III Вычисление объёмов тел вращения
Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры  вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.
Ось вращения может и пересекать фигуру, если это ось симметрии фигуры.
Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции 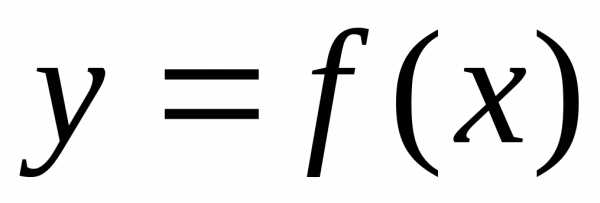 ,
осью
,
осью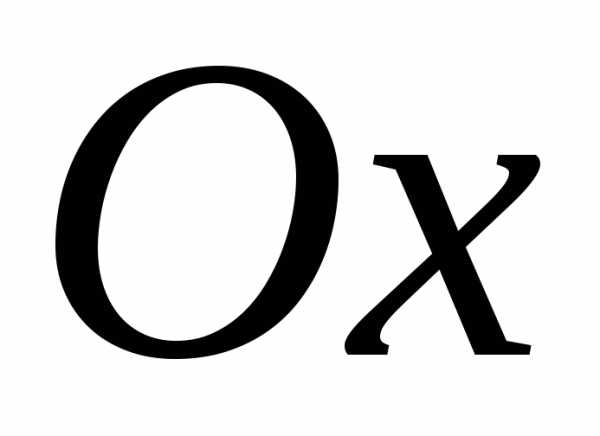 и отрезками прямых
и отрезками прямых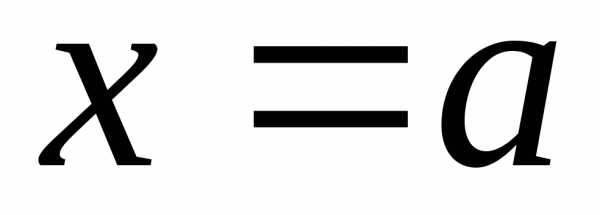 и
и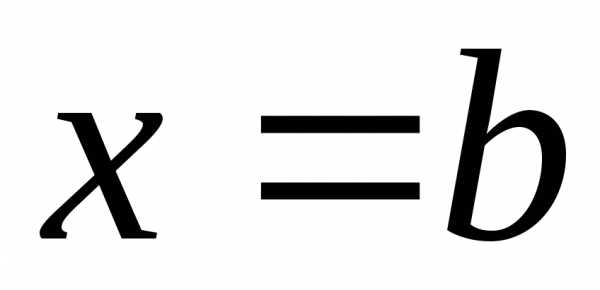
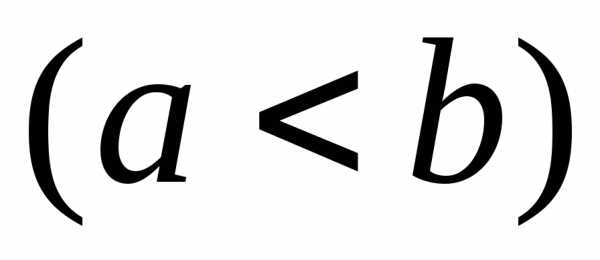
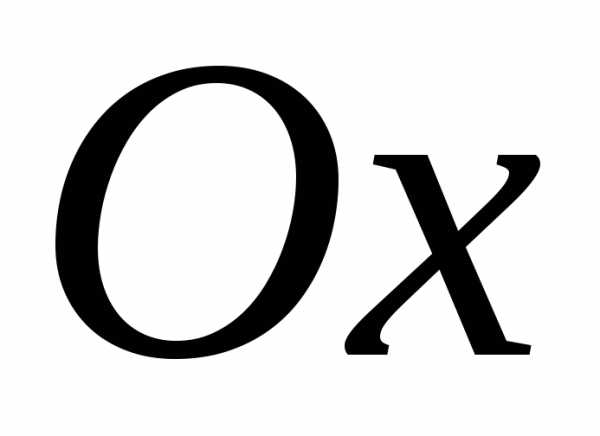 .
Тогда объём получающегося тела вращения
можно вычислить по формуле
.
Тогда объём получающегося тела вращения
можно вычислить по формуле 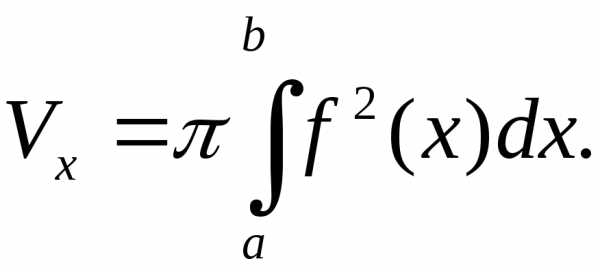 (2)
(2)
Доказательство. Для такого тела сечение с абсциссой 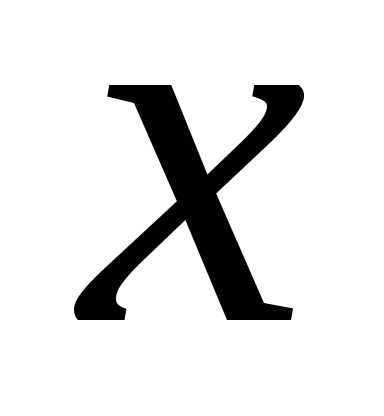 – это круг радиуса
– это круг радиуса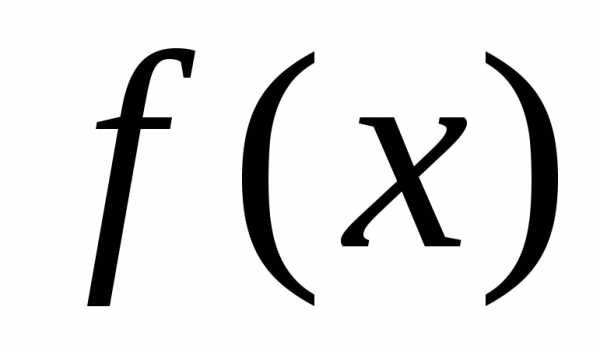 ,
значити формула (1) даёт требуемый результат.
,
значити формула (1) даёт требуемый результат.
Если фигура
ограничена графиками двух непрерывных
функций 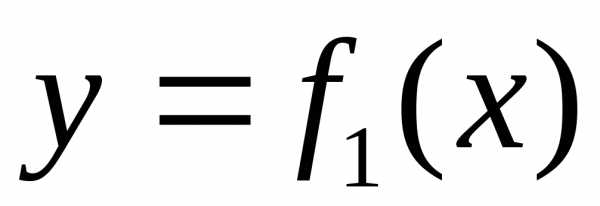 и,
и отрезками прямых
и,
и отрезками прямых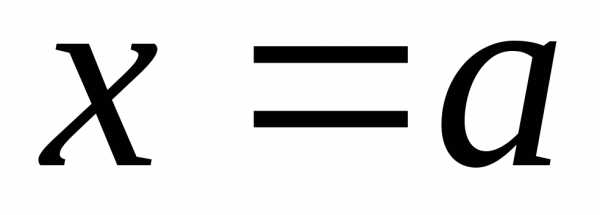 и,
причём
и,
причём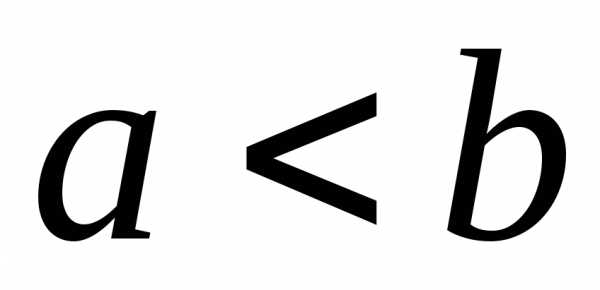 и,
то при вращении вокруг оси абсцисс
получим тело, объём которого
и,
то при вращении вокруг оси абсцисс
получим тело, объём которого
Пример 3. Вычислить объём тора, полученного вращением круга, ограниченного окружностью ,вокруг оси абсцисс.
Решение. Указанный круг снизу ограничен графиком функции , а сверху –. Разность квадратов этих функций:
Искомый объём
(графиком подынтегральной функции является верхняя полуокружность, поэтому написанный выше интеграл – это площадь полукруга).
Пример 4. Параболический сегмент с основанием 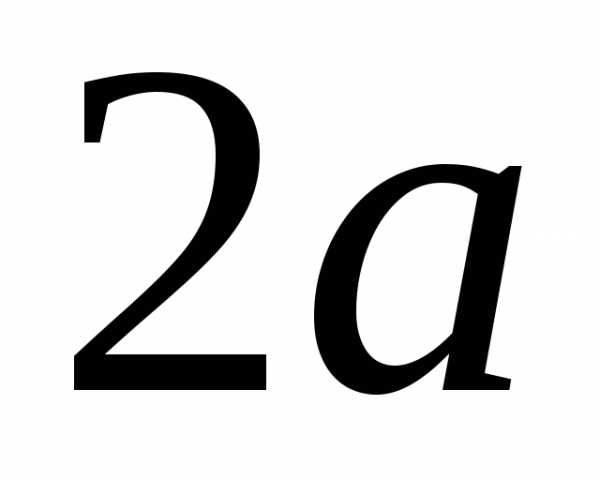 и высотой
и высотой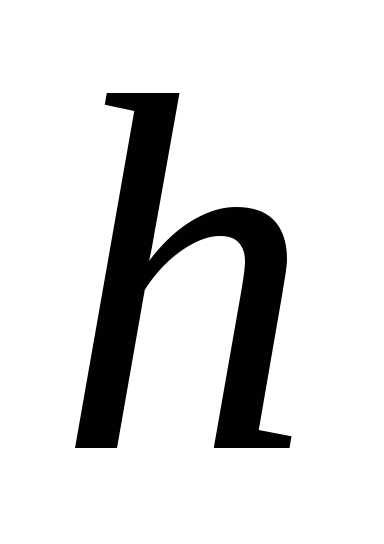 ,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).
Решение. Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем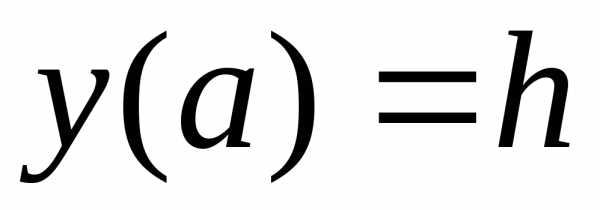
 :.
Итак, искомый объём:
:.
Итак, искомый объём: Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции 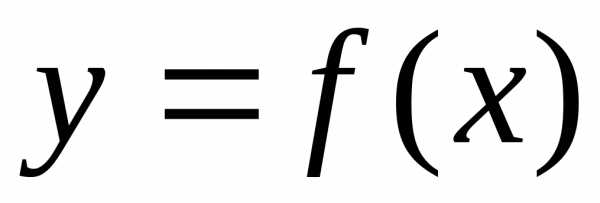 ,
осью
,
осью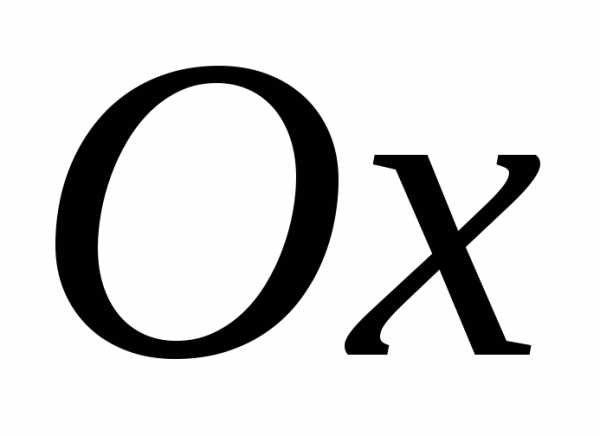 и отрезками прямых
и отрезками прямых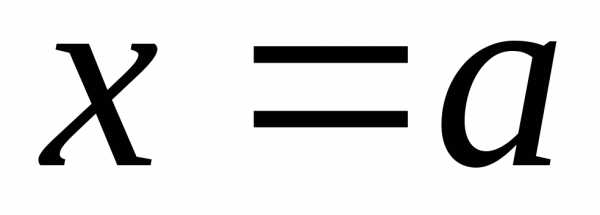 и
и ,
причём,
вращается вокруг оси
,
причём,
вращается вокруг оси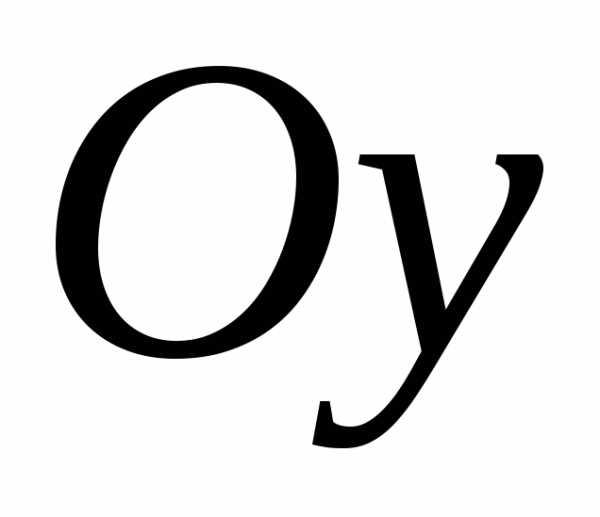 .
Тогда объём получающегося тела вращения
может быть найден по формуле
.
Тогда объём получающегося тела вращения
может быть найден по формуле
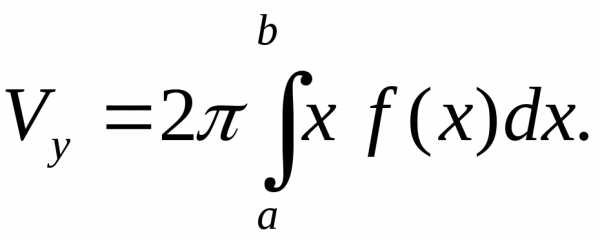
Идея
доказательства. Разбиваем отрезок  точками
точками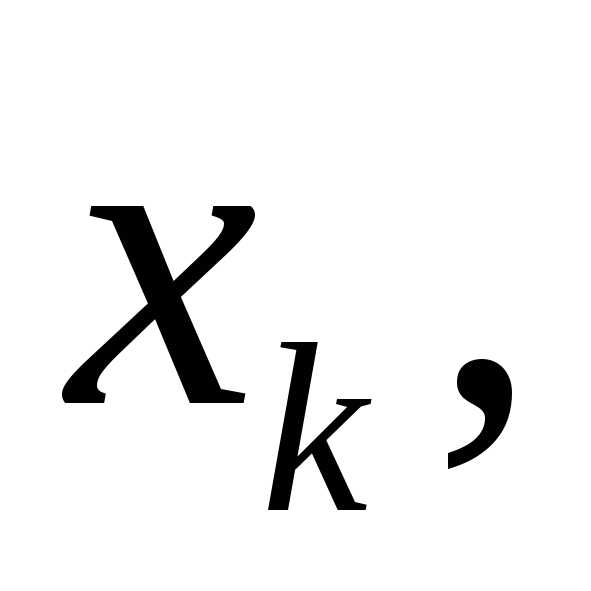 ,
на части и проводим прямые
,
на части и проводим прямые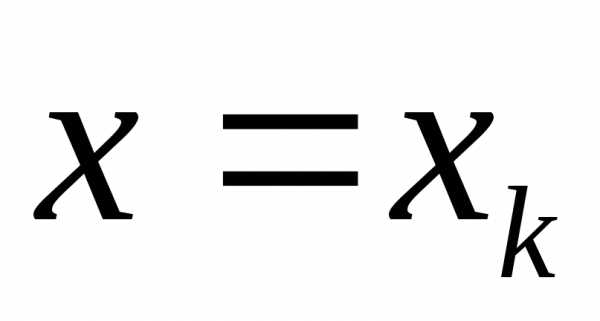 .
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основанием
.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основанием и высотой
и высотой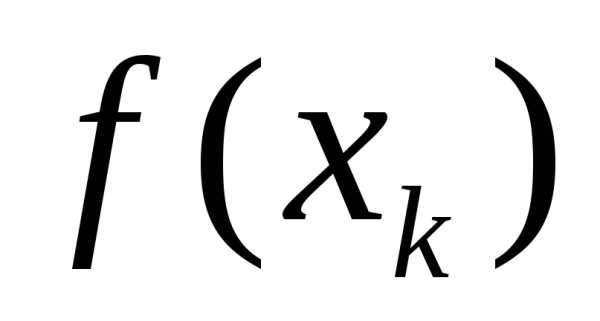 .
.
Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами: 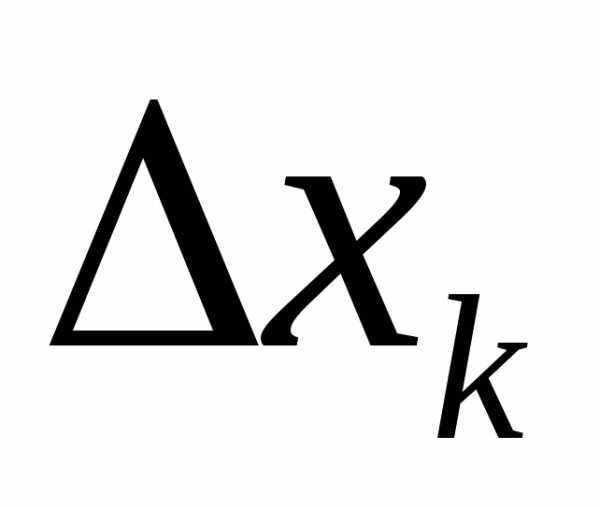 ,
,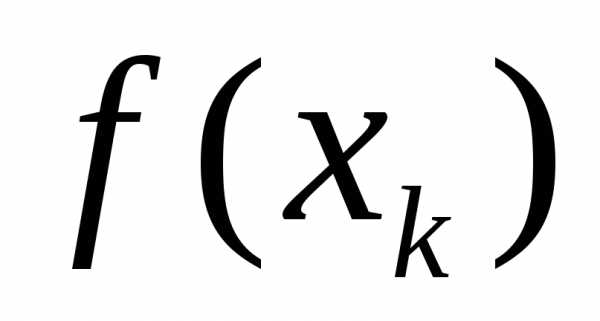 и
и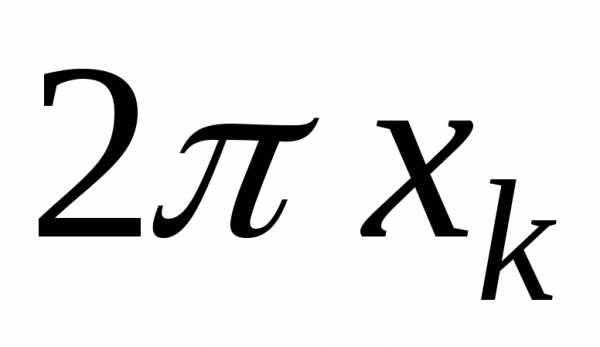 .
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство
Для получения точного равенства надо перейти к пределу при . Написанная выше сумма есть интегральная сумма для функции , следовательно, в пределе получим интеграл из формулы (3). Теорема доказана.
Замечание
1. В теоремах
2 и 3 условие 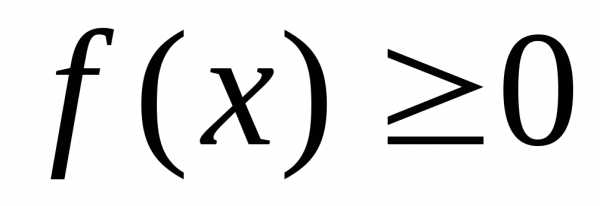 можно опустить: формула (2) вообще
нечувствительна к знаку
можно опустить: формула (2) вообще
нечувствительна к знаку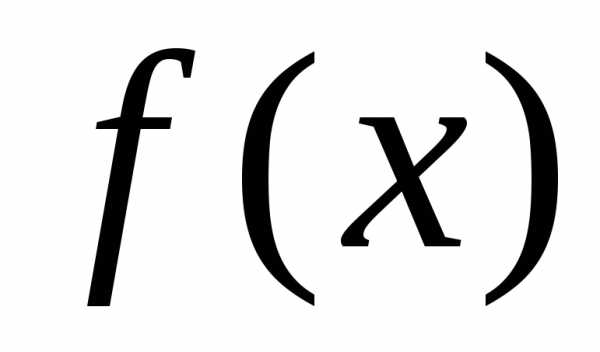 ,
а в формуле (3) достаточно
,
а в формуле (3) достаточно заменить на
заменить на .
.
Пример
5. Параболический сегмент (основание 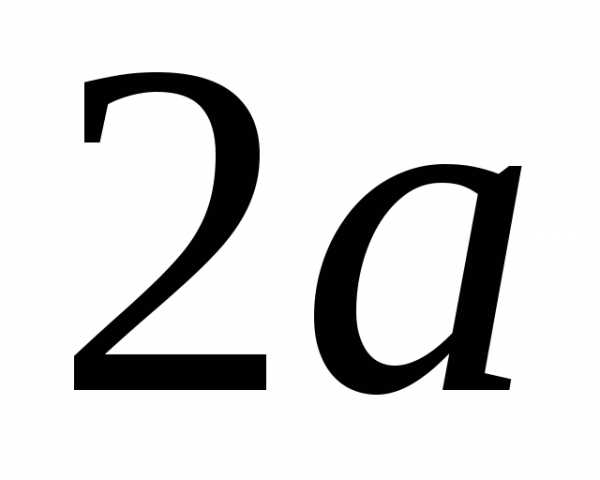 ,
высота
,
высота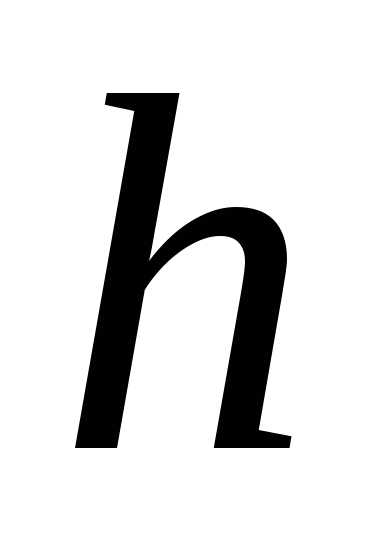
Решение. Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем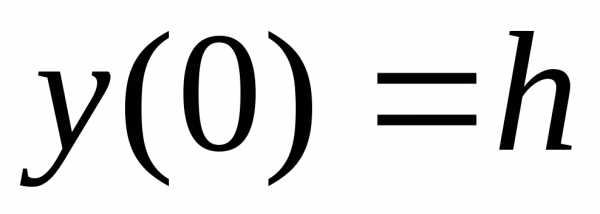 ,
значит
,
значит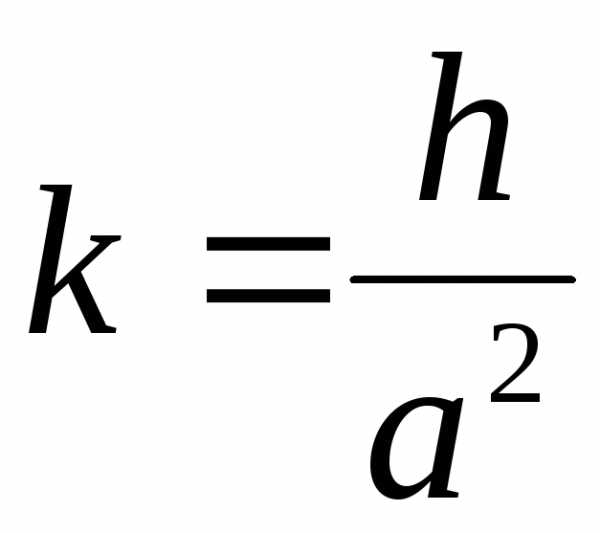 .
Имеем для объёма:
.
Имеем для объёма:
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями 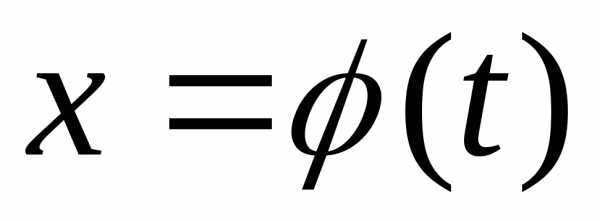 ,
, ,и,
,и,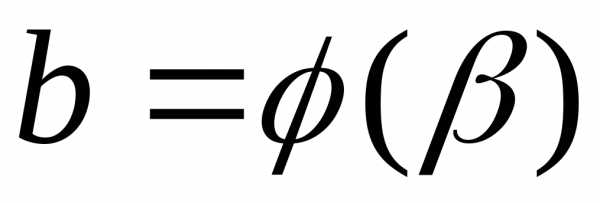 то можно использовать формулы (2) и (3) с
заменой
то можно использовать формулы (2) и (3) с
заменой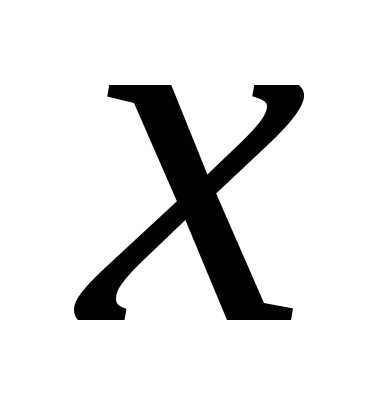
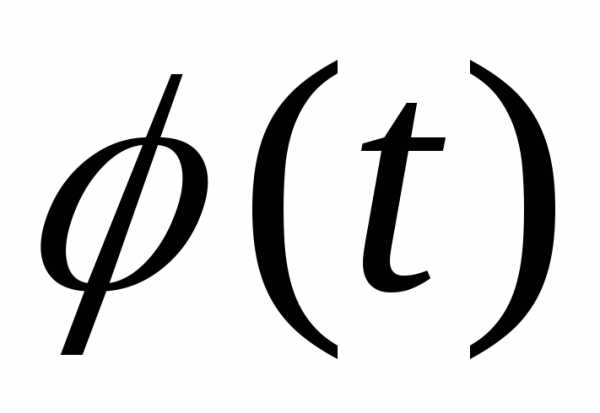 и
и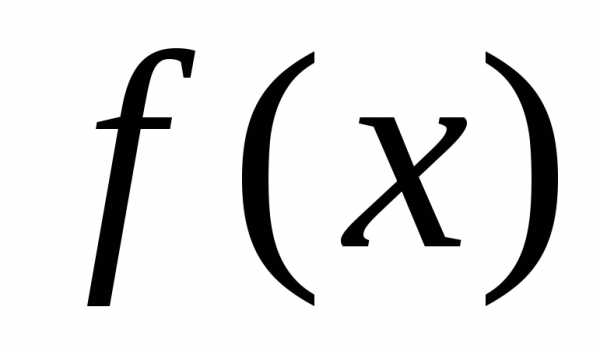 на
на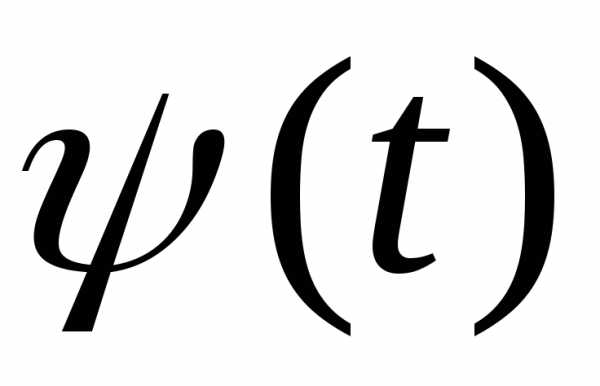 при измененииt от
при измененииt от  до
до .
. Пример
6. Фигура
ограничена первой аркой циклоиды
,,,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси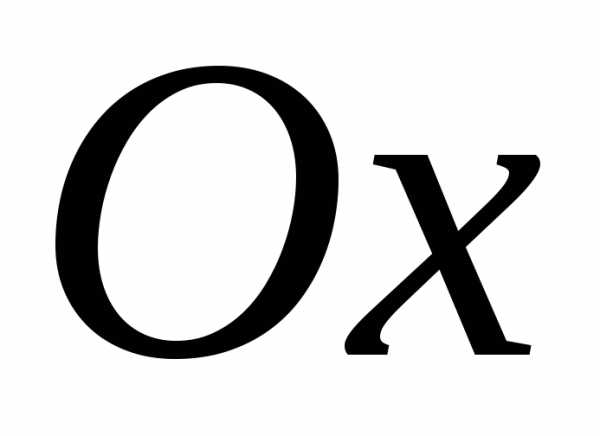 ;
2) оси
;
2) оси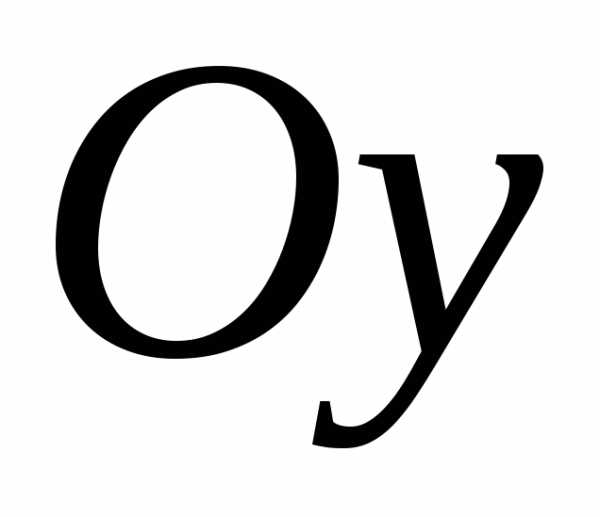 .
.
Решение. 1) Общая формула 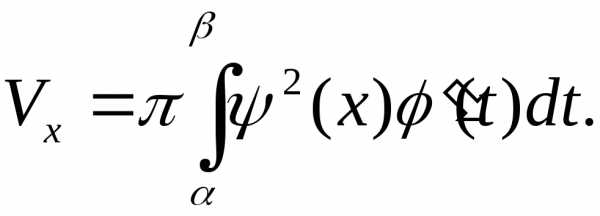 В нашем случае:
В нашем случае:
2) Общая формула Для нашей фигуры:
Предлагаем студентам самостоятельно провести все вычисления. Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами ,
,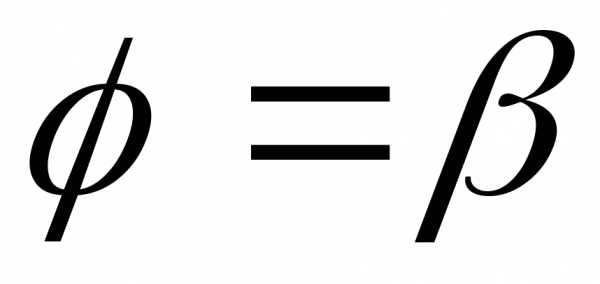 ,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.
Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности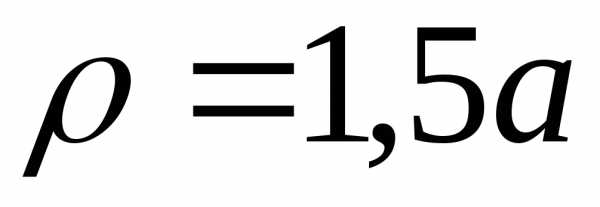 ,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.
Решение. Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой .
Кривые пересекаются при
при 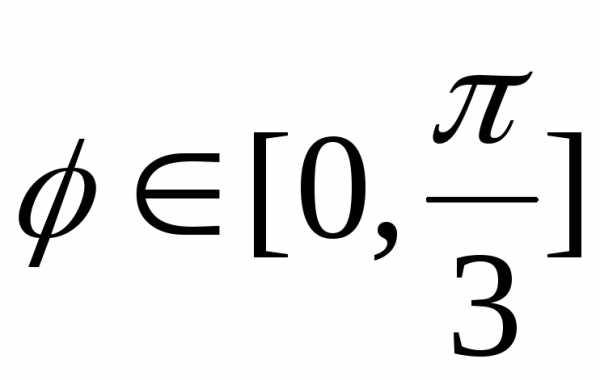 .
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:
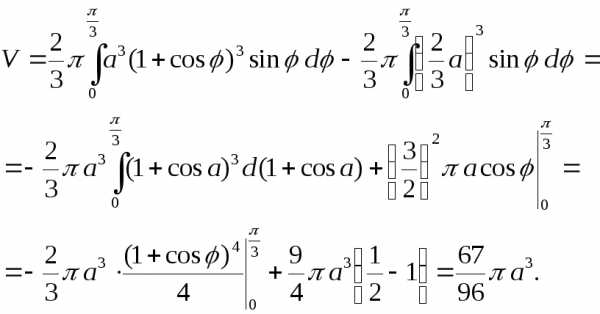
Задачи для самостоятельного решения.
1. Круговой сегмент,
основание которого 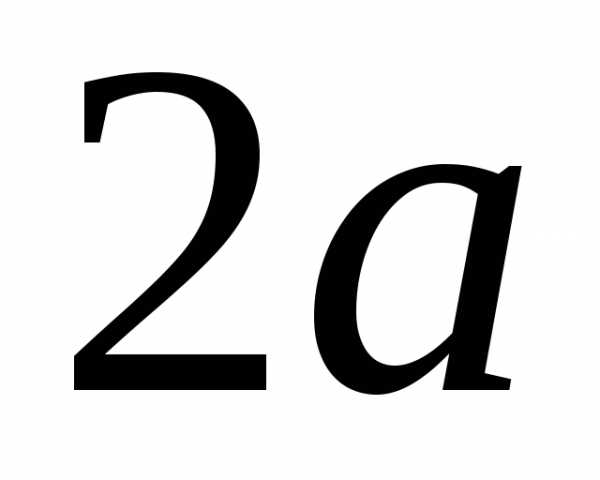 ,
высота
,
высота 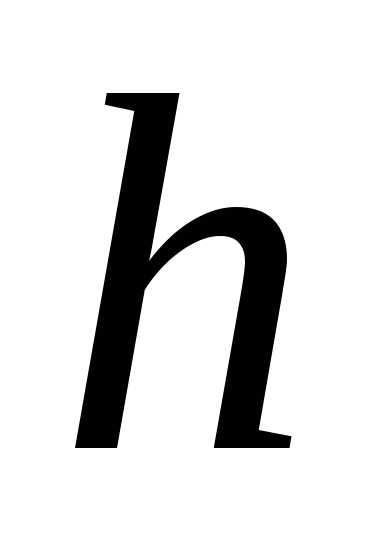 ,
вращается вокруг основания. Найти объём
тела вращения.
,
вращается вокруг основания. Найти объём
тела вращения.
2. Найти объём
параболоида вращения, площадь основания
которого равна  ,
а высота равна
,
а высота равна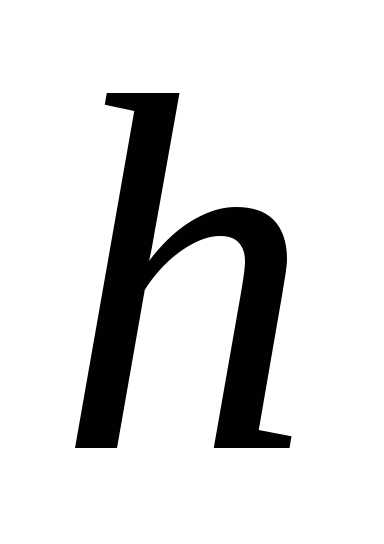 .
.
3. Фигура, ограниченная астроидой ,вращает-ся вокруг оси абсцисс. Найти объём тела, которое получается при этом.
4. Фигура, ограниченная
линиями 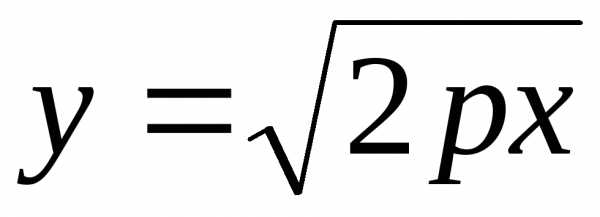 и
и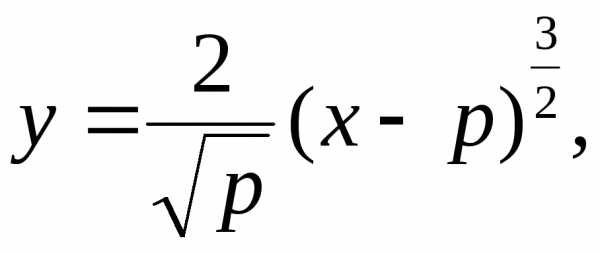 вращается вокруг оси абсцисс. Найти
объём тела вращения.
вращается вокруг оси абсцисс. Найти
объём тела вращения.
studfiles.net
объем тела вращения — ПриМат
Пусть на отрезке $\left[a,b\right]$ задана непрерывная неотрицательная функция $f$. Рассмотрим криволинейную трапецию, или подграфик функции $f$. Будем вращать эту трапецию вокруг оси $Ox$. Полученное тело вращения обозначим через $E$. Выведем формулу для его объема. Разобьем отрезок $\left[a,b\right]$ точками $a= x_0 < x_1 <\ldots < x_n = b$ и обозначим $m_i = \inf f(x), M_i = \sup f(x)$. В результате вращения получаем два прямых круговых цилиндра и один “цилиндр” с криволинейной образующей. Объемы меньшего и большего круговых цилиндров равны соответственно $\pi m_i^2\Delta x_i$ и $\pi M_i^2\Delta x_i$. Из круговых прямых цилиндров составим две области: одна из них имеет объем V=$\pi\sum\limits_{i=1}^{n-1}m_i^2\Delta x_i$ ,а другая $\overline{V}=\pi\sum\limits_{i=1}^{n-1}M_i^2\Delta x_i$ (Если у Вас возникли проблемы, то просмотрите этот материал Суммы Дарбу). Ясно, что наше тело вращения $E$ содержит в себе меньшее из этих кусочно цилиндрических тел и содержится в большем кусочно цилиндрическом теле. Таким образом, объем $V$ тела $E$ удовлетворяет неравенству V $\leq$ V $\leq$ $\overline{V}$. Понятно, что суммы V и $\overline{V}$ соответственно нижняя и верхняя суммы Дарбу для интеграла $\pi\int\limits^a_b f(x)^2\,dx.$, так что они обе стремятся к этому интегралу при стремлении к нулю диаметра разбиения.
Итак, мы получаем следующую формулу для нахождения объема тела вращения:
$$V=\pi\int\limits^a_b f(x)^2\,dx$$
Примеры решения задач
- Пример 1.Найти объем тела вращения вокруг оси абсцисс ограниченного функциями $y=2x-x^2, o<x<2;$
РешениеВыполним чертеж:
Объем тела вращения:
$V=\pi\int\limits^a_b f(x)^2\,dx = \pi\int\limits^2_0 (2x-x^2)^2\,dx$ =
=$\pi\int\limits^2_0 4x^2-4x^3+x^4\,dx = \pi (\frac{32}{3}-16 +\frac{32}{5}) =\frac{ 16\pi}{15}$ - Пример 2.Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры ограниченной линиями $y=2x+1$, $y=x+4$, $x=0$, $x=1$.
Решение$$V=V_1 — V_2$$
Найдем фигуру ограниченную сверху прямой $y=x+4$ :
$$ V_1 = \pi\int\limits^1_0 (x+4)^2\,dx = \pi (\frac{x^3}{3}+4x^2 +16x)|_0^1 =\frac{61\pi}{3}$$
Найдем фигуру ограниченную сверху прямой $y=2x+1$ :
$$ V_2 = \pi\int\limits^1_0 (2x+1)^2\,dx = \pi (\frac{4x^3}{3}+2x^2 +x)|_0^1 =\frac{61\pi}{3} =\frac{13\pi}{3}$$
$$ V = \frac{61\pi}{3} — \frac{13\pi}{3} = 16\pi$$
Объем тела вращения
Лимит времени: 0
Информация
Пройдите этот тест, чтобы проверить свои знания по только что прочитанной теме.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
См. также
Поделиться ссылкой:
ib.mazurok.com
Объем тела вращения

Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции, ограниченной кривойy = f (x) , непрерывной на[a;b], прямымиx = a ,x = b и осьюOx (рис. 4.4.16).
у |
|
|
|
|
| y=f (x) |
|
0 | a | b | х |
|
z
| Рис. 4.4.16. |
Тогда объем тела вращения равен | V = πb∫(f(x))2 dx. |
| a |
ЗАМЕЧАНИЕ 1
Объем тела, образованного вращением вокруг оси Оу криволинейной трапеции, построенной на отрезке[c; d ] оси ординат и ограниченной кривойx = f ( y) , вычисляется по формуле
V = πd∫(f( y))2 dy.
с
ЗАМЕЧАНИЕ 2
Если криволинейная трапеция ограничена кривой, заданной параметрическими уравнениями
| х = ϕ(t) | , где α ≤ t ≤β и | ϕ(α) =a; ϕ(β) =b , |
|
| ||
y = ψ(t) |
|
| |
тогда объем тела вращения вокруг оси Ох определяется формулой
V = π β∫(ψ(t))2 ϕt′ dx
α
Пример 4.4.7
Найти объем тела, полученного при вращении вокруг оси Оу криволинейной трапеции, ограниченной дугой параболыу = х2 − 4 , заключенной между точкой(0; − 4) и осьюОх.
Решение
Изобразим тело вращения (рис. 4.4.17).
4
Рис. 4.4.17.
Из уравнения у = х2 − 4 найдемx2 = y + 4 , т.е.(f ( y))2 = y + 4 . Вычислим объем:
30
studfiles.net
4.4. Объемы и поверхности тел вращения
I. Объемы тел вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п°п° 197, 198* Разберите подробно примеры, приведенные в п° 198.
508. Вычислить объем тела, образуемого вращением эллипсаВокруг оси Ох.
Решение. При вращении эллипса вокруг оси Ox образуется тело, называемое эллипсоидом вращении. Как известно, объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной сверху кривой у = f{x), ординатами х = а, х = Ь и осью Ох, вычисляется по формуле:
Из уравнения эллипса видно, что большая его полуось равна 2, следовательно,. Разрешив уравнение
эллипса относительно, получимОбъем
эллипсоида вращения равен:
509. Найти объем тора, образованного вращением круга
Вокруг оси Ox (рис. 18). Решение. Искомый объем тора равен разности объемов, полученных от вращения верхнего и нижнего полукругов. Так как для верхнего полукруга
, а для нижнего, то
(см. задачу 388).
Б10. Вычислить объем прямого конуса, высота которого h и радиус основания г, рассматривая конус как тело вращения прямоугольного треугольника около одного из катетов.
Решение. Выберем систему координат так, чтобы ось Ox совпала с высотой h (рис. 19), а вершину конуса
примем за начало координат. Тогда уравнение прямой OA
Следовательно, объем конуса
запишется так: будет равен:
511. Вычислить объемы тел, образованных вращением около осей Ox и Oy сегмента AOB параболы, от
секаемого хордой AFB, проходящей через фокус параболы перпендикулярно к оси Ox (рис. 20, а, б).
Решение I. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Ох, пользуясь формулой:
Найдем пределы интегрирования. Прямая AB параллельна оси Oy. Ее уравнение. Для того чтобы
найти точки пересечения этой прямой с параболой, решим совместно систему уравнений:
мя я AB проходит через фокус параболы, то координаты точки F будутСледовательно,
Получим точки. Так Kaw пря
2. Вычислим объем тела, получаемого при вращении сегмента AOB вокруг оси Oy. Учитывая симметрию сегмента относительно оси Oxi найдем сначала половину искомого объема. Она равна разности объемов тел, получаемых от вращения вокруг оси Oy прямоугольника OFBD и криволинейного тоеугольника OBD. Так как объем цилиндра равен, а объемТела, полученного от вращения криволинейного треугольника OBD вокруг оси Oy, будет:
512. Фигура, ограниченная гиперболойИ
то половина искомого объема равна:
Следовательно, весь искомый объем
прямыми, вращается вокруг оси
Ох. Найти объем тела вращения.
Решение. В результате вращения данной фигуры вокруг оси Ox образуются два тела вращения, имеющие равные объемыТогда
Найдем объем V1 тела (рис. 21), сбразованного вращением площади, ограниченной правей ветвью гиперболы И прямейПределы интегрирова
ния найдем из геометрических соображений:
. Таким образом,
513. Вычислить объем тела, образованного вращением вокруг оси Ox одной полуволны синусоиды у = sin х.
514. Найти объем конуса, производимого вращением вокруг оси Ox части прямой _, содержащейся между осями координат.
515. Криволинейная трапеция, ограниченная срерху параболой,с боков—ординатами х = — I и х—\, снизу — осью Ох, вращается вокруг оси Ох. Найти объем полученного тела вращения.
516. Вычислить объем тела, образованного вращением вокруг оси Ox площади, ограниченной цепной линией
, ординатами X = — а, х = а и осью Ох.
517. Прямой параболический сегмент, основание которого а, а высота R, вращается вокруг основания. Определить объем полученного тела вращения.
518. Найти объем цирка, осевое сечение которого — парабола. Высота цирка 30 м. Диаметр основания 50 м.
519. Найти объем тела, образованного вращением кривойВокруг оси абсцисс.
520. Вычислить объем тела, полученного вращением
астроидыВокруг оси Oy.
521. На кривойВзяты две точки А и В, абсциссы которых соответственно а = I и Ь = 2. Найти объем тела, полученного вращением криволинейной трапеции аАВЬ вокруг оси Ох.
522. Найти объем тела, производимого вращением площади, ограниченной дугой циклоиды,
И осью Ox вокруг ее основания.
523. Вычислить объем тела, образованного вращением вокруг оси ординат дуги OM циклоиды,
, ограниченной точками О (0, 0) и M (та*, 2а).
524. Найти объем тела, ограниченного поверхностью, полученной при вращении линии
вокруг оси абсцисс.
2. Площадь поверхности тела вращения. Предварительно изучите по учебнику Г. М. Фихтенгольца главу XII, п° 205. В теоретическом курсе показано, что площадь поверхности тела вращения определяется по формуле:
52$. Определить площадь поверхности параболоида, образованного вращением дуги параболы у2 = 2х вокруг оси Ox от х = 0 до х = 2.
Решение. В нашем случае . Поэтому
526. Найти площадь поверхности шара радиуса R. Решение. Поместим начало координат в центре шара. Будем рассматривать поверхность шара как поверхность, полученную в результате вращения полуокружностиВокруг оси Ох. Тогда площадь поверхности шара найдется по формуле:
T ак как
И, следовательно,
527. Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Ох.
Решение. Из уравнения эллипса имеем:
. Найдем производную:
Тогда. Так как полуось эллипса
И, следовательно,
Если кривая задана параметрически, то, заменяя переменную под знаком определенного интеграла, получим для площади поверхности следующую формулу:
528 Вычислить площадь поверхности, сбразованной вращением одной арки циклоиды
Вокруг оси Ox (см. рис. 13).
Решение. Найдем:
Тогда. Искомая по
верхность равна:
Решение. Построим данную кривую. Найдем точки пересечения ее с осями координат.
нием петли кривой х = /2, у
(/2— 3) вокруг оси Ох.
При у — 0 находим t = 0 и t = ±}/ 3 . Следовательно, X1 = 0 и X2 -= 3* т. е. кривая пересекает ось Ox в двух точках О (0, 0) и А (3, 0).
При х = 0 находим / = 0, следовательно, у = 0. Мы получили ту же точку О (0, 0).
При люб dx вещественных значениях параметра / будут вещественны х и у Так как х — четная функция параметра /, у — нечетная функция параметра /, то график расположен симметрично относительно оси Ох.
Исследуем данную функцию на экстремум. Находим производную:
dy = /2-dx 21
Легко видеть, что у = 0 при / = + I и, следовательно^
У
у — + —; когда X= I; у’-* оо, когда / —> 0, следовательно,
когда х -> 0, то и у 0. Это значит, что в начале координат касательная к данной кривой вертикальна. В точке
А (3; 0) будет у’ = — J=, это значит, что касательная У з
к данной кривой в этой точке образует с положительным направлением оси Ox угол в 30°.
Полученных данных достаточно для построения графика данной функции (рис. 22).
Найдем площадь данной поверхности. Имеем: х’ = 21, y’ = f — I; х’% -(-y’z = (I +12 )а.
З о
Таким образом,
Р=2* Jyj/T^T |±(<*_3)(1+/«)Л =
0 KT
IrF ^ з
3 Ik 2 2 2 /
530. Найти площадь поверхности, образованной вращением вокруг оси Ox дуги синусоиды у = sin х от точки X = 0 до точки X = It.
531. Вычислить площадь поверхности конуса с высотой h и радиусом г.
532. Вычислить площадь поверхности, образованной
2_ 2_ 2_
вращением астроиды х3 -)- у* — а3 вокруг оси Ох.
533. Вычислить площадь поверхности, образованной цращением петли кривой 18 уг — х (6 — х)г вокруг оси Ох.
534. Найти поверхность тора, производимого вращением круга X2 — j — (у—З)2 = 4 вокруг оси Ох.
535. Вычислить площадь поверхности, образованной вращением окружности X = a cost, y = asint вокруг оси Ох.
536. Вычислить площадь поверхности, образованной вращением петли кривой х = 9t2, у = St — 9t3 вокруг оси Ох.
537. Найти площадь поверхности, образованной вращением дуги кривой х = е*sint, у = el cost вокруг оси Ox
от t = 0 до t = —.
2
538. Показать, что поверхность, производимая вращением дуги циклоиды х = a (q> —sin ф), у = а (I — cos ф) вокруг оси Oy, равна 16 и2 о2.
539. Найти поверхность, полученную вращением кардиоидыВокруг полярной оси.
540. Найти площадь поверхности, образованной вращением лемнискатыВокруг полярной оси.
Дополнительные задачи к главе IV
Площади плоских фигур
541. Найтивсю площадь области, ограниченной кривойИ осью Ох.
542. Найти площадь области, ограниченной кривой
И осью Ох.
543. Найти часть площади области, расположенной в первом квадранте и ограниченной кривой
л осями координат.
544. Найти площадь области, содержащейся внутри
петли:
545. Найти площадь области, ограниченной одной петлей кривой:
546. Найти площадь области, содержащейся внутри петли:
547. Найти площадь области, ограниченной кривой
И осью Ох.
548. Найти площадь области, ограниченной кривой
И осью Ох.
549. Найти площадь области, ограниченной осью Oxr
прямойИ кривой
550. Найти площадь области, ограниченной кривыми.
И осью Oy.
Вычисление длины дуги
551. Найти длину дуги кривойОт точки А(0: до точки В (I: 6).
552. Найти длину дуги CD кривой, где
Дать геометрическую иллюстрацию.
553. Найти длину дуги OA кривойГде
554. Найти длину дуги AB кривой у = еху где А (0; I), В (I; 2)
555. Нгйти длину дуги AB кривой, где
556. Нгйти длину дуги кривой, отсеченной прямей X = — I.
557. Нгйти длину дуги кривойОт
До
Объем тела вращения
558. Нгйти объем тела, полученного вращением вокруг юси Ox п/ощоди, сграниченной крквой
559. Нййти объем тела, полученного от вращения рокруг сси Ox площади, ограниченной кривой
560. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченной кривой
ц прямыми
561. Найти объем тела, образованного вращением вокруг оси Oy площади, ограниченней эллипсом
562. Нгйти объем тела, полученного вращением вокруг оси Oy плещади, ограниченной кривой
И отрезком оси Oy.
563. Найти объем тела, полученного вращением вокруг оси Ox площади, ограниченной кривой
564. Круг радиуса 2 с центром в точке (7; 0) вращается вокруг оси Oy. Определить объем полученного тела вращения.
565. Нлйти объем тела, полученного вращением вокруг оси Ox площади, расположенной в первом квадранте и
ограниченной кривой(эволюта
эллипса).
Площадь поверхности вращения
566. Найти площадь поверхности, образованной вращением дуги кривой, отсеченной прямой
567. Найти площадь поверхности шаоовой чаши, полученной при вращении кругаВокруг оси Ox в пределах от 0 до h.
568. Найти площадь поверхности катеноида, образованного вращением вокруг оси абсцисс цепной линии
От точкиДо точки
569. Найти площадь поверхности эллипсоида, образованного вращением эллипсаВокруг оси Oy.
570. Найти площадь поверхности, образованной вращением вокруг оси Ox петли кривой
571. Найти площадь поверхности, образованной вращением вокруг оси Ox кривой
572. Найти площадь поверхности, образованной вращениемВокруг полярной оси.
ПРИЛОЖЕНИЯ К ВОПРОСАМ ФИЗИКИ
| < Предыдущая | Следующая > |
|---|
matica.org.ua
07.5.2. Объем тела вращения | Решение задач по математике и другим предме
Рассмотрим тело, которое образуется при вращении вокруг оси Ох криволинейной трапеции, ограниченной сверху непрерывной и положительной на отрезке [А, b] функцией F(X) (рис. 7.5). Объем этого тела вращения определяется формулой
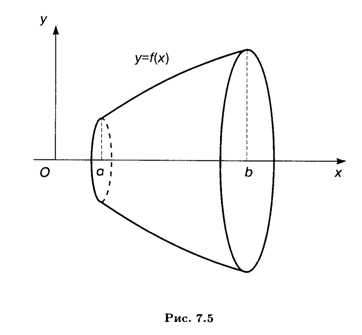
Если тело образовано вращением криволинейной трапеции вокруг оси Оу, то, выражая Х через У как обратную функцию, мы можем получить аналогичным образом формулу для объема тела вращения:
Где [C, D] — область изменения функции У = F(X).
Рассмотрим примеры вычисления объемов тел, образованных вращением фигур, ограниченных следующими линиями.
Пример 3. У = х2, у = вокруг оси Ох.
Решение. Искомый объем вращения равен разности объемов, образованных вращением криволинейных трапеций с верхними границами соответственно У = и У = Х2. Пределы интегрирования определяются по точкам пересечения этих кривых: А = 0 и B = 1. По формуле (7.15) получаем
Пример 4. У = eх, х = 0, Х = 1, У = 0 вокруг оси Оу.
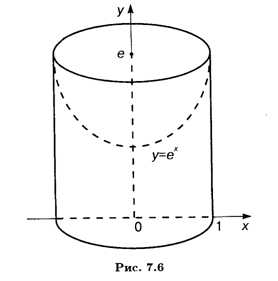
Ррешение. Выражаем Х через У: х = ln У; промежуток интегрирования [1, Е] определяется очевидным образом. Объем тела вращения (рис. 7.6) равен разности объемов соответственно цилиндра радиуса 1 и высоты Е и тела вращения вокруг оси Оу криволинейной трапеции, ограниченной сверху кривой Х = ln У. Согласно формуле (7.15) получаем
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Шпаргалка математика — Стр 2
Если же вокруг оси Оу вращается криволинейная трапеция, ограниченная графиком непрерывной на [c,d] функцией, то объём такого тела вращения:
Этот
же объём может быть вычислен по формуле:  .
Если линия задана параметрическими
уравнениями :
.
Если линия задана параметрическими
уравнениями :
Делая замену переменной получим:
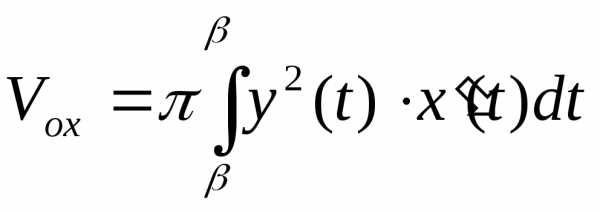
Если линия задана параметрическими уравнениями :
y(α)=c, y(β)=d. Делая замену y=y(t) получим:
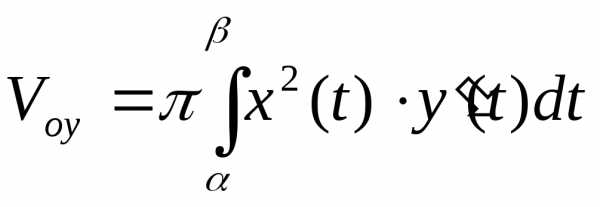
Вычислить тела вращения вокруг оси ОУ параболы,.
1способ:
2способ:
2)Вычислить Vтела вращения вокруг оси ОХ криволинейной трапеции, ограниченной прямой у=0, дугой( с центом в точке(1;0), и радиусом=1), при.
Площадь поверхности тела вращения
Пусть заданна поверхность образованная вращением кривой у =f(х)вокруг оси Ох. Необходимо определитьSэтой поверхности при.
Пусть функция у =f(х) определенна и непрерывна, имеет неприр.и неотрицательна во всех точках отрезка [а;в]
Проведем хорды длины которых обозначим соответственно (n-хорд)
по теореме Лагранжа:
Тогда:
Площадь поверхности всей описанной ломанной будет равна
Определение: предел этой суммы, если он и конечен, когда наибольшее звено ломанойmax,называется площадью рассматриваемой поверхности вращения.
Можно доказать, сто предел суммы равен приделу интегрированной суммы для р-ий
формула дляSповерхности тела вращения =
Sповерхности образованной Вращением дуги кривой х=g(x) вокруг оси Оу при
Непрерывна со своей производной
Если кривая заданна параметрически ур-ми x=x(t) , y=t(t) ф-ии x’(t), y’(t),x(t),y(t) определенны на отрезке [a;b],x(a)=a, x(b)=b то сделав замену переменой x=x(t)
Если кривая заданна параметрически сделав замену в формуле получим:
Если уравнение кривой заданно в полярной системе координат
S поверхности вращения вокруг оси будет равно
studfiles.net
ВЫЧИСЛЕНИЕ ОБЪЕМОВ ТЕЛ ВРАЩЕНИЯ
Поиск ЛекцийОбъем тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной кривой , прямыми выражается интегралом
Объем тела, образованный вращением вокруг оси ОУ криволинейной трапеции, ограниченной кривой и прямыми определяется формулой
.
5.2(1). , ,
Решение.
На рис. 2 изображена область, ограниченная параболой и прямой , на рис. 3 — тело, полученное вращением вокруг оси фигуры, изображенной на рис.2.
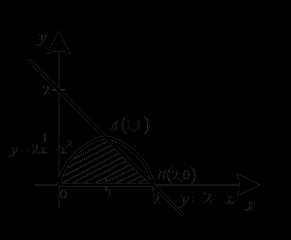
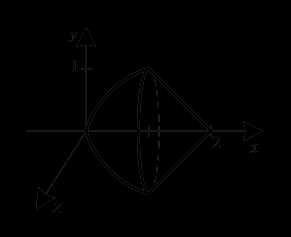
Рис. 2. Рис. 3.
Объем тела вращения вокруг оси состоит из двух частей – тела, полученного вращением вокруг оси параболы (параболоида вращения) и конуса — тела, полученного вращением вокруг оси ОХ прямой . Следовательно,
Ответ: (куб. ед.).
5.2(2).
Решение.
На рис. 4 изображена область, ограниченная параболой и прямыми линиями: и На рис. 5 изображено тело вращения вокруг оси
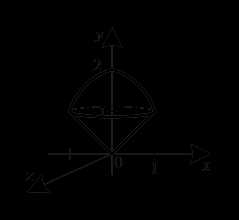
Рис. 4 Рис. 5.
Согласно правилу вычисления объемов вращения вокруг оси , получим
Ответ: (куб. ед.).
ДВОЙНОЙ ИНТЕГРАЛ.
Обобщением определенного интеграла на случай функции двух переменных является двойной интеграл [2]:
.
Область интегрирования называется правильной, если прямые, проведенные через любую внутреннюю точку области параллельно осям и пересекают границу области не более чем в двух точках. Двойной интеграл от непрерывной в правильной области функции сводится к повторному интегралу [2], т.е. к последовательному вычислению двух определенных интегралов.
Задание 6. 6.1 .Изменить порядок интегрирования в повторном интеграле; 6.2. Найти среднее значение функции в области: .
6.1.а. ,
6.1.b. .
6.1.а. ,
Решение.
Опишем область интегрирования .
Уравнение нижней границы: если и , т.е. , если . Уравнение верхней границы области :
если и , т.е. , если .
Область изображена на рис.6. Область правильная, ее можно
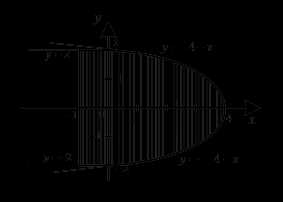
Рис. 6 Рис. 7
описать и так (рис. 7):
Согласно правилу расстановки пределов в повторных интегралах, получим
.
Ответ: .
6.1.b. .
Решение. Область интегрирования определяется соотношениями:
Кривая левая ветвь параболы (рис. 9).

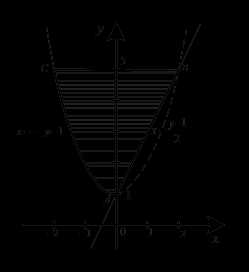
Рис. 8 Рис. 9
Уравнение прямой : или
Точки — это точки пересечения параболы с прямыми и
Область состоит из двух областей: : и .
На рис. 8 указаны уравнения границ области, которые надо использовать для области, правильной в направлении оси .
Следуя правилам составления повторного интеграла, получим
Ответ:
Средним значением функции в области называется выражение
.
Здесь площадь области .
6.2. Найти среднее значение функции в области: .
Решение. Область интегрирования — прямоугольник, изображена на рис. 10. Очевидно,
Рис. 10 Рис. 11
Сведением к повторному интегралу, вычислим двойной интеграл
=
Внутренний интеграл вычисляем при фиксированных значениях « ».
Тогда
Отсюда по формуле Ньютона — Лейбница получим
Следовательно, среднее значение функции
Ответ: 1.
ТРОЙНОЙ ИНТЕГРАЛ.
Тройной интеграл — обобщение определенного интеграла на трехмерную область . Как и в двойном интеграле, он сводится к повторному (трехкратному) интегралу от непрерывной функции по правильной области Область называется правильной, если прямые, проведенные через любую внутреннюю точку области параллельно координатным осям, пересекают границу области не более, чем в двух точках.
Объем области выражается тройным интегралом
.
Задание 7. Изобразить проекцию области на координатную плоскость и область интегрирования . Вычислить объем тела, ограниченного поверхностями:
Решение.
На рис. 11, 12, 13 изображены проекции области на координатные плоскости , на рис. 14 — область .
Рис. 12 Рис. 13
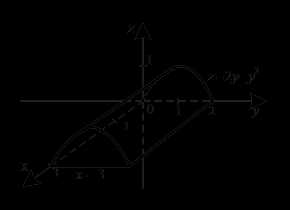
Рис. 14
Объем тела вычисляем по формуле: .
Перейдем к повторному интегралу:
.
Вычисляем внутренний интеграл при постоянных значениях и :
Переходим к повторному интегралу по области :
Вычисляем внутренний интеграл по переменной
Ответ: 4 (куб. ед.).
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
