О красивых пагодах вдоль дороги
В Мьянме, по моим наблюдениям, существует несколько вариантов возведения пагоды Самая простая — со ступой-конусом в центре, но есть и другие варианты. Например, когда основание имеет форму квадрата с продолжением в виде «обтесанного» конуса с углами, эдакая вытянутая объемная трапеция (или как так штука в геометрии называется?) , причем на таких же основания стоят мелкие ступы по периметру , а в нишах еще и Будды сидят. Что-то подобное я видел в городе Таунчжи , когда шел к автостанции в центре.
Пагода данного типа попалась мне по дороге из Таунгу в Баго на просторах одноименной провинции среди полей с рисом и бахчи.

Решил поискать ее точное место на карте, хотя шансы на это были довольно низкие. В альбоме все фотографии идут подряд. Перед Баго какой-то населенный пункт, перед ним — китайский храм и стандартная пагода со ступой. Поставил сильное увеличение на гугле и «пошел» вдоль дороги от Баго на север. В автобусе я сидел у окна на западную сторону.
Так вот пагода нашлась около населенного пункта с меткой «Ballni Junction Bus Stop». Он расположен на берегу одноименной реки Ballni после населенного пункта Pyin Ma Lwin.
Все точно видно на карте — поле, пагода, река. Белая стрелка на пагоду указывает.
Как называется населенный пункт я так и не понял. Деревня это , на другой стороне реки остановка называется «Kadoak Ywama», а на километр южнее ж/д станция Ka Toke с монастырем , пагодами и китайским храмом.
Теперь пагода белой стрелкой в верхней части карты указана, а внизу все остальное.

Речка , она в верхней части карты

Красиво, однако, со ступой на золотом камне и круглой ступой-пешкой поблизости.

Хинты у входнйо арки
glebwiktorow.livejournal.com
Плоские и объемные геометрические фигуры :: SYL.ru
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
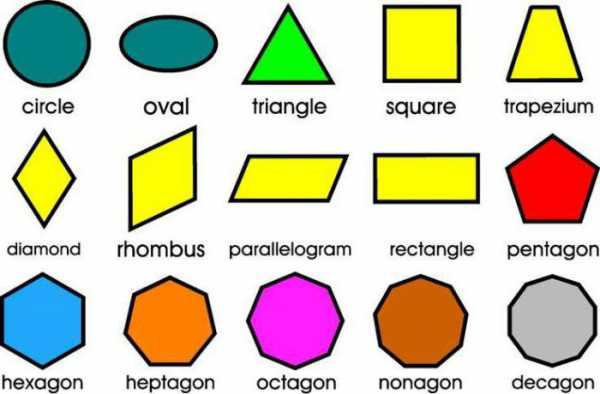
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка – это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка – это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.

Угол – это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость – это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм – это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник – это параллелограмм, у которого все стороны соприкасаются под прямым углом.

Квадрат – это четырехугольник с равными сторонами и углами.
Ромб – это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция – это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
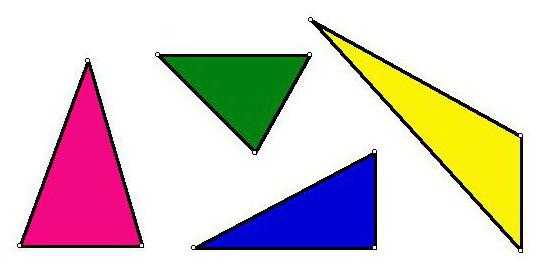
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
К этой категории стоит отнести геометрические фигуры разнообразных форм, ломаная линия контуров которых замыкается.
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
К этой категории причисляют следующие конструкции:
- куб;
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
- тор.
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.

Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
www.syl.ru
Все формулы диагоналей трапеции
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2.
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Все формулы сторон трапеции
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
www-formula.ru
Прямоугольная трапеция | Треугольники
Что такое прямоугольная трапеция и какими свойствами она обладает?
Определение.
Рисунок прямоугольной трапеции
ABCD- прямоугольная трапеция,
AD ∥ BC — основания трапеции,
AB и CD — ее боковые стороны,
Свойства прямоугольной трапеции:
1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.
AB — высота трапеции ABCD.
2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.
∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.
3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.
ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.
FCD — прямоугольный треугольник. FD=AD-AF,
отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то
и по теореме Пифагора
4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.
Треугольник ABC — прямоугольный.
По теореме Пифагора,
5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.
Треугольник ABD — прямоугольный.
По теореме Пифагора,
www.treugolniki.ru
