Область определения функции y f x – Область определения функции | Онлайн калькулятор

Область определения функции

Множество всех значений X (xX), которые может принимать аргумент функции x, называется областью определения этой функции.

Множество всех значений Y (yY), которые может принимать функция f(x), называется областью значений этой функции.

 Примеры: Областью определения функции y = x² является интервал (– ; ), а областью значений функции – интервал [0; ).

 Задача 1. Найти область определения функции .

Решение: Область определения функции находится как решение неравенства 2x – 4 

0  x  2, т.е. x  [2; ).

 Задача 2. Найти область определения функции .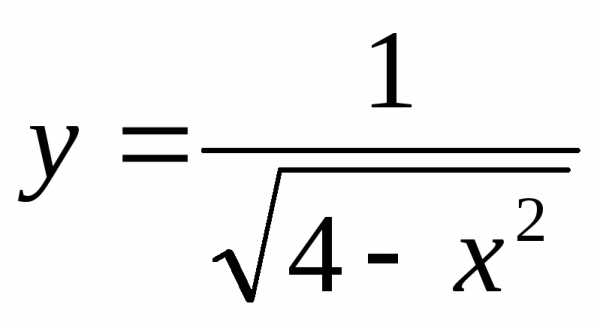

Решение: Область определения функции находится как решение неравенства 4 – x² > 0  – 2 < x < 2, т.е. x  (–2; 2).

Элементарные функции

Степенная функция: y = xⁿ (n — степень, nR)

Линейная y = x, квадратичная y = x², кубическая y = x³, гиперболическая 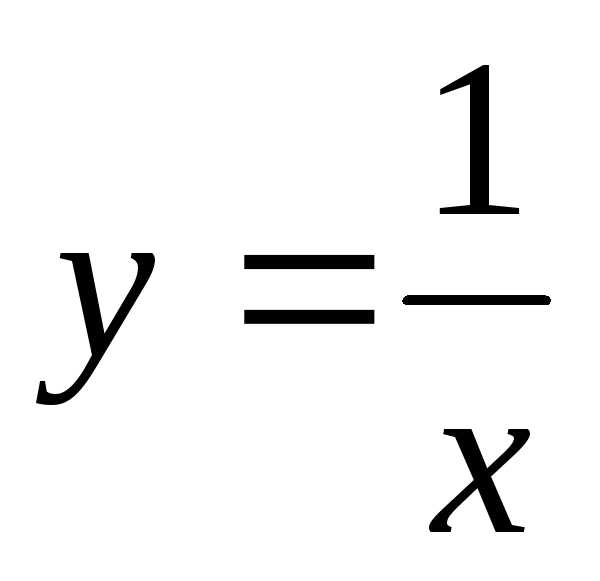и постояннаяy = 1 функции являются частными случаями степенной функции со степенями n = 1; 2; 3; –1; 0.

Показательная функция: y = a^x (a — основание степени, a > 0, a  1).

Показательная функция с основанием a = e = 2,718… называется экспоненциальной функцией y = e^x.

Областью определения показательной функции является интервал (– ; ), а областью значений функции – интервал (0; ).

Логарифмическая функция: y = log_ax (a — основание логарифма, a > 0, a  1).

Логарифмическая функция с основанием a = e = 2,718… называется натуральным логарифмом: y = lnx, а логарифмическая функция с основанием a = 10 — десятичным логарифмом:

y = lgx.

Областью определения логарифмической функции является интервал (0; ), а областью значений функции интервал (– ; ).

Тригонометрические функции: y = sinx, y = cosx, y = tgx, y = ctgx.

Областью определения функций y = sinx, y = cosx является интервал (– ; ), а областью значений функций – интервал [– 1; 1]. Областью определения функции y = tgx является интервал (– /2 + n; /2 + n), а областью значений функции — (– ; ). Областью определения функции y = ctgx является интервал (n;  + n), а областью значений функции — (– ; ).

Обратные тригонометрические функции: y = arcsinx, y

 = arccosx, y = arctgx, y = arcctgx.

Областью определения функций y = arcsinx, y = arccosx является интервал [– 1; 1], а областью значений функций – интервал (– ; ). Областью определения функции y = arctgx является интервал (– ; ), а областью значений функции — (– /2 + n; /2 + n). Областью определения функции y = arcctgx является интервал (– ; ), а областью значений функции — (n;  + n).

 Пример функции прибыли: В наиболее общем виде прибыль П (profit) определяется как разность между полным доходом (выручкой) от реализации продукции или услуг R (revenue) и полными издержками (затратами) C (cost): П = R – C. С учетом кривой спроса R = pQ = (p

0 – aQ)Q, где Q (quantity) — объем реализации, p (price) — цена. С другой стороны издержки делятся на постоянные и переменные, т.е. C = C_f + C_vQ. Таким образом, П = – aQ²+ (p₀ – C_vQ) – C_f, т.е. зависимость П от Q квадратичная.

Обратная функция

Если из зависимости y = f(x) вытекает соотношение x = g(y), то функция g(y) называется обратной функцией (относительно функции f(x)).

 Пример: Обратной функцией линейной функции y = 2x + 4 является функция .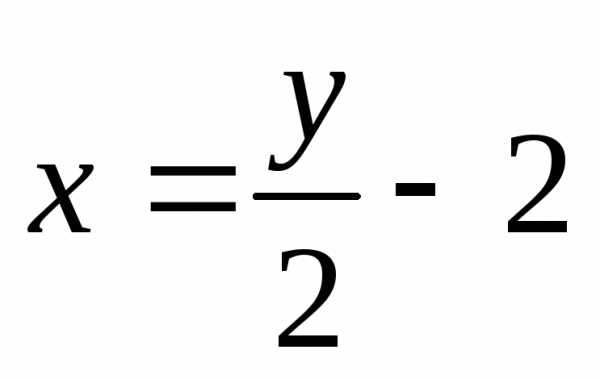

Показательная и логарифмическая функции, тригонометрические и обратные тригонометрические функции являются обратными.

Область определения X функции f(x) является областью значений Y обратной функции g(y) и наоборот.

studfiles.net

Понятие функции. Способы задания функции

Понятие функции является одним из важнейших понятий математики и её приложений. С помощью различных функций могут быть описаны многие процессы и явления реального мира.

Пусть X и Y — какие-то

множества. Имеет место функция, определённая на множестве X со значениями на множестве Y, если в силу некоторого закона f каждому элементу x∈X ставится в соответствие один и только один элемент y∈Y.

Это записывается в виде

y = f(x).

Другими словами, с помощью функции y = f(x) множество X отображается в множество Y. Поэтому функцию называют также отображением.

Например, авиапассажиры сидят в креслах салона пассажирского самолёта. Пусть X — множество пассажиров, а Y — множество кресел салона. Тогда возникает соответствие f : каждому пассажиру x∈X сопоставляется то кресло y = f

(x), в котором он сидит.

Наблюдается, таким образом, простой пример функции, областью определения которой является множество X пассажиров, а областью значений — множество f(X) занимаемых ими кресел. Если заполнены не все кресла Y, то множество значений функции будет подмножеством Y, не совпадающим со всем множеством Y.

Если, однако, какому-то пассажиру удастся сесть сразу в два кресла и , то нарушится принцип однозначной определённости значений функции, поэтому такая ситуация не является функциональной в смысле данного выше определения функций, поскольку требуется, чтобы каждому значению x аргумента соответствовало бы одно определённое значение y = f(x) функции.

В математическом анализе часто

X обозначают как D (область определения функции), а Y как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел). На сайте есть урок Как найти область определения функции.

Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от икса или f(x). И это неслучайно. Функции составляют бОльшую часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления в функции.

Пример 1. Даны множества A = {a, b, c, d, e} и L = {l

, m, n}. Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому соответствует.

Решение. Итак, множество A содержит 5 элементов, а множество L — 3 элемента. Если мы поставим стрелки, ведущие от каждого элемента множества L к элементам множества A, то некоторым элементам L будут соответствовать более одного элемента A. Такое соответствие не является функцией по определению. Но если мы проведём стрелки от элементов A к элементам L, то некоторым элементам A будут соответствовать одни и те же элементы L, но при этом каждому элементу A будет соответствовать не более одного элемента L. Такое соответствие не противоречит определение функции, следовательно, ответ на вопрос задания — положительный.

Можно задать, например, такое соответствите между элементами данных множеств, которое будет функцией:

Пример 2. Даны множества A = {70, 140, 30, 48} и В = {35, 15, 12}. Установить между элементами множеств соответствие, заданное правилом «элемент A можно нацело поделить на элемент В«. Будет ли такое соответствие функцией?

Решение. Между элементами множеств A и В устанавливается следующее соответствие:

Это соответствие является функцией, так как каждому элементу из множества A соответствует не более одного элемента из множества В.

Аналитическое задание функции.

Функция задана аналитически, если функциональная зависимость выражена в виде формулы, которая указывает совокупность тех математических операций, которые должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение функции.

При аналитическом задании функции указывают область определения, либо не указывают. В первом случае функция задаётся в виде y = f(x), x∈D, где D — область определения функции, во втором случае — в виде y = f(x). Во втором случае областью определения функции считается наибольшее множество, на котором имеет смысл формула, которой задана функция, то есть наибольшее множество аргумента, которое приводит к действительным значениям функции.

Важно, что функцию не следует отождествлять с формулой, с помощью которой она задана. Например, функции y = x², x∈]-∞,+∞[ и y = x², x∈[2, 4], выраженные одной и той же формулой y = x², так как они имеют разные области определения.

Наоборот, одна и та же функция может быть задана разными формулами на различных участках области определения. Пусть, например,

Здесь две формулы задают одну функцию, определённую на всей числовой прямой. При x≤0 значения этой функции определяются по первой формуле, а при x>0 — по второй.

Аналитический способ задания функции удобен тем, что значения функции можно вычислить при любых значениях аргумента. Недостатком этого способа задания функции является его малая наглядность.

Графический способ задания функции

График функции даёт наглядное представление о её свойствах. Например, график линейной функции y = kx + b — прямая линия, график квадратичной функции y = ax² + bx + c — парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде формул или уравнений. Таким образом, под графиком функции понимается множество точек плоскости, декартовы координаты которых удовлетворяют заданному уравнению.

Графический способ задания функции помимо геометрического изображения функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически. Задать функцию графически — это значит построить её график. Это часто делают самопишущие приборы. Например, в медицине электрокардиограф строит электрокардиограмму — кривую изменения электрических импульсов сердечной мышцы.

Графиком числовой функции y = f(x) называется множество точек плоскости с координатами (x; f(x)), абсциссы которых — числа из области определения функции, а ординаты — соответствующие значения функции.

Не всякое множество точек координатной плоскости, даже не всякая линия может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая, параллельная оси 0y, пересекает её не более чем в одной точке.

Пример 4. На рисунке ниже — график параболы, заданной уравнением y² = 2x. Является ли этот график графиком функции?

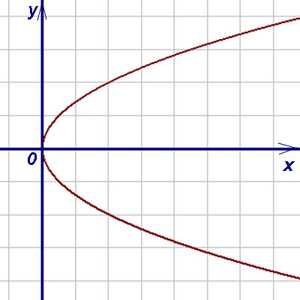
Решение. График параболы, заданной уравнением y² = 2x, не является графиком функции, поскольку прямая, параллельная оси 0y, пересекает его в двух точках при всех значениях x, кроме x = 0. Заданное уравнение эквивалентно двум уравнениям , каждое из которых определяет функцию. Графиком функции служит верхняя половина параболы, а графиком функции — её нижняя половина.

Табличный способ задания функции

При табличном способе задания функции рядом с числовым значением аргумента записывается соответствующее значение функции. Широко известных таблицы квадратов и кубов чисел, квадратных корней, то есть таблицы функций , , .

Недостатком табличного способа задания функции является то, что в таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности изменения функции при этом могут быть искажены или утрачены.

Если функция y зависит от переменной u, то есть y = f(u), а u, в свою очередь, является какой-либо функцией от независимой переменной x, то есть u = g(x), то переменная y называется функцией от функции или сложной функцией от x.

Это записывается в виде

y = f(u), u = g(x)

или

y = f[g(x)].

Таким образом, сложной называется функция, аргументом которой является не независимая переменная, а некоторая функция от неё.

Область определения сложной функции — это множество тех значений x из X, для которых соответствующие значения u принадлежат области определения U функции y = f(u). Ни для каких других значений x сложная функция не имеет смысла.

Из определения следует, что сложная функция y = f[g(x)] может быть представлена в виде цепочки простых функций y = f(u), u = g(x). Переменную u принято называть промежуточным аргументом в отличие от независимой переменной x. Цепочка, составляющая сложную функцию, может состоять не только из двух, но и из большего числа звеньев.

Например, функция состоит из трёх звеньев: , , .

Пример 5. Представить сложную функцию в виде звеньев — простых функций.

Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:

Пример 6. Представить сложную функцию в виде звеньев — простых функций.

Решение. Цепочка, составляющая данную функцию, состоит из следующих звеньев:

Если функция y задана уравнением вида f(x, y) =0, не разрешённым относительно y, то она называется неявной функцией аргумента x (Что такое разрешить уравнение относительно одной из переменных — в примере 8).

Пусть задана некоторая функция y = f(x), т. е. некоторое соответствие между множествами D(f) (область определения) и E(f) (множество значений). Если обратное соответствие есть функция, т. е. каждому значению y∈E(f) соответствует одно единственное значение x∈E(f), то её называют обратной функцией по отношению к функции f(x).

В этом случае уравнение y = f(x) определяет x как неявную функцию от y. Если это уравнение разрешимо относительно x, то получим явное выражение обратной функции: x = g(y).

Пример 7. Будет ли функцией соответствие, обратное функции ? А соответствие, обратное функции ?

Решение. Соответствие, обратное функции, заданной в первом условии, также является функцией:

.

Соответствие, обратное функции, заданной во втором условии, не является функцией, так как , то есть значениям икса, кроме нуля, соответствуют два значения игрека.

Весь раздел «Исследование функций»

function-x.ru

Понятие функции. Область определения функции. Способы задания функции

ИНСТИТУТ БИЗНЕСА, ПРАВА И ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИЙ

КОНТРОЛЬНАЯ РАБОТА

по дисциплине

МАТЕМАТИКА

на тему

Понятие функции. Область определения функции.

Способы задания функции

Выполнил: Мальский Эдуард Александрович,

студент 2 курса

юридического факультета

заочного отделения

группа 25-ЮЗП

Преподаватель:

Оценка:_______________

Подпись преподавателя:_______________

2004 г.

Оглавление

контрольной работы по дисциплине «Математика»

на тему «Понятие функции. Область определения функции.

Способы задания функции»

Введение……………………………………………………………………………3

1. Функция и её свойства……………………………………………………..4

2. Способы задания функции…………………………………………………..5

3. Виды функций и их свойства………………………………………………6

Заключение……………………………………………………………………….11

Список использованной литературы……………………………………………12

Введение.

Функция — одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.

Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r² . Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции — теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

Раздел 1. Функция и её свойства.

Функция- зависимость переменной у от переменной x , если каждому значению х соответствует единственное значение у .

Переменная х- независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у , соответствующее заданному значению х .

Область определения функции- все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х из области определения функции выполняется равенство f ( x )= f (- x )

Функция является нечетной- если для любого х из области определения функции выполняется равенство f (- x )=- f ( x )

Возрастающая функция- если для любых х₁ и х₂ , таких, что х₁ < х₂ , выполняется неравенство f (х₁ )< f (х₂ )

Убывающая функция- если для любых х₁ и х₂ , таких, что х₁ < х₂ , выполняется неравенство f (х₁ )> f (х₂ )

Раздел 2. Способы задания функции.

Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у= f ( x ) , где f ( x )- с переменной х . В таком случае говорят, что функция задана формулой или что функция задана аналитически.

На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Раздел 2. Виды функций и их свойства.

1) Постоянная функция- функция, заданная формулой у= b , где b — некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у= kx , где к¹0. Число k называется коэффициентом пропорциональности .

Cвойства функции y=kx :

1. Область определения функции- множество всех действительных чисел

2. y=kx — нечетная функция

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

3)Линейная функция- функция, которая задана формулой y = kx + b , где k иb — действительные числа. Если в частности, k =0 , то получаем постоянную функцию y = b ; если b =0 , то получаем прямую пропорциональность y = kx .

Свойства функции y = kx + b :

1. Область определения- множество всех действительных чисел

2. Функция y = kx + b общего вида, т.е. ни чётна, ни нечётна.

3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой

Графиком функции является прямая .

4)Обратная пропорциональность- функция, заданная формулой y = k /х, где k¹0 Число k называют коэффициентом обратной пропорциональности.

Свойства функции y = k / x :

1. Область определения- множество всех действительных чисел кроме нуля

2. y=k / x — нечетная функция

3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).

Графиком функции является гипербола .

5)Функция y = x ²

Свойства функции y=x² :

1. Область определения- вся числовая прямая

2. y=x² — четная функция

3. На промежутке [0;+¥) функция возрастает

4. На промежутке (-¥;0] функция убывает

Графиком функции является парабола .

6)Функция y=x³

Свойства функции y=x³ :

1. Область определения- вся числовая прямая

2. y=x³ — нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой y = xⁿ , где n — натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x² ; y=x³ . Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8… В этом случае функция y = xⁿ обладает теми же свойствами, что и функция y=x² . График функции напоминает параболу y=x² , только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем “теснее прижимаются” к оси Х, чем больше n.

Пусть n- произвольное нечетное число, большее трех: 5,7,9… В этом случае функция y = xⁿ обладает теми же свойствами, что и функция y=x³ . График функции напоминает кубическую параболу.

8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y = x ^{— n} , где n — натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.

Пусть n- нечетное число, большее единицы: 3,5,7… В этом случае функция y = x ^{— n} обладает в основном теми же свойствами, что и функция y=1/х.

Пусть n- четное число, например n=2.

Свойства функции y=x^-2 :

1. Функция определена при всех x¹0

2. y=x^-2 — четная функция

3. Функция убывает на (0;+¥) и возрастает на (-¥;0).

Теми же свойствами обладают любые функции при четном n, большем двух.

9)Функция y = Ö х

Свойства функции y = Ö х:

1. Область определения — луч [0;+¥).

2. Функция y= Ö х — общего вида

3. Функция возрастает на луче [0;+¥).

10)Функция y =³ Ö х

Свойства функции y =³ Ö х:

1. Область определения- вся числовая прямая

2. Функция y= ³ Ö х нечетна.

3. Функция возрастает на всей числовой прямой.

11)Функция y=ⁿ Ö х

При четном n функция обладает теми же свойствами, что и функция y = Ö х . При нечетном n функция y = ⁿ Ö х обладает теми же свойствами, что и функция y =³ Ö х.

12)Степенная функция с положительным дробным показателем- функция, заданная формулой y = x^r , где r — положительная несократимая дробь.

Свойства функции y=x^r :

1. Область определения- луч [0;+¥).

2. Функция общего вида

3. Функция возрастает на [0;+¥).

На рисунке изображен график функции y=x^5/2 . Он заключен между графиками функций y=x² и y=x³ , заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y = x^r , где r>1.

На рисунке изображен график функции y=x^2/3 . Подобный вид имеет график любой степенной функции y = x^r , где 0<r<1

13)Степенная функция с отрицательным дробным показателем- функция, заданная формулой y = x ^{— r} , где r — положительная несократимая дробь.

Свойства функции y = x ^{— r} :

1. Обл. определения -промежуток (0;+¥)

2. Функция общего вида

3. Функция убывает на (0;+¥)

14)Обратная функция

Если функция y = f ( x ) такова, что для любого ее значения y_o уравнениеf ( x )= y_o имеет относительно х единственный корень, то говорят, что функция f обратима.

Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.

mirznanii.com

Укажите область определения функции y=f(x)

область определения функции — это означает какие значения может принимать х. те все ли действия. записанные в формуле выполнимы. невыполнимыми мб извлечение корня из отрицательного числа .при четной степени корня ( на множестве действительных чисел) ; а также деление на ноль. Пример: у=к\х обл. опр х не равно 0. для у=кх; у=кх+в; у=х»2 область опр. от минус до плюс бесконечности. те любое число.

вот твой х и определяет область f)))

в каких пределах х действует функция. ну, например, от 0 до 5. (зависит от конкретной функции)

А ты вообще знаешь, что такое ООФ — область определения функции?

touch.otvet.mail.ru