Как найти область значения функции
Лекция 19. Функция. Область определения и множество значений функции.
Функция — одно из важнейших математических понятий.
Определение: Если каждому числу из некоторого множества x поставлено в соответствие единственное число y, то говорят, что на этом множестве задана функция y(x). При этом x называют независимой переменной или аргументом, а y — зависимой переменной или значением функции или простофункцией.
Говорят также, что переменная y является функцией от переменной x.
Обозначив соответствие некоторой буквой, например f, удобно писать: y=f (x), то есть, значение y получается из аргумента x с помощью соответствия f. (Читают: y равно f от x.) Символом f (x) обозначают значение функции, соответствующее значению аргумента, равному x.
Пример 1 Пусть функция задается формулой y=2×2–6. Тогда можно записать, что f(x)=2×2–6. Найдем значения функции для значений х, равных, например, 1; 2,5;–3; т. е. найдем f(1), f(2,5), f(–3):
f(1)=2•12–6=–4;
f(2,5)=2•2,52–6=6,5;
f(–3)=2•(–3)2–6= 12.
Заметим, что в записи вида y=f (x) вместо f употребляют и другие буквы: g, и т. п.
Определение: Область определения функции — это все значения x, при которых существует функция.
Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.
Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.
Определение: Все значения, которые принимает зависимая переменная образуют область значения функции.
Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой , где l 0 начальная длина стержня, а —коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функцииl=g(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.
Пример.
Укажите область значений функции y = arcsinx.
Решение.
Областью определения арксинуса является отрезок [-1; 1]. Найдем наибольшее и наименьшее значение функции на этом отрезке.
Производная положительна для всех x из интервала (-1; 1), то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1, а наибольшее при x = 1.
Мы получили область значений функции арксинуса
.Найдите множество значений функции
на отрезке [1; 4].Решение.
Найдем наибольшее и наименьшее значение функции на данном отрезке.
Определим точки экстремума, принадлежащие отрезку [1; 4]:
Вычисляем значения исходной функции на концах отрезка и в точках
: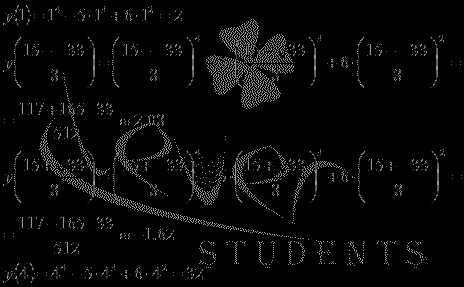
Следовательно, множеством значений функции на отрезке является интервал
.Сейчас покажем, как находить множество значений непрерывной функции y = f(x) на открытых интервалах (a; b),
.Сначала определяем точки экстремума, экстремумы функции, промежутки возрастания и убывания функции на данном интервале. Далее вычисляем односторонние пределы на концах интервала и (или) пределы на бесконечности (то есть, исследуем поведение функции на границах открытого интервала или на бесконечности). Этой информации достаточно, чтобы найти множество значений функции на таких промежутках.
studopedia.ru>
Область значений функции
Область значений (или множество значений) функции — множество, состоящее из всех значений, которые принимает функция[1][2][3].
Определение
Пусть на множестве X {\displaystyle X} з
zna4enie.ru
Область определения и область значения
Понятие и свойства функции. Область определения и область значения
Основные данные о работе
| Версия шаблона | 2.1 |
| ЦДОР | |
| Вид работы | Творческое эссе |
| Название дисциплины | Математика (курс 13) |
| Тема | Понятие и свойства функции. Область определения и область значения. |
| Фамилия | |
| Имя | |
| Отчество | |
| № контракта |
Содержание
Понятие и свойства функции. Область определения и область значения……………3
Список использованных интернет-ресурсов……………………………………………9
Основная часть
Понятие и свойства функции. Область определения и область значения
1.Фукция и её свойства.
Функция (отображение, оператор, преобразование) — это математическое понятие, отражающее связь между элементами множеств. Так же можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения, а значение месяца однозначно определяет значение следующего за ним месяца, а также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем в 1692 год. В свою очередь, Иоганн Бернулли в письме к Лейбницу употребил этот термин в смысле, более близком к современному.
Первоначально, понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, которое дал Эйлер в 1751 год, затем — Лакруа в 1806 год — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским в 1834 году и Дирихле в 1837 году.
К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
Часто под термином «функция» понимается числовая функция; то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
Функция – это одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира.
Функция — это зависимость переменной у от переменной х, если каждому значению х соответствует единственное значение у.
Переменная х – это независимая переменная или аргумент.
Переменная у – это зависимая переменная.
Значение функции – это значение у, соответствующее заданному значению х.
Область определения функции – это все значения, которые принимает независимая переменная.
Область значений функции (множество значений)- это все значения, которые принимает функция.
Функция является четной — если для любого х из области определения функции выполняется равенство f(х)=f(-х)
Функция является нечетной — если для любого х из области определения функции выполняется равенство f(-х)=-f(х)
Возрастающая функция — если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)
Убывающая функция — если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2)
2. Способы задания функции.
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее часто употребительным является способ задания функции с помощью формулы у=f(х), где f(х) – с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При данном способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами такого табличного задания функции являются: таблица квадратов и таблица кубов.
2. Виды функций и их свойства.
1) Постоянная функция- это функция, заданная формулой у=b, где b- это некоторое число.
Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат.
2) Прямая пропорциональность – это функция, заданная формулой у=kx, где к¹0. Число k называется коэффициентом пропорциональности.
Cвойства функции y=kx:
1. Область определения функции- множество всех действительных чисел;
2. y=kx — нечетная функция;
3. При k>0 функция возрастает, а при k
3)Линейная функция- это функция, которая задана формулой y=kx+b, где k и b- это действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b ; если b=0, то получаем прямую пропорциональность y=kx.
Свойства функции y=kx+
zna4enie.ru
Функция. Область определения и область значений функции
Определение:
Зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение y, называют функцией.
В определении сказано, что только та зависимость является функцией, у которой каждому значению аргумента соответствует единственное значение функции.
Рассмотрим первый график. Видим, что одному значению x может соответствовать несколько значений y. Значит, данная зависимость не является функцией.
Обратимся ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них соответствует только одно значение функции. Можно сказать, что эта зависимость является функцией.
В общем виде любую функцию можно записать так:
Например:
Понятно, что функция может принимать различные значения в зависимости от значения аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы заметили, что в этом задании функции названы разными буквами. Действительно, функцию можно называть любой буквой латинского алфавита.
Ранее вами были изучены несколько важных функций. Вспомним их.
Сейчас попробуем выяснить, как же получается график функции, и дадим определение этому понятию.
Можно записать её в таком виде:
Это линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.
Получаем точки с координатами (1;3) и (-1;-11).
Проведём прямую через полученные точки.
Мы изобразили график функции.
Определение:
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — значениям функции, называют графиком функции.
Все значения аргумента, т.е. переменной x образуют область определения функции, а все значения зависимой переменной, т.е. y, — область значений функции.
В данном случае x и y могут быть любыми числами, т.е. областью определения и областью значений является множество всех действительных чисел.
Потренируемся находить область определения и область значений функции по её графику.
Область определения можно находить не только по графику функции, но и по формуле, с помощью которой задана функция.
videouroki.net
Как найти область значений функции?
<a href=»/» rel=»nofollow» title=»10122400:##:http://www.ipo.spb.ru/internet-school/a/bashm/3-7.htm» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> Область определения — это значения «Х» (т. е. какие значения может принимать Х) А область значения — это «у» (т. е. какие «у» при этом получаются)
Прировнять функцию к нулю и посмотреть при каких значениях есть решения при каких нету.
насколько помню, область значений это те значения, которые может принимать игрек. ну например если у=корень из х, то игрек будет неотрицательным числом. так и искать
Множество всех тех значений, которые принимает сама функция, называется областью значений (изменения) этой функции. Если по графику — то это проекция графика на ось Оу
область значение — это у
touch.otvet.mail.ru
Как находить область определения функции ???
Область определения и область значений функции. Пусть нам дана функция y = f(x). Все значения независимой переменной (х) образуют область определения функции — D( f ). Все значения, которые принимает зависимая переменная (у) , образуют область значений функции – Е ( f ). При нахождении области определения функции надо обращать внимание на следующие моменты: 1. Пусть дана функция в виде многочлена у = Р (х) . (у = ах^n + bx^k + … + c). В этом случае при любом значении х данная функция всегда будет иметь определенное значение. Это значит, что D(f) = (-беск; +беск) 2. Пусть дана функция в виде дроби f(x)/q(x) . В этом случае g(x) не=0. 3. Пусть дана функция вида кор из f(x). В этом случае должно выполняться условие f(x) >= 0. (Подкоренное выражение должно принимать неотрицательные значения) . 4. При нахождении области определения логарифмической функции у = log (осн g(x)) f(x) надо учитывать, что f(x)>0, g(x) > 0, f(x) не=1. А производная находится при другом исследовании функции.
Производная тут вообще не причём. Область определения зависит от значений, которые может принимать аргумент, что бы функция не потеряла смысл. Например для функции у=1/х область определения (-бесконечность, 0)(0,+бесконечность) то есть при х=0 функция не определена.
Нет, это все возможные значения у.
область определения — все возможные значения х. чтобы их найти, нужно найти все х, при которых функция будет иметь смысл, например все х, при которых знаменатель дроби не равен 0, подкоренное выражение неотрицательное и др.
touch.otvet.mail.ru
