Тригонометрический круг — материалы для подготовки к ЕГЭ по Математике
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
- Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.
- Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .
- И синус, и косинус принимают значения от до .
- Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.
- Знаки синуса, косинуса, тангенса и котангенса.
- Синус — функция нечётная, косинус — чётная.
- Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .
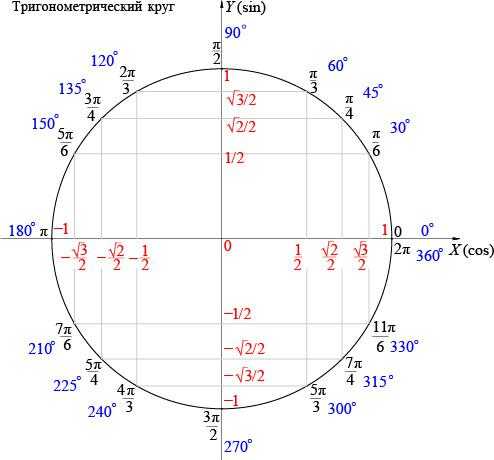
Вот что мы видим на этом рисунке:
Ты нашел то, что искал? Поделись с друзьями!
А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Например:
;
;
;
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
,
.
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
,
.
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
,
,
где — целое число. То же самое можно записать в радианах:
,
.
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
,
.
В результате получим следующую таблицу.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Тригонометрический круг со всеми значениями
Тригонометрический круг — один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
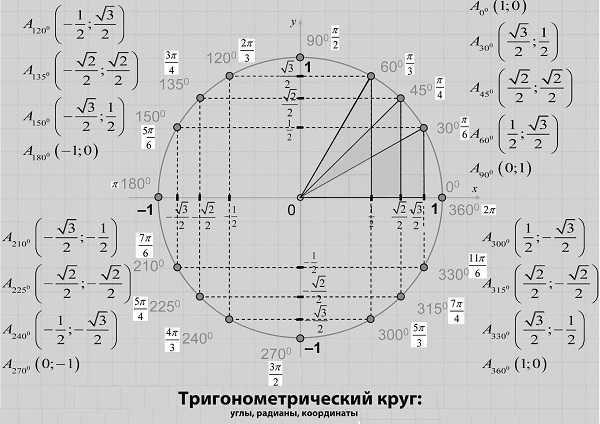
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты — две стороны треугольника, которые прилегают к углу 90°, а третья — гипотенуза, она всегда длиннее катетов.

Синусом называется отношение одного из катетов к гипотенузе, косинусом — отношение другого катета к ней, а тангенсом — отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.

Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х — косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто — полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
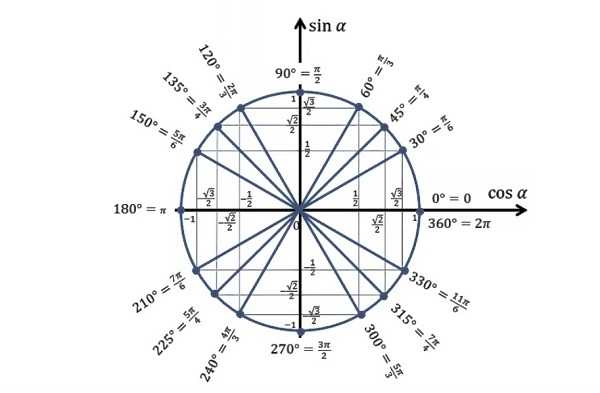
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три — 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° — значения углов от 0 до ∏/2;
- от 90 до 180° — значения углов от ∏/2 до ∏;
- от 180 до 270° — от ∏ до 3*∏/2;
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.

Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности — функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.




Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
1001student.ru
Тригонометрический круг (окружность)
ОПРЕДЕЛЕНИЕТригонометрический круг (окружность) – круг радиуса один (единичная окружность), с центром в начале координат (рисунок 1).
За нулевое положение радиуса, принимается его положение на положительном направлении оси Ox. Угол поворота радиуса отсчитывается от положительного направления оси Ox: с плюсом – против часовой стрелки, с минусом – по часовой стрелке. Полный круг – это . Каждому углу от до соответствует точка на единичной окружности.
Синусом угла есть ордината точки , а косинусом угла есть абсцисса точки .
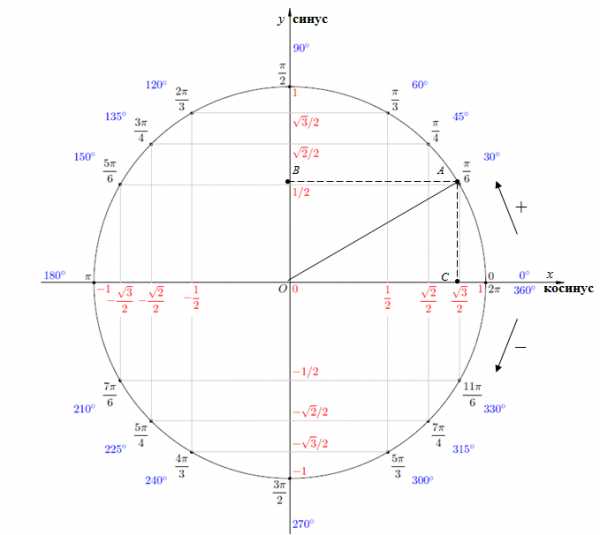
Рис. 1
Примеры решения задач
ПРИМЕР 1| Задание | Используя единичную окружность, определить синус и косинус угла . |
| Решение | Отложим на единичной окружности угол равный (рис. 1), ему будет соответствовать точка A окружности. Найдем синус заданного угла. Для этого найдем проекцию точки A на ось Oy, ею будет точка . Значит, ордината точки A равна и значение .
Для нахождения косинуса заданного угла, найдем проекцию точки A на ось Ox. Ею будет точка , тогда абсцисса точка A равна и, соответственно, . |
| Ответ |
Единицы измерения углов
Углы обычно измеряются либо в градусах, либо в радианах. Перевести градусы в радианы просто: 360 градусов (полный круг) соответствует радиан.
ПРИМЕР 2| Задание | Перевести:
1) угол в градусы; 2) угол в радианы. |
| Решение | 1) Для того чтобы перевести угол из радиан в градусы, умножим данный угол на . Получим
2) Для того чтобы перевести заданный угол из градусов в радианы, умножим его на . Получим
|
| Ответ |
На единичной окружности также можно находить углы, которые больше 360 градусов. Поскольку, значения синуса и косинуса на тригонометрическом круге повторяются каждые .
ПРИМЕР 3| Задание | Найти с помощью единичной окружности синус угла . |
| Решение | Представим данный угол следующим образом
Таким образом, необходимо сделать два полных обхода окружности, а затем остановиться в точке соответствующей углу в (рис. 1). Синусу соответствует ордината этой точки, то есть . |
| Ответ |
Тригонометрические функции
Тригонометрические уравнения и их решение
Косинус 45 градусов
Основное тригонометрическое тождество
Обратные тригонометрические функции
Синус угла
ru.solverbook.com
Основные значения тригонометрических функций. Часть 2
Продолжение (начало здесь)
Перевод радиан в градусы и градусы в радианы
На тригонометрическом круге помимо углов в градусы мы наблюдаем радианы.
 Подробнее про радианы:+ показать
Подробнее про радианы:+ показать

1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.
Все знают, что радиан – это
Так вот, например, , а . Так, мы научились переводить радианы в углы.
Теперь наоборот, давайте переводить градусы в радианы.
Допустим, нам надо перевести в радианы. Нам поможет пропорция. Поступаем следующим образом:
Так как, радиан, то заполним таблицу:
Откуда
Тренируемся находить значения синуса и косинуса по кругу
Давайте еще уточним следующее.
Ну хорошо, если нас просят вычислить, скажем, , – здесь обычно путаницы не возникает – все начинают первым делом искать на круге.
А если просят вычислить, например, … Многие, вдруг, начинают не понимают где искать этот ноль… Частенько ищут его в начале координат. Почему?
1) Давайте договоримся раз и навсегда! То, что стоит после или – это аргумент=угол, а углы у нас располагаются на круге, не ищите их на осяx! (Просто отдельные точки попадают и на круг, и на ось…) А сами значения синусов и косинусов – ищем на осях!
2) И еще! Если мы от точки «старт» отправляемся против часовой стрелки (основное направление обхода тригонометрического круга), то мы откладываем положительные значения углов, значения углов растут при движении в этом направлении.
Если же мы от точки «старт» отправляемся по часовой стрелке, то мы откладываем отрицательные значения углов.
Пример 1.
Найти значение .
Решение:
Находим на круге . Проецируем точку на ось синусов (то есть проводим перпендикуляр из точки к оси синусов (оу)).

Приходим в 0. Значит, .
Пример 2.
Найти значение .
Решение:
Находим на круге (проходим против часовой стрелки и еще ). Проецируем точку на ось синусов (а она уже лежит на оси синусов).

Попадаем в -1 по оси синусов.
Значит, .
Заметим, за точкой «скрываются» такие точки, как (мы могли бы пойти в точку, помеченную как , по часовой стрелке, а значит появляется знак минус), и бесконечно много других.
Можно привести такую аналогию:
Представим тригонометрический круг как беговую дорожку стадиона.

Вы ведь можете оказаться в точке «Флажок», отправляюсь со старта против часовой стрелки, пробежав, допустим, 300 м. Или пробежав, скажем, 100м по часовой стрелке (считаем длину дорожки 400 м).
А также вы можете оказаться в точке «Флажок» (после «старт»), пробежав, скажем, 700 м, 1100 м, 1500 м и т. д. против часовой стрелки. Вы можете оказаться в точке «Флажок», пробежав 500 м или 900 м и т. д. по часовой стрелке от «старт».
Разверните мысленно беговую дорожку стадиона в числовую прямую. Представьте, где на этой прямой будут, например, значения 300, 700, 1100, 1500 и т.д. Мы увидим точки на числовой прямой, равноотстоящие друг от друга. Свернем обратно в круг. Точки «cлепятся» в одну.
Так и с тригонометрическим кругом. За каждой точкой скрыто бесконечно много других.
Скажем, углы , , , и т.д. изображаются одной точкой. И значения синуса, косинуса в них, конечно же, совпадают. (Вы заметили, что мы прибавляли/вычитали или ? Это период для функции синус и косинус.)
Пример 3.
Найти значение .
Решение:
Переведем для простоты в градусы
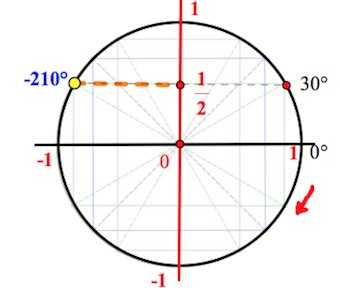 (позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):
(позже, когда вы привыкнете к тригонометрическому кругу, вам не потребуется переводить радианы в градусы):
Двигаться будем по часовой стрелки от точки Пройдем полкруга () и еще
Понимаем, что значение синуса совпадает со значением синуса и равняется
.
Заметим, если б мы взяли, например, или и т.д., то мы получили бы все тоже значение синуса.
Пример 4.
Найти значение .
Решение:
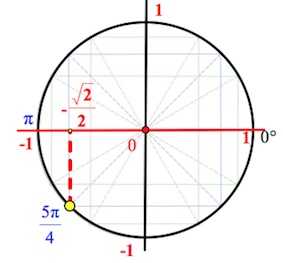 Все же, не будем переводить радианы в градусы, как в предыдущем примере.
Все же, не будем переводить радианы в градусы, как в предыдущем примере.
.
То есть нам надо пройти против часовой стрелки полкруга и еще четверть полкруга и спроецировать полученную точку на ось косинусов (горизонтальная ось).
Пример 5.
Найти значение .
Решение:
Как отложить на тригонометрическом круге ?
 Если мы пройдем или , да хоть , мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге
Если мы пройдем или , да хоть , мы все равно окажемся в точке, которую мы обозначили как «старт». Поэтому, можно сразу пройти в точку на круге
Пример 6.
Найти значение .
Решение:
Мы окажемся в точке ( приведет нас все равно в точку ноль). Проецируем точку круга на ось косинусов (смотри тригонометрический круг), попадаем в . То есть .
Тригонометрический круг – у вас в руках
Вы же уже поняли, что главное – запомнить значения тригонометрических функций первой четверти. В остальных четвертях все аналогично, нужно лишь следить за знаками. А «цепочку-лесенку» значений тригонометрических функций, вы, надеюсь уже не забудете. 
Как находить значения тангенса и котангенса основных углов смотрите здесь.
После чего, познакомившись с основными значениями тангенса и котангенса, вы можете пройти тест по теме «Нахождение значений косинусов, синусов, тангенсов и котангенсов различных углов»
Ссылочка на пустой шаблон круга. Тренируйтесь!
egemaximum.ru
Тригонометрический круг. Основные значения тригонометрических функций
Если вы уже знакомы с тригонометрическим кругом, и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, тригонометрический круг:
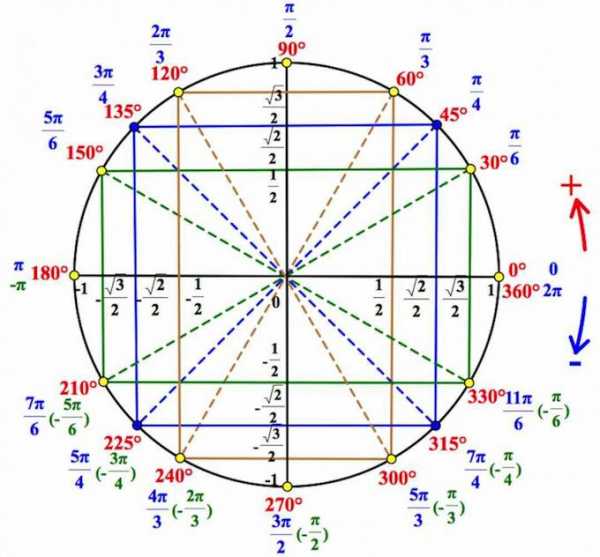
Мы же здесь будем все подробно разбирать шаг за шагом.
Тригонометрический круг – не роскошь, а необходимость
Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Очень важно не махать рукой на значения тригонометрических функций, – мол, всегда можно посмотреть в шпору с таблицей значений.
Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!
Нас выручит тригонометрический круг! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!
К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул, чему равен синус, скажем, 300 градусов, или -45.
Никак?.. можно, конечно, подключить формулы приведения… А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!
А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.
Знакомство с тригонометрическим кругом
Давайте по порядку.
Сначала выпишем вот такой ряд чисел:
А теперь такой:
И, наконец, такой:
Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .
Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».
И зачем оно нам?
Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.
Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).
От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .
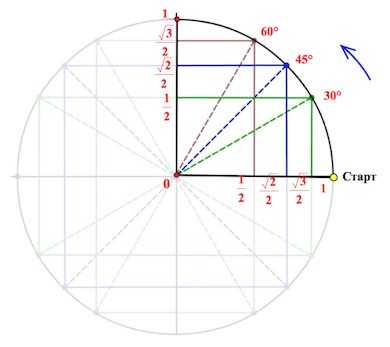 Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.
Это почему же, спросите вы?
Не будем разбирать все. Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
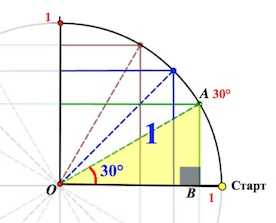
Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).
Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора
Надеюсь, уже что-то становится понятно?
Наконец, что такое синус, косинус в прямоугольном треугольнике?
Так вот точка В и будет соответствовать значению , а точка М – значению
Аналогично с остальными значениями первой четверти.
Как вы понимаете, привычная нам ось (ox) будет осью косинусов, а ось (oy) – осью синусов. Про тангенс и котангенс позже.
Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.
Итак, вот он, ВСЕМОГУЩИЙ тригонометрический круг, без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в следующей статье.
egemaximum.ru
Тригонометрический круг. Значения тангенса и котангенса на круге
В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.
Как же быть с тангенсом и котангенсом? Об этом и поговорим сегодня.
Где же на тригонометрическом круге оси тангенсов и котангенсов?
Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).
Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).
На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?
Я думаю, вы легко сообразите и сами. 🙂 Можно по-разному рассуждать. Можете, например, использовать тот факт, что и
Изучаем картинку:
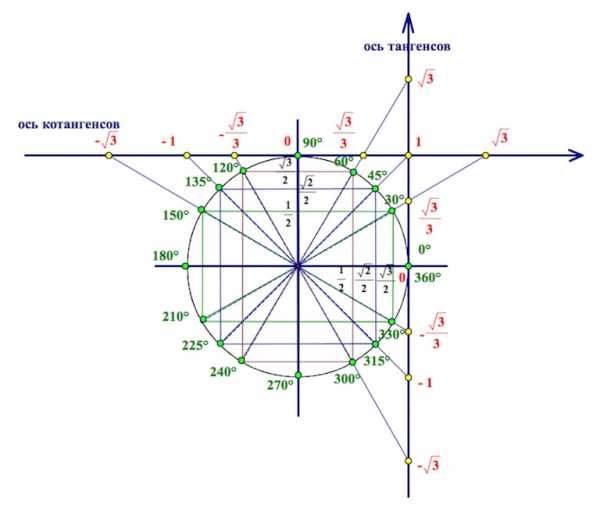
Собственно, картинка за себя сама говорит.
Если не очень все же понятно, разберем примеры:
Пример 1.
Вычислить
Решение:
Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что
Ответ:
Пример 2.
Вычислить
Решение:
Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.
не существует.
Ответ: не существует
Пример 3.
Вычислить
Решение:
Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .
Так значит,
Ответ:
Пример 4.
Вычислить
Решение:
Поэтому от точки (именно там будет ) откладываем против часовой стрелки .
Выходим на ось котангенсов, получаем, что
Ответ:
Пример 5.
Вычислить
Решение:
Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что
Ответ:
Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройти тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».
egemaximum.ru
Окружность, радиус, диаметр, число Пи, сектор, касательная
Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
Центр окръжности
Радиус: расстояние от центра окружности до его границы.
Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
$d = 2\cdot r$
Периметр (длина окружности): длина границы окружности.
Длина окружности $= \pi \cdot$ диаметр $= 2 \cdot \pi \cdot$ радиус
Длина окружности $= \pi \cdot d = 2 \cdot \pi \cdot r$
$\pi$ — pi: число, равное 3,141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности.
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $\frac{\pi}{2}$ — четверть круга,
180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360° или $2\pi$
Хорда: отрезок прямой, соединяющей две точки на окружности.
Сектор: похож на часть пирога (клин).
Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.
Формулы
Длина окружности $=\pi \cdot \text{диаметр} = 2\cdot \pi \cdot \text{радиус}$
Площадь круга $= \pi \cdot$ радиус2
Радиус обозначается как r, диаметр как d, длина окружности как P и площадь как S.
$P = \pi \cdot d = 2\cdot \pi \cdot r$
$S = \pi \cdot r^2$
Площадь сектора круга
Площадь сектора круга K: (с центральным углом $\theta$ и радиусом $r$).
Если угол $\theta$ в градусах, тогда площадь = $\frac{\theta}{360} \pi r^2$
Если угол $\theta$ в радианах, тогда площадь, тогда площадь = $\frac{\theta}{2} r^2$
Углы
Центральный угол
Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).
Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:
$\theta = 360 \cdot \frac{l}{P} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r}$
$l$ — длина дуги.
Вписанный угол
Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.
На рисунке, угол APB это вписанный угол.
 Величина вписанного угла равна половине дуги, на которую он опирается.
Величина вписанного угла равна половине дуги, на которую он опирается. Пример:
$\widehat{AB} = 84^\circ$
$\angle APB = \frac{84}{2} = 42^\circ$
Углы между двумя хордами
Случай 1: два секущие пересекаются внутри окружности.
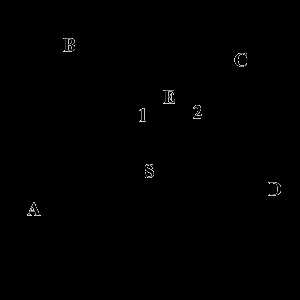
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$
Случай 2: две секущие пересекаются вне окружности.
Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.
$\angle ABC =\frac{1}{2}(x — y)$
На рисунке дуга AB=80° и дуги CD=30°.
$\angle ABC = \frac{1}{2}(80 — 30) = \frac{1}{2} \cdot 50 = 25^\circ$
Хорды
Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:
$AX \cdot XB = CX \cdot XD$
www.math10.com