Решение задач по теме «Уравнение окружности». Видеоурок. Геометрия 9 Класс
Уравнение окружности с центром в точке и радиусом имеет вид:
и – это координаты точки , лежащей на этой окружности.
Выясните, какие из данных уравнений являются уравнениями окружности, найдите центр окружности и ее радиус:
1.
2.
Решение
1.
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
2.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Воспользуемся формулой квадрата суммы и разности. В обеих скобках есть квадрат первого выражения и удвоенное произведение, не хватает квадрата второго выражения, прибавим и отнимем его:
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
Задачи с использованием метода выделения полного квадрата
Выясните, является ли данное уравнение уравнением окружности, найдите центр окружности и ее радиус:
1.
2.
Решение
1.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Так как и (квадрат выражения больше или равен нулю), то выражение в левой части уравнения больше нуля. Следовательно, это уравнение не имеет решения и не является уравнением окружности.
Доказать отсутствие решений у исходного уравнения можно также с помощью дискриминанта. Для этого рассмотрим это уравнение как квадратное относительно с параметром .
Мы получили квадратный трехчлен с такими коэффициентами:
— коэффициент при – ;
— свободный член зависит от параметра – .
Найдем корни данного уравнения по известной формуле:
Выделим полный квадрат в подкоренном выражении:
Видно, что подкоренное выражение меньше нуля. А так как подкоренное выражение равно четверти дискриминанта, то и дискриминант будет отрицательным числом.
Следовательно, исходное уравнение не имеет решений.
2.
Преобразуем данное уравнение с помощью метода выделения полного квадрата:
Данное уравнение является уравнением окружности. Центр окружности – это точка с координатами ; радиус окружности – .
Напишите уравнение окружности, проходящей через три заданные точки.
Дано: ; ; .
Найти: уравнение окружности, проходящей через данные точки.
Решение
Уравнение окружности задается тремя параметрами , , , поэтому необходимо найти эти параметры.
Так как данные точки лежат на окружности, то их координаты удовлетворяют уравнению искомой окружности. Подставим координаты точек в уравнение окружности в общем виде:
:
:
:
Мы получили систему из трех уравнений относительно трех неизвестных:
Решим эту систему. Вычтем из третьего уравнения первое:
Разложим выражение как разность квадратов:
Подставляем найденное значение во все три уравнения системы:
Видно, что первое и третье уравнение одинаковые, поэтому оставляем только одно из них:
Вычтем из первого уравнение второе:
Подставим найденное значение a в уравнение системы:
Радиус больше нуля, следовательно:
Мы нашли необходимые три параметра, поэтому можно выписать искомое уравнение окружности:
Ответ:
Типовые задачи на нахождение координат точек на окружности
Задача А
Дано: – центр окружности; – точка на окружности (см. Рис. 1).
Найти: уравнение окружности.
Рис. 1. Иллюстрация к задаче
Решение
Уравнение окружности в общем виде:
Так как координаты центра окружности , то ; . Необходимо найти – радиус данной окружности.
Нам известны две точки, поэтому радиус определим по формуле:
Выпишем уравнение окружности:
Ответ: .
Уравнение окружности позволяет найти точки на окружности по одной из координат этих точек.
Задача Б
Дано: – уравнение окружности; ордината искомых точек равна 3 (см. Рис. 2).
Найти: точки окружности с ординатой, равной 3.
Рис. 2. Иллюстрация к задаче
Решение
Уравнение данной окружности , следовательно, координаты ее центра , а радиус равен 5.
На рисунке видно, что необходимо найти координаты точек и (абсциссы данных точек).
Точки и лежат на окружности, поэтому их координаты удовлетворяют уравнению этой окружности. Для этих точек известно, что их ординаты равны 3. Получаем систему уравнений:
или
Таким образом, координаты точки , а координаты точки .
Ответ: , .
Напишите уравнение окружности, проходящей через две заданные точки , , если известно, что центр окружности лежит на оси ординат.
Дано:, , (см. Рис. 3).
Найти: уравнение окружности.
Рис. 3. Иллюстрация к задаче
Решение
Уравнение данной окружности будет иметь следующий вид:
Нам необходимо найти и .
1-й способ:
Так как окружность проходит через точки и , то их координаты удовлетворяют уравнению окружности. Подставляем эти координаты в уравнение и получаем систему уравнений:
Правые части данных уравнений равны, поэтому равны и левые части:
interneturok.ru
Уравнение окружности
Пусть
окружность имеет радиус 
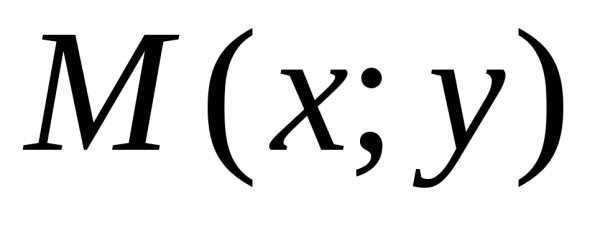 лежит на окружности тогда и только
тогда, когда модуль вектора
лежит на окружности тогда и только
тогда, когда модуль вектора равен
равен ,
то есть.
Последнее равенство выполнено тогда и
только тогда, когда
,
то есть.
Последнее равенство выполнено тогда и
только тогда, когда(1)
Уравнение (1) и является искомым уравнением окружности.
Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору
Пусть
прямая проходит через точку перпендикулярно вектору 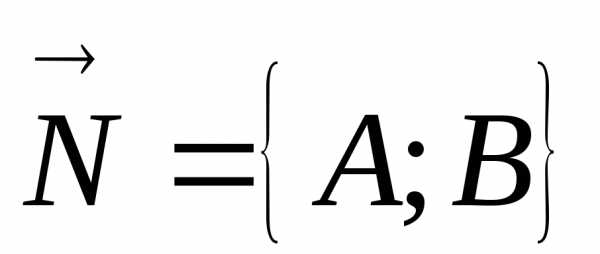 .
.

Точка 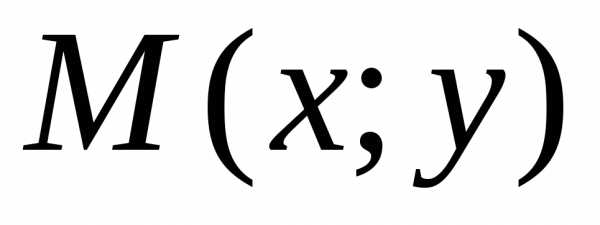 лежит на прямой тогда и только тогда,
когда векторы
лежит на прямой тогда и только тогда,
когда векторы 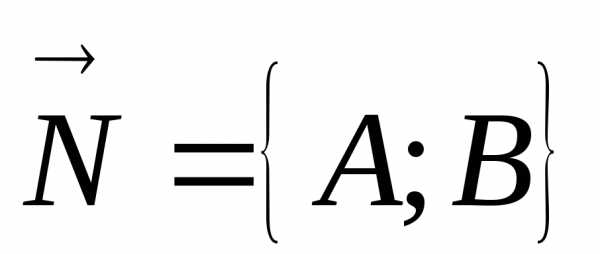 иперпендикулярны. Векторы
иперпендикулярны. Векторы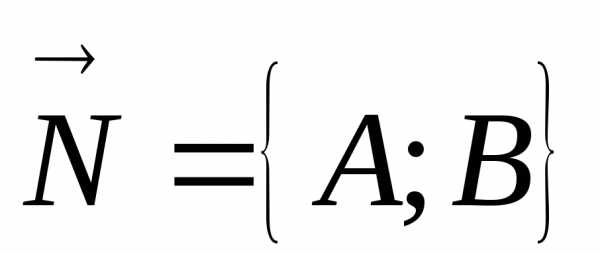 иперпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю, то есть
иперпендикулярны тогда и только тогда,
когда их скалярное произведение равно
нулю, то есть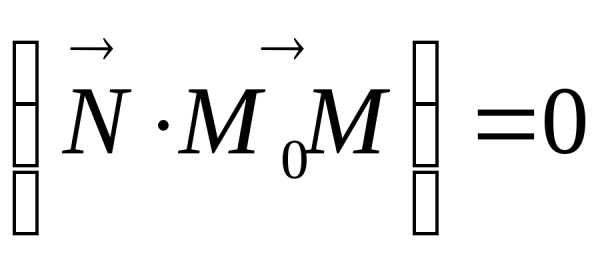 .
Используя формулу вычисления скалярного
произведения векторов, заданных своими
координатами, уравнение искомой прямой
записываем в виде
.
Используя формулу вычисления скалярного
произведения векторов, заданных своими
координатами, уравнение искомой прямой
записываем в виде
(2)
Рассмотрим пример. Найти уравнение прямой, проходящей через
середину отрезка АВ перпендикулярно этому отрезку если координаты точек соответственно равны А(1;6), В(5;4).
Будем
рассуждать следующим образом. Чтобы
найти уравнение прямой мы должны знать
точку, через которую эта прямая проходит,
и вектор перпендикулярный этой прямой.
Вектором, перпендикулярным данной
прямой, будет вектор
,
поскольку, по условию задачи, прямая
перпендикулярна отрезку АВ. Точкуопределим
из условия, что прямая проходит через
середину АВ. Имеем
.
Таким образом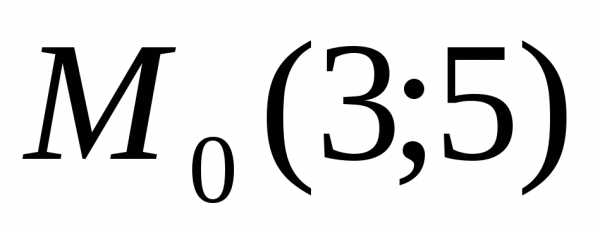 и уравнение примет вид.
и уравнение примет вид.
Выясним вопрос, проходит ли эта прямая через точку М(7;3).
Имеем , значит, эта прямая не проходит через указанную точку.
Уравнение прямой, проходящей через данную точку, параллельно данному вектору
Пусть
прямая проходит через точку параллельно вектору 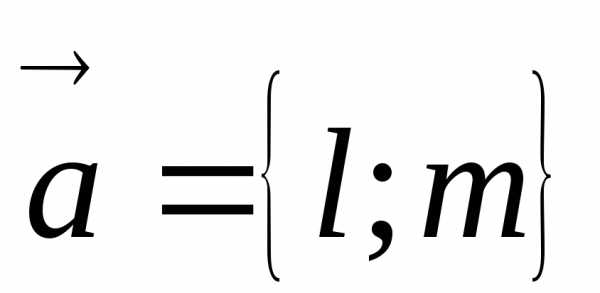 .
.
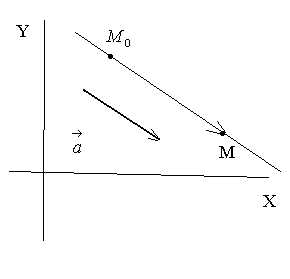
Точка  лежит на прямой тогда и только тогда,
когда векторы
иколинеарны. Векторы
лежит на прямой тогда и только тогда,
когда векторы
иколинеарны. Векторы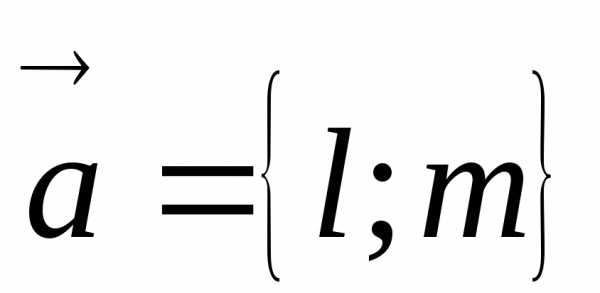 иколинеарны тогда и только тогда, когда
их координаты пропорциональны, то есть
иколинеарны тогда и только тогда, когда
их координаты пропорциональны, то есть
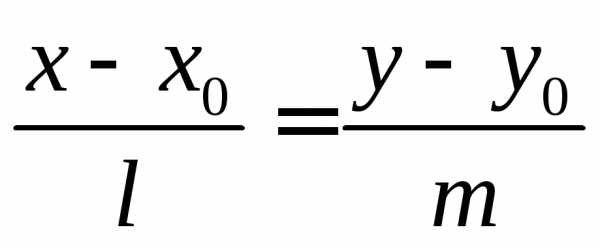 (3)
(3)
Полученное уравнение и является уравнением искомой прямой.
Уравнение (3) представим в виде
,
где  принимает любые значения.
принимает любые значения.
Следовательно, можем записать
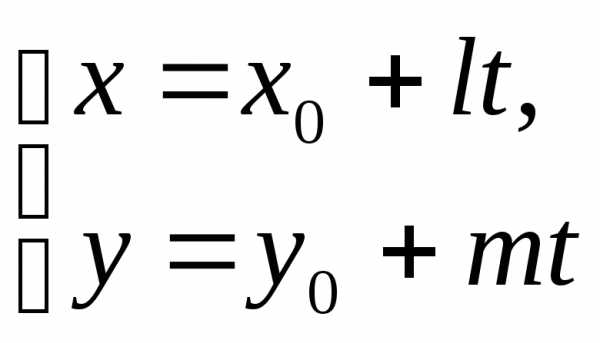 ,
где
(4)
,
где
(4)
Система уравнений (4) называется параметрическими уравнениями прямой.
Рассмотрим
пример. Найти
уравнение прямой, проходящей через
точки
.
Мы можем построить уравнение прямой,
если знаем точку и параллельный или
перпендикулярный ей вектор. Точек в
наличии целых две. Но если две точки
лежат на прямой, то вектор, их соединяющий
будет параллелен этой прямой. Поэтому
воспользуемся уравнением (3), взяв в
качестве вектора 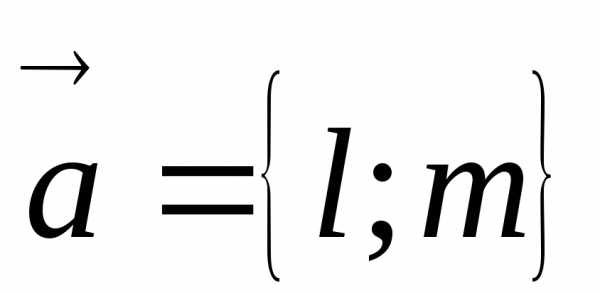 вектор.
Получаем
вектор.
Получаем
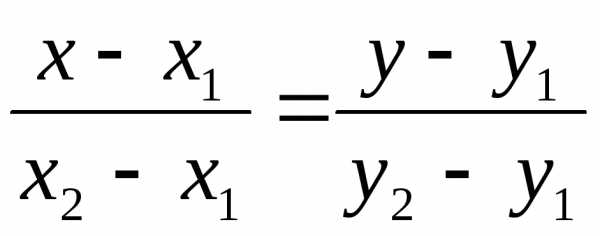 (5)
(5)
Уравнение (5) называется уравнением прямой, проходящей через две данные точки.
Общее уравнение прямой
Определение. Общим уравнением линии первого порядка на плоскости называется уравнение вида , где.
Теорема. Всякая прямая на плоскости может быть задана в виде уравнения линии первого порядка, и всякое уравнение линии первого порядка является уравнением некоторой прямой на плоскости.
Первая
часть этой теоремы доказывается просто.
На всякой прямой можно указать некоторую
точку
перпендикулярный
ей вектор 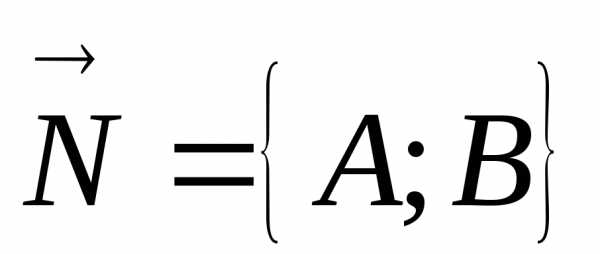 .
Тогда, согласно (2), уравнение такой
прямой имеет вид.
Обозначим.
Тогда уравнение примет вид
.
.
Тогда, согласно (2), уравнение такой
прямой имеет вид.
Обозначим.
Тогда уравнение примет вид
.
Теперь
перейдем ко второй части теоремы. Пусть
имеется уравнение ,
где.
Будем считать для определенности .
.
Перепишем уравнение в виде:
;
;
.
Рассмотрим
на плоскости точку
,
где.
Тогда полученное уравнение имеет вид
,
и является уравнением прямой, проходящей
через точку
перпендикулярно вектору  .
Теорема доказана.
.
Теорема доказана.
В процессе доказательства теоремы мы попутно доказали
Утверждение. Если имеется уравнение прямой вида
,
то вектор 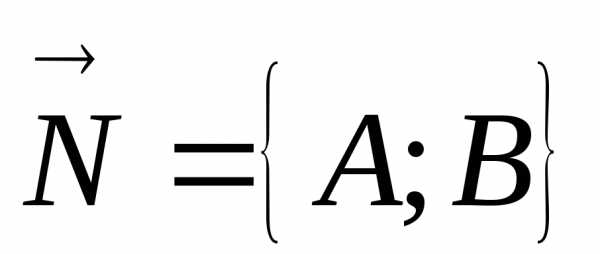 перпендикулярен данной прямой.
перпендикулярен данной прямой.
Уравнение вида называется общим уравнением прямой на плоскости.
Далее выведем формулу вычисления расстояния от произвольной точки плоскости до прямой, заданной общим уравнением.
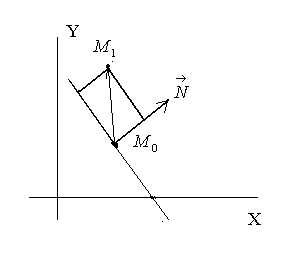
Пусть имеется прямая и точка. Требуется определить расстояние от указанной точки до прямой.
Рассмотрим
произвольную точку
на прямой. Имеем.
Расстояние от точки
от точки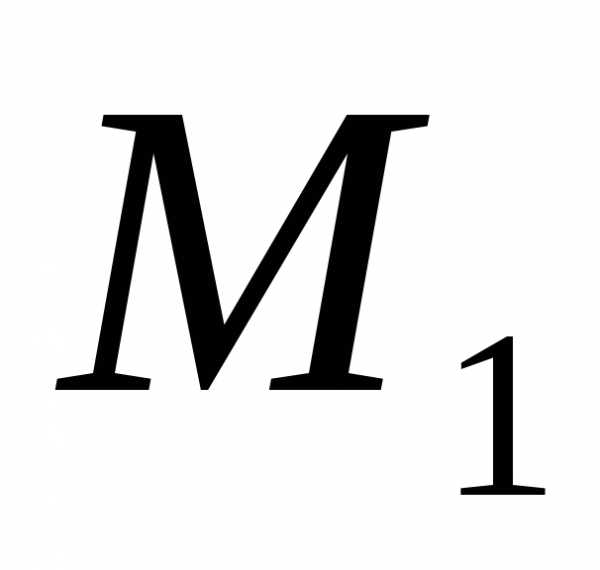 до прямой равно модулю проекции векторана вектор
до прямой равно модулю проекции векторана вектор 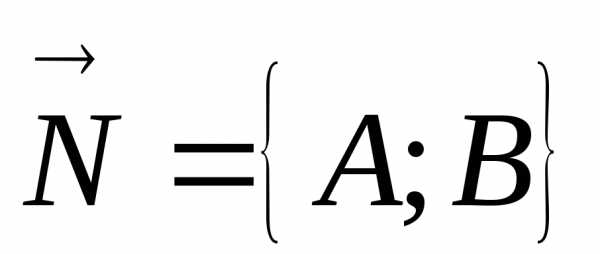 ,
перпендикулярный данной прямой. Имеем
,
перпендикулярный данной прямой. Имеем
,
преобразуя, получаем формулу:
.
Пусть даны две прямые, заданные общими уравнениями
,
. Тогда векторы 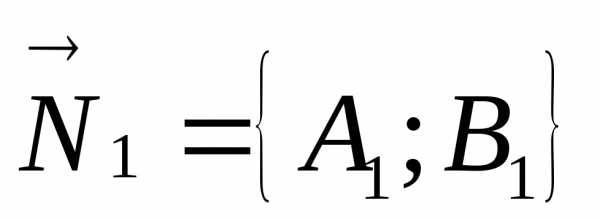
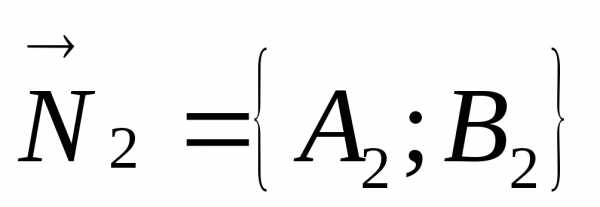 перпендикулярны первой и второй прямой
соответственно. Угол
перпендикулярны первой и второй прямой
соответственно. Угол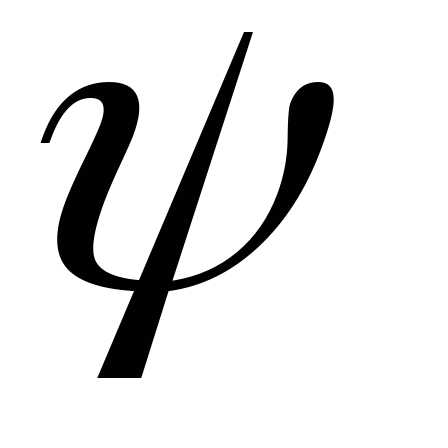 между прямыми равен углу между векторами
между прямыми равен углу между векторами ,
,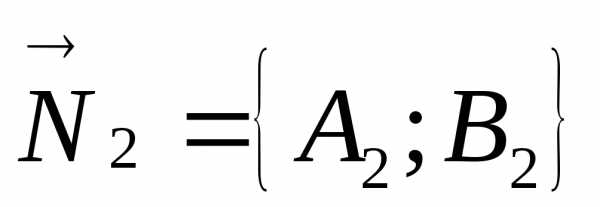 .
.
Тогда формула для определения угла между прямыми имеет вид:
.
Условие перпендикулярности прямых имеет вид:
.
Прямые
параллельны или совпадают тогда и только
тогда, когда векторы 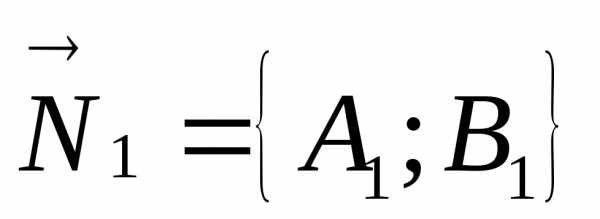
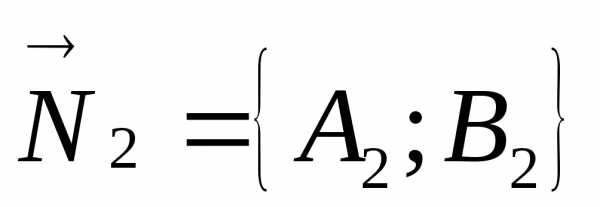 колинеарны. При этомусловие
совпадения прямых имеет вид:
колинеарны. При этомусловие
совпадения прямых имеет вид: 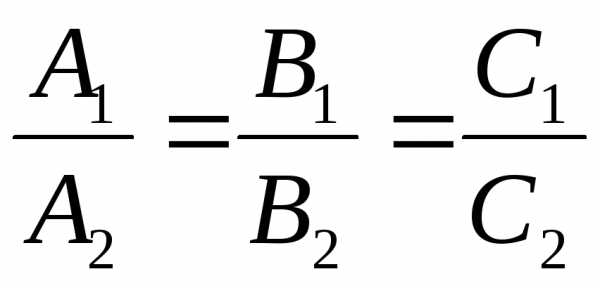 ,
,
а
условие отсутствия пересечения
записывается в виде: 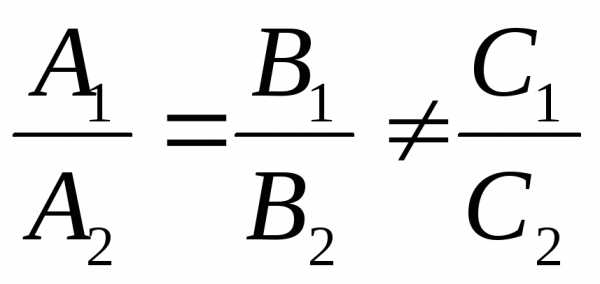 .
Последние два условия докажите
самостоятельно.
.
Последние два условия докажите
самостоятельно.
Исследуем характер поведения прямой по ее общему уравнению.
Пусть
дано общее уравнение прямой
.
Если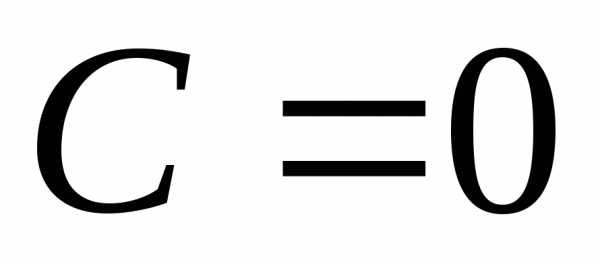 ,
то прямая проходит через начало координат.
,
то прямая проходит через начало координат.
Рассмотрим случай, когда ни один из коэффициентов не равен нулю . Уравнение перепишем в виде:
,
 ,
,
Где
.
Выясним смысл параметров 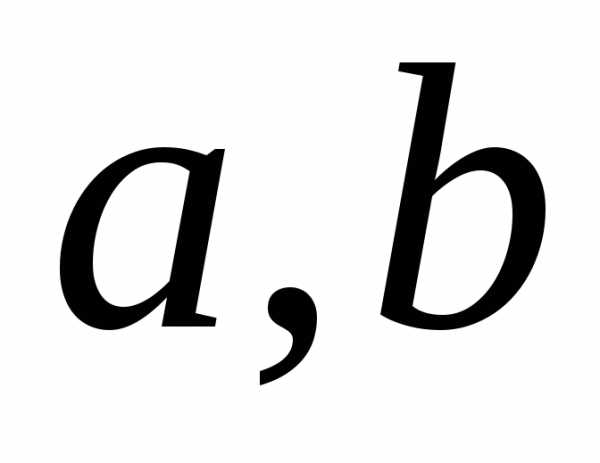 .
Найдем точки пересечения прямой с осями
координат. При
.
Найдем точки пересечения прямой с осями
координат. При имеем
имеем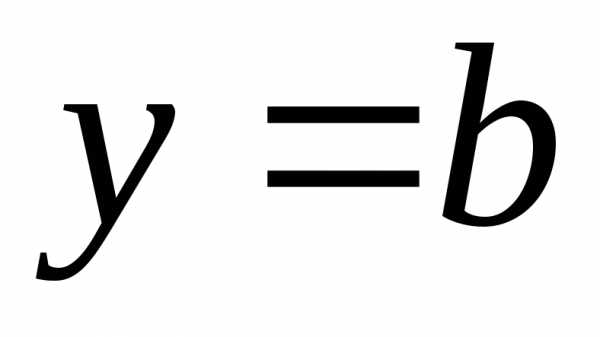 ,
а при
,
а при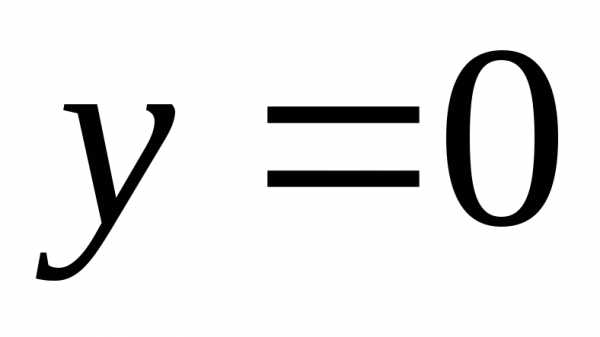 имеем
имеем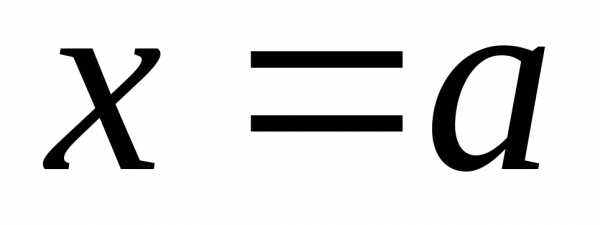 .
То есть
.
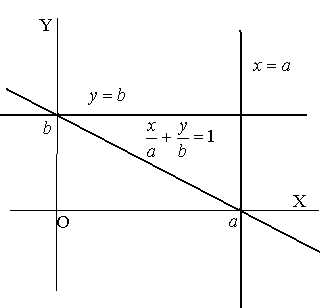
То есть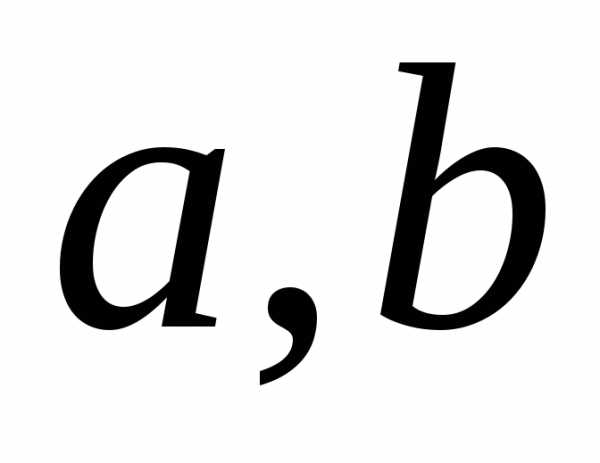 — это отрезки, которые отсекает прямая
на координатных осях.Поэтому
уравнение
— это отрезки, которые отсекает прямая
на координатных осях.Поэтому
уравнение 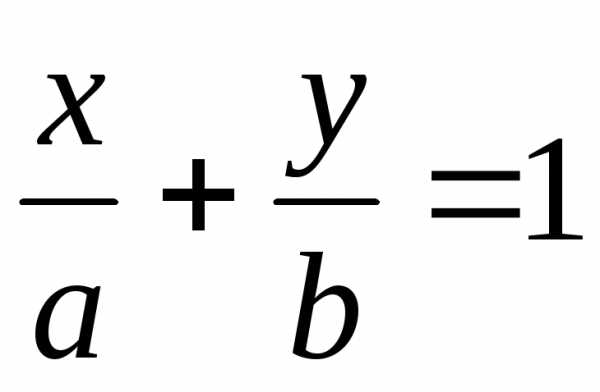 называется
уравнением прямой в отрезках.
называется
уравнением прямой в отрезках.
В
случае 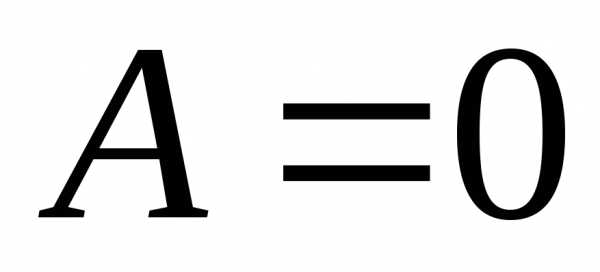 имеем
.
То есть прямая будет параллельна оси
имеем
.
То есть прямая будет параллельна оси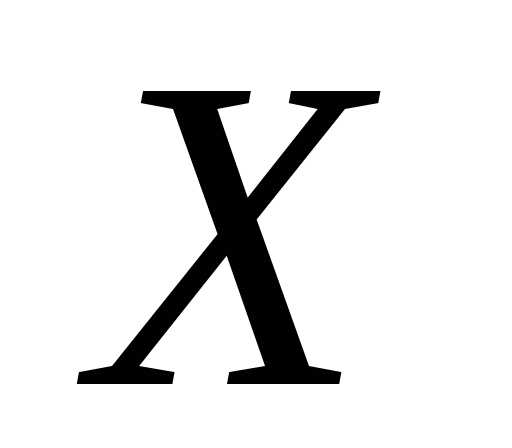 .
В случае
.
В случае 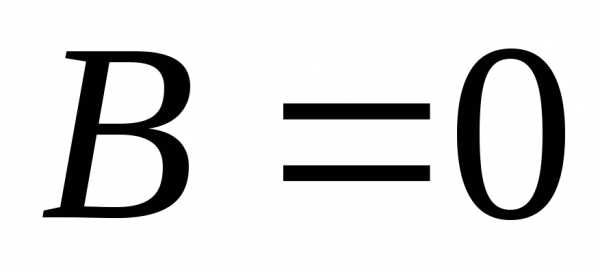 имеем
.
То есть прямая будет параллельна оси
имеем
.
То есть прямая будет параллельна оси .
.
Напомним,
что угловым
коэффициентом прямой  называется тангенс угла наклона этой
прямой к оси
называется тангенс угла наклона этой
прямой к оси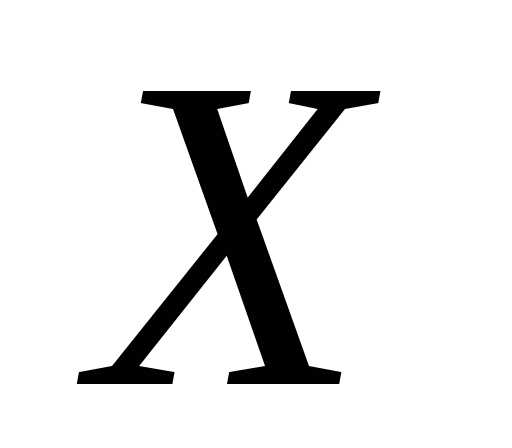 .
Пусть прямая отсекает на оси
.
Пусть прямая отсекает на оси отрезок
отрезок и имеет угловой коэффициент
и имеет угловой коэффициент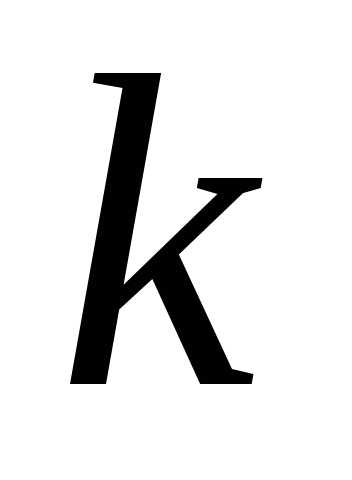 .
Пусть точка
.
Пусть точка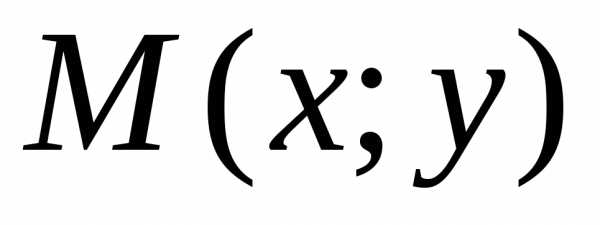 лежит на данной
лежит на данной
прямой.
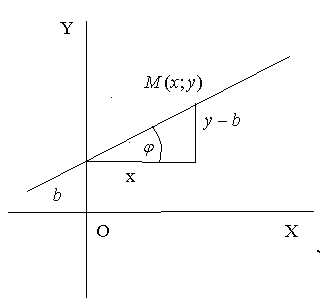
Тогда 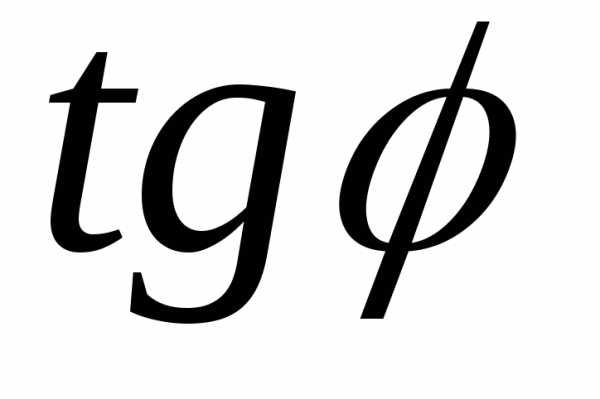 =
=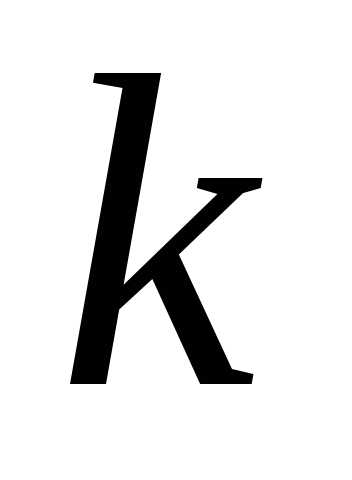 =
=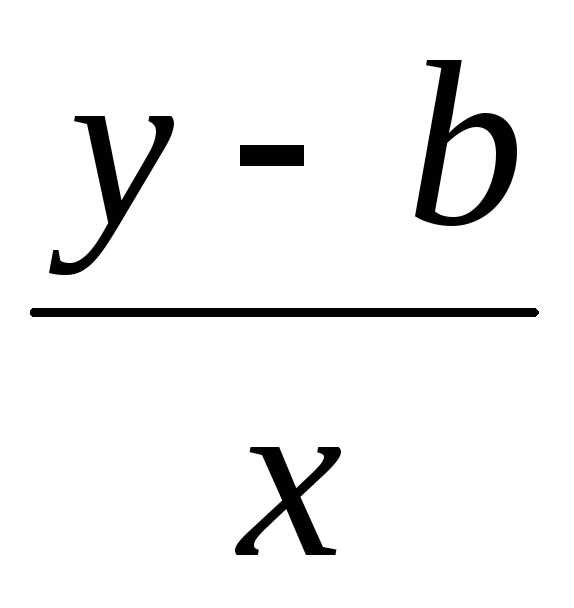 .
И уравнение прямой запишется в виде
.
И уравнение прямой запишется в виде
.
Пусть
прямая проходит через точку
и имеет угловой коэффициент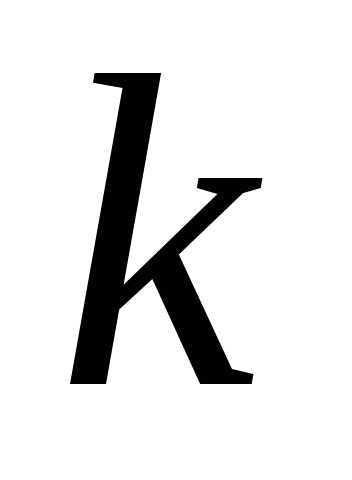 .
Пусть точка
.
Пусть точка лежит на этой прямой.
лежит на этой прямой.
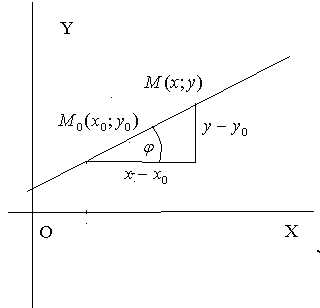
Тогда 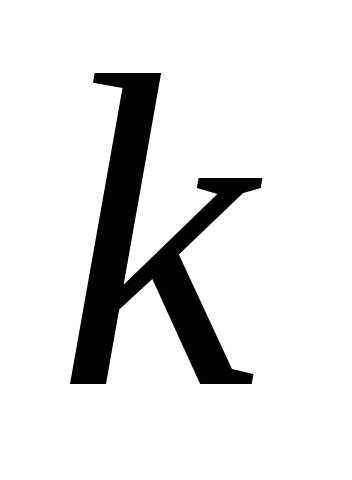 =.
=.
Полученное уравнение называется уравнением прямой, проходящей через данную точку с заданным угловым коэффициентом.
Пусть
даны две прямые
,.
Обозначим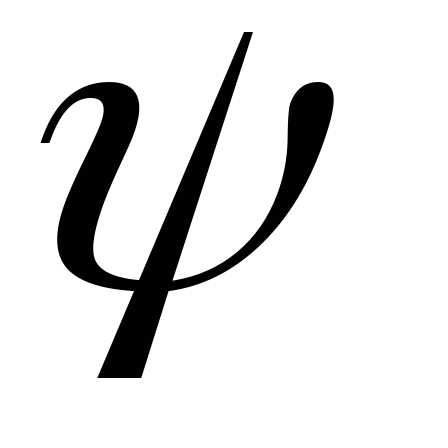 — угол между ними. Пусть
— угол между ними. Пусть ,
,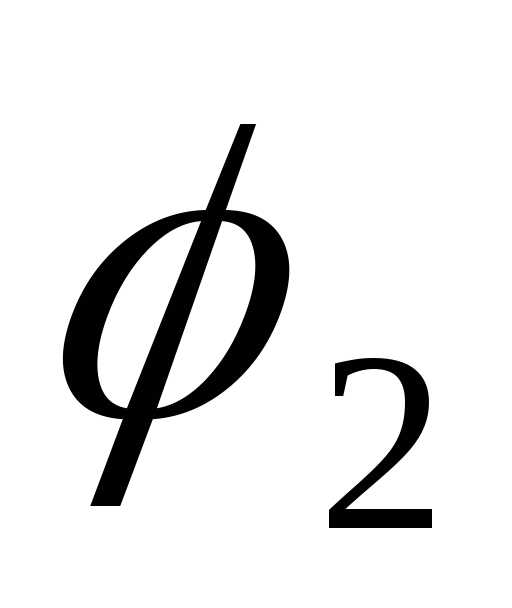 углы наклона к оси Х соответствующих
прямых
углы наклона к оси Х соответствующих
прямых
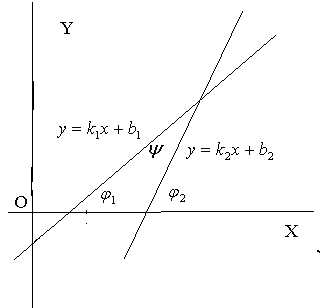
Тогда 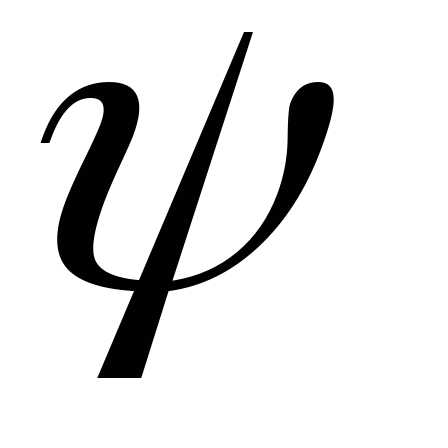 =
=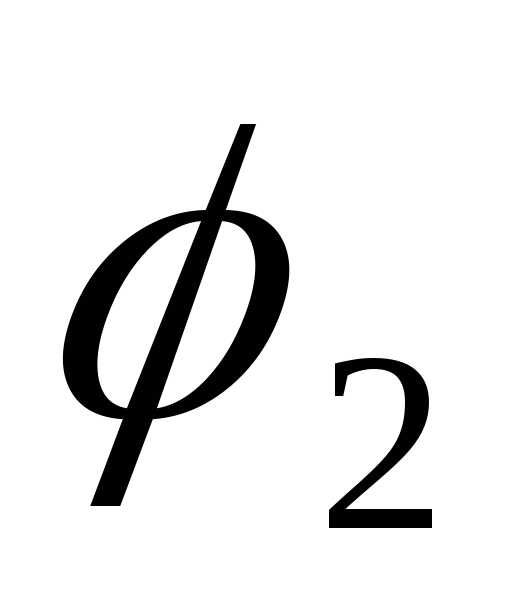
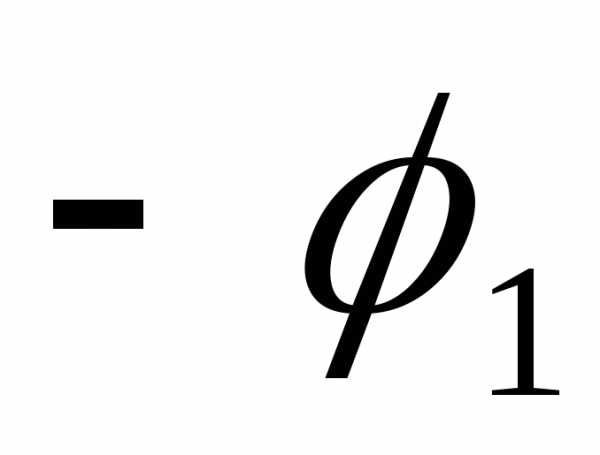 ,.
,.
Тогда
условие параллельности прямых имеет
вид 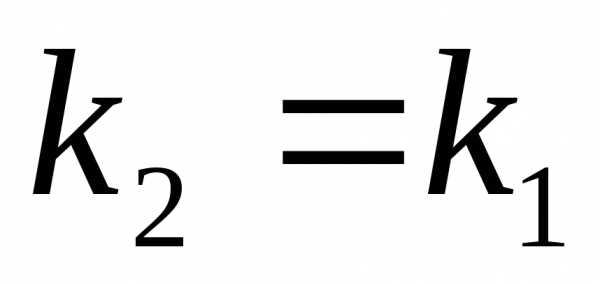 ,
а условие перпендикулярности
,
а условие перпендикулярности
В заключение рассмотрим две задачи.
Задача. Вершины треугольника АВС имеют координаты: A(4;2), B(10;10), C(20;14).
Найти: а) уравнение и длину медианы, проведенной из вершины А;
б) уравнение и длину высоты, проведенной из вершины А;
в) уравнение биссектрисы, проведенной из вершины А;
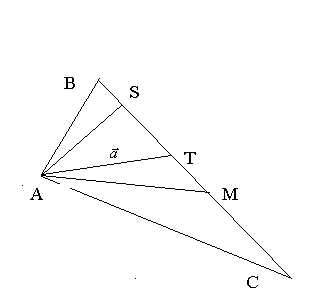
Определим уравнение медианы АМ.
Точка М() середина отрезка ВС.
Тогда , . Следовательно, точка М имеет координаты M(15;17). Уравнение медианы на языке аналитической геометрии это уравнение прямой, проходящей через точку А(4;2) параллельно вектору ={11;15}. Тогда уравнение медианы имеет вид. Длина медианы АМ=.
Уравнение высоты AS — это уравнение прямой, проходящей через точку А(4;2) перпендикулярно вектору ={10;4}. Тогда уравнение высоты имеет вид 10(x-4)+4(y-2)=0, 5x+2y-24=0.
Длина высоты — это расстояние от точки А(4;2) до прямой ВС. Данная прямая проходит через точку B(10;10) параллельно вектору ={10;4}. Ее уравнение имеет вид, 2x-5y+30=0. Расстояние AS от точки А(4;2) до прямой ВС, следовательно, равно AS=.
Для определения уравнения биссектрисы найдем вектор параллельный этой прямой. Для этого воспользуемся свойством диагонали ромба. Если от точки А отложить единичные векторы одинаково направленные с векторамии, то вектор, равный их сумме, будет параллелен биссектрисе. Тогда имеем=+.
={6;8}, , ={16,12}, .
Тогда =В качестве направляющего вектора искомой прямой может служить вектор={1;1}, коллинеарный данному. Тогда уравнение искомой прямой имеет видилиx-y-2=0.
Задача. Река протекает по прямой линии, проходящей через точки А(4;3) и В(20;11). В точке С(4;8) живет Красная Шапочка, а в точке D(13;20) ее бабушка. Каждое утро Красная Шапочка берет пустое ведро из дома, идет на реку, черпает воду и относит ее бабушке. Найти самую короткую дорогу для Красной Шапочки.
Найдем точку Е, симметричную бабушке, относительно реки.
Для этого сначала найдем уравнение прямой, по которой течет река. Это уравнение можно рассматривать, как уравнение прямой, проходящей через точку А(4;3) параллельно вектору . Тогда уравнение прямой АВ имеет вид.
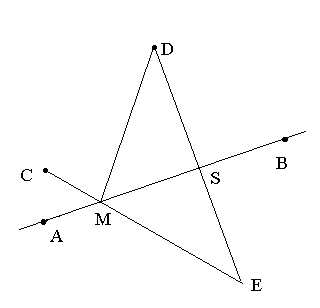
Далее
найдем уравнение прямой DE,
проходящей через точку D
перпендикулярно АВ. Его можно рассматривать,
как уравнение прямой, проходящей через
точку D,
перпендикулярно вектору  .
Имеем
.
Имеем
.
Теперь найдем точку S — проекцию точки D на прямую АВ, как пересечение прямых АВ и DE. Имеем систему уравнений
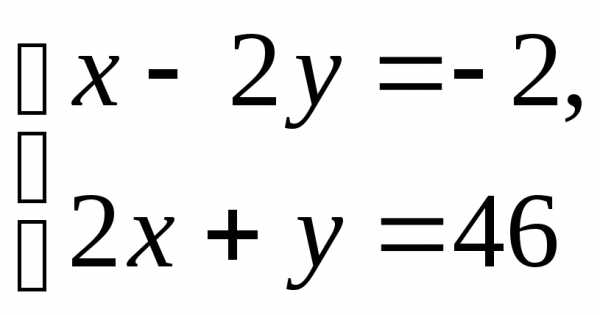 .
.
Следовательно, точка S имеет координаты S(18;10).
Поскольку S середина отрезка DE, то .
Аналогично .
Следовательно, точка Е имеет координаты Е(23;0).
Найдем уравнение прямой СЕ, зная координаты двух точек этой прямой
.
Точку М найдем как пересечение прямых АВ и СЕ.
Имеем систему уравнений
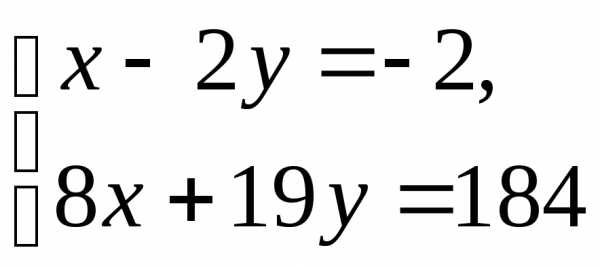 .
.
Следовательно,
точка М имеет координаты 
 .
.
Тема 2. Понятие об уравнении поверхности в пространстве. Уравнение сферы. Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору. Общее уравнение плоскости и его исследование Условие параллельности двух плоскостей. Расстояние от точки до плоскости. Понятие об уравнении линии. Прямая линия в пространстве. Канонические и параметрические уравнения прямой в пространстве. Уравнения прямой, проходящей через две данные точки. Условия параллельности и перпендикулярности прямой и плоскости.
Вначале, дадим определение понятия уравнения поверхности в пространстве.
Пусть
в
пространстве 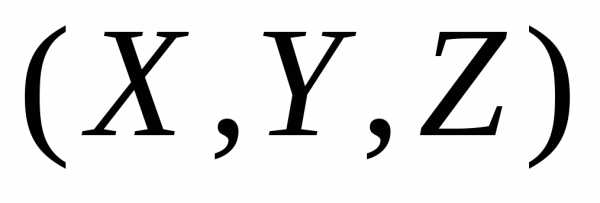 задана некотораяповерхность
задана некотораяповерхность  .
Уравнениеназывается уравнениемповерхности
.
Уравнениеназывается уравнениемповерхности 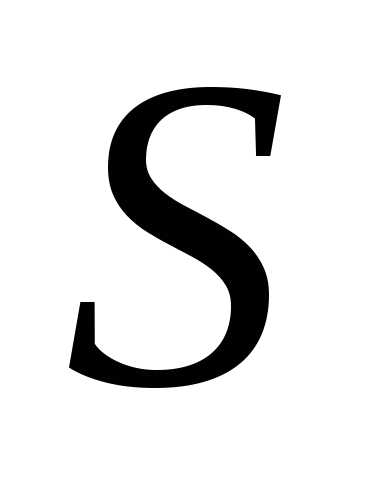 ,
если выполнены два условия:
,
если выполнены два условия:
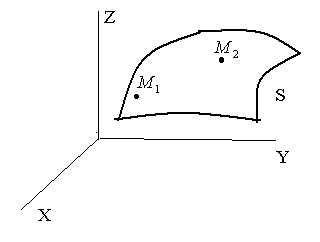
1.для
любой точки 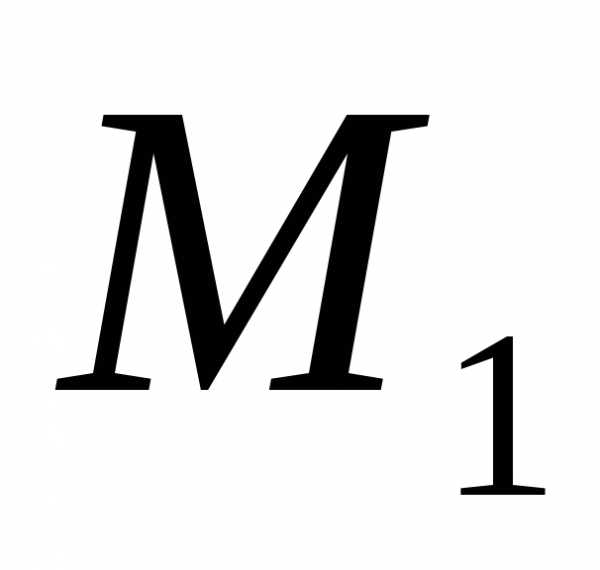 с координатами,
лежащей наповерхности,
выполнено
,
то есть ее координаты удовлетворяют
уравнениюповерхности;
с координатами,
лежащей наповерхности,
выполнено
,
то есть ее координаты удовлетворяют
уравнениюповерхности;
2. любая точка , координаты которой удовлетворяют уравнению, лежит на линии.
studfiles.net
Уравнение окружности | Треугольники
Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид
Доказательство:
1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).
Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).
По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.
По формуле расстояния между точками
откуда
Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.
2. Если пара чисел (xo;yo) удовлетворяет данному уравнению, то
А это значит, что расстояние между точками C(xo;yo) и A(a;b) равно R. Значит, точка C(xo;yo) принадлежит окружности с центром в точке A(a;b) и радиусом R.
Следовательно, данное уравнение фигуры является уравнением окружности.
Что и требовалось доказать.
www.treugolniki.ru
Уравнение окружности и прямой
Уравнение линии на плоскости
Введем для начала понятие уравнения линии в двумерной системе координат. Пусть в декартовой системе координат построена произвольная линия $L$ (Рис. 1).
Рисунок 1. Произвольная линия в системе координат
Определение 1
Уравнение с двумя переменными $x$ и $y$ называется уравнением линии $L$, если этому уравнению удовлетворяют координаты любой точки, принадлежащей линии $L$ и не удовлетворяет ни одна точка, не принадлежащая линии $L.$
Уравнение окружности
Выведем уравнение окружности в декартовой системе координат $xOy$. Пусть центр окружности $C$ имеет координаты $(x_0,y_0)$, а радиус окружности равен $r$. Пусть точка $M$ с координатами $(x,y)$ — произвольная точка этой окружности (рис. 2).
Рисунок 2. Окружность в декартовой системе координат
Расстояние от центра окружности до точки $M$ вычисляется следующим образом
Но, так как $M$ лежит на окружности, то получаем $CM=r$. Тогда получим следующее
Уравнение (1) и есть уравнение окружности с центром в точке $(x_0,y_0)$ и радиусом $r$.
В частности, если центр окружности совпадает с началом координат. То уравнение окружности имеет вид
Уравнение прямой.
Выведем уравнение прямой $l$ в декартовой системе координат $xOy$. Пусть точки $A$ и $B$ имеют координаты $\left\{x_1,\ y_1\right\}$ и $\{x_2,\ y_2\}$ соответственно, причем точки $A$ и $B$ выбраны так, что прямая $l$ — серединный перпендикуляр к отрезку $AB$. Выберем произвольную точку $M=\{x,y\}$, принадлежащую прямой $l$ (рис. 3).
Рисунок 3. Прямая в декартовой системе координат
Так как прямая $l$ — серединный перпендикуляр к отрезку $AB$, то точка $M$ равноудалена от концов этого отрезка, то есть $AM=BM$.
Найдем длины данных сторон по формуле расстояния между точками:
Следовательно
Обозначим через $a=2\left(x_1-x_2\right),\ b=2\left(y_1-y_2\right),\ c={x_2}^2+{y_2}^2-{x_1}^2-{y_1}^2$, Получаем, что уравнение прямой в декартовой системе координат имеет следующий вид:
Замечание 1
Здесь можно выделить два частных случая для уравнения прямой. Пусть прямая $l$ проходит через точку $M=\{x_0,y_0\}$, тогда
Если прямая $l$ параллельна оси $Ox$, то она имеет вид
\[y=y_0\]Если прямая $l$ параллельна оси $Oy$, то она имеет вид
\[x=x_0\]
Пример задачи на нахождение уравнений линий в декартовой системе координат
Пример 1
Найти уравнение окружности с центром в точке $(2,\ 4)$. Проходящей через начало координат и прямую, параллельную оси $Ox,$ проходящей через её центр.
Решение.
Найдем сначала уравнение данной окружности. Для этого будем использовать общее уравнение окружности (выведенное выше). Так как центр окружности лежит в точке $(2,\ 4)$, получим
\[{(x-2)}^2+{(y-4)}^2=r^2\]Найдем радиус окружности как расстояние от точки $(2,\ 4)$ до точки $(0,0)$
\[r=\sqrt{{(2-0)}^2+{(4-0)}^2}=\sqrt{20}=2\sqrt{5}\]Получаем, уравнение окружности имеет вид:
\[{(x-2)}^2+{(y-4)}^2=20\]Найдем теперь уравнение окружности, используя частный случай 1. Получим
\[y=4\]spravochnick.ru
Окружность. Уравнение окружности
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.Решение.
Обратимся к формуле уравнения окружности:
R2 = (x-a)2 + (y-b)2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2)2 + (y — (-3))2 = 42
или
(x — 2)2 + (y + 3)2 = 16.
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2)2 + (y + 3)2 = 16.Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение (x — 2)2 + (y + 3)2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
(x — 2)2 + (y + 3)2 = 16
(2 — 2)2 + (3 + 3)2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Содержание главы:Площадь геометрической фигуры | Описание курса | Задачи про окружность
profmeter.com.ua
7_54-63
Выделяют четыре основных типа кривых второго порядка: окружность, эллипс, гипербола и парабола.
1. Окружность
Определение. Окружностью называется множество, состоящее из всех точек плоскости, находящихся на равном расстоянии R от фиксированной точки С.
Число R называется радиусом окружности, точка С – центром.
Воспользуемся определением окружности для вывода ее уравнения.
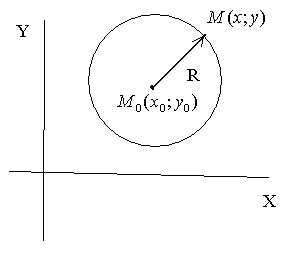
П
Рис. 5
усть точка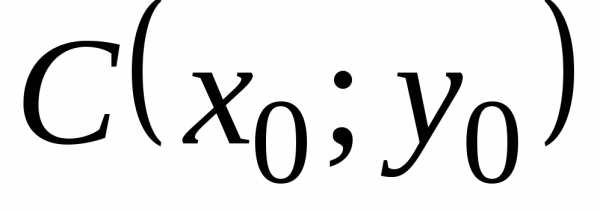 – центр окружности. Точка
– центр окружности. Точка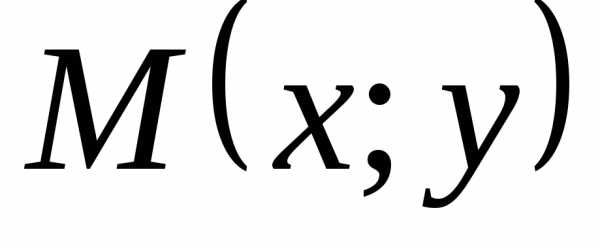 – произвольная точка окружности, а
радиус этой окружности равен
– произвольная точка окружности, а
радиус этой окружности равен .
По определению
.
По определению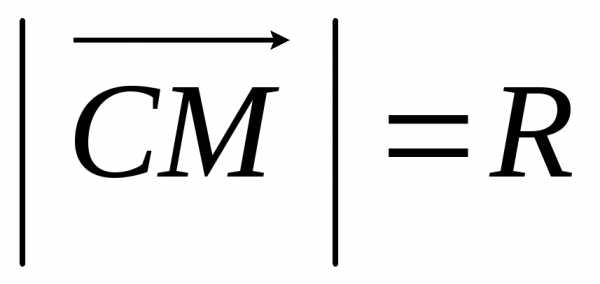 ,
тогда, используя формулу вычисления
длины вектора
,
тогда, используя формулу вычисления
длины вектора ,
имеем,
тогда
,
имеем,
тогда .
Возведем обе части равенства в квадрат.
Тогда уравнение окружности с центром
в точке 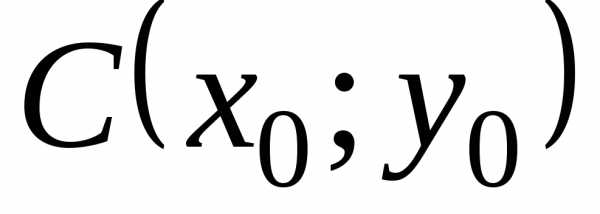 и радиусомR имеет вид:
и радиусомR имеет вид:
каноническое уравнение окружности
В частности, уравнение окружности с центром в начале координат и радиусом R имеет вид: .
Пример
Составить
каноническое уравнение окружности,
центр которой находится в точке  ,
а диаметр
,
а диаметр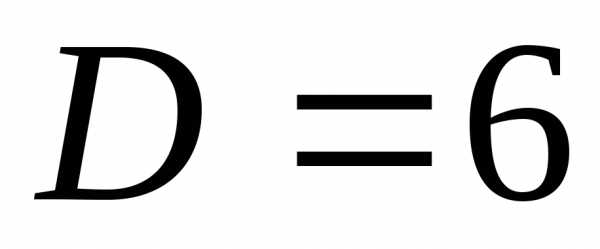 .
.
Решение:
Найдем радиус 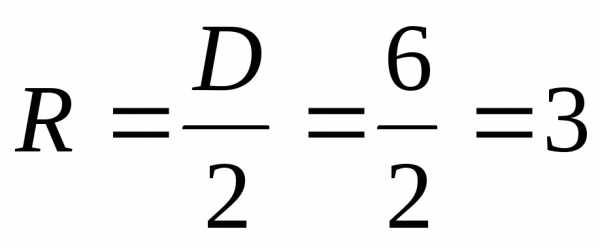 ,
тогда уравнение окружности имеет вид
,
тогда уравнение окружности имеет вид
или .
Пример
Построить окружность по заданному уравнению . Привести каноническое уравнение к общему виду.
Решение:
П
Рис. 6
о заданному уравнению определяем, что центр окружности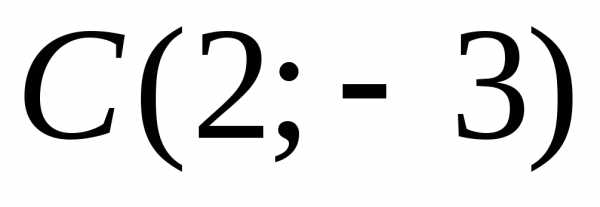 ,
а радиус
,
а радиус .
Теперь преобразуем каноническое
уравнение к общему видуили,
полученное уравнение является общим
уравнением окружности с центром в точке
.
Теперь преобразуем каноническое
уравнение к общему видуили,
полученное уравнение является общим
уравнением окружности с центром в точке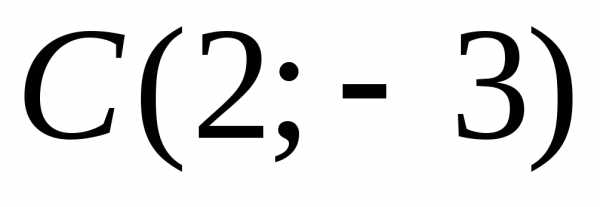 и радиусом
и радиусом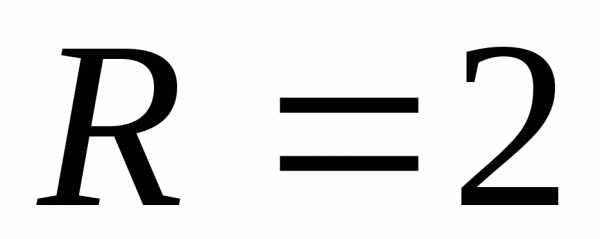 .
.Возможно решение обратной задачи: общее уравнение преобразовать в каноническое.
2. Эллипс
Определение 1. Эллипсом называется множество, состоящее из всех точек плоскости, сумма расстояний от каждой из которых до двух заданных точек плоскости и, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
В случае, когда
фокусы эллипса 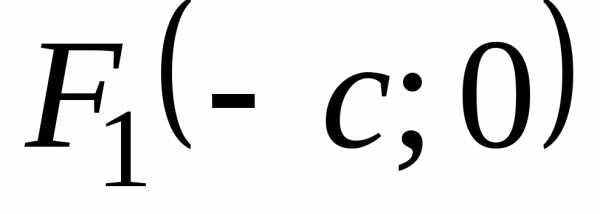 и
и 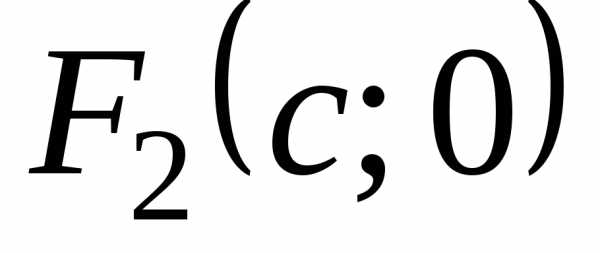 расположены
на оси Ox (или на оси Oy)
симметрично относительно начала
координат, его уравнение называется каноническим и имеет
вид:
расположены
на оси Ox (или на оси Oy)
симметрично относительно начала
координат, его уравнение называется каноническим и имеет
вид:
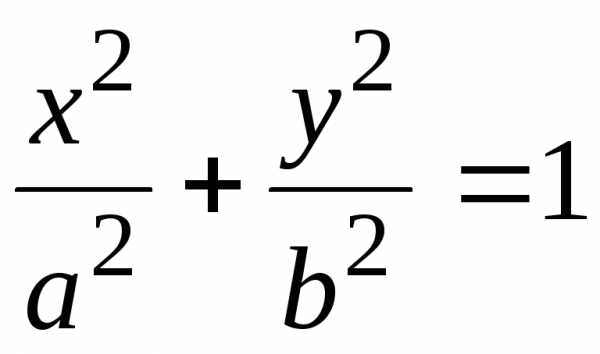 .
.
Обозначим через 2с расстояние между фокусами эллипса. Если a > b (a < b), то фокусы эллипса расположены на оси Ox (на оси Oy) и (cм. рис. 7). Фокусы эллипса всегда лежат на большей оси. ОтрезкиОА и ОВ называются полуосями эллипса. Точки пересечения линии эллипса с осями координат А, В, А1, В1 называются вершинами эллипса. Эллипс имеет две оси симметрии (в случае, если эллипс задается каноническим уравнением, оси симметрии совпадают с осями координат) и центр симметрии (в случае, если эллипс задается каноническим уравнением, центр симметрии совпадает с началом координат).
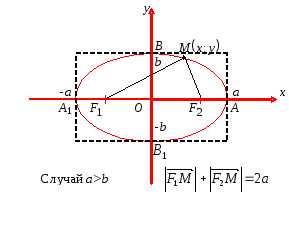
Рис. 7
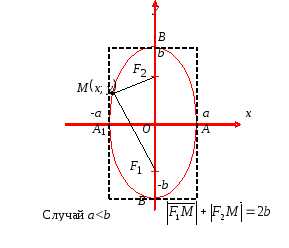
Для количественной оценки формы эллипса введена величина, называемая эксцентриситетом эллипса.
Определение 2. Эксцентриситетом эллипса называется величина, равная отношению расстояния между фокусами к длине его большей оси.
Обозначим эксцентриситет эллипса через . Пусть a > b (a < b). Тогда (). Так как 0< с < a (0 < с < b) , то 0 < < 1. Чем ближе эксцентриситет к единице, тем эллипс более вытянут вдоль большей оси.
3. Гипербола
Определение 1. Гиперболой называется множество, состоящее из всех точек плоскости, модуль разности расстояний от которых до двух фиксированных точек и, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами, и отличная от нуля.
Каноническое уравнение гиперболы имеет вид:
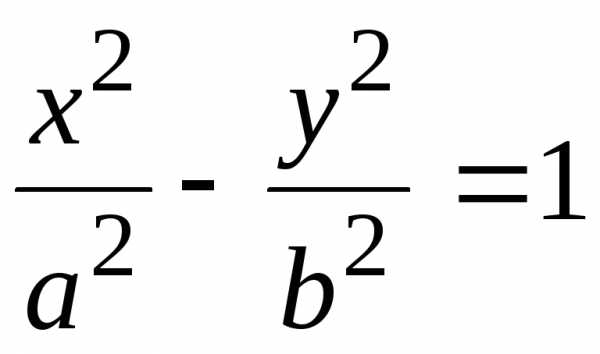 (1)
(1)
(в случае, если
фокусы 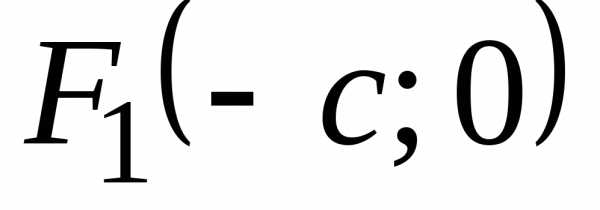 и
и 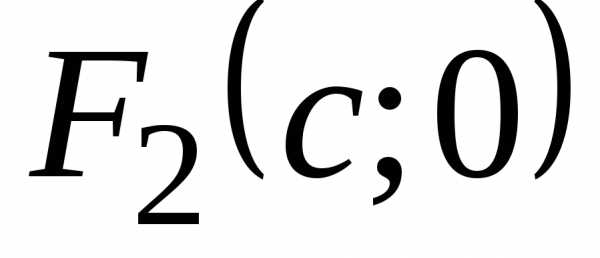 расположены
на оси Ох симметрично относительно начала
координат, см. рис. 8) или
расположены
на оси Ох симметрично относительно начала
координат, см. рис. 8) или
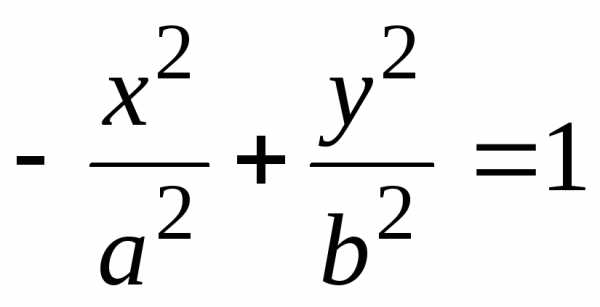 (2)
(2)
(в случае, если
фокусы 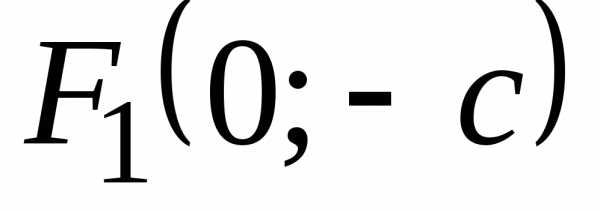 и
и 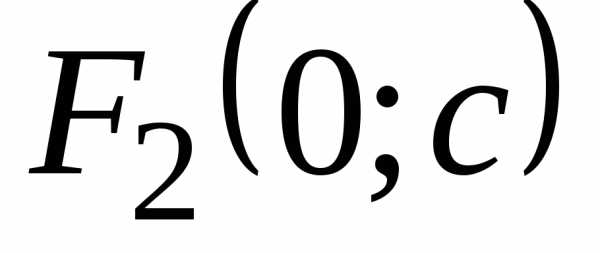 расположены
на оси Оу симметрично
относительно начала координат, см. рис.
9).
расположены
на оси Оу симметрично
относительно начала координат, см. рис.
9).
Гиперболы, заданные уравнениями (1) и (2), называются сопряженными относительно друг друга.
Обозначим через 2с расстояние между фокусами гиперболы. Тогда .
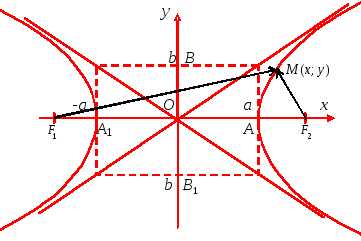
Рис. 8 Рис. 9
Точки А иА1–вершиныгиперболы. ТочкиВиВ1 –вершиныгиперболы.
Прямоугольник,
составленный прямыми 
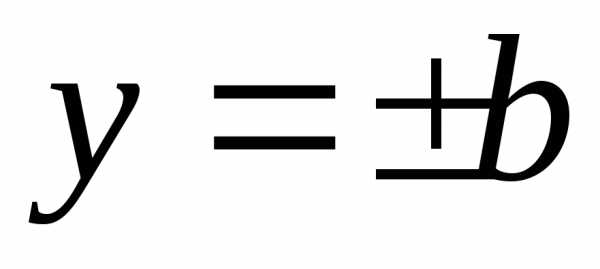 ,
называетсяосновным
прямоугольником гиперболы.
Его диагонали совпадают с прямыми
,
называетсяосновным
прямоугольником гиперболы.
Его диагонали совпадают с прямыми 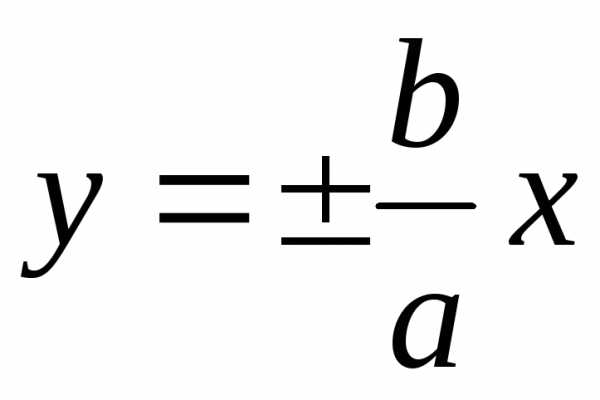 ,
которые являютсяасимптотами гиперболы. Отрезки ОА
= a и OB = b называются полуосями гиперболы. Ось координат, на которой
расположены фокусы гиперболы (и которую
пересекает гипербола) называется действительной,
другая ось координат (с которой у
гиперболы нет общих точек) – мнимой.
,
которые являютсяасимптотами гиперболы. Отрезки ОА
= a и OB = b называются полуосями гиперболы. Ось координат, на которой
расположены фокусы гиперболы (и которую
пересекает гипербола) называется действительной,
другая ось координат (с которой у
гиперболы нет общих точек) – мнимой.
Гипербола называется равносторонней, если длины осей равны 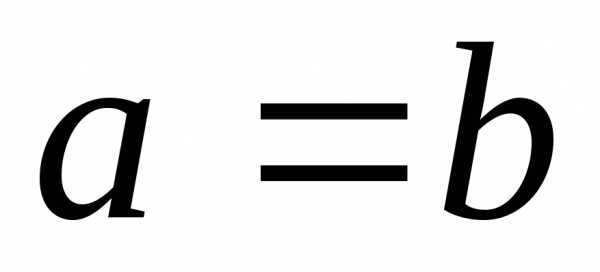 .
.
Форму гиперболы определяет отношение длин основного прямоугольника. Для количественной оценки формы гиперболы, как и в случае эллипса, вводится понятие эксцентриситета.
Определение 2. Эксцентриситетом гиперболы называется величина, равная отношению половины расстояния между фокусами к длине действительной полуоси.
Обозначим эксцентриситет гиперболы через . Для гиперболы, заданной уравнением (1), ; для гиперболы, заданной уравнением (2). Так как 0< а < с и 0 < b < с, то > 1. Чем ближе эксцентриситет к единице, тем основной прямоугольник гиперболы более вытянут вдоль ее оси, соединяющей вершины.
4. Парабола
Определение. Параболой называется множество, состоящее из всех точек на плоскости, для которых расстояние до некоторой фиксированной точки F, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.
На рисунках 10–13 представлены все простейшие случаи расположения параболы и соответствующие им канонические уравнения.
p – параметр, он равен расстоянию между фокусом и директрисой;
точка F – фокус.

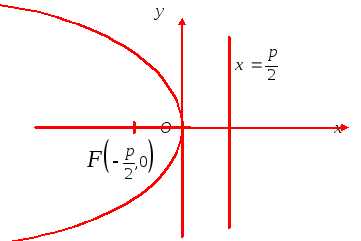
Рис. 10 Рис. 11
На рис. 10 парабола
;
уравнение директрисы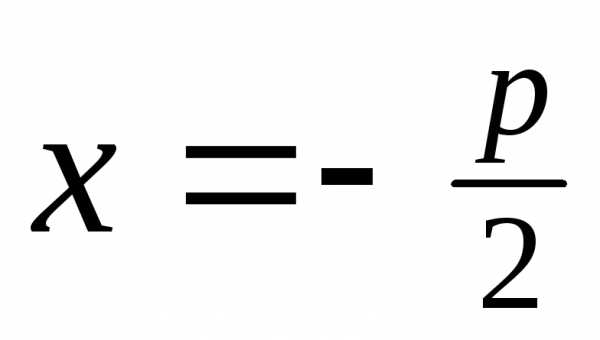 .
.
На рис. 11 парабола
;
уравнение директрисы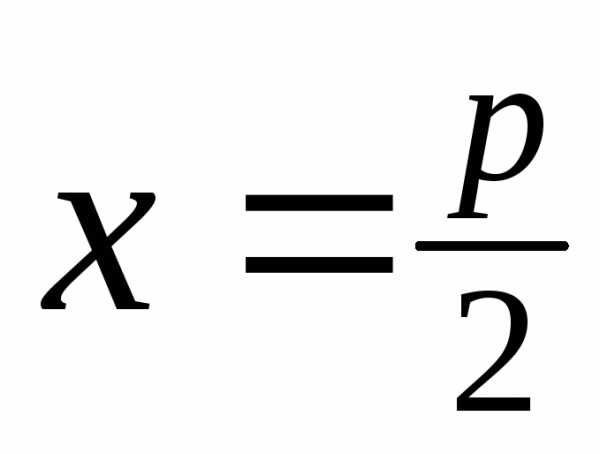 .
.
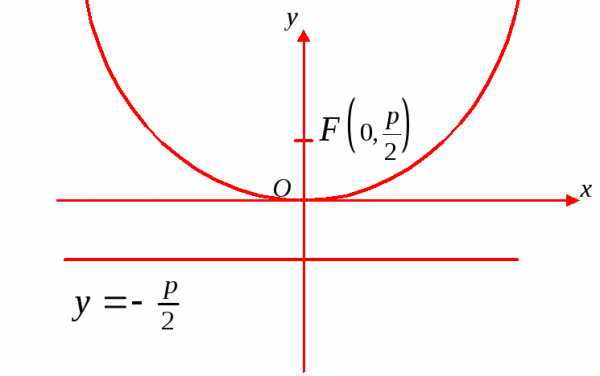
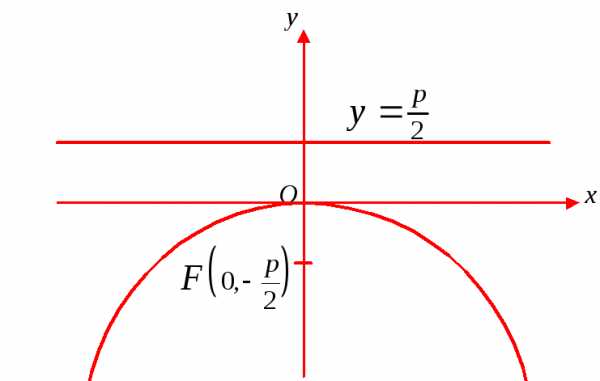
Рис. 12 Рис. 13
На рис. 12 парабола ; уравнение директрисы.
На рис. 13 парабола ; уравнение директрисы.
Пример
По заданному
каноническому уравнению  построить кривую,
найти координаты фокусов.
построить кривую,
найти координаты фокусов.
Решение:
Заданное
уравнение есть уравнение эллипса, где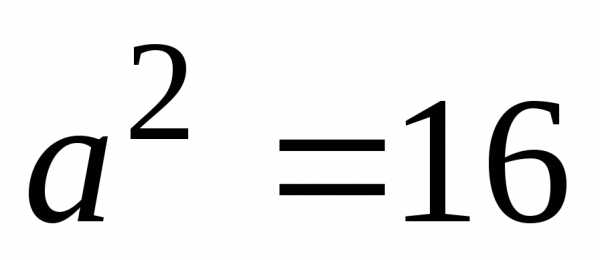 ,
,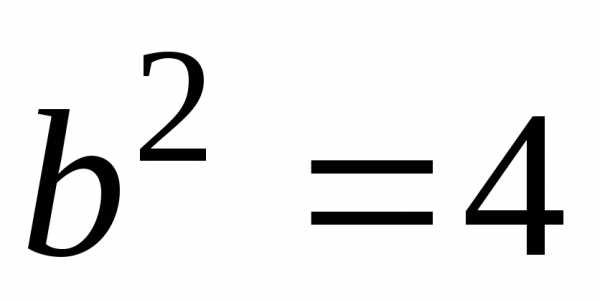 ,
следовательно,
,
следовательно,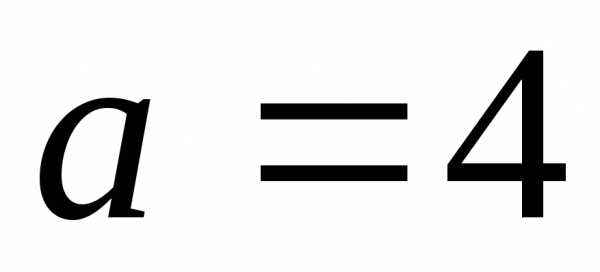 ,
,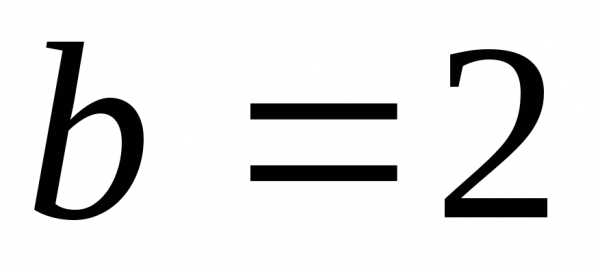 ,
тогда.
,
тогда.
На оси 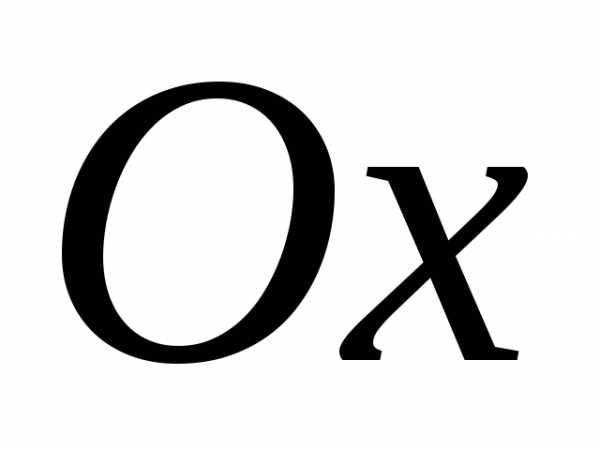 отметим точки
отметим точки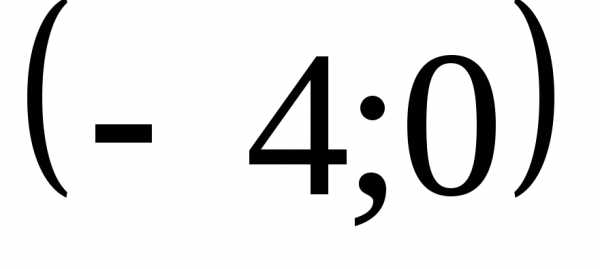 и
и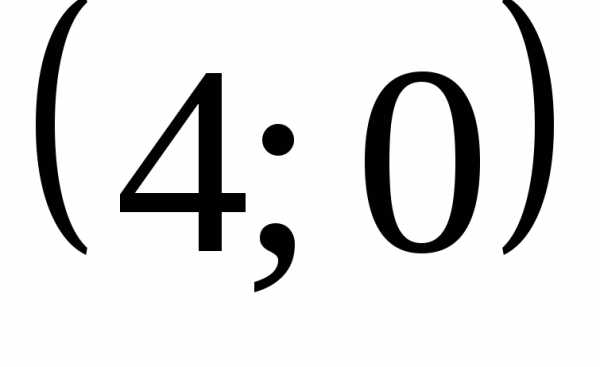 ,
а на оси
,
а на оси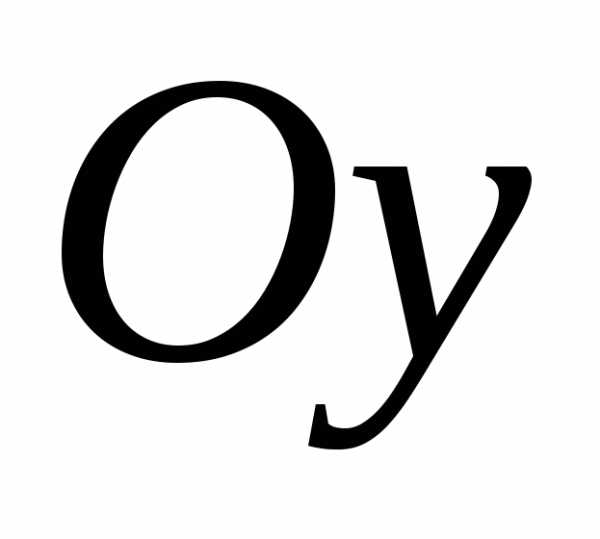 отметим
отметим и
и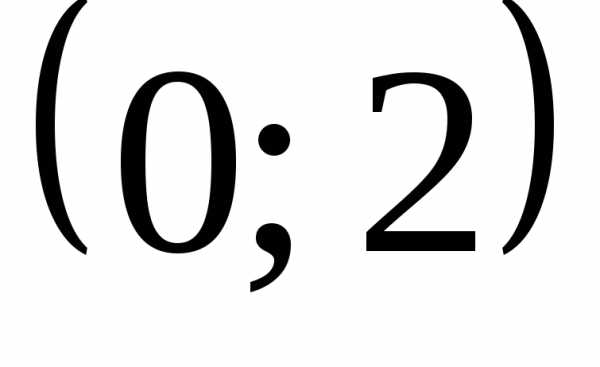 это вершины эллипса.
это вершины эллипса.
Соединим полученные точки плавной линией. Прямоугольных участков быть не должно. Эллипс – это сжатая окружность.
Найдем фокусы
эллипса, так как  ,
то фокусы располагаются на оси
,
то фокусы располагаются на оси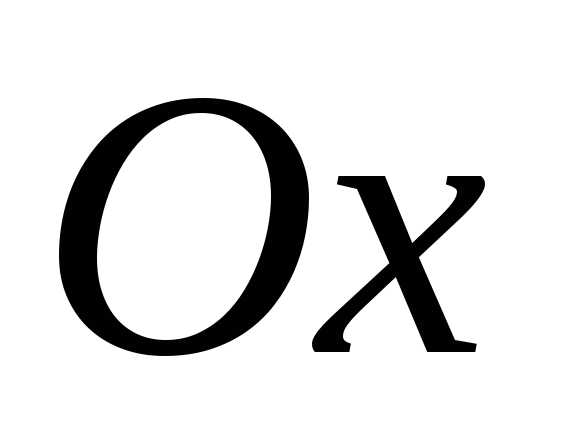 и имеют координатыи
и имеют координатыи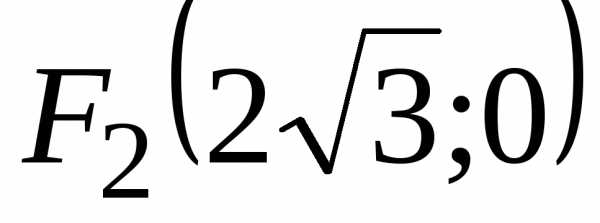 .
.
Пример
Общее уравнение кривой привести к каноническому виду, построить кривую, найти координаты фокусов.
Решение:
Перенесем свободный
член вправо
.
Разделим слагаемое уравнения на 225,
получим 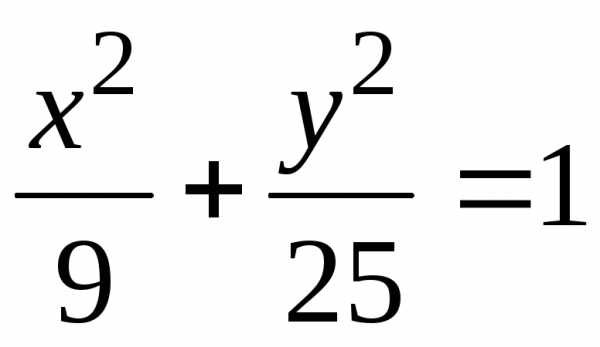 ,это уравнение соответствует
каноническому уравнению эллипса, где
,это уравнение соответствует
каноническому уравнению эллипса, где 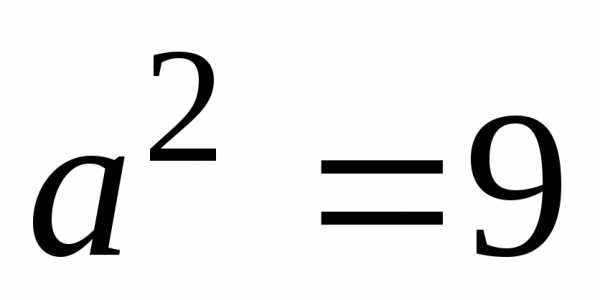 ,
,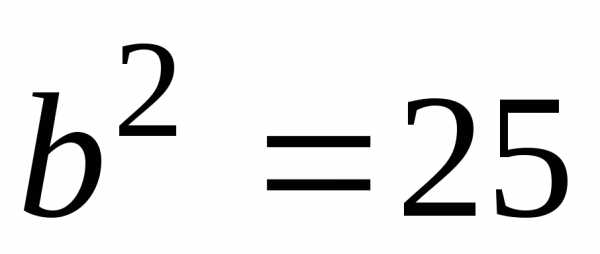 ,
следовательно,
,
следовательно,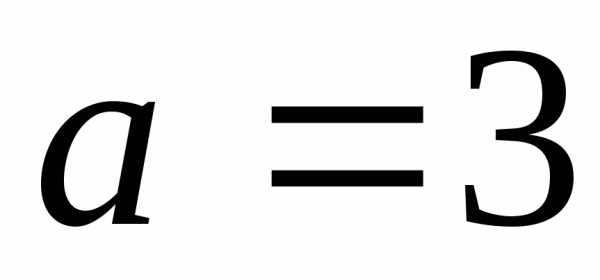 ,
,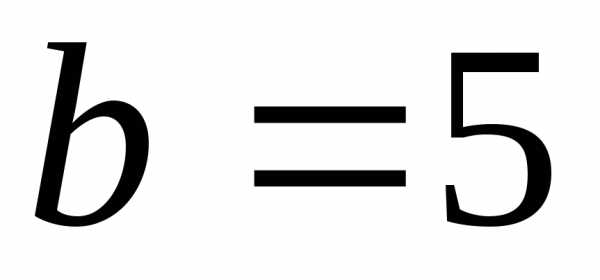 ,
тогда.
,
тогда.
На оси 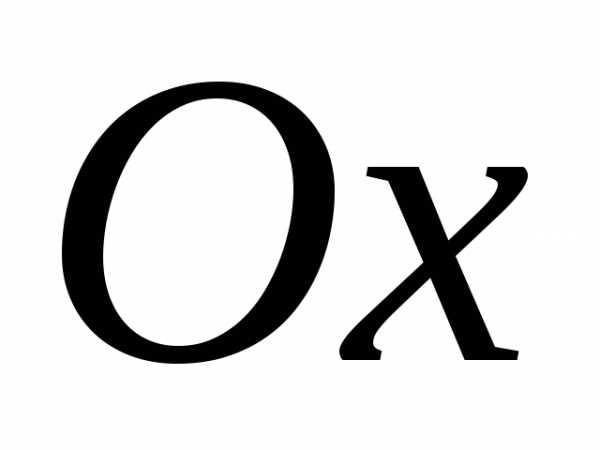 отметим точки
отметим точки и
и ,
а на оси
,
а на оси отметим
отметим и
и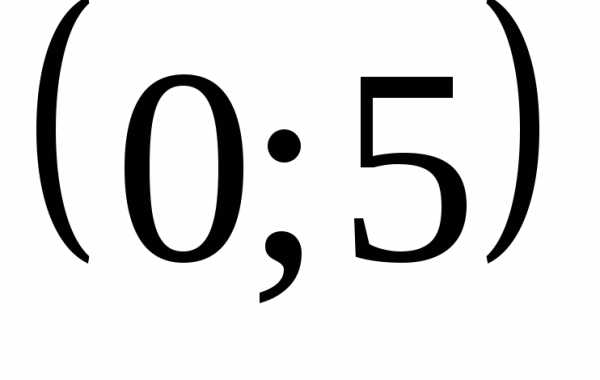 – это вершины эллипса.
– это вершины эллипса.
Найдем фокусы
эллипса, так как  ,
то фокусы располагаются на оси
,
то фокусы располагаются на оси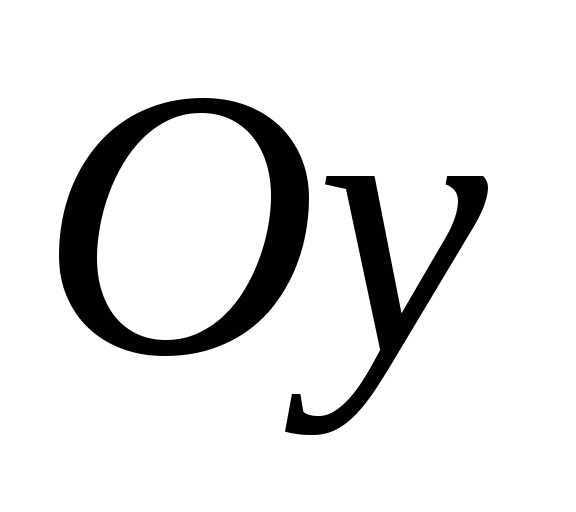 и имеют координаты
и имеют координаты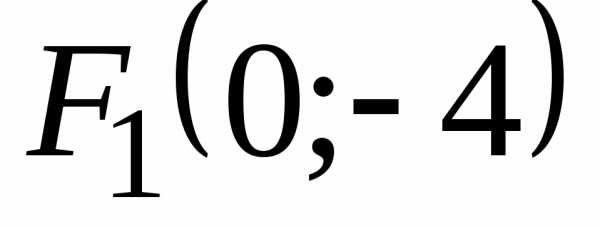 и
и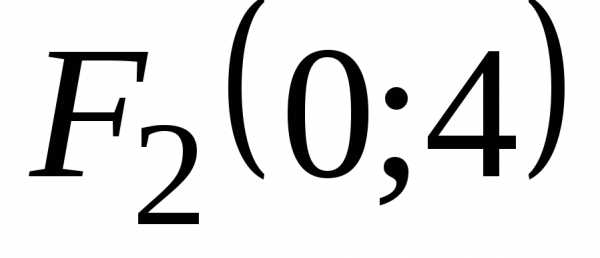 .
.
Пример
Дано каноническое
уравнение гиперболы 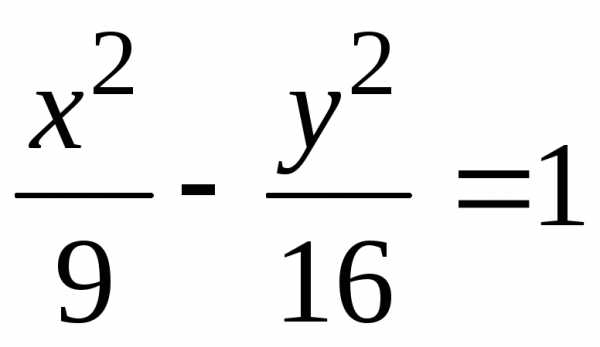 .
Записать уравнение гиперболы, сопряженной
с заданной. Найти координаты фокусов и
построить обе гиперболы.
.
Записать уравнение гиперболы, сопряженной
с заданной. Найти координаты фокусов и
построить обе гиперболы.
Решение:
Уравнение 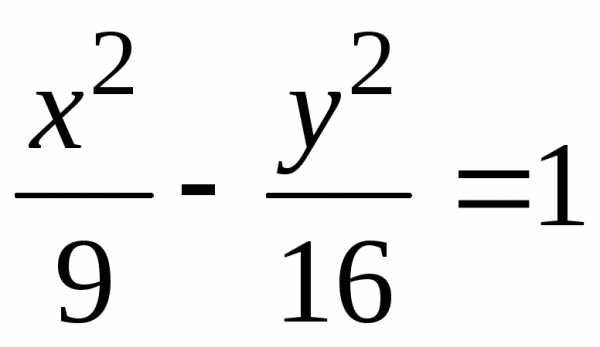 соответствует гиперболе, у которой
действительная ось симметрии есть ось
соответствует гиперболе, у которой
действительная ось симметрии есть ось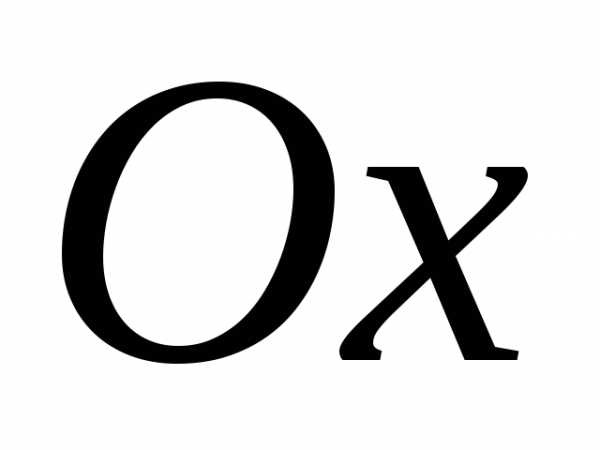 .
Следовательно, уравнение сопряженной
гиперболы
.
Следовательно, уравнение сопряженной
гиперболы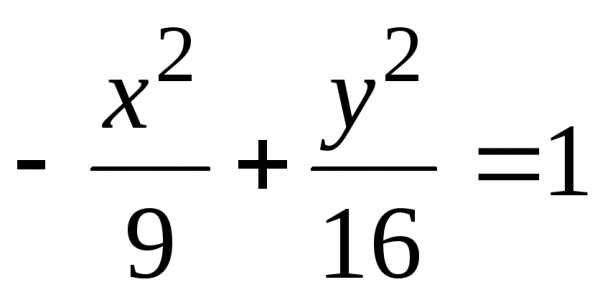 ,
у которой действительная ось симметрии
есть ось
,
у которой действительная ось симметрии
есть ось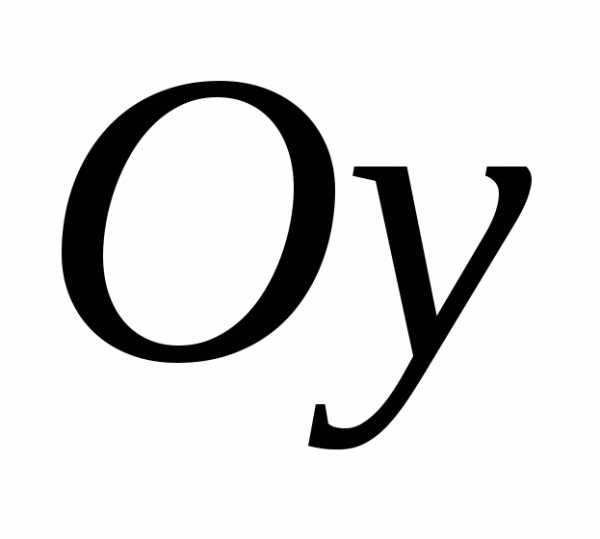 .
Межфокусное расстояние у сопряженных
гипербол одинаковое, равно
.
Межфокусное расстояние у сопряженных
гипербол одинаковое, равно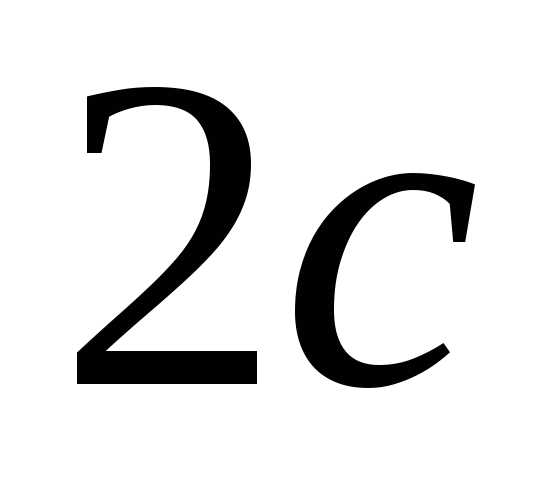 ,
где.
,
где.
Подготовка
к построению сопряженных гипербол
одинаковая. На осях координат строим
основной прямоугольник со сторонамии.
Прямоугольник строится так, чтобы точка
пересечения его диагоналей совпадала
с началом координат. Продолжение
диагоналей являются асимптотами
гиперболы. В нашем случае уравнения
асимптот имеют вид: .
Для уравнения заданной гиперболы вершины
гиперболы
.
Для уравнения заданной гиперболы вершины
гиперболы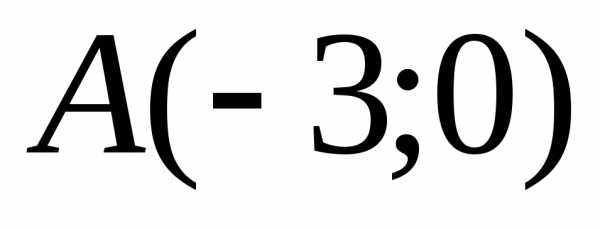 и
и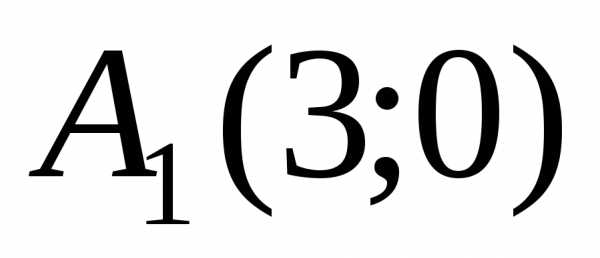 ,
так же как и фокусы
,
так же как и фокусы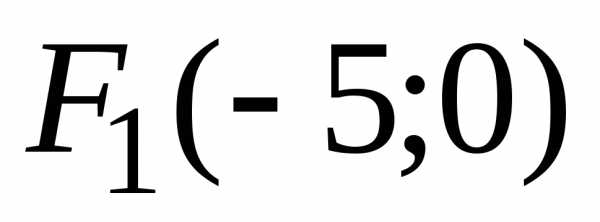 и
и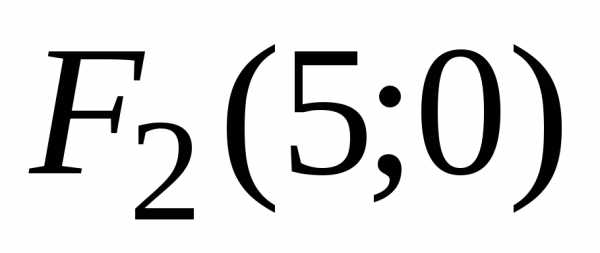 ,
находятся на оси
,
находятся на оси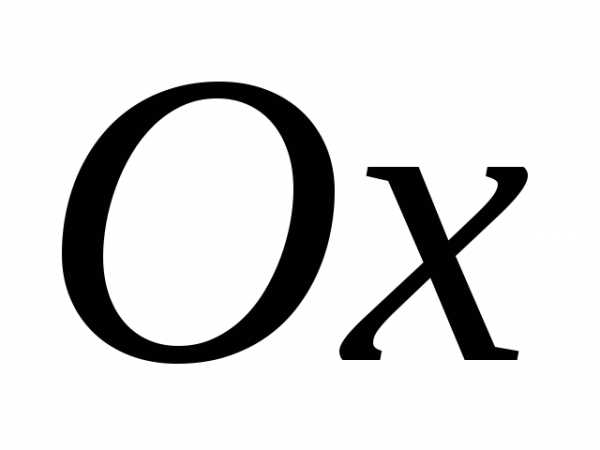 .
Линия гиперболы касается вспомогательного
прямоугольника только в одной точке
(вершине) и плавно стремится к асимптотам.
Для уравнения сопряженной гиперболы
вершины гиперболы
.
Линия гиперболы касается вспомогательного
прямоугольника только в одной точке
(вершине) и плавно стремится к асимптотам.
Для уравнения сопряженной гиперболы
вершины гиперболы и
и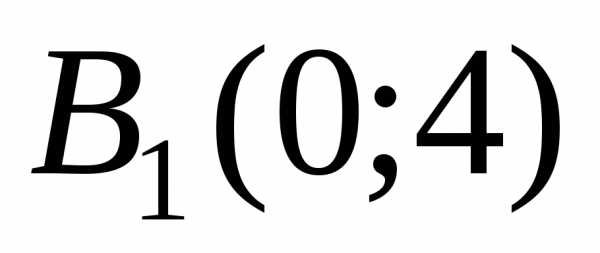 ,
так же как и фокусы
,
так же как и фокусы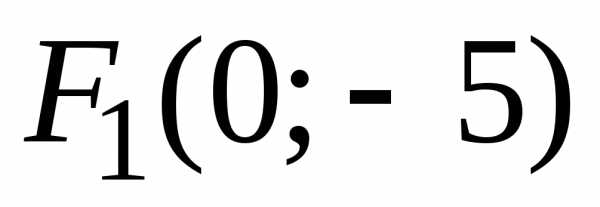 и
и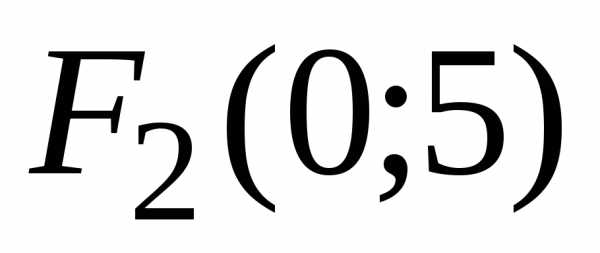 ,
находятся на оси
,
находятся на оси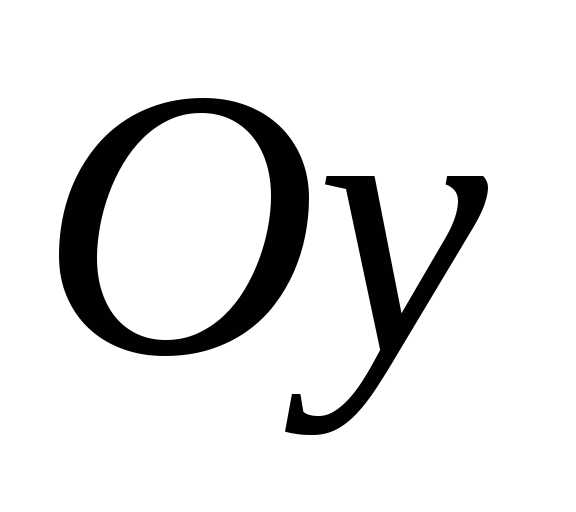 .
.
Рис. 16
Пример
Построить
по заданному уравнению параболы 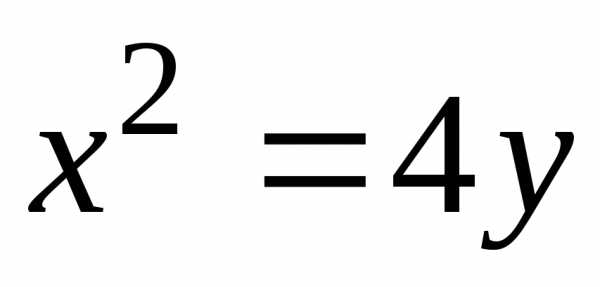 ,
определить координаты фокуса, составить
уравнение директрисы.
,
определить координаты фокуса, составить
уравнение директрисы.
Решение:
Данное
уравнение 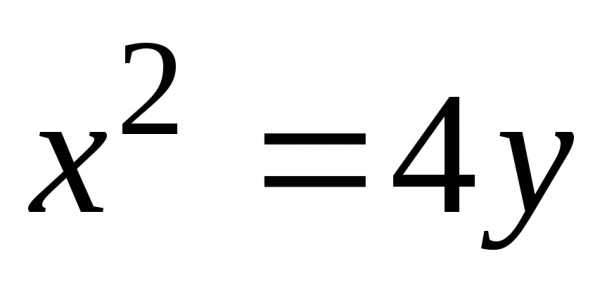 – это уравнение параболы с осью симметрии
– это уравнение параболы с осью симметрии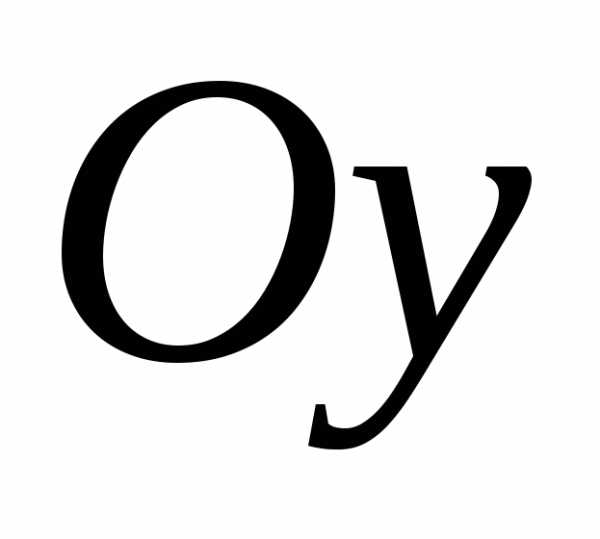 .
Для нахождения координат фокуса надо
найти параметр
.
Для нахождения координат фокуса надо
найти параметр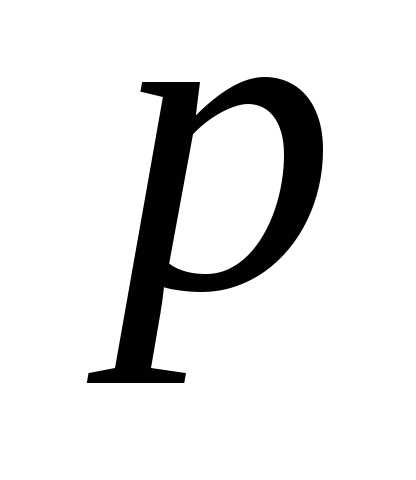 .
Сравнивая каноническое уравнение
параболы
и заданное уравнение
.
Сравнивая каноническое уравнение
параболы
и заданное уравнение 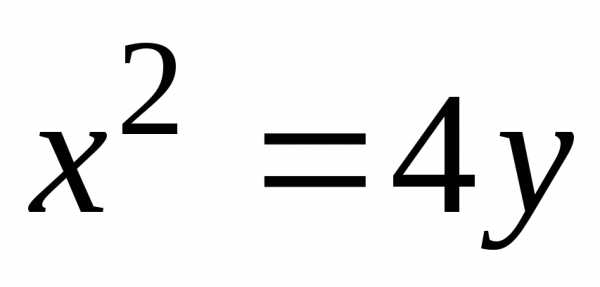 ,
находим
,
находим ,
откуда
,
откуда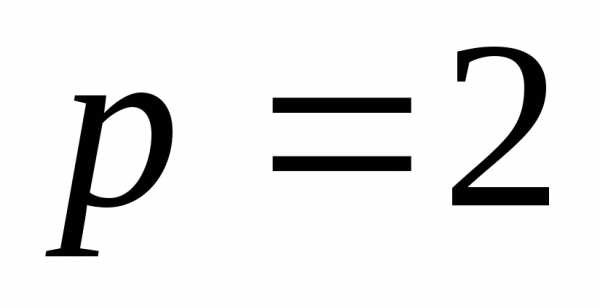 .
Следовательно,
.
Следовательно,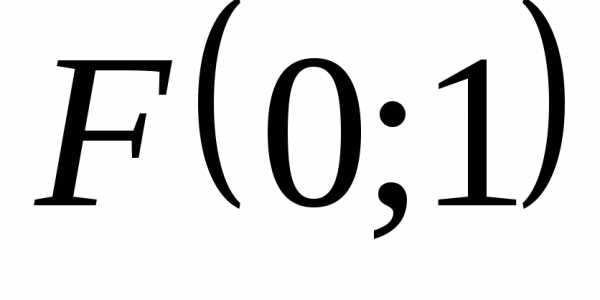 и уравнение директрисы
и уравнение директрисы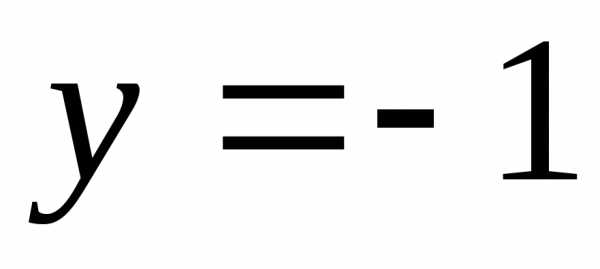 ,
а ветви параболы направлены вверх. Кроме
вершины
,
а ветви параболы направлены вверх. Кроме
вершины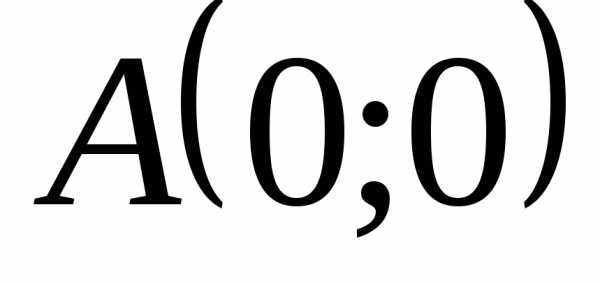 найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 17). Для этого
составим таблицу
найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 17). Для этого
составим таблицу
Пример
Привести уравнение к каноническому виду и выполнить задания предыдущего примера.
Решение:
Преобразуем
уравнение к каноническому виду 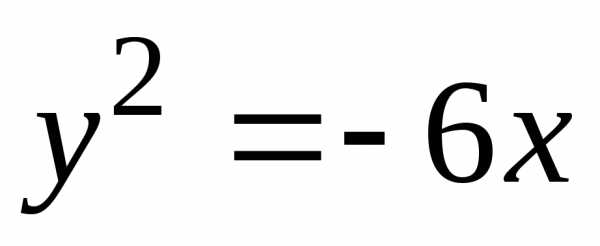 .
Это уравнение соответствует уравнению
,
то есть уравнению параболы с осью
симметрии
.
Это уравнение соответствует уравнению
,
то есть уравнению параболы с осью
симметрии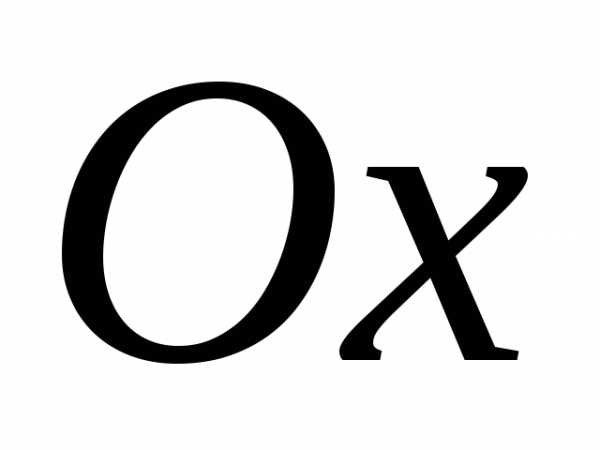 .
Аналогично предыдущему примерунаходим
.
Аналогично предыдущему примерунаходим  ,
откуда
,
откуда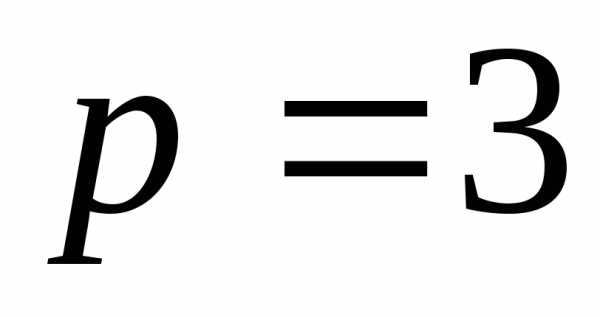 .
Следовательно,
.
Следовательно, и уравнение директрисы
и уравнение директрисы ,
а ветви параболы направлены влево. Кроме
вершины
,
а ветви параболы направлены влево. Кроме
вершины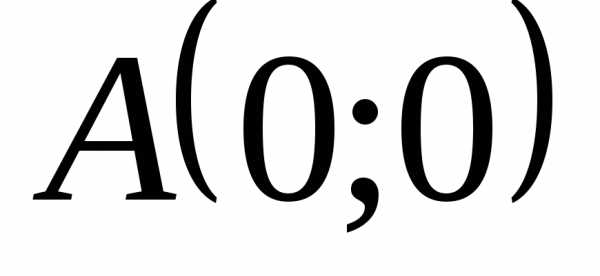 найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 18). Для этого
составим таблицу
найдем еще хотя бы 4 точки, принадлежащие
данной параболе (рис. 18). Для этого
составим таблицу
62
studfiles.net
Уравнение окружности
Прежде всего, давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.
Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.
В качестве линии рассмотрим окружность радиуса с центром в точке .
Пусть центр окружности имеет координаты . Возьмем на окружности произвольную точку . Запишем формулу расстояния между точками C и M. Мы знаем, что длина отрезка, который соединяет любую точку на окружности с центром окружности – это радиус. Поэтому можно записать, что MC равно r. Возведем MC в квадрат и получим уравнение MC2 = r2. Заменим MC2 квадрат на выражение и получим, что если точка лежит на окружности с радиусом r и центром в точке C, то координаты этой точки удовлетворяют уравнению . Если точка не лежит на окружности, то расстояние от этой точки до центра окружности не равно радиусу, поэтому координаты таких точек не будут удовлетворять полученному уравнению. Поэтому можно сказать, что в прямоугольной системе координат уравнение окружности радиуса r с центром в точке C с координатами имеет вид: .
Задача. Записать уравнение окружности с радиусом и центром в начале координат.
Решение.
Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид
.
Задача. Начертить окружность, заданную уравнением .
Решение.
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.
Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.
Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.
Задача. Начертить окружность, заданную уравнением .
Решение.
Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.
Это будут числа -4 и 2. Теперь давайте определим величину радиуса окружности.
Задача. Начертить окружность, заданную уравнением .
Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.
Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.
Теперь давайте попробуем решить задачу обратную данным.
Задача. Составить уравнение окружности, которая показана на рисунке.
Как и в предыдущих задачах мы начнем с определения координат центра окружности. Сделать это нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр окружности имеет координаты (0;0).
Нетрудно заметить, что радиус окружности равен 4.
Запишем уравнение окружности и подставим найденные значения.
Ответ: .
Решим еще одну задачу.
Задача. Составить уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Задача. Составить уравнение окружности, которая показана на рисунке.
Решение.
– центр окружности
– радиус окружности
Ответ:.
Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.
Для того, что бы составить уравнение окружности и построить ее надо:
1. Найти координаты центра окружности.
2. Найти длину радиуса этой окружности.
3. Записать уравнение окружности.
4. Подставить полученные значения в уравнение окружности.
5. Построить окружность, если это требуется для решения задачи.
Рассмотрим еще одну задачу.
Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.
Задача. Написать уравнение окружности с диаметром , если , .
Решение.
Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.
Получим, что центр окружности имеет координаты .
Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.
Запишем общее уравнение окружности и подставим в него найденные значения. Тогда получим, что уравнение данной окружности имеет вид:
Ответ: .
Подведем итоги урока.
На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x0; y0) и радиусом r.
Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.
Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.
videouroki.net
