Создание математических формул онлайн
| Полученная формула |
Создание математических формул
Бот позволяет отображать математически формулы и графики записанные в формате LaTEX.
Хотелось бы заметить что в поле можно писать достаточно много формул одновременно. Для того что бы каждая формула была расположена на новой строки Вам следует использовать «разделитель» \\
Синтаксис
Синтаксис очень прост
WEB: <Формула в формате Latex>
Примеры
запрос: \begin{pmatrix} 1-i & 12+2i \\ 3-1.5i & -2.5i \end{pmatrix}
Ответ:
Запрос: \int_0^1 f(x)dx
Ответ:
Запрос: \usepackage{color} \color{blue} x^2+y^2
Ответ:
Запрос: f(x)=\int_{-\infty}^xe^{-t^2/m}dt
Ответ:
\usepackage{color}\color{red}\Large e^x=\sum_{n=0}^\infty\frac{x^n}{n!}
\large f^\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\parstyle\begin{eqnarray*} x+y+z&=&3\\2y&=&x+z\\2x+y&=&z\end{eqnarray*}
- Создание QR кодов онлайн >>
abakbot.ru
Площадь треугольника онлайн расчет
Данная страница посвящена достаточно распространенному информационному ресурсу — описанию и расчету площади произвольного треугольника. Отличие от других ресурсов, это расчет площади онлайн, непосредственно в процессе прочтения статьи
Площадь через высоту и основание
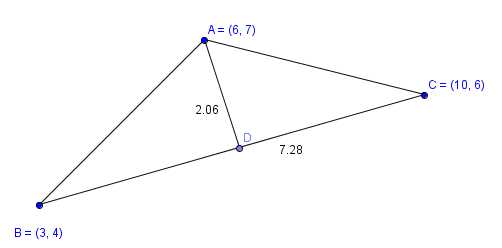
Это самая простая для запоминания формула. Словами эта формула звучит так — площадь треугольника равна половине произведения основания треугольника на его высоту.
В случае прямоугольного треугольника это выражение приобретает еще более простой смысл: Площадь прямоугольного треугольника равна половине произведения двух катетов
площадь через стороны треугольника
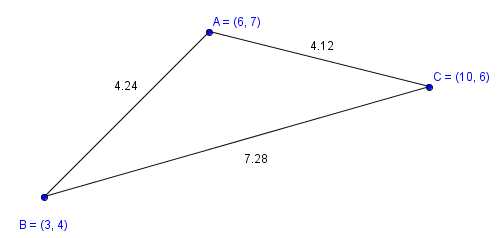
Площадь треугольника выраженная через стороны известна очень давно — она фигурирует в книгах, датированных 1 веком до нашей эры.
Эту формулу можно выразить по разному, благо формул расчета параметров треугольника достаточно.
Но если попытаться мыслить категориями времен до нашей эры, когда не было формул в современном преставлении, не было переменных и знаков корня, то единственной аксимомой, на базе которого, Герон, создал свою формулу, была теорема Пифагора. А так как в те времена, еще не знали иррациональных чисел, да к отрицательным у ученых было достаточно скептическое видение, то для размышлений использовались целые числа.
Самого доказательства здесь не будет, предположив только что Герон, дополнял произвольный пифагоровый треугольник до прямоугольника высчитывал его площадь, и делил на два.
Площадь через координаты вершин
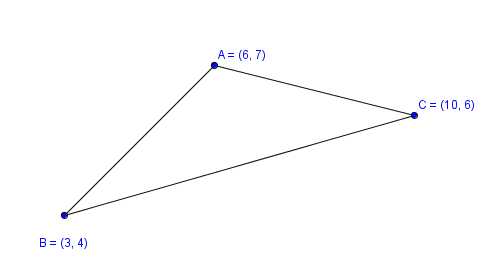
Когда известны координаты вершин треугольника, формула площади может быть выражена вот такой формулой
Определитель третьего порядка легко раскладывается, и поэтому расчет площади даже в ручном режиме не вызовет никаких затруднений.
Площадь через две стороны и угол между ними
Площадь через сторону и два угла
Редко встречающаяся задача, но и для таких исходных данных высчитали формулу. Внимательный читатаель сразу видит «ошибку». Заголовок гласит, что площадь узнается через сторону и два угла, то есть через три переменных, а в формуле присутствут все четыре. Как же так?
На самом деле ошибки никакой нет, зная одну из основных аксиом треугольника, гласящая, что сумма внутренних углов треугольника всегда(!!) равна 180 градусов
Поэтому нет ничего сложного, зная два угла треугольника, узнать третий.
Площадь через медианы треугольника
Заменив квадраты сторон на дополнительные переменные, система превращается в систему линейных уравнений, которые легко решить.
А узнав все стороны, легко определить площадь по сторонам треугольника
Как её выводили неизвестно, то что что она по своему элеганта, это не подвергается сомнению.
abakbot.ru
Создание математических формул онлайн
| Полученная формула |
Создание математических формул
Бот позволяет отображать математически формулы и графики записанные в формате LaTEX.
Хотелось бы заметить что в поле можно писать достаточно много формул одновременно. Для того что бы каждая формула была расположена на новой строки Вам следует использовать «разделитель» \\
Синтаксис
Синтаксис очень прост
WEB: <Формула в формате Latex>
Примеры
запрос: \begin{pmatrix} 1-i & 12+2i \\ 3-1.5i & -2.5i \end{pmatrix}
Ответ:
Запрос: \int_0^1 f(x)dx
Ответ:
Запрос: \usepackage{color} \color{blue} x^2+y^2
Ответ:
Запрос: f(x)=\int_{-\infty}^xe^{-t^2/m}dt
Ответ:
\usepackage{color}\color{red}\Large e^x=\sum_{n=0}^\infty\frac{x^n}{n!}
\large f^\prime(x)\ = \lim_{\Delta x\to0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
\parstyle\begin{eqnarray*} x+y+z&=&3\\2y&=&x+z\\2x+y&=&z\end{eqnarray*}
abakbot.ru
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
$ 1 рад = 57.3° $ | $ 1° = 17.45 мрад $ | $ 1´ = 291 мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
В помощь студенту
Вращательное движение (движение тела по окружности) |
стр. 421 |
|---|
www.fxyz.ru
