Чётность и нечётность функций
Привет всем посетителям! Сегодня рассматриваем вопрос четности и нечетности функций.
Правило:
Если , то функция четная.
Если , то функция нечетная.
При этом важно, чтобы область определения функции была бы симметричной относительно оси ординат, а при наличии в ней выколотых точек или интервалов они также должны располагаться симметрично.
Алгоритм исследования:
Установить, симметрична ли область определения функции. Если это так, то найти и сравнить с
Если то функция — четная.
Если , то функция нечетная.
Функция совсем не обязана быть четной или нечетной, она может быть «никакой», несмотря на то, что область определения симметрична.
Примеры:
1. Определить, является ли четной функция: .
Область определения этой функции – все действительные числа, то есть она симметрична. Теперь подставим вместо x – (-x) и посмотрим, что получится:
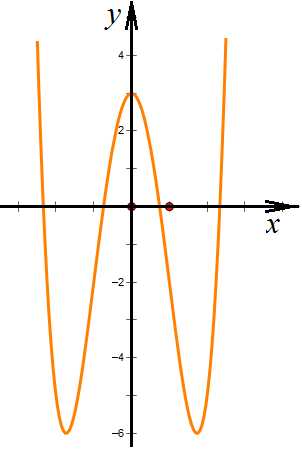
– функция четна.
Надо отметить, что график четной функции симметричен относительно оси ординат, она для него словно зеркало. Поэтому графики таких функций можно строить в правой полуплоскости, а в левую просто отражать.
Верно и следующее: если функция задана графиком, который симметричен относительно оси ординат, то она четная.
2. Определить, является ли четной функция: .
Область определения этой функции может быть найдена из системы неравенств:
Оба неравенства всегда соблюдаются, так как дискриминант обоих трехчленов всегда меньше 0, и ветви парабол направлены вверх – таким образом, мы установили, что область определения симметрична – это вся числовая ось.
Теперь подставим вместо x – (-x): – данная функция нечетна.
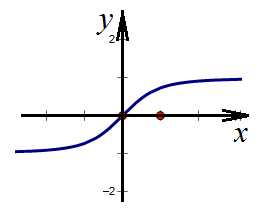
График нечетной функции симметричен относительно начала координат, то есть каждой его точке соответствует точка, получить которую можно поворотом на 180 градусов относительно начала координат. Поэтому графики таких функций можно строить в правой полуплоскости, а изображение в левой полуплоскости получить, повернув картинку на 180 градусов.
Верно и следующее: если функция задана графиком, который симметричен относительно начала координат, то она нечетная.
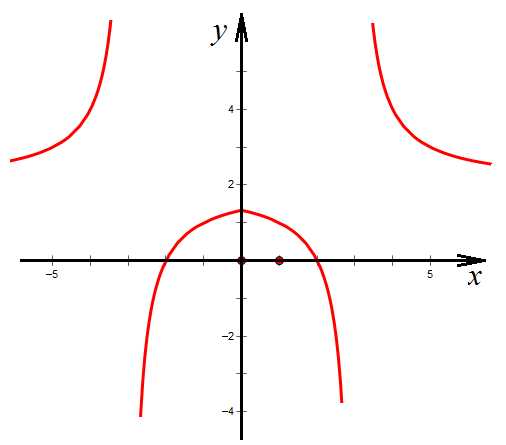
3. Определить, является ли четной функция: .
Область определения может быть найдена из системы неравенств:
Таким образом, область определения симметрична, и не содержит выколотые точки (1) и (-1).
Подставляем (-х) вместо х:
– исходную функцию не получили, а получили совсем другую – значит, исходная функция не является ни четной, ни нечетной (что и подтверждает график). Мы убедились, что симметрия области определения еще не означает, что функция четная или же нечетная.
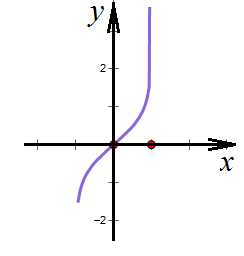
4. Определить, является ли четной функция: .
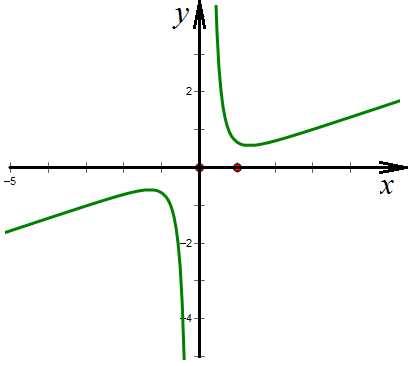
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетна.
5. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме точек 3 и (-3) – симметричная.
Подставляем (-х) вместо х:
– функция четная.
6. Определить, является ли четной функция: .

Область определения – вся числовая ось – симметричная.
Подставляем (-х) вместо х:
– функция четная.
7. Определить, является ли четной функция: .
Область определения – вся числовая ось, кроме 0 – симметричная.
Подставляем (-х) вместо х:
– функция нечетная.
Кроме того, здесь мы имеем дело с суммой двух функций.
Правило:
Сумма двух нечётных функций – нечётна.
Сумма двух чётных функций – чётна.
А вот сумма двух функций разной четности – как правило, ни четна, ни нечетна.
Определим четность этих функций по отдельности.
– функция нечетная.
– функция нечетная.
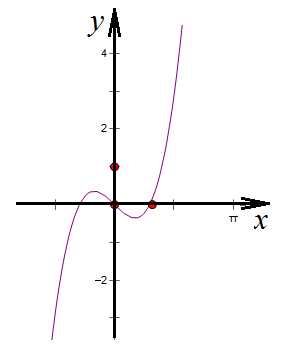
8. Исследуем теперь такую функцию:
Одна из них нечётна – это мы только что показали, а вторая?
Область определения функции симметрична, функция нечётна, так как . Тогда по правилу сложение двух нечетных функций даст функцию нечетную.
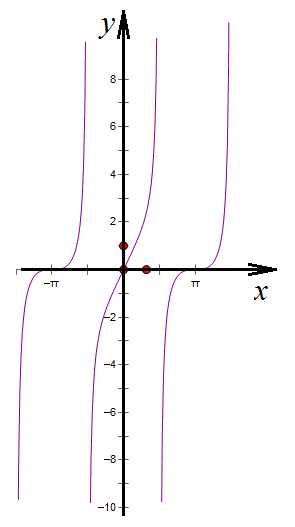
9. Наконец, последняя:
– имеем произведение двух функций.
Правило:
Произведение или частное двух нечётных функций чётно.
Произведение или частное двух чётных функций чётно.
Произведение или частное нечётной и чётной функций нечётно.
Так как обе функции являются чётными, то и их произведение чётно.
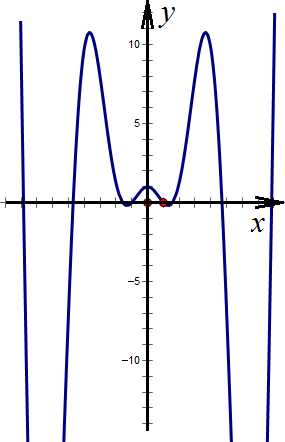
Проверим?
Область определения – вся числовая ось. Производим подстановку:
– функция четная.
easy-physic.ru
Как проверить функцию на четность и нечетность
Крупную часть школьной программы математики занимает изыскание функций, в частности, проверка на четность и нечетность . Данный способ является значимой составляющей процесса постижения нрава поведения функции и построения ее графика.

Инструкция
1. Свойства четности и нечетности функции определяется исходя из могущества знака довода на ее значение. Это могущество отображается на графике функции в определенной симметрии. Иными словами, выполняется качество четности, если f(-x) = f(x), т.е. знак довода не влияет на значение функции, и нечетности, если объективно равенство f(-x) = -f(x).
2. Нечетная функция графически выглядит симметричной касательно точки пересечения координатных осей, четная – касательно оси ординат. Примером четной функции может служить парабола x², нечетной – f = x³.
3. Пример № 1Исследовать на четность функцию x²/(4·x² – 1).Решение:Подставьте в данную функцию –x взамен x. Вы увидите, что знак функции не изменится, от того что довод в обоих случаях присутствует в четной степени, которая нейтрализует негативный знак. Следственно, исследуемая функция является четной.
4. Пример № 2Проверить функцию на четность и нечетность: f = -x² + 5·x.Решение:Как и в предыдущем примере, подставьте –x взамен x: f(-x) = -x² – 5·x. Видимо, что f(x) ? f(-x) и f(-x) ? -f(x), следственно, функция не владеет свойствами ни четности, ни нечетности. Такая функция именуется индифферентной либо функцией всеобщего вида.
5. Изучать функцию на четность и нечетность дозволено также наглядным образом при построении графика либо нахождении области определения функции. В первом примере областью определения является уйма x ∈ (-?; 1/2) ∪ (1/2; +?). График функции симметричен касательно оси Oy, значит, функция четная.
6. В курсе математики вначале постигают свойства элементарных функций, а после этого полученные познания переносят на изыскание больше трудных функций. Элементарными являются степенные функции с целым показателем, показательные вида a^x при a>0, логарифмические и тригонометрические функции.
Изысканием функции называют особое задание в школьном курсе математики, в ходе которого выявляются основные параметры функции и строится ее график. Ранее целью данного изыскания было построение графика, сегодня же эта задача решается с подмогой специализированных компьютерных программ. Но все же не лишним будет ознакомиться с всеобщей схемой изыскания функции.

Инструкция
1. Находится область определения функции, т.е. диапазон значений x, при которых функция принимает какое либо значение.
2. Определяются области непрерывности и точки обрыва. При этом обыкновенно области непрерывности совпадают с областью определения функции, нужно изучать левые и правые приделы изолированных точек.
3. Проверяется присутствие вертикальных асимптот. Если функция имеет обрывы, то нужно изучать концы соответствующих интервалов.
4. Четность и нечетность функции проверяется по определению. Функция y = f(x) именуется четной, если для всякого x из области определения правильно равенство f(-x) = f(x).
5. Функция проверяется на периодичность. Для этого x меняется на x + T и ищется наименьшее правильное число T. Если такое число существует, то функция периодична, а число T – период функции.
6. Функция проверяется на монотонность, находятся точки экстремума. При этом производную функции приравнивают к нулю, обнаруженные при этом точки, выставляют на числовой прямой и добавляют к ним точки, в которых производная не определена. Знаки производной на получившихся интервалах определяют области монотонности, а точки перехода между различными областями являются экстремумами функции.
7. Изучается выпуклость функции, находятся точки перегиба. Изыскание производится подобно изысканию на монотонность, но при этом рассматривается вторая производная.
8. Находятся точки пересечения с осями OX и OY, при этом y = f(0) – пересечение с осью OY, f(x) = 0 – пересечение с осью OX.
9. Определяются пределы на концах области определения.
10. Строится график функции.
11. По графику определяется область значений функции и сжатость функции.
Чётные и нечётные функции – это числовые функции, области определения которых (и в первом, и во втором случае) симметричны касательно системы координат. Как же определить, какая из 2-х представленных числовых функций является чётной?
Вам понадобится
- лист бумаги, функция, ручка
Инструкция
1. Для того дабы определить чётную функцию , раньше каждого запомните её определение. Функцию f (x) дозволено назвать чётной, если для всякого значения х (икс) из области определения выполняются оба равенства: а) -x € D;б) f (-x) = f (x).
2. Запомните, что если при противоположных значениях x (икс) значения y (игрек) равны, то исследуемая функция является чётной.
3. Разглядите пример чётной функции. Y = x?. В этом случае при значении x = -3, y = 9, и при противоположном значении x = 3 y = 9. Обратите внимание, данный пример доказывает, что при противоположных значениях x (икс) (3 и -3) значения y (игрек) равны.
4. Обратите внимание, что на каждой области определения график чётной функции симметричен оси OY, в то время как график нечётной функции на все области определения симметричен касательно начала координат. Простейшим примером чётной функции служат функции y = cos x; y = ?x?; y = x? + ?x?.
5. Если точка (a; b) принадлежит графику чётной функции, то и симметричная ей касательно оси ординат точка(-a; b) также принадлежит данному графику, из чего следует, что график чётной функции симметричен касательно оси ординат.
6. Помните, что не всякая функция непременно является либо чётной, либо нечётной. Некоторые из функций могут быть суммой чётной и нечётной функций (примером может служить функция f (x) = 0).
7. При изысканий функции на чётность, запомните и оперируйте следующими заявлениями: а) сумма чётных (нечётных) функций также является чётной (нечётной) функцией; б) произведение 2-х чётных либо нечётных фунций является чётной функцией; в) произведение нечётной и чётной функций является нечётной функцией; г) если функция f чётна (либо нечётна), то и функция 1/f также является чётной (либо нечётной).
8. Функция именуется чётной, если при изменении знака довода значение функции остаётся непоколебимым. f (x) = f (-x). Используйте данный легкой метод для определения чётности функции: если значение останется непоколебимым при умножении на -1, то функция – чётная.
Видео по теме
Изыскание функции на четность либо нечетность – один из шагов всеобщего алгорифма изыскания функции, нужного для построения графика функции и постижения её свойств. В этом шаге нужно определить, является ли функция четной либо нечетной. Если про функцию невозможно сказать, что она является четной либо нечетной, то говорят, что это функция всеобщего вида.

Инструкция
1. Запишите функцию в виде зависимости y=y(x). Скажем, y=x+5.
2. Подставьте взамен довода x довод (-x) и посмотрите, что получилось в результате. Сравните с первоначальной функцией y(x). Если y(-x)=y(x), имеем четную функцию. Если y(-x)=-y(x), имеем нечетную функцию. Если y(-x) не равняется y(x) и не равняется -y(x), имеем функцию всеобщего вида.
3. Запишите итог к данному шагу изыскания функции. Допустимые варианты итога:y(x) – четная функция,y(x) – нечетная функция,y(x) – функция всеобщего вида.
4. Переходите к дальнейшему шагу изыскания функции, применяя типовой алгорифм.
Изыскание функции на четность и нечетность помогает строить график функции и постигать нрав ее поведения. Для этого изыскания нужно сравнить данную функцию, записанную для довода “х” и для довода “-х”.

Инструкция
1. Запишите функцию, изыскание над которой нужно провести, в виде y=y(x).
2. Замените довод функции на “-х”. Подставьте данный довод в функциональное выражение.
3. Упростите выражение.
4. Таким образом, вы получили одну и ту же функцию, записанную для доводов “х” и “-х”. Посмотрите на две эти записи.Если y(-x)=y(x), то это четная функция.Если y(-x)=-y(x), то это нечетная функция.Если же про функцию невозможно сказать, что y(-x)=y(x) либо y(-x)=-y(x), то по свойству четности это функция всеобщего вида. То есть, она не является ни четной, ни нечетной.
5. Запишите сделанные вами итоги. Сейчас вы можете их применять в построении графика функции либо же в будущем аналитическом изыскании свойств функции.
6. Говорить о четности и нечетности функции дозволено также и в том случае, когда теснее задан график функции. Скажем, график послужил итогом физического эксперимента.Если график функции симметричен касательно оси ординат, то y(x) – четная функция.Если график функции симметричен касательно оси абсцисс, то x(y) – четная функция. x(y) – функция, обратная функции y(x).Если график функции симметричен касательно начала координат (0,0), то y(x) – нечетная функция. Нечетной будет также обратная функция x(y).
7. Главно помнить, что представление о четности и нечетности функции имеет прямую связь с областью определения функции. Если, скажем, четная либо нечетная функция не существует при х=5, то она не существует и при х=-5, чего невозможно сказать про функцию всеобщего вида. При установлении четности и нечетности обращайте внимание на область определения функции.
8. Изыскание функции на четность и нечетность коррелирует с нахождением множества значений функции. Для нахождения множества значений четной функции довольно разглядеть половину функции, правее либо левее нуля. Если при x>0 четная функция y(x) принимает значения от А до В, то те же значения она будет принимать и при x<0.Для нахождения множества значений, принимаемых нечетной функцией, тоже довольно разглядеть только одну часть функции. Если при x>0 нечетная функция y(x) принимает диапазон значений от А до В, то при x<0 она будет принимать симметричный диапазон значений от (-В) до (-А).
jprosto.ru
2. Исследование функции на четность и нечетность.
Функция 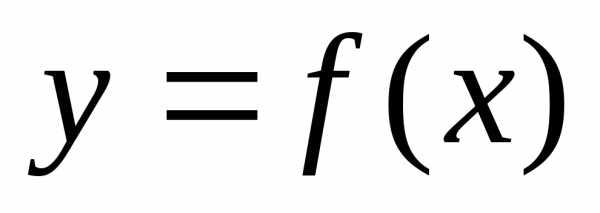 называется четной (нечетной), если для
любогои выполняется равенство
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси  .
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2);
3)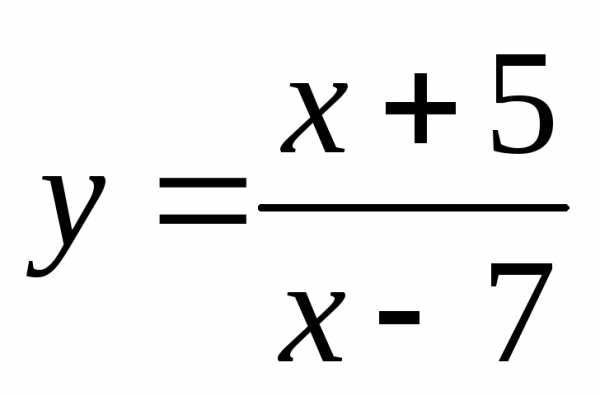
Решение.
1) Функция определена
при
.
Найдем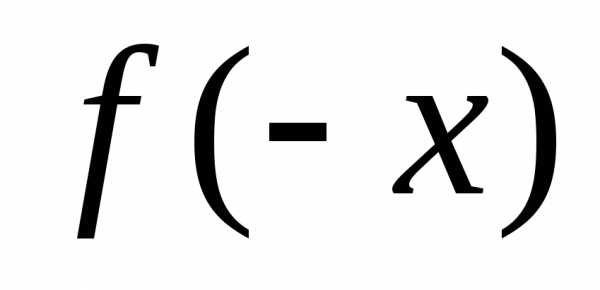 .
.
, т.е. . Значит, данная функция является четной.
2) Функция определена при
, т.е. . Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
, . Поэтому функция не является ни четной, ни нечетной. Назовем ее функцией общего вида.
3. Исследование функции на монотонность.
Функция 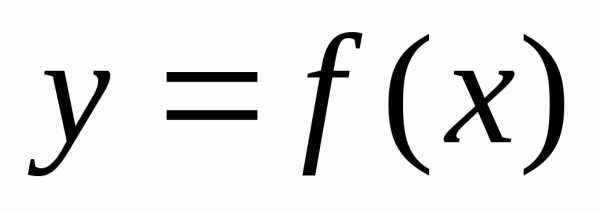 называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие (убывающие) на некотором интервале называются монотонными.
Если функция 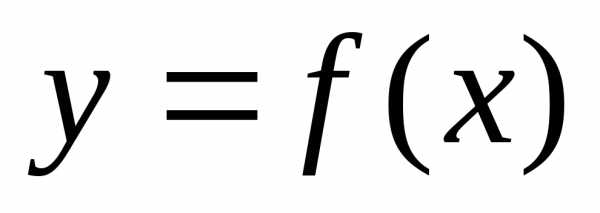 дифференцируема на интервале
дифференцируема на интервале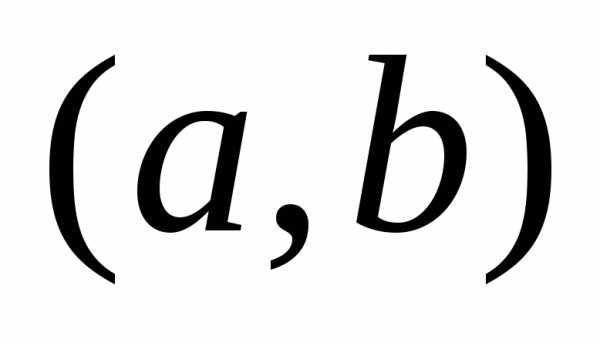 и имеет положительную (отрицательную)
производную
и имеет положительную (отрицательную)
производную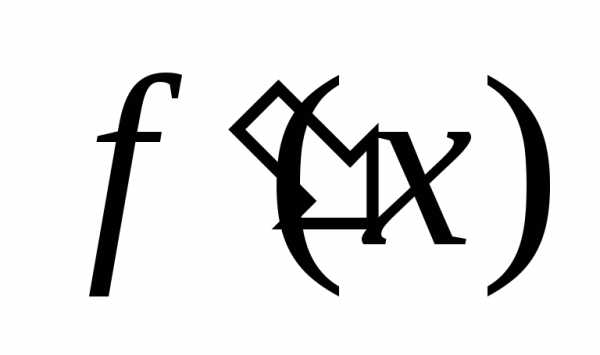 ,
то функция
,
то функция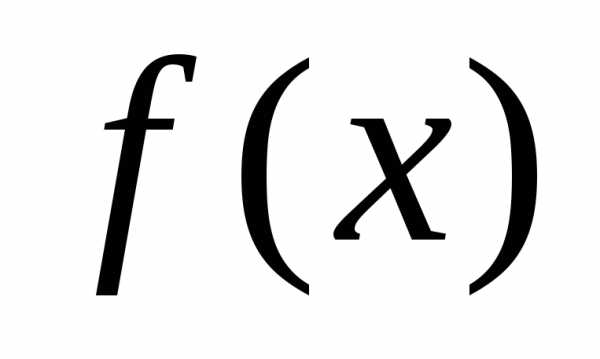 возрастает (убывает) на этом интервале.
возрастает (убывает) на этом интервале.
Пример 6.3. Найти интервалы монотонности функций
1) 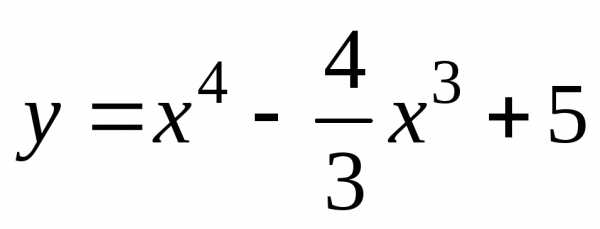 ;
3).
;
3).
Решение.
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если  и
и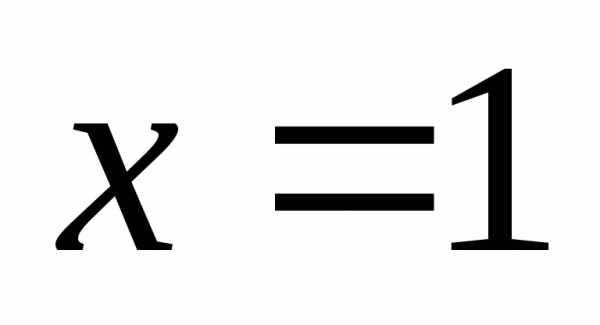 .
Область определения – числовая ось,
разбивается точками
.
Область определения – числовая ось,
разбивается точками ,
, на интервалы. Определим знак производной
в каждом интервале.
на интервалы. Определим знак производной
в каждом интервале.
В интервале 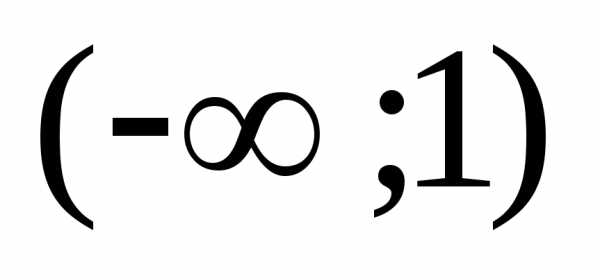 производная отрицательна, функция на
этом интервале убывает.
производная отрицательна, функция на
этом интервале убывает.
В интервале 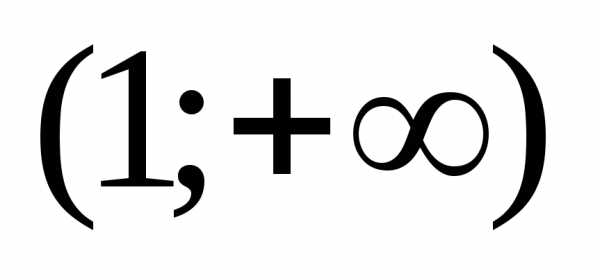 производная положительна, следовательно,
функция на этом интервале возрастает.
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция определена, если или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
.
Найдем производную  ,
,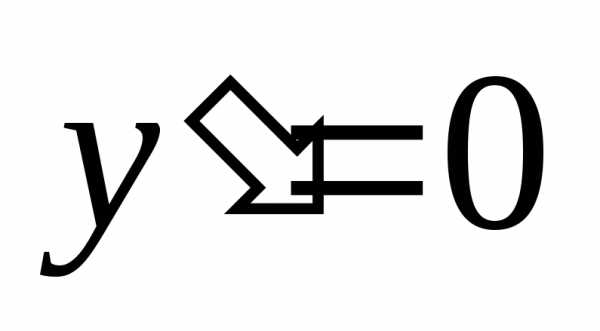 ,
если,
т.е.
,
если,
т.е.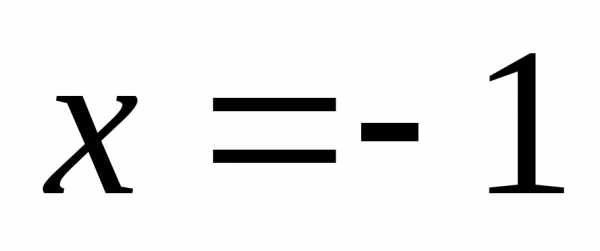 ,
но.
Определим знак производной в интервалах.
,
но.
Определим знак производной в интервалах.
В интервале 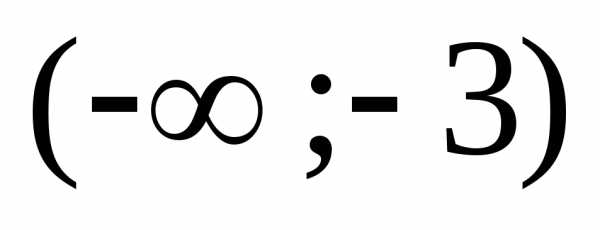 производная отрицательна, следовательно,
функция убывает на интервале.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале.
В интервале производная положительна, функция
возрастает на интервале
производная положительна, функция
возрастает на интервале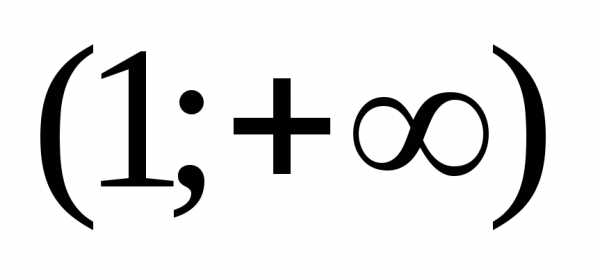 .
.
4. Исследование функции на экстремум.
Точка 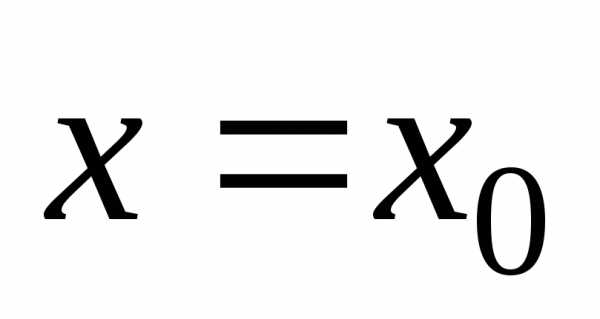 называется точкой максимума (минимума)
функции
называется точкой максимума (минимума)
функции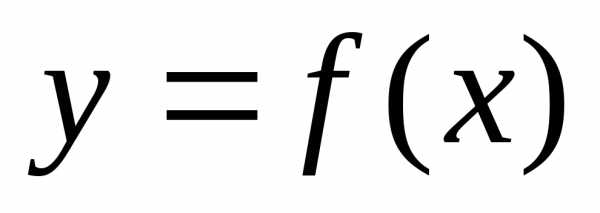 ,
если существует такая окрестность точки
,
если существует такая окрестность точки ,
что для всех
,
что для всех из этой окрестности выполняется
неравенство.
из этой окрестности выполняется
неравенство.
Точки максимума и минимума функции называются точками экстремума.
Если функция 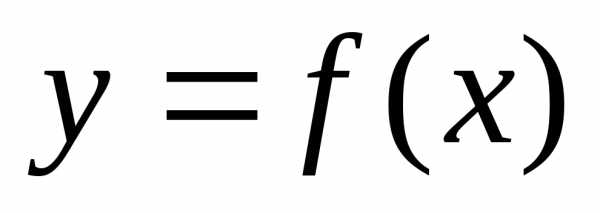 в точке
в точке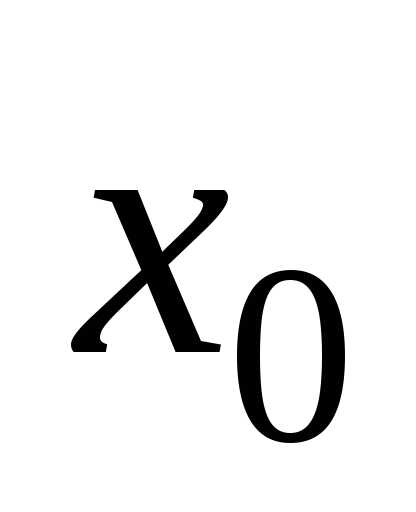 имеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
имеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1.
Если при переходе (слева направо) через
критическую точку 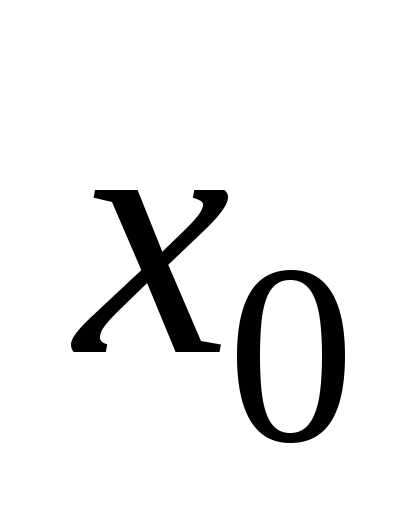 производная
производная меняет знак с «+» на «–», то в точке
меняет знак с «+» на «–», то в точке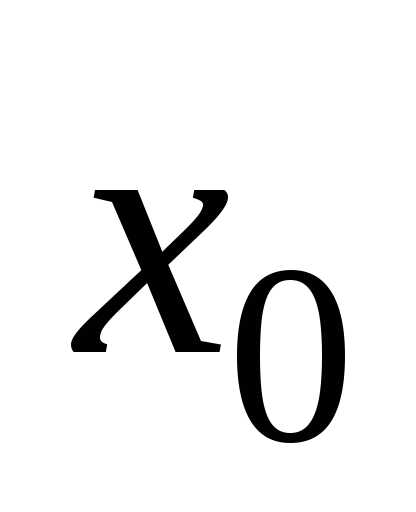 функция
функция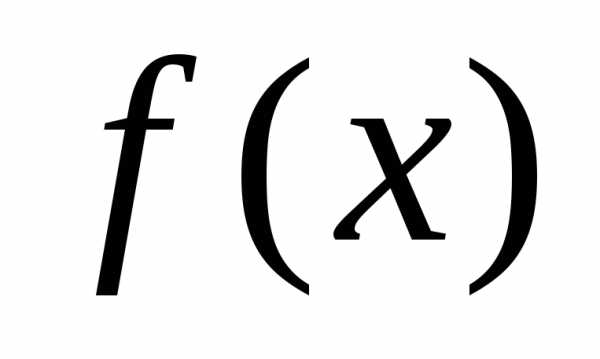 имеет максимум; если с «–» на «+», то
минимум; если
имеет максимум; если с «–» на «+», то
минимум; если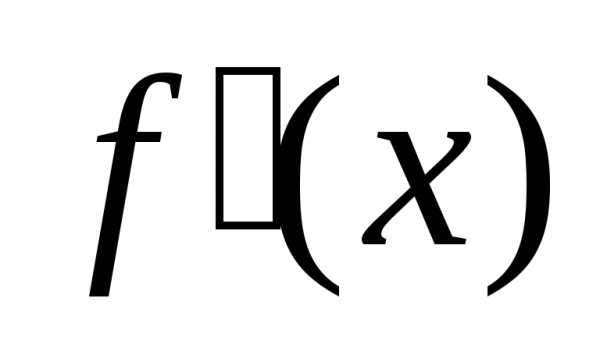 не меняет знак, то экстремума нет.
не меняет знак, то экстремума нет.
Правило 2.
Пусть в точке 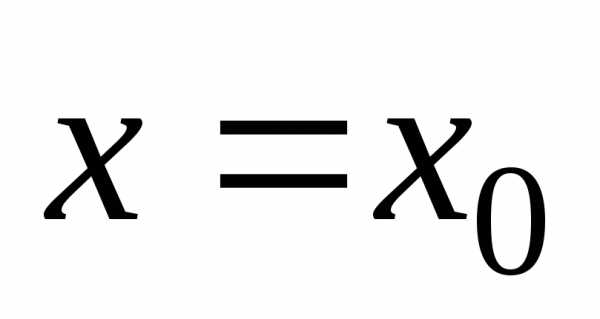 первая производная функции
первая производная функции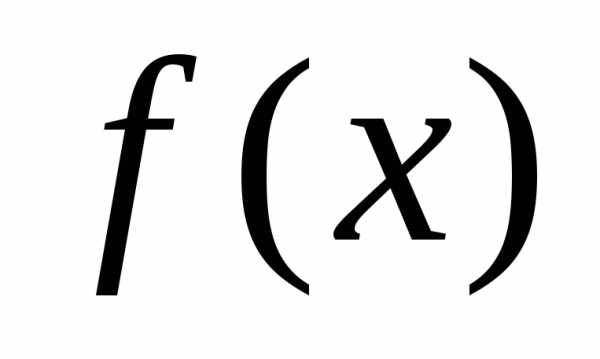 равна нулю,
а вторая производная существует и
отлична от нуля. Если,
то
равна нулю,
а вторая производная существует и
отлична от нуля. Если,
то – точка максимума, если,
то
– точка максимума, если,
то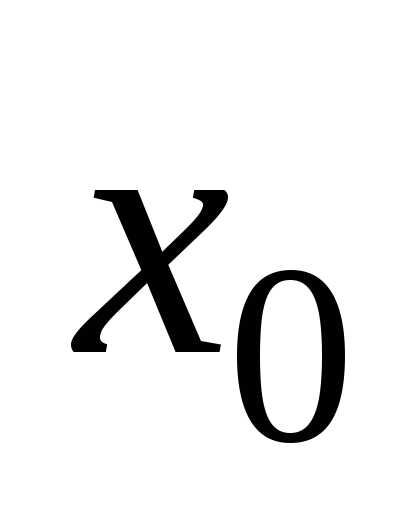 – точка минимума функции.
– точка минимума функции.
Пример 6.4. Исследовать на максимум и минимум функции:
1) 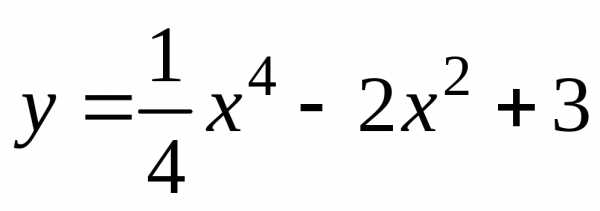 ;
2);
3)
;
2);
3)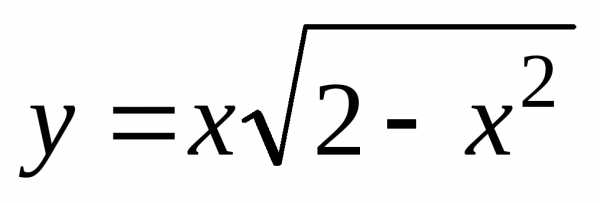 ;
;
4) .
Решение.
1) Функция определена
и непрерывна на интервале  .
.
Найдем производную 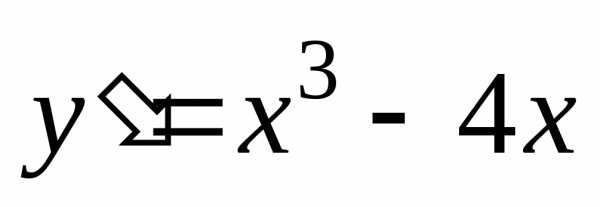 и решим уравнение
и решим уравнение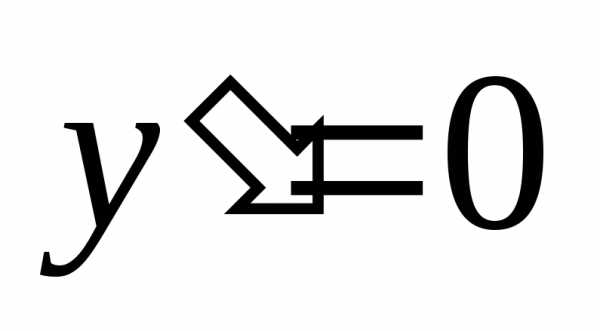 ,
т.е..Отсюда– критические точки.
,
т.е..Отсюда– критические точки.
Определим знак
производной в интервалах
, .
.
При переходе через
точки
и производная меняет знак с «–» на «+»,
поэтому по правилу 1
производная меняет знак с «–» на «+»,
поэтому по правилу 1 – точки минимума.
– точки минимума.
При переходе через
точку 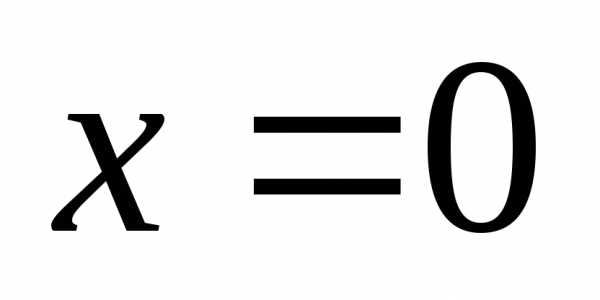 производная меняет знак с «+» на «–»,
поэтому
производная меняет знак с «+» на «–»,
поэтому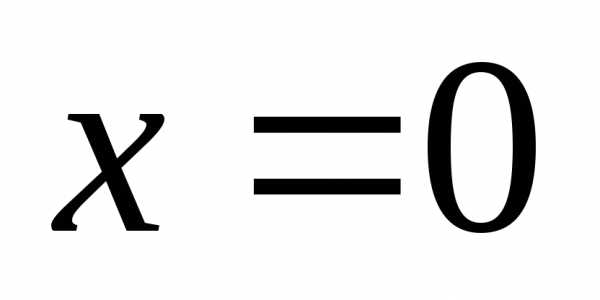 – точка максимума.
– точка максимума.
, .
2) Функция определена
и непрерывна в интервале 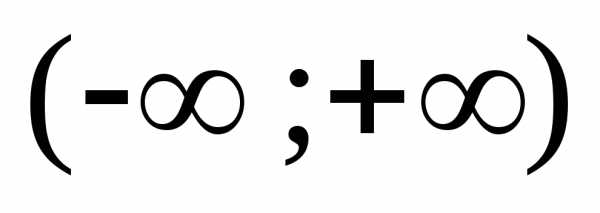 .
Найдем производную.
.
Найдем производную.
Решив уравнение 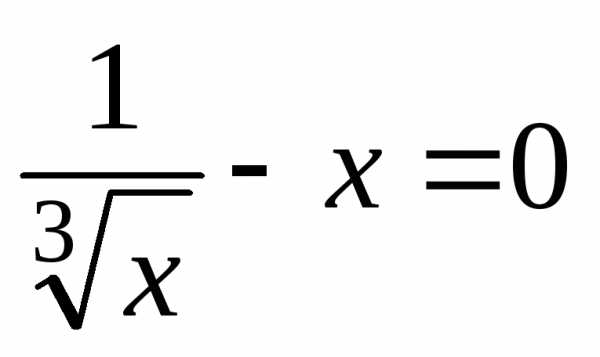 ,
найдем
,
найдем и
и – критические точки. Если знаменатель
– критические точки. Если знаменатель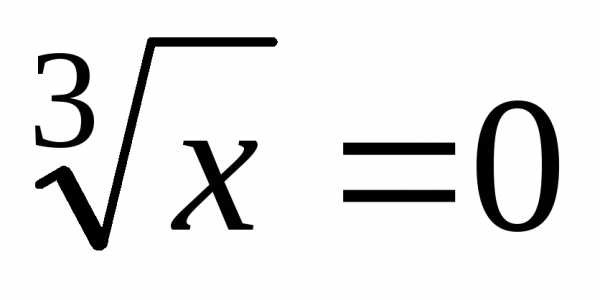 ,
т.е.
,
т.е.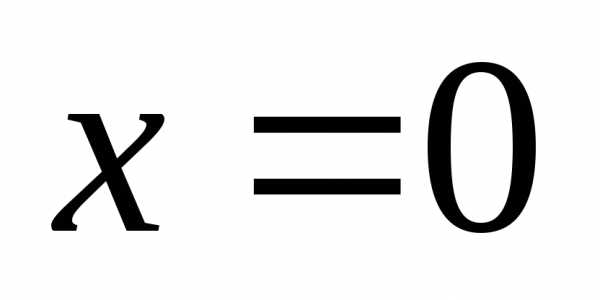 ,
то производная не существует. Итак,
,
то производная не существует. Итак,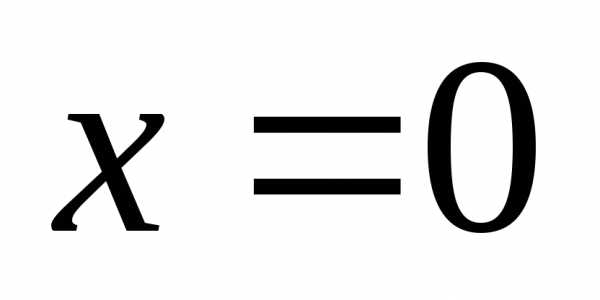 – третья критическая точка. Определим
знак производной в интервалах.
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке 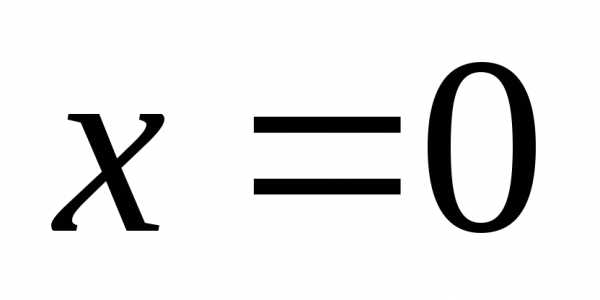 ,
максимум в точках
,
максимум в точках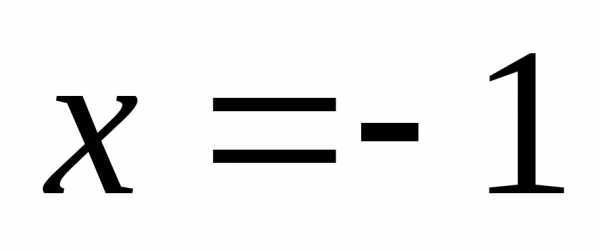 и
и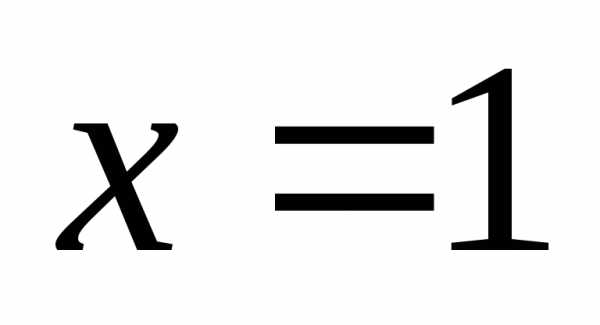 .
.
.
3) Функция определена
и непрерывна, если 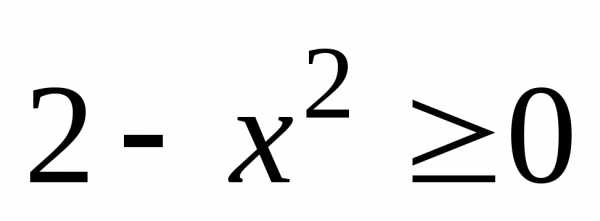 ,
т.е. при.
,
т.е. при.
Найдем производную
.
Найдем критические
точки: 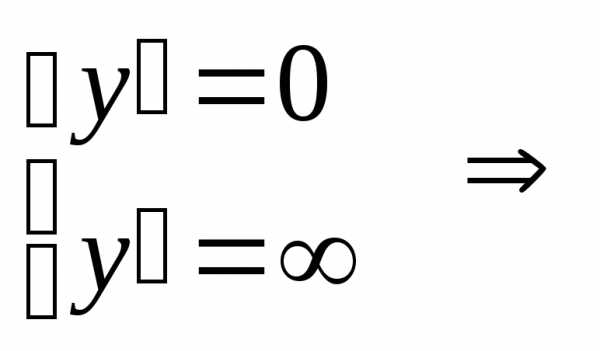
Окрестности точек  не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки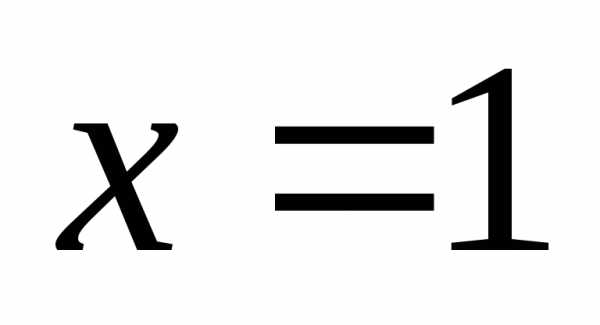 и
и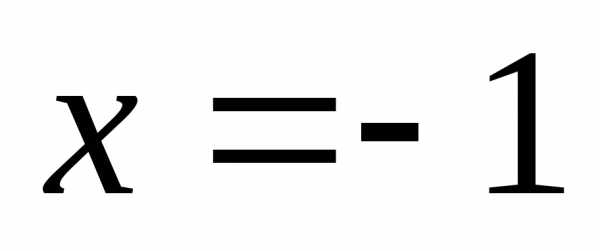 .
.
.
4) Функция определена
и непрерывна на интервале 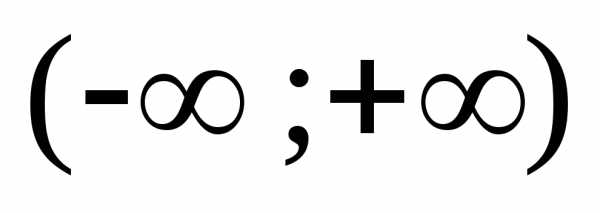 .
Используем правило 2. Найдем производную.
.
Используем правило 2. Найдем производную.
Найдем критические точки:
Найдем вторую производную и определим ее знак в точках
.
В точках функция имеет минимум.
.
В точках функция имеет максимум.
studfiles.net
