Решить уравнение Эйлера онлайн калькулятор
Леонард Эйлер швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук, а также физики, астрономии и других. Эйлер — автор более чем 850 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, и математической физике. Он глубоко изучал медицину, химию, ботанику, воздухоплавание, теорию музыки, множество европейских и древних языков. Решение уравнений Эйлера является весьма нетривиальной задачей и требует определенных знаний. Уравнения данного рода имеют средний уровень сложности и изучаются в старших классах школы.

Так же читайте нашу статью «Решить уравнения с помощью обратной матрицы онлайн»
Уравнение Эйлера имеет следующий вид:
\[x^ny^{(n)}+p_{n-1}x^{n-1}y^{n-1}+ \cdots +p_1xy ‘+p_0y=0 \]
\[P_2, P_2, \cdots ,P_{n-1}\] — постоянные числа.
Благодаря замене \[x = e^t\] данное уравнение преобразуется к уравнению с постоянными коэффициентами:
\[y(x)=y(e^t)=v(t).\]
Получаем:
\[y ‘(x)= v ‘(t)dt/dx=v ‘(t) \cdot e^-t ; xy'(x) =v'(t) \]
\[y»(x)=v»(t)e^{-2t}-v ‘(t)e^-t ; x^2y» (x) =v» (t)-v'(t) \]
Подставив эти значения, мы получим уравнение с постоянными коэффициентами относительно функции \[v(t).\]
Допустим, дано такое уравнение Эйлера:
\[x^2y»+3y ‘+y=0\]
Решение данного уравнения будем искать в виде \[y =x^k,\] поэтому:
\[y ‘=kx^{k-1}, y ‘=k(k-1)x^{k-2}\]
Вставив эти значения производных получим:
\[x^2k(k-1)x^k-2+3kx \cdot x^{k-1}+x^kx^k[k(k-1)+3k+1]=0\]
Соответственно, если \[x \ne 0 k(k-1)+3k+3=0.\] Поскольку \[k = -1\] второй кратности, то\[ y = \frac{1}{x}\] является решением уравнения Эйлера. Другое решение \[y =\frac {(ln x)}{x}\]. В этом можно убедиться, поскольку \[\frac {1}{x}\] и \[ \frac {(ln x)}{x}\] линейно независимые, то:
\[y=\frac {C_1}{x} +\frac {C_2lnx}{x}\]
Это и есть общее решение данного вида уравнения Эйлера.
Где можно решить уравнение Эйлера онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
КРУГИ ЭЙЛЕРА | Matemat.me
Этот урок посвящен одному очень необычному и красивому способу решения задач.
В 18 веке один из величайших математиков — Леонард Эйлер использовал идею изображения множеств с помощью кругов, которые и получили название: «круги Эйлера». Подробнее кто такой Эйлер, и чем он знаменит вы можете узнать из видеоролика который размещен ниже.
В конце урока вам нужно будет ответить на вопросы по биографии Эйлера: Кто такой Эйлер и что он сделал для России?
Вы узнали кто такой Леонард Эйлер, чем он знаменит и сколько он сделал для науки.
Леонард Эйлер «Письма к немецкой принцессе» — скачайте книгу. Посмотрите содержание писем. Обратите внимание на стиль изложения.Есть ли среди писем такие, темы, которых вам показались интересными, и вы бы захотели расширить свои знания о устройстве нашего мира?
Задачи на круги Эйлера это тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие.
Ниже представлен видеоролик с разбором нескольких задач, посвященных кругам Эйлера.
Посмотрев видео, пройдите тестирование по подобным задачам.
для прохождения тестирования введите свое имя. Тест будет открыт. Возможно, чтобы увидеть вопросы теста, вам придется немного прокрутить информацию вниз.
БОНУС: Я хочу показать вам прекрасное датское видео, которое является хорошей иллюстрацией к теме «Круги Эйлера».
В нем показывается, как у людей из разных слоев общества, с разными интересами, из разных социальных и политических кругов, вдруг находится много общего друг с другом. И, казалось бы, совсем разные группы людей, могут удивительным образом объединяться и пересекаться.
Приведите один-два примера объединения совершенно разных, казалось бы, групп людей.
Перейдем к задачам посложнее. Ниже представлены задачи, в которых речь идет уже о пересечениях и объединениях трех множеств.
три круга нов
Пройдите тестирование по подобным задачам.
для прохождения тестирования введите свое имя. Тест будет открыт. Возможно, чтобы увидеть вопросы теста, вам придется прокрутить информацию вниз.
Домашнее задание:
I) Дайте ответы на вопросы либо с помощью Googl формы, либо просто вышлите ответы по почте [email protected].
1.Посмотрите видеоролик «Биография Эйлера» и дайте ответ на вопрос :» Кто такой Леонард Эйлер».
2. Что он сделал для России?
3. Скачайте, или пролистайте книгу Эйлера «Письма к немецкой принцессе» Посмотрите содержание писем. Есть ли среди писем такие, темы, которых вам показались интересными? И вы бы захотели расширить свои знания о устройстве нашего мира. Напишите название одной-двух тем.
4. Посмотрите видеоролик датского телевидения. Приведите один-два примера объединения совершенно разных, казалось бы, групп людей.
Критерии оценивания домашнего задания.
Домашняя работа состоит из двух уровней. Свой уровень выбирайте сами. При желании, можете выполнить задания из обоих уровней.
1 уровень — Ответить на вопросы и пройти тест по теме «Круги Эйлера. 2 множества.»
2 уровень — Самому составить и решить задачу на пересечение трех кругов. Выслать электронный вариант оформленной и решенной задачи (в форме презентации, в формате word или каком то другом — выбирайте сами ) мне на почту: [email protected]
Урок закончен! 🙂
Здесь представлена коллекция задач, составленная учащимися Гуманитарного Лицея г Ижевска в 2016-2017 году как итог нашего занятия по кругам Эйлера. Нажмите на выделенный текст для того, чтобы посмотреть коллекцию.
matemat.me
Круги Эйлера в информатике
Сегодня разберём задачу на круги Эйлера в информатике.
Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.
Рассмотрим метод Эйлера на примере:
Задача: В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных страниц некоторого сегмента сети интернет.
| Запрос | Найдено страниц (В тысячах) |
| (Информатика & ОГЭ) | (Информатика & ЕГЭ) | 1100 |
| Информатика & ЕГЭ | 600 |
| Информатика & ОГЭ & ЕГЭ | 50 |
Какое количество страниц (в тыс.) будет найдено по запросу Информатика & ОГЭ
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменился за время выполнения запросов.
Решение: Рассмотрим первый запрос: (Информатика & ОГЭ) | (Информатика & ЕГЭ). Нарисуем первую и вторую часть запроса отдельно в виде кругов Эйлера.
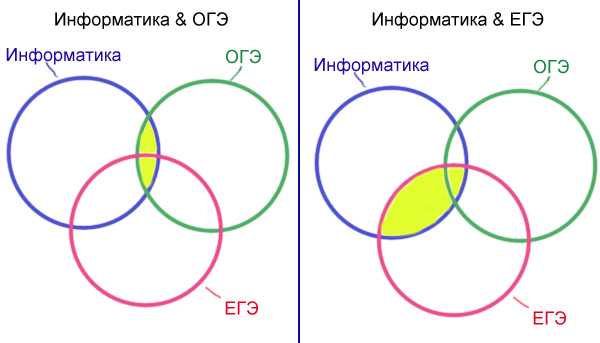
Чтобы применить операцию «И», необходимо закрасить только ту область, которая является общей для двух множеств, к которым применяется эта логическая операция. Чтобы применить операцию «ИЛИ» к двум или нескольким множествам, необходимо объединить эти области. У нас на рисунке изображено (Информатика & ОГЭ) и (Информатика & ЕГЭ) жёлтым цветом. Теперь необходимо применить к этим областям операцию «ИЛИ», т.е. объеднить эти области.

Второй запрос Информатика & ЕГЭ
у нас уже нарисован на первой картинке справа. Теперь изобразим третий запрос Информатика & ОГЭ & ЕГЭ. Пересечение всех трёх окружностей.
Нас спрашивают, какое количество страниц (в тыс.) будет найдено по запросу Информатика & ОГЭ. Из рисунков видно, пересечение Информатика & ОГЭ состоит из двух частей: (Информатика & ОГЭ) | (Информатика & ЕГЭ) — (Информатика & ЕГЭ) и (Информатика & ОГЭ & ЕГЭ).
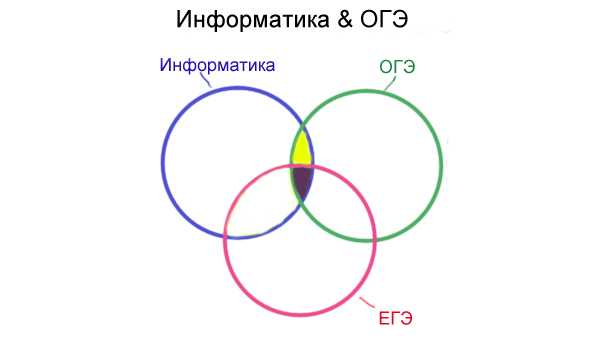
Тогда ответ будет (1100 — 600) + 50 = 550.
На этом всё. Не пропустите новые статьи!
Шифр Виженера на C#
Шифруем сообщение методом Виженера с помощью ключа….Категория: Алгоритмы Подкатегория: ЗадачиДата: 15-01-2018 в 16:47:34 0
«Построение множеств с помощью кругов Эйлера»
Задание. Ученик по заданному логическому выражению построил круги Эйлера, до ошибся и неверно закрасил области.
а) Выполните правильно закрашивание кругов на схеме справа.
б) По начальному рисунку напишите логическое выражение.

Построение кругов Эйлера
1 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
С & В | А
(А | С) & В
А | С | В
№2. Постройте круги Эйлера для множеств из таблицы.
A | тетради | учебники |
Б | тетради |
В | тетради & учебники |
№3. Постройте круги Эйлера для множеств из таблицы.
A | файлы & папки |
Б | файлы | папки |
В | файлы |
Построение кругов Эйлера
2 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
А & С | В
(А | В) & С
А & В & С
№2. Постройте круги Эйлера для множеств из таблицы.
A | ручки | карандаши |
Б | ручки & карандаши |
В | ручки |
№3. Постройте круги Эйлера для множеств из таблицы.
A | банты & ленты |
Б | банты |
В | банты | ленты |
Построение кругов Эйлера
3 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Построить круги Эйлера для множеств:
А | С | В
А & В & С
В & (А | С)
№2. Постройте круги Эйлера для множеств из таблицы.
A | телевизор & холодильник |
Б | телевизор |
В | телевизор | холодильник |
№3. Постройте круги Эйлера для множеств из таблицы.
A | клавиатура | мышь |
Б | клавиатура & мышь |
В | клавиатура |
Построение кругов Эйлера
4 вариант
№1. Заданы три множества А, В, С. Известно, что есть элементы, входящие в множества А, В, С одновременно. Постройте круги Эйлера для множеств:
А & С & В
А | В & С
С & (А | В)
№2. Постройте круги Эйлера для множеств из таблицы.
A | маркер & фломастер |
Б | маркер | фломастер |
В | маркер |
№3. Постройте круги Эйлера для множеств из таблицы.
A | открытка | визитка |
Б | открытка |
В | открытка & визитка |
multiurok.ru
Сайт учителя математики Комаровой Натальи Алексеевны
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью
которой можно изобразить отношения между подмножествами, для наглядного
представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает
рассуждения. Однако, прежде чем приступить к решению задачи, нужно
проанализировать условие. Иногда с помощью арифметических действий решить
задачу легче.
Рассмотрим этот метод на примере решения задачи:
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:
Ответ: человек смотрели только «Стиляги».
Эйлер Леонард (1707-1783), г.Базель,Германия.
Математик, механик, физик. Адъюнкт по физиологии, профессор физики, профессор высшей математики.
В математике рисунки в виде кругов, изображающих множества, используются очень давно. Одним из первых, кто пользовался этим методом, был выдающийся немецкий математик и философ Готфрид Вильгельм Лейбниц (1646 — 1716). В его черновых набросках были обнаружены рисунки с такими кругами. Затем этот метод довольно основательно развил и Леонард Эйлер. Он долгие годы работал в Петербургской Академии наук. К этому времени относятся его знаменитые «Письма к немецкой принцессе», написанные в период с 1761 по 1768 год. В некоторых из этих «Писем…» Эйлер как раз и рассказывает о своем методе. После Эйлера этот же метод разрабатывал чешский математик Бернард Больцано (1781 — 1848). Только в отличие от Эйлера он рисовал не круговые, а прямоугольные схемы. Методом кругов Эйлера пользовался и немецкий математик Эрнест Шредер (1841 — 1902). Этот метод широко используется в книге «Алгебра логики». Но наибольшего расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843 — 1923). С наибольшей полнотой этот метод изложен им в книге «Символическая логика», изданной в Лондоне в 1881 году. В честь Венна вместо кругов Эйлера соответствующие рисунки называют иногда диаграммами Венна; в некоторых книгах их называют также диаграммами (или кругами) Эйлера-Венна.
Джон Венн (1834 — 1923), английский логик.
Работал в области логики классов, где создал особый графический аппарат (так называемые диаграммы Венна), нашедший применение в логико-математической теории «формальных нейронных сетей». В. принадлежит обоснование обратных операций в логическом исчислении Дж. Буля. Основной областью интереса Джона была логика, и он опубликовал три работы по этой теме. Это были «Логика случая», в которой вводится интерпретация частоты или частотная теория вероятностей в 1866; «Символьная логика», с которой были введены диаграммы Венна в 1881; «Принципы эмпирической логики» в 1889, в которой приводятся обоснования обратных операций в булевой логике.
На данной странице можно найти примеры задач:
komarovana.ucoz.ru
