Периметр фигуры найти – — как найти периметр различных геометрических форм. Простая задача: как найти периметр

Содержание

— как найти периметр различных геометрических форм. Простая задача: как найти периметр

Периметр фигуры это длина всех ее сторон. Не все фигуры имеют периметр, например, шар не имеет периметра. Стандартное обозначение периметра в математике — буква P

Периметр квадрата

Пусть длина стороны квадрата равна a . Квадрат имеет четыре равных стороны, поэтому периметр квадрата есть P = a + a + a +a или:

Периметр прямоугольника

Пусть длины сторон прямоугольника равны a иb .
Длина всех его сторон есть P = a + b + a + b или:

Периметр параллелограмма

Пусть длины сторон параллелограмма равны a и b
Длина всех его сторон есть P = a + b + a + b , поэтому периметр параллелограмма есть:

Как видно, периметр параллелограмма равен периметру прямоугольника.

Периметр равнобедренной трапеции

Пускай длины параллельных сторон трапеции a и b , а длины двух других сторон равна c (Как известно, равнобедренная трапеция имеет две равные стороны).

P = a + b + c + c = a + b + 2c

Периметр равностороннего треугольника

Как известно, равносторонний треугольник имеет 3 равные стороны. Если длина стороны равна a , тогда формула нахождения периметра есть P = a + a + a

Периметр параллелепипеда

Параллелепипед есть призма, все стороны которой являются параллелограммами. (Прямоугольный параллелепипед это фигура, стороны которой — прямоугольники.)
Если стороны основания имеют длину a и b тогда периметр основания есть P = 2a + 2b . Каждый параллелепипед имеет два основания, поэтому периметр двух оснований равен (2a + 2b).2 = 4a + 4b . Как мы знаем, параметр это сумма всех сторон. Таким образом, мы должны сложить четыре раза c

P = 4a + 4b + 4c

Периметр куба

Куб это параллелепипед, все стороны которого являются квадратами (все грани равны).
Тогда, периметр куба есть число сторон*длина.
Каждый куб имеет 12 сторон.
Тогда, формула нахождения периметра куба имеет вид:

Где a — длина его стороны.

Как найти Периметр различных геометрических форм

Возникли проблемы в понимании того, как найти периметр различных геометрических фигур? Бизнес сайт приходит к вам на помощь посредством облегчения геометрии, чем когда-либо!Удовольствие FactThe периметру или окружности Земли составляет 24,901 миль, я. э. почти 40,075 км!В математике, геометрии рассматриваются формы, размеры, взаиморасположение, трехмерная ориентация фигур в пространстве. Она имеет дело с тремя основными измерениями фигур:площади, объема и периметра.

Площадь является мерой степени двумерной фигуры или формы; поверхность может быть описана как степень поверхности объекта. Это мера в трехмерном пространстве вблизи объекта.

По периметру можно просто охарактеризовать как длина пути, который окружает двумерной формы. Другими словами, это расстояние вокруг фигуры. Давайте теперь взглянем на Как найти периметр различных геометрических форм.

Индекс
Площадь
Прямоугольник
Круг
Полуокружность

Сектор
Треугольник
Трапециевидные
Полигон

Площадь
Квадрат-это четырехугольник, который имеет все четыре стороны и четыре угла равны (все 90°).

Пример: чтобы найти периметр квадрата со стороной 5 см, мы используем формулу, показанную на рис..
Р = А + А + А + А
Р = 5 + 5 + 5 + 5
Р = 20 см
Эта же формула может использоваться для вычисления периметра ромба..
Обратно в индекс
Прямоугольник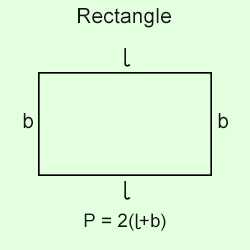

pedkolledj.ru

Найти периметр фигуры

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

Показать решение

C).

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a.

Показать решение

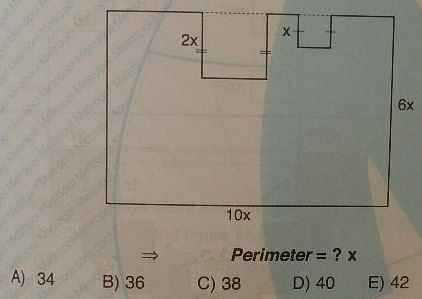
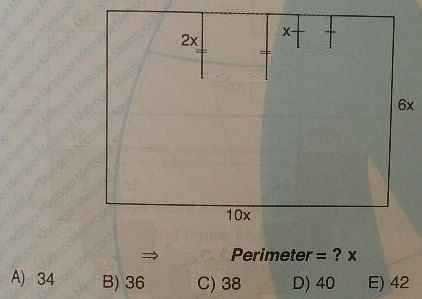
C).

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x.

Показать решение

?).

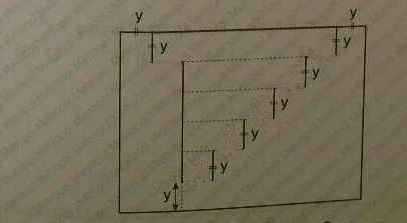
Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y.

Показать решение

D).

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x.

Показать решение

E).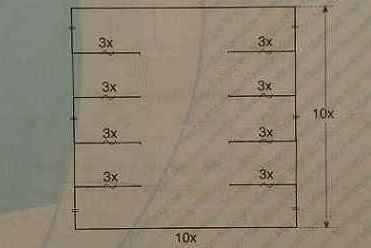

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x.

Показать решение

B).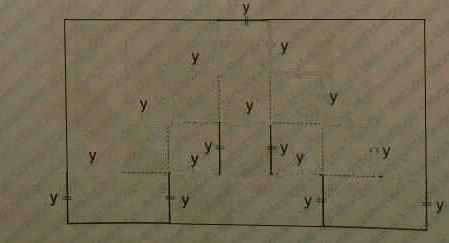

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y.

Показать решение

D).

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z.

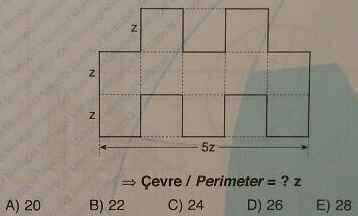
Показать решение

B).

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z.

www.uznateshe.ru

как найти периметр? :: SYL.ru

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение. Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

www.syl.ru

Периметр фигуры найти – — как найти периметр различных геометрических форм. Простая задача: как найти периметр

— как найти периметр различных геометрических форм. Простая задача: как найти периметр

Периметр квадрата

Периметр прямоугольника

Периметр параллелограмма

Периметр равнобедренной трапеции

Периметр равностороннего треугольника

Периметр параллелепипеда

Периметр куба

Найти периметр фигуры

как найти периметр? :: SYL.ru

Общая для всех фигур теория

Формулы периметров разных фигур

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Примеры задач

как найти периметр фигуры — Лучшее видео смотреть онлайн

Добавить комментарий Отменить ответ