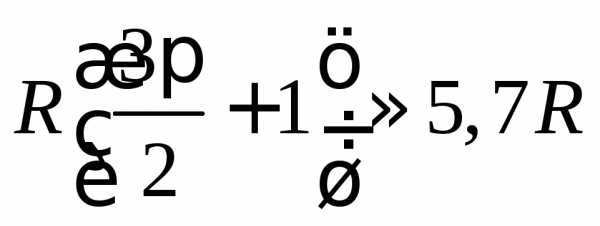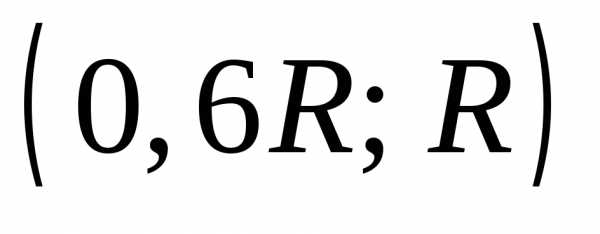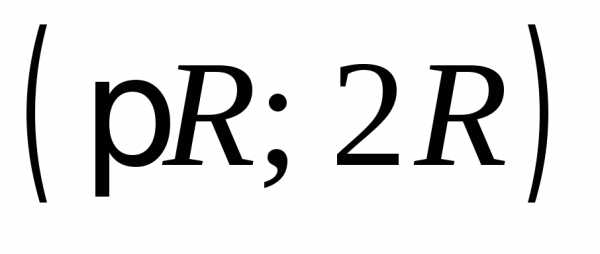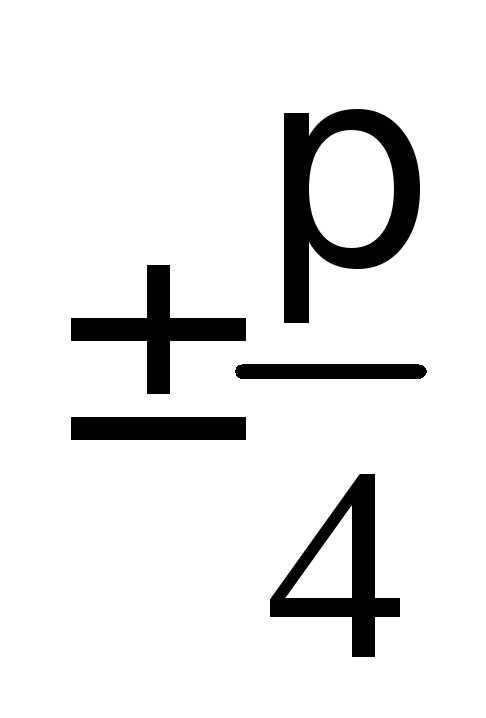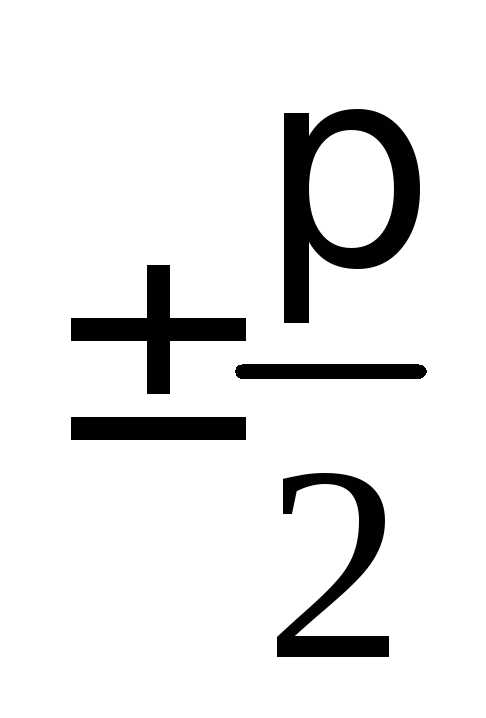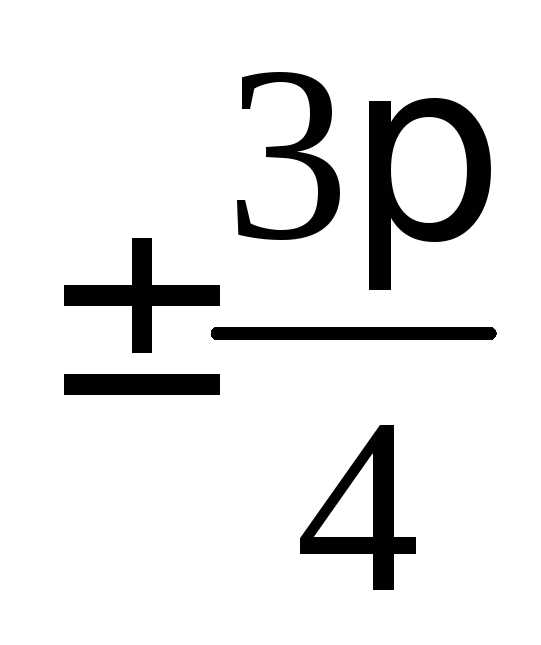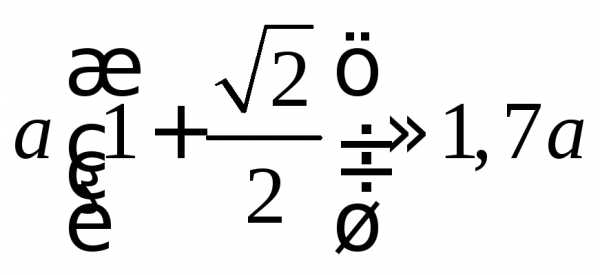Как построить график функции у = f(x) + m, если известен график функции у = f(x)
На этом уроке вы узнаете, как построить график функции y=f (x) + m, если известен график функции y= f(x)
На прошлом уроке мы научились график функции . Сейчас же наша задача – научиться строить график функции . Рассмотрим пример:
Дано:
у = х2(графиком данной функции будет парабола) (рис. 1)
Рис. 1. Иллюстрация к задаче
Построить:
а) у = х2 + 1
б) у = х2 — 1
Решение: Поясним характер кривых, их взаимное расположение поясним с помощью таблицы:
|
х |
0 |
1 |
-1 |
2 |
-2 |
|
у = х2 |
0 |
1 |
1 |
4 |
4 |
|
у = х2 + 1 |
1 |
2 |
2 |
5 |
5 |
|
у = х2 – 1 |
-1 |
0 |
0 |
3 |
3 |
Строим график функции у = х2 + 1 (рис. 2):
Рис. 2. График функции у = х2 + 1
График этой функции получается с помощью сдвига вверх на 1 единицу графика исходной функции.
График же следующей функции мы получим сдвигом исходной функции вниз на 1 единицу (рис. 3):
Рис. 3. График функции у = х2 – 1
Итак, чтобы построить график функции у = х2 + 1, надо график исходной функции сдвинуть на 1 единицу вверх. Чтобы построить график функции у = х2 – 1, необходимо график исходной функции сдвинуть на 1 единицу вниз.
Сдвиги вверх и вниз приводят к изменению множества значений. Множество значений иллюстрирует эти сдвиги:
;
;
Мы рассмотрели частный случай, когда к х2 прибавляли или отнимали единицу. Отсюда следует правило:
Правило построения не изменится при . Правило также не изменится, если мы возьмем любую другую функцию.
Сформулируем важное для нас правило:
Чтобы получить у = f(х) + m
— сдвинуть на единиц вверх, если m > 0,
— сдвинуть на единиц вниз, если m < 0
Рисунок отображает графически данное правило (рис. 4):
Рис. 4. Иллюстрация правила
Дана кривая . Построить кривые: а) ; б)
Построение:
а) Строим график функции и сдвигаем его на 1 единицу вверх (согласно правилу) (рис. 5):
Рис. 5. Иллюстрация к задаче а)
График функции а) построен сдвигом графика исходной функции на 1 единицу вверх.
б) Строим график функции и сдвигаем его на 1 единицу вниз (согласно правилу) (рис. 6):
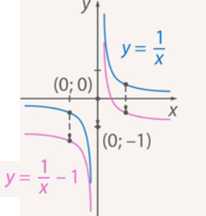
Рис. 6. Иллюстрация к задаче б)
Кривые а) и б) построены. Сделаем некоторый анализ:
У нас есть 3 кривые (у = ;
у = и у = . Каждая из них есть гипербола. Шаблоном для всех остальных является гипербола . Но у каждой гиперболы есть свой центр симметрии. Отметим их:(0; 0) –
(0; 1) –
(0; -1) –
Итак, построены 3 гиперболы, и для каждой из них указан центр.
Далее рассмотрим горизонтальные асимптоты:
Теперь проанализируем множества значений для каждой из функций:
Найти все значения параметра а, при которых уравнения: а) ;
б) = а; в) = а не имеют решений.
Решение:
а)
Ответ для этой задачи ясен сразу. Уравнение , если .
Ответ: это уравнение не имеет решений, когда .
б) Преобразуем левую часть:
=>
Эту функцию мы уже рассматривали в задаче 2. Эта функция принимает все значения, кроме 1.
Если , то это уравнение не имеет решений.
= + 1 => = => => = 1 =>
Ответ: это уравнение не имеет решений, когда .
в) Запишем его следующим образом:
=>
Мы только что рассматривали эту функцию в задаче 2 и выяснили, что она принимает все значения, кроме -1.
Если , то это уравнение не имеет решений.
Ответ: это уравнение не имеет решений, когда .
Дадим геометрическую интерпретацию каждой из задач (рис. 7)
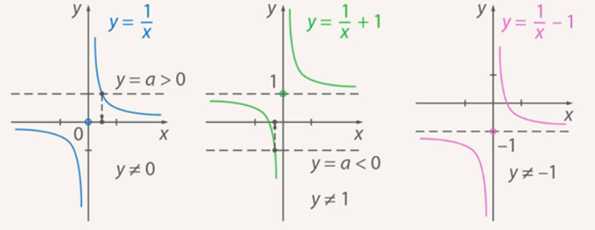
Рис. 7. Иллюстрация к задачам
Итак, мы решили 3 задачи и дали иллюстрации к каждой из них.
Решить уравнение .
Решение:
Для начала попробуем решить аналитическим методом.
а) Приведем к общему знаменателю и получим:
= 0
Дробь равна 0 тогда, и только тогда, когда числитель ( равен 0, а знаменатель (х) не равен 0. Но уравнения третьей степени мы сейчас решать не можем. Значит, единственным возможным методом остается графический.
б) Перепишем данное уравнение
График функции как из левой, так и из пр
interneturok.ru
Где построить график функции?
 |
Раньше, когда все работы выполнялись в тетрадках, такого вопроса, где построить график функции (в каком редакторе) не возникало. Сейчас нам больше нравится тыкать на кнопки клавиатуры, нежели писать ручками. Оформленная на компьютере работа выглядит аккуратно, а если немного приноровиться, то скорость выполнения будет выше рукописной.
Каждый из нас знает в каком редакторе набрать текст, но вот с графиками дело обстоит чуть хуже. Я использую для этих целей Geogebra. Определение с Википедии: GeoGebra — свободно распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки. Скачать ее можно тут совершенно бесплатно: http://www.geogebra.org/cms/ru/ |
Это очень простая в использовании программа, не требующая каких либо дополнительных знаний.
Для того, чтобы скачать ее и понять как построить график функции на плоскости, вам достаточно будет пяти минут.
Если она вас заинтересует, то можно заняться ей более плотно, так как она обладает огромными возможностями.
Пример построения:
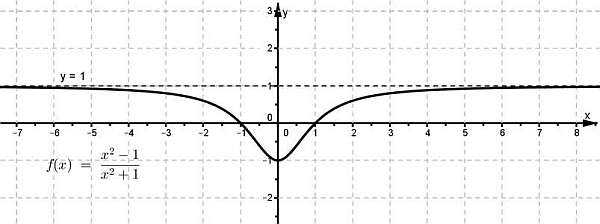 |
Разберем по шагам как это сделать.
| После скачивания и установки программы на рабочем столе появится вот такой ярлык: |
Кликаем по нему. Запускается Geogebra. Открывается вот такое окно программы:
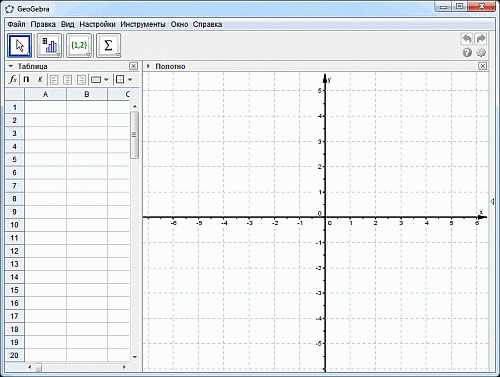
Закрываем ненужное окно таблиц, оно не понадобиться для нашего построения.
Добавляем нужные объекты: панель объектов и строку ввода. Находятся данные пункты на вкладке Вид.
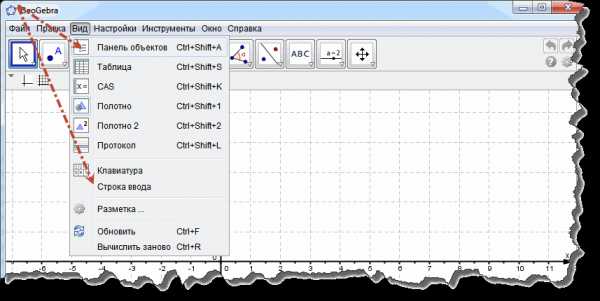
Рабочее окно программы теперь выглядит так:
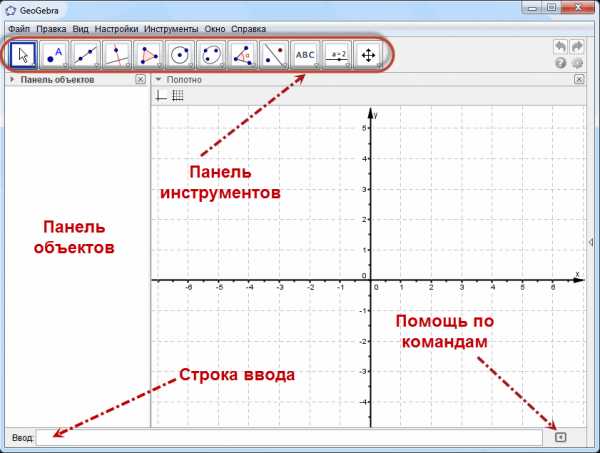
Чтобы каждый раз при запуске программы не производить вышеописанные действия, необходимо сохранить настройки.
Пункт меню Настройки → Сохранить настройки.
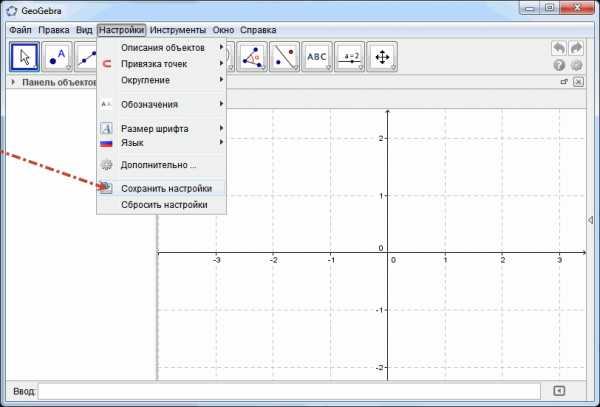
В строке ввода пишем функцию, которую хотим построить.
Например: y=x3 . Степень вводим значком ^. Для этого на клавиатуре одновременно нажимаем [Shift] и [6].
Имеем в строке y=x^3. Жмем Enter. График функции построен.

Немного подкорректируем график: добавим подпись, линию графика сделаем чуть толще.
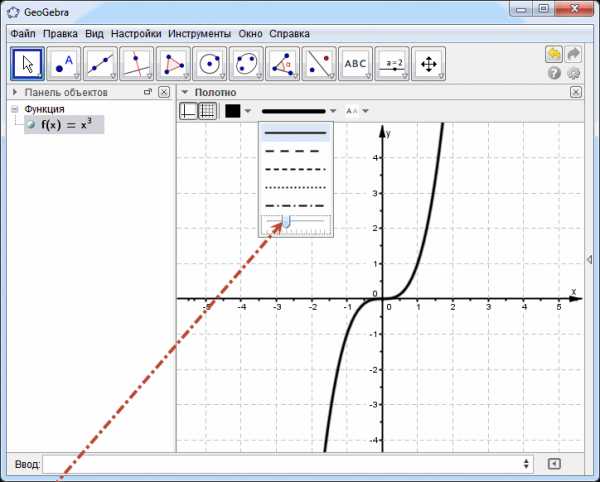
Перемещая бегунок регулируем толщину линии. При желании можно выбрать другой тип линии.
Если толщина линии по умолчанию вас не устраивает, то лучше изменить ее в настройках программы один раз, а не править для каждого графика функций.
Пункт меню Настройки → Дополнительно → Настройки по умолчанию
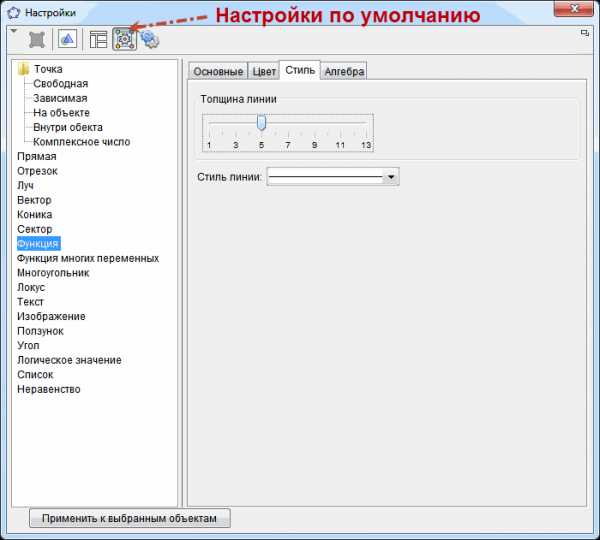
Не забываем после изменения, сохранить настройки.
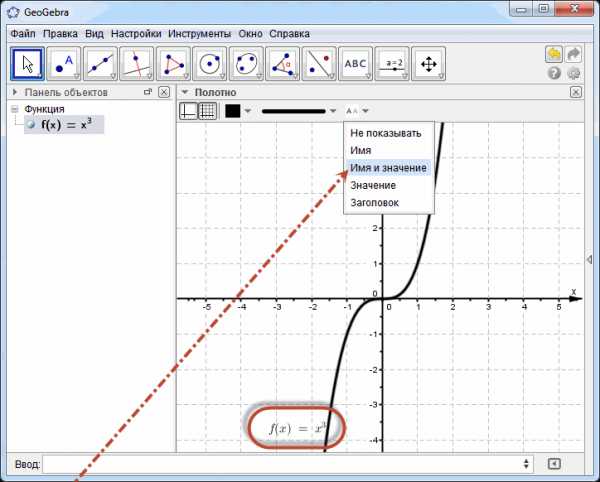
В раскрывающимся списке выбираем «Имя и значение» для добавления подписи к построенному графику. Подпись можем перемещать мышкой вдоль графика по своему усмотрению.
Если удерживать клавишу [Ctrl] и левую кнопку мыши, то можно перемещать рабочую область построения.
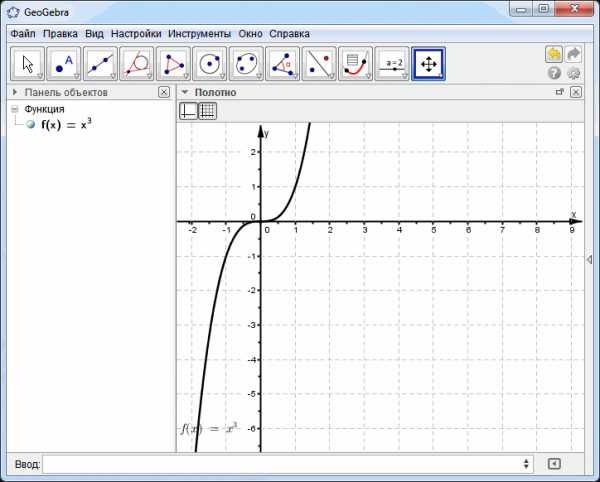
Можно изменить масштаб построения одновременно удерживая [Ctrl] и крутя колесико мыши.
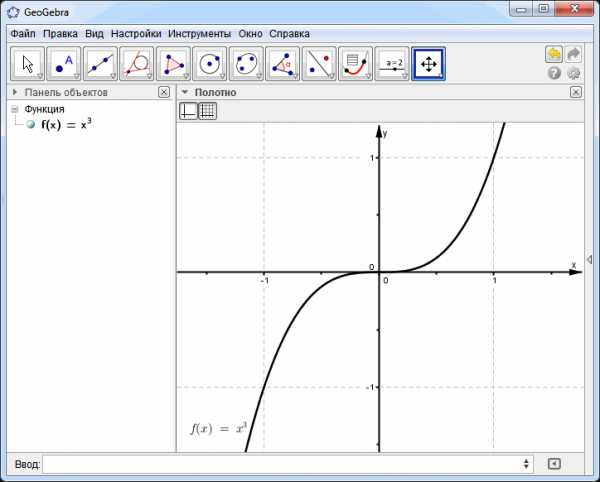
Операции перемещения и изменения масштаба можно найти и в раскрывающимся списке панели инструментов:
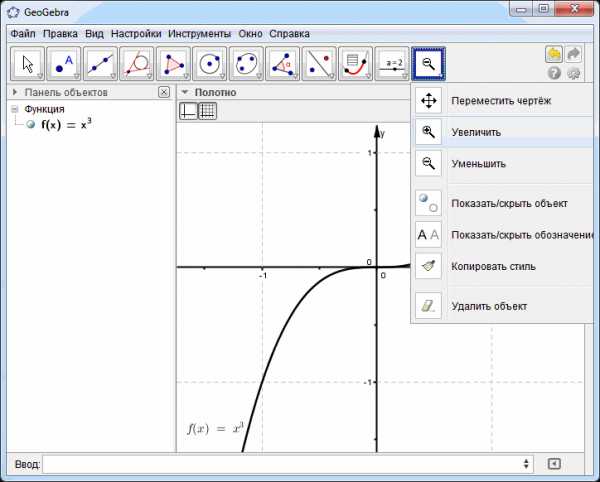
Построим еще один график функции, приведенный как пример в начале статьи.
В новом окне в строке ввода пишем: y=(x^2-1)/(x^2+1)
Незабываем, что «крышечка» ^ означает степень числа.
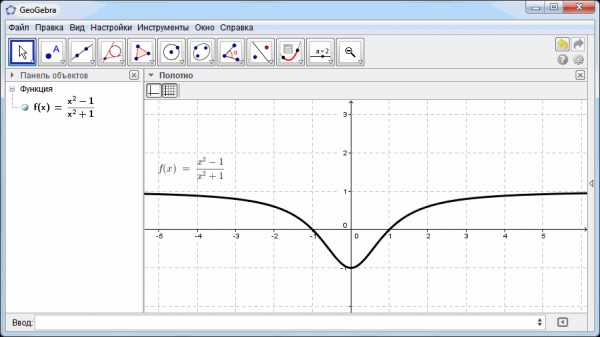
Допустим необходимо добавить на график горизонтальную асимптоту: y=1
Вводим это уравнение в строке ввода. Подкорректируем тип, толщину и цвет линии. Добавим подпись к графику.
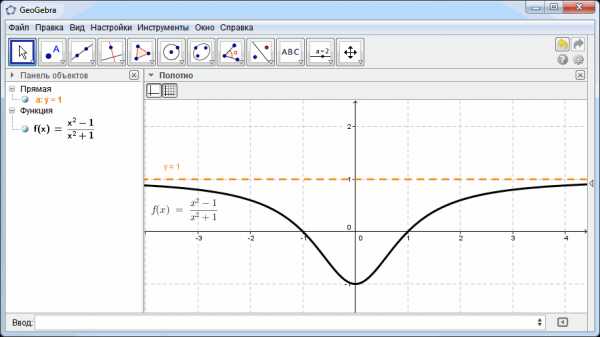
Пока на этом все. Возникли вопросы? Пишите.
matecos.ru
Графики функций. Простейшие построения
 |
График функции — это наглядный образ некоторой функции f(x). Здесь каждому значению х соответствует единственное значение y. Это множество точек на плоскости, координаты которых удовлетворяют заданному уравнению y = f(x).График уравнения — это множество всех точек плоскости, которые удовлетворяют заданному уравнению, т.е. обращают уравнение в верное числовое равенство. Зависимость в данном случае не обязательно является функцией.Рассмотрим ряд элементарных функций, таких, как прямая, парабола, гипербола, их свойства и правила построения. |
1. Прямая.
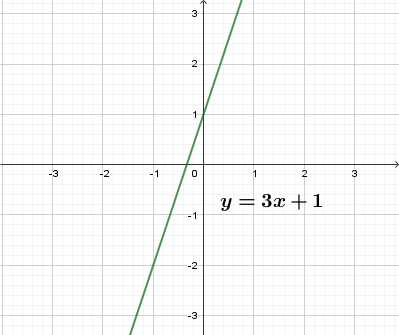
Прямая задается линейной функцией , т.е. уравнением первой степени вида y = ax + b.
при a>0 график функции возрастает (y=3x+1, a=3, a>0), при a


Рассмотрим частные случаи расположения линейных функций.
y = ax — график функции проходит через начало координат, т.е. точку О(0;0),
y = c (c = const) — график функции параллелен оси Ox,
x = c (c = const) — график функции параллелен оси Oy.
Для построения прямой достаточно получить координаты двух точек, принадлежащих заданному уравнению.
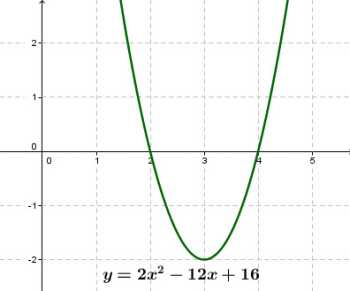
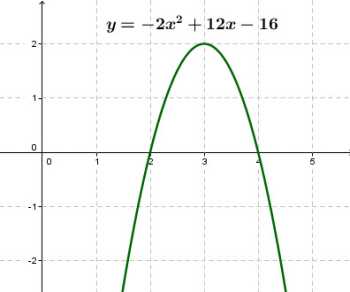
2. Парабола.
Парабола задается квадратичной функцией вида y = ax2 + bx + c.
|
при a > 0 ветви параболы направлены вверх,
|
при a < 0 ветви параболы направлены вниз.
|
 |
 |
3. Гипербола.
not found
4. Кубическая парабола.
matecos.ru
Примеры построения графиков функций
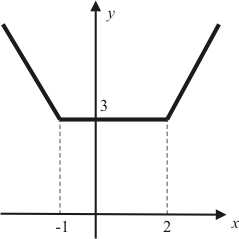
1.Построить график функции
Такая функция, задаваемая явно, но несколькими формулами, называетсякусочно заданной функцией.
Решение
Чтобы построить график этой кусочно заданной функции, нужно
построить графики известных функций
 ,
, ,
, ;
;выделить сужение каждой из этих функций на указанное множество;
объединить сужения в общий график.
Таким образом, график кусочно заданной функции получается компиляцией (объединением, склеиванием) «кусков» графиков известных функций.
2.Перейти от неявно заданной функцииy(x)уравнением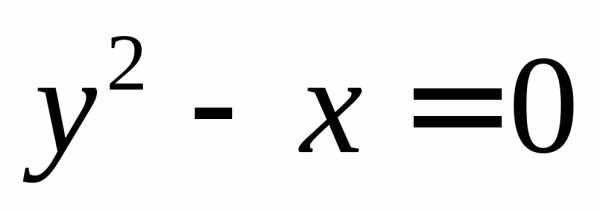 к явному заданию и построить график.
к явному заданию и построить график.
Решение
Решаем данное уравнение относительно y:
,
где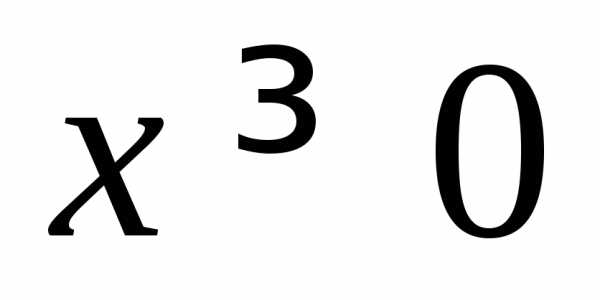 .
.
Получили равенство, которое каждому
значению 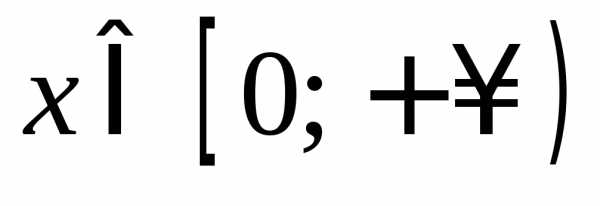 ставит в соответствие два значенияy.
Можно было бы его истолковать как
двузначную функцию. Но функциональная
зависимость по определению однозначная,
т. к. этим определением каждому
значениюxставится
в соответствие единственное значениеy. Поэтому нужно перейти
от якобы двузначной функции к совокупности
двух однозначных функций:
ставит в соответствие два значенияy.
Можно было бы его истолковать как
двузначную функцию. Но функциональная
зависимость по определению однозначная,
т. к. этим определением каждому
значениюxставится
в соответствие единственное значениеy. Поэтому нужно перейти
от якобы двузначной функции к совокупности
двух однозначных функций:
3.Построить график функции.
Решение
По определению модулей имеем, что
Преобразуем данную функцию, раскрыв оба модуля на каждом из промежутков знакопостоянства подмодульных выражений:
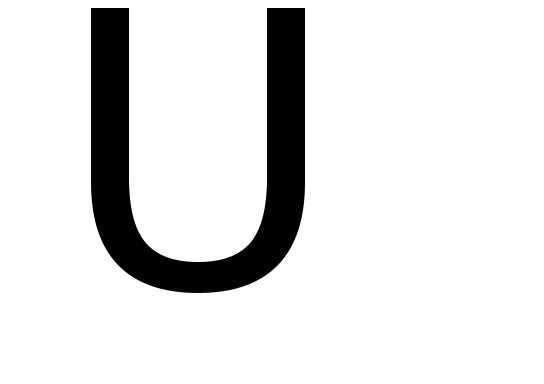
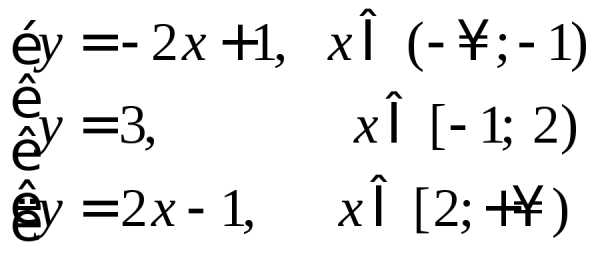 .
.
Строим график получившейся кусочно-заданной функции:
| |
4.Построить график функции, заданной параметрически
Линия, описываемая этими уравнениями, называетсяциклоидой.
Решение
Построение графика любой функции, заданной параметрически, проводится поточечно с помощью таблицы соответствующих значений параметра, аргумента и функции.
t | 0 | | | | 2 |
0 | | R | | 2R | |
0 | 2R | R | 0 | ||
Точки графика | (0; 0) | | | | |
Нетрудно видеть, что эта функция является периодической с наименьшим периодом .
Известно геометрическое определение циклоиды как линии, которую описывает фиксированная точка окружности радиуса R, если окружность катится без скольжения по прямой:
фиксированная точка окружности в начальный момент времени.
5.Построить график функциив полярной системе координат.
Решение
Построение линии в полярной системе
координат выполняется по точкам с
помощью таблицы соответствующих друг
другу значений аргумента и функции. При
построении таблицы учтем, что функция  является четной, поэтому.
является четной, поэтому.
| 0 | | | | |
2a | | a | | 0 | |
Точка на графике | T2, T3 | T4, T5 | T6, T7 | О |
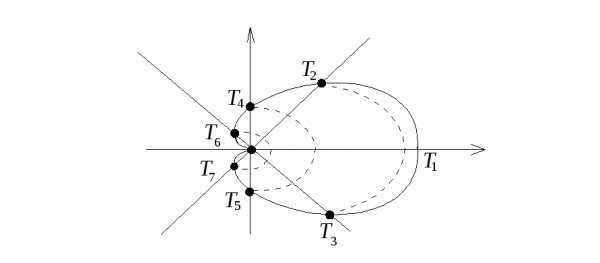
Линия, описываемая уравнением, называетсякардиоидой.
studfiles.net


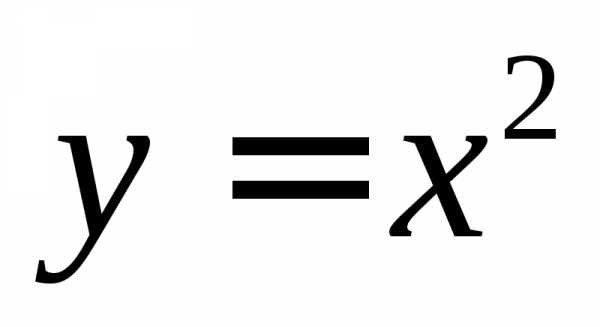 ,
, ,
,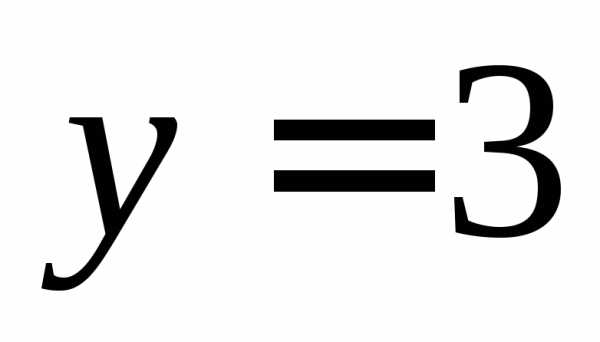 ;
; график функции
график функции