Ряд распределения случайной величины X
xi | 0 | 1 | 2 | 3 | 4 | 5 |
P(xi)= pi | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,1 |
Поскольку появление различных значений случайной величины X – несовместные события, то вероятность того, что число опрошенных на уроке учеников равно 2 или 3, равна сумме вероятностей этих значений СВ Х (по теореме сложения вероятностей). Тогда P(Х=2 или Х=3) = P(Х=2) + P(Х=3) = 0,3 + 0,2 = 0,5.
Вероятность того, что число опрошенных на уроке учеников будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, т.к.P(1≤X≤4)= P(Х=1) + P(Х=2)+ P(Х=3) + P(Х=4) = 0,8. Вероятность того ни один ученик не будет опрошенP(X= 0) = 0,1.
Задание:
Построить многоугольник (или полигон) распределения СВ X– числа опрошенных учеников.
Построить функцию распределения СВ Xчисла опрошенных учеников.
Используя функцию распределения, найти вероятность того, что число опрошенных на уроке учеников будет не меньше одного, но меньше трех, т.е. Р(1 ≤Х< 3).
Решение.
1). Построение многоугольника (полигона) распределения СВX – число опрошенных на уроке учеников приведено на рис.1.1..
Рис.1.1. Полигон распределения для данных примера 1.1.
2). Построение F(х) — функции распределения СВX – числа опрошенныхна уроке учеников.
По определению . Как следует из табл.1.2. случайная величинаХ не принимает значений, меньших 0. Следовательно, еслих < 0, то событиеX < х невозможно, а вероятность его равна нулю. Для всех значений
Если значение х удовлетворяет двойному неравенству, 0 ≤х < 2, тоF(х) = P(Х=0) + P(Х=1) = 0,1 + 0,2 = 0,3.
Пусть, например, х = 2. Тогда F(2) есть вероятность события X < 2. Это событие возможно в двух случаях: случайная величина X принимает значение 0 (с вероятностью 0,1), или 1 (с вероятностью 0,2). Применив теорему сложения вероятностей, получим F(2) = P(Х=0 и Х=1) = 0,1 + 0,2 = 0,3. Аналогичные рассуждения позволяют найти функцию распределения для данных табл. 1.1. Результат приведен в табл. 1.3.
Функция распределения (интегральная функция распределения) для примера 1.1 приведена в таблице 1.3.
Таблица 1.3
x | | | |||||
F(х) | 0,1 | 0,3 | 0,6 | 0,8 | 0,9 | 1,0 |
На рис.1.2. представлен график функции распределения F(x). Функция распределенияF(x)– неубывающая функция, её значение равно единице прих, большем наибольшего возможного значения случайной величины или равном ему (рис.1.2).
Рис.1.2. График функции распределения F(x).
График F(x) имеет ступенчатый вид. Функция распределения каждой дискретной случайной величины постоянна на интервалах и имеет скачки на границах, соответствующих значениям СВ. Величина скачков равна вероятностям конкретныxзначений СВ (табл. 1.3).
3). Как следует из таблиц 1.2. и 1.3, вероятность того, что число опрошенных на уроке учеников в определенный день будет меньше трех, можно найти по формуле Р(Х < 3) =F(3)= 0,6. С другой стороны, эту же вероятность можно найти. используяпо теорему сложения вероятностей:
Р(Х < 3) =P(Х=0 или Х=1 или Х=2) = 0,1 + 0,2 + 0,3 = 0,6.
Вероятность того, что на уроке будет опрошено не менее одного ученика, когда вероятность события X ≥ 1 вычисляется по формуле
P(X ≥ 1) = 1– P(X < 1) = 1 – 0,1 = 0,9
где P(X < 1) вероятность того, что на уроке будет опрошено менее одного ученика, т.е. не будет опрошен ни один ученик. Вероятность событияP(X ≥ 1) также можно найти по формуле
P(X ≥ 1) = 1– P(X < 1) = 1–F(1) = 1 – 0,1 = 0,9
Вероятность того, что число опрошенных учеников в определенный день будет не меньше одного, но меньше трех, можно найти по формуле Р(1 ≤Х <3) =F(3)–F(1) = 0,6 – 0,1 = 0,5.
Этот же результат может быть получен непосредственно по ряду распределения СВ Х(табл.1.2):
Р(1 ≤Х <3)=P(X=1)+P(X=2)=0,2+0,3=0,5
studfiles.net
Случайные величины. Закон распределения. Ряд распределения дискретной случайной величины. Смешанная случайная величина.
Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество Ξ, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z.В зависимости от вида множества Ξ случайные величины могут быть дискретными и недискретными
. СВ Х называется дискретной, если множество ее возможных значений Ξ – счетное или конечное. Если множество возможных значений СВ несчетно, то такая СВ является недискретной.В теоретико-множественной трактовке основных понятий теории вероятностей случайная величина Х есть функция элементарного события: X=φ(ω), где ω – элементарное событие, принадлежащее пространству Ω. При этом множество Ξ возможных значений СВ Х состоит из всех значений, которые принимает функция φ(ω).Закон распределения случайной величины.Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной. (То есть, всякое соотношение, устанавливающее связь между возможными значениями СВ и их вероятностями.)СВ будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое событие. Про случайную величину мы будем говорить, что она
| X | x1 | x2 | … | xn | … |
| P | p1 | p2 | … | pn | … |
Ряд распределения дискретной случайной величины.Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x1, x2, …, xn,
… и вероятности этих значений p1, p2, …, pn, …, где pi=P{X=xi} – вероятность того, что в результате опыта СВ Х примет значение xi (i=1,2,…, n, …).Ряд распределения записывается в виде таблицы:
Так как события {X=x1}, {X=x2}, … несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке равна единице:
Смешанная случайная величина.
Случайная величина называется смешанной, если функция распределения F(x) на некоторых участках непрерывна, а в отдельных точках имеет разрывы (скачки).
На тех участках, где F(x) непрерывна, вероятность каждого отдельного значения случайной величины равна нулю. Вероятность тех значений, где функция распределения совершает скачки, отличны от нуля и равны величине скачка.
7.Функция распределения случайной величины и ее свойства.
F(x)=P{X<x}.
Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.
1. F(-¥ ) = 0. (5.2)
2. F(+¥ ) = 1. (5.3)
3.F(x) – неубывающая функция своего аргумента, т.е. при x1 < x2
F(x1) £ F(x2).
Доказательство этого свойства иллюстрируется рис. 5.2.
Представим событие C={X<x2} как сумму двух несовместных событий С=A+B, где A={X<x1} и B={x1£X<x2}.
По правилу сложения вероятностей
P(C)=P(A)+P(B),
т.е. P{X<x2}=P{X<x1}+P{ x1£X<x2}, или
F(x2)=F(x1)+P{x1£X<x2}.
Но P{x1£X<x2}£0, следовательно, F(x1) £ F(x2)
4. P(α£ X < β) = F(β) — F(α), для «[α,β[ÎR. (5.4)
Доказательство этого свойства вытекает из предыдущего доказательства.Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α) равна приращению функции распределения на этом участке.Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1.
8.Непрерывная случайная величина. Плотность распределения случайной величины и ее свойства.
Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю
P{X=α}=0 для любого α.В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.
Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:
P{x£ X <x+Dx}=F(x+Dx) — F(x).
Плотность вероятности на этом участке определяется отношением
(5.6)
Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.
Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.
Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:
(5.7)
В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).
Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:
(5.8)
В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).
Основные свойства плотности распределения:
1. Плотность распределения неотрицательна: f(x) ³ 0.
Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.
2. Условие нормировки: Это свойство следует из формулы (5.8), если положить в ней x=∞.
Геометрически основные свойства плотности f(x) интерпретируются так:1.вся кривая распределения лежит не ниже оси абсцисс;2полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
1. 9. Числовые характеристики случайных величин.Математическое ожидание. Свойства математического ожидания.
Законы распределения случайной величины являются исчерпывающими характеристиками. Каждый закон распределения представляет собой некоторую функцию, указание которой полностью описывает случайную величину с вероятностной точки зрения.
Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями; зачастую достаточно бывает только отдельные числовые параметры, характеризующие отдельные черты распределения; например, среднее значение или разброс случайной величины («степень случайности»). Такие числа называются числовыми характеристиками случайной величины.
Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y=φ(X).
Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:
| Xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
| φ(X)i | φ(x1) | φ(x2) | … | φ(xn) |
| pi | p1 | p2 | … | pn |
Определяем вероятности появления различных значений случайной величины У
Тогда математическое ожидание случайной величины Y определяется так:
(9.1)
Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности pi элементом вероятности f(x)dx, а сумму – интегралом, получаем:
. (9.2)
Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:
(9.3)
Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидания, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента.
Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины.
Для вычисления математического ожидания для ДСВ каждое значение xi учитывается с «весом», пропорциональным вероятности этого значения.
(6.1)
M[X]-оператор математического ожидания;
mx — число, полученное после вычислений по формуле.
Для НСВ заменим отдельные значения непрерывно изменяющимся параметром , соответствующие вероятности — элементом вероятности , а конечную сумму – интегралом: (6.2)
Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами , в которых сосредоточены соответственно массы р1, р2,…., причем . Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью .
Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.
, (6.3)
где сумма распространяется на все значения xi, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.
Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.
cyberpedia.su
Лекция № 4 Случайные величины. Определение и формы задания законов распределения. Числовые характеристики. Определение случайной величины
Случайная величина – это величина, которая в результате опыта принимает заранее неизвестное значение.
Примеры:
Количество студентов, присутствующих на лекции.
Количество домов, сданных в эксплуатацию в текущем месяце.
Температура окружающей среды.
Вес осколка разорвавшегося снаряда.
Случайные величины делятся на дискретные и непрерывные.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или счетным.
Непрерывной называют случайную величину, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, число возможных значений непрерывной случайной величины бесконечно.
В приведенных примерах: 1 и 2 – дискретные случайные величины, 3 и 4 – непрерывные случайные величины.
В дальнейшем, вместо слов «случайная величина» часто будем пользоваться сокращением с. в.
Как правило, случайные величины будем обозначать большими буквами, а их возможные значения – маленькими.
В теоретико-множественной трактовке основных понятий теории вероятностей случайная величина Х есть функция элементарного события: Х =φ(ω), где ω – элементарное событие принадлежащее пространству Ω ( ω Ω). При этом множество Ξ возможных значений с. в. Х состоит из всех значений, которые принимает функция φ(ω).
Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (например, вероятность того, что она примет какое-то значение или попадет на какой-то интервал).
Формы задания законов распределения случайных величин. Ряд распределения.
Это таблица в верхней строке которой перечислены в порядке возрастания все возможные значения случайной величины Х: х1, х2, …, хn, а в нижней – вероятности этих значений: p1, p2, …, pn , где pi = Р{Х = xi}.
Х | x1 | x2 | …… | xn |
Р | p1 | p2 | …… | pn |
Так как события {Х = x1}, {Х = x2}, … несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке ряда распределения, равна единице
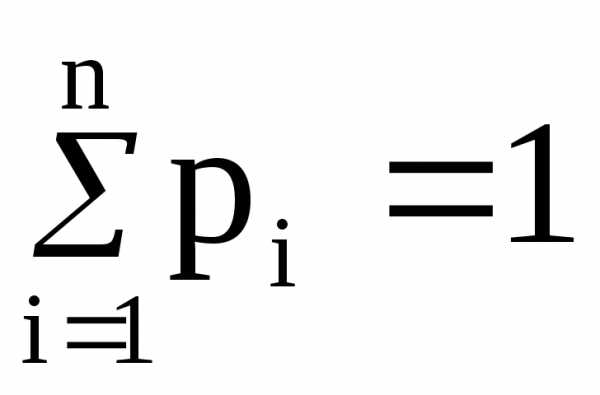 .
.
Ряд распеделения используется для задания закона распределения только дискретных случайных величин.
Многоугольник распределения
Графическое изображение ряда распределения называется многоугольником распределения. Строится он так: для каждого возможного значения с. в. восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения с. в. Полученные точки для наглядности (и только для наглядности! ) соединяются отрезками прямых.
Интегральная функция распределения (или просто функция распределения).
Это функция, которая при каждом значении аргумента х численно равна вероятности того, что случайная величина окажется меньше, чем значение аргумента х.
Функция распределения обозначается F(x): F(x) = P {X x}.
Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Функция распределения – это наиболее универсальная форма задания с. в., которая может использоваться для задания законов распределения как дискретных, так и непрерывных с. в.
studfiles.net
ТВ5
ЧАСТЬ 4
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Лекция 5
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ. ЗАКОНЫ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНЫХ ВЕЛИЧИН
ЦЕЛЬ ЛЕКЦИИ: ввести понятие случайной величины и закона распределения; для дискретной случайной величины определить ряд распределения; ввести понятие функции распределения и плотности распределения вероятностей и определить их свойства.
Под случайной величиной понимается
величина, которая в результате опыта
со случайным исходом принимает то или
иное значение. Возможные значения
случайной величины образуют множество  ,
которое называютмножеством возможных
значенийслучайной величины.
,
которое называютмножеством возможных
значенийслучайной величины.
Пример 1. Для игральной кости случайной величинойХбудет число выпавших очков. Множество возможных значений.
Пример 2. Тестирование изделия до появления первого исправного. Случайная величинаY– число тестов, которое будет произведено. Множество возможных значенийбесконечное, но счетное.
Впредь случайную величину будем
обозначать большими буквами, например Х,
а их возможные значения – малыми; в
приведенных примерах–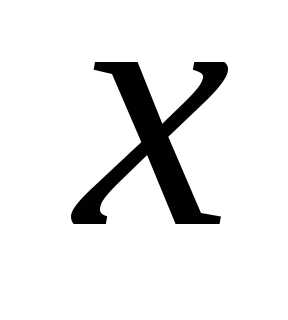 и
и .
.
Случайные величины могут быть дискретными
и недискретными. В теоретико-множественной
трактовке основных понятий теории
вероятностей случайная величина Хесть функция элементарного события,
где – элементарное событие, принадлежащее
пространству.
При этом множество
– элементарное событие, принадлежащее
пространству.
При этом множество возможных значений случайной величины
состоит из тех значений, которые принимает
функция
возможных значений случайной величины
состоит из тех значений, которые принимает
функция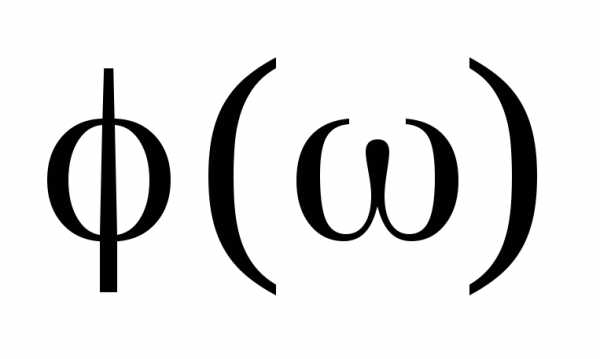 .Если множество
.Если множество  счетное или конечное, то случайная
величинаХ называется дискретной, если несчетное
– недискретной.При этом случайные
величины могут иметь различные
распределения.
счетное или конечное, то случайная
величинаХ называется дискретной, если несчетное
– недискретной.При этом случайные
величины могут иметь различные
распределения.
Закон распределения. Ряд распределения
дискретной случайной величины
Законом распределенияслучайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.
Рядом распределениядискретной случайной величиныХназывается таблица, в верхней строке которой перечислены в порядке возрастания всевозможные значения случайной величины а в нижней – вероятности этих значений:При этом– вероятность того, что в результате опыта случайная величинаХпримет значение.
Ряд распределения записывается в виде таблицы
(4.1)
События 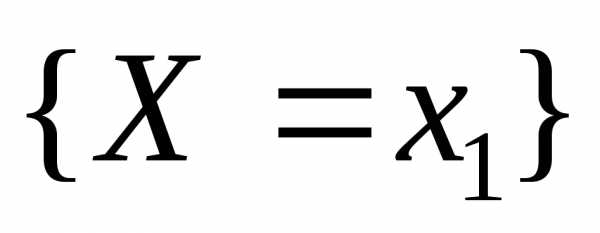 ;
;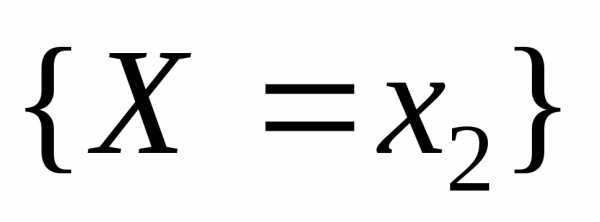 ;
… несовместны и образуют полную группу,
поэтому сумма всех вероятностей
;
… несовместны и образуют полную группу,
поэтому сумма всех вероятностей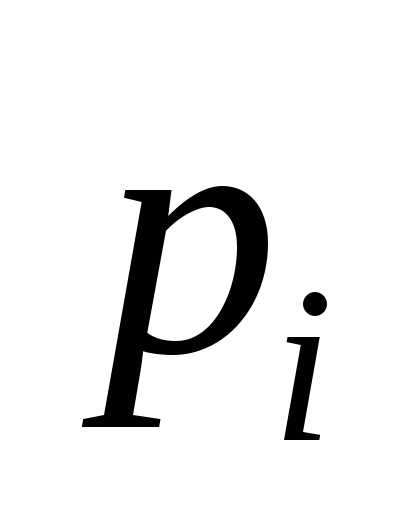 в (4.1) будет равна единице:
в (4.1) будет равна единице:
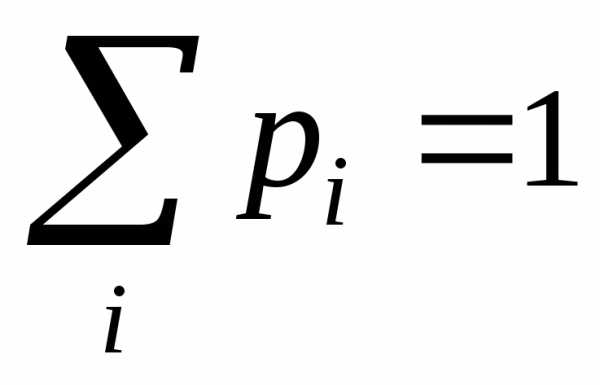 . (4.2)
. (4.2)
Отсюда следует, что единица распределена между возможными значениями случайной величины.
Пример. Ряд распределения случайной величиныХ
Х: | 0 | 1 | 2 | 3 | |
0,24 | 0,46 | 0,26 | 0,04 | . |
(4.3)
Графическое изображение ряда распределения называется многоугольником распределения.
Строится он так: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения случайной величины. Полученные точки для наглядности соединяются отрезками прямых (см. рис. 4.1).
Кроме этой геометрической интерпретации, часто полезнамеханическая интерпретация, при которой ряд распределения рассматривается как ряд материальных точек на оси абсцисс, имеющих значения, и соответственно массыв сумме составляющие единицу (см. рис. 4.2).
Функция распределения
Наиболее общей формой закона распределения, пригодной как для дискретных, так и недискретных случайных величин, является функция распределения.
Функцией распределенияслучайной величиныХназывается вероятность того, что она примет значение меньшее, чем заданноех(аргумент функции)
. (4.4)
Геометрически определение (4.4) интерпретируется как вероятность того, что случайная точка попадает левее заданной точки (см. рис. 4.3).
Свойства функции распределения выводятся из геометрической интерпретации (см. рис. 4.3–4.4):
1. 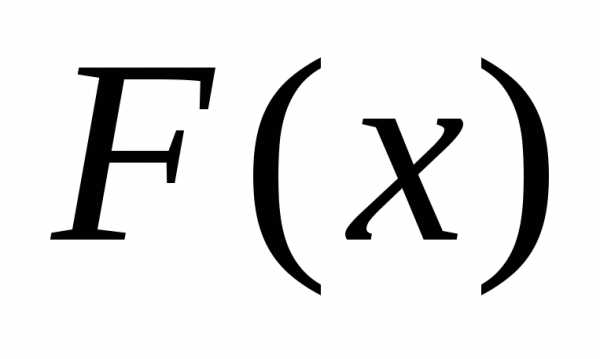 – неубывающая функция своего аргумента,
т. е. если
– неубывающая функция своего аргумента,
т. е. если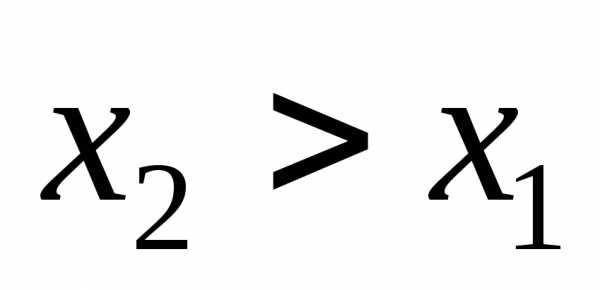 ,
то.
,
то.
Для доказательства представим событие как сумму двух несовместных событий (см. рис. 4.4)
,
где
.
По правилу сложения вероятностей
;
.
Учитывая выражение (4.4), получаем
, (4.5)
но так как , то окончательно имеем, что
.
2. ;.
Перемещая 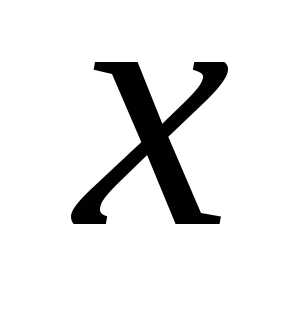 до бесконечности влево (при)
или вправо (при),
можно убедиться, что событие становится
либо невозможным,
либо достоверным.
до бесконечности влево (при)
или вправо (при),
можно убедиться, что событие становится
либо невозможным,
либо достоверным.
Функция
распределения 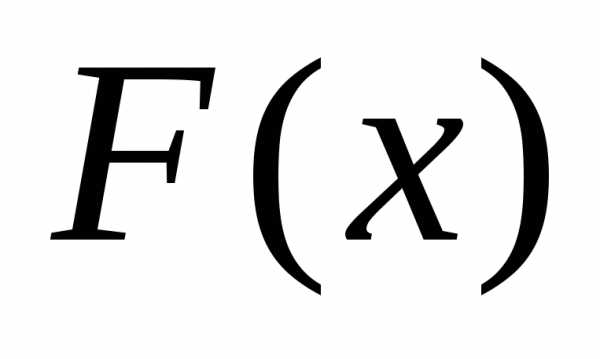 любой случайной величины есть неубывающая
функция своего аргумента, значения
которой заключены между нулем и единицей;
причем,
а.
В отдельных точках эта функция может
иметь скачки (разрывы первого рода), на
некоторых участках она может быть
постоянной, на других – монотонно
возрастать (см. рис. 4.5).
любой случайной величины есть неубывающая
функция своего аргумента, значения
которой заключены между нулем и единицей;
причем,
а.
В отдельных точках эта функция может
иметь скачки (разрывы первого рода), на
некоторых участках она может быть
постоянной, на других – монотонно
возрастать (см. рис. 4.5).
Спомощью функции распределения можно
вычислить вероятность попадания
случайной точки на участок от до
до .
Для определенности левый конец участка
будем включать в него, а правый – нет.
.
Для определенности левый конец участка
будем включать в него, а правый – нет.
Искомую
вероятность получаем из выражения
(4.5), положив 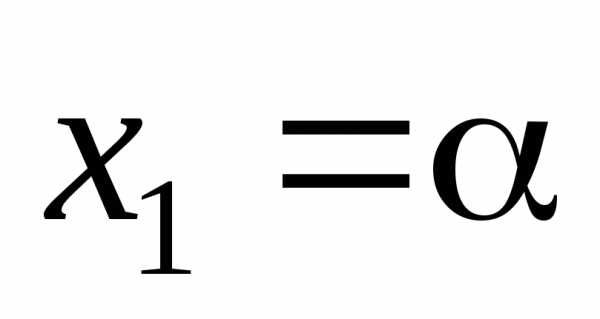 и
и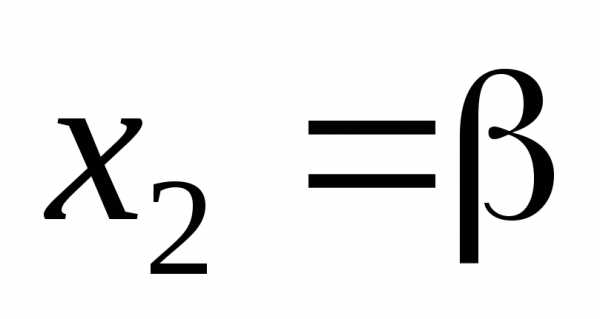 ,
,
,
откуда
. (4.6)
Таким
образом, вероятность того, что случайная
величинаХв результате опыта попадет на участок
от до
до (включая
(включая ),
равна приращению функции распределения
на этом участке (см. рис. 4.6). Другая запись
выражения (4.6)
),
равна приращению функции распределения
на этом участке (см. рис. 4.6). Другая запись
выражения (4.6)
,
где квадратная скобка означает, что данный конец включается в участок, а круглая – что не включается.
Вероятность отдельного значения
случайной величины. Если взять любую
точку и примыкающий к ней участок
и примыкающий к ней участок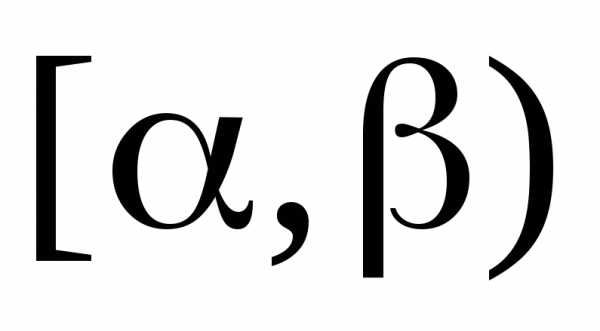 ,
то, приближая
,
то, приближая к
к ,
в пределе получаем
,
в пределе получаем
. (4.7)
Значение этого
предела зависит от того, непрерывна ли
функция 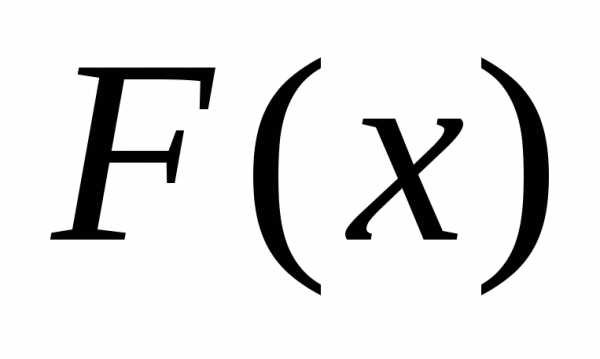 в точке
в точке или терпит разрыв. Если функция в точке
или терпит разрыв. Если функция в точке совершает скачок, то предел (4.7) равен
величине этого скачка. Если же
совершает скачок, то предел (4.7) равен
величине этого скачка. Если же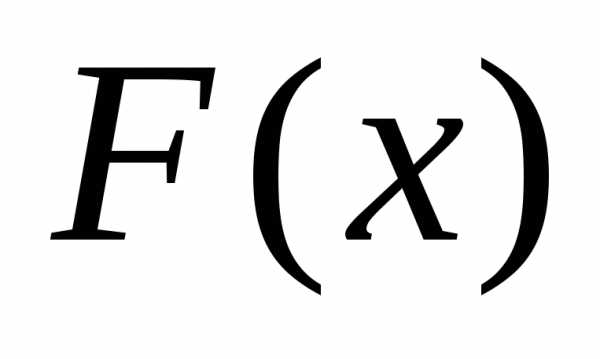 везде непрерывна, то вероятность каждого
отдельного значения случайной величиныХ равна нулю. Последнее утверждение не
означает, что событие
везде непрерывна, то вероятность каждого
отдельного значения случайной величиныХ равна нулю. Последнее утверждение не
означает, что событие 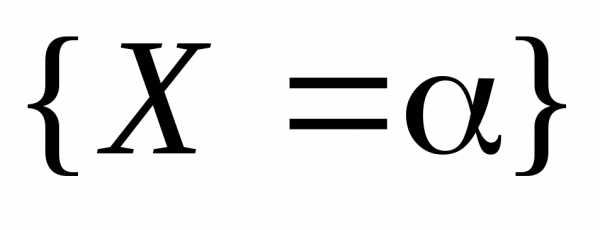 невозможно; оно возможно, но с нулевой
вероятностью.
невозможно; оно возможно, но с нулевой
вероятностью.
Функция распределения дискретной
случайной величины
Для случайной величины Х, представленной рядом распределения
Х : | 0 | 1 | 2 | 3 | |
0,24 | 0,46 | 0,26 | 0,04 | , |
можно, задаваясь различными значениями х, вычислить функцию распределения:
;
;
;
;
.
На
рис. 4.7 приведена рассчитанная функция
распределения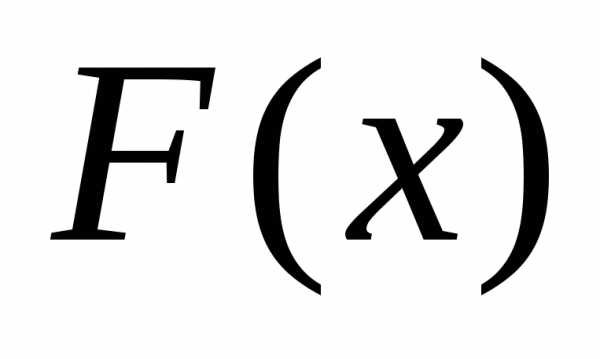 .
Жирными точками отмечены значения в
точках разрыва; функция
.
Жирными точками отмечены значения в
точках разрыва; функция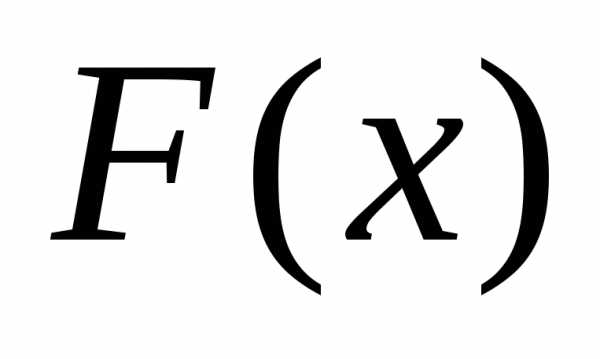 при подходе к точке разрыва слева
сохраняет свое значение (функция
«непрерывна
слева»). Заметим, что между скачками
функция
при подходе к точке разрыва слева
сохраняет свое значение (функция
«непрерывна
слева»). Заметим, что между скачками
функция 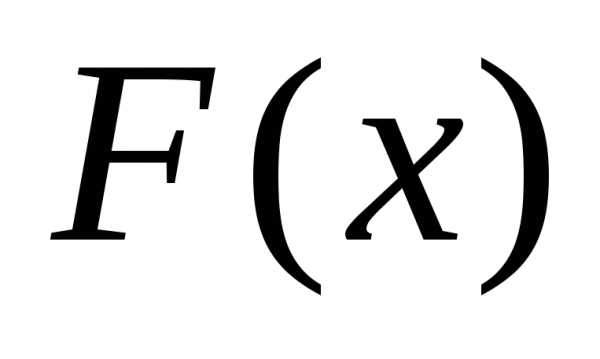 постоянна.
постоянна.
Функция распределения любой дискретной случайной величины есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции распределения равна единице.
Индикатор события. Индикатором
событияАназывается случайная величина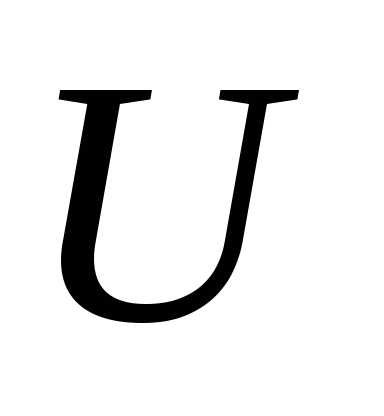 ,
равная единице, если в результате опыта
событиеАпроизошло, и – нулю, если не произошло:
,
равная единице, если в результате опыта
событиеАпроизошло, и – нулю, если не произошло:
Ряд распределения случайной величины 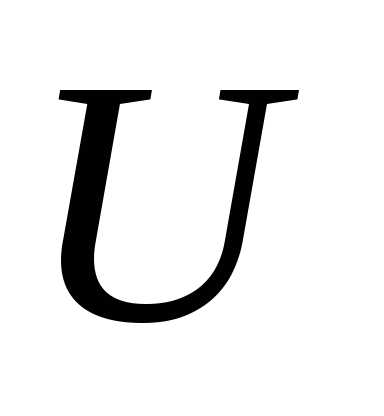 с вероятностью событияА,равной
с вероятностью событияА,равной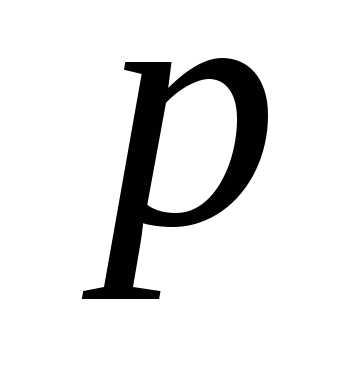 ,
имеет вид
,
имеет вид
Многоугольник
распределения случайной величины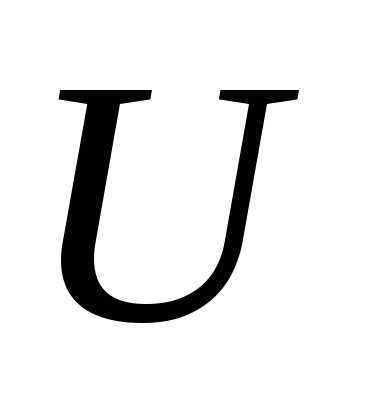 приведен на рис. 4.9, а функция распределения
– на рис. 4.10.
приведен на рис. 4.9, а функция распределения
– на рис. 4.10.
Непрерывная случайная величина.
Плотность распределения
Случайная величинаХназываетсянепрерывной, если функция распределения не только непрерывна в любой точке, но и дифференцируема всюду, кроме, может быть, отдельных точек, где она терпит излом (см. рис. 4.11). Так как скачков эта функция не имеет, то вероятность любого отдельного значения непрерывнойслучайной величины равна нулю, т. е.
.
Поэтому говорить о распределении вероятностей отдельных значений не имеет смысла. В качестве закона распределения непрерывных случайных величин вводится понятие плотности распределения вероятностей или плотности распределения.
Исходим из механической
интерпретации распределения вероятностей.Для дискретной случайной величиныХв точкахсосредоточены
массы,
сумма которых равна единице. Для
непрерывной случайной величины масса,
равная 1, «размазана» по числовой
оси с непрерывной в общем случае
плотностью (см. рис. 4.12). Вероятность
попадания случайной величиныХна любой участок может быть интерпретирована как масса,
приходящаяся на этот участок, а средняя
плотность на этом участке – как отношение
массы к его длине. Для участка
может быть интерпретирована как масса,
приходящаяся на этот участок, а средняя
плотность на этом участке – как отношение
массы к его длине. Для участка
.
Но вероятность определяется как приращение функции распределения на этом участке
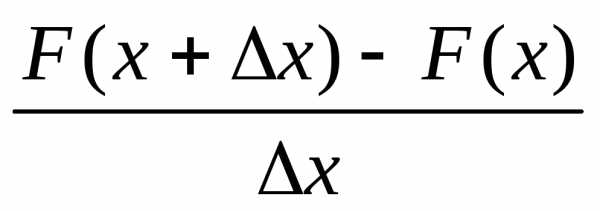 ,
,
и, переходя к пределу при 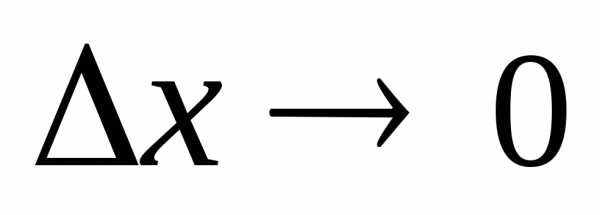 ,
получаем плотность в точке
,
получаем плотность в точке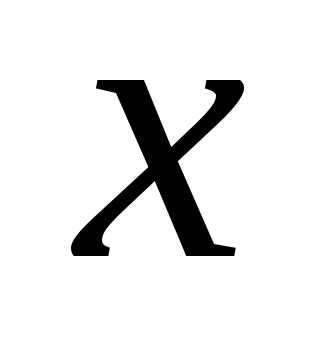
,
т. е. производную функции распределения.
Плотностью
распределения 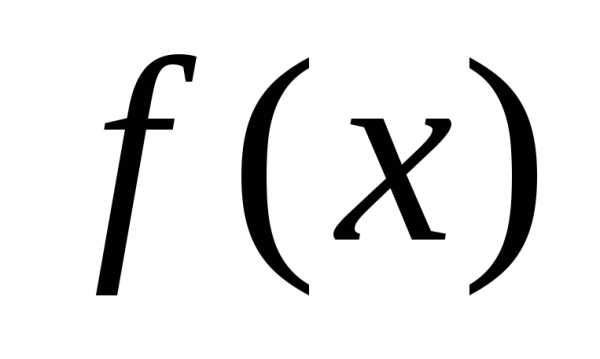 непрерывной случайной величиныХ в точке х называется производная ее функции
распределения в этой точке
непрерывной случайной величиныХ в точке х называется производная ее функции
распределения в этой точке
. (4.8)
Плотность распределения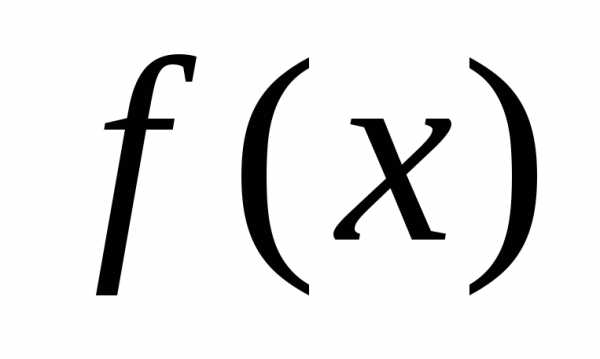 ,
как и функция распределения
,
как и функция распределения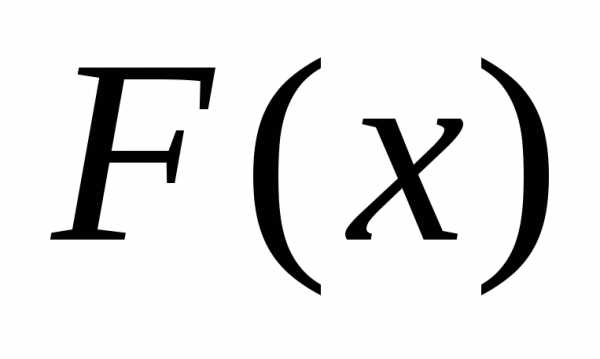 ,
является одной из форм закона распределения,
но она существует только для непрерывных
случайных величин. График плотности
распределения
,
является одной из форм закона распределения,
но она существует только для непрерывных
случайных величин. График плотности
распределения  называется кривой распределения
(см. рис. 4.13).
называется кривой распределения
(см. рис. 4.13).
Вероятность
попадания случайной величиныХ на участок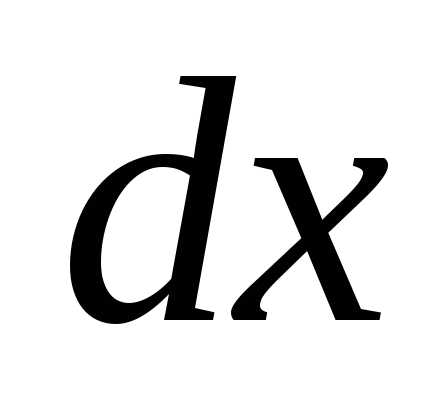 с точностью до бесконечно малых высших
порядков равна
с точностью до бесконечно малых высших
порядков равна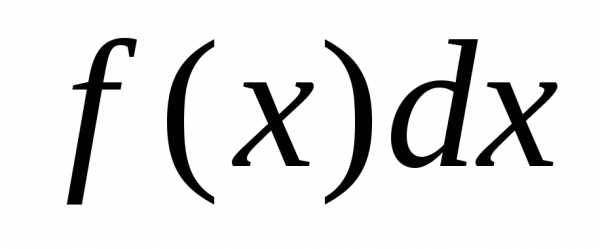 .
Эта величина
.
Эта величина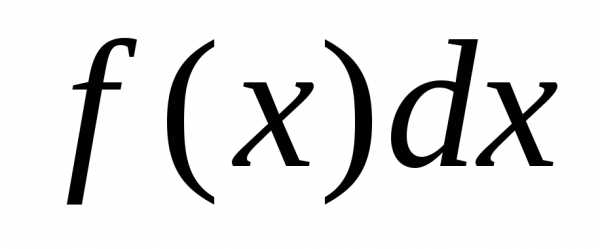 называется элементом вероятности и
геометрически равна (приближенно)
площади элементарного прямоугольника,
опирающегося на отрезок длиной
называется элементом вероятности и
геометрически равна (приближенно)
площади элементарного прямоугольника,
опирающегося на отрезок длиной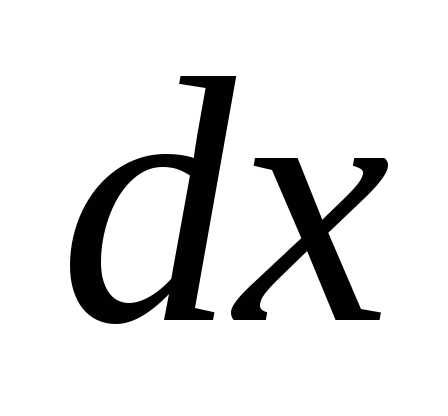 и примыкающего к точке
и примыкающего к точке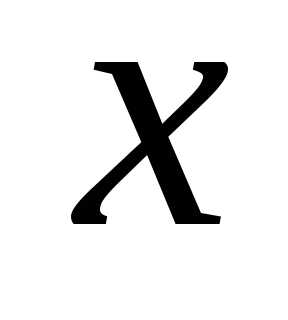 (см. рис. 4.13).
(см. рис. 4.13).
Вероятность попадания случайной величины Хна участок от до
до равна сумме элементов вероятности на
всем этом участке, т. е. интегралу вида
равна сумме элементов вероятности на
всем этом участке, т. е. интегралу вида
. (4.9)
В геометрической
интерпретации эта вероятность равна
площади фигуры, ограниченной сверху
кривой распределения и опирающейся на
участок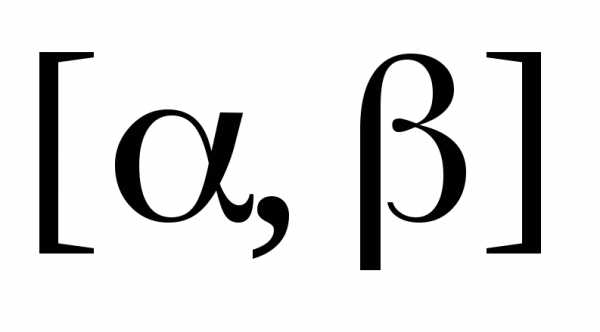 (см. рис. 4.14). Функция распределения
теперь может быть вычислена следующим
образом:
(см. рис. 4.14). Функция распределения
теперь может быть вычислена следующим
образом:
. (4.10)
Геометрически (см. рис. 4.14) – это площадь,
ограниченная сверху кривой распределения
и лежащая левее точки 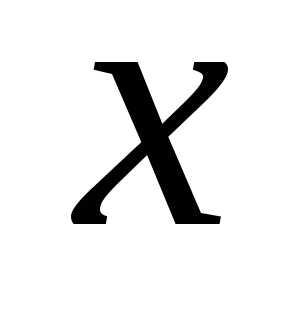 .
.
Свойства плотности распределения.
1. Плотность распределения – неотрицательная функция
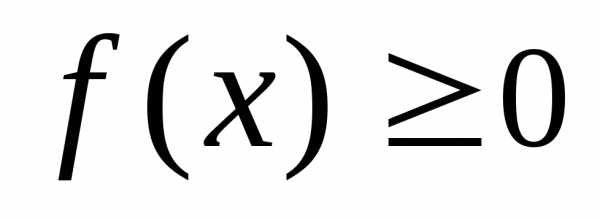 ,
,
как производная от неубывающей функции, и еще потому, что плотность, как физическая величина, не может быть отрицательной.
2. Интеграл в бесконечных пределах от плотности вероятности равен единице, т. е.
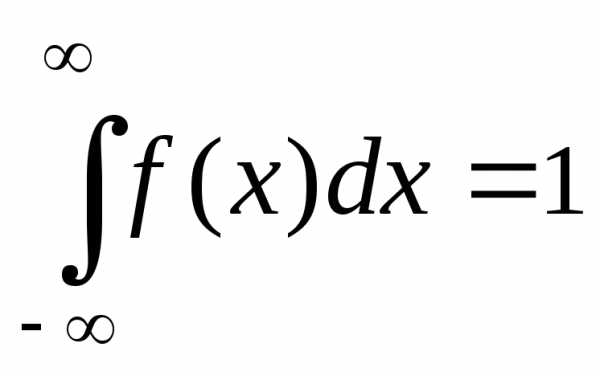 . (4.11)
. (4.11)
Это
свойство вытекает из выражения (4.10),
если верхний предел будет  и если учесть, что
и если учесть, что .
.
44
studfiles.net
Дан ряд распределения дискретной случайной величины найти недостающую вероятность и построить график функции распределения вычислить математическое ожидание и дисперсию этой величины
Дан ряд распределения дискретной случайной величины. Найти недостающую вероятность и построить график функции распределения. Вычислить математическое ожидание и дисперсию этой величины.
Х | -4 | -3 | 1 | 2 |
Р | 0,3 | ? | 0,1 | 0,4 |
Решение
Случайная величина Х принимает только четыре значения: -4, -3, 1 и 2. Каждое из этих значений она принимает с определенной вероятностью. Так как сумма всех вероятностей должна быть равна 1, то недостающая вероятность равна:
0,3 + ? + 0,1 + 0,4 = 1,
? = 0,2.
Составим функцию распределения случайной величины Х. Известно, что функция распределения , тогда:
при
 ,
так как ни одно значение х (-4, -3, 1 и
2) не являются меньше х, значит
,
так как ни одно значение х (-4, -3, 1 и
2) не являются меньше х, значит  ;
;при , так как только значение –4 будет меньше х, а событие Х=1 появляется с вероятностью, равной 0,3, то есть ;
при , так как значениями, меньшими х, будут Х=-4 и Х=-3, и случайная величина Х может принять либо первое, либо второе значение, то ;
при , поэтому :
при
 и
и  .
.
Следовательно,
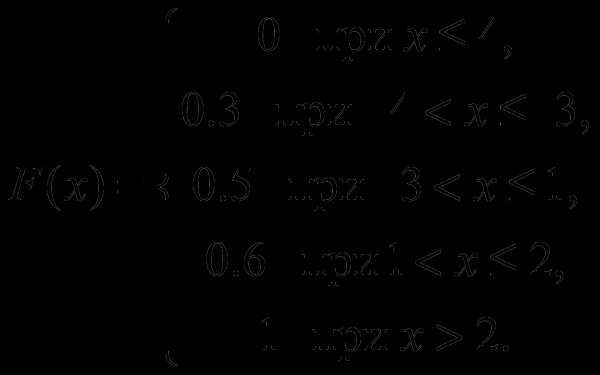
Построим график функции F(x).
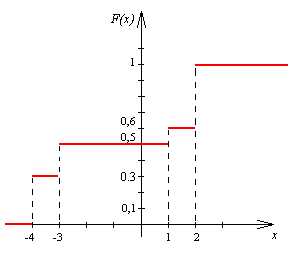
Математическое ожидание дискретной случайной величины равно сумме произведений значения случайной величины на соответствующую вероятность, т.е.
.
Значит, .
Дисперсию дискретной случайной величины найдем по формуле:
.
.
ПРИЛОЖЕНИЕ
Элементы комбинаторики
Здесь:
— факториал числа |
Действия над событиямиСобытие – это всякий факт, который может произойти или не произойти в результате опыта.
Обозначение: ; Обозначение: ; |
Классическое определение вероятности Вероятность события А – это
отношение числа опытов
|
Формула умножения вероятностейВероятность события можно найти по формуле: , — вероятность события А, — вероятность события В,
Если события А и В – независимы (появление одного не влияет на появление другого), то вероятность события равна: |
Формула сложения вероятностейВероятность события можно найти по формуле: , — вероятность события А, — вероятность события В,
Если события А и В – несовместны (не могут появиться одновременно), то вероятность события равна: |
Формула полной вероятностиПусть
событие А может произойти
одновременно с одним из событий |
Схема БернуллиПусть проводится n независимых испытаний. Вероятность появления (успеха) события А в каждом из них постоянна и равна p, вероятность неудачи (т.е. не появления события А) q =1 — p. Тогда вероятность появления k успехов в n испытаниях можно найти по формуле Бернулли: Наивероятнейшее
число успехов . |
Случайные величиныдискретные непрерывные (н-р, число девочек в семье с 5 детьми) (н-р, время исправной работы чайника) Числовые характеристики дискретных случайных величинПусть дискретная величина задана рядом распределения:
Функция распределения Функцией распределения случайной
величины Х называется функция |
Вопросы к экзамену
Событие. Операции над случайными событиями.
Понятие вероятности события.
Правила сложения и умножения вероятностей. Условные вероятности.
Формула полной вероятности. Формула Байеса.
Схема Бернулли.
Случайная величина, ее функция распределения и ряд распределения.
Основные свойства функции распределения.
Математическое ожидание. Свойства математического ожидания.
Дисперсия. Свойства дисперсии.
Плотность распределения вероятностей одномерной случайной величины.
Виды распределений: равномерное, экспоненциальное, нормальное, биномиальное и распределение Пуассона.
Локальная и интегральные теоремы Муавра-Лапласа.
Закон и функция распределения системы двух случайных величин.
Плотность распределения системы двух случайных величин.
Условные законы распределения, условное математическое ожидание.
Зависимые и независимые случайные величины. Коэффициент корреляции.
Выборка. Обработка выборки. Полигон и гистограмма частот. Эмпирическая функция распределения.
Понятие оценки параметров распределения. Требования к оценке. Доверительный интервал. Построение интервалов для оценки математического ожидания и среднего квадратического отклонения.
Статистические гипотезы. Критерии согласия.
gigabaza.ru
7. Примеры распределения случайных величин
Дискретная случайная величина называется распределенной побиномиальному закону, если ее возможные значения 0, 1, …, n , а вероятность того, что , выражается формулой
,
где .
Математическое ожидание случайной величины , распределенной по биномиальному закону, равно, а дисперсия.
Дискретная случайная величина называется распределенной по законуПуассона, если ее возможные значения 0, 1, …, m, …, а вероятность того, что выражается формулой
,
где — параметр закона Пуассона.
Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны параметру .
Непрерывная случайная величина называетсяравномерно распределенной в интервале , если ее плотность распределения в этом интервале постоянна.
Математическое ожидание и дисперсия случайной величины, распределенной равномерно на участке , равны соответственно
.
Непрерывная случайная величина называется распределенной попоказательному закону, если ее плотность распределения
где — параметр показательного закона.
Для случайной величины , распределенной по показательному закону,
.
Функция распределения имеет вид
Непрерывная случайная величина называется распределенной понормальному закону, если ее плотность распределения
.
Математическое ожидание случайной величины , распределенной по нормальному закону, равно, а дисперсия.
Вероятность попадания случайной величины , распределенной по нормальному закону, в интервалравна
,
где — табулирована,
отсюда .
Типовые задачи для решения в аудитории
1. Стрелок делает по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения числа попаданий и вычислить математическое ожидание и дисперсию указанной случайной величины.
Решение. Случайная величина — число попаданий в мишень при 3-х выстрелах, распределена по биномиальному закону, ее возможные значения 0, 1, 2, 3.
;
;
;
.
Ряд распределения случайной величины :
0
1
2
3
0,343
0,441
0,189
0,027
; .
2. Длина заготовляемой автоматом детали представляет собой случайную величину, распределенную по нормальному закону с параметрами ,. Найти вероятность брака, если допускаемые размеры детали должны быть. Какую точность длины можно гарантировать с вероятностью 0,97?
Решение. а) .
.
Вероятность брака .
б)
.
Следовательно, с вероятностью 0,97 можно гарантировать размеры .
3. Снайпер стреляет по замаскированному противнику до первого попадания. Вероятность промаха при отдельном выстреле равна . Найти математическое ожидание числа промахов.
Решение. Возможные значения случайной величины — числа промахов:.
Ряд распределения случайной величины :
Полученное распределение носит название геометрического распределения.
.
Для вычисления суммы полученного ряда рассмотрим ряд
.
Отсюда .
studfiles.net
Случайная величина ряд распределения — Энциклопедия по экономике
Случайные величины. Функция распределения и ее свойства. Дискретные и абсолютно непрерывные распределения случайных величин. Ряд и плотность распределения, их свойства. Примеры распределений. Нормальное распределение. [c.30]Вероятностно-статистические методы воспроизводят как устойчивые, так и временные зависимости между экономическими явлениями и факторами. С помощью этих моделей можно обрабатывать данные статистического анализа, исследования закона распределения некоторой случайной величины, корреляционного (регрессионного) анализа получения количественной характеристики связей и зависимостей между различными технико-экономическими показателями. Кроме того, можно определять степень влияния каждого производственного фактора на изучаемый показатель или одновременно действующих факторов (для дисперсионного анализа) на технико-экономические показатели и выбирать из ряда факторов наиболее важные. [c.346]
Однако для обеспечения надежности прогнозирования необходимо исследовать случайную компоненту временного ряда, определить характер (закон) распределения случайных величин. Если случайные величины е f нормально распределены и между собой независимы, тогда определяются интервалы [34, 54], в которые с определенной вероятностью попадают значения полученного нами прогноза. [c.54]
Первая причина если случайная величина (X, Y) имеет совместное нормальное распределение, то, как известно, уравнения регрессии линейные (см. 2.5). Предположение о нормальном распределении является вполне естественным и в ряде случаев может быть обосновано с помощью предельных теорем теории вероятностей (см. 2.6). [c.18]
Такая таблица называется рядом распределения дискретной случайной величины. [c.25]
Закон (ряд) распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной. Однако такой закон (ряд) распределения бывает трудно обозримым, не всегда удобным (и даже необходимым) для анализа. [c.26]
Пример 2.5. Дан ряд распределения случайной величины [c.29]
Упражнения 2.9. Дан ряд распределения случайной величины X [c.48]
Построить ряды распределения случайных величин X и Y. Найти М(Х), D(X) M(Y), D(Y) P(X1). [c.49]
Мы будем предполагать, что x w. yt— стационарные временные ряды, т. е. все случайные величины xt имеют одно и то же распределение (и аналогично >>,). [c.191]
Вероятностное описание случайных величин, т. е. закон их распределения и его основные параметры — математическое ожидание, дисперсию и др., можно получить статистической обработкой их массовых реализаций в прошлом. Однако корректно применить этот метод к плановым показателям развития отрасли весьма затруднительно. По многим показателям либо вообще отсутствуют аналоги в прошлом, либо число наблюдений оказывается недостаточным, чтобы можно было выяснить закон распределения. Но даже если статистические характеристики колебания тех или иных показателей развития отрасли в прошлом найдены, возникает вопрос о допустимости их распространения на будущее, так как меняются и сами условия развития отрасли. Существует и ряд трудностей чисто практического характера. В частности, отклонение отчетных показателей от плановых может быть обусловлено не только объектив- [c.82]
В результате анализа, проведенного методом Монте-Карло, эксперт получает значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако этих данных недостаточно для того, чтобы аналитик установил, действительно ли прибыльность проекта настолько велика, что компенсирует риск по проекту, оцененный стандартным отклонением и коэффициентом вариации. Ряд исследователей избегает использования данного метода ввиду сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности). [c.252]
Регрессионный анализ — один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, х[,х2,…,хп у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида [c.101]
Рассмотрим сумму X+(f0,t) = x(l)(t0,t)+…+xM(t0,t) депозитов, лежащих на счетах потенциальных вкладчиков к моменту времени t. Эта. случайная величина получена с учетом возможности и того, что счета некоторых потенциальных вкладчиков не будут открыты к моменту времени t, и того, что счета ряда потенциальных вкладчиков, открытые в некоторый момент времени те [t0,t], будут ликвидированы к указанному моменту t. Предполагается, что случайные величины x(i)(t0,t), i = 1,.., s+ независимы в совокупности и имеют одинаковое распределение — распределение случайной величины x(t0,f). [c.198]
Составить таблицу распределения или построить многоугольник для непрерывной случайной величины невозможно, так как отдельные ее значения имеют вероятности, стремящиеся к нулю. В то же время при решении ряда практических задач и при переходе к обобщениям пользуются понятием как непрерывной, так и дискретной случайной величины. [c.18]
Тогда по выборке этих случайных величин, которая может быть получена из ценового ряда, можно определить их закон распределения. [c.85]
При обработке движения марки готовой продукции на складе предприятия-изготовителя определим для каждого из нормообразующих факторов его вариации в течение отчетного года (объемы суточного производства, объемы отгрузок, интервалы отгрузок и т.д.), т.е. определим вариационные ряды, а по ним построим графики плотности распределения вариаций случайных величин, как это было сделано в разд. 1.2. [c.221]
По рассчитанному статистическому ряду (значений суммарных объемов суточных отпусков в интервалах поставки — X и их частот — Р(Х ), формула (6.87)) необходимо определить плотность распределения суммарных объемов суточных отпусков в интервалах между поставками. Границы диапазонов, на которые делится размах вариаций суммарных объемов суточных отпусков U принять такие же, как при расчете плотности распределения двухмерной случайной величины QU, вычисляемой по формуле (6.40) [c.366]
Пример. Прибыль, получаемая компанией при реализации 1-го решения, является случайной величиной Е с рядом распределения [c.88]
Далее рассмотрим ряд распределения случайной величины х— числа распределения баллов [c.155]
Очевидно, в схеме В (наблюдения производятся в фиксированных точках Хь. .., Хп без случайных ошибок в регистрации независимой переменной) случайную величину следует рассматривать как дискретную с областью мыслимых значений В — (Хь Х2,. .., Хп (не исключается возможность повторения одинаковых значений в этом ряду) и с частным законом распределения г ) (X), задаваемым вероятностями [c.57]
Последовательность наблюдений типа (12.1) принято называть временным рядом. Он имеет два главных отличия от рассматриваемых наблюдений анализируемого признака, образующих случайные выборки а) образующие временной ряд наблюдения л ь х2,. .., хп, рассматриваемые как случайные величины, не являются взаимно независимыми, и, в частности, значение, которое мы получим в момент времени th (k = 1, 2,. .., я), может существенно зависеть от того, какие значения были зарегистрированы до этого момента времени б) наблюдения временного ряда (в отличие от элементов случайной выборки), вообще говоря, не образуют стационарной последовательности, т. е. закон распределения вероятностей k-ro члена временного ряда (случайной величины xh x (tk)) не остается одним и тем же при изменении его номера в частности, от tk могут зависеть основные числовые характеристики случайной переменной xk — ее среднее значение Ex (tk) и дисперсия Dx (tk) (функцию от аргумента /, описывающую зависимость Ел (/) от времени, часто называют трендом временного ряда). [c.362]
С содержательной точки зрения однофакторный анализ можно рассматривать как / рядов (каждый ряд длины Jt) независимых наблюдений над нормально распределенными случайными величинами со средними 9ДО +ЭД и дисперсией а2. [c.375]
И теоретические формулы, аналогичные формуле (2.10), и ряд распределений — все это различные формы описания законов распределения случайных величин. Но наиболее универсальной и часто применяемой на практике формой описания распределений является функция распределения. [c.48]
Расширительным теоретико-вероятностным толкованием феномена лотереи является понятие вероятностного распределения случайной величины. С его помощью определяют вероятности того, что случайная величина примет те или иные свой возможные значения. Обозначим через у случайную величину, а через у — ее возможные значения. Тогда для дискретной случайной величины, которая может принимать возможные значения У , у2, УЗ,. .., уп удобной формой вероятностного распределения следует считать зависимость Р(у = у ), которую обычно называют вероятностным рядом, шт рядом распределения. На практике для оперативной обобщенной оценки вероятностного распределения величин риска часто используют так называемые числовые и другие характеристики распределения случайных результатов математическое ожидание, дисперсия, среднее квадратическое (стандартное) отклонение, коэффициент вариации, мода, медиана и др. (см., например, [13,10, 54] и др.). Иными словами, для быстрого и целостного восприятия предприниматель стремится (или просто вы- [c.246]
Следовательно, рассмотренный нами для дискретной случайной величины вероятностный ряд распределения совершенно не пригоден в качестве характеристики распределения непрерывных случайных величин. Однако для непрерывной случайной величины вероятность попадания в некоторый интервал ненулевой длины — это [c.250]
Конечно, проще анализировать внезапные отказы, оперируя субъективными вероятностями на уровне событий. Здесь не приходится применять сложные методы анализа временных рядов и учитывать корреляцию случайных величин. А по своей полезности результаты ничуть не хуже некоторых сложных социологических исследований. Кроме того, иногда определить субъективное распределение вероятностей предполагаемого результата просто нельзя. Например, предприниматель не имеет опыта вынесения подобных количественных суждений и в то же время не считает возможным полагать, что будущие исходы имеют равные вероятности (т.е. он не согласен следовать принципу недостаточного основания Лапласа). Тогда тоже хорошо использовать алгебру субъективной вероятности на уровне событий. [c.267]
В каких графических формах могут отображаться ряды распределений случайных величин [c.276]
Ряд литературных источников [4, 20] указывают, что в силу упомянутых выше причин можно полагать эту случайную величину распределенной по нормальному закону. Это подтверждается и результатами статистических исследований. [c.99]
Более подходящей является в этом отношении аналогичная процедура, применяемая не к самому ряду Xt, а к остаткам, полученным при оценивании специфицированной модели ряда Xt. В моделях AR и МА остатки состоятельно оценивают инновации st, которые, в предположении нормальности, являются независимыми, одинаково распределенными случайными величинами, имеющими распределение N(0, сг2). Поэтому при применении метода Ломницкого для проверки предположения о нормальности инноваций, мы получаем [c.52]
Регрессионный анализ — один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регресси-онногс анализа необходимо выполнение ряда специальных требований (в частности, Х1,Х2,…х , у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. [c.122]
Временной (динамический) рад (time-series data). Временным (динамическим) рядом называется выборка наблюдений, в которой важны не только сами наблюдаемые значения случайных величин, но и порядок их следования друг за другом. Чаще всего упорядоченность обусловлена тем, что экспериментальные данные представляют собой серию наблюдений одной и той же случайной величины в последовательные моменты времени. В этом случае динамический ряд называется временным рядом. При этом предполагается, что тип распределения наблюдаемой случайной величины остается одним и тем же (например, нормальным), но параметры его меняются в зависимости от времени. [c.16]
Если выборка у, У2,…, Уь-.., уп рассматривается как одна из реализаций случайной величины Y, временной ряд у, Уг,…, Уь—> Уп рассматривается как одна из реализаций (траекторий) случайного процесса1 Y(t). Вместе с тем следует иметь в виду принципиальные отличия временного ряда у, (t= 1,2,…, п) от последовательности наблюдений у, уг,…, у , образующих случайную выборку. Во-первых, в отличие от элементов случайной выборки члены временного ряда, как правило, не являются статистически независимыми. Во-вторых, члены временного ряда не являются одинаково распределенными. [c.135]
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ (в математической статистике) [probability distribution] — ряд чисел, показывающих, как часто встречается то или иное значение случайной величины, или соответствующая таблица, диаграмма или математическая формула, их заменяющая. Различают эмпирические Р.в., получаемые в результате экспериментов и измерений, и теоретические Р.в. (к которым бывает удобно с той или иной точностью приводить эмпирические Р.в.) Если, напр., при обработке результатов наблюдения получены некоторые число- [c.300]
СЛУЧАЙНАЯ ФУНКЦИЯ [random fun tion] — «функция X t) произвольного аргумента t, t е Т, значения которой при любом t являются случайной величиной с определенным распределением вероятностей»76. Если t принимает числовые значения, которые интерпретируются как время, имеем случайный процесс (напр., в частном случае — временной ряд) если значения t рассматриваются как точки из некоторой области многомерного пространства — имеем случайное поле. [c.332]
Определение вида закона распределения случайной величины по опытным данным занимает одно из центральных мест при обработке результатов экспериментов статистическими методами. Традиционный подход при решении задачи сводится к расчету параметров эмпирического распределения, принятию их в качестве оценок параметров генеральной совокупности с последующей проверкой сходимости эмпирического распределения с предполагаемым теоретическим по критериям х2 (Пирсона), А. (Колмогорова), со2. Такой подход имеет следующие недостатки зависимость методики обработки результатов эксперимента от предполагаемого теоретического распределения, большой объем вычислений, особенно при использовании критериев со2 и %2. Некоторые новые критерии [82] не имеют удовлетворительного теоретического обоснования, а в ряде случаев, как это показано в работе [82], не обладают достаточной мощностью. Б.Е. Янковский [133] предложил информационный способ определения закона распределения. Суть его в следующем. Если имеется выборка с распределением частос-тей Р, Р2> . Рп > то энтропия эмпирического распределения должна совпадать с энтропией предполагаемого теоретического распределения при верной нулевой гипотезе, т. е. должно выполняться равенство [c.27]
Пусть реализации (А, Ь,с) условий задачи соответствует оптимальный план к. Оптимальное значение линейной формы L =L(x )= x как функция случайных величин А, Ь, с является случайной величиной. Пассивный подход к стохастическому линейному программированию заключается в вычислении функции распределения (L ) по заданному совместному распределению случайных параметров условий задачи. Решение этой задачи представляет значительные, иногда непреодолимые вычислительные трудности. Имеются работы, изучающие область изменения функции L и некоторые характеристики распределения (L ) ([50, 176, 130]). Функции 8(L ) получены при некоторых ограничивающих предположениях на совместную функцию распределения F(A, b, с) ( 21, 23, 39, 267, 249, 251, 269, 26, 274]). Ряд работ (см., например, [176]) лтосвящен методам приближенного вычисления (L ). [c.276]
Тинтнер предлагает для задачи стохастического программирования со случайной матрицей Л с независимыми нормально распределенными элементами и детерминированными векторами бис следующий приближенный метод вычисления Q(L ). Составим матрицу Аг=А+фоА, где элементы ац матрицы А — математические ожидания элементов оц матрицы А, а элементы матрицы СТА — среднеквадратические отклонения элементов йц от ац. Решим детерминированные задачи линейного программирования с матрицей условий At для ряда значений параметра t — реализаций некоторой случайной величины с заданной функцией распределения. Рассматривая полученные при этом оптимальные значения L t как случайную выборку, можно, используя соответствующие методы математической статистики, получить и оценить приближенное значение для (Ь ). Полученный таким образом закон распределения оптимального значения линейной формы для рассмотренного выше (см. п. 4.5) численного примера практически не отличается от функции Q(L ), изображенной на рис. 13.1. [c.299]
Сказанное не умаляет значения средней арифметической (гармонической). Она является в большинстве случаев наилучшей характеристикой центрального и наиболее типичного значения уровня изучаемого признака, поскольку исчисляется исходя из суммы всех его конкретных значений, охватывает все его имеющиеся варианты, обобщает весь ряд распределения значений признака. В ней взаимопогашаются случайные индивидуальные различия, что особенно важно для изучения общественных процессов. К. Маркс писал Труд, овеществленный в стоимости, есть труд среднего общественного качества, т. е. проявление средней рабочей силы. Но средняя величина есть всегда средняя многих различных индивидуальных величин одного и того же вида. В каждой отрасли промышленности индивидуальный рабочий, Петр или Павел, более или менее отклоняется от среднего рабочего. Такие индивидуальные отклонения, называемые на языке математиков погрешностями», взаимно погашаются и уничтожаются, раз мы берем значительное число рабочих 1. [c.45]
Батер [80] показал, что критерий геометрического скользящего среднего является оптимальным для процесса, в котором изменение параметра в течение единичного интервала времени представляет нормально распределенную случайную величину с известными математическим ожиданием и дисперсией. Для этого случая он получил зависимость весового множителя в скользящем геометрическом среднем от указанных параметров нормального распределения. Результат Батера имеет много общего с приложениями теории сглаживания и предсказания стационарных временных рядов (см. [78], замечания Дженкинса). [c.123]
Наиболее полное представление о сложившихся в данный. момент соотношениях в заработной плате н доходах дают статистич. ряды распределения рабочих н служащих по размерам заработной платы и их семей (а также членов семей) по величине среднедушевого дохода. Для получения таких рядов органы ЦСУ СССР периодически проводят спец. единовременные обследования. Текущие сведения о доходах семей представляет йюИжпнная статистика, на основе к-рой строятся экономим, группировки населения СССР н союзных республик. Ряды распределения н исчисляемые по ним статистич. характеристики являются обобщающими, интегральными они отражают в сводном виде весь комплекс различий в величине рассматриваемого признака. 1-]слп исследованию подлежит совершенно однородная статистич. совокупность (напр., рабочие одной и той же квалификации, работающие при одинаковых условиях), то для измерения разброса их заработной платы могут быть использованы показатели отклонения от ср. арифметической (дисперсия, коэффициент вариации). Но эти показатели имеют смысл только в тех случаях, когда вариация признака носит более млн менее случайный характер. Если же различия между отд. элементами совокупности внутренне обусловлены, закономерны, н задача состоит именно в том, чтобы установить величину этих различий, т. е. если речь идёт о дифференциации признака, а не о просто колеблемости (вариации), то приходится прибегать к др. приёмам измерения. [c.441]
Случайные процессы. В экономике проблема изучения поведения объектов во времени — одна из важнейших. Очевидно, что и здесь вероятностные модели могут оказаться пригодными для их описания. Изучением соответств. математич. проблем занимается теория случайных процессов. В Т. в. под случайным процессом понимается параметрич. семейство случайных величин (t). В приложениях обычно параметр t — время (при этом говорят о случайной функции, при многомерном t — процесс (t) чаще называют случайным полем). В случаях, когда t дискретно, последовательность Si = I (h), ( 2), — li = i (li)— называют временным рядом. Случайный процесс может быть полностью охарактеризован совокупностью совместных функций распределения случайных величин (ti), (г2),. .., (tn) для всевозможных моментов времени и любого п > 0. [c.110]
Для вычислений вероятностей Р(у = у ) ряда распределения Пуассона удобно использовать функцию ПУАССОН(х среднее …) пакета Mi rosoft Ex el. Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, равны между собой ШУ = Dy = а. График вероятностного ряда распределения Пуассона для среднего значения а=1,7 представлен на рис. 7.5. [c.250]
economy-ru.info

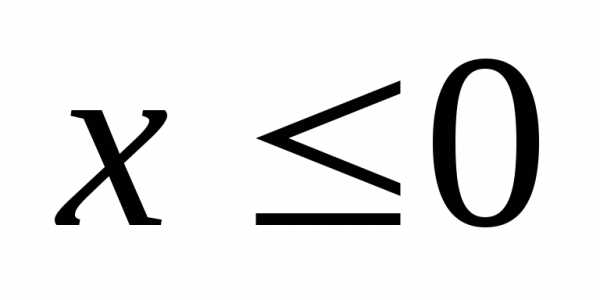
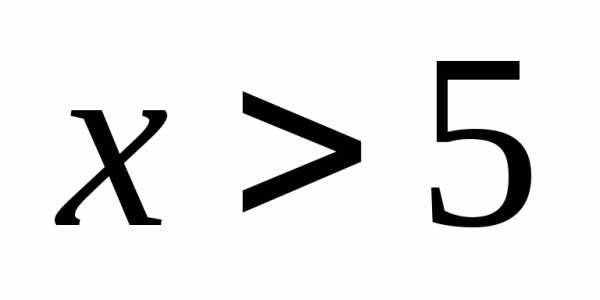
 ,
так как ни одно значение х (-4, -3, 1 и
2) не являются меньше х, значит
,
так как ни одно значение х (-4, -3, 1 и
2) не являются меньше х, значит 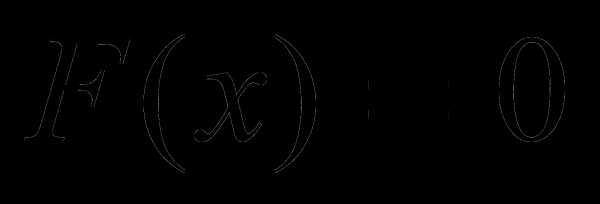 ;
; и
и  .
.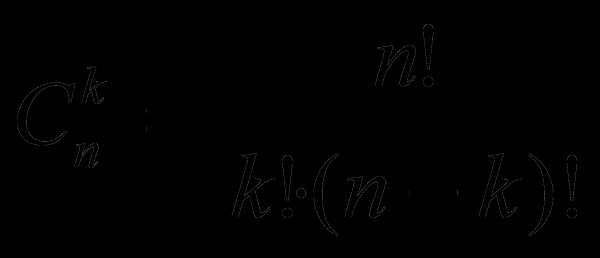 — это число способов, с помощью которых
можно выбрать k различных элементов из имеющихся n элементов без учета порядка выборки.
— это число способов, с помощью которых
можно выбрать k различных элементов из имеющихся n элементов без учета порядка выборки.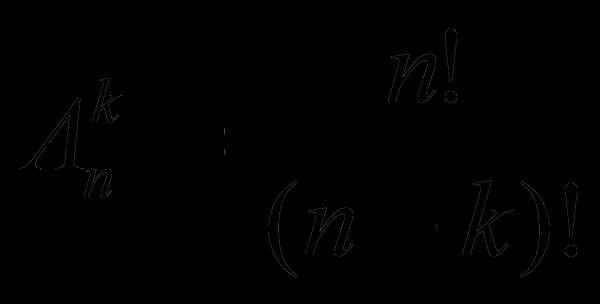
 — это число способов, с помощью которых
можно выбрать k различных элементов из имеющихся n элементов с учетом порядка выборки.
— это число способов, с помощью которых
можно выбрать k различных элементов из имеющихся n элементов с учетом порядка выборки. —
это число способов, с помощью которых
можно выбрать n различных элементов из имеющихся n элементов с учетом порядка выборки.
—
это число способов, с помощью которых
можно выбрать n различных элементов из имеющихся n элементов с учетом порядка выборки.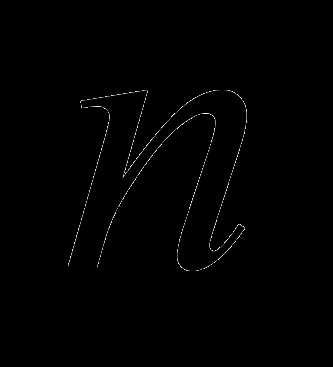
 , благоприятствующих появлению события А, к общему числу опытов
, благоприятствующих появлению события А, к общему числу опытов  :
: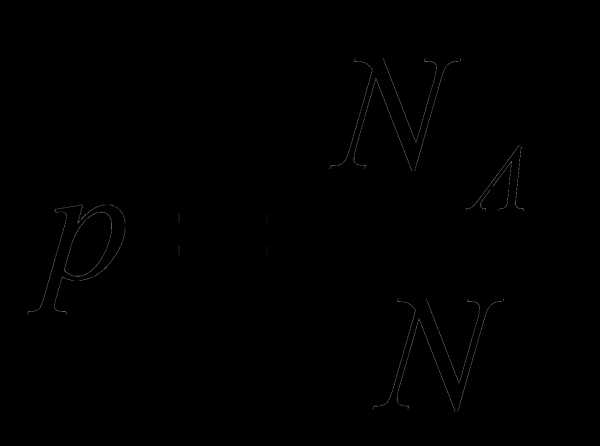
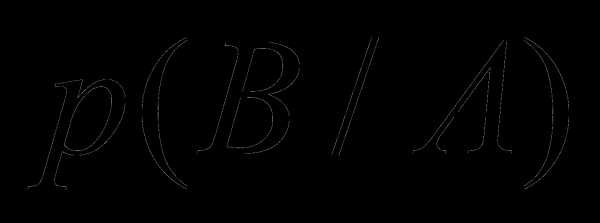 — вероятность события В при условии,
что событие А уже произошло.
— вероятность события В при условии,
что событие А уже произошло. — вероятность совместного появления
событий А и В.
— вероятность совместного появления
событий А и В. ,
,  ,
…,
,
…,  — назовем их гипотезами. Также известны
— назовем их гипотезами. Также известны 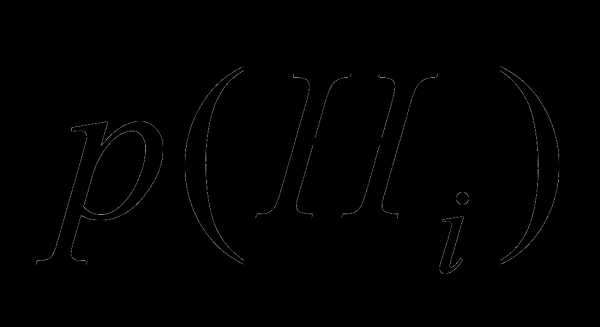 — вероятность выполнения i-ой
гипотезы и
— вероятность выполнения i-ой
гипотезы и 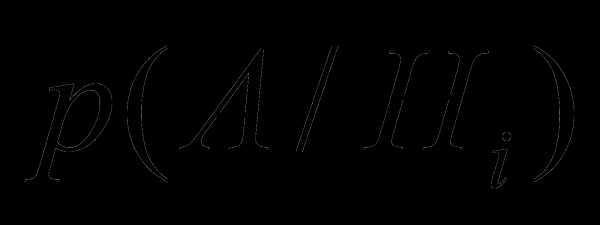 — вероятность появления события А при
выполнении i-ой
гипотезы. Тогда вероятность события А может быть найдена по формуле:
— вероятность появления события А при
выполнении i-ой
гипотезы. Тогда вероятность события А может быть найдена по формуле: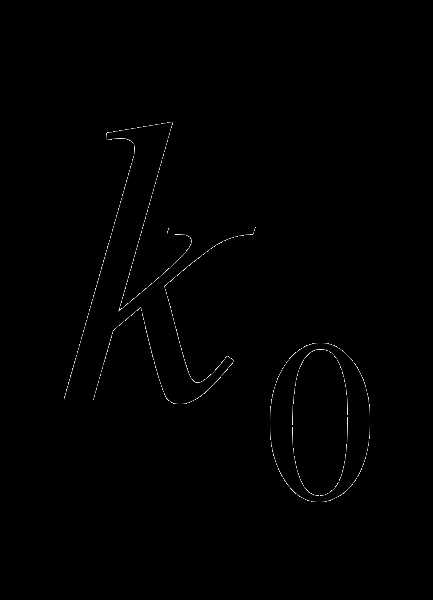 в схеме Бернулли – это число появлений
некоторого события, которому
соответствует наибольшая вероятность.
Можно найти по формуле:
в схеме Бернулли – это число появлений
некоторого события, которому
соответствует наибольшая вероятность.
Можно найти по формуле: ,
, 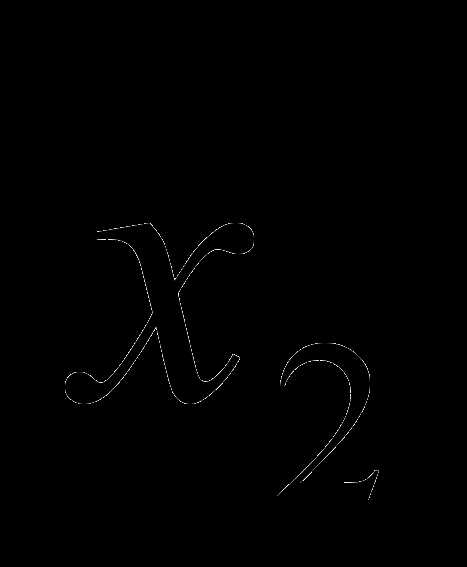 ,
…,
,
…, 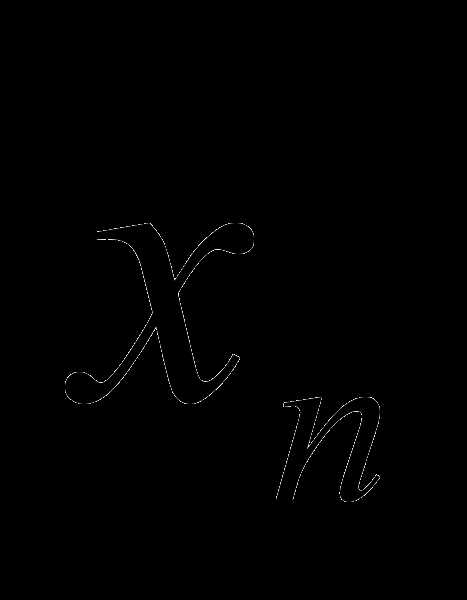 — значения случайной величины Х;
— значения случайной величины Х; ,
, 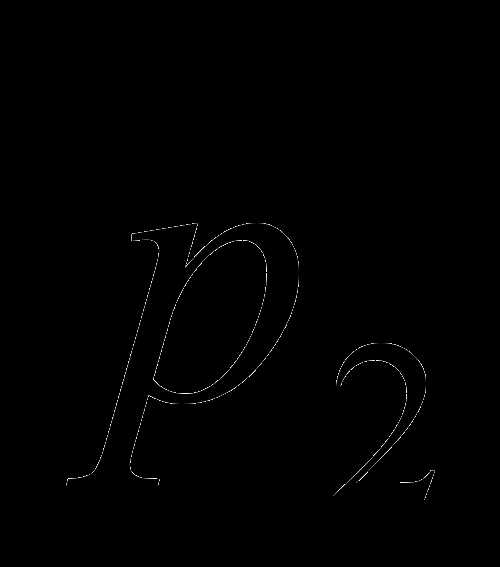 ,
…,
,
…, 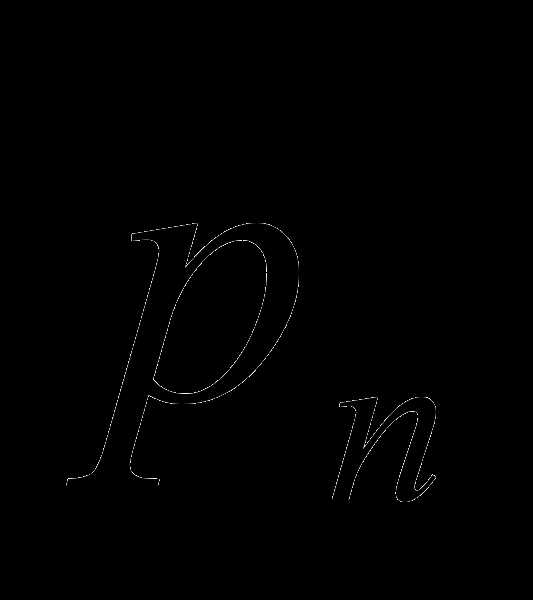 — соответствующие им значения
вероятностей.
— соответствующие им значения
вероятностей.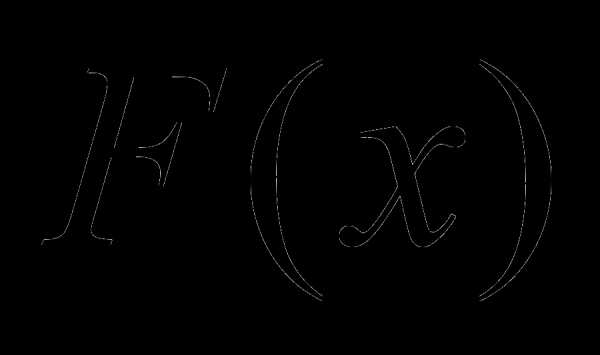 ,
заданная на всей числовой прямой и
равная вероятности того, что Х будет меньше х:
,
заданная на всей числовой прямой и
равная вероятности того, что Х будет меньше х: