Задания
Задание 1.1Вычислить предел числовой последовательности
Ответы:1.,2.,3.4.5.6.7.8.9.10.11.12.13.14.15.16.17..
2. Предел функции.
Приведем два определения предела функции:
Определение 4 (по Коши). Числоназывается пределом функциипри, если для любого сколь угодно малогонайдется такое, что для всехудовлетворяющих неравенствувыполняется:
. (14)
Определение 5 (по Гейне).Числоназывается пределом функции, при стремлениик, если какую бы последовательностьс пределом, извлеченную из множества, ни пробегала независимая переменная, соответствующая последовательность значений функции,… всегда имеет предел.
Обозначают этот факт так:
. (15)
Из определения предела функции по Гейне следует, что все теоремы о пределах последовательности можно обобщить на случай предела функции.
Далее приведем несколько примеров вычисления предела функции.
Пример 8
Вычислить предел функции
Решение:
При подстановке в числитель и знаменатель мы получаем неопределенность типа.
Выделяем критический множитель , разложив на множители квадратный трехчлен в знаменателе и воспользовавшись формулой разности кубов в числителе. Затем сократим полученное выражение на.
Ответ:
Пример 9
Вычислить предел функции
Решение:
При подстановке в предел мы получаем неопределенность типа. Числитель разложим на множители:; далее знаменатель и числитель нашей дроби умножим на величину сопряженную знаменателю, т.е.
Ответ:
Задания
Задание 2.1Вычислить предел функции
Ответы:18.,19.,20.21.22.23.24.25.26.27.28.29.30.31.32.33.34., 35..
2.1 Первый замечательный предел.
Первым замечательным пределом называют предел вида:
. (16)
Следствия первого замечательного предела.
1.
2.
3.
4.
5.
6.
7.
Для пределов, содержащих , справедливы свойства, аналогичные 4 – 7.
Определение 6. Функцияназывается бесконечно малой при, если
(17)
Определение 7.Если отношение бесконечно малыхстремится к единице при:
, (18)
то бесконечно малые иназываются эквивалентными бесконечно малыми,и пишут
при.
На основании приведенных определений и первого замечательного предела (16) можно записать следующие соотношения эквивалентности при :
(19)
(20)
(21)
(22)
Пример 10
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
Здесь мы воспользовались эквивалентностью (19) ~при.
Ответ:
Пример 11
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
Ответ:
Пример 12
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
В данном примере мы не можем применить первый замечательный предел, так как , в подобных случаях необходимо сделать замену переменной. Причем, новая переменная должна стремиться к нулю.
Ответ:
studfiles.net
Задания
Задание 1.1Вычислить предел числовой последовательности
Ответы:
2. Предел функции.
Приведем два определения предела функции:
Определение 4 (по Коши). Числоназывается пределом функциипри, если для любого сколь угодно малогонайдется такое, что для всехудовлетворяющих неравенствувыполняется:
. (14)
Определение 5 (по Гейне).Числоназывается пределом функции, при стремлениик, если какую бы последовательностьс пределом, извлеченную из множества, ни пробегала независимая переменная, соответствующая последовательность значений функции,… всегда имеет предел.
Обозначают этот факт так:
. (15)
Из определения предела функции по Гейне следует, что все теоремы о пределах последовательности можно обобщить на случай предела функции.
Далее приведем несколько примеров вычисления предела функции.
Пример 8
Вычислить предел функции
Решение:
При подстановке в числитель и знаменатель мы получаем неопределенность типа.
Выделяем критический множитель , разложив на множители квадратный трехчлен в знаменателе и воспользовавшись формулой разности кубов в числителе. Затем сократим полученное выражение на.
Ответ:
Пример 9
Вычислить предел функции
Решение:
При подстановке в предел мы получаем неопределенность типа. Числитель разложим на множители:; далее знаменатель и числитель нашей дроби умножим на величину сопряженную знаменателю, т.е.
Ответ:
Задания
Задание 2.1Вычислить предел функции
Ответы:18.,19.,20.21.22.23.24.25.26.27.28.29.30.31.32.33.34., 35..
2.1 Первый замечательный предел.
Первым замечательным пределом называют предел вида:
. (16)
Следствия первого замечательного предела.
1.
2.
3.
4.
5.
6.
7.
Для пределов, содержащих , справедливы свойства, аналогичные 4 – 7.
Определение 6. Функцияназывается бесконечно малой при, если
(17)
Определение 7.Если отношение бесконечно малыхстремится к единице при:
, (18)
то бесконечно малые иназываются эквивалентными бесконечно малыми,и пишут
при.
На основании приведенных определений и первого замечательного предела (16) можно записать следующие соотношения эквивалентности при :
(19)
(20)
(21)
(22)
Пример 10
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
Здесь мы воспользовались эквивалентностью (19) ~при.
Ответ:
Пример 11
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
Ответ:
Пример 12
Вычислить предел функции
Решение:
При подстановке имеем неопределенность типа.
В данном примере мы не можем применить первый замечательный предел, так как , в подобных случаях необходимо сделать замену переменной. Причем, новая переменная должна стремиться к нулю.
Ответ:
studfiles.net
Практическое занятие №3 предел функции
Цель:
решения задач по нахождению пределов
функции с неопределенностью вида:  и
и .
.
Контрольные вопросы
1. Сформулируйте понятие числовой последовательности. 2. Какая числовая последовательность называется ограниченной? 3. Какая точка называется предельной для данной числовой последовательности. 4. Сформулируйте теорему Больцано-Вейерштрассе. 5. Сформулируйте понятие предела числовой последовательности. 6. В чем заключается геометрический смысл предела числовой последовательности? 7. Сформулируйте понятие функции. Способы задания функции. 8. Сформулируйте понятие предела функции. 9. Запишите основные свойства пределов. 10. Запишите первый и второй замечательные пределы.
Примеры решения типовых задач
Пример
3.1. Вычислить
предел:  .
.
Решение:
.
Пример
3.2. Вычислить
предел: 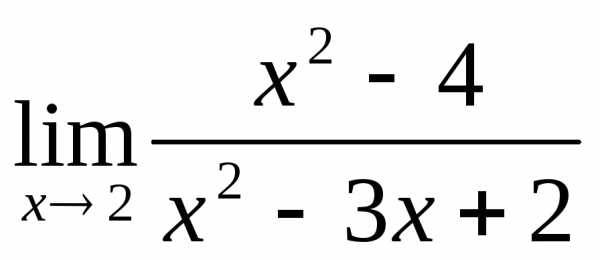 .
.
Решение:
Если
вместо 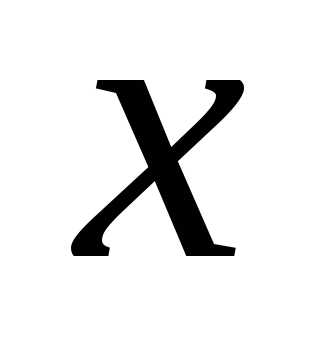 подставить 2, то получится неопределенность
вида
подставить 2, то получится неопределенность
вида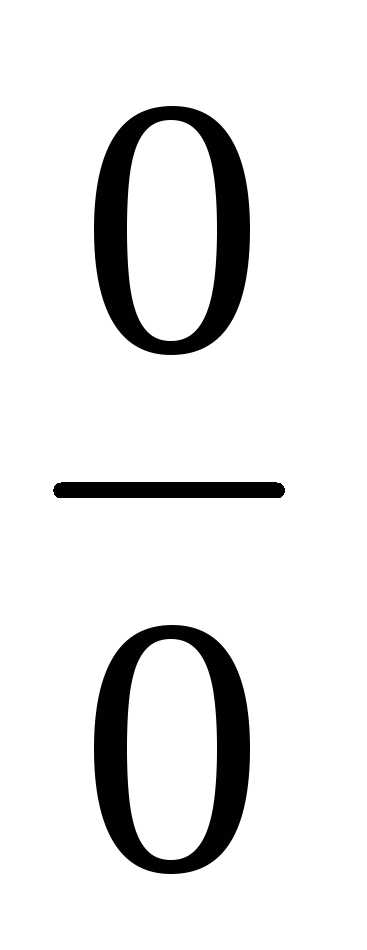
Числитель:
Знаменатель:
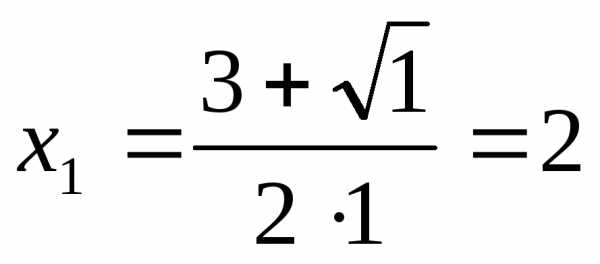 ,
, 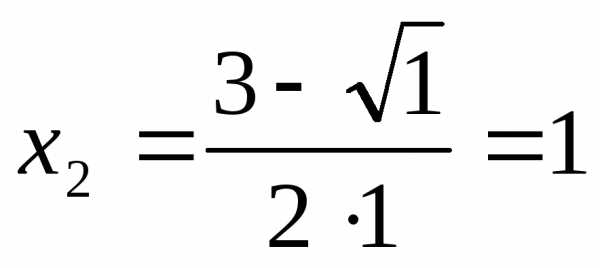
Таким образом:
.
Пример
3.3. Вычислить
предел:  .
.
Решение:
Если
вместо 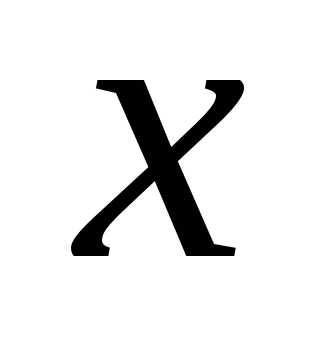 подставить
подставить ,
то получится неопределенность вида
,
то получится неопределенность вида .
Чтобы избавится от нее разделим числитель
и знаменатель на
.
Чтобы избавится от нее разделим числитель
и знаменатель на :
:

Пример
3.4. Вычислить
предел: 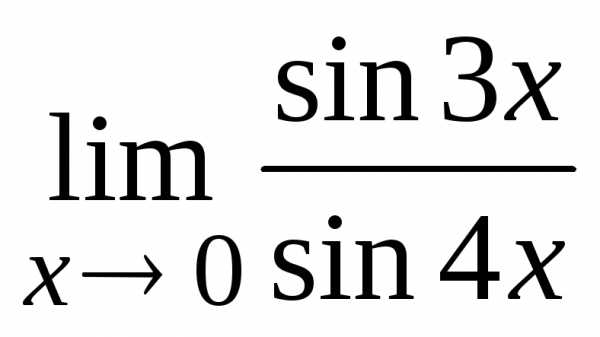 .
.
Решение:
Если
вместо 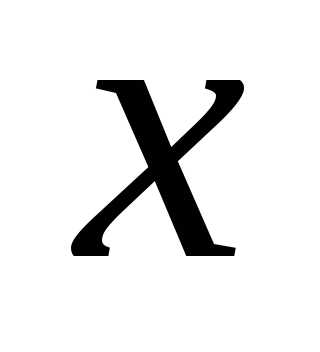 подставить 0, то получится неопределенность
вида
подставить 0, то получится неопределенность
вида .
.
Преобразуем данный предел:
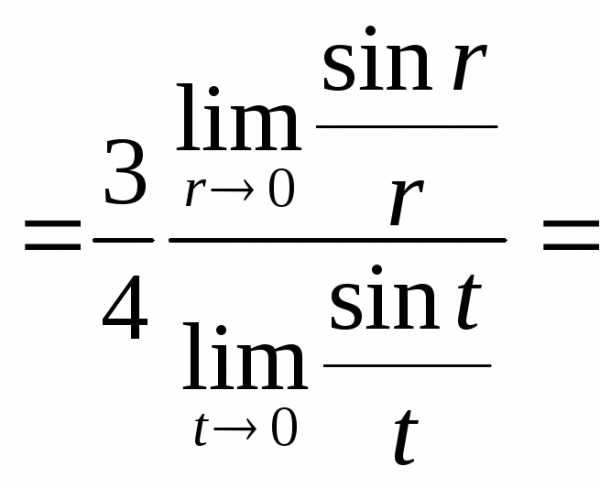
 .
.
Здесь использовали замену и первый замечательный предел.
Пример
3.5. Вычислить
предел: 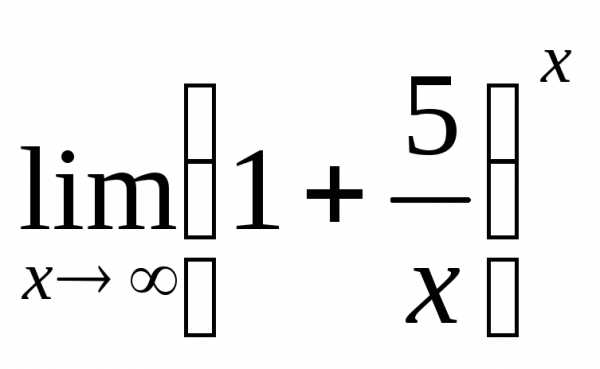 .
.
Решение:
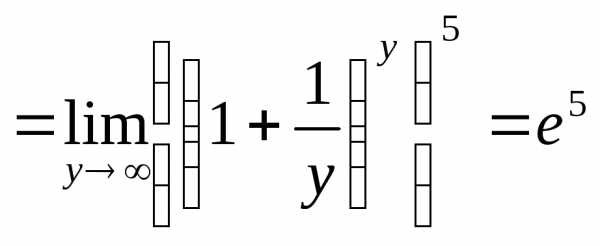 .
.
Здесь
выполнили замену 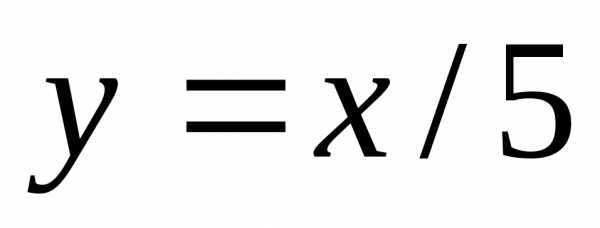 и второй замечательный предел.
и второй замечательный предел.
Задачи для самостоятельного решения
3.1. 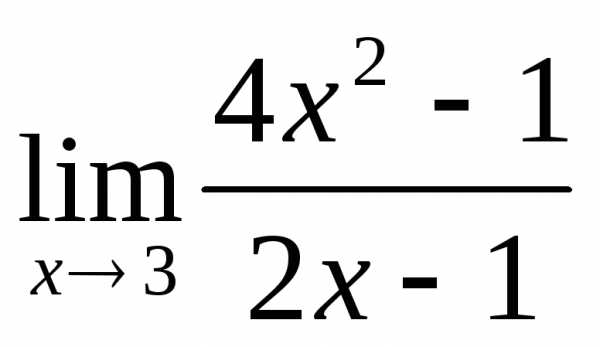 .3.2.
.3.2. 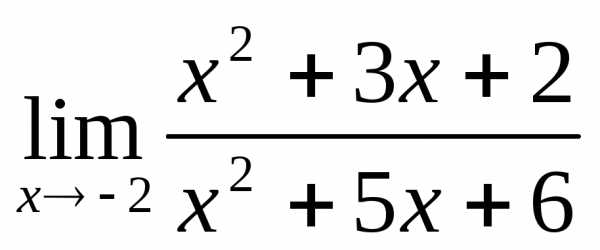 .3.3.
.3.3.  .3.4.
.3.4. 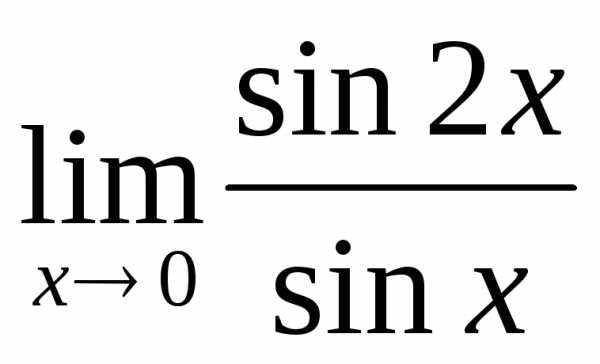 .3.5.
.3.5.  .3.6.
.3.6. 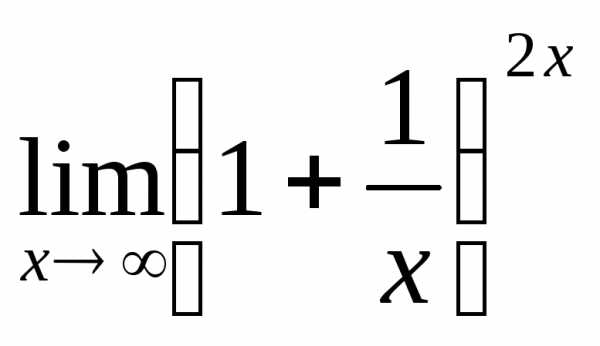 .
.
Практическое занятие №4 дифференциальное исчисление функции одной переменной
Цель: решение задач по нахождению производной от функции, а также исследовании функции на точки максимумов и минимумов, интервалы возрастания и убывания.
Контрольные вопросы
1. Сформулируйте понятие непрерывной функции в данной точке. 2. Сформулируйте понятие точки разрыва функции. 3. В чем принципиальное различие между точками разрыва первого и второго рода? 4. Сформулируйте понятие производной функции одной переменной. 5. Какая функция называется дифференцируемой в данной точке? 6. В чем состоит геометрический смысл производной? 7. Запишите правило дифференцирования суммы функций. 8. Запишите правило дифференцирования частного функций. 9. Запишите правило нахождения производной от произведения функций. 10. Сформулируйте правило дифференцирования сложных функций. 11. Сформулируйте понятие дифференциала функции одной переменной. 12. Сформулируйте понятие точек максимумов и минимумов функции. 13. Запишите необходимый и достаточный признаки существования точек экстремумов функции.
Примеры решения типовых задач
Пример 4.1. Найти производную функции:
Решение:
 .
.
Пример 4.2. Найти производную функции: .
Решение:
Воспользуемся правилом дифференцирования произведения функций:
Пример
4.3. Найти
производную функции:  .
.
Решение:
Воспользуемся
правилом дифференцирования частного  .
.
.
Пример 4.4. Найти производную сложной функции: .
Решение:
Пример 4.5. Исследовать на максимум и минимум функцию: .
Решение:
Находим критические точки. Продифференцируем данную функцию:
.
Находим действительные корни производной:
 ;
;  .
.
Производная всюду непрерывна, значит, других критических точек нет.
Исследуем первую критическую точку . Так как, то:
При  имеем;
имеем;
При 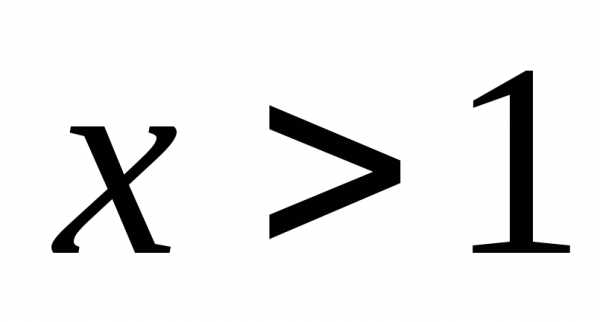 имеем.
имеем.
Значит,
при переходе (слева направо) через
значение 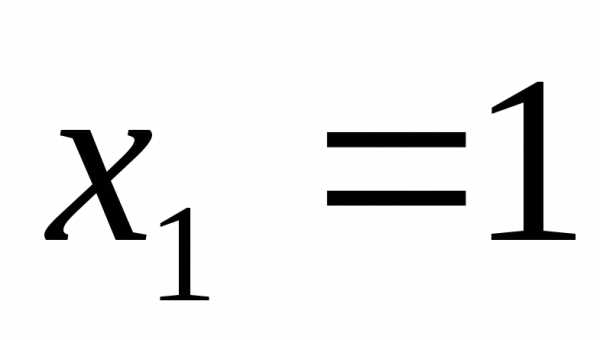 производная меняет знак с плюса на
минус. Следовательно, при
производная меняет знак с плюса на
минус. Следовательно, при функция имеет максимум.
функция имеет максимум.
Исследуем
вторую критическую точку  :
:
При  имеем;
имеем;
При 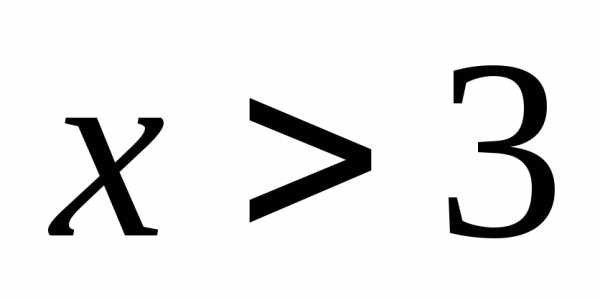 имеем.
имеем.
Значит,
при переходе (слева направо) через
значение 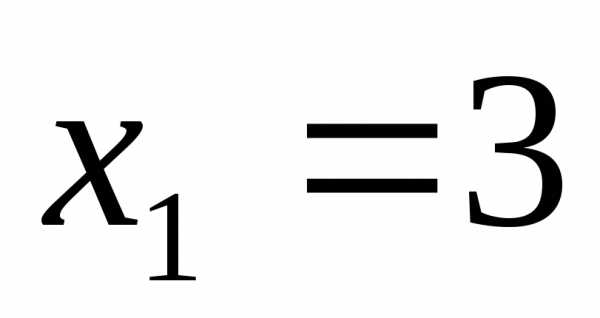 производная меняет знак с минуса на
плюс. Следовательно, при
производная меняет знак с минуса на
плюс. Следовательно, при функция имеет минимум.
функция имеет минимум.
.
Пример 4.6. Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузу, равную 10 см.
Решение:
Площадь
прямоугольного треугольника  можно найти по формуле:
можно найти по формуле:
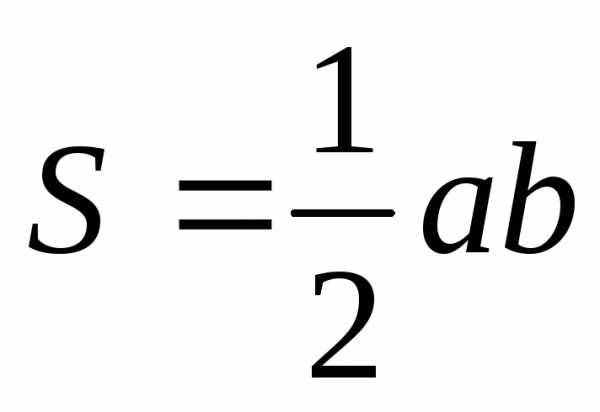 ,
где
,
где  и
и длины катетов. Согласно теореме Пифагора:
длины катетов. Согласно теореме Пифагора:
,
где  – длина гипотенузы.
– длина гипотенузы.
Таким образом, подставив данное выражение в формулу для нахождения площади, получим функцию одной переменной:
.
Нам
необходимо найти прямоугольный
треугольник наибольшей площади, т.е. по
сути, нам необходимо исследовать на
экстремумы функцию 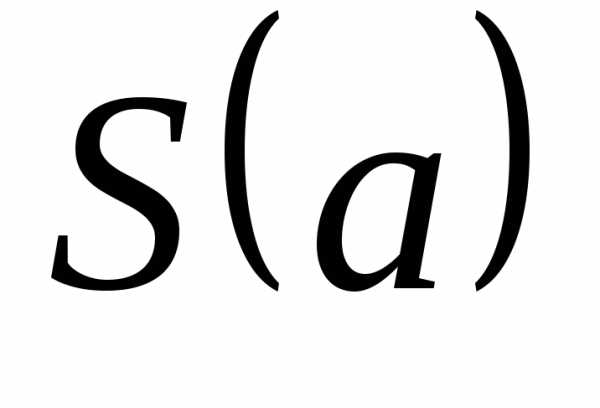 и найти при каком значении
и найти при каком значении она максимальна.
она максимальна.
Находим
производную от функции 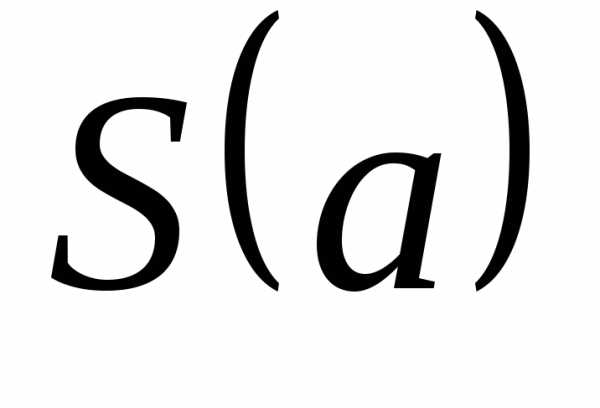 :
:
Находим критические точки: ,, Используя достаточный признак существования экстремума функции, можно определить, что точкой максимума будет. Тогда длина второго катета будет равна:. Таким образом, максимальная площадь будет равна:
см2.
Задачи для самостоятельного решения
4.1. Найти производные функций:
а) ; б) 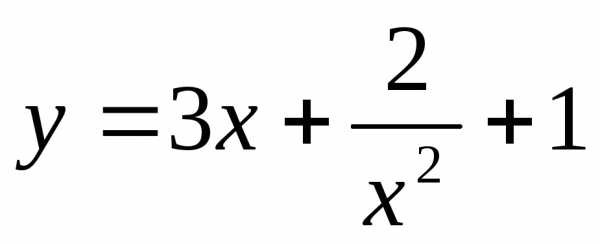 ;
;
в)
;г) 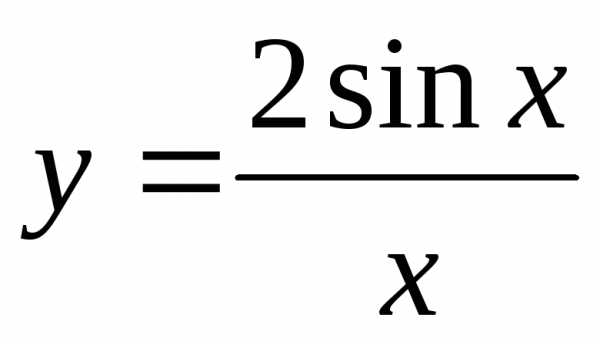 .
.
4.2. Найти производную сложной функции:
а) 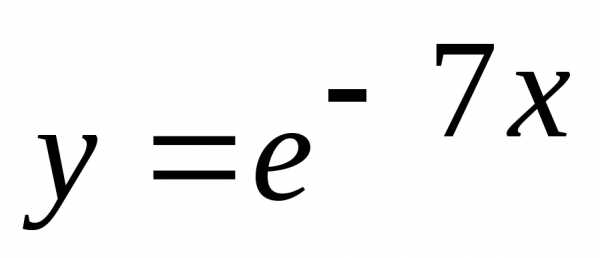 ; б)
;
; б)
;
в) 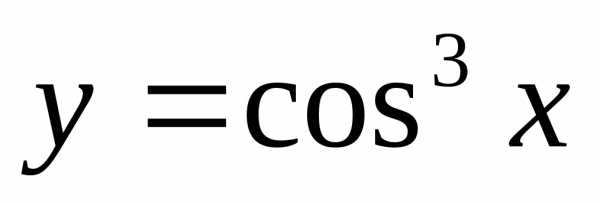 ;г)
.
;г)
.
4.3. Найти экстремумы функции:
а) ;б) .
4.4. Найти наибольшее и наименьшее значения функции на отрезке.
4.5. В тюрьме города Ленинск собрались строить железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры должна быть не менее 2,5 м, а ее площадь – не менее 6 м2?
studfiles.net
Творческие задания по теме «Предел»
Является ли число 0,8 пределом последовательности 0,7; 0,77; 0,777; … ? Почему?
Найти предел последовательности
0,03; 0,033; 0,0333 ; …
Функция Е(х) или [х] – целая часть числа х, т.е. наибольшее целое число, не превосходящее х. Найти:
А)
Б)
В)
4. Найти
А)
Б)
5. Найти
6. Доказать, что функция не является ограниченной в любой окрестности точки х=0, однако не является бесконечно большой при х.
7. Доказать, что не существует.
8. Доказать, что функция не имеет предела при х.
9. Доказать, что , указавN=N , если , а=2 .
10. Докажите, что если последовательность имеет предел, то она ограниченна. Верно ли обратное утверждение?
11. Пусть , aне существует. Доказать, чтоне существует.
12. Придумайте последовательности {xn} , {yn} для которых ,, и такие, что
А)
Б)
В)
Г)
13. Найдите
14. Найти предел последовательности
1; 1+; 1++; 1+++; …
15. Доказать, что процесс, описываемый фикцией
f(t)=sin(ln t)-sin(ln(t-1))
является затухающим.
16. Доказать, что уравнение имеет хотя бы один корень припри любом значениии при условии.
17. Найти число n , такое, что
18. Построить график функции
19. Найти числа , чтобы
Дополнительные задачи на пределы
Доказать, что следующие пределы не существуют
А)
Б)
В) 2.
Найти постоянные a и b из условия :
А)
Б)
Найти односторонние пределы функций
А) при x
Б) при x
В) при x
Найти пределы
Доказать, что при
А)
Б)
В)
Определить при порядок малости по отношению к бесконечно малойследующих бесконечно малых:
А)
Б)
Доказать, что функция tgx-sinx будет бесконечно малой третьего порядка относительно х при .
Доказать эквивалентность бесконечно малых функций
А) иx при
Б) иx при
Определить, при каком значении постоянных с и k функция эквивалентна функциипри
А)
Б) )
В) sin3x-3cosx)
Г)
Найти пределы
А)
Б
В)
Г)
Д)
Е)
Ж)
З)
И)
К)
Л)
М)
Н)
О)
П)
Р)
С)
Верно ли соотношение при?
Задачи на пределы (3й уровень)
Найти
x1=0, x2=1, xn=1/2(xn-1+xn-2)
Найти (n=2,3,…)
Найти (n=1,2,…)
X0=1, xn=
y0=1, yn=1/2((n=1, 2, … ) , x>0.
Найти
26-36 Построить графики функций
, x
, x
, x
, x
, x
, x>0
, x
, где
Задачи третьего уровня сложности по теме «пределы»
№1.
Доказать, что уравнение
,
где ω > 0 – частота, а b – постоянная, удовлетворяющая условию b > , имеет хотя бы один корень приx>0.
№2.
При каких значениях параметра а процесс h(t), задаваемый функцией
(t>0),
обладает свойством h(0+0)=h(+∞) ?
№3.
Является ли процесс f(t), описываемый функцией
(t≥0)?
затухающим?
№4.
При каких значениях параметра k≥0 процесс u(t), задаваемый функцией
(t≥0),
является затухающим? Существует ли такое значение параметра k, при котором процесс u(t) стремится с возрастанием времени к некоторому постоянному режиму u1(t)=u0 — const ?
№5.
При каком значении постоянной а процесс u(t) является затухающим, если
А)
Б)
№6.
Какие из приведенных ниже процессов являются затухающими?
А) ,t≥0
Б) ,t≥0
В) ,t≥0
Г) ,t≥0
№7.
Дискретный процесс {un}, n=1, 2, … задается так:
Найти .
№8.
Чему равно n, если и
?
№9.
Постройте график функции:
№10.
Постройте график функции: .
№11.
При каких значениях параметров процессh(t), задаваемый аналитической формулой
является затухающим?
№12.
Вычислить предел:
№13.
Вычислить предел:
№14.
Доказать, что числовая последовательность имеет предел и найти его.
№15.
Найти предел суммы:
№16.
Найти предел:
№17.
Вычислить предел: .
№18.
Вычислить пределы:
А)
Б)
В)
Г)
Д)
№19.
Является ли процесс h(t), задаваемый формулой
,
непрерывным при t≥0? Если нет, то укажите точки разрыва h(t) и найдите величину скачка в этих точках.
№20.
Можно ли непрерывную на некотором отрезке функцию представить в виде суммы двух разрывных функций, заданных на том же отрезке? Если «да», то приведите какой-либо конкретный пример.
№21.
Можно ли разрывную функцию на отрезке функцию представить в виде:
А) суммы конечного числа непрерывных на отрезке функций
Б) суммы бесконечного числа непрерывных на функций?
№22.
Имеет ли уравнение корни на отрезке? Если «да», то укажите их число.
№23.
Непрерывная функция f(x) обладает свойством: . Найти все такие функции.
№24.
Найти ограниченную при x=0 функцию, удовлетворяющую функциональному уравнению
.
Творческие задания по теме «Предел» — ответы.
Не является
1/30
-2, не сущ, 1
Не сущ, 1
b, -b или не сущ.
Можно взять 1/х=2πk и 1/x =π/2 + πk
Например, x=πk и x =π/2 + 2πk
Можно взять 1/х = πk и 1/x =π/2 + 2πk
Например, xn=sin πn. Обратное не верно.
Док-во от противного
Очевидные последовательности
0
2
f(0)f(+, f(+) =, f(0)
2000
Дополнительные задачи на пределы – ответы.
2. а) (1;1) б) (1;-1/2)
3. а) f(-0) =1/2; f(+0)=0
б) f(-0) =0; f(+0)=+
в) f(-0) =-1; f(+0)=1
4. 4.1 54
4.2
4.3 1
4.4 1/8
4.5 -2
4.6 1/2
4.7 3/5
6. а) 1
б) 2
9. а) (1;2)
б)
в) (-1/4; 3)
г) (1; 2)
10. а) 9/2
б) -2
в) 3/4
г) 1
д) 4/5
е) 1
ж) 1
з)
и) 1/а
к)
л) а
м)
н)
о) ((2lna)/b)
п)
р) π
с)
studfiles.net
Тестовые задания по теме: «Пределы функций»
Тестовые задания по теме «Пределы функций»
Одним из видов контроля является тестирование, позволяющее оперативно и достаточно определить уровень знаний студента.
Данная работа посвящена теме «Предел функции» и дается в 8 вариантах. Каждый вариант содержит 7 заданий с четырьмя вариантами ответов, один из которых правильный.
Выборочная система ответов обеспечивает возможность экспресс-контроля, т.е. немедленной проверки и оценки выполненного задания.
Задания составлены таким образом, что в них отражены узловые, идейно важные моменты данной темы, на которые следует обратить внимание в первую очередь.
Основное назначение тестовых заданий – помочь преподавателю в проведении систематического и оперативного контроля текущей успеваемости студентов.
Вариант 1
1) Вычислите
ответы: А) – 3; Б) ; В) – 4; Г) 8
2) Вычислите:
ответы: А) – 3; Б) ; В) ; Г) другой ответ
3) Дано:
Вычислите:
ответы: А) – 15; Б) 15; В) 1,5; Г) – 1,5
4) Вычислите:
ответы: А) 0; Б) 2; В) ; Г)
5) Вычислите:
ответы: А) 0; Б) ; В) 1,5; Г)
6) Вычислите:
ответы: А) ; Б) ; В) 0; Г)
7) Вычислите:
ответы: А) ; Б) 2; В) 0; Г)
Вариант 2
1) Вычислите
ответы: А) 1; Б) – 23; В) – 19; Г) 3
2) Вычислите:
ответы: А) 1; Б) – 3; В) – 1; Г) 0
3) Дано:
Вычислите:
ответы: А) ; Б) ; В) ; Г)
4) Вычислите:
ответы: А) 0; Б) ; В)– ; Г)
5) Вычислите:
ответы: А) 0; Б) ; В) ; Г)
6) Вычислите:
ответы: А) ; Б)1; В) ; Г)
7) Вычислите:
ответы: A) ; Б) ; В) 1; Г) 0
Вариант 3
1) Вычислите
ответы: А) 2; Б) – 10; В) – ; Г)
2) Вычислите:
ответы: А) ; Б) ; В) ; Г) другой ответ
3) Дано:
Вычислите:
ответы: А) –18; Б) 6; В) – 6; Г)
4) Вычислите:
ответы: А) 0; Б) ; В) ; Г) другой ответ
5) Вычислите:
ответы: А) ; Б) 0; В) 3; Г)
6) Вычислите:
ответы: А) 1; Б) ; В) ; Г)
7) Вычислите:
ответы: A) ; Б) ; В) ; Г) 5
Вариант 4
1) Вычислите
ответы: А) 20; Б) 8; В) –10; Г) 10
2) Вычислите:
ответы: А) 3; Б) ; В) ; Г) другой ответ
3) Дано:
Вычислите:
ответы: А) 2; Б) 12; В) ; Г) 4
4) Вычислите:
ответы: А) 0; Б) 4; В) ; Г)
5) Вычислите:
ответы: А) ; Б) ; В) –5; Г) 0
6) Вычислите:
ответы: А) 1; Б) ; В) 0; Г)
7) Вычислите:
ответы: A) ; Б) ; В) 0; Г) 1
Вариант 5
1) Вычислите
ответы: А) 0; Б) 6; В) 18; Г) 9
2) Вычислите:
ответы: А) ; Б) 1; В) 3; Г) –1
3) Дано:
Вычислите:
ответы: А) –2; Б) ; В) 0; Г) –8
4) Вычислите:
ответы: А) 3; Б) ; В) ; Г) другой ответ
5) Вычислите:
ответы: А) 5; Б) ; В) –1; Г) –5
6) Вычислите:
ответы: A) 1; Б) ; В) 2; Г)
7) Вычислите:
ответы: А) ; Б) 0; В) ; Г) другой ответ
Вариант 6
1) Вычислите
ответы: А) 4; Б) –54; В) –24; Г) 26
2) Вычислите:
ответы: А) 6; Б) –4; В) 2; Г) другой ответ
3) Дано:
Вычислите:
ответы: А) –8; Б) 9; В) 0; Г)
4) Вычислите:
ответы: А) ; Б) ; В) 1; Г) –1
5) Вычислите:
ответы: А) ; Б) ; В) 1; Г) другой ответ
6) Вычислите:
ответы: A) 8; Б) 0; В) ; Г) 6
7) Вычислите:
ответы: А) –4; Б) 0; В) 5; Г)
Вариант 7
1) Вычислите
ответы: А) 4; Б) 0; В) 8; Г) –6
2) Вычислите:
ответы: А) 10; Б) 6; В) ; Г) 5
3) Дано:
Вычислите:
ответы: А) 1; Б) ; В) ; Г)
4) Вычислите:
ответы: А) –5; Б) ; В) –2; Г)
5) Вычислите:
ответы: А) ; Б) ; В) ; Г) другой ответ
6) Вычислите:
ответы: A) 1; Б) ; В) 2; Г)
7) Вычислите:
ответы: А) ; Б) 2; В) 4; Г)
Вариант 8
1) Вычислите
ответы: А) –18; Б) 128; В) 30; Г) –22
2) Вычислите:
ответы: А) 0; Б) 11; В) –8; Г) 23
3) Дано:
Вычислите:
ответы: А) –2; Б) 2; В) ; Г) другой ответ
4) Вычислите:
ответы: А) 1; Б) 2; В) ; Г)
5) Вычислите:
ответы: А) 5; Б) ; В) ; Г) 2
6) Вычислите:
ответы: A) 1; Б) 2; В) ; Г)
7) Вычислите:
ответы: А) ; Б) ; В) ; Г)
Ответы:
В-1 | В-2 | В-3 | В-4 | В-5 | В-6 | В-7 | В-8 | |
1 | А | А | А | Б | Б | Б | В | Б |
2 | Б | Б | Б | А | В | А | А | В |
3 | Б | Г | А | Б | Г | Б | Б | А |
4 | А | В | А | А | Б | А | Б | Г |
5 | Б | А | В | А | А | Б | В | А |
6 | Б | А | А | Б | Б | А | В | В |
7 | Б | А | Б | А | В | А | В | Б |
xn--j1ahfl.xn--p1ai
задачи по пределам
Пределы
Задача 1. Доказать, что (указать ).
Задача 2. Вычислить пределы числовых последовательностей.
Задача 3. Вычислить пределы числовых последовательностей.
Задача 4. Вычислить пределы числовых последовательностей.
Задача 5. Вычислить пределы числовых последовательностей.
Задача 6. Вычислить пределы числовых последовательностей.
Задача 7. Доказать (найти ), что:
Задача 8. Доказать, что функция непрерывна в точке(найти).
Задача 9. Вычислить пределы функций.
Задача 10.(3.20 МАДИ) Вычислить пределы функций.
Задача 11. Вычислить пределы функций.
Задача 12. Вычислить пределы функций.
Задача 13.15 Вычислить пределы функций.
Задача 14. Вычислить пределы функций.
Задача 15. Вычислить пределы функций.
Задача 16. Вычислить пределы функций.
Задача 17. Вычислить пределы функций.
Задача 20. Вычислить предел функции или числовой последовательности.
studfiles.net
IZ_1_PREDELY
ИЗ № 1
Пределы числовых последовательностей и функций.
Образец выполнения ИЗ № 1.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
Решение:
Данную
последовательность можно представить
как произведение ограниченной
последовательности
,
предел которой не определён, и сходящейся
последовательности ,
предел которой равен нулю. Согласно
одному из свойств сходящихся
последовательностей, произведение
ограниченной и сходящейся последовательности
есть также сходящаяся последовательность,
предел которой равен пределу последней.
,
предел которой равен нулю. Согласно
одному из свойств сходящихся
последовательностей, произведение
ограниченной и сходящейся последовательности
есть также сходящаяся последовательность,
предел которой равен пределу последней.
Тогда: .
1.2. 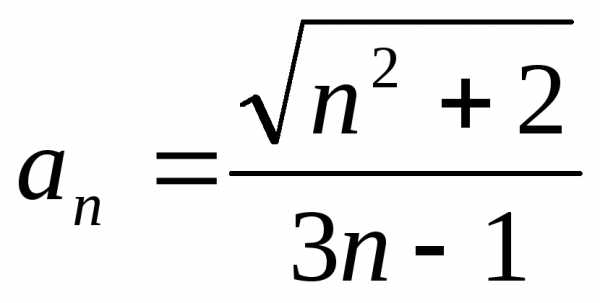 .
.
Решение:
.
1.3. .
Решение:
Как и в первом
пункте данного задания, представим
данную последовательность в виде
произведения двух последовательностей:
,
где.
Очевидно, .
Последовательность
.
Последовательность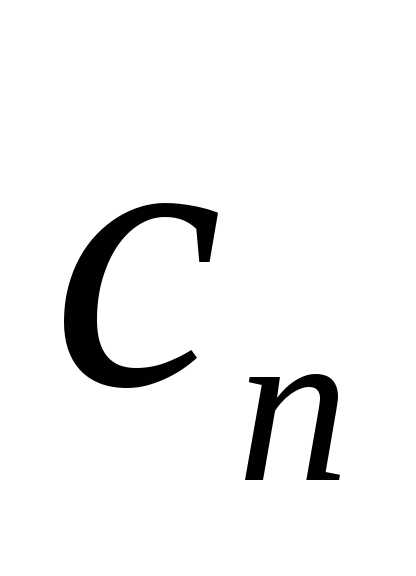 в силу свойств косинуса является
ограниченной:.
Таким образом, члены последовательности
в силу свойств косинуса является
ограниченной:.
Таким образом, члены последовательности прибудут принимать как неограниченно
большие, так и неограниченно малые
значения. Следовательно, данная
последовательность является расходящейся
и предел её не определён.
прибудут принимать как неограниченно
большие, так и неограниченно малые
значения. Следовательно, данная
последовательность является расходящейся
и предел её не определён.
Задание 2. Найти пределы функций:
2.1. .
Решение:
В данном случае
имеем неопределённость вида  .
Для её раскрытия используем следующее
известное свойство.
.
Для её раскрытия используем следующее
известное свойство.
Пусть дана
дробно-рациональная функция  ,
гденекоторые многочлены. Тогда:
,
гденекоторые многочлены. Тогда:
Если степень многочлена
 больше степени многочлена
больше степени многочлена ,
то.
,
то.Если степень многочлена
 меньше степени многочлена
меньше степени многочлена ,
то
,
то .
.Если степень многочлена
 равна степени многочлена
равна степени многочлена ,
то
,
то ,
где
,
где числовые
коэффициенты при наивысших степенях
числовые
коэффициенты при наивысших степенях в данных многочленах.
в данных многочленах.
В данном случае
степени числителя и знаменателя равны
двум, поэтому  .
.
2.2.  .
.
Решение:
В данном случае
снова имеем неопределённость вида  .
Для её раскрытия используем то же
известное свойство, что и в предыдущем
случае. Степень числителя равна двум,
а степень знаменателя – трём. Поэтому.
.
Для её раскрытия используем то же
известное свойство, что и в предыдущем
случае. Степень числителя равна двум,
а степень знаменателя – трём. Поэтому.
2.3.  .
.
Решение:
В данном случае
снова имеем неопределённость вида 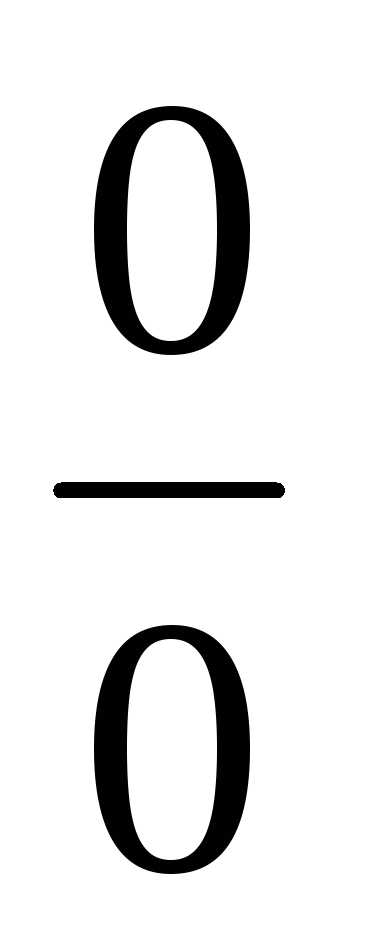 .
Чтобы раскрыть её, преобразуем данную
функцию, предварительно разложив на
множители числитель и знаменатель:.
.
Чтобы раскрыть её, преобразуем данную
функцию, предварительно разложив на
множители числитель и знаменатель:.
2.4. .
.
Решение:
В данном случае
имеем неопределённость вида 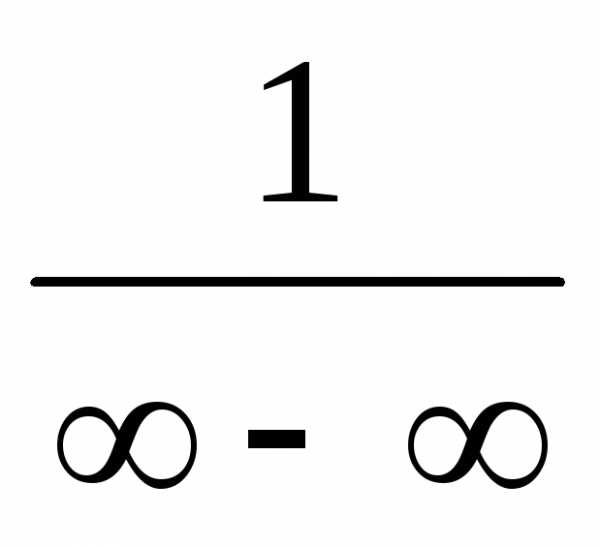 .
Чтобы раскрыть её, домножим данную дробь
на дробь, сопряжённую её знаменателю:
.
Чтобы раскрыть её, домножим данную дробь
на дробь, сопряжённую её знаменателю:
.
2.5. 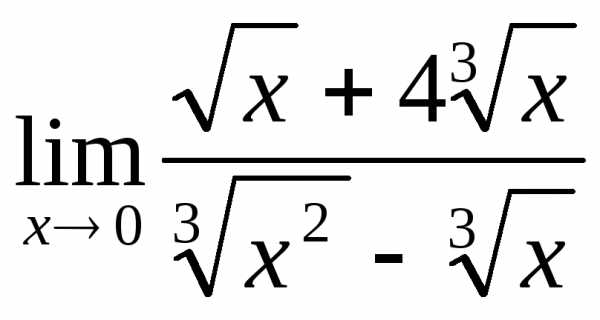 .
.
Решение:
В данном случае
имеем неопределённость вида 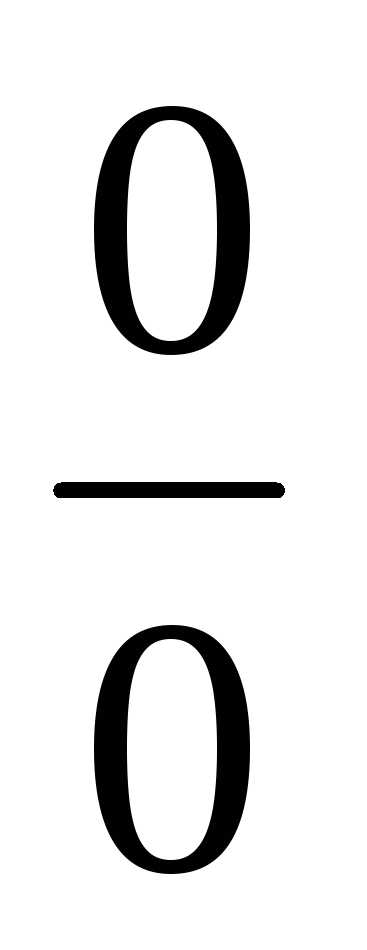 .
Чтобы раскрыть её, введём подстановку
.
Чтобы раскрыть её, введём подстановку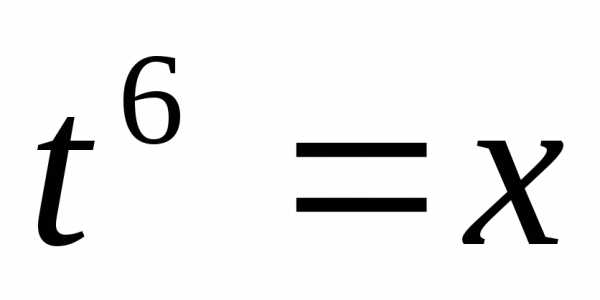 .
Заметим, что
.
Заметим, что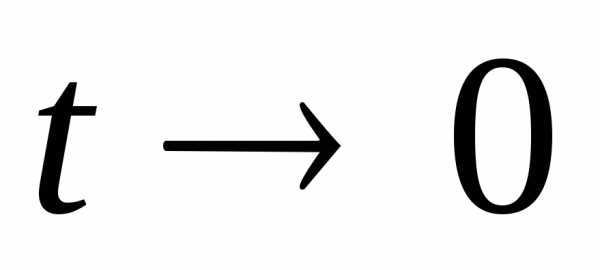 ,
при
,
при .
Получим:
.
Получим:
.
2.6. 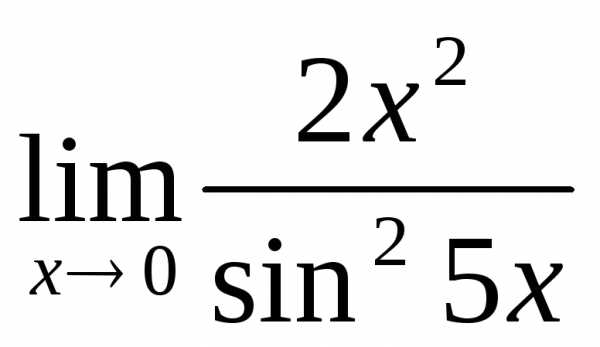 .
.
Решение:
Имеем неопределённость
вида  .
Чтобы раскрыть её, приведём данную дробь
к виду, который допускал бы применение
первого замечательного предела
.
Чтобы раскрыть её, приведём данную дробь
к виду, который допускал бы применение
первого замечательного предела .
.
.
Замечание. При выполнении этого задания и заданий, подобных ему, можно использовать и другие способы решения – например, применить правило Лопиталя или эквивалентность бесконечно малых функций.
2.7.  .
.
Решение:
Имеем неопределённость
вида  .
Чтобы раскрыть её, как и в предыдущем
задании, приведём данную дробь к виду,
который допускал бы применение первого
замечательного предела
.
Чтобы раскрыть её, как и в предыдущем
задании, приведём данную дробь к виду,
который допускал бы применение первого
замечательного предела .
Введём подстановку
.
Введём подстановку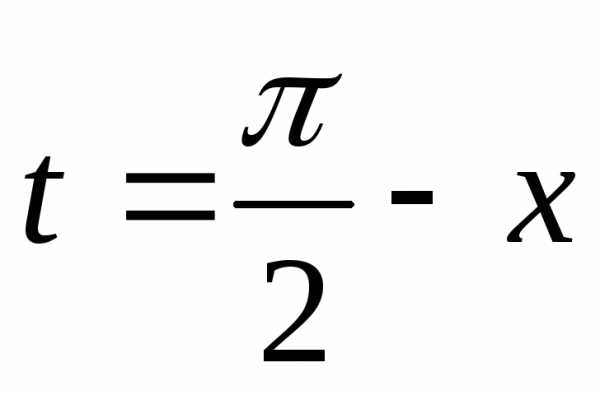 .
Заметим, что
.
Заметим, что ,
при
,
при .
Получим:
.
Получим:
.
2.8.  .
.
Решение:
Имеем неопределённость
вида 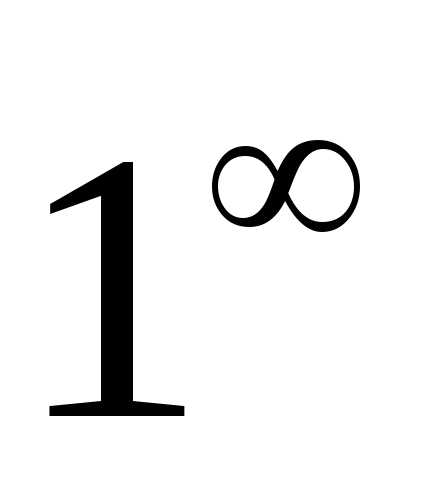 .
Чтобы раскрыть её, приведём данную дробь
к виду, который допускал бы применение
второго замечательного предела
.
Чтобы раскрыть её, приведём данную дробь
к виду, который допускал бы применение
второго замечательного предела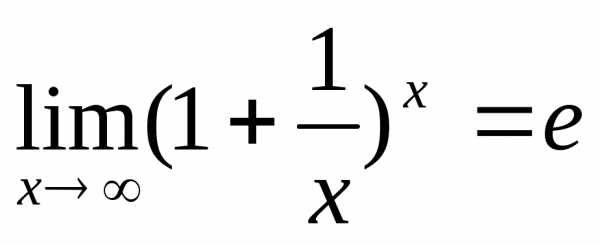 .
.
.
Далее, воспользовавшись равенствами  и
и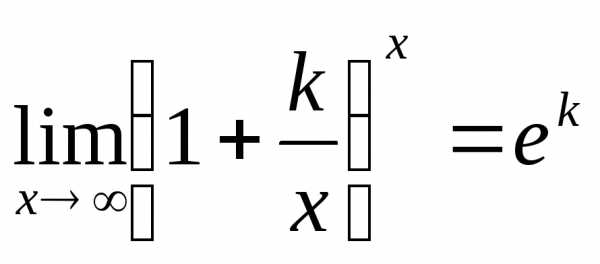 ,
получим:
,
получим: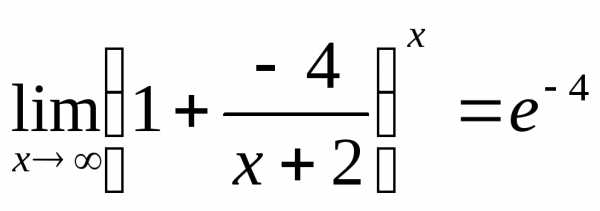 .
.
2.9.  .
.
Решение:
Обратим внимание,
что в данном случае  ,
поэтому нет необходимости использовать
второй замечательный предел, поскольку
нет никакой неопределённости, и предел
может быть вычислен непосредственно.
,
поэтому нет необходимости использовать
второй замечательный предел, поскольку
нет никакой неопределённости, и предел
может быть вычислен непосредственно.
.
2.10. 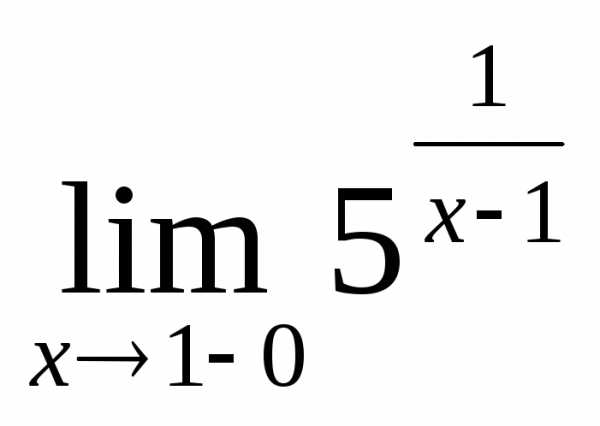 .
.
Решение:
Прежде всего,
заметим, что если  стремится к единице слева, то
стремится к единице слева, то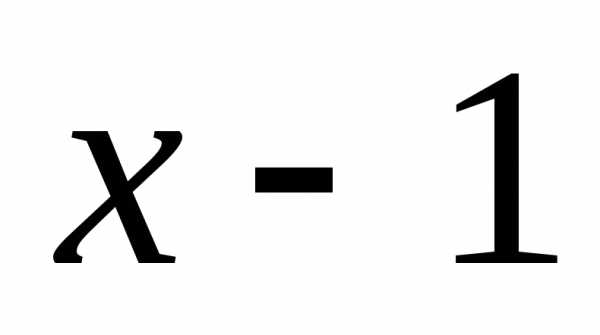 будет принимать близкие к нулю
отрицательные значения, и выражение
будет принимать близкие к нулю
отрицательные значения, и выражение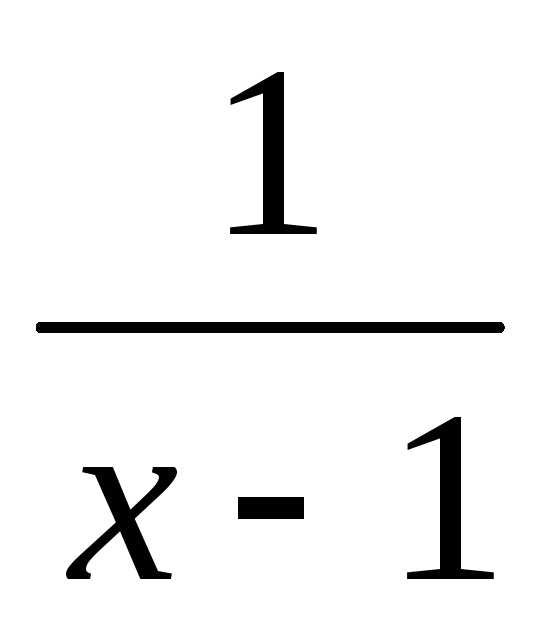 ,
очевидно, стремится к
,
очевидно, стремится к .
Тогда:.
.
Тогда:.
Задание 3. Исследовать функцию на непрерывность:
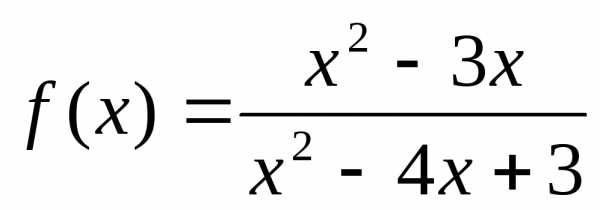 .
.
Решение:
Найдём область
определения данной функции.
.
Итак, имеем две точки разрыва: и
и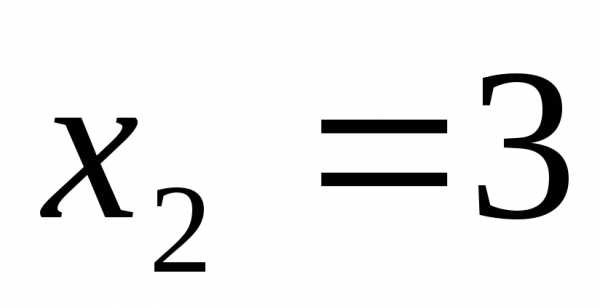 .
Теперь определим, каков характер разрыва
функции в каждой из этих точек.
.
Теперь определим, каков характер разрыва
функции в каждой из этих точек.
Точка  является точкой бесконечного разрыва
(второго рода), так как:.
является точкой бесконечного разрыва
(второго рода), так как:.
Точка 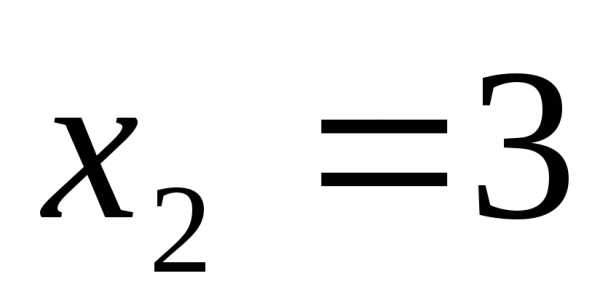 является точкой устранимого разрыва,
так как:
является точкой устранимого разрыва,
так как:
.
Окончательный
ответ: функция непрерывна при
;
точка является точкой бесконечного разрыва;
точка
является точкой бесконечного разрыва;
точка является точкой устранимого разрыва и.
является точкой устранимого разрыва и.
Вариант № 1.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3. .
.
Задание 2. Найти пределы функций:
2.1. 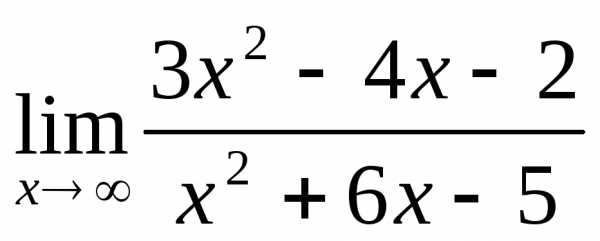 .
2.2.
.
2.2. .
2.3.
.
2.3. .
2.4.
.
2.4.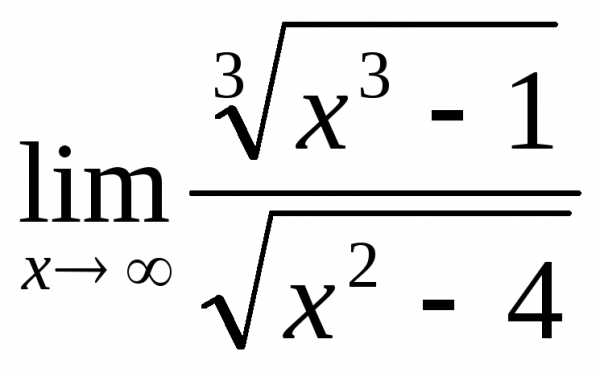 .
2.5.
.
2.5. .
2.6.
.
2.6. .
2.7.
.
2.7.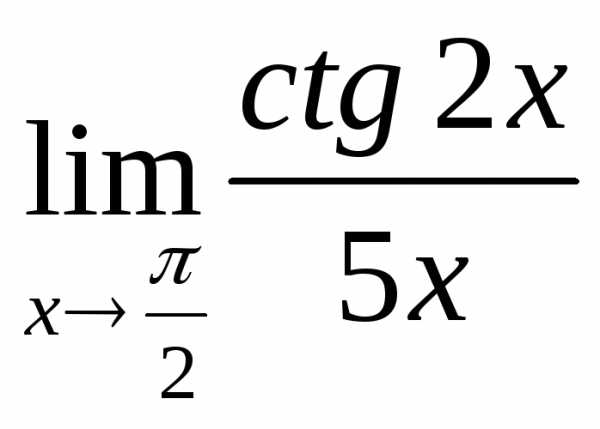 .
2.8.
.
2.8. .
2.9.
.
2.9. .
2.10.
.
2.10. .
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 2.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.  .
1.2.
.
1.2.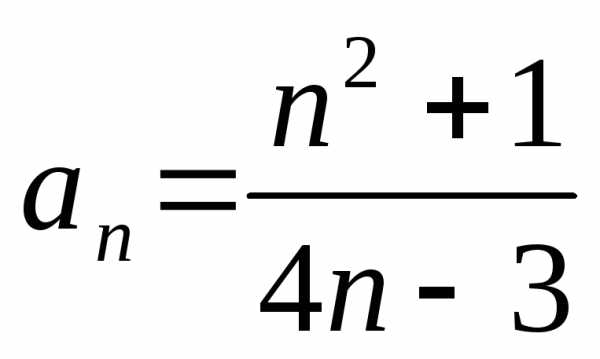 ;
1.3.
;
1.3.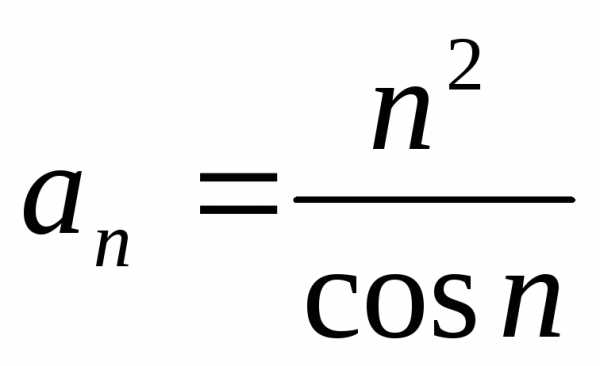 .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2. .
2.3.
.
2.3. .
2.4.
.
2.4.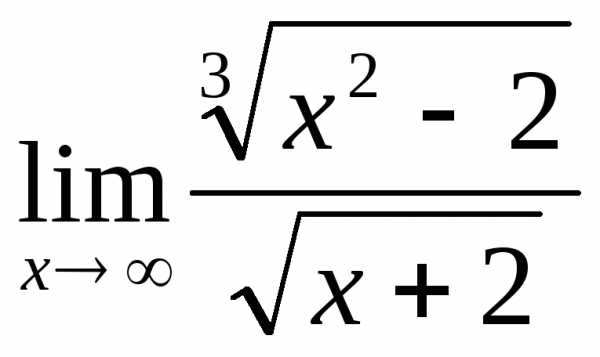 .
2.5.
.
2.5.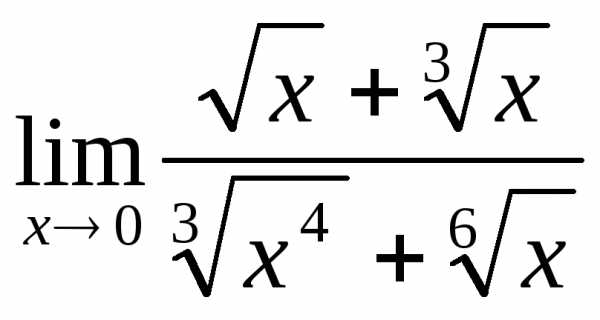 .
2.6.
.
2.6.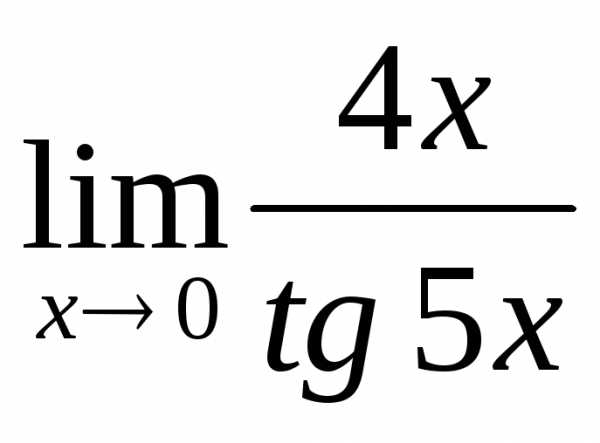 .
2.7.
.
2.7.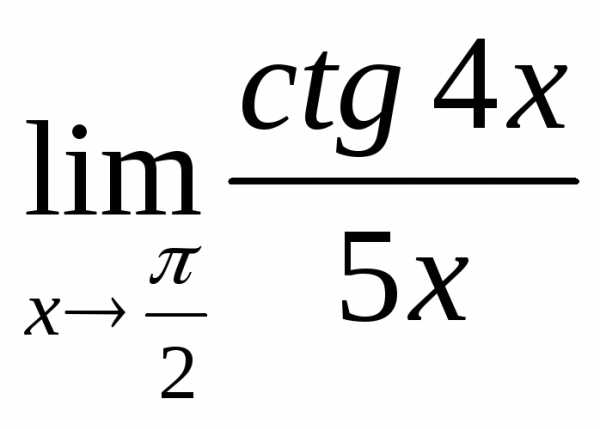 .
2.8.
.
2.8. .
2.9.
.
2.9. .
2.10.
.
2.10. .
.
Задание 3. Исследовать функцию на непрерывность:
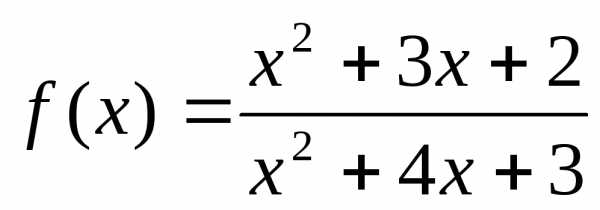 .
.
Вариант № 3.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3. .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2.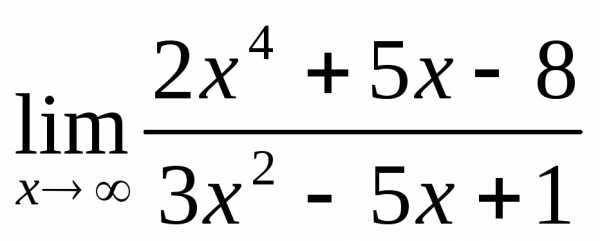 .
2.3.
.
2.3. .
2.4.
.
2.4. .
2.5.
.
2.5. .
2.6.
.
2.6.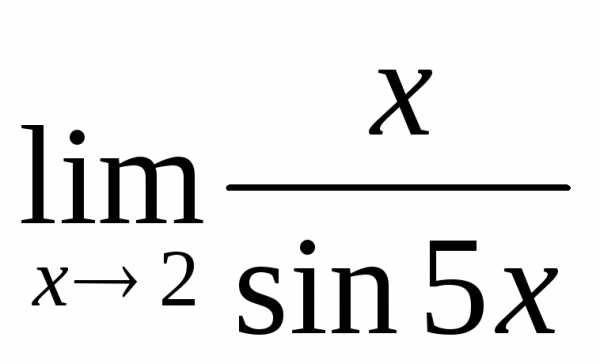 .
2.7.
.
2.7. .
2.8.
.
2.8.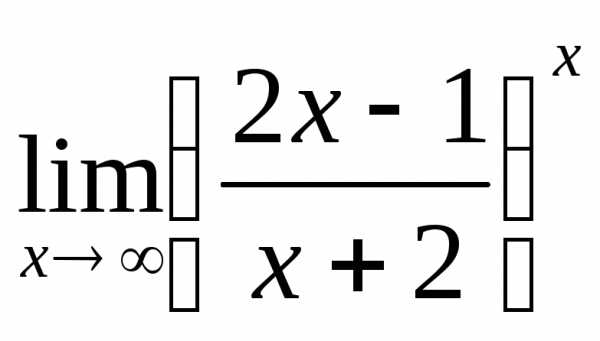 .
2.9.
.
2.9.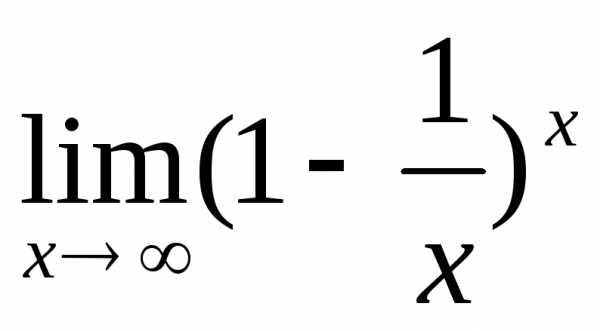 .
2.10.
.
2.10. .
.
Задание 3. Исследовать функцию на непрерывность:
.
Вариант № 4.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.  .
1.2.
.
1.2. ;
1.3.
;
1.3. .
.
Задание 2. Найти пределы функций:
2.1. 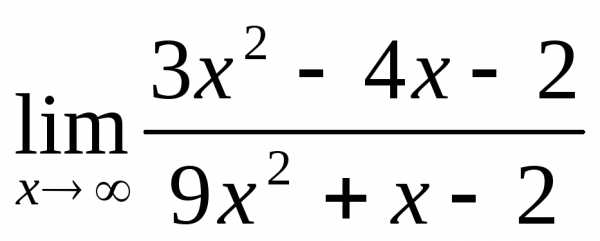 .
2.2.
.
2.2. .
2.3.
.
2.3. .
2.4.
.
2.4. .
2.5.
.
2.5. .
2.6.
.
2.6.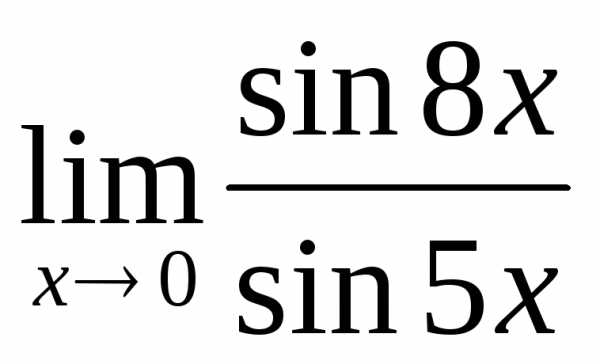 .
2.7.
.
2.7.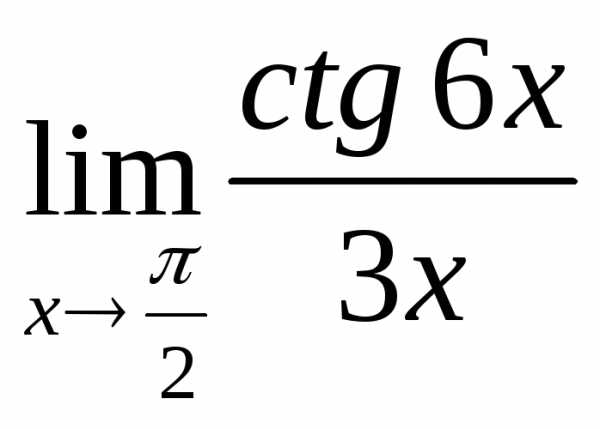 .
2.8.
.
2.8.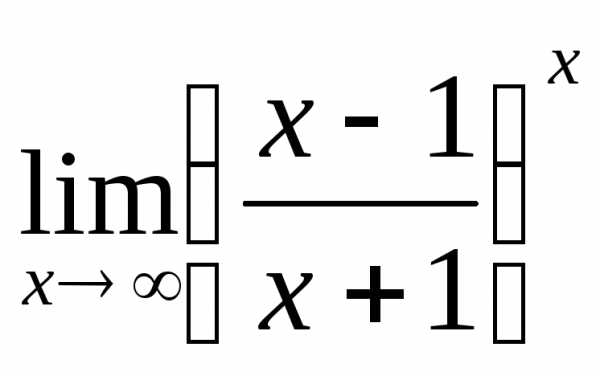 .
2.9.
.
2.9.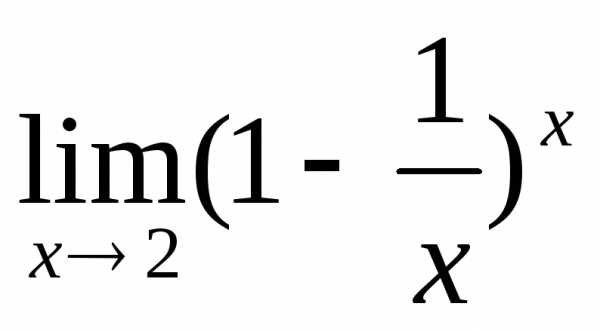 .
2.10.
.
2.10. .
.
Задание 3. Исследовать функцию на непрерывность:
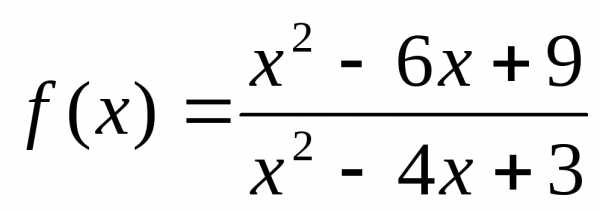 .
.
Вариант № 5.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3. .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2. .
2.3.
.
2.3.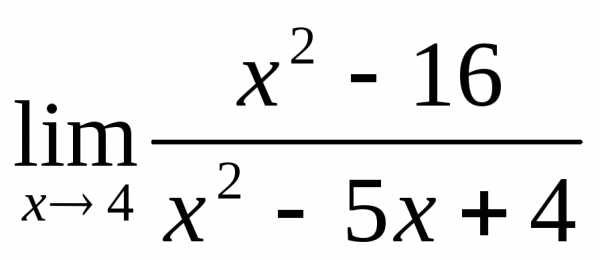 .
2.4.
.
2.4.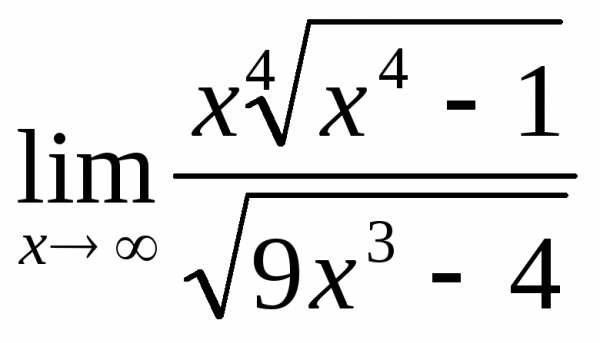 .
2.5.
.
2.5. .
2.6.
.
2.6. .
2.7.
.
2.7. .
2.8.
.
2.8.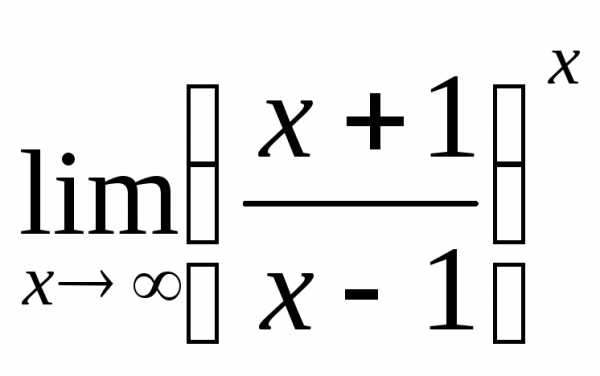 .
2.9.
.
2.9. .
2.10.
.
2.10.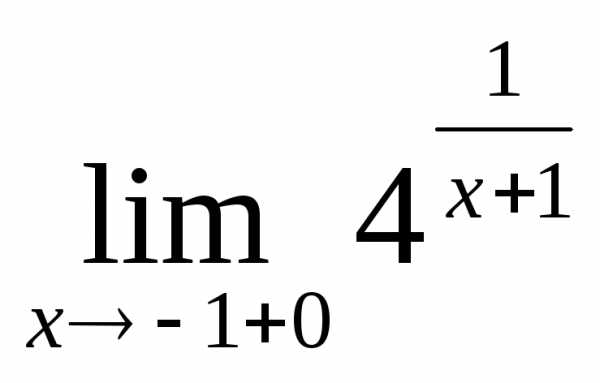 .
.
Задание 3. Исследовать функцию на непрерывность:
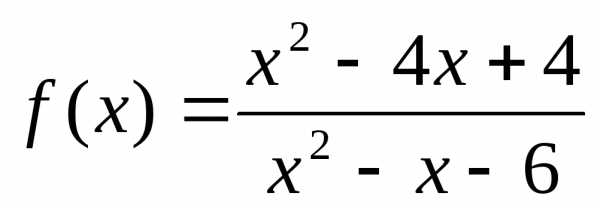 .
.
Вариант № 6.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3.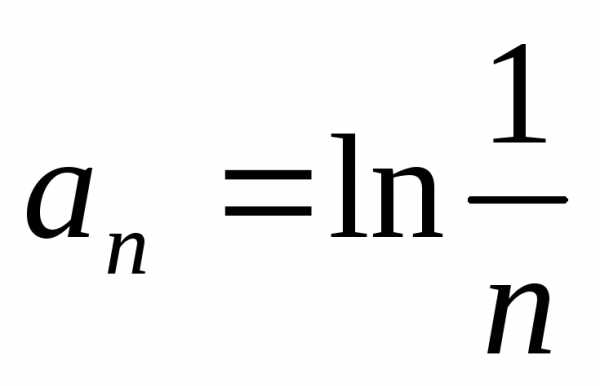 .
.
Задание 2. Найти пределы функций:
2.1. 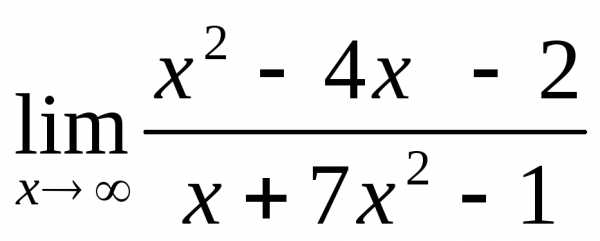 .
2.2.
.
2.2.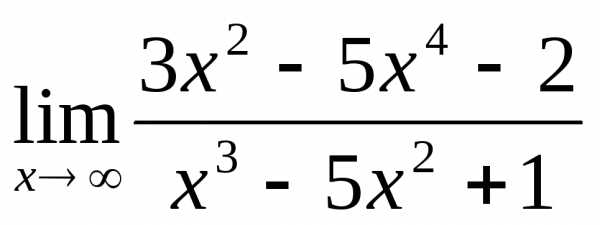 .
2.3.
.
2.3. .
2.4..
2.5.
.
2.4..
2.5.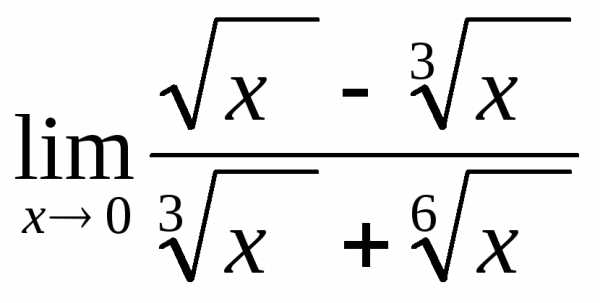 .
2.6.
.
2.6.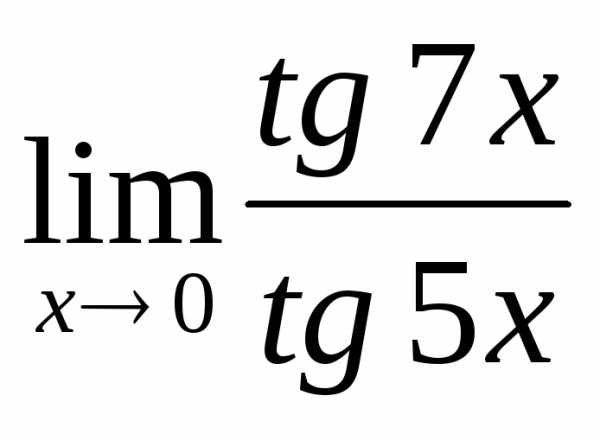 .
2.7.
.
2.7.  .
2.8.
.
2.8.  .
2.9.
.
2.9.  .
2.10.
.
2.10.  .
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 7.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3.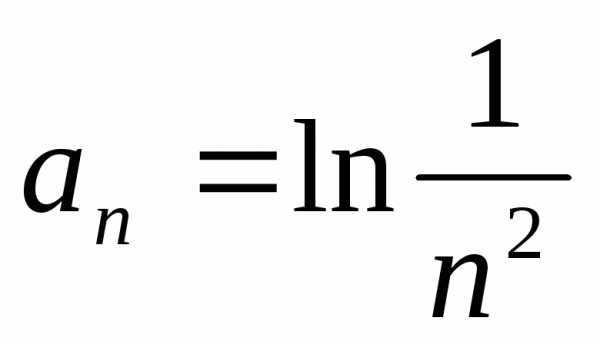 .
.
Задание 2. Найти пределы функций:
2.1.
.
2.2. .
2.3.
.
2.3.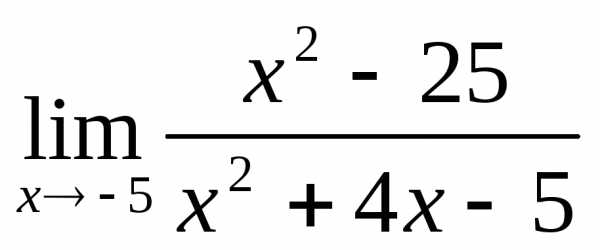 .
2.4.
.
2.5.
.
2.4.
.
2.5. 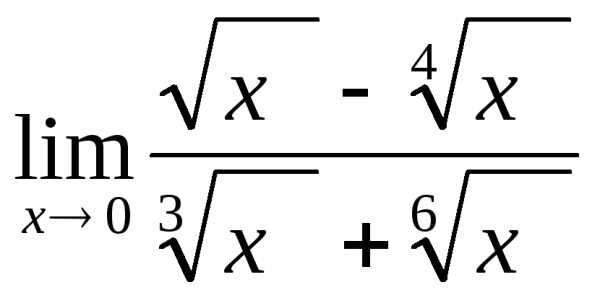 .
2.6.
.
2.6.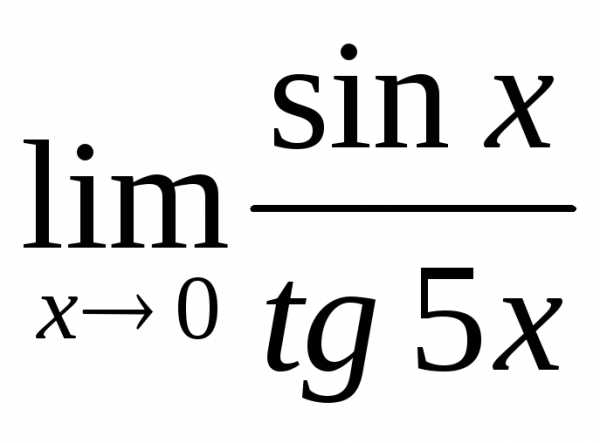 .
2.7.
.
2.7.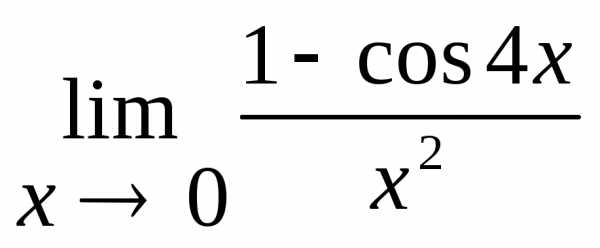 .
2.8.
.
2.8.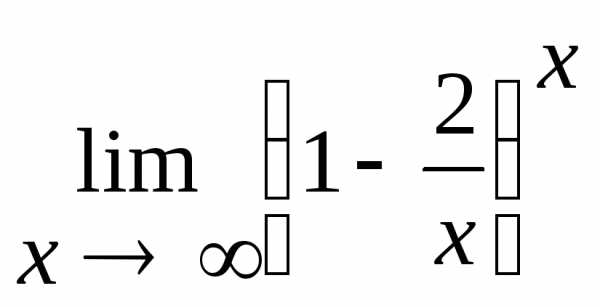 .
2.9.
.
2.9. 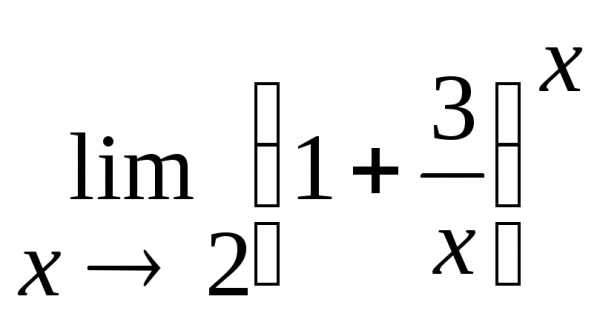 .
2.10.
.
2.10.  .
.
Задание 3. Исследовать функцию на непрерывность:
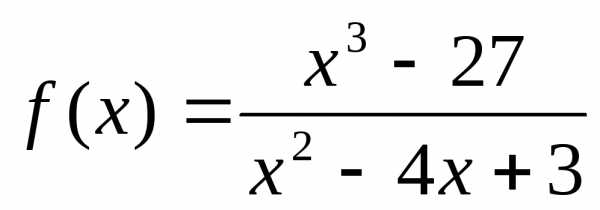 .
.
Вариант № 8.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2.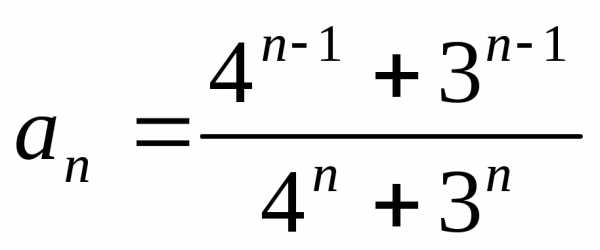 ;
1.3..
;
1.3..
Задание 2. Найти пределы функций:
2.1.
.
2.2.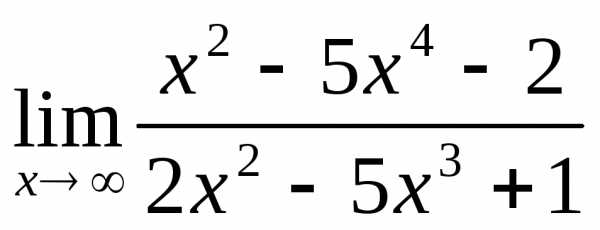 .
2.3.
.
2.3. .
2.4.
.
2.5.
.
2.4.
.
2.5.  .
2.6.
.
2.6. .
2.7.
.
2.7. 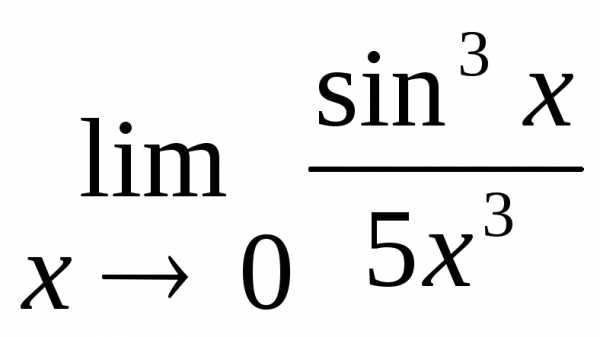 .
2.8.
.
2.8. 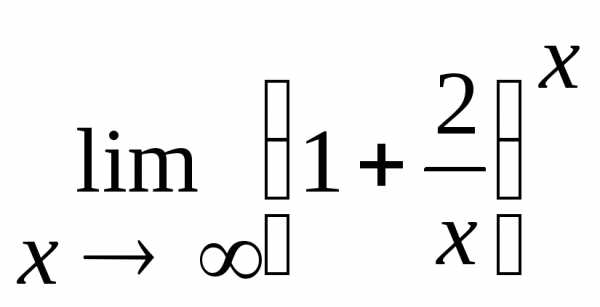 .
2.9.
.
2.9. 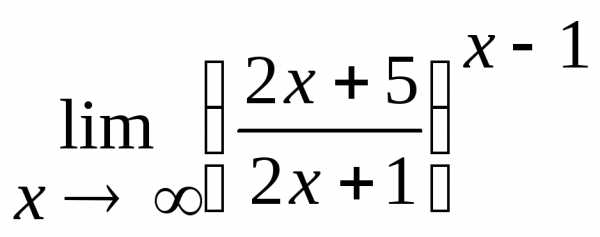 .
2.10.
.
.
2.10.
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 9.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3..
;
1.3..
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2. .
2.3.
.
2.3.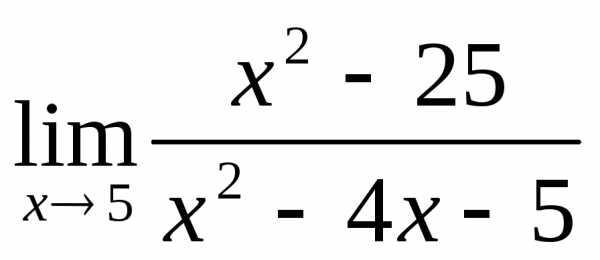 .
2.4.
.
2.4. 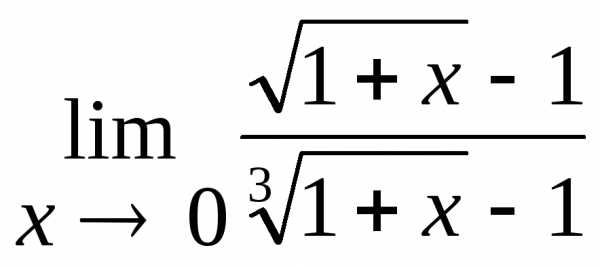 .
2.5.
.
2.5. 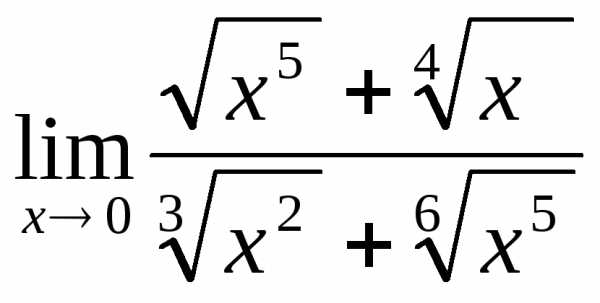 .
2.6.
.
2.6.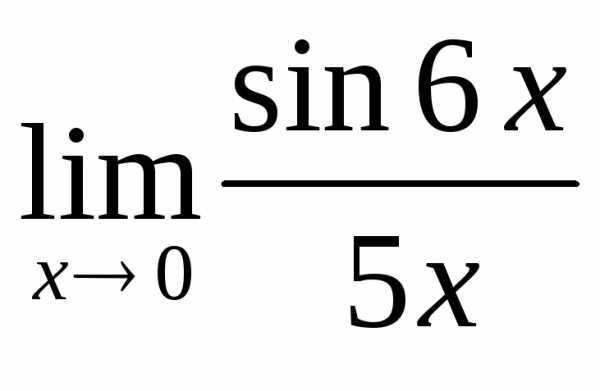 .
2.7.
.
2.7.  .
2.8.
.
2.8.  .
2.9.
.
2.9. 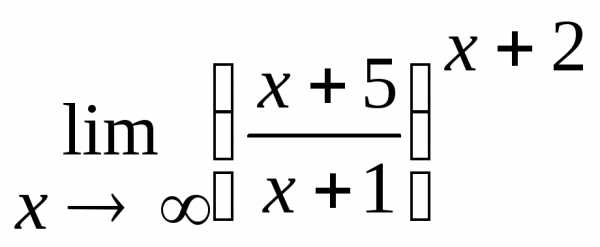 .
2.10.
.
2.10. 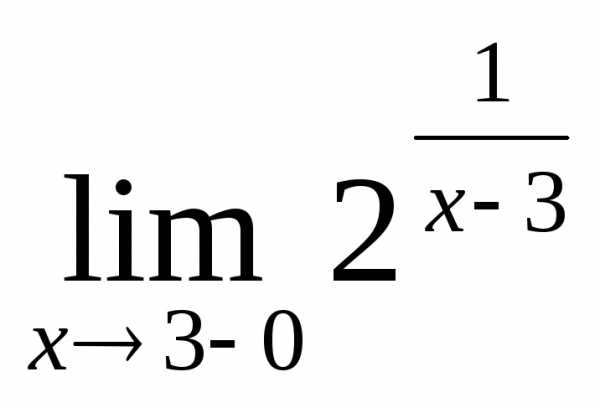 .
.
Задание 3. Исследовать функцию на непрерывность:
.
Вариант № 10.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2.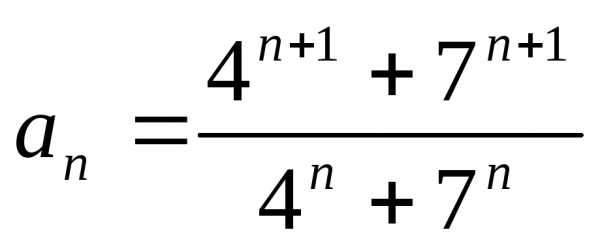 ;
1.3.
;
1.3. .
.
Задание 2. Найти пределы функций:
2.1.
.
2.2.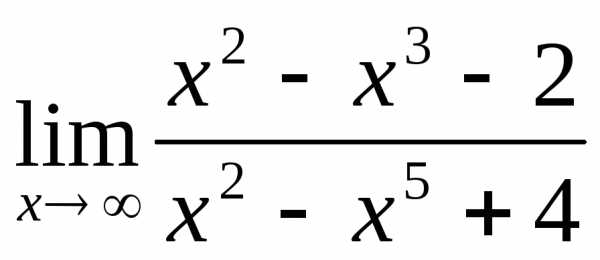 .
2.3.
.
2.3. .
2.4.
.
2.5.
.
2.4.
.
2.5. 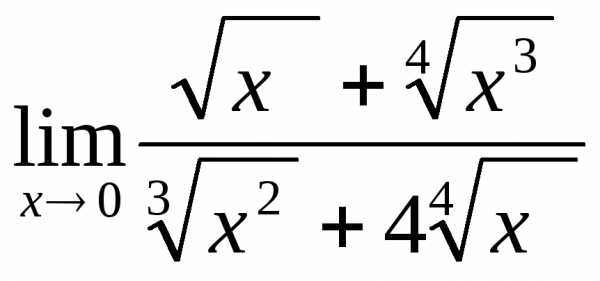 .
2.6.
.
2.6.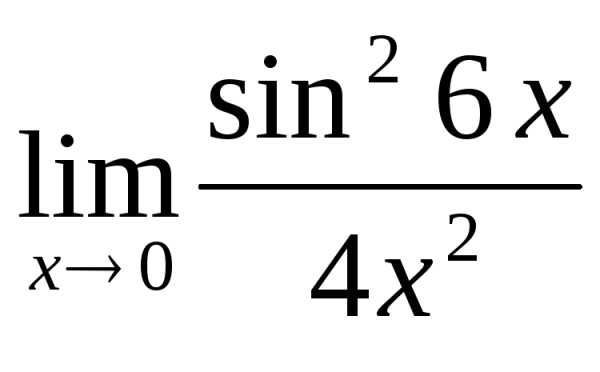 .
2.7.
.
2.7.  .
2.8.
.
2.8. 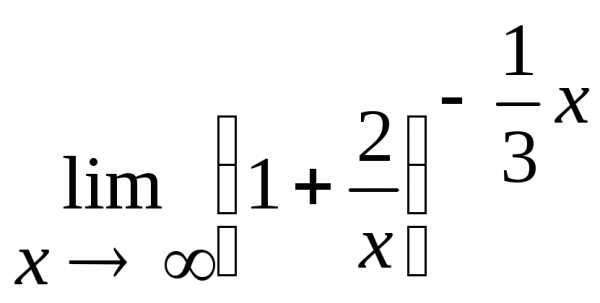 .
2.9.
.
2.9. 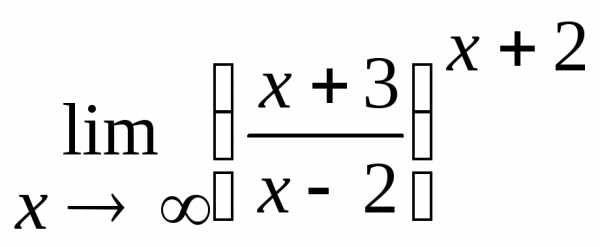 .
2.10.
.
2.10.  .
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 11.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2.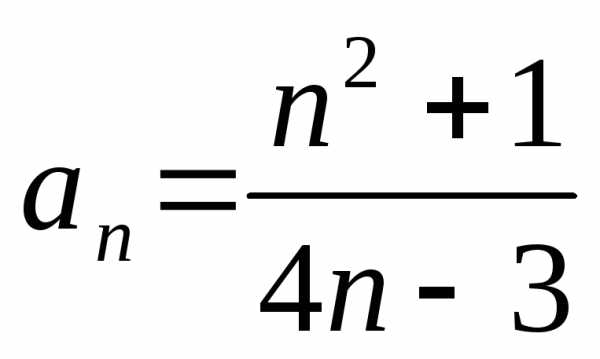 ;
1.3.
;
1.3.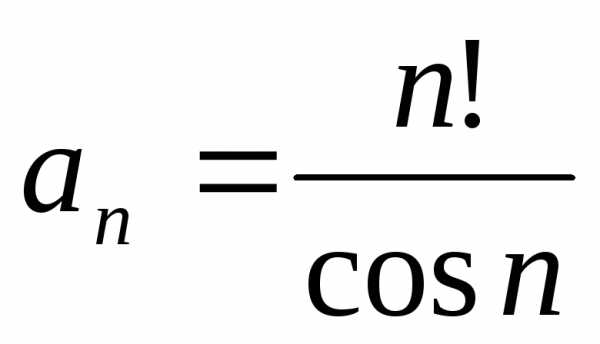 .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2.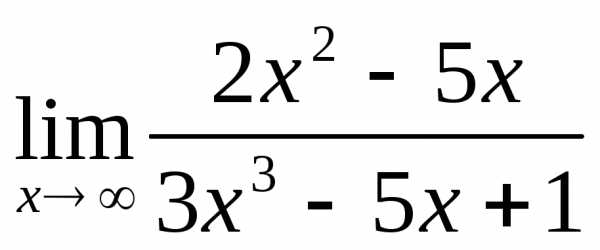 .
2.3.
.
2.3.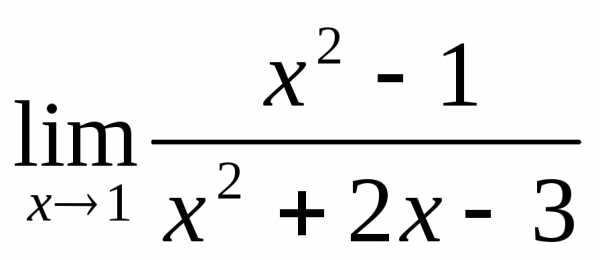 .
2.4.
.
2.4.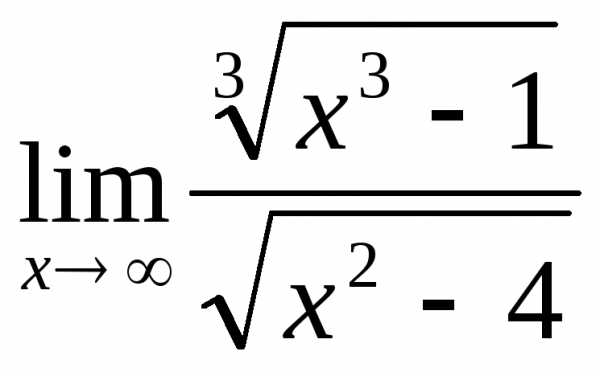 .
2.5.
.
2.5.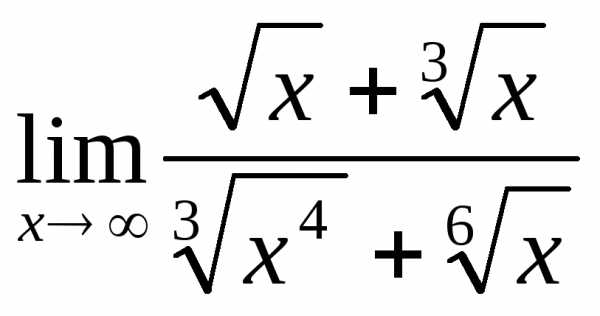 .
2.6.
.
2.6. .
2.7.
.
2.7.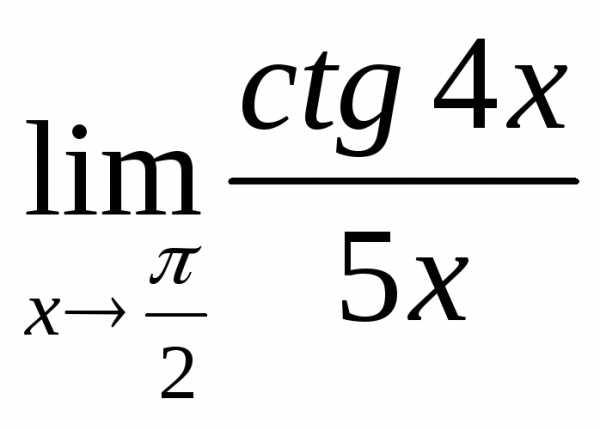 .
2.8.
.
2.8.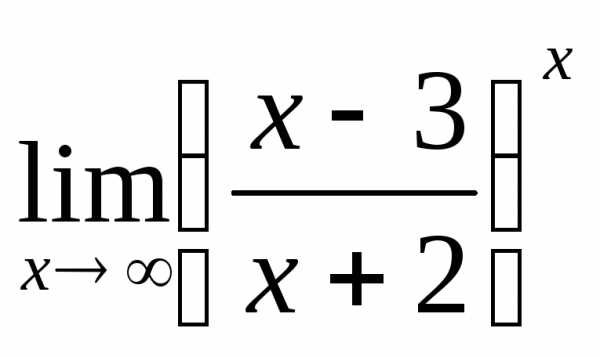 .
2.9.
.
2.9.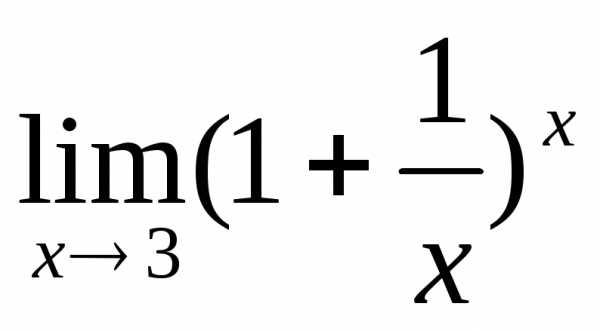 .
2.10.
.
2.10.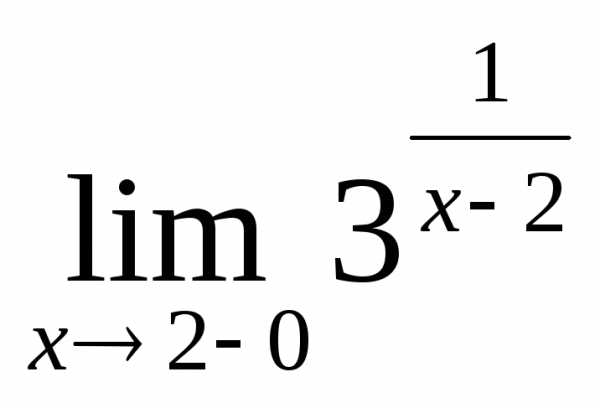 .
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 12.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2.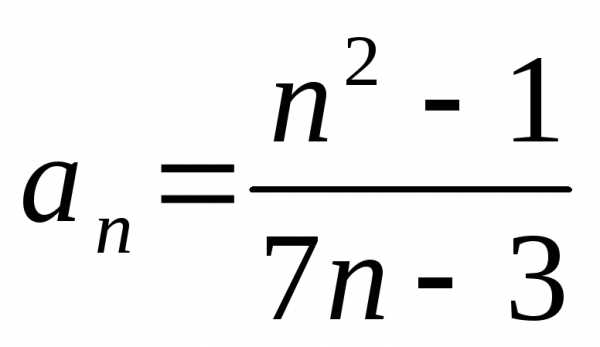 ;
1.3.
;
1.3.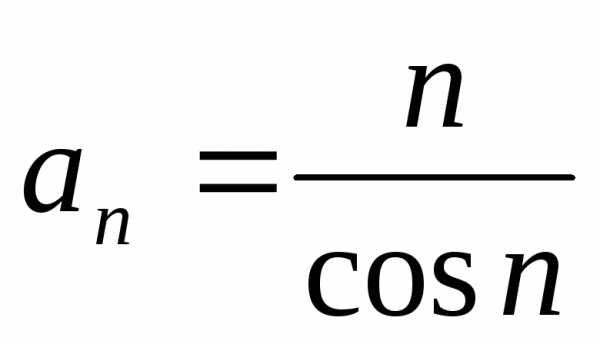 .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2.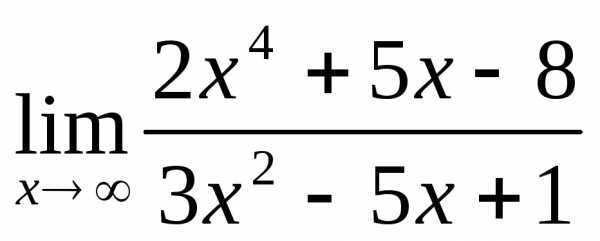 .
2.3.
.
2.3.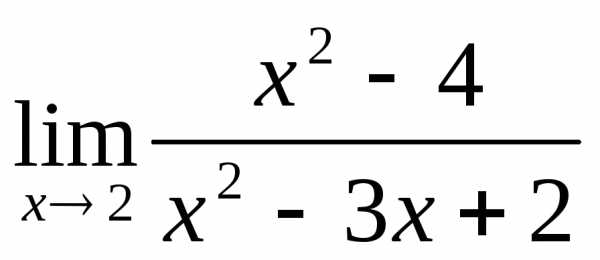 .
2.4.
.
2.4. .
2.5.
.
2.5. .
2.6.
.
2.6.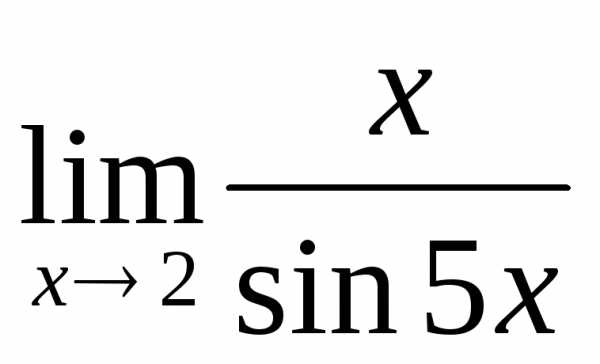 .
2.7.
.
2.7.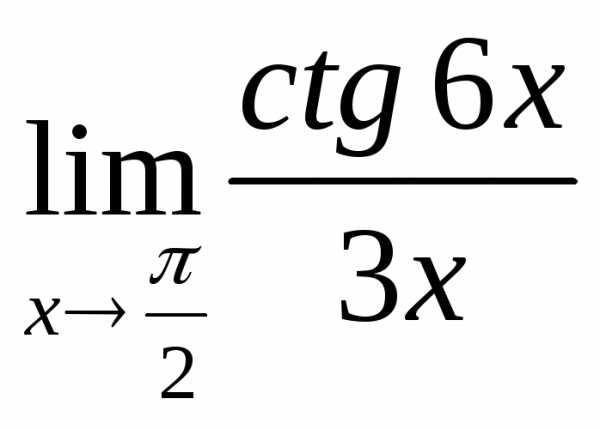 .
2.8.
.
2.8. .
2.9.
.
2.9. .
2.10.
.
2.10. .
.
Задание 3. Исследовать функцию на непрерывность:
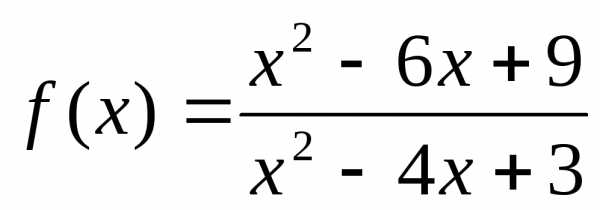 .
.
Вариант № 13.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2. ;
1.3.
;
1.3.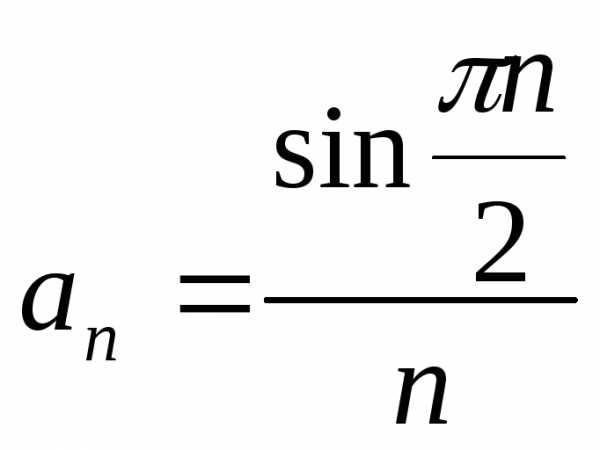 .
.
Задание 2. Найти пределы функций:
2.1.  .
2.2.
.
2.2.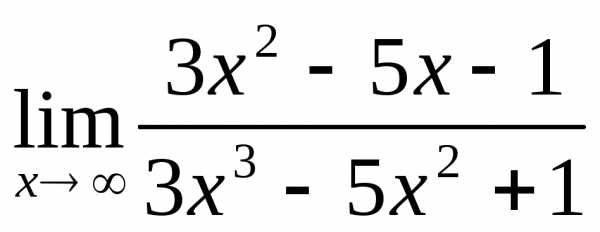 .
2.3.
.
2.3. .
2.4.
.
2.4.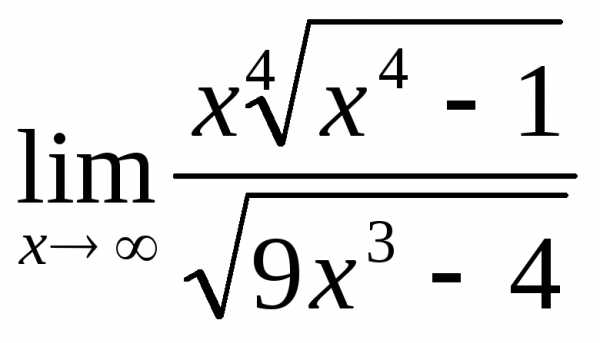 .
2.5.
.
2.5. .
2.6.
.
2.6.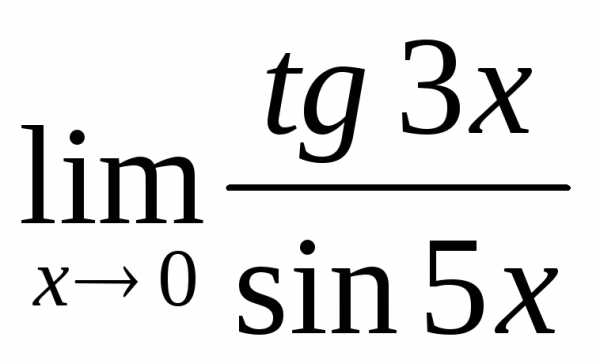 .
2.7.
.
2.7. 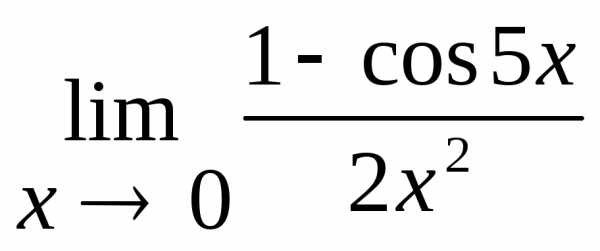 .
2.8.
.
2.8. 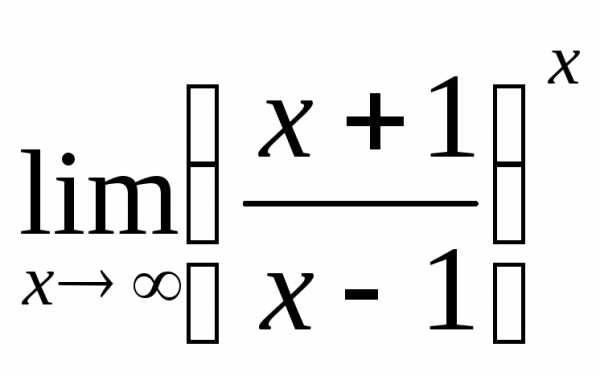 .
2.9.
.
2.9.  .
2.10.
.
2.10. 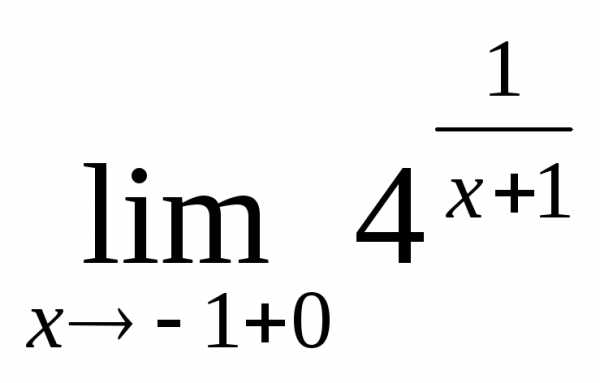 .
.
Задание 3. Исследовать функцию на непрерывность:
 .
.
Вариант № 14.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
.
1.2.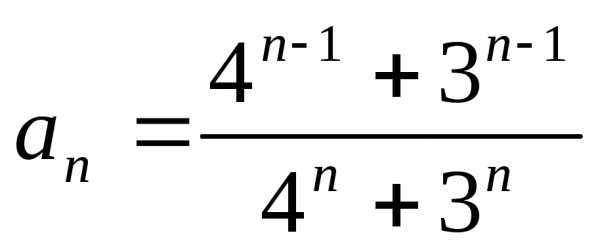 ;
1.3.
;
1.3. .
.
studfiles.net

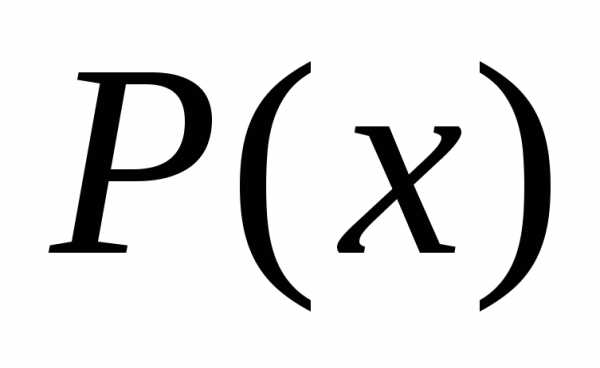 больше степени многочлена
больше степени многочлена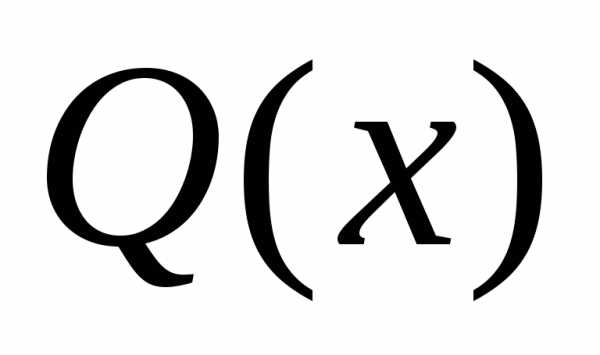 ,
то.
,
то.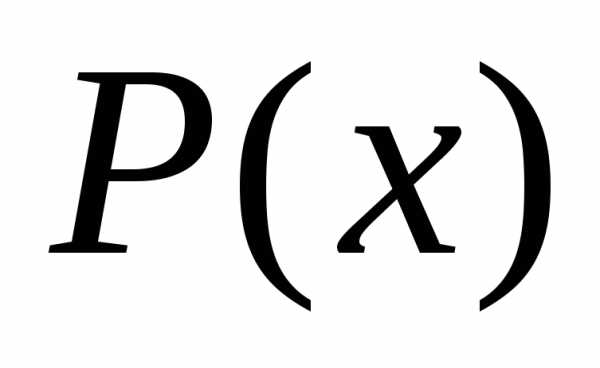 меньше степени многочлена
меньше степени многочлена ,
то
,
то .
. равна степени многочлена
равна степени многочлена ,
то
,
то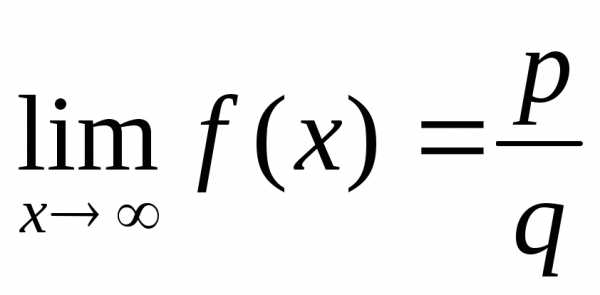 ,
где
,
где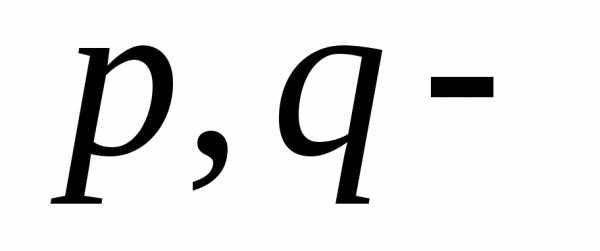 числовые
коэффициенты при наивысших степенях
числовые
коэффициенты при наивысших степенях в данных многочленах.
в данных многочленах.