Примеры дискретная математика – Страница не найдена | Алматинский филиал Санкт-Петербургского Гуманитарного университета профсоюзов

Содержание

ДИСКРЕТНАЯ МАТЕМАТИКА • Большая российская энциклопедия

ДИСКРЕ́ТНАЯ МАТЕМА́ТИКА, раздел математики, изучающий свойства дискретных структур, которые возникают как в самой математике, так и в её приложениях. При этом дискретными структурами называются объекты, для которых важнейшие характеристики принимают конечное или счётное число значений. К числу таких структур относятся, напр., конечные группы, конечные графы, некоторые математич. модели преобразователей информации, конечные автоматы, Тьюринга машины. Это примеры структур финитного (конечного) характера. Часть Д. м., изучающая их, иногда называется конечной математикой. Помимо финитных структур, Д. м. изучает также дискретные бесконечные структуры (напр., бесконечные алгебраич. системы, бесконечные графы, бесконечные автоматы).

Предмет и методы дискретной математики

Значит. часть классич. математики занимается изучением свойств объектов непрерывного характера. Использование дискретной или непрерывной модели изучаемого объекта связано как с самим объектом, так и с тем, какие задачи ставит перед собой исследователь. Само деление математики на Д. м. и математику, занимающуюся непрерывными моделями, в значит. мере условно, поскольку, с одной стороны, происходит обмен идеями и методами между ними, а с другой – часто возникает необходимость исследования моделей, обладающих как дискретными, так и непрерывными свойствами одновременно. В математике существуют разделы, использующие средства Д. м. для изучения непрерывных моделей (напр., алгебраическая геометрия), и наоборот, часто методы, развитые для анализа непрерывных моделей, используются при изучении дискретных структур (напр., асимптотические методы в теории чисел, в перечислительных задачах комбинаторики). Однако специфика мн. разделов Д. м. связана с необходимостью отказа от таких фундам. понятий классич. математики, как предел и непрерывность, в связи с чем для мн. задач Д. м. некоторые методы классич. математики оказываются неприменимыми.

Наряду с выделением Д. м. путём указания её предмета можно также описать Д. м. перечислением составляющих её частей. К ним относятся комбинаторный анализ, графов теория, теория кодирования, теория функциональных систем, теория управляющих систем, автоматов теория, алгоритмов теория. При более широком толковании к Д. м. могут быть отнесены как целые разделы математики, напр. математич. логика, так и части таких разделов, как теория чисел, алгебра, вычислительная математика, теория вероятностей, в которых изучаемые объекты имеют дискретный характер.

Исторический очерк

Элементы Д. м. возникли в глубокой древности; развиваясь параллельно с др. разделами математики, они являлись их составной частью. Типичными были задачи, связанные со свойствами целых чисел, позднее эти задачи привели к созданию теории чисел. Примеры таких задач: отыскание алгоритмов сложения и умножения натуральных чисел у древних египтян, вопросы делимости натуральных чисел и задачи суммирования в пифагорейской школе, а в более позднее время – вопросы, связанные с разрешимостью уравнений в целых числах. Этот этап развития Д. м. связан с именами Диофанта, Евлида, Пифагора и Эратосфена. В 17–18 вв., в осн. в связи с игровыми задачами, появились элементы комбинаторного анализа и дискретной теории вероятностей, а в связи с общими проблемами теории чисел, алгебры и геометрии в 18–19 вв. возникли такие важнейшие понятия алгебры, как группа, поле, кольцо, определившие дальнейшее развитие и содержание алгебры и имевшие, по существу, дискретную природу. На протяжении 17–19 вв. развитие Д. м. связано с именами Н.
Абеля, Э. Варинга, У. Гамильтона, Э. Галуа, А. Кэли, Ж. Лагранжа, А. Лежандра, П. Ферма, Л. Эйлера. В 19–20 вв. стремление к строгости математич. рассуждений и анализ методов математики привели к выделению ещё одного раздела – математич. логики. В это время проблемами Д. м. занимались Л. Брауэр, Дж. Буль, Н. Винер, К. Гёдель, Д. Гильберт, А. Чёрч, К. Шеннон. В создании рос. школы Д. м. участвовали И. М. Виноградов, А. Н. Колмогоров, О. Б. Лупанов и С. В. Яблонский.

Современные задачи дискретной математики

информации теории, теории кодирования и теоретич. криптографии. Экономич. задачи, задачи электротехники, равно как и внутренние проблемы математики, потребовали развития теории графов. Задачи описания работы и конструирования сложных управляющих систем составили предмет теории управляющих систем и теории автоматов.

Одна из особенностей Д. м. состоит в том, что вместе с задачами типа задач существования, имеющими общематематич. характер, важное место в Д. м. занимают задачи, связанные с алгоритмич. разрешимостью и построением конкретных решающих алгоритмов. Др. особенностью Д. м. является то, что в ней впервые начались исследования т. н. дискретных многоэкстремальных задач. Соответствующие методы поиска экстремумов, использующие гладкость функций, в этих случаях оказываются неприменимыми. Типичными задачами такого рода в Д. м. являются, напр., задачи отыскания в некотором смысле оптимальных стратегий в шахматах, а также задачи построения минимальных дизъюнктивных нормальных форм для булевых функций (см. также Алгебра логики).

Особенностью Д. м., связанной с задачами для конечных структур, является то, что для многих из них существуют алгоритмы решения, в то время как для задач с элементами непрерывности, как правило, полное решение возможно лишь при весьма жёстких ограничениях. Примером такого алгоритма может служить алгоритм просмотра всех возможных вариантов, т. е. алгоритм полного перебора. К задачам, в которых может быть применён алгоритм полного перебора, относятся упомянутые задачи о стратегиях в шахматной партии с ограниченным числом ходов и о минимизации дизъюнктивных нормальных форм для булевых функций. Алгоритмы полного перебора трудоёмки и часто не могут быть реализованы на практике, в связи с чем возникает ряд задач, связанных с нахождением условий, ограничивающих перебор.

bigenc.ru

Примеры Дискретная математика. диаграммы Эйлера-Венна

Примеры предназначены для самостоятельного изучения Дискретной математики

Если некоторые задачи по Дискретной математике все-таки вызывают у Вас затруднения и Вы не можете разобраться с их решением самостоятельно,

то Вы можете заказать у нас помощь в решении задач по Дискретной математике

Группа студентов из 25 человек сдала экзаменационную сессию следующими результатами: 2 человека получили только «отлично», 3 человека получили отличные, хорошие и удовлетворительные оценки; 4 человека только “хорошо”; 3 человека только хорошие и удовлетворительные оценки; число студентов, сдавших сессию только на “отлично”, «хорошо», равно числу студентов, сдавших сессию только на «удовлетворительно». Студентов, получивших только отличные и удовлетворительные оценки — нет. Удовлетворительные или хорошие оценки получили 22 студента. Сколько студентов не явилось на экзамены? Сколько студентов сдали сессию только на удовлетворительно?

Посмотреть решение

В графе, представленном следующей матрицей смежности, найти все максимальные независимые множества

1	2	3	4	5	6	7	8	9	10
0	0	0	0	1	1	0	1	0	1	1
0	0	0	1	1	0	1	0	0	0	2
0	0	0	0	0	1	1	0	0	0	3
0	1	0	0	1	0	0	0	1	1	4
1	1	0	1	0	0	1	0	1	0	5
1	0	1	0	0	0	0	1	1	1	6
0	1	1	0	1	0	0	0	0	0	7
1	0	0	0	0	0	0	0	0	0	8
0	0	0	1	1	1	0	0	0	1	9
1	0	0	1	0	1	0	0	1	0	10

Посмотреть решение

Получить минимальную систему ДНФ для следующей системы полностью определённых булевых функций:

Х₁	Х₂	Х₃	Х₄		f₁	f₂	f₃
0	0	1	1	1	1	0	1
1	0	1	1	2	1	0	0
1	0	0	0	3	0	1	0
0	0	1	0	4	0	0	1
0	0	0	0	5	1	0	0
0	0	0	1	6	1	1	0
1	0	0	1	7	1	1	0
1	1	0	0	8	0	0	1

Посмотреть решение

Упростить выражение. Задача на множества

Посмотреть решение

Если все же Вы не смогли разобраться самостоятельно с какими-либо задачами по Дискретной математике,

то Вы можете заказать у нас решение задач по Дискретной математике

zadanie.by

Дискретная математика

Министерство образования и науки

Российской Федерации

Российский химико-технологический университет

им. Д.И. Менделеева

Новомосковский институт

Издательский центр

T.П. Тюрина, В.И. Емельянов

Дискретная математика

(часть 3)

Учебное пособие

Новомосковск 2004

Содержание

Часть 3. Элементы алгебры логики…………………………………………………… 3

3.1 Введение в алгебру логики…………………………………………………………….. 3

3.2 Основные функции алгебры логики………………………………………………… 5

3.3 Формулы алгебры логики……………………………………………………………… 9

Контрольные вопросы………………………………………………………………………. 12

3.4 Законы алгебры логики и следствия из них……………………………………. 12

Контрольные вопросы………………………………………………………………………. 16

3.5 Логические функции многих переменных………………………………………. 16

3.6 Построение формул алгебры логики по заданной таблице истинности 18

Контрольные вопросы и упражнения…………………………………………………. 26

3.7 Некоторые замкнутые классы (классы Поста). Понятие базиса………… 26

Контрольные вопросы и упражнения…………………………………………………. 34

3.8 Методы минимизации логических функций……………………………………. 34

Контрольные вопросы………………………………………………………………………. 39

3.9 Неполностью определенные логические функции…………………………… 40

3.10 Формы представления булевых функций…………………………………….. 41

3.10.1 Семантические деревья……………………………………………………………. 42

3.10.2 Бинарные диаграммы решений (БДР)……………………………………….. 45

3.11 Построение логических схем………………………………………………………. 45

Контрольные вопросы………………………………………………………………………. 45

3.12 Логические конечные автоматы…………………………………………………… 46

3.12.1 Процессы……………………………………………………………………………….. 50

3.12.2 Конечные автоматы…………………………………………………………………. 52

Контрольные вопросы………………………………………………………………………. 55

БИБЛИОГРАФИЧЕСКИЙ СПИСОК………………………………………………….. 60

3.1 Введение в алгебру логики

Алгебру логики иначе еще называют алгеброй высказываний, логикой высказываний. Алгебра логики начала формироваться в 19 веке в трудах английского математика Дж. Буля.

Прежде всего, благодаря труду английского логика Джорджа Буля «Математический анализ логики», был достигнут подлинный прогресс науки, называемый математической логикой. Он перенёс на логику законы и правила математических действий, ввёл логические операции, предложил способ записи высказываний в символической форме.

В трудах Джорджа Буля и О. де Моргана математическая логика представлена как своеобразная алгебра – алгебра логики (алгебра высказываний).

Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Джордж Буль (1815–1864) родился в Линкольне (Англия). Сын сапожного мастера. Окончил только начальную школу и дальнейшие знания приобретал самоучкой. С 1849 г. Буль – профессор математики в Куинс – колледже в Корке (Ирландия), где преподавал до конца жизни. Буля почти в равной степени интересовали логика, математический анализ, теория вероятностей, этика Б. Спинозы, философские работы Аристотеля и Цицерона. Он считается несомненным создателем современной символической (математической) логики.

Огастес де Морган (1806–1871) родился в Индии в семье полковника английских войск. Получил образование в Кембриджском университете. Был профессором математики Лондонского университета. Математику и логику де Морган назвал азами точного знания и выражал сожаление, что математики не более заботятся о логике, чем логики о математике. Сам он стремился сблизить обе науки, и его главной заслугой явилось построение логики по образу и подобию математических наук. Независимо от Дж. Буля он открыл основные идеи алгебры логики.

«Логика Буля» основывается на отношении эквивалентности, при котором правая часть равенства всегда содержит ровно столько же «истин», сколько и левая.

Высказывание – это имеющее смысл языковое выражение (повествовательное предложение), относительно которого в данной ситуации можно утверждать, что оно либо истинно, либо ложно, т. е. каждому высказыванию можно приписать истинное значение И (истина) или Л (ложь), но не то и другое одновременно.

Примеры:

1. НГТУ – крупнейший «вуз Новосибирска».

2. «Снег зелёный».

3. Р= «Чтобы подключиться к Интернету с домашнего компьютера, необходим модем и соответствующее ПО».

4. Крокодилы летают очень низко.

«А ты любишь информатику?» – это предложение не является высказыванием.

Уравнение 2+х=4 не является высказыванием. Однако, всякий раз, придавая переменной х определенное числовое значение, будем получать высказывание. Используя частицу «не», а также союзы «и», «или», связки «если …., то…», «тогда и только тогда, когда…» и т. п., можно из одних высказываний строить другие высказывания.

Изучением высказываний занимается Булева алгебра, в которой предполагается, что уже имеется некоторый запас высказываний, для каждого из которых известно истинно оно или ложно. Такие высказывания называют элементарными высказываниями. Из элементарных высказываний могут быть построены сложные с помощью операций алгебры логики.

Знаки логических операций называют логическими связками (или просто связками). Логические связки могут быть одноместные (унарные), двухместные (бинарные), трехместные (тернарные) и т. д.

В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности, содержащих все наборы значений переменных и значения функции этих наборов. Алгебра логики не занимается обоснованием того, почему тому или иному элементарному высказыванию приписано значение истины или лжи. Этот вопрос решается за пределами алгебры логики.

Например: сумма углов в треугольнике – 180 градусов. Алгебра логики отвлекается и от смысловой содержательности высказывания. Она интересуется только одним свойством сложных высказываний: быть истинным (True – 1) или ложным (False – 0).

Основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых. Этот метод основан на изучении свойств булевых функций.

Основными символами алгебры высказываний являются:

а) пропозиционные переменные Р1, Р2, Р3 , …;

б) одноместная связка – (ù) и двуместные связки Ù (и), Ú (или), ®, Þ, Û;

в) скобки ().

Переменная, значениями которой являются высказывания, называется пропозиционной переменной.

Пусть А, В- некоторые элементарные высказывания.

Определим новое высказывание Ā (т. е. не А ), будем называть его отрицанием (инверсия:

, Ā ), представим таблицы значений функции отрицания:

Рассмотрим наборы истинных значений элементарных функций на наборах аргументов:

Таблица 1

mirznanii.com

Дискретная математика

\bookfoldsheets0Федеральное агентство по образованию РФ

«ДИСКРЕТНАЯ МАТЕМАТИКА»

(КОНСПЕКТ ЛЕКЦИЙ)

Преподаватель: профессор,

Архипов Игорь Константинович

1. МНОЖЕСТВА

Множество – совокупность элементов, обладающих каким-то одним общим свойством. (Это определение не является строгим, оно лишь показывает особенности построения множеств, т.е. для построения множества важно указать свойство, которым обладают все его элементы).

Если каждому элементу множества можно присвоить номер и этот номер не повторяется, то такое множество называется счетным или конечным .

Если такого номера для каждого элемента не существует, то такое множество называется бесконечным .

Бесконечное множество часто называют континуумом (например: совокупность точек на плоскости).

Если можно пересчитать все число элементов в счетном множестве, то эта сумма называется мощностью множества.

Множества задаются различными способами:

1. С помощью перечисления всех его элементов.

{0,1,2,3,4,5,6,7,8,9}

2. Алгоритмическая форма (в виде последовательности или фомул).

а) конечное

М ={2;4;6;8} <=> М ={m|2n;n-целое;1<=n<=4}

б) бесконечное

А ={х| |х-1|<3}

2. СВОЙСТВА СЧЕТНЫХ МНОЖЕСТВ

1. Всякое подмножество счетного множества конечно или счетно

Подмножеством множества А называется множество А` все элементы которого принадлежат множеству А

Пример:

2. Сумма конечного или счетного числа конечных или счетных множеств есть конечное или счетное множество.

3. Множество всех рациональных чисел счетно .

4. Алфавитом называется любое непустое множество.

Пустое множество – множество, которое не содержит ни одного элемента.

Элементы множества под названием АЛФАВИТ называют буквами (символами) .

Символом в данном алфавите любая конечная последовательность букв.

Для каждого множества А существуют множества, элементами которого являются только все его подмножества.

Такое подмножество называют семейством множеств А или булеаном. (обозначается В(А) )

Будем называть вектором (кортежем) упорядоченный набор элементов и обозначать его

, заметим, что в отличие от множества, элементы в векторе могут повторяться. Эти элементы называются координатами или проекциями.

Количество элементов в векторе называется его длиной, если в векторе 2 элемента, то двойка, если n элементов, то n-ка.

Теория множеств строится на основе систем аксиом.

1. Аксиома существования: Существует по крайней мере одно множество.

2. Аксиома объемности: Если множества А и В составлены из одних и тех же элементов, то они совпадают.

3. Аксиома объединения: Для произвольных множеств А и В существует множество, элементами которого являются все элементы множества А и все элементы множества В и никакие другие элементы множество не содержит.

4. Аксиома разности: Для произвольных множеств А и В существует множество, элементами которого являются те и только те элементы множества А , которые не содержатся в множестве В .

5. Аксиома существования пустого множества: Существует множество не содержащее ни одного элемента.

3. ОСНОВНЫЕ ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

1. Включение (объединение)

Множество А входит (включено) в множество В , или А является подмножеством В .

Если всякий объект, обладающий свойством

, также обладает свойством , то говорят, что свойство включает свойство , т.е.

2. Сумма

Сумма множеств А и В есть множество С , включающее в себя все элементы множество А и В .

Объект входит во множество если он входит во множество А или во множество В .

3. Пересечение (произведение)

Пересечением множество А и В называется новое множество С . Элементы множества С принадлежат множеству А (обладают его свойствами) и множеству В (обладают его свойствами).

4. Вычитание (разность)

Разность множеств А и В есть множество С , элементы которого обладают свойствами множества А и не обладают свойствами множества В или принадлежат множеству А и не принадлежат множеству В .

5. Дополнение

Если имеется некоторое универсальное множество (универсум) U и все рассматриваемые множества есть его подмножества, то дополнением

называется такое множество, элементы которого не входят в А , но принадлежат U .

ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

(Диаграммы Эймера, Венна)

4. ПРЯМОЕ ПРОИЗВЕДЕНИЕ А х В

Прямым произведением множеств А и В называется множество М всех пар (

), таких, что

Если А=В , то такое произведение называется

Аналогично можно вывести операцию прямого произведения большего числа множеств.

Если в частности

одинаковы то получаем

(Например, множество точек на плоскости являются прямым произведением двух множеств).

Если множества конечные, мощность произведений

равна мощности произведений

5. ОСНОВНЫЕ ТОЖДЕСТВА АЛГЕБРЫ МНОЖЕСТВ

Независимость расположения:

(1) (2)

Ассоциативно

mirznanii.com

Дискретная математика

Задача1. Решить рекуррентное соотношение методом производящих функций:

$$u_{n+2}-15u_{n+1}+56u_n=42 \cdot 5^n,\:n=0,1,2,…;$$ $$n_0=3,\:u_1=9$$

Решение, скачать (формат .docx)

Задача2. Решить рекуррентное соотношение с помощью характеристических чисел:

$$u_{n+2}-15u_{n+1}+56u_n=-35 \cdot 7^n,\:n=0,1,2,…;$$ $$n_0=-3,\:u_1=9$$

Решение, скачать (формат .docx)

ЗАДАНИЯ
по контрольной работе
«СПЕЦИАЛЬНАЯ МАТЕМАТИКА»

Все варианты СКАЧАТЬ

В каждом варианте подробно решены все задачи. Контрольные работы выполнены в формате Word. Стоимость решения одного варианта, или аналогичной работы от 500р,, срок выполнения не более 1 дня (можно заказать задачи выборочно, из любого варианта), ОФОРМИТЬ ЗАКАЗ

Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями. Представляет собой операции попарного неполного склеивания и элементарного поглощения.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.

Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.

Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки, которые содержат нули.

Алгоритм минимизации по методу карт Карно:

… Смотреть решение »

Определение. Двойственной для функции f(x1, x2, …, xn) называется функция$f^*(x_1, x_2,…, x_n)=\overline{f\left ( \bar{x_1}, \bar{x_2},… \bar{x_n} \right )}$

Пример. Построить функцию, двойственную данной:

$1.\, f=x\vee y;$
$2. \, f=x\rightarrow y.$

Решение.

$1. f^*=\overline{\bar{x}\vee \bar{y}}=\bar{\bar{x}}\wedge\bar{\bar{y}} ;$
$2. f^*=\overline{\bar{x}\rightarrow \bar{y}}=\overline{\bar{\bar{x}} \vee \bar{y}}=\bar{\bar{\bar{x}}}\wedge \bar{\bar{y}}=\bar{x}\wedge y.$

Определение. Функция, совпадающая со своей двойственной, называется самодвойственной.
Утверждение. Если функция f(x1, x2, …, xn) самодвойственна, то функция $\bar{f} тоже самодвойственна.
Утверждение. Чтобы функция была самодвойственной необходимо и достаточно, чтобы на всяких двух противоположных наборах она принимала разные значения.
Противоположными называются те наборы, которые в сумме дают двоичный код числа (2ⁿ-1).

Пример. Выяснить являются ли функции самодвойственными:

$1.\, f=\left ( \bar{x} \approx y\right )\rightarrow \bar{z};$
$2\, f … Смотреть решение »

www.reshim.su

ДИСКРЕТНАЯ МАТЕМАТИКА • Большая российская энциклопедия

Предмет и методы дискретной математики

Исторический очерк

Элементы Д. м. возникли в глубокой древности; развиваясь параллельно с др. разделами математики, они являлись их составной частью. Типичными были задачи, связанные со свойствами целых чисел, позднее эти задачи привели к созданию теории чисел. Примеры таких задач: отыскание алгоритмов сложения и умножения натуральных чисел у древних египтян, вопросы делимости натуральных чисел и задачи суммирования в пифагорейской школе, а в более позднее время – вопросы, связанные с разрешимостью уравнений в целых числах. Этот этап развития Д. м. связан с именами Диофанта, Евлида, Пифагора и Эратосфена. В 17–18 вв., в осн. в связи с игровыми задачами, появились элементы комбинаторного анализа и дискретной теории вероятностей, а в связи с общими проблемами теории чисел, алгебры и геометрии в 18–19 вв. возникли такие важнейшие понятия алгебры, как группа, поле, кольцо, определившие дальнейшее развитие и содержание алгебры и имевшие, по существу, дискретную природу. На протяжении 17–19 вв. развитие Д. м. связано с именами Н. Абеля, Э. Варинга, У. Гамильтона, Э. Галуа, А. Кэли, Ж. Лагранжа, А. Лежандра, П. Ферма, Л. Эйлера. В 19–20 вв. стремление к строгости математич. рассуждений и анализ методов математики привели к выделению ещё одного раздела – математич. логики. В это время проблемами Д. м. занимались Л. Брауэр, Дж. Буль, Н. Винер, К. Гёдель, Д. Гильберт, А. Чёрч, К. Шеннон. В создании рос. школы Д. м. участвовали И. М. Виноградов, А. Н. Колмогоров, О. Б. Лупанов и С. В. Яблонский.

Современные задачи дискретной математики

В 20 в. развитие Д. м. определялось гл. обр. запросами практики. Возникла новая наука – кибернетика и её теоретич. часть – математич. кибернетика, изучающая математич. методами разнообразные проблемы, которые ставит перед кибернетикой практич. деятельность человека. Математич. кибернетика является поставщиком идей и задач Д. м. Так, прикладные вопросы, требующие больших вычислений, стимулировали появление и развитие численных методов решения задач, что привело к созданию вычислительной математики. Анализ понятий «вычислимость» и «алгоритм» привёл к созданию теории алгоритмов. Задачи хранения, обработки и передачи информации способствовали возникновению информации теории, теории кодирования и теоретич. криптографии. Экономич. задачи, задачи электротехники, равно как и внутренние проблемы математики, потребовали развития теории графов. Задачи описания работы и конструирования сложных управляющих систем составили предмет теории управляющих систем и теории автоматов.

dev.bigenc.ru

Конспект лекций (Описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике)

Министерство образования Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

______________________________________________________________________

С.В. РЕНИН

ДИСКРЕТНАЯ МАТЕМАТИКА

Конспект лекций для студентов II курса

Института социальной реабилитации

Новосибирск

2002

УДК 51 (076.1)

Рецензент ………………………………………………..

Работа выполнена на кафедре
автоматизированных систем управления
для студентов II курса Института социальной реабилитации

Ренин С.В.

Дискретная математика. Конспект лекций. – Новосибирск:
Изд-во НГТУ, 2000.

Конспект лекций содержит описание основных понятий и методов решения задач дискретной математики, относящихся к теории множеств, отношениям на множествах, теории графов и комбинаторике и предназначается студентам Института социальной реабилитации НГТУ , обучающимся по направлению 5528 «Информатика и вычислительная техника», для использования при подготовке к практическим занятиям и при самостоятельной работе над курсом.

УДК 51 (076.1)

ОГЛАВЛЕНИЕ

1. МНОЖЕСТВА. ОТНОШЕНИЯ НА МНОЖЕСТВАХ

1.1. Основные понятия теории множеств

Множество – совокупность объектов любой природы, называемых элементами данного множества.

Обозначение – большие буквы латинского алфавита для множеств, малые – для его элементов.

Способы задания: 1) перечисление элементов; 2) указание свойства, которым обладают все элементы множества.

Примеры. 1) Множество Х, состоящее из элементов х₁, х₂, х₃, обозначают:

Х = {х₁, х₂, х₃}

2) Множество простых чисел Х = {x|x — простое число}.

Принадлежность элемента х множеству Х записывается как хÎХ.

Если элемент х не принадлежит Х, то пишут хÏХ.

Множество называется конечным, если оно состоит из конечного числа элементов. Например, множество жителей г. Новосибирска, множество студентов группы ВИ-51.

Множество называется бесконечным, если число его элементов бесконечно. Например, множество натуральных чисел N = {1,2,3,…}.

Бесконечное множество называется счетным, если его элементы можно перечислять. Например, множество натуральных чисел N, множество целых чисел
Z = {…,-3,-2,-1,0,1,2,3,…}.

В противном случае оно называется несчетным. Например, множество точек плоскости, множество вещественных чисел.

Если множество не содержит ни одного элемента, то оно называется пустым и обозначается Æ. Например, пусто множество людей, имеющих рост выше 3 метров. Пусто множество студентов группы ВИ-51, имеющих диплом о высшем образовании.

Множество А называется подмножеством множества В, если любой элемент А является и элементом множества В. Это обозначается так:

АÌВ. Например, множество студентов группы ВИ-51 есть подмножество множества студентов ИСР и НГТУ.

Если множество А является подмножеством множества В и при этом может совпадать с В, то знак Ì подчеркивают: Í.

Множество называется универсальным, если все другие рассматриваемые в данной задаче множества являются его подмножествами. Обозначается такое множество латинской буквой I. Например, если в задаче рассматриваются множество вещественных чисел R, множество целых чисел Z, множество натуральных чисел N и множество рациональных чисел F, то для всех этих множеств множество R является универсальным, так как ZÌR, NÌR и FÌR. Т.е. в данном случае I=R.

1.2. Операции над множествами

1.2.1. Объединение

Обозначение:

Определение. Объединением двух множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые входят во множество А или во множество В или в оба вместе, причем элементы, принадлежащие обоим множествам одновременно, входят в объединение только один раз.

Если С = А В, то С = {c| cÎА или сÎВ или сÎА и В одновременно}.

Операции над множествами можно наглядно изобразить с помощью диаграмм Эйлера-Венна. На этих диаграммах универсальное множество изображается в виде прямоугольника, а множества, участвующие в операции — кругами.

Представление объединения на диаграмме Эйлера-Венна (результат объединения закрашен):

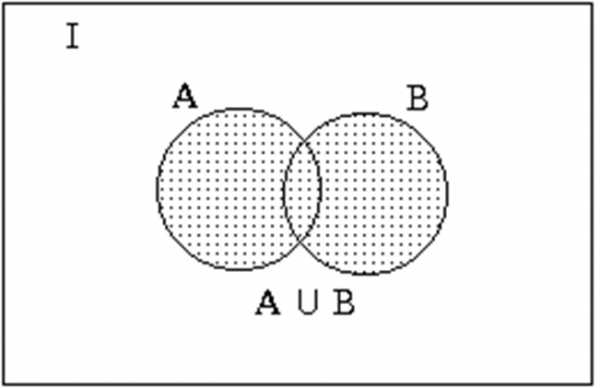
Примеры:

1) А = {a, b, c, d}, B = {c, d, e, f}, C=A B={a, b, c, d, e, f}

2) Z⁺ – множество целых положительных чисел;

Z^— – множество целых отрицательных чисел;

О = {0};

C = Z⁺Z^—O = Z – множество всех целых чисел.

3) А – множество студентов гр. ВИ-51, учащихся на отлично;

В – множество студентов гр. ВИ-51, учащихся без троек;

С – множество студентов гр. ВИ-51, имеющих удовлетворительные оценки;

D – множество студентов гр. ВИ-51, имеющих неудовлетворительные оценки;

E = A B C D — множество всех студентов группы ВИ-51.

Свойства: 1) коммутативность (переместительный закон)

А В = В А

2) ассоциативность (сочетательный закон)

А В С = (А В) С = А (В С)

3) если АÌВ, то А В=В;

vunivere.ru

ДИСКРЕТНАЯ МАТЕМАТИКА • Большая российская энциклопедия

Предмет и методы дискретной математики

Исторический очерк

Современные задачи дискретной математики

Примеры Дискретная математика. диаграммы Эйлера-Венна

Дискретная математика

3.1 Введение в алгебру логики

Дискретная математика

Преподаватель: профессор,

Архипов Игорь Константинович

ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ

Дискретная математика

Алгоритм минимизации по методу карт Карно:

ДИСКРЕТНАЯ МАТЕМАТИКА • Большая российская энциклопедия

Предмет и методы дискретной математики

Исторический очерк

Современные задачи дискретной математики

1. МНОЖЕСТВА. ОТНОШЕНИЯ НА МНОЖЕСТВАХ

Добавить комментарий Отменить ответ