Сложение дробей | tutomath
Разные действия с дробями можно выполнять, например, сложение дробей. Сложение дробей можно разделить на несколько видов. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
Сложение дробей с одинаковыми знаменателями.
На примере посмотрим, как складывать дроби с общим знаменателем.
Туристы пошли в поход из точки A в точку E. В первый день они прошли от точки A до B или \(\frac{1}{5}\) от всего пути. Во второй день они прошли от точки B до D или \(\frac{2}{5}\) от всего пути. Какое расстояние они прошли от начала пути до точки D?
Решение:
Чтобы найти расстояние от точки A до точки D нужно сложить дроби \(\frac{1}{5} + \frac{2}{5}\).
Сложение дробей с одинаковыми знаменателями заключается в том, что нужно числители этих дробей сложить, а знаменатель останется прежний.
\(\frac{1}{5} + \frac{2}{5} = \frac{1 + 2}{5} = \frac{3}{5}\)В буквенном виде сумма дробей с одинаковыми знаменателями будет выглядеть так:
Ответ: туристы прошли \(\frac{3}{5}\) всего пути.
Сложение дробей с разными знаменателями.
Рассмотрим пример:
Нужно сложить две дроби \(\frac{3}{4}\) и \(\frac{2}{7}\).
Чтобы сложить дроби с разными знаменателями нужно сначала найти общий знаменатель, а потом воспользоваться правилом сложения дробей с одинаковыми знаменателями.
Как найти общий знаменатель можно посмотреть здесь, нажав на ссылку>>
Для знаменателей 4 и 7 общим знаменателем будет число 28. Первую дробь \(\frac{3}{4}\) нужно умножить на 7. Вторую дробь \(\frac{2}{7}\) нужно умножить на 4.
\(\frac{3}{4} + \frac{2}{7} = \frac{3 \times \color{red} {7} + 2 \times \color{red} {4}}{4 \times \color{red} {7}} = \frac{21 + 8}{28} = \frac{29}{28} = 1\frac{1}{28}\)В буквенном виде получаем такую формулу:
\(\bf \frac{a}{b} + \frac{c}{d} = \frac{a \times d + c \times b}{b \times d}\)Сложение смешанных чисел или смешанных дробей.
Сложение смешанных дробей происходит по закону сложения.
У смешанных дробей складываем целые части с целыми и дробные части с дробными.
Если дробные части смешанных чисел имеют одинаковые знаменатели, то числители складываем, а знаменатель остается тот же.
Сложим смешанные числа \(3\frac{6}{11}\) и \(1\frac{3}{11}\).
\(3\frac{6}{11} + 1\frac{3}{11} = (\color{red} {3} + \color{blue} {\frac{6}{11}}) + (\color{red} {1} + \color{blue} {\frac{3}{11}}) = (\color{red} {3} + \color{red} {1}) + (\color{blue} {\frac{6}{11}} + \color{blue} {\frac{3}{11}}) = \color{red}{4} + (\color{blue} {\frac{6 + 3}{11}}) = \color{red}{4} + \color{blue} {\frac{9}{11}} = \color{red}{4} \color{blue} {\frac{9}{11}}\)Если дробные части смешанных чисел имею разные знаменатели, то находим общий знаменатель.
Выполним сложение смешанных чисел \(7\frac{1}{8}\) и \(2\frac{1}{6}\).
Знаменатель разный, поэтому нужно найти общий знаменатель, он равен 24. Умножим первую дробь \(7\frac{1}{8}\) на дополнительный множитель 3, а вторую дробь \(2\frac{1}{6}\) на 4.
Вопросы по теме:
Как складывать дроби?
Ответ: сначала надо определиться к какому типу относиться выражение: у дробей одинаковые знаменатели, разные знаменатели или смешанные дроби. В зависимости от типа выражения переходим к алгоритму решения.
Как решать дроби с разными знаменателями?
Ответ: необходимо найти общий знаменатель, а дальше по правилу сложения дробей с одинаковыми знаменателями.
Как решать смешанные дроби?
Ответ: складываем целые части с целыми и дробные части с дробными.
Пример №1:
Может ли сумма двух правильных дробей в результате получить правильную дробь? Неправильную дробь? Приведите примеры.
Решение:
\(\frac{2}{7} + \frac{3}{7} = \frac{2 + 3}{7} = \frac{5}{7}\)Дробь \(\frac{5}{7}\) это правильная дробь, она является результатом суммы двух правильных дробей \(\frac{2}{7}\) и \(\frac{3}{7}\).
\(\frac{2}{5} + \frac{8}{9} = \frac{2 \times 9 + 8 \times 5}{5 \times 9} =\frac{18 + 40}{45} = \frac{58}{45}\)Дробь \(\frac{58}{45}\) является неправильной дроби, она получилась в результате суммы правильных дробей \(\frac{2}{5}\) и \(\frac{8}{9}\).
Ответ: на оба вопроса ответ да.
Пример №2:
Сложите дроби: а) \(\frac{3}{11} + \frac{5}{11}\) б) \(\frac{1}{3} + \frac{2}{9}\).
а) \(\frac{3}{11} + \frac{5}{11} = \frac{3 + 5}{11} = \frac{8}{11}\)
б) \(\frac{1}{3} + \frac{2}{9} = \frac{1 \times \color{red} {3}}{3 \times \color{red} {3}} + \frac{2}{9} = \frac{3}{9} + \frac{2}{9} = \frac{5}{9}\)
Пример №3:
Запишите смешанную дробь в виде суммы натурального числа и правильной дроби: а) \(1\frac{9}{47}\) б) \(5\frac{1}{3}\)
а) \(1\frac{9}{47} = 1 + \frac{9}{47}\)
б) \(5\frac{1}{3} = 5 + \frac{1}{3}\)
Пример №4:
Вычислите сумму: а) \(8\frac{5}{7} + 2\frac{1}{7}\) б) \(2\frac{9}{13} + \frac{2}{13}\) в) \(7\frac{2}{5} + 3\frac{4}{15}\)
Решение:
а) \(8\frac{5}{7} + 2\frac{1}{7} = (8 + 2) + (\frac{5}{7} + \frac{1}{7}) = 10 + \frac{6}{7} = 10\frac{6}{7}\)
б) \(2\frac{9}{13} + \frac{2}{13} = 2 + (\frac{9}{13} + \frac{2}{13}) = 2\frac{11}{13} \)
в) \(7\frac{2}{5} + 3\frac{4}{15} = 7\frac{2 \times 3}{5 \times 3} + 3\frac{4}{15} = 7\frac{6}{15} + 3\frac{4}{15} = (7 + 3)+(\frac{6}{15} + \frac{4}{15}) = 10 + \frac{10}{15} = 10\frac{10}{15} = 10\frac{2}{3}\)
Задача №1:
За обедам съели \(\frac{8}{11}\) от торта, а вечером за ужином съели \(\frac{3}{11}\). Как вы думаете торт полностью съели или нет?
Решение:
Знаменатель дроби равен 11, он указывает на сколько частей разделили торт. В обед съели 8 кусочков торта из 11. За ужином съели 3 кусочка торта из 11. Сложим 8 + 3 = 11, съели кусочков торта из 11, то есть весь торт.
Ответ: весь торт съели.
tutomath.ru
Тема сложение дробей. Сложение и вычитание дробей с разными знаменателями.
Сложение – это арифметическое действие, в результате которого получают новое число, содержащее столько единиц, сколько было во всех заданных числах вместе взятых.
Дробь обозначает тип деления, который рассматривается как часть целого и указывает на разделение целого на равные доли или части, где знаменатель показывает, на сколько частей мы разделили, а числитель — сколько взяли частей от этого целого.
Сложение или вычитание дробей могут быть двух видов:
- знаменатели одинаковые;
- знаменатели разные;
Правила сложения дробей:
- Одинаковые знаменатели. Складываем числители этих дробей.
- Разные знаменатели. Находим общий знаменатель с помощью наименьшего общего кратного чисел, и складываем их числители.
Чтобы вычислить НОК, необходимо разбить числа на простые множители и найти разложение большего числа, добавив к нему простые недостающие множители другого разложения. Полученные числа перемножить. Алгоритм решения для двух, трех и более чисел одинаков, если числа простые, то надо перемножить их.
Примеры решения задач: сложение дробей с одинаковым знаменателем.
Задача 1. Сложить две дроби с одинаковыми знаменателями \(\frac{7}{8}\) и \(\frac{1}{8}\).
Решение:
\(\frac{7}{8}+\frac{1}{8}=\)\(\frac{(7+1)}{8}\)\(=\frac{8}{8}=\frac{1}{1}\)
Ответ:\(1\).
Задача 2. Сложить две дроби с одинаковыми знаменателями \(\frac{6}{5}\)и \(\frac{3}{5}\).
Решение:
\(\frac{6}{5} +\frac{3}{5}\)\(=\frac{(6+3)}{5}\)\(=\frac{9}{5}=1\frac{4}{5}\)
Ответ:\(1\frac{4}{5}\).
3адача 3. Сложить две дроби \(\frac{11}{3}\) и \(\frac{5}{3}\).
Решение:
\(\frac{11}{3}\) + \(\frac{5}{3}\)\(=\)\(\frac{(11+5)}{3}=\frac{16}{3}=5\frac{1}{3}\)
16/3
Ответ:\(5\frac{1}{3}\).
3адача 4. Сложить две дроби с разными знаменателями \(\frac{11}{3}\) и \(\frac{5}{8}\).
Решение:
НОК\((3;8)\) \(=24\)
\(\frac{11*8}{3*8}+\frac{5*3}{8*3}\)\(=\)\(\frac{88}{24}+\frac{15}{24}=\)\(\frac{88+15}{24}\)\(=\frac{103}{24}=4\frac{7}{24}\)
Ответ: \(4\frac{7}{24}\)
Задача 5. Сложить две дроби с разными знаменателями \(\frac{27}{3}\) и \(\frac{55}{13}\).
Решение.
\(НОК(3;13) =39\)
\(\frac{(27*13)}{3*13} +\frac{(55*3)}{13*3}=\)\(\frac{351}{39}+\frac{165}{39}\)\(=\frac{351+165}{39}=\)
\(=\frac{516}{39}-\) сокращаем обе части дроби на 3
\(\frac{175}{13}=13\frac{6}{13}\)
Ответ: \(13\frac{6}{13}\).
Выводы:
для того чтобы сложить или вычесть два и более дробных числа нам необходимо привести их к общему знаменателю;
основное свойство дробей: значение дробного числа не изменится, если числитель и знаменатель умножить или разделить на одно и то же число.
`
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
myalfaschool.ru
Сложение и вычитание дробей с одинаковыми знаменателями
Что можно складывать? Все, что угодно. Числа: . Яблоки: Сантиметры: . Даже что-то, про что мы вообще ничего не знаем: .
Самое важное при сложении, чтобы объекты для сложения были одинаковые. Так как сложно сложить , или , или .
Итак, одинаковое можно складывать. Это относится и к дробям.
Вспомним, что мы уже знаем про дроби: знаменатель (нижняя часть дроби) указывает, на сколько частей мы делили, какие доли мы получили. Числитель (верхняя часть) указывает, сколько таких долей взяли, сколько их содержит дробь (см. рис. 1).
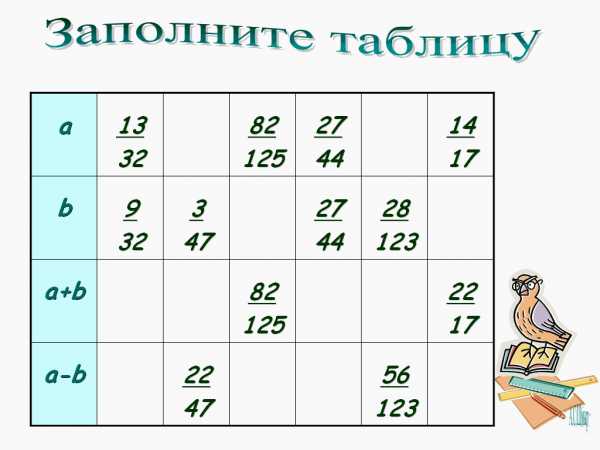
Рис. 1. Дробь
Сколько долей в дроби ? Пять, так как .
Во сколько раз больше, чем ? В 4 раза. Так как дробь .
Чему равна сумма ?
Два одинаковых объекта можно сложить: .
Чему равна сумма ? Одинаковых слагаемых пять штук.
Получаем: .
Сложим . Сколько всего семнадцатых? Пять и три. Пять и три семнадцатых. , всего восемь семнадцатых: .
Сложим . Сколько всего двенадцатых?
Итак, чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители.
У дробей одинаковые знаменатели, значит, чтобы сложить эти дроби, нужно сложить их числители: .
Знаменатели одинаковые, значит, можно складывать числители:
Вычитать дроби с одинаковыми знаменателями так же просто, как и складывать.
Выполнить вычитание: .
Вычтем из числителя первой дроби числитель второй дроби: .
Выполним вычитание числителей: .
Вычитаем числители . Но обычно такую запись редко используют. Пишут просто ноль: .
Итак, чтобы сложить или вычесть дроби с одинаковым знаменателем, нужно сложить или вычесть их числители соответственно. Открытым остался вопрос: А что делать, если знаменатели разные? Если нужно сложить, например, и ? Мы пока не умеем решать такие примеры.
Список рекомендованной литературы
- Математика. 5 класс. Зубарева И.И., Мордкович А.Г. 14-е изд., испр. и доп. — М.: 2013. – 270
- Математика. 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: 2014. — 304 с.
- Математика. 5 класс. Виленкин Н.Я., Жохов В.И. и др. 24-е изд., испр. — М: 2008. — 280с.
Домашнее задание
Вычислите:
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Urokimatematiki.ru (Источник).
- Интернет-портал Festival.1september.ru (Источник).
- Интернет-портал Onlinegdz.net (Источник).
interneturok.ru
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями (более сложные случаи)
Данный урок является логическим продолжением предыдущего, т. к. на прошлом уроке рассматривалась техника сложения и вычитания алгебраических дробей, а в рамках сегодняшнего урока будут рассмотрены более сложные случаи тех же операций над дробями. Дополнительно в рассматриваемых примерах будет делаться акцент на применение формул сокращенного умножения и на замену знака множителя на противоположный. Оказывается, что подобные процедуры могут существенно помочь при решении сложных примеров на сложение и вычитание алгебраических дробей.
Вспомним изученное на прошлом уроке правило сложения и вычитания алгебраических дробей с одинаковым знаменателем:
Примечательно то, что оно одинаково применимо и для простейших случаев, рассмотренных ранее, и для более сложных, которые мы сейчас разберем на примерах.
Пример 1. Сложить и вычесть указанные дроби: .
Решение. Очевидно, что указанные дроби уже с одинаковым (общим) знаменателем, и мы можем воспользоваться упомянутым ранее правилом их сложения/вычитания.
.
Прокомментируем последовательность действий. В процессе применения правила сложения/вычитания дробей следует помнить, что такой знак, как минус перед дробью, относится ко всему числителю, и вычитать его необходимо в скобках. После приведения подобных слагаемых необходимо попытаться разложить знаменатель и числитель дроби на множители в надежде сократить на какой-то из них, что мы успешно и проделали. Затем при удачном стечении обстоятельств дробь сокращается, как в нашем случае, например, на . При этом стоит помнить, что любые сокращенные элементы необходимо учесть в области недопустимых значений переменных, так как они пропадают из дроби, и о них можно забыть. В нашем случае запишем, что .
Ответ..
Пример 2. Сложить и вычесть указанные дроби:.
Решение. В указанном условии неочевидно, одинаковы ли знаменатели у дробей. Чтобы это проверить, разложим их на множители. При разложении на множители первого знаменателя видим, что он почти такой же, как и у второй дроби, противоположен только знак второго множителя. Чтобы привести знаменатели к одинаковому виду, вынесем минус из второго множителя второй дроби, и он окажется перед дробью, так как знак знаменателя и числителя относятся и ко всей дроби сразу:
.
Знаменатель третьей дроби тоже очень похож на знаменатель первой до разложения. Поступим с ним аналогично – вынесем минус и разложим на множители:
.
Все полученные преобразования дробей подставим в исходное условие (знак перед третьей дробью получится положительным, т. к. «минус на минус дает плюс»).
.
В числителе воспользовались формулой квадрата разности. После сокращения учтем, что
Ответ. .
Рассмотрим теперь пример на применение умения складывать дроби с одинаковыми знаменателями в других целях.
Пример 3. Доказать, что выражение принимает положительные значения при всех допустимых значениях переменной.
Решение. Поскольку необходимо исследовать выражение при всех допустимых значениях переменной, определим эти значения. По уже известному принципу, это все значения , кроме . Следовательно, . Выполним действия:
.
После приведения подобных слагаемых мы воспользовались формулой квадрата разности , далее, т. к. , то . Числитель и знаменатель положительные числа, значит, и дробь положительна.
Доказано.
На следующих уроках мы поговорим уже о сложении и вычитании дробей с разными знаменателями, используя похожую на изученную нами технику.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Сайт учителя математики Зубаревой Веры Анатольевны (Источник).
Домашнее задание
- №58, 59, 60. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Упростить выражение .
- Упростить выражение .
- Упростить выражение .
interneturok.ru
Сложение дробей с одинаковыми знаменателями
Рассмотрим, как проводится сложение дробей с одинаковыми знаменателями.
Правило.
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.
С помощью букв правило сложения дробей с одинаковыми знаменателями можно записать так:
Примеры.
Выполнить сложение дробей:
Решение:
Чтобы выполнить сложение дробей с одинаковыми знаменателями, сложим числители, а знаменатель оставим без изменения:
Если при сложении дробей получаем дробь, у которой числитель равен знаменателю, то такая дробь равна единице.
Примеры.
Если при сложении дробей получаем дробь, у которой числитель больше знаменателя, надо представить ее виде смешанной дроби.
Для этого нужно выделить из дроби целую часть.
Например,
www.for6cl.uznateshe.ru
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (3,9 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока.
сформулировать правила
сложения и вычитания дробей с одинаковыми
знаменателями; научить применять их при решении
задач и нахождении значений выражений.
Тип урока: урок усвоения новых знаний.
Структура урока:
- Организационный момент (1 мин.)
- Актуализация опорных знаний. (7 мин.)
- Гимнастика для глаз. (1 мин.)
- Сообщение темы и цели урока. (2 мин.)
- Изучение нового материала. (14 мин.)
- Физкультминутка. (1 мин.)
- Применение полученных знаний при решении задач.
- Тренировочные упражнения. (4 мин.)
- Самостоятельная работа. (9 мин.)
- Проверка самостоятельной работы. (3 мин.)
Оборудование: презентация, интерактивная доска, карточки.
Ход урока
1. Организационный момент.
Сегодня у нас необычный урок к нам в гости пришли герои мультфильма “Смешарики”.
Слайд 1
Давайте откроем тетради, запишем число и классная работа.
2. Актуализация опорных знаний.
Как обычно урок мы начнем с повторения.
Слайд 2 [3]
Каждый может за версту
Видеть дробную черту.
Над чертой – числитель, знайте,
Под чертою – знаменатель.
Дробь такую, непременно,
Надо звать обыкновенной.
Число, которое показывает, на сколько равных частей разделили целое, называется знаменатель.
Число, которое показывает, сколько равных частей взято, называется числитель.
Слайд 3
1) Какая часть фигуры закрашена?
2) Расположите дроби в порядке возрастания:
Слайд 4
Задача 1.
В огороде у Копатыча 10 грядок с овощами. грядок засажено капустой. Сколько грядок в огороде у Копатыча с капустой? (Ответ: 4 шт.)
Краткая запись условия записана на доске с обратной стороны.
Задача 2.
Ежик собирает фантики. Нюша подарила ему 34 штуки, Крош на 8 штук больше, чем Нюша, а Бараш на 12 меньше, чем Крош. Сколько всего фантиков подарили друзья Ежику?
(1. 34+8=42; 2. 42-12=30 3. 34+42+30=106)
Краткая запись условия записана на доске с обратной стороны.
Задача 3.
Кар Карыч забыл порядок действий. Помогите ему.
444:4+(45•51-232:2)•6
Гимнастика для глаз.
3. Сообщение темы и цели урока.
В начале года мы с вами изучили натуральные числа, а затем все действия с ними. Теперь мы изучаем обыкновенные дроби, а значит будем изучать и действия с ними.
У многих народов в древности дроби называли ломаными числами. Правил действий с дробями было так много, что умение оперировать ими воспринималось как чудо! Поэтому всегда и везде знание дробей пользовалось особым почетом и уважением.
Сегодня мы начинаем изучать первые действия с ними — это сложение и вычитание.
Слайд 5
Итак, тема нашего урока “Сложение и вычитание дробей с одинаковыми знаменателями”.
Мы должны:
- сформулировать правила сложения и вычитания дробей с одинаковыми знаменателями;
- научиться применять их при решении задач и вычислении значений выражений.
4. Изучение нового материала
Слайд 6
Нюша и Бараш раскрашивали квадрат. Нюша раскрашивала красным цветов, а Бараш зеленым.
Какую часть квадрата закрасила Нюша? (7/25)
Какую часть – Бараш? (10/25)
Какую часть они всего закрасили? (17/25)
Какое арифметическое действие используют, если нужно найти сколько всего в задачах? (сложение).
Значит получаем, что 7/25 +10/25 =17/25.
Теперь попробуем сформулировать правило сложения обыкновенных дробей с одинаковыми знаменателями.
Слайд 7
Чтобы сложить две дроби с одинаковыми знаменателями надо:
- сложить числители,
- знаменатель оставить прежним.
[1]
Например: 3/14 +5/14 = 8/14
Отработка правила учащиеся решают примеры у доски и записывают в тетради
19/24 + 3/24 = 22/24
17/29 + 9/29 = 26/29
21/45 + 17/45 = 38/45
А теперь вернемся к Нюше и Барашу.
Слайд 8
На сколько частей Бараш закрасил больше, чем Нюша? (3/25)
Какое арифметическое действие используют, если нужно найти на сколько одно число больше другого? (Вычитание)
Значит получаем, что 10/25 -7/25 = 3/25.
Теперь попробуем сформулировать правило вычитания обыкновенных дробей с одинаковыми знаменателями.
Слайд 9
Чтобы вычесть две дроби с одинаковыми знаменателями надо:
- вычесть числители этих дробей,
- знаменатель оставить прежним.
[1]
Например: 7/15 – 4/15 = 3/15
Отработка правила учащиеся решают примеры у доски и записывают в тетради.
Те же примеры, что и на сложение, только меняем знак на минус.
19/24 — 3/24 = 16/24
17/29 — 9/29 = 8/29
21/45 — 17/45 = 4/45
Слайд 10
Теперь настало время для физкультминутки.
5. Применение полученных знаний при решении задач.
1. Тренировочные упражнения.
Давайте еще раз повторим:
1. Как сложить две дроби с одинаковыми знаменателями?
2. Как вычесть дроби с одинаковыми знаменателями?
Откроем учебники №1005, №1008 (краткая запись обоих задач приготовлена на ватманах).
2. Самостоятельная работа.
(Приложение 1)
Раздать карточки учащимся.
Вариант 1 [3]
Вычислите
1.
2.
3.
4.
5. В книге у Совуньи несколько рассказов.
Первый рассказ занимает 7/17 частей книги, а второй на 3/17 меньше.
Какую часть занимает второй рассказ?
(Ответы: 1. 7/10; 2. 2/14; 3. 4/5; 4. 1/4; 5. 4/17)
Вариант 2
Вычислите
1.
2.
3.
4.
5. Дорога от домика Нюши до домика Бараша равна км,
а от домика Бараша до домика Кроша км.
Сколько метров занимает дорога от домика Нюши до домика Кроша? (Ответы: 1. 15/13; 2. 1/15; 3. 5/10; 4. 3/7; 5. 13/19)
Проверка варианта осуществляется на интерактивной доске, с использованием приготовленного файла Excel. (Приложение 2)
Ученик заполняет места предназначенные для ответов, при этом правильность примера и оценка закрыты “Шторкой”. Как только ученик все заполнит, учитель открывает “шторку”, где можно будет увидеть успешность выполнения работы и оценка за нее.
Ученикам, быстро справившимся с заданием дать дополнительное задание.
1. На первой тарелке было 7/25 фунта сливочного масла, на второй тарелке на 3/25 фунта меньше, а на третьей – 4/25 фунта больше, чем на первой. Сколько граммов масла было на трех тарелках вместе, если считать фунт равным 400 г? (22/25 фунта, 352 г)
2. Решите уравнение (7/8)
6. Домашнее задание.
Слайд 11
П 26, №1041(а-г), 1039, 1043 (с комментариями).
7. Итог урока.
Подведение итога урока можно закончить.
Слайдом 12
Дроби всякие нужны,
Дроби разные важны.
Дробь учи, тогда сверкнёт тебе удача.
Если будешь дроби знать,
Точно смысл их понимать,
Станет лёгкой даже трудная задача.
Слайд13 можно использовать, если остается несколько секунд до звонка, или совсем не показывать.
Например:
1 вариант. Герои мультика говорят нам: “Спасибо за внимание!” На этом наш урок закончен.
2 вариант. Герои мультика говорят нам: “Спасибо за внимание!” Давайте сосчитаем, сколько здесь изображений Ежика, Бараша, Нюши, Совуньи, Каркарыча, Лосяша, Каркарыча.
Используемые источники:
1. http://festival.1september.ru/articles/510161/
2. 173/kolobova/DswMedia/prezent.ppt
3. http://festival.1september.ru/articles/577803/
20.03.2013
xn--i1abbnckbmcl9fb.xn--p1ai
Сложение дробей | Формулы с примерами
Сложение дробей
С одинаковыми знаменателями
Определение
Что бы найти сумму дробей с одинаковыми знаменателями, нужно просто сложить их числители. Знаменатель останется прежним.
Найдем, во сколько раз каждый знаменатель меньше общего
и умножим каждую дробь на это число.
Пример 27 + 47 = 2 + 47 = 67;
46 + 96 = 4 + 96 = 136 = 216;
72 + 122 = 7 + 122 = 192 = 912.
С разными знаменателями
Определение
Необходимо привести к общему знаменателю и сложить полученные дроби.
1. Преобразуем смешанную дробь в неправильную;
2. Находим общий знаменатель;
3. Приводим дроби к общему знаменателю;
4. Выполняем действия с числителями;
5. Приводим получившуюся неправильную дробь к смешанной.
12 + 34 = 48 + 68 = 108 = 128 = 114;
34 + 57 = 2128 + 2028 = 4128 = 11 13;
23 + 74 = 8 12 + 2112 = 2912 = 25 12.
formula-xyz.ru
