Примеры системы массового обслуживания – —

Системы массового обслуживания

Применение различных математических методов к формализации. Акцент на сложную систему — непредсказуемую. Носитель неопределенности является человек.

Характерным примером стохастических (случайные, вероятностные) задач являются модели систем массового обслуживания.

СМО имеют повсеместное распространение. Это телефонные сети, автозаправочные станции, предприятия бытового обслуживания, билетные кассы, торговые мероприятия и т.д.

С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если такое имеется в блоке ожидания. Цикл функционирования СМО подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.

Примерами СМО могут служить:

• посты технического обслуживания автомобилей;

• посты ремонта автомобилей;

• аудиторские фирмы и т.д.

Основоположником теории массового обслуживания, в частности, теории очередей, является известный датский ученый А.К.Эрланг (1878-1929), который исследовал процессы обслуживания на телефонных станциях.

Системы, в которых имеют место процессы обслуживания, называют системами массового обслуживания (СМО).

Чтобы описать систему массового обслуживания, необходимо задать:

— входной поток заявок;

— дисциплину обслуживания;

— время обслуживания

— количество каналов обслуживания.

Входной поток требований (заявок) описывается путем выявления как вероятностного закона распределения моментов поступления требований в систему, так и количества требований в каждом поступлении.

При задании дисциплины обслуживания (ДО) необходимо описать правила постановки требований в очередь и обслуживания их в системе. При этом длина очереди может быть как ограниченной, так и неограниченной. В случае ограничений на длину очереди поступившая на вход СМО заявка получает отказ. Чаще всего используются ДО, определяемые следующими правилами:

первым пришел – первым обслуживаешься;

• пришел последним — обслуживаешься первым; (коробочка для теннисных шариков, стек в технике)

• случайный отбор заявок;

• отбор заявок по критерию приоритетности.

Время обслуживания заявки в СМО является случайной величиной. Наиболее распространенным законом распределения является экспоненциальный закон.  — скорость обслуживания. =количество заявок обслуживания/ед. времени.

Каналы обслуживания, могут быть расположены параллельно и последовательно. При последовательном расположении каналов каждая заявка проходит обслуживание на всех каналах последовательно. При параллельном расположении каналов обслуживание производится на всех каналах одновременно по мере их освобождения.

Обобщенная структура СМО представлена на рис.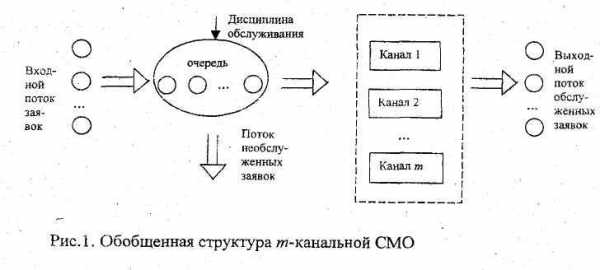

Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности СМО, и эффективностью ее функционирования.

Проблемы проектирования СМО.

К задачам определения характеристик структуры СМО относятся задача выбора количества каналов обслуживания (базовых элементов {Ф_i}), задача определения способа соединения каналов (множества элементов связей {Hj}), а также задача определения пропускной способности каналов.

1). Выбор структуры. Если каналы работают параллельно, то проблема выбора Str сводится к определению количества каналов в обслуживающей части исходя из условия обеспечения работоспособности СМО. (Если очередь не является бесконечно растущей).

Отметим, что при определении количества каналов системы, в случае их параллельного расположения, необходимо соблюдать условие работоспособности системы. Обозначим:  — среднее число заявок, поступающих в единицу времени, т.е. интенсивность входного потока;  — среднее число заявок, удовлетворяемых в единицу времени, т.е. интенсивность обслуживания; S — количество каналов обслуживания. Тогда условие работоспособности СМО запишется

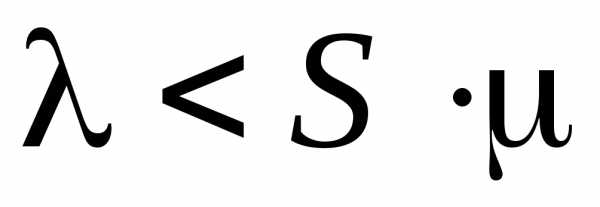или 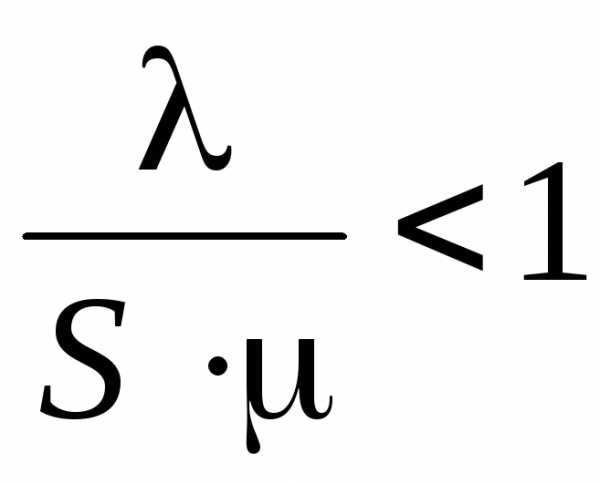. Выполнение этого условия позволяет вычислить нижнюю границу количества каналов.

В случае, если 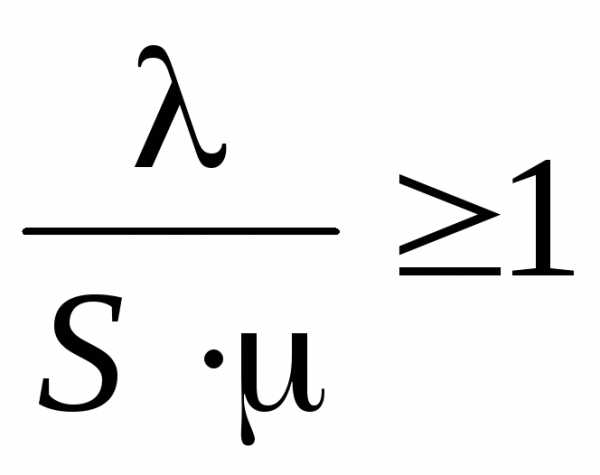, система не справляется с очередью. Очередь при этом растет безгранично.

2). Необходимо определить критерий эффективности функционирования

СМО с учетом затрат на потери времени как со стороны заявок, так и со стороны обслуживающей части.

В качестве показателей эффективности функционирования СМО рассматриваются следующие три основные группы показателей:

1. Показатели эффективности использования СМО.

1. Абсолютная пропускная способность СМО — среднее число заявок, которое может обслужить СМО в единицу времени.

2. Относительная пропускная способность СМО – отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших заявок за это время.

3. Средняя продолжительность периода занятости СМО.

4. Коэффициент использования СМО — средняя доля времени, в течение которого СМО занята обслуживанием заявок.

2. Показатели качества обслуживания заявок.

1. Среднее время ожидания заявки в очереди.

2. Среднее время пребывания заявки в СМО.

3. Вероятность отказа заявке в обслуживании без ожидания.

4. Вероятность того, что поступившая заявка немедленно будет принята к обслуживанию.

5. Закон распределения времени ожидания заявки в очереди.

6. Закон распределения времени пребывания заявки в СМО.

7. Среднее число заявок, находящихся в очереди.

8. Среднее число заявок, находящихся в СМО.

3. Показатели эффективности функционирования пары «СМО — потребитель».

При выборе критерия эффективности функционирования СМО необходимо учесть двойственный подход к рассмотрению систем массового обслуживания. Например, работу универсама, как СМО, можно рассматривать с противоположных сторон. С одной, традиционно принятой, стороны покупатель, ожидающий свою очередь у кассы, представляет собой заявку на обслуживание, а кассир — канал обслуживания. С другой стороны, кассир, который ожидает покупателей, может быть рассмотрен в качестве заявки на обслуживание, а покупатель — обслуживающее устройство, способное удовлетворить заявку, т.е. подойти к кассе и прекратить вынужденный простой кассира. (традиционно – покупателей > чем кассиров, если кассиров > чем покупателей, они ждут покупателей).

С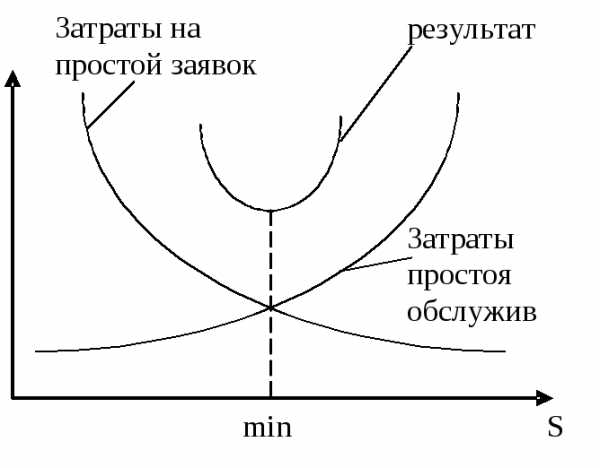учетом этого целесообразно минимизировать обе части СМО одновременно.

Применение такого двойственного подхода предполагает необходимость учета при формировании критерия эффективности не только перечисленных выше показателей в отдельности, но и одновременно нескольких показателей, отражающих интересы как обслуживающей, так и обслуживаемой подсистем СМО. Например, показано, что наиболее важным критерием эффективности в задачах массового обслуживания является суммарное время нахождения клиента в очереди, с одной стороны, и простоя каналов обслуживания — с другой.

Классификация систем массового обслуживания

1. По характеру обслуживания выделяют следующие виды СМО:

1.1. Системы с ожиданием или системы с очередью. Требования, поступившие в систему и не принятые немедленно к обслуживанию, накапливаются в очереди. Если каналы свободны, то заявка обслуживается. Если же все каналы заняты в момент поступления заявки, то очередная заявка будет обслужена после завершения обслуживания предыдущей. Такая система называется полнодоступной (с неограниченной очередью).

Существуют системы с автономным обслуживанием, когда обслуживание начинается в определенные моменты времени;

2. Системы с ограниченной очередью. (ремонт в гараже)

3. Системы с отказами. Все заявки, прибывшие в момент обслуживания заявки, получают отказ. (ГТС)

4. Системы с групповым входным потоком и групповым обслуживанием. В таких системах заявки поступают группами в моменты времени, обслуживание также происходит группами.

2. По количеству каналов обслуживания СМО подразделяются на следующие группы.

Одноканальные СМО.

Многоканальные СМО. Обслуживание очередной заявки может начаться до окончания обслуживания предыдущей заявки. Каждый канал действует как самостоятельное обслуживающее устройство.

3. По кругу обслуживаемых объектов различают два вида.

Замкнутые СМО. Замкнутая система массового обслуживания — это система массового обслуживания, в которой обслуженные требования могут возвращаться в систему и вновь поступать на обслуживание. Примерами замкнутой СМО являются ремонтные мастерские, сберегательные банки.

Открытые СМО.

4. По количеству этапов обслуживания различают однофазные и многофазные СМО.

Однофазные СМО — это однородные системы, которые выполняют одну и ту же операцию обслуживания.

Многофазные СМО — это системы, в которых каналы обслуживания расположены последовательно и выполняют различные операции обслуживания. Примером многофазной СМО являются станции технического обслуживания автомобилей.

Приведенная классификация СМО является условной. На практике чаще всего СМО выступают в качестве смешанных систем. Например, заявки ожидают начала обслуживания до определенного момента, после чего система начинает работать как система с отказами.

studfiles.net

3.4.5. Примеры систем массового обслуживания с отказами

Пример 3.1. Рассматривается работа районной автоматической телефонной станции (АТС), которая обеспечивает не более 120 переговоров одновременно. Средняя длительность переговоров 1/μ = 1 мин. Вызовы на станцию поступают через 0,5 с, т.е. 1/λ = 0,5 с. Требуется найти характеристики работы АТС: ,,,,.

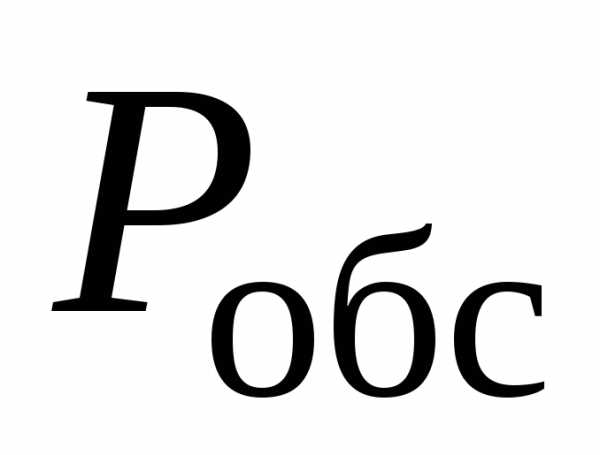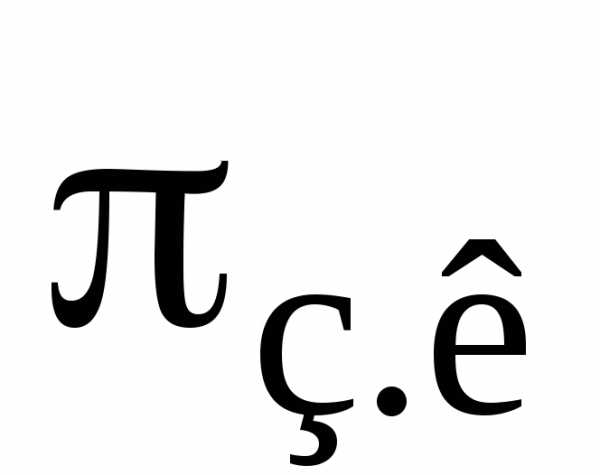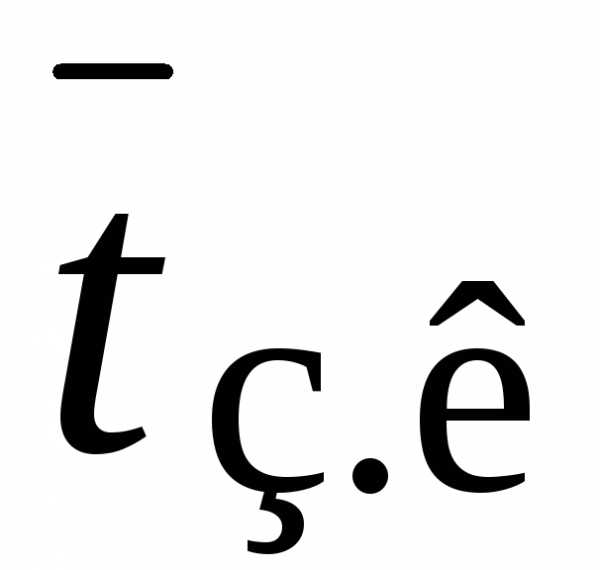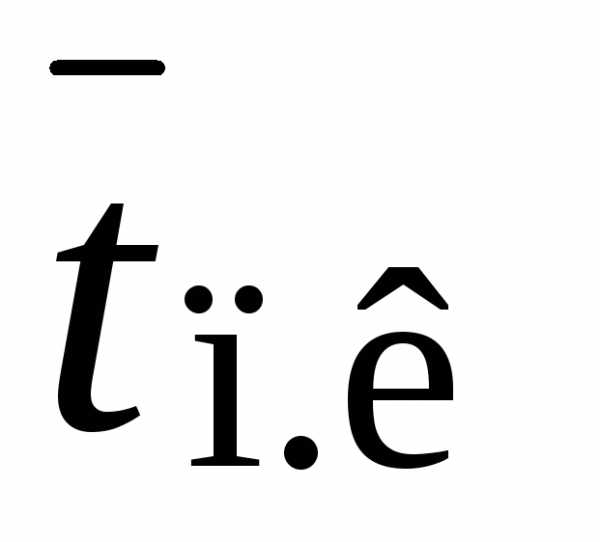Решение

АТС представляет собой 120-канальную СМО с отказами. Параметры системы следующие: n = 120; λ = 2 сооб/с; μ = 1/60 сооб/с; ρ = λ/μ = 120.

Среднее число занятых каналов

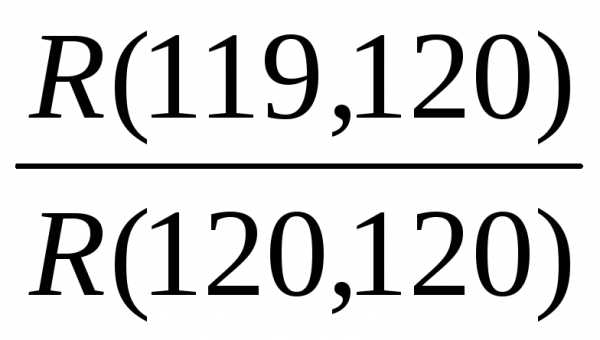= ρР_обс = ρ= 120≈ 120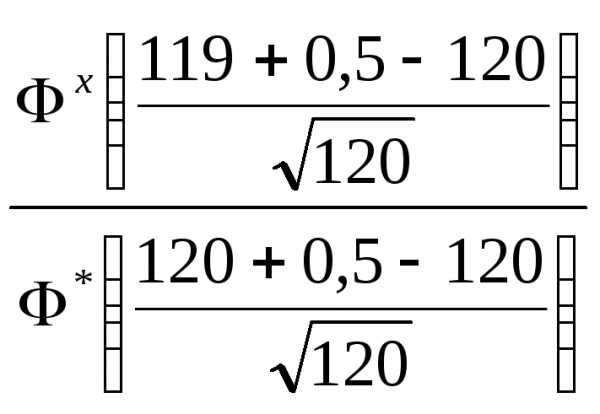≈ 112.

Вероятность обслуживания

Р_обс = /ρ =.

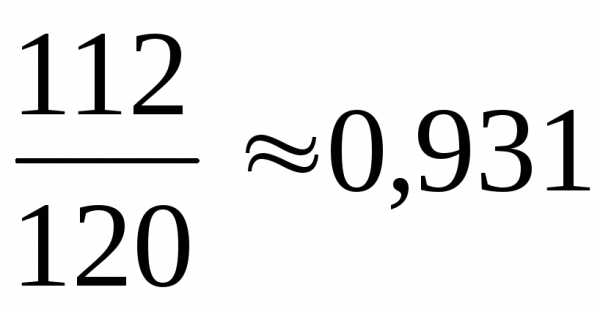Вероятность занятости канала

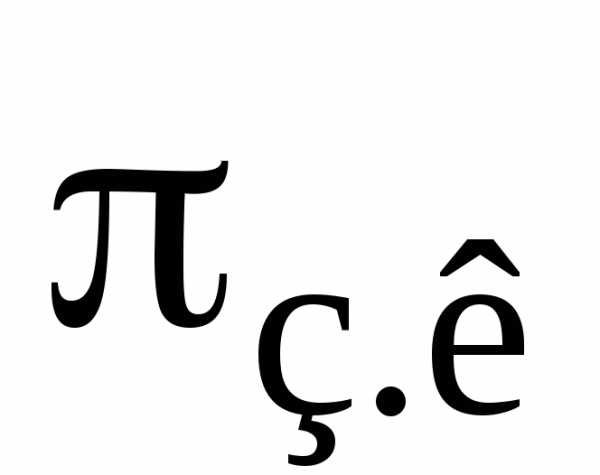=/n.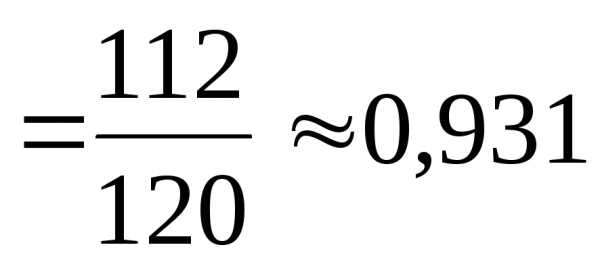

Среднее время занятости канала

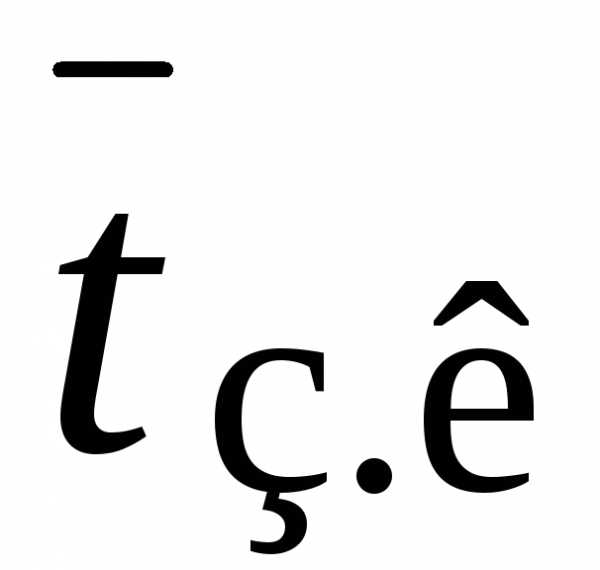= 1/μ = 1 мин = 60 с.

Среднее время простоя канала

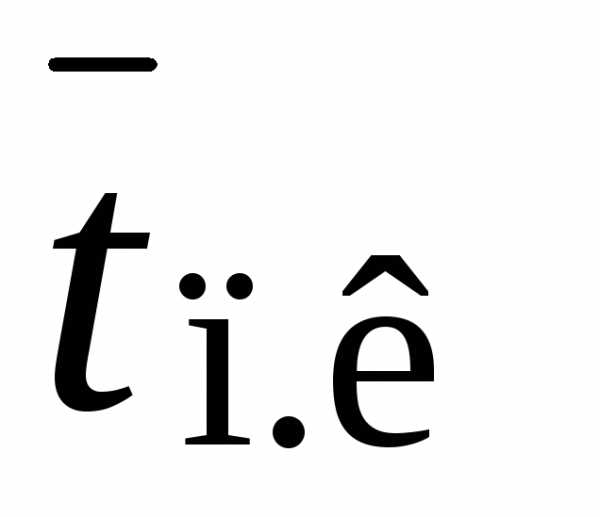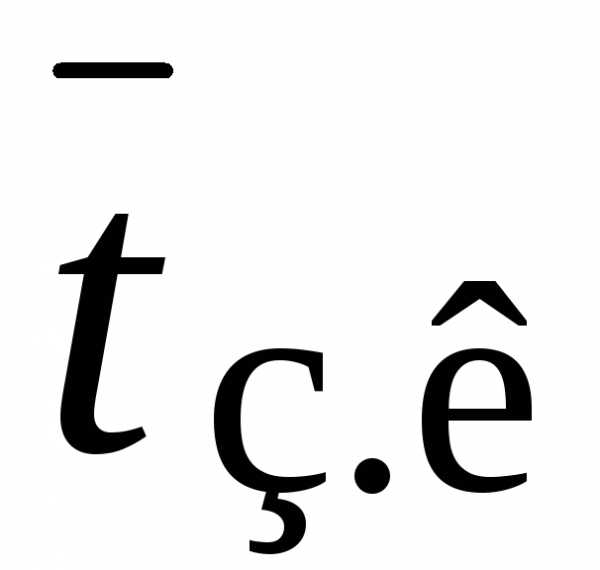
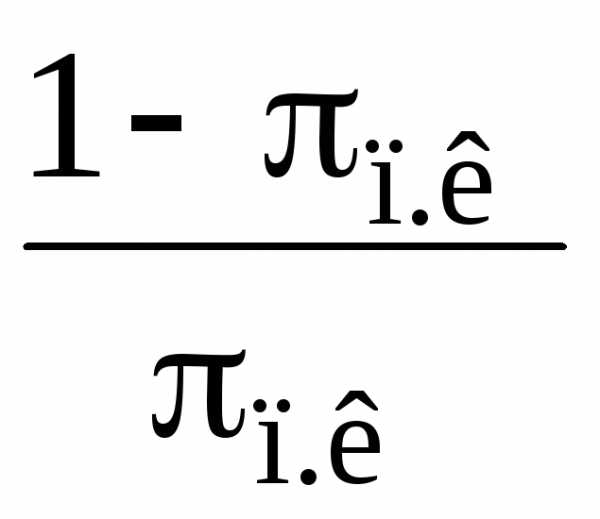= ≈ 4,5 с.

Пример 3.2. Обслуживание заявок производится СМО с отказами, параметрами системы n, λ, μ. Обслуживание каждой заявки приносит среднюю прибыль С₁. С целью увеличения доходов обслуживания предлагается провести реорганизацию, состоящую в том, что система будет допускать взаимопомощь между каналами. На преобразование СМО с отказами в СМО с отказами и взаимопомощью требуется израсходовать стоимость С₂. Переоборудование занимает время τ_п. Определить, по истечении какого срока времени t после начала преобразования вновь организованная СМО с отказами и взаимопомощью начнет приносить прибыль.

Решение

Задачу будем решать при условии, что время установления стационарного режима в системах мало по сравнению со временем переоборудования τ_п и временем t (t > τ_п). Начало отсчета для времени τ_п и t одно. В этом случае можно записать следующее уравнение:

С₁λ₀⁽¹⁾ t = –С₂ + С₁ λ₀⁽²⁾( t – τ_п),

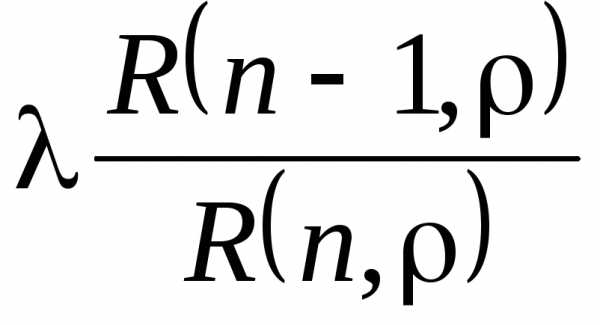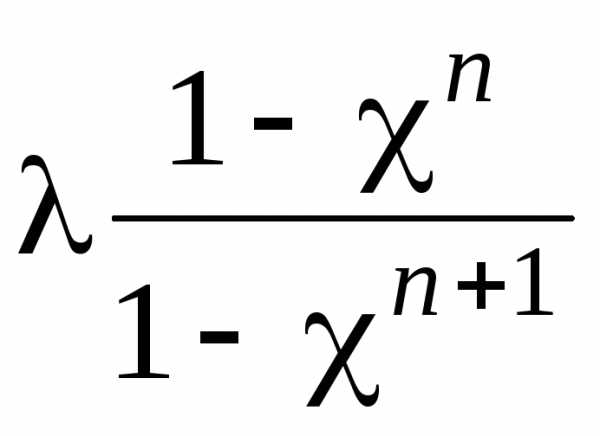где ₀⁽¹⁾ = – абсолютная пропускная способность СМО с отказами; λ₀⁽²⁾ = – абсолютная пропускная способность СМО с отказами и взаимопомощью; ρ = λ/μ; χ = λ/nμ.

Решая это уравнение, получим t, по истечении которого реорганизация начнет приносить прибыль:

.

Пример 3.3. Определить, насколько увеличится вероятность обслуживания для СМО с отказами, имеющей следующие параметры: n = 10, λ = = 8 сооб/мин; μ = 0,8 сооб/мин, если обеспечить взаимопомощь группы из двух каналов (l = 2).

Решение

Для СМО с отказами без взаимопомощи вероятность обслуживания

Р_обс⁽¹⁾ = .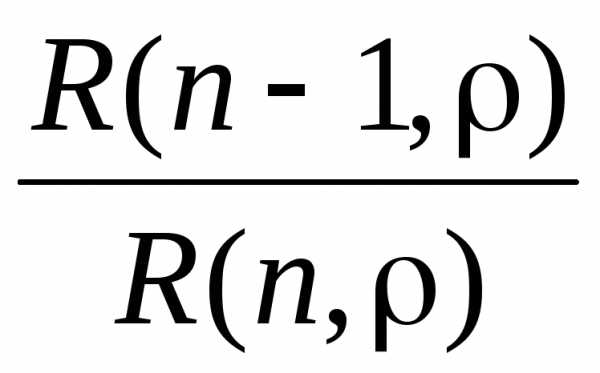

Для примера

Р_обс⁽¹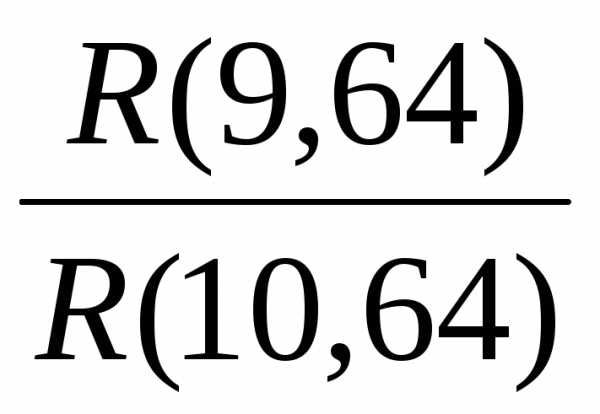⁾ = = 0,795.

Для системы с частичной взаимопомощью имеем

N = 10; χ = λ / nμ = 1; ρ_l = λ / lμ = 0,5; h = ]n / l[ = 5.

Для этой системы в случае, когда χ = 1, вероятность обслуживания

Р_обс⁽²⁾ = = 0,883.

Таким образом,

Р_обс⁽²⁾ – Р_обс⁽¹⁾ = 0,883 – 0,795 = 0,088.

Пример 3.4. Рассматривается система ПВО с нарушенным управлением. Нарушение управления состоит в том, что каждую влетающую в зону обстрела цель обстреливают все свободные к этому времени каналы. Обстрел цели каждым каналом длится случайное время, распределенное по показательному закону с параметром . За это время каждый канал поражает цель с вероятностью р независимо от других каналов, принимающих участие в обстреле. Определить характеристики работы системы, если параметры системы ПВО следующие: n = 4;  = 4 1/мин;  = 1 1/мин;  = = 0,5.

Решение

В рассматриваемом примере величина 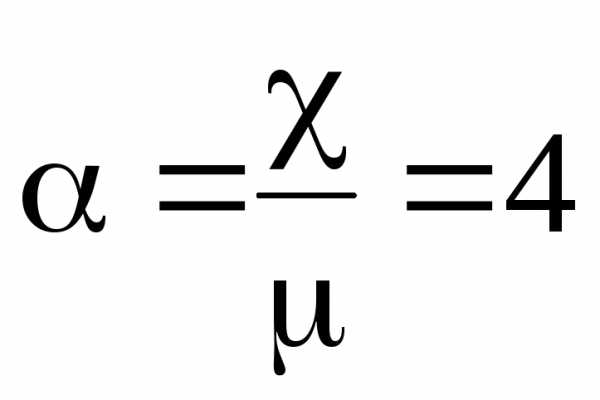– целое число. Вероятности различных состояний системы следующие:

; ;

;;

.

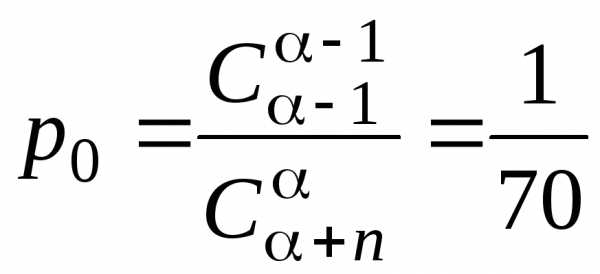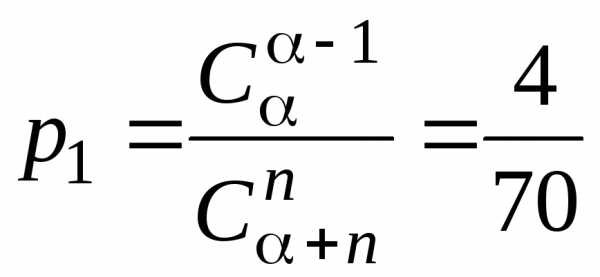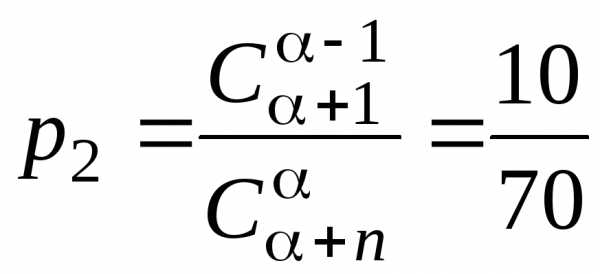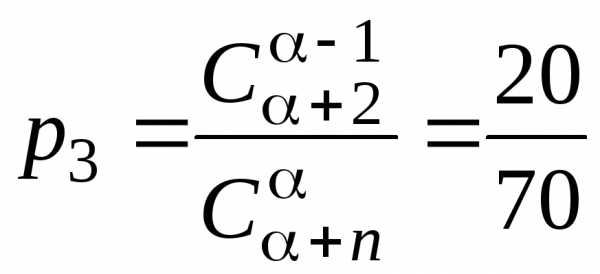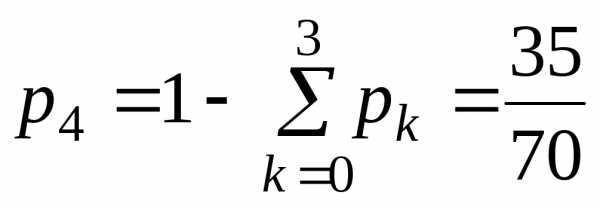Вероятности поражения цели

.

Вероятность полной загрузки системы

.

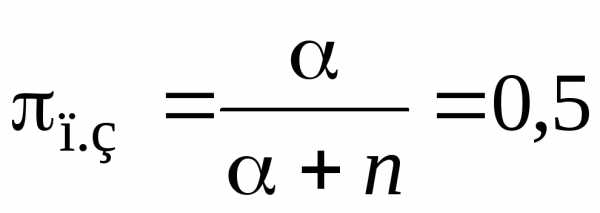studfiles.net

3.1 Модели систем массового обслуживания (смо)

Во многих областях экономики, финансов, производства и быта важную роль играют системы, реализующие многократное выполнение однотипных задач. Такие системы называются системами массового обслуживания (СМО). Примерами СМО являются: банки различных типов, страховые организации, налоговые инспекции, аудиторские службы, различные системы связи, погрузочно-разгрузочные комплексы, автозаправочные станции, различные предприятия и организации сферы обслуживания.

3.1.1 Общие сведения о системах массового обслуживания

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а в случайные моменты времени. Обслуживание заявок также длится не постоянное, заранее известное время, а случайное, которое зависит от многих случайных, порой неизвестных нам, причин. После обслуживания заявки канал освобождается и готов к приёму следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО. В некоторые промежутки времени на входе СМО могут скапливаться заявки, что приводит к перегрузке СМО, в некоторые же другие интервалы времени при свободных каналах (устройствах обслуживания) на входе СМО заявок не будет, что приводит к недогрузке СМО, т.е. к простаиванию её каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по какой-то причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными.

На рис 3.1 изображена схема СМО.

Основными элементами (признаками) систем массового обслуживания являются:

Обслуживающий узел (блок),

Поток заявок,

Очередь в ожидании обслуживания (дисциплина очереди).

Обслуживающий блок предназначен для осуществления действий согласно требованиям поступающих в систему заявок.

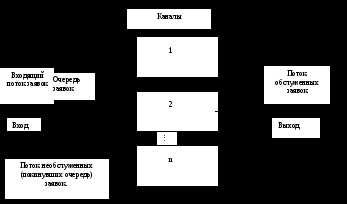
Рис. 3.1 Схема системы массового обслуживания

Вторая составляющая систем массового обслуживания — входной поток заявок. Заявки поступают в систему случайным образом. Обычно предполагают, что входной поток подчиняется некоторому вероятностному закону для длительности интервалов между двумя последовательно поступающими заявками, причем закон распределения считается не изменяющимся в течение некоторого достаточно продолжительного времени. Источник заявок — неограничен.

Третья составляющая — дисциплина очереди. Эта характеристика описывает порядок обслуживания заявок, поступающих на вход системы. Поскольку обслуживающий блок, как правило, имеет ограниченную пропускную способность, а заявки поступают нерегулярно, то периодически создается очередь заявок в ожидании обслуживания, а иногда обслуживающая система простаивает в ожидании заявок.

Главная особенность процессов массового обслуживания – случайность. При этом имеются две взаимодействующие стороны: обслуживаемая и обслуживающая. Случайное поведение хотя бы одной из сторон приводит к случайному характеру протекания процесса обслуживания в целом. Источниками случайности взаимодействия этих двух сторон являются случайные события двух типов.

1. Появление заявки (требования) на обслуживание. Причиной случайности данного события часто является массовый характер потребности в обслуживании.

2. Окончание обслуживания очередной заявки. Причинами случайности этого события является как случайность начала обслуживания, так и случайная продолжительность самого обслуживания.

Указанные случайные события составляют систему двух потоков в СМО: входного потока заявок на обслуживание и выходного потока обслуженных заявок.

Результатом взаимодействия указанных потоков случайных событий является число находящихся в СМО заявок в данный момент, которое принято называть состоянием системы.

Каждая СМО в зависимости от своих параметров ­ характера потока заявок, числа каналов обслуживания и их производительности, от правил организации работы, ­ обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей успешно справляться с потоком заявок.

Специальная область прикладной математики ­ теория массового обслуживания (ТМО) – занимается анализом процессов в системах массового обслуживания. Предметом изучения теории массового обслуживания является СМО.

Цель теории массового обслуживания ­ выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО. Для достижения этой цели ставятся задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от её организации.

Задачи теории массового обслуживания носят оптимизационный характер и в конечном счете направлены на определение такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и от простоя обслуживающего блока. Знание таких характеристик дает менеджеру информацию для выработки направленного воздействия на эти характеристики для управления эффективностью процессов массового обслуживания.

В качестве характеристик эффективности функционирования СМО обычно выбираются три следующие основные группы (обычно средних) показателей:

1. Показатели эффективности использования СМО:

• Абсолютная пропускная способность СМО — среднее число заявок, которое сможет обслужить СМО в единицу времени.

• Относительная пропускная способность СМО — отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу заявок поступивших за это же время.

• Средняя продолжительность периода занятости СМО.

• Коэффициент использования СМО — средняя доля времени, в течении которого СМО занята обслуживанием заявок, и т.п.

2. Показатели качества обслуживания заявок:

• Среднее время ожидания заявки в очереди.

• Среднее время пребывания заявки в СМО.

• Вероятность отказа заявке в обслуживании без ожидания.

• Вероятность того, что поступившая заявка немедленно будет принята к обслуживанию.

• Закон распределения времени пребывания заявки в очереди.

• Закон распределения времени пребывания заявки в СМО.

• Среднее число заявок, пребывающих в очереди.

• Среднее число заявок, находящихся в СМО, и т.п.

3. Показатели эффективности функционирования пары «СМО − потребитель», где под «потребителем» понимают всю совокупность заявок или некий их источник: средний доход, приносимый СМО в единицу времени и т.п.

Отметим, что третья группа показателей оказывается полезной в тех случаях, когда некоторый доход, получаемый от обслуживания заявок и затраты на обслуживание измеряются в одних и тех же единицах. Эти показатели обычно носят вполне конкретный характер и определяются спецификой СМО, обслуживаемых заявок и дисциплиной обслуживания.

Впервые задачи такого типа были решены в работах А. К. Эрланга в начале прошлого века и легли в основу «Теории массового обслуживания», которая успешно развивается в настоящее время. Большой вклад в развитие этой теории внесли российские математики А.Я.Хинчин, Б.В.Гнеденко, А.Н.Колмогоров, Е.С.Вентцель и др.

studfiles.net

Системы массового обслуживания — Энциклопедия по экономике

Называется также моделью очереди. Используются в системах массового обслуживания, часто называемых «теорией очередей» (см. [Т 38]).  [c.179]
Многие компании пытались снизить себестоимость перед лицом постоянного роста цен на нефть и сырье, большую часть которых приходится импортировать. Расходы на каналы системы массового обслуживания, которые в Японии весьма велики, стали основной целью. Для правительства настоятельная потребность — отреагировать на жалобы и критику зарубежных сбытовиков и разработать эффективную систему каналов массового обслуживания, управляемую соответствующей информационному веку системой ЭВМ.  [c.252]

В рассматриваемом примере системой массового обслуживания является служба испытания, а в качестве каналов обслуживания приняты бригады по испытанию с соответствующим буровым оборудованием.  [c.64]

Каждая система массового обслуживания в зависимости от числа каналов и их производительности обладает пропускной способностью, позволяющей ей более или менее успешно справляться с обслуживанием. Пользуясь методами теории массового обслуживания, можно установить зависимость между ха-  [c.64]

Модели со случайными факторами системы массового обслуживания  [c.200]

В этом параграфе мы рассмотрим наиболее распространенный в экономических (и не только экономических) исследованиях класс стохастических моделей модели систем массового обслуживания. Системы массового обслуживания встречаются повсеместно. Читатель сотни и тысячи раз пользовался такими системами, не догадываясь, видимо, что они являются объектом исследования одного и того же раздела теории принятия решения.  [c.200]

Основным признаком системы массового обслуживания является наличие некоторой системы (обслуживающей системы), которая предназначена для осуществления действий, совершаемых согласно требованиям (называемым заявками), которые поступают нерегулярным образом. Поскольку обслуживающая система обычно имеет ограниченную пропускную способность, а заявки поступают нерегулярно, время от времени создается очередь заявок в ожидании обслуживающего устройства иногда же оборудование простаивает в ожидании заявок. Наиболее часто предполагается, что известен вероятностный закон, управляющий поступлением заявок. Впервые такой подход был применен датским математиком А. К. Эрлангом в начале нашего века для анализа работы телефонной станции. С тех пор методы теории массового обслуживания распространились на широкий круг разнообразных проблем, включающий в себя столь разнородные задачи, как анализ очереди в магазине и исследование пропускной способности дорог, мостов и перекрестков, исследование эффективности работы большого морского порта и небольшой автозаправочной станции, анализ работы ремонтной бригады на предприятии и кассира в кинотеатре и т. д. Делаются попытки проанализировать с помощью методов теории массового обслуживания даже такие вопросы, как эффективность работы промышленного предприятия в целом.  [c.200]

Системы массового обслуживания имеют место практически везде, где есть или может возникнуть очередь. На  [c.200]

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 201  [c.201]

Итак, система массового обслуживания состоит из блока обслуживания, на который поступают заявки, из потока заявок и из очереди в ожидании обслуживания. Рассмотрим эти три основные составляющие системы массового обслуживания более подробно.  [c.201]

Блоки обслуживания в соответствии с тем, что системы массового обслуживания встречаются в различных непохожих ситуациях, различаются между собой по многим показателям.  [c.201]

Во-вторых, системы массового обслуживания могут быть однофазными и многофазными. В первом случае заявка обслуживается только одним прибором , после чего покидает систему например, покупатель билета в театре. Во втором случае заявка должна пройти некоторую последовательность приборов . Например, в сберкассе, прежде чем получить деньги, человек сначала должен быть обслужен контролером и только потом — кассиром.  [c.202]

Для описания другой важнейшей составной части любой системы массового обслуживания, — входного потока заявок, — обычно задают вероятностный закон, которому удовлетворяют длительности интервалов между двумя последовательно поступающими заявками. Эти длительности обычно являются статистически независимыми и их распределение не изменяется в течение некоторого достаточно продолжительного промежутка времени. Иногда встречаются системы, в которых заявки могут поступать группами (например, посетители в кафе). Обычно предполагается, что источник, из которого поступают заявки, практически  [c.202]

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 203  [c.203]

Итак, в жизни встречается огромное число систем, которые могут быть описаны математически как системы массового обслуживания одного из типов. После того как  [c.203]

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 205  [c.205]

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 207  [c.207]

Величину р часто называют нагрузкой системы. Итак, мы получили интересующее нас распределение длины очереди. Найдем некоторые из характеристик нашей системы массового обслуживания.  [c.208]

СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ 211  [c.211]

Описание этапов имитационного исследования мы будем проводить на примере двух конкретных задач. Первая из них — принятие решения о варианте системы массового обслуживания. Пусть планируется строительство автозаправочной станции, предназначенной для заправки автомобилей бензином. Имеется конечное число вариантов АЗС, которые могут быть построены в интересующем заказчика пункте. Перед ним стоит проблема — выбрать один из этих вариантов. Как читатель знает, анализ систем такого рода обычно относится к исследованию моделей со случайными воздействиями, которые были уже рассмотрены нами. Полученные читателем знания помогут построить модель и оценить преимущества и недостатки имитационного исследования в этом случае. Надо подчеркнуть, что изучение стохастических моделей было первым объектом приложения имитационных исследований к экономическим задачам. Такие исследования относятся к наиболее широко применяемым методам имитации и по настоящее время.  [c.239]

Некоторые закономерности становятся ясны при внимательном анализе структуры изучаемых систем. Например, в нашей системе массового обслуживания можно сформулировать следующий факт, дающий возможность понять зависимость времени нахождения в очереди г -го автомобиля г,- и времени простоя оборудования в ожидании i-ro автомобиля У в зависимости от времени нахождения в очереди z/.j и времени обслуживания e/-i (i— l)-ro автомобиля и промежутка между этими автомобилями х вопрос о том, будет ли стоять в очереди i-й автомобиль, зависит лишь от соотношения между величиной tt и полным временем нахождения у колонки (i — 1)-го автомобиля Xi-i, а точнее  [c.252]

Модель системы массового обслуживания, для которой может не быть реального аналога, можно проверить при упрощающих предположениях. Обычно распределение промежутков времени между автомобилями, прибывающими на автозаправочную станцию, имеет какой-либо сложный вид. Модель будем проверять при упрощающих предположениях относительно распределения интервалов между прибытием автомобилей. Например, известно, что при экспоненциальном распределении эту модель можно исследовать теоретически. Тогда необходимо проделать это исследование, провести имитационный расчет при таком распределении интервалов и сравнить полученные в обоих случаях средние величины, интересующие нас в исследовании.  [c.280]

Нагрузка системы массового обслуживания 208  [c.302]

Системы массового обслуживания 200  [c.302]

В этом параграфе описано несколько моделей, в которых учитываются неопределенные факторы. Приведенные модели являются иллюстрацией общих принципов описания и исследования систем с неопределенными факторами (см. гл. 2). Рассматриваются системы массового обслуживания и хранения запасов, а также приводится пример принятия решения в условиях неопределенности.  [c.201]

Системы массового обслуживания встречаются практически везде, где есть или может возникнуть очередь. На Западе методы массового обслуживания даже получили название теория очередей . Поскольку обычно очередь — явление нежелательное, то для ее ликвидации естественно предложить увеличить мощность (пропускную способность) обслуживающих устройств. Однако поскольку заявки поступают нерегулярно, то с увеличением своей мощности оборудование все большую долю, времени будет простаивать, что также нежелательно. Таким образом, с экономической точки зрения задачи массового обслуживания сводятся к нахождению компромисса между двумя противоречивыми требованиями требованием ликвидировать очередь и требованием полной загрузки оборудования. Убытки от возникновения очереди связаны с потерей времени покупателями в магазинах, простоем автолюбителей на автозаправочных станциях, у мостов и перекрестков, кораблей в ожидании разгрузки и погрузки, затратами горючего самолетами в полете над аэропортом в ожидании посадки. Простой оборудования означает непродуктивное использование вложенных в него средств, которые в другом месте могли бы приносить пользу.  [c.202]

Каждый прибор может обслужить одновременно одну или несколько заявок. Например, лифт высотного здания обслуживает сразу несколько человек, а кассир — только одного. Во-вторых, системы массового обслуживания могут быть однофазными и многофазными В первом случае заявка обслуживается только одним прибором после чего покидает систему, например, покупатель билета в театре. Во втором случае заявка должна пройти некоторую последовательность приборов . Например, в сберкассе, прежде чем получить деньги, человек сначала должен быть обслужен контролером и только потом кассиром. В-третьих, каждый прибор обслуживает заявку в течение некоторого промежутка времени. Иногда продолжительность этого промежутка является заданной, иногда ее считают случайной величиной с заданным распределением. В некоторых моделях продолжительность обслуживания считают зависящей от длины очереди (кассир в магазине, например, в случае роста очереди начинает работать быстрее), а в некоторых случаях учитывают возможности выхода обслуживающего- прибора из строя.  [c.203]

Поэтому получаем Р(0) = 1 — р, Р(п) = рп(1 — р), п = 1, 2,. .. Величину р часто называют нагрузкой системы. Итак, интересующее нас распределение длины очереди получено. Найдем некоторые из характеристик системы массового обслуживания.  [c.208]

Системы массового обслуживания 201  [c.392]

Работа системы массового обслуживания.  [c.309]

Ни одна из вышеперечисленных методик, включая линейное и целочисленное программирование и др., не позволяет описывать динамические процессы. Динамика развития рынка привносит более высокую степень сложности, связанную с принятием последовательности взаимосвязанных решений в течение нескольких временных периодов. При принятии последовательных и взаимосвязанных решений управляющий должен учитывать не только необходимость оптимизации деятельности компании при принятии отдельных решений, но и координировать каждое отдельное решение с другими связанными с ним решениями. Динамические модели (которые могут использоваться для принятия решений в условиях как определенности, так и неопределенности) включают модели управления складскими запасами, методы управления проектом, системы массового обслуживания. Каждая из этих моделей разработана специально для решения задач, описываемых их областью применения.  [c.257]

Рассмотрим модель МПС с общей памятью. Процесс обслуживания заявок в режиме разделения нагрузки можно рассматривать как процесс функционирования одной многоканальной системы массового обслуживания (рис. 3.23) с интенсивностью X входящего потока, общей очередью О, заявки из которой выбираются в порядке поступления их в систему, и средней длительностью обслуживания заявки Каждым 108  [c.108]

Суммарная загрузка R в отношении W-канальной системы массового обслуживания определяет среднее число каналов, которые заняты обслуживанием заявок. Для стационарного режима R[c.111]

Задача определения оптимальности может считаться решенной, если будут найдены количественные характеристики работы обслуживающей системы (резервуарной емкости) и если удается выразить их через величины, характеризующие входящий и выходящий потоки заявок на обслуживание и саму обслуживающую систему. Различные процессы в системах массового обслуживания содержат много общего, поэтому достаточно исследовать типичные случаи и разработать методы решения, которые были бы приемлемы для выполнения конкретных задач.  [c.104]

Изложенные обстоятельства позволяют для моделирования науки в регионе использовать математический аппарат теории очередей. Согласно этой теории, науку можно считать системой массового обслуживания (СМО). СМО, как известно, называется любая система, предназначенная для обслуживания каких-либо заявок, поступающих в нее в случайные моменты времени.  [c.172]

Газпром представим в виде системы массового обслуживания (СМО).  [c.61]

Системы массового обслуживания могут быть одноканальными или  [c.61]

Поток железнодорожных цистерн, прибывающих на пункт перевалки под налив, как показано в [1], можно считать простейшим. Т. е. он обладает всеми свойствами этого потока стационарностью, ординарностью и отсутствием последействия. Операция налива нефтепродуктов в вагоны-цистерны является системой массового обслуживания с ожиданием, т. к. вероятность того, что цистерна уйдет неналитой, из-за того, что все наливщики будут заняты, равна нулю.  [c.70]

В данном примере мы рассмотрели самый простой случай пуассоновский входной поток, экспоненциальное время обслуживания, одна обслуживающая установка. На самом деле, в реальности, и распределения бывают значительно сложнее, и АЗС включают в себя большее число бензоколонок. Для того чтобы упорядочить классификацию систем массового обслуживания, американский математик Д. Кен-далл предложил удобную систему обозначений, широко распространившуюся к настоящему времени. Тип системы массового обслуживания Кендалл обозначил с помощью трех символов, первый из которых описывает тип входного потока, второй — тип вероятностного описания системы обслуживания, а третий — количество обслуживающих приборов. Символом М он обозначал пуассоновское распределение входного потока (с экспоненциальным распределением интервалов между заявками), этот же символ применялся и для экспоненциального распределения продолжительности обслуживания. Таким образом, описанная и изученная в этом параграфе система массового обслуживания имеет обозначение М/М/1. Система M/G/3, например, расшифровывается как система с пуассоновским входным потоком, общей (по-английски — general) функцией распределения времени обслуживания и тремя обслуживающими устройствами. Встречаются и другие обозначения D —детерминированное распределение интервалов между поступлением заявок или длительностей обслуживания, Е — распределение Эрланга порядка п и т. д.  [c.211]

Блоки обслуживания в соответствии с тем, что системы массового обслуживания встречаются в различных, непохожих ситуациях, различаются между собой по многим показателям. Во-первых, блок обслуживания может состоять из одного или нескольких приборов . Под прибором имеется в виду устройство или человек, обслуживающий заявки. Например, билеты в кинотеатре могут продаваться в одной или нескольких кассах. В первом случае блок обслуживания называют одноканалъным, во втором — многоканальным. Примеры однокапальных блоков автозаправочная станция, па которой каждый вид бензина продается лишь одной бензоколонкой, речной вокзал небольшого городка с одним причалом, газетный киоск с одним продавцом, аэродром с одной посадочной полосой, узкий мост па шоссе и т. д. Многоканальные системы обслуживания встречаются еще чаще турникеты в метро, которые всегда встречаются в виде батарей из нескольких устройств, морской порт с большим числом причалов, аэродром с несколькими работающими одновременно посадочными полосами, парикмахерская с несколькими мастерами п т. д.  [c.203]

Для описния другой важнейшей составной части любой системы массового обслуживания — входного потока заявок — обыч-  [c.203]

Итак, в жизни встречается огромное число систем, которые могут быть математически описаны как системы массового обслуживания одного из типов. После того как модель построена, возникает вопрос о методах ее псследования. При исследовании моделей массового обслуживания обычно используется следующая методика предполагается, что обслуживающая система имеет конечное число вариантов, после чего для каждого варианта исследуют средние характеристики системы например, средняя продолжительность нахождения заявки в очереди, средняя доля вре-  [c.204]

economy-ru.info