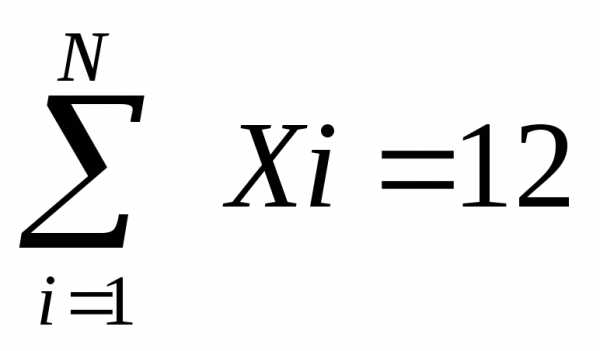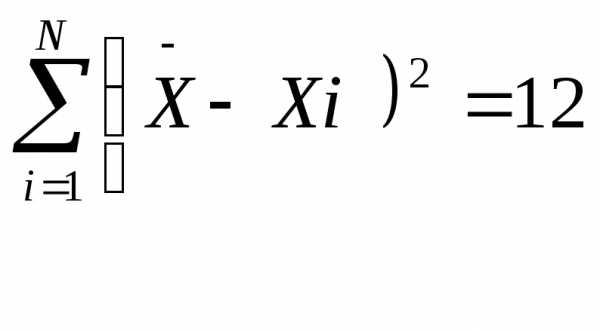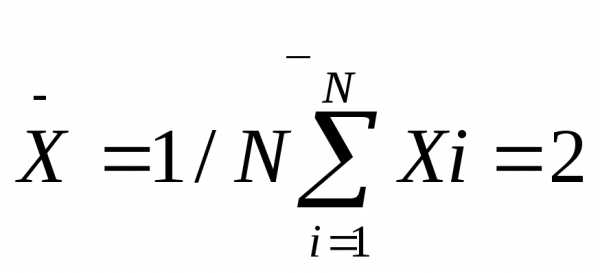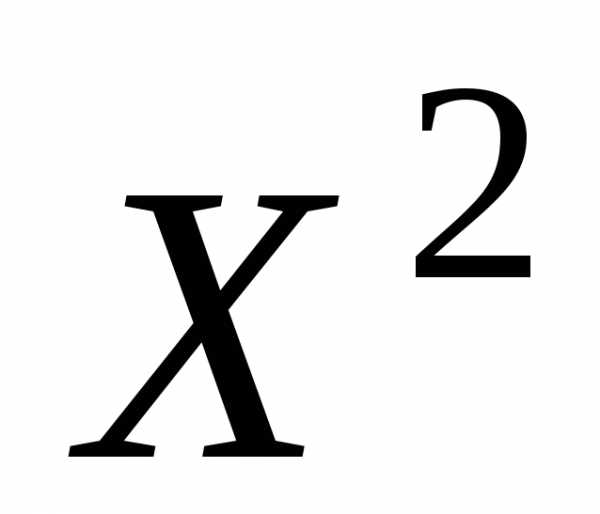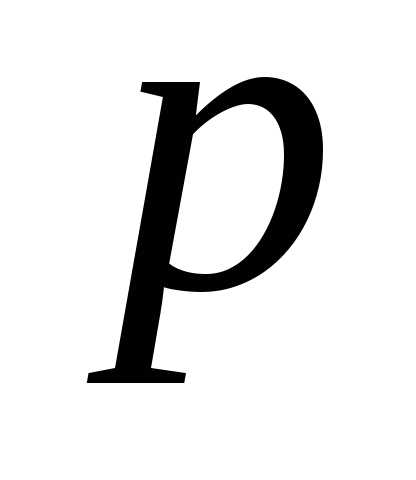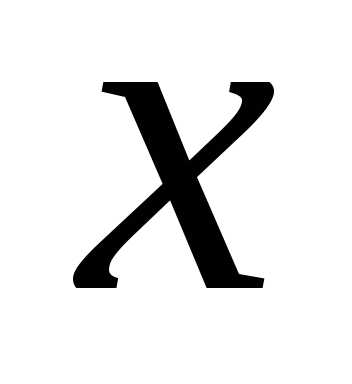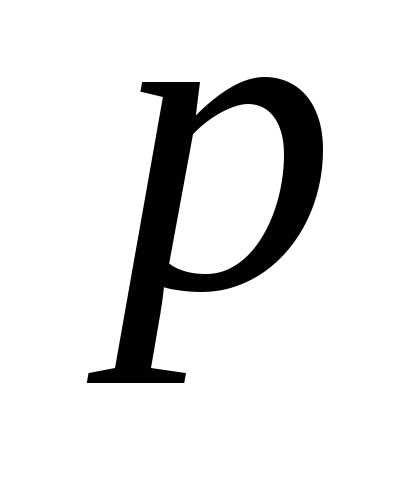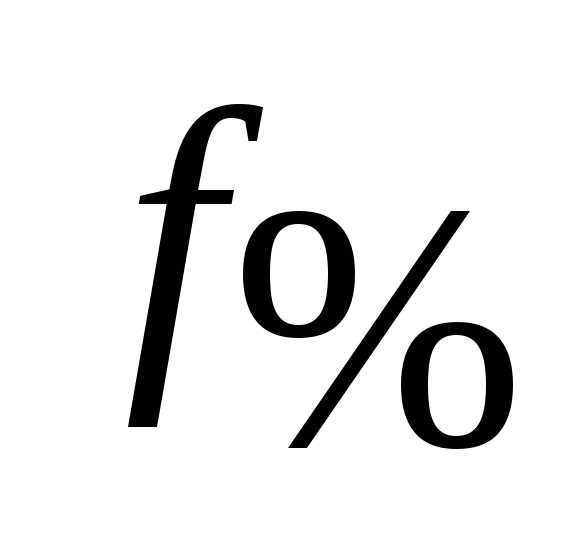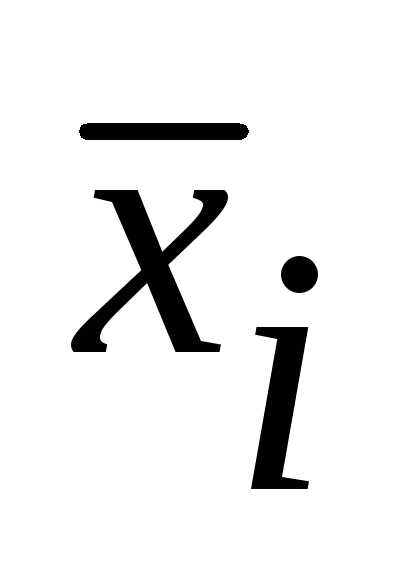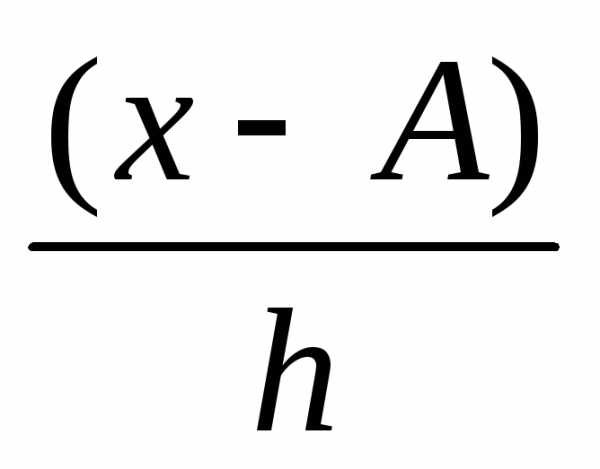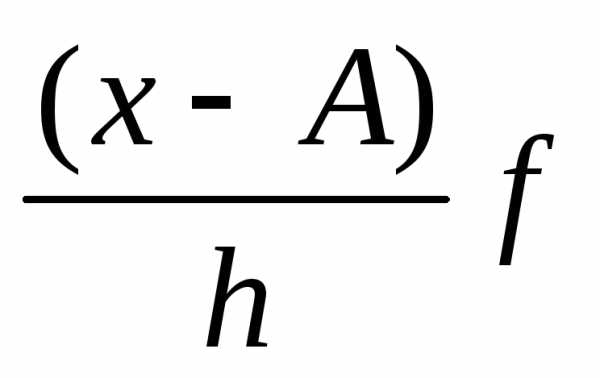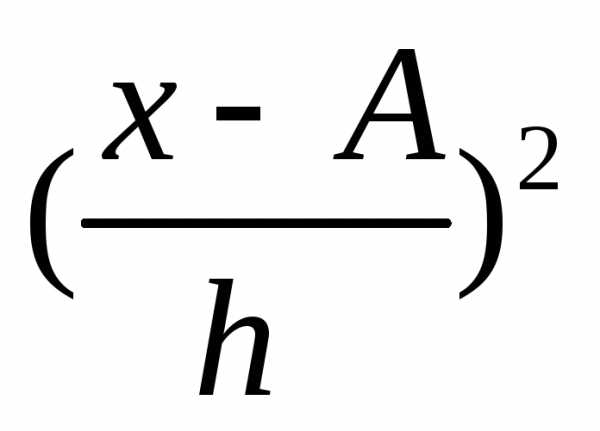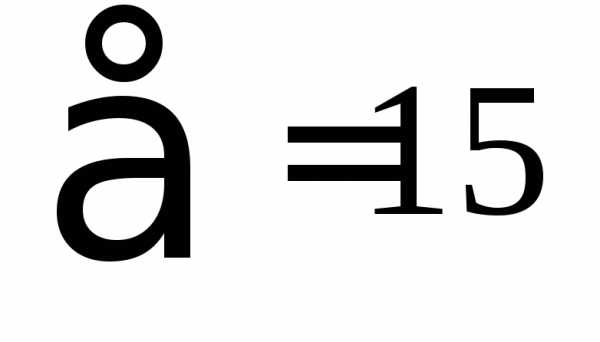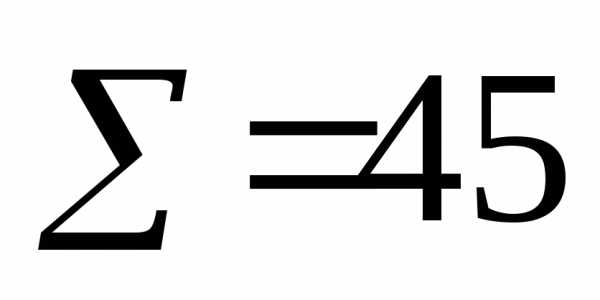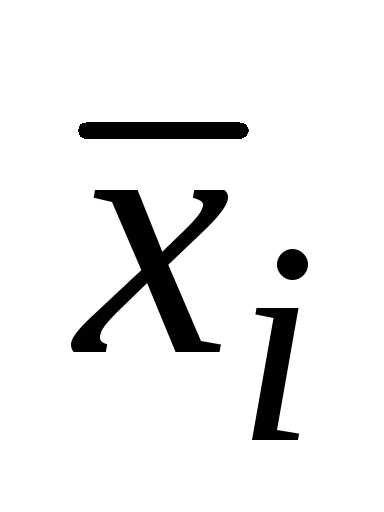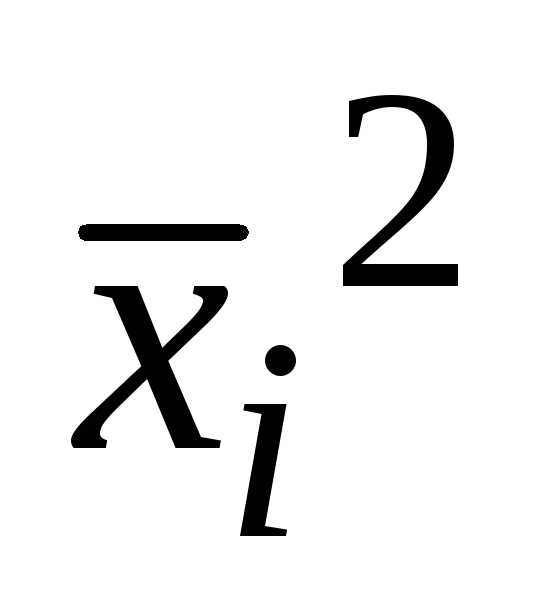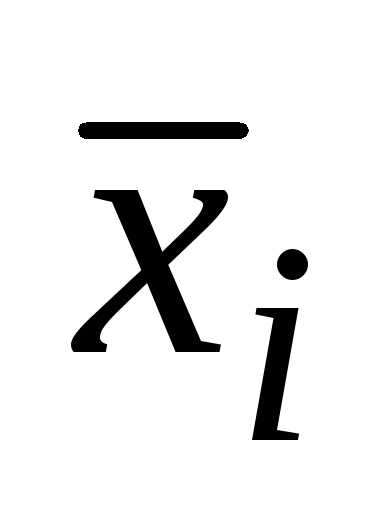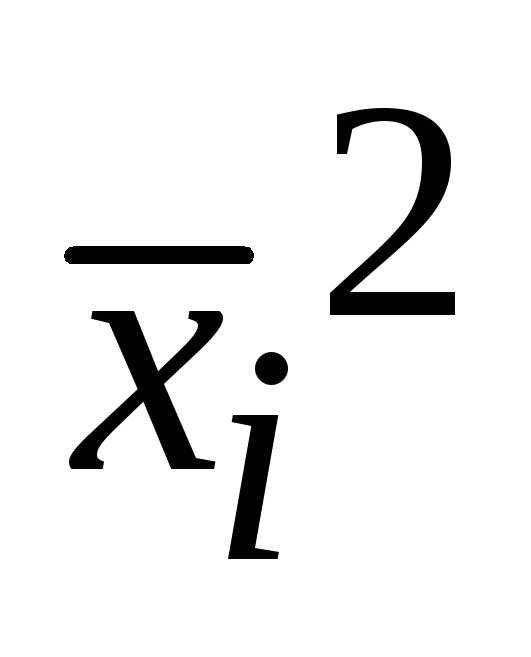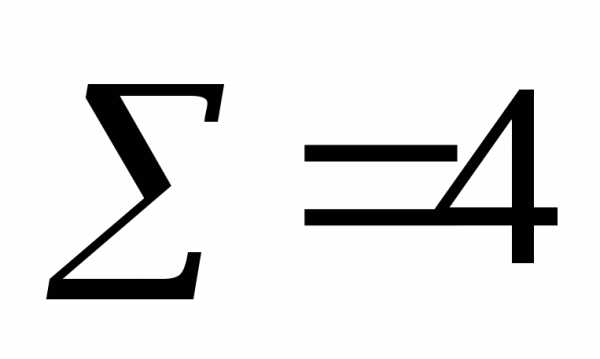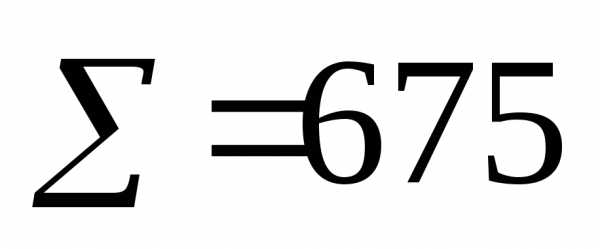Дисперсия, формула дисперсии, виды дисперсии, простая дисперсия, взвешенная дисперсия
Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда): где n — частота (повторяемость фактора Х)Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
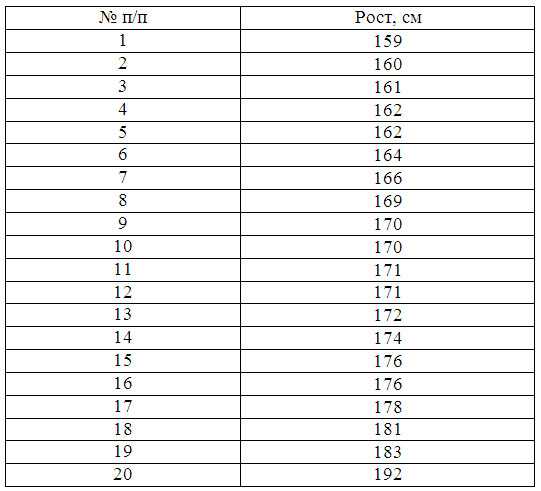Построим интервальную группировку. Определим размах интервала по формуле:
где X max– максимальное значение группировочного признака;n – количество интервалов: Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
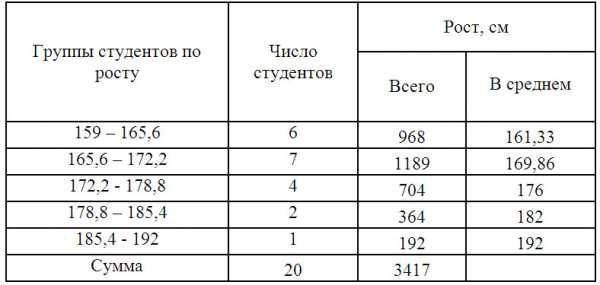Для дальнейших расчетов построим вспомогательную таблицу:
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
Определим дисперсию по формуле:Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 4. Нахождение дисперсии в дискретном ряду
Формулу дисперсии можно преобразовать так: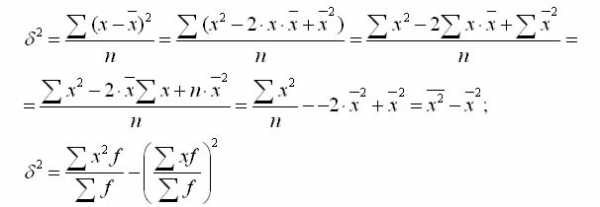
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала;
А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя;
ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.
Свойства дисперсии
1. Если все значения признака уменьшить (увеличить) на одну и ту же постоянную величину, то дисперсия от этого не изменится.
2. Если все значения признака уменьшить (увеличить) в одно и то же число раз n, то дисперсия соответственно уменьшится (увеличить) в n^2 раз.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.
univer-nn.ru
Задача №22. Виды дисперсии и их расчёт
Имеются данные о распределении семей сотрудников финансовой корпорации по количеству детей:
| Число детей | Число семей сотрудников по подразделениям | ||
|---|---|---|---|
| первое | второе | третье | |
| 0 | 4 | 7 | 5 |
| 1 | 6 | 10 | 13 |
| 2 | 3 | 3 | 3 |
| 3 | 2 | 1 | — |
Вычислить:
а) внутригрупповые дисперсии;
б) среднюю из внутригрупповых дисперсий;
в) межгрупповую дисперсию;
г) общую дисперсию;
Проверьте правильность произведения расчётов с помощью правила сложения дисперсий.
Решение:
Совокупность семей сотрудников финансовой корпорации разбита на три группы по количеству детей.
а) Групповая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы от средней арифметической этой группы. Внутригрупповые дисперсии вычисляются по формуле:
Нахождению внутригрупповой дисперсии предшествует расчёт средней арифметической по каждой группе.
Рассчитаем внутригрупповые дисперсии:
б) Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых:
в) Межгрупповая дисперсия равна среднему квадрату отклонений групповых средних от общей средней:
Для её расчета необходимо вычислить общую среднюю:
Определим межгрупповую дисперсию:
Вычислим общую дисперсию обычным способом:
Проверим полученный результат, исчислив общую дисперсию по правилу сложения дисперсий: общая дисперсия равна сумме средней из внутригрупповых дисперсий и межгрупповой дисперсии:
ecson.ru
Пример вычисления дисперсии
№ п/п | Значение показателя | Отклонение от среднего | Квадрат отклонения |
1 2 3 4 5 6 | 1 3 3 0 4 1 | 2 – 1 = +1 2 – 3 = –1 2 – 3 = – 1 2 – 0 = +2 2 – 4 = –2 2 – 1 = +1 | 1 1 1 4 4 1 |
|
| ||
| |||
Среднее квадратичное отклонение подтверждает типичность и показательность средней арифметической, отражает меру колебания численных значений признаков, из которых выводится средняя величина. Оно равно корню квадратному из дисперсии и определяется по формуле:
;
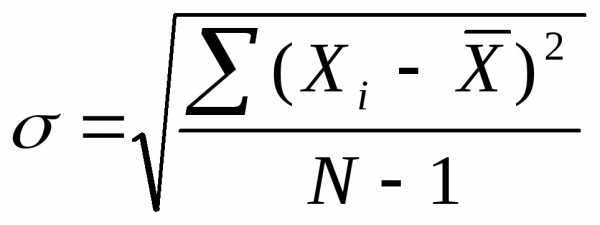(2)
где: s – средняя квадратическая. При малом числе наблюдения (действий) – менее 100 – в значении формулы следует ставить не «N», а «N – 1».
Средняя арифметическая и средняя квадратическая являются основными характеристиками полученных результатов в ходе исследования. Они позволяют обобщить данные, сравнить их, установить преимущества одной психолого-педагогической системы (программы) над другой.
Среднее квадратическое (стандартное) отклонение широко применяется как мера разброса для различных характеристик.
Оценивая результаты исследования важно определить рассеивание случайной величины около среднего значения. Это рассеивание описывается с помощью закона Гауса (закона нормального распределения вероятности случайной величины). Суть закона заключается в том, что при измерении некоторого признака в данной совокупности элементов всегда имеют место отклонения в обе стороны от нормы вследствие множества неконтролируемых причин, при этом, чем больше отклонения, тем реже они встречаются.
При дальнейшей обработке данных могут быть выявлены: коэффициент вариации (устойчивости) исследуемого явления, представляющий собой процентное отношение среднеквадратического отклонения к средней арифметической; мера косости, показывающая, в какую сторону направлено преимущественное число отклонений; мера крутости, которая показывает степень скопления значений случайной величины около среднего и др. Все эти статистические данные помогают более полно выявить признаки изучаемых явлений.
Меры связи между переменными. Связи (зависимости) между двумя и более переменными в статистике называют корреляцией. Она оценивается с помощью значения коэффициента корреляции, который является мерой степени и величины этой связи.
Коэффициентов корреляции много. Рассмотрим лишь часть из них, которые учитывают наличие линейной связи между переменными. Их выбор зависит от шкал измерения переменных, зависимость между которыми необходимо оценить. Наиболее часто в психологии и педагогике применяются коэффициенты Пирсона и Спирмена.
Рассмотрим вычисление значений коэффициентов корреляции на конкретных примерах.
Пример 1. Пусть две сравниваемые переменные X (семейное положение) и Y (исключение из университета) измеряются в дихотомической шкале (частный случай шкалы наименований). Для определения связи используем коэффициент Пирсона.
В тех случаях, когда нет необходимости подсчитывать частоту появления различных значений переменных X и Y, удобно проводить вычисления коэффициента корреляции с помощью таблицы сопряженности (см. табл. 6.2, 6.3, 6.4)1, показывающей количество совместных появлений пар значений по двум переменным (признакам). А – количество случаев, когда переменная X имеет значение равное нулю, и, одновременно переменная Y имеет значение равное единице; В – количество случаев, когда переменные X и Y имеют одновременно значения, равные единице; С – количество случаев, когда переменные X и Y имеют одновременно значения равные нулю; D – количество случаев, когда переменная X имеет значение, равное единице, и, одновременно, переменная Y имеет значение, равное нулю.
Таблица 6.2
studfiles.net
Вычисление дисперсии
Теорема. Дисперсия
равна разности между математическим
ожиданием квадрата случайной величины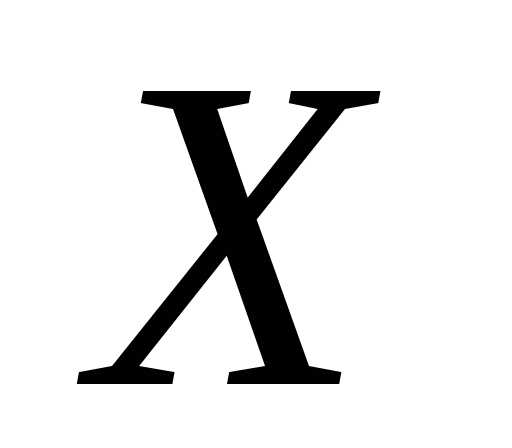 
и квадратом ее математического ожидания.
Доказательство.
С учетом того, что математическое
ожидание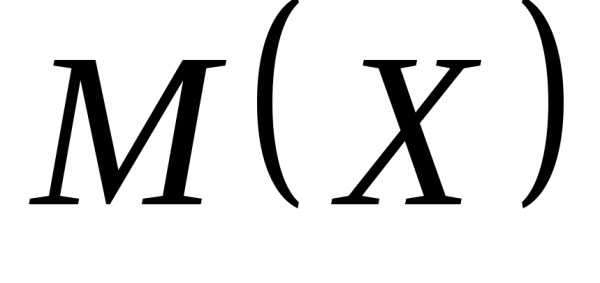 
и квадрат математического ожидания
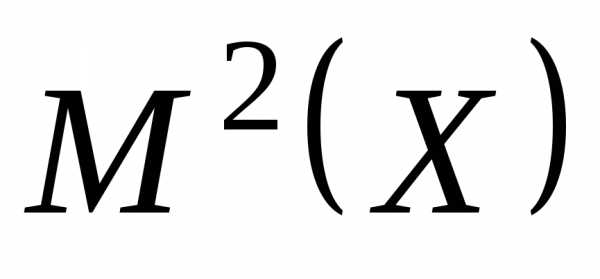– величины постоянные, можно записать:
Применим эту формулу для рассмотренного выше примера:
0
1
2
0
1
4
0,0625
0,375
0,5625
Свойства дисперсии
Дисперсия постоянной величины равна нулю.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия
числа появления события 
в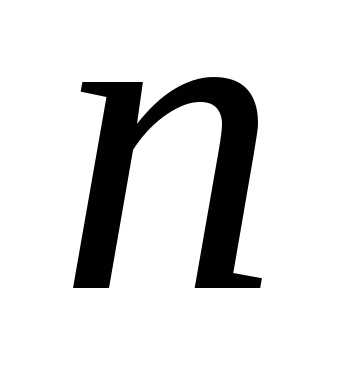 
независимых испытаний, в каждом из
которых вероятность 
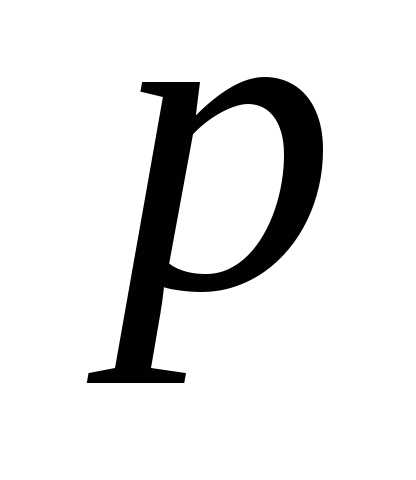появления события постоянна, равна
произведению числа испытаний на
вероятности появления и не появления
события в каждом испытании.
Среднее квадратическое отклонение
Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.
Пример
18. Завод
выпускает 96% изделий первого сорта и 4%
изделий второго сорта. Наугад выбирают
1000 изделий. Пусть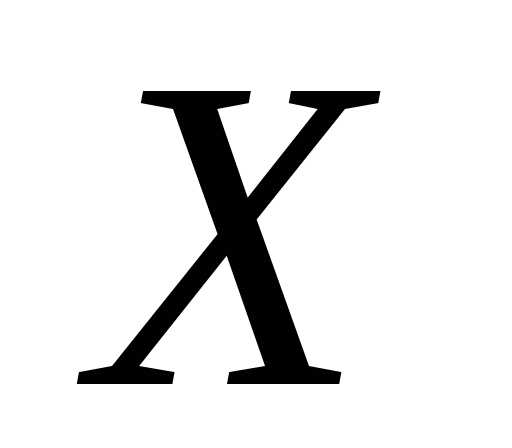 
– число изделий первого сорта в данной
выборке. Найти закон распределения,
математическое ожидание и дисперсию
случайной величины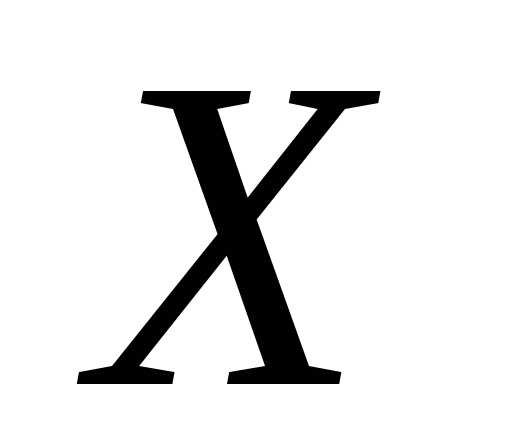
.
Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.
Таким образом, закон распределения может считаться биноминальным.
Пример
19. Найти
дисперсию дискретной случайной величины 
– числа появлений события
в двух независимых испытаниях, если
вероятности появления этого события в
каждом испытании равны и известно, что.
Так
как случайная величина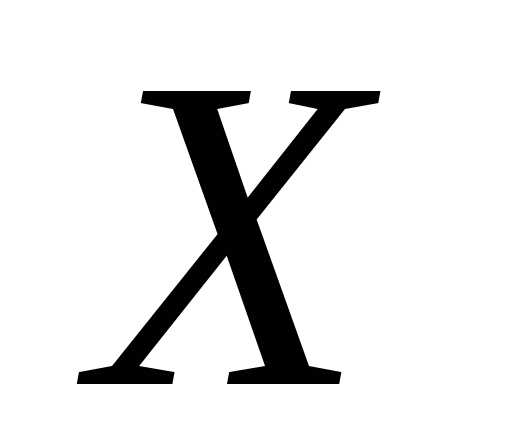 
распределена по биноминальному закону,
то
Функция распределения
Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений.
Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.
Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?
Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.
Пусть х – действительное число. Вероятность
события, состоящего в том, что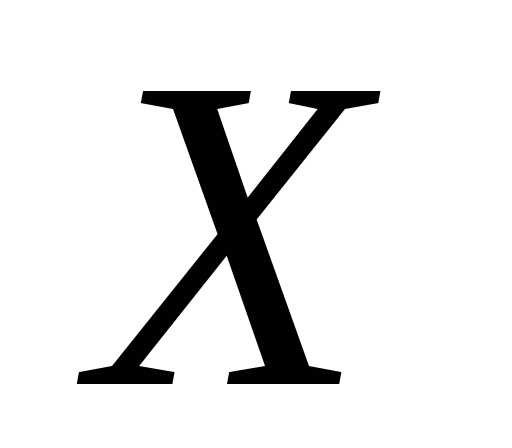 
примет значение, меньшеех,
то есть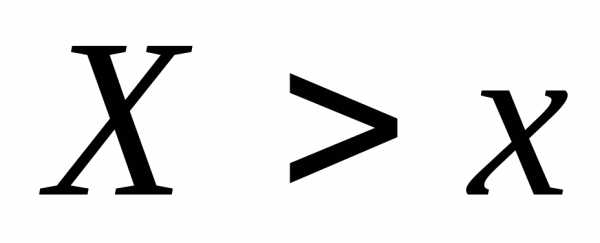 
,
обозначим через
.
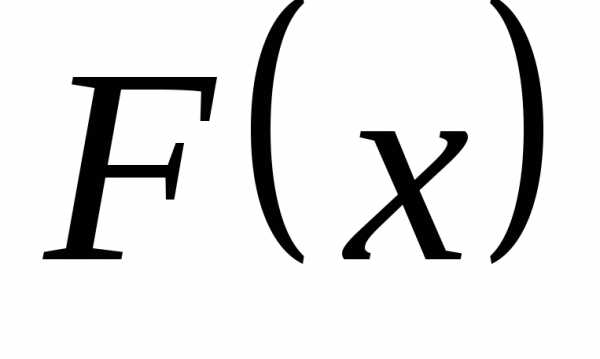Определение. Функцией
распределения называют функцию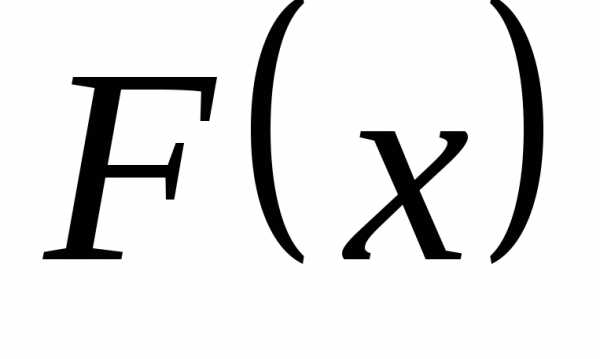 
,
определяющую вероятность того, что
случайная величина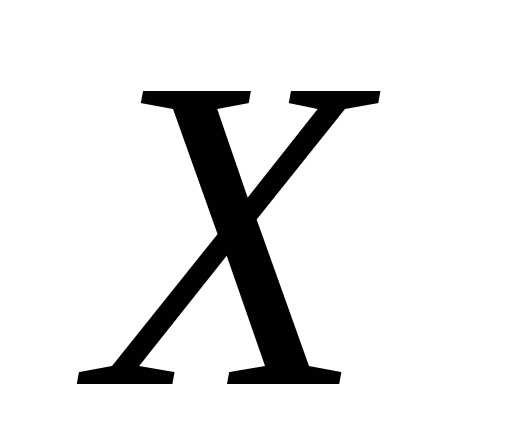
в результате испытания примет значение,
меньшеех.
Функцию распределения также называют интегральной функцией.
Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.
Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция
распределения дискретной случайной
величины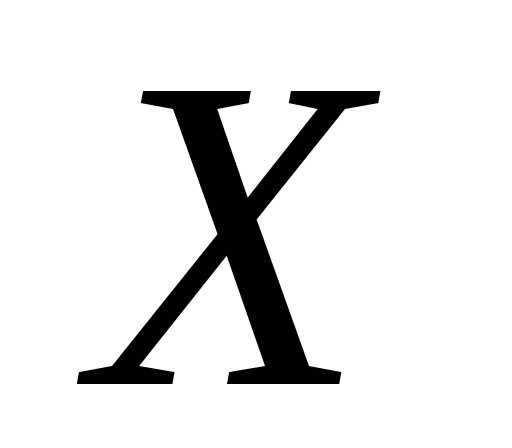 
разрывна и возрастает скачками при
переходе через каждое значениехi.
Пример 20. Задана интегральная функция распределения:
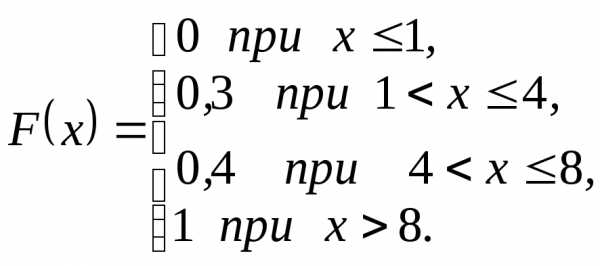
П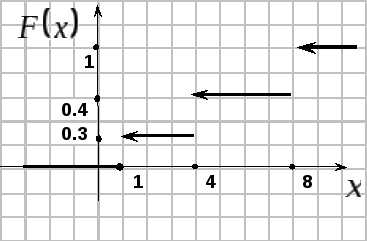
остроить
ее график.
| 1 | 4 | 8 |
| 0,3 | 0,1 | 0,6 |
studfiles.net
Свойства плотности вероятности[править]
.
Обратно, если — неотрицательная п.в. функция, такая что , то существует абсолютно непрерывная вероятностная мера на такая, что является её плотностью.
,
где любая борелевская функция, интегрируемая относительно вероятностной меры .
Дисперсия, виды и свойства дисперсии Понятие дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий:
1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле:
2. Взвешенная дисперсия (для вариационного ряда):
где n — частота (повторяемость фактора Х)
Пример нахождения дисперсии
На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение
Пример 1. Определение групповой, средней из групповой, межгрупповой и общей дисперсии
Пример 2. Нахождение дисперсии и коэффициента вариации в группировочной таблице
Пример 3. Нахождение дисперсии в дискретном ряду
Пример 4. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию
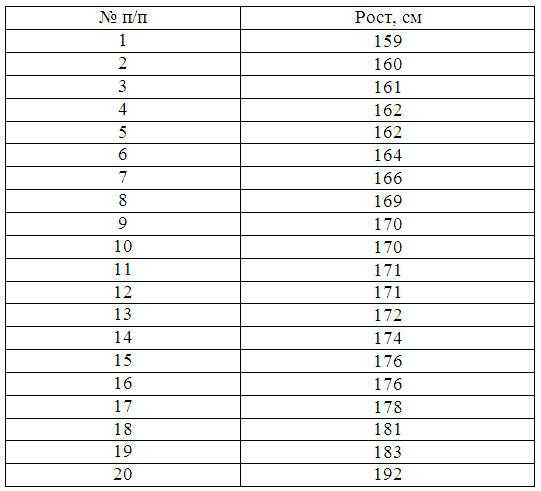
Построим интервальную группировку. Определим размах интервала по формуле:
где X max– максимальное значение группировочного признака; X min–минимальное значение группировочного признака; n – количество интервалов:
Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
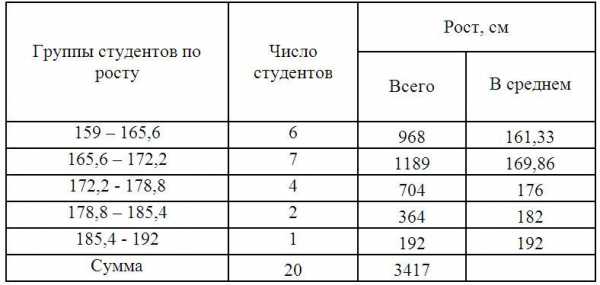
Для дальнейших расчетов построим вспомогательную таблицу:
X’i– середина интервала. (например середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
Определим дисперсию по формуле:
Формулу можно преобразовать так:
Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок:
где i — величина интервала; А — условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой; m1 — квадрат момента первого порядка; m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:
Виды дисперсии
Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия.
Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле:
где хi — групповая средняя; ni — число единиц в группе.
Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
studfiles.net
5.2. Свойства и методы расчета дисперсии
Свойства дисперсии:
Величина дисперсии не изменится, если из всех значений вариант отнять какое–либо число А.
Если все значения вариант увеличить или уменьшить в А раз, то σ2 увеличится (уменьшится) в А2 раз, а σ— в А раз.
.
Если все частоты увеличить (уменьшить) в А раз, то σ2 и σ не изменятся.
Дисперсия равна разности среднего квадрата и квадрата средней величины.
,
где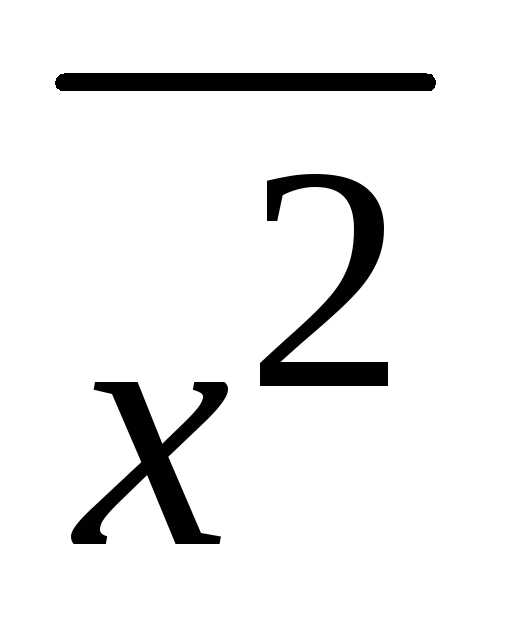 
– средний квадрат индивидуальных
значений признака;
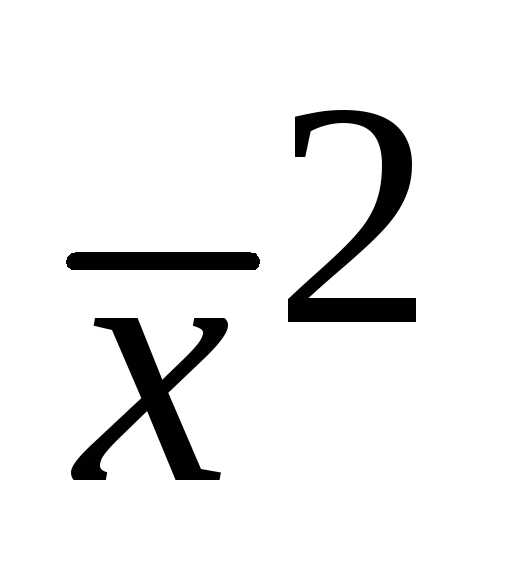–квадрат
средней величины.
Расчет дисперсии методом моментов
, где
,
.
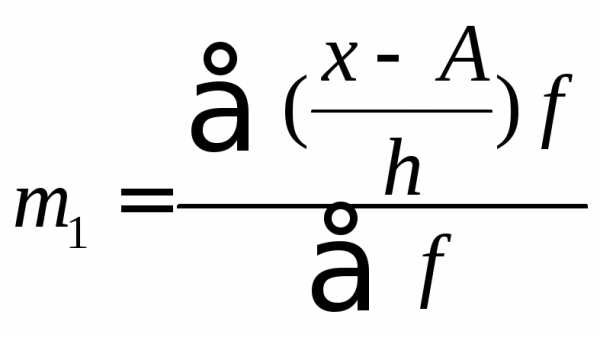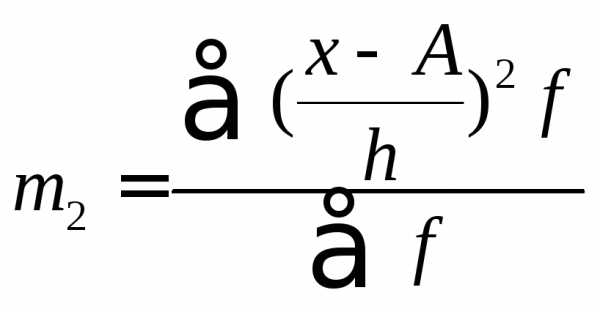Пример 5.2
Оценить
надежность средней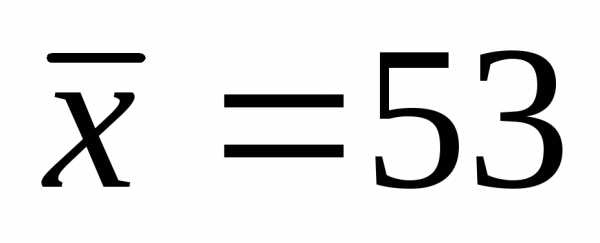 
кг
для группировки
населения по мясопотреблению (табл.11).
Таблица 11
Объем потребления мяса | | | | | | |
20–40 кг | 10 | 30 | –1 | –10 | 1 | 10 |
40–60 кг | 70 | 50 | 0 | 0 | 0 | 0 |
60–80 кг | 15 | 70 | 1 | 15 | 1 | 15 |
80–100 кг | 5 | 90 | 2 | 10 | 4 | 20 |
Итого: | | | |
Решение: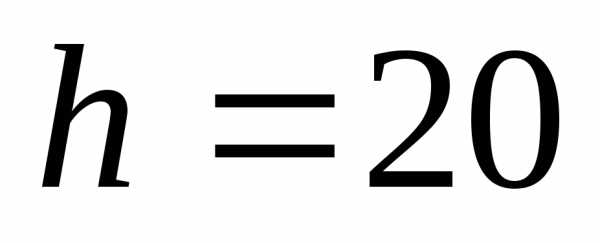 
, 
, ,
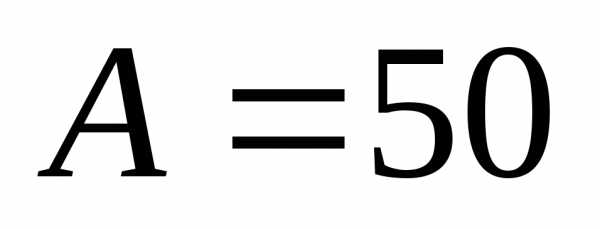
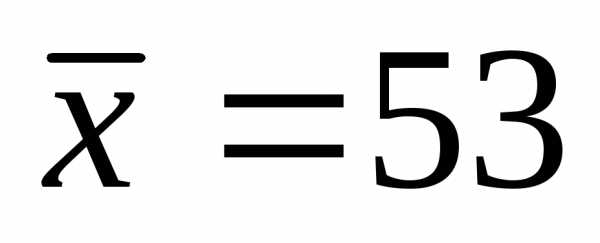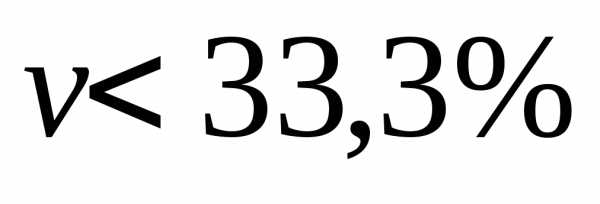
Вывод: средняя надежна и типична для данной группировки.
5.3. Дисперсия альтернативного признака
Единицы совокупности могут либо обладать альтернативным признаком, либо нет.
Приняты обозначения:
1 – наличие признака, 0 – отсутствие признака.
p
– доля единиц, обладающих данным
признаком, q – доля единиц, не обладающих
данным признаком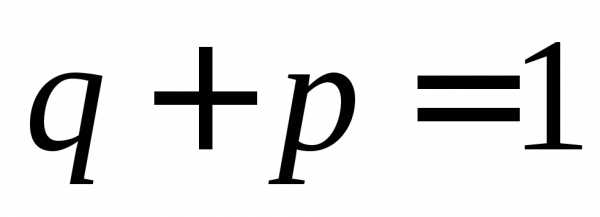 
(или
100%)
.
Для альтернативного признака средняя величина равна доле единиц, обладающих данным признаком.
Дисперсию альтернативного признака рассчитывают следующим образом:
.
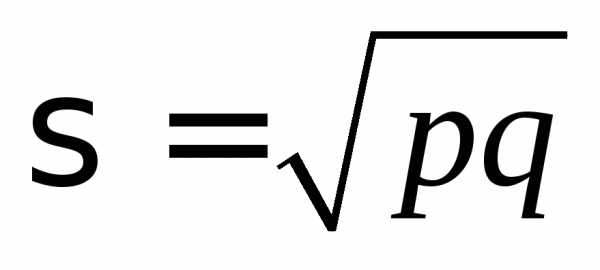5.4. Правило сложения дисперсий
Если совокупность разбить на группы, то средние величины и дисперсию можно рассчитать как для всей совокупности, так и для каждой группы.
Различают среднюю из групповых, межгрупповую и общую дисперсии. Общая дисперсия отражает влияние всех возможных факторов. Внутригрупповая дисперсия отражает влияние всех факторов, кроме группировочного признака. Средняя из групповых аналогична внутригрупповым дисперсиям. Межгрупповая дисперсия характеризует влияние только группировочного признака.
В соответствии с правилом сложения дисперсии: общая дисперсия равна сумме средней из групповых и межгрупповой дисперсии.
,
где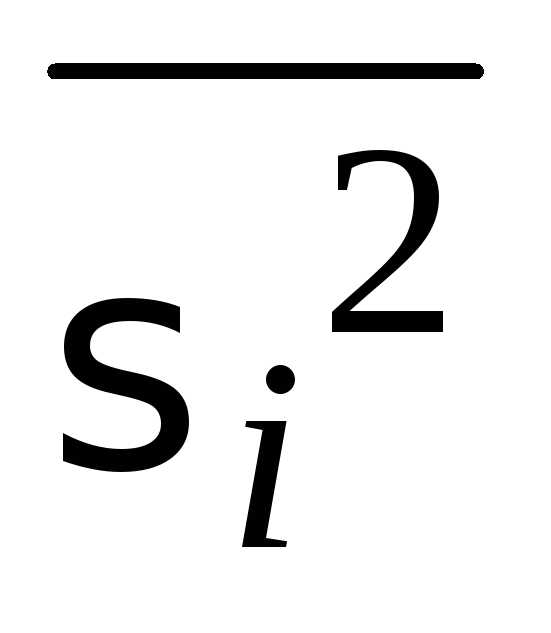 
– средняя из групповых дисперсий,
–межгрупповая
дисперсия
Средняя из групповых дисперсий определяется по формуле:
.
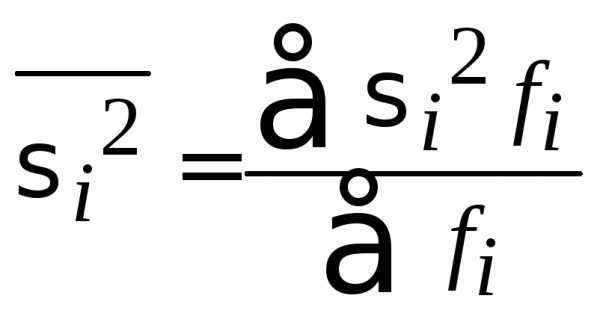Межгрупповая дисперсия определяется по формуле:
.
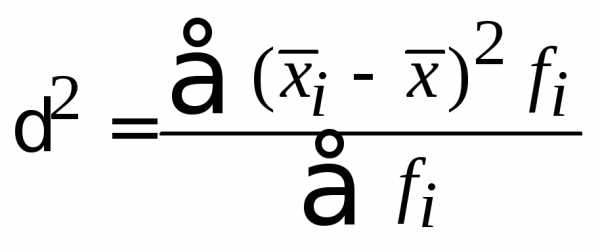Пример 5.3
Проверим правило сложения дисперсий на примере группировки рабочих по уровню квалификации (табл.12).
Решение
Рассчитаем групповые средние:
,
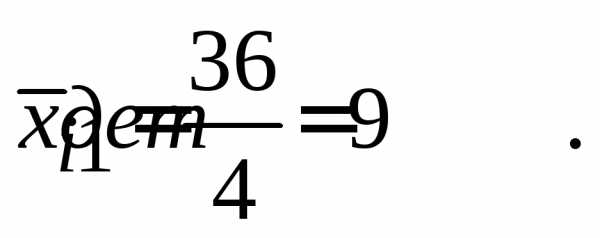Таблица 12
Рабочие 5–ого разряда | Рабочие 6–ого разряда | ||||
№ п\п | Количество деталей | | № п\п | Количество
деталей | |
1 | 8 | 64 | 1 | 9 | 81 |
2 | 8 | 64 | 2 | 9 | 81 |
3 | 9 | 81 | 3 | 10 | 100 |
4 | 11 | 121 | 4 | 10 | 100 |
— | — | — | 5 | 12 | 144 |
— | — | — | 6 | 13 | 169 |
| | | | | |
Определим групповые дисперсии методом разности:
Рассчитаем межгрупповую дисперсию:
Общая дисперсия равна
, что подтверждает правило сложения дисперсий.
Для
оценки влияния группировочного признака
(уровень квалификации) используют
показатели, построенные на соотношении
межгрупповой и общей дисперсии: эмпирический
коэффициент детерминации (
)
и эмпирическое корреляционное отношение
(
).
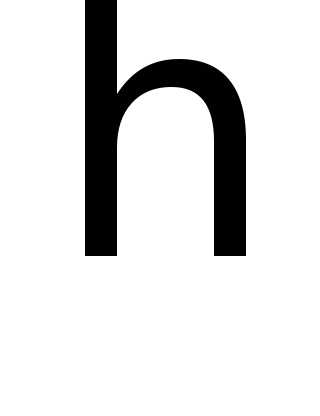Эмпирический
коэффициент детерминации (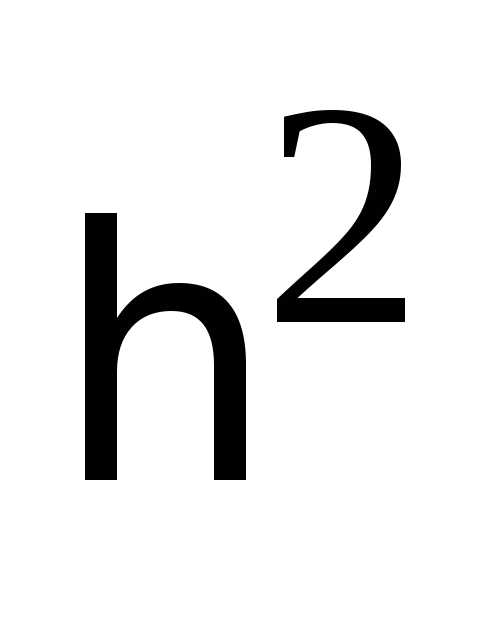
)рассчитывается
по формуле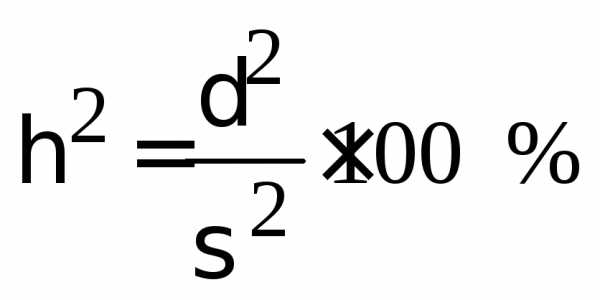
и показывает, какой процент общей
вариации изучаемого признака определяется
вариацией группировочного признака.
Для рассматриваемого примера , т.е. вариация выработки рабочих на 21,7% определяется вариацией уровня их квалификации.
Эмпирическое
корреляционное отношение () характеризует тесноту связи между
признаками и рассчитывается по формуле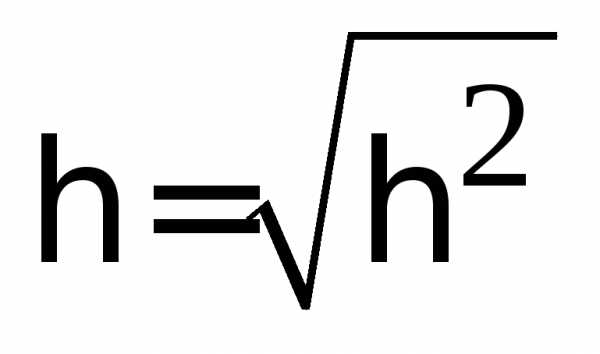 
.
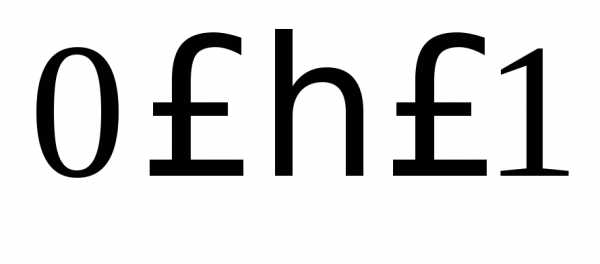Связь отсутствует, если 
,
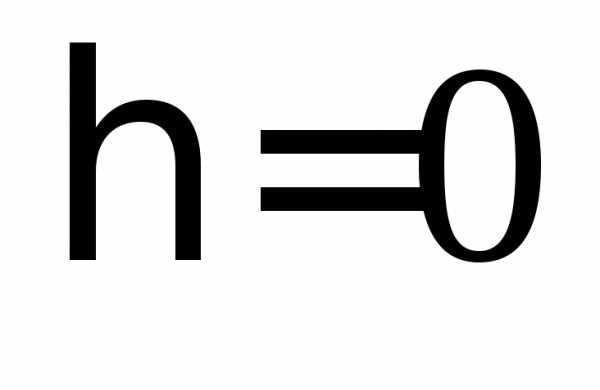связь функциональная, если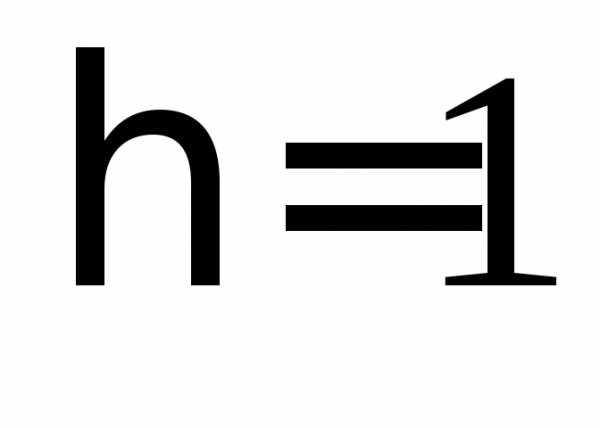
Сила связи определяется в соответствии со шкалой Чеддока, которая представлена в таблице 12.
Таблица 12
Шкала Чеддока для определения силы связи
η | Сила связи |
0,1-0,3 | слабая |
0,3-0,5 | умеренная |
0,5-0,7 | заметная |
0,7-0,9 | высокая |
0,9-0,99 | очень высокая |
В
рассматриваемом примере связь выработки
рабочих с уровнем квалификации умеренная,
так как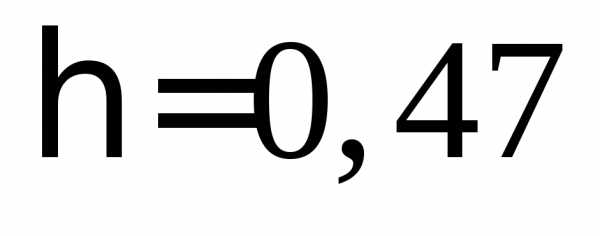 
.
studfiles.net
Решение задач по статистике: Правило сложения дисперсий
Решение задач по статистике: Правило сложения дисперсий
Количественный признак
Задача по статистике № 1
Определим групповые дисперсии, среднюю из групповых дисперсий,
межгрупповую дисперсию, общую дисперсию по данным табл.
Производительность труда двух бригад рабочих-токарей
Решение. Для расчета групповых дисперсий вычислим средние по каждой группе:
шт.; шт.
|
1-я бригада |
2-я бригада |
||||||
|
№ п/п |
Изготовлено деталей за час, шт. |
xi— |
(xi-)2 |
№ п/п |
Изготовлено деталей за час, шт. |
xi— |
(xi-)2 |
|
1 |
13 |
-2 |
4 |
7 |
18 |
-3 |
9 |
|
2 |
14 |
-1 |
1 |
8 |
19 |
-2 |
4 |
|
3 |
15 |
0 |
0 |
9 |
22 |
1 |
1 |
|
4 |
17 |
2 |
4 |
10 |
20 |
-1 |
1 |
|
5 |
16 |
1 |
1 |
11 |
24 |
3 |
9 |
|
6 |
15 |
0 |
0 |
12 |
23 |
2 |
4 |
|
90 |
10 |
126 |
28 |
||||
Промежуточные расчеты дисперсий по группам представлены в табл. 7.4. Подставив полученные значения в формулу, получим:
Средняя из групповых дисперсий
Затем рассчитаем межгрупповую дисперсию. Для этого предварительно определим общую среднюю как среднюю взвешенную из групповых средних:
шт.
Теперь определим межгрупповую дисперсию:
Таким образом, общая дисперсия по правилу сложения дисперсий
Проверим полученный результат, исчислив общую дисперсию обычным способом:
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результативным признаками. Он называется эмпирическим корреляционным отношением, обозначается («эта») и
рассчитывается по формуле . Для нашего примера эмпирическое корреляционное отношение — тесная связь на основе расчета между разбивкой на бригады и производительностью труда.
Измеряет какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Отношение факторной дисперсии к общей дисперсии результативного признака
Альтернативный признак
Задача № 2
Определить дисперсию альтернативного признака
|
Хозяйство |
Удельный вес всех дойных коров, pi= |
Всего коров в хозяйстве |
|
1 |
90 |
50 |
|
2 |
95 |
20 |
|
3 |
80 |
30 |
Решение
= p – среднее значение равно доле.
– общая средняя доля по хозяйствам
Межгрупповая дисперсия
–
обусловлена влиянием факторного признака – разбиения дойных коров по хозяйствам.
— внутригрупповая дисперсия по 1-му хозяйству
0.1=100%-90%
— внутригрупповая дисперсия по 2-му хозяйству
100%-95%
— внутригрупповая дисперсия по 3-му хозяйству
100%-80%
— дисперсия обусловленная влиянием результативного признака – удельный вес дойных коров
— общая дисперсия
Коэффициент детерминации:
Т.о. общая вариация на 97% обусловлена влиянием прочих неучтенных факторов, а разбивка на группы никак не зависит от количества дойных коров.
www.goodstudents.ru