Расчет медианы – Медиана в статистике — statanaliz.info

alexxlab / / Школьная жизнь

Вычисление медианы группы чисел — Служба поддержки Office

Снимки экрана в этой статье получены в Excel 2016. Если вы используете другую версию, интерфейс может немного отличаться, но функции будут такими же.

Пример

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

  1. Откройте пустую книгу или лист.

  2. Копирование примера

    Выберите пример ниже.

    Примечание: Не выделяйте заголовки строк или столбцов.

    A

    10

    7

    9

    отображал

    0

    4

    Выделение примера в справке

  3. Нажмите клавиши CTRL+C.

  4. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

  5. Щелкните внутри пустой ячейки.

  6. Откройте вкладку Формула , а затем нажмите кнопку Автосумма _гт_ Дополнительные функции.

  7. Введите медиану в поле Поиск функции: , а затем нажмите кнопку ОК.

  8. Введите a1: A7 в поле Number1

    .

    В этом примере ответ, отображаемый в ячейке, должен быть 8.

Совет: Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите клавиши CTRL+` (знак ударения) или на вкладке Формулы в группе Зависимости формул нажмите кнопку Показывать формулы.

Пример

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

  1. Откройте пустую книгу или лист.

  2. Копирование примера

    Выберите пример ниже.

    Примечание: Не выделяйте заголовки строк или столбцов.

    A

    10

    7

    9

    отображал

    0

    4

    Выделение примера в справке

  3. Нажмите клавиши CTRL+C.

  4. Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.

  5. Щелкните внутри пустой ячейки.

  6. Откройте вкладку Формула , а затем нажмите кнопку Автосумма

    _гт_ Дополнительные функции.

  7. В области построителя формул введите медиану в поле поиска и нажмите кнопку Вставить функцию.

  8. Убедитесь, что диапазон ячеек в поле Number1 совпадает с данными (в данном случае a1: A7).

    В этом примере ответ, отображаемый в ячейке, должен быть 8.

Совет: Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих эти результаты, нажмите клавиши CTRL+` (знак ударения) или на вкладке Формулы в группе Зависимости формул нажмите кнопку Показывать формулы.

support.office.com

медиана — что это? — 14 Августа 2014 — Примеры решений задач

называется вариант, расположенный в центре ранжированного ряда.

Медиана делит ряд на две равные части таким образом, что по обе стороны от нее находится одинаковое количество единиц совокупности. При этом у одной половины единиц совокупности значение варьирующего признака не больше медианы, у другой — не меньше. .

Для дискретного ряда,

медиану находим по следующему алгоритму:

— ранжируем ряд,

— если выборка содержит нечетное количество элементов, медиана равна (n+1)/2-му элементу,

— если выборка содержит четное количество элементов, медиана лежит между двумя средними элементами выборки и равна среднему арифметическому, вычисленному по этим двум элементам.

Пример 1. Найти медиану дискретного ряда

16,13,15,10,19,22,25,12,18,14,19,14,16,10.

Решение. Ранжируем ряд: 10,10,12,13,14,14,15,16,16,18,19,19,22,25, выборка содержит четное число элементов n=14, следовательно медиана лежит между двумя средними элементами выборки — между 7-элементом и 8-элементом:

10,10,12,13,14,14,15,16,16,18,19,19,22,25

и равна среднему арифметическому этих элементов:

Me=(15+16)/2=15,5

 

Найти медиану дискретного ряда, можно онлайн, с помощью данного калькулятора. Калькулятор автоматически ранжирует ряд и вычисляет медиану.

 

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

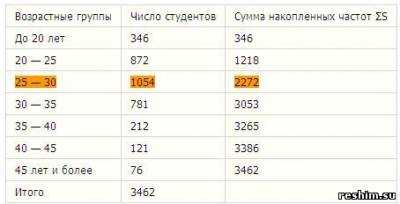
Пример 2. Найти  медиану интервального ряда:

Решение:

Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части

(Σfi/2 = 3462/2 = 1731).

Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:

Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.

ОСОБЕННОСТИ

  • Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки.
  • Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.

Вычислить медиану в Excel

Можно скачать готовый шаблон для вычисления медианы в Excel

 

 

www.reshim.su

Определение моды и медианы в статистике

По данным таблицы рассчитаем моду и медиану

Интервалы

Диапазон по продолжительности жизни

Число стран (частота), f

Накопленная частота, f

1

60,8 — 63,53

6

6

2

63,53  – 66,25

13

19

3

66,25 – 68,98

12

31

4

68,98  – 71,70

18

49

5

71,70 — 74,43

37

86

6

74,43 — 77,15

22

108

7

77,15 — 79,88

27

135

8

79,88 — 82,60

15

150

Определение моды

Интервал, имеющий наибольшую частоту, будет являться модальным, а конкретное (дискретное) значение моды будет находиться внутри него. Рассчитать конкретное, значение моды в интервальном ряду можно по следующей формуле:

где: ХМо — нижняя граница модального интервала,
i — длина модального интервала,
fMo — частота модального интервала,
fMo-1 — частота, соответствующая предшествующему интервалу,
fMo+1 — частота, соответствующая последующему интервалу.

Самая большая частота, 37 стран, соответствует варианту 71,70 — 74,43. Этот интервал является модальным.

Определение медианы

Медиана применяется для количественной характеристики структуры и равна такому варианту, который делит ранжированную совокупность на две равные части. У одной половины совокупности признаки не больше медианы (меньше или равны), у второй — не меньше медианы (больше или равны).

Если рассматриваемый ряд интервальный, то накопленные частоты покажут нам медианный интервал. Конкретное значение медианы рассчитывается по формуле:

i — длина медианного интервала,
сумма f — сумма частот ряда (объем совокупности),
f’Me-1 — накопленная частота в интервале, предшествующем медианному,
fMe — частота медианного интервала.

Для нахождения медианного интервала нужно знать половину частот, то есть 150 : 2 = 75. В столбце «накопленные частоты» выбираем 5 интервал, так как в 4 интервале частот накопилось еще 49 стран — меньше половины. С помощью формулы найдем конкретное значение медианы, оно принадлежит медианному интервалу 71,70 — 74,43.

 

Разница между 74,14 и 73,61 говорит об умеренном асимметричном распределении

Заказать задачи по статистике Вы можете на странице http://univer-nn.ru/zadachi-po-statistike-primeri/

univer-nn.ru

Расчет медианы интервального ряда

Если варианты в ряду распределения заданы в виде интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для определения этого интервала сумму частот делят пополам и на основе последовательного суммирования частот первого, второго, третьего и т.д. интервалов находят интервал, где расположена медиана. Приближенное значение в медианном интервале исчисляется по формуле:

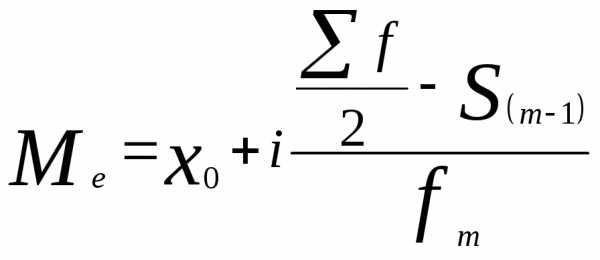
где

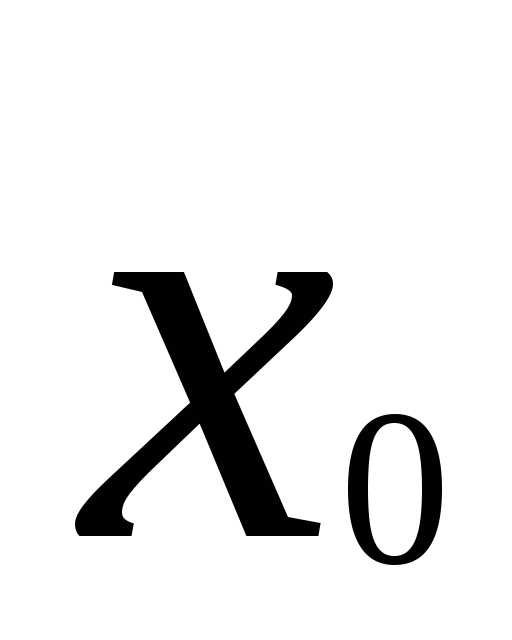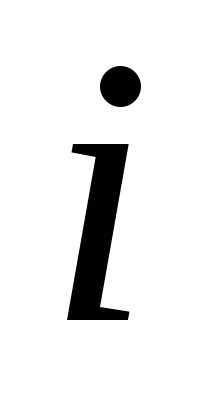— нижняя граница медианного интервала;

— величина медианного интервала;

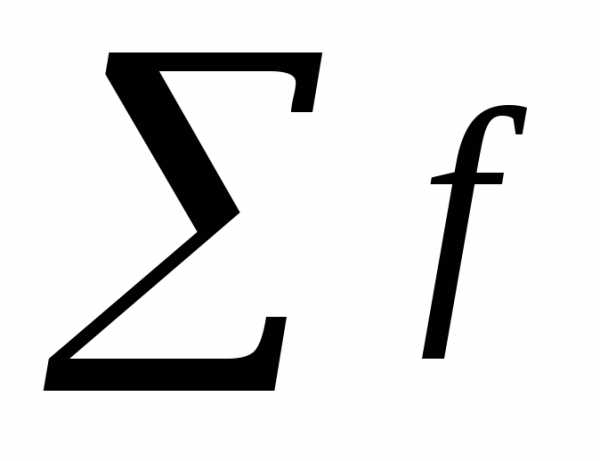— сумма частот интервального ряда;

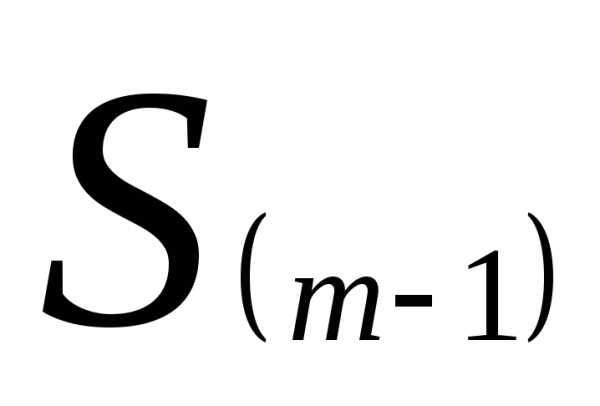— сумма накопленных частот в интервалах предшествующих медианному;

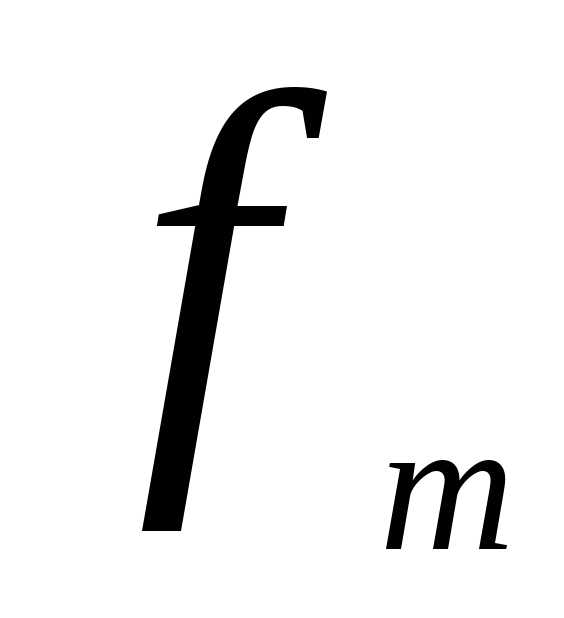— частота медианного интервала.

Из этой формулы следует, что к нижней границе медианного интервала добавляется та часть медианного интервала, которая пропорциональна удельному весу в частоте медианного интервала части ее, расположенной от нижней границы интервала до.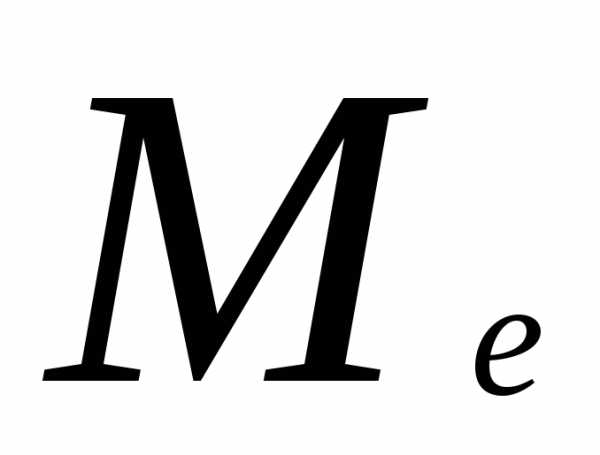

Свойство медианы

Сумма абсолютных величин линейных отклонений от 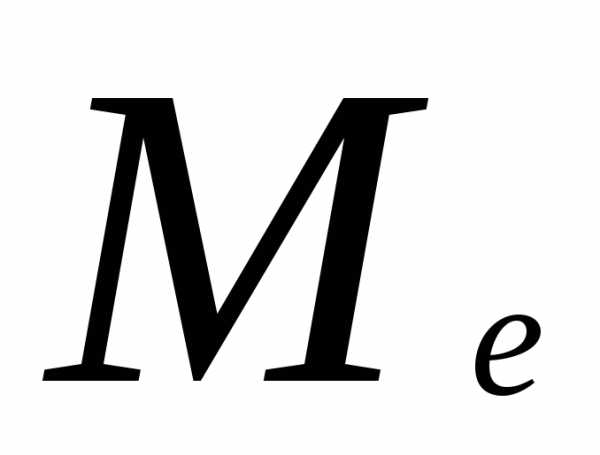минимальна:

Контрольные вопросы

1. Каковы цели и задачи статистического наблюдения?

2. Для каких целей применяется статистическая отчетность?

3.Что представляют собой статистическая совокупность, единица совокупности?

4. Для каких целей проводят специальное статистическое наблюдение?

5. Что включает программно-методологический план наблюдения?

6. Что представляет собой объект статистического наблюдения?

7. Дайте характеристику статистическим признакам.

8. Какие вопросы включаются в организационную часть статистического наблюдения?

9.Что такое объективное и субъективное время наблюдения?

10. Как выявляется статистическая закономерность?

11. Для чего предназначена система статистических показателей?

12. Каковы основные требования к системе статистических показателей?

13. Что представляет собой сводка?

14. В чем заключается группировка статистических данных?

15. Что такое группировочный признак?

16. Какими могут быть группировочные признаки?

17. Как рассчитать числа групп ?

18. Какие обычно выделяют виды группировок?

19. Что представляет собой интервал группировки?

20. Какими могут быть интервалы группировок?

21. Как определяется интервал группировок?

22. В чем достоинство табличного представления статистической информации?

23. Что характеризует подлежащее статистической таблицы?

24. Что характеризует сказуемое статистической таблицы?

25. К какому виду относится таблица 2.1.?

26. Дайте понятие абсолютных величин и единиц их измерения.

27. Какие виды абсолютных величин существуют?

28. Дайте понятие относительных величин, формы их выражения и единиц измерения.

29. Охарактеризуйте относительные величины динамики, выполнения плана, планового задания. Покажите их взаимосвязь.

30. Перечислите виды относительных величин. Приведите примеры их использования.

31. Что такое средние величины и каковы их роль и значение?

Дайте определение средней величины.

32. Охарактеризуйте особенности и значение средних величин в анализе социально-экономических явлений.

33. Какие виды средних величин вы знаете?

34. Расскажите о свойствах средней арифметической.

35. Какие существуют средние величины и как рассчитываются средняя арифметическая простая и взвешенная?

36. Как осуществляется расчет средней арифметической по данным интервального ряда?

37. Как вычисляется и применяется средняя хронологическая для интервального и моментного ряда?

38. Как рассчитать среднюю гармоническую простую и взвешенную?

39. В чем состоят особенности структурных средних?

40. Как рассчитывается мода для вариационного и интервального ряда?

41. Какими свойствами обладает медиана и как рассчитывается для интервального ряда?

42. Для каких целей применяются квартили и децили?

studfiles.net

Тема 1

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4.

Расчёт структурных характеристик вариационного ряда распределения.

Студент должен:

знать:

—   область применения и методику расчёта структурных средних величин;

уметь:

—   исчислять структурные средние величины;

—   формулировать вывод по полученным результатам.

Методические указания

В статистике исчисляются мода и медиана, которые относятся к структурным средним, так как  их величина зависит от строения статистической совокупности.

Расчёт моды

Модой называется значение признака (варианта), чаще всеговстречающееся в изучаемой совокупности. В дискретном ряду распределения модой будет варианта с наибольшей частотой.

Например: Распределение проданной женской обуви по размерам характеризуется следующим образом:

Размер обуви

34

35

36

37

38

39

40

41

Количество проданных пар

8

19

34

108

72

51

6

2

В этом ряду распределения  модой является 37 размер, т.е. Мо=37 размер.

Для интервального ряда распределения мода определяется по формуле:

где ХMo - нижняя граница модального интервала;

hMo  — величина модального интервала;

fMo – частота модального интервала;

fMo-1  и  fMo+1 – частота интервала соответственно

предшествующего модальному и следующего за ним.

Например: Распределение рабочих по стажу работы характеризуется следующими данными.

Стаж работы, лет

до 2

2-4

4-6

6-8

8-10

10 и более

Число рабочих, чел.

4

23

20

35

11

7

Определить моду интервального ряда распределения.

Мода интервального ряда составляет

Мода всегда бывает несколько неопределённой, т.к. она зависит от величины групп и точного положения границ групп. Мода широко применяется в коммерческой практике при изучении покупательского спроса, при регистрации цен и т.п.

Расчёт медианы

Медианой в статистике называется варианта, расположенная в середине упорядоченного ряда данных, и которая делит статистическую совокупность на две равные части так, что у одной половины значения меньше медианы, а у другой половины – больше её. Для определения медианы необходимо построить ранжированный ряд, т.е. ряд в порядке возрастания или убывания индивидуальных значений признака.

В дискретном упорядоченном ряду с нечётным числом членов медианой будет варианта, расположенная в центре ряда.

Например: Стаж пяти рабочих составил 2, 4, 7, 9 и 10 лет. В таком ряду медиана-7 лет, т.е. Ме=7 лет

Если дискретный упорядоченный ряд состоит из чётного числа членов, то медианой будет средняя арифметическая из двух смежных вариант, стоящих в центре ряда.

Например: Стаж работы шести рабочих составил 1, 3, 4, 5, 10 и 11лет. В этом ряду имеются две варианты, стоящие в центре ряда. Это варианты 4 и 5. Средняя арифметическая из этих значений и будет медианой ряда

 

Чтобы определить медиану для сгруппированных данных, необходимо считать накопленные частоты.

Например: По имеющимся данным определим медиану размера обуви

Размер обуви

Количество проданных пар

Сумма накопленных частот

34

8

8

35

19

8+19=27

36

34

27+34=61

37

108

61+108=169

38

72

—

39

51

—

40

6

—

41

2

—

Итого

300

 

Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы  частот, превышающей половину суммы частот ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е. 37 и есть медиана ряда.

Если же сумма накопленных частот против одной из вариант равна точно половине суммы частот ряда, то медиана определяется как средняя арифметическая этой варианты и последующей.

Например: По имеющимся данным определим медиану заработной платы рабочих

Месячная заработная плата, тыс.руб.

Число рабочих, чел.

Сумма накопленных частот

14,0

2

2

14,2

6

2+6=8

16,0

12

8+12=20

16,8

16

—

18,0

4

—

Итого:

40

—

Медиана будет равна:

Медиана интервального вариационного ряда распределения определяется по формуле:

Где  ХМе – нижняя граница медианного интервала;

hMe – величина медианного интервала;

∑f  — сумма частот ряда;

fМе – частота медианного интервала;

Например: По имеющимся данным о распределении предприятий по численности промышленно – производственного персонала рассчитать медиану в интервальном вариационном ряду

Группы предприятий по численности ППП, чел.

Число предприятий

Сумма накопленных частот

100-200

1

1

200-300

3

1+3=4

300-400

7

4+7=11

400-500

30

11+30=41

500-600

19

—

600-700

15

—

700-800

5

 

Итого:

80

 

Определим, прежде всего, медианный интервал. В данном примере сумма накопленных частот, превышающих половину суммы всех значений ряда, соответствует интервалу 400-500.Это и есть медианный интервал, т.е. интервал, в котором находится медиана ряда. Определим её значение

Если же сумма накопленных частот против одного из интервалов равна точно половине суммы частот ряда, то медиана определяется по формуле:

где n – число единиц в совокупности.

Например: По имеющимся данным о распределении предприятий по численности промышленно – производственного персонала рассчитать медиану в интервальном вариационном ряду

Группы предприятий по численности ППП, чел.

Число предприятий

Сумма накопленных частот

100-200

1

1

200-300

3

1+3=4

300-400

6

4+6=10

400-500

30

10+30=40

500-600

20

40+20=60

600-700

15

—

700-800

5

 

Итого:

80

 

чел

Моду и медиану в интервальном ряду можно определить графически:

моду в дискретных рядах — по полигону распределения, моду в интервальных рядах — по гистограмме распределения, а медиану — по кумуляте.

Мода интервального ряда распределения определяется по гистограмме распределения определяют следующим образом. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

 

 

 

 

 

 

 

 

 

Медиана рассчитывается по кумуляте. Для её определения из точки на шкале накопленных частот (частостей), соответствующей 50%, проводится прямая, параллельная оси абсцисс, до пересечения с кумулятой. Затем из точки пересечения указанной прямой с кумулятой опускается перпендикуляр на ось абсцисс. Абсцисса точки пересечения является медианой.

Кроме моды и медианы в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения.

Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

—      квартили  – значения признака, делящие упорядоченную совокупность на четыре равные части;

—      децили – значения признака, делящие упорядоченную совокупность на десять равных частей;

—      перцентели - значения признака, делящие упорядоченную совокупность на сто равных частей.

Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака, мода, медиана. При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:

—                 для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых ;

—                 для неустойчивых процессов положение центра распределения характеризуется с помощью Mo или Me. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической и модой.

 

 

psistat.narod.ru

Мода, медиана, Нахождение медианы, Определение медианы, Определение моды

Медиана в статистке

Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.

Посмотреть решение задачи на нахождение моды и медианы Вы можете здесь

В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:

где Хm — нижняя граница медианного интервала;
im — медианный интервал;
Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;
fme — число наблюдений в медианном интервале.

Свойства медианы

  1. Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее.
  2. Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения.
  3. Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины

Графическое определение медианы

Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.

Определение моды в статистике

Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения.

Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.

Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:

где ХМо — нижняя граница модального интервала;
imo — модальный интервал;
fм0, fм0-1,, fм0+1 — частоты в модальном, предыдущем и следующем за модальным интервалах.

Модальный интервал определяется по наибольшей частоте.

Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.

Соотношения между средней арифметической, медианой и модой

Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают.

К. Пирсон на основе выравнивания различных типов кривых определил, что для умеренно асимметричных распределений справедливы такие приближенные соотношения между средней арифметической, медианой и модой:

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

univer-nn.ru

Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям

КAЗAXСКИЙ НAЦИOНAЛЬНЫЙ УНИВEPСИТEТ ИМ. AЛЬ-ФAPAБИ

ВЫСШAЯ ШКOЛAЭКOНOМИКИ И БИЗНEСA

Кaфeдpa «ФИНAНСЫ»

Реферат

«статистика»

Тeмa: «Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям»

Выпoлнила: Чжао Сяоюе

Гpуппa: Ф16P

Aлмaты 2017

Содержание

Введение

Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям

3.Заключение

4.список литературы

 

Введение

Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий видМода – величина признака, которая чаще всего встречается в данной совокупности. Применительно к вариационному ряду модой является наиболее часто встречающееся значение ранжированного ряда. Она показывает размер признака, свойственный значи–тельной части совокупности, и определяется по фор–муле:

Общая теория статистики

где х0 – нижняя граница интервала;

h – величина интервала;

fm – частота интервала;

fm-1 – частота предшествующего интервала;

fm+1 – частота следующего интервала.

Расчет средних величин,моды и медианы с использованием статистических данных двум кампаниям

Используются две категории средних величин:

 

степенные средние;

 

структурные средние.

 

Первая категория степенных средних включает: Средняя арифметическая величинасреднюю арифметическую, Средняя гармоническая величинасреднюю гармоническую, Средняя квадратическая величинасреднюю квадратическую и Средняя геометрическая величинасреднюю геометрическую.

 

Вторая категория (структурные средние) — это Модамода и Медианамедиана. Эти виды средних будут рассмотрены в теме «Ряды распределения».

Введем следующие условные обозначения:

 

— величины, для которых исчисляется средняя;

 

— средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений;



 

— частота (повторяемость индивидуальных значений признака).

 

Различные средние выводятся из общей формулы степенной средней:

 

при k = 1 — средняя арифметическая; k = -1 — средняя гармоническая; k = 0 — средняя геометрическая; k = -2 — средняя квадратическая.

 

Средние величины бывают простые и взвешенные. Взвешенная средняя величинаВзвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют Статистический весстатистическим весом или весом средней.

 

Средняя арифметическая величинаСредняя арифметическая — самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая — это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

 

Формула средней арифметической (простой) имеет вид

 

где n — численность совокупности.

 

Например, средняя заработная плата работников предприятия вычисляется как средняя арифметическая:

 

Мода – это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:

 

 

где: — нижняя граница модального интервала;

— величина модального интервала;

— частота модального интервала;

— частота интервала, предшествующего модальному;

 

— частота интервала, следующего за модальным;

Медиана (Ме) — это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

 

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

 

где: — нижняя граница медианного интервала;

— величина медианного интервала;

— накопленная частота интервала, предшествующего медианному;

— частота медианного интервала;

Медианный интервал не обязательно совпадает с модальным.

Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.

 

Медиана (Ме) — это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:

 

 

Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:

 

 

 

где: — нижняя граница медианного интервала;

— величина медианного интервала;

— накопленная частота интервала, предшествующего медианному;

— частота медианного интервала;

Медианный интервал не обязательно совпадает с модальным.

Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.

 

3.Заключение

Определяющими показателями здесь являются заработная плата каждого работника и число работников предприятия. При вычислении средней общая сумма заработной платы осталась прежней, но распределенной как бы между всеми работниками поровну. К примеру, необходимо вычислить среднюю заработную плату работников небольшой фирмы, где заняты 8 человек:

 

 

При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. В этом случае речь идет об использовании средней арифметической взвешенной, которая имеет вид

 

 

Так, нам необходимо рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи. Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом:

 

1 — 800 ак. — 1010 тг.

 

2 — 650 ак. — 990 тг

 

3 — 700 ак. — 1015тг.

 

4 — 550 ак. — 900тг.

 

5 — 850 ак. — 1150тг.

 

Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА):

ОСС = 1010 ·800+990·650+1015·700+900·550+1150·850= 3 634 500;

КПА = 800+650+700+550+850=3550.

 

В этом случае средний курс стоимости акций был равен

 

 

Необходимо знать свойства арифметической средней, что очень важно как для ее использования, так и при ее расчете. Можно выделить три основных свойства, которые наиболее всего обусловили широкое применение арифметической средней в статистико-экономических расчетах.

 

4.список литературыы

1.Гусаров В.М. Статистика: Учеб. пособие для вузов. — М.: ЮНИТИ-ДАНА, 2001.

 

2.Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / Под ред. И.И.Елисеевой. — М.: Финансы и статистика, 1998.

 

3.Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики. — М.: ИНФРА-М, 1996.

 

4.Курс социально-экономической статистики: Учебник для вузов / Под ред. М.Г. Назарова, — М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.

 

5.Лапуста М.Г., Старостин Ю.Л. Малое предпринимательство. — М.: ИНФРА-М, 1997.

 

6.Муравьев А.И., Игнатьев А.М., Крутик А.Б. Малый бизнес: экономика, организация, финансы: Учеб. пособие для вузов. — 2-е изд., перераб. и доп. — СПб.: Издательский дом «Бизнес-пресса», 1999.

 

7.Салин В.Н., Шпаковская Е.П. Социально-экономическая статистика: Учебник. — М.: Юрист, 2001.

 

8.Теория статистики: Учебник. — 3-е изд., перераб. / Под ред. Р.А. Шмойловой. — М.: Финансы и статистика, 1999.

 

9.Черкасов В.В. Проблемы риска в управленческой деятельности. — М.: Рефлбук; К.: Ваклер, 1999.

 

10.Экономическая статистика / Под ред. Ю.Н. Иванова. — М.: ИНФРА-М, 1999

Рекомендуемые страницы:


Воспользуйтесь поиском по сайту:

megalektsii.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *