Теория вероятности формулы и определения: Основные формулы теории вероятности / Блог :: Бингоскул

Основные формулы теории вероятности / Блог :: Бингоскул

Классическое определение вероятности

Случайное событие – любое событие, которое может произойти, а может и не произойти в результате какого-либо опыта.

Вероятность события р равна отношению числа благоприятных исходов k к числу всевозможных исходов n, т.е.

p=\frac{k}{n}

 

Формулы сложения и умножения теории вероятности

Событие \bar{A} называется противоположным событию A, если не произошло событие A.

Сумма вероятностей противоположных событий равна единице, т.е.

 

P(\bar{A}) + P(A) =1

• Вероятность события не может быть больше 1.
• Если вероятность события равна 0, то оно не случится.
• Если вероятность события равна 1, то оно произойдет.

---

Теорема сложения вероятностей:

«Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий.»

 

P(A+B) = P(A) + P(B)

 

Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:

 

P(A+B) = P(A) + P(B) — P(AB)

---

Теорема умножения вероятностей

«Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.»

 

P(AB)=P(A)*P(B)

События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.

События называются совместными, если наступление одного из них не исключает наступления другого.

Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.

 

Смотри также: Основные формулы по математике

примеры задач с решением на математические классические формулы комбинаторики Пуассона или Лапласа

События, которые происходят реально или в нашем воображении, можно разделить на 3 группы. Это достоверные события, которые обязательно произойдут, невозможные события и случайные события. Теория вероятностей изучает случайные события, т.е. события, которые могут произойти или не произойти.

В данной статье будет представлена в кратком виде теория вероятности формулы и примеры решения задач по теории вероятности, которые будут в 4 задании ЕГЭ по математике (профильный уровень).

Зачем нужна теория вероятности

Исторически потребность исследования этих проблем возникла в XVII веке в связи с развитием и профессионализацией азартных игр и появлением казино. Это было реальное явление, которое требовало своего изучения и исследования.

Игра в карты, кости, рулетку создавала ситуации, когда могло произойти любое из конечного числа равновозможных событий. Возникла необходимость дать числовые оценки возможности наступления того или иного события.

В XX веке выяснилось, что эта, казалось бы, легкомысленная наука играет важную роль в познании фундаментальных процессов, протекающих в микромире. Была создана современная теория вероятностей.

Основные понятия теории вероятности

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

События А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом .

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом .

Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.

Вероятность принимает значения на отрезке от 0 до 1, т.е.

Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е.

Важным частным случаем является ситуация, когда имеется равновероятных элементарных исходов, и произвольные  из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле . Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов , прямо в условии написано число всех исходов .

Пример задачи из ЕГЭ по математике по определению вероятности

На столе лежат 20 пирожков — 5 с капустой, 7 с яблоками и 8 с рисом. Марина хочет взять пирожок. Какова вероятность, что она возьмет пирожок с рисом?

Решение

Всего равновероятных элементарных исходов 20, то есть Марина может взять любой из 20 пирожков. Но нам нужно оценить вероятность того, что Марина возьмет пирожок с рисом, то есть , где А — это выбор пирожка с рисом. Значит у нас количество благоприятных исходов (выборов пирожков с рисом) всего 8. Тогда вероятность будет определяться по формуле:

Ответ: 0,4

Независимые, противоположные и произвольные события

Однако в открытом банке заданий стали встречаться и более сложные задания. Поэтому обратим внимание читателя и на другие вопросы, изучаемые в теории вероятностей.

События А и В называется независимыми, если вероятность каждого из них не зависит от того, произошло ли другое событие.

Теоремы сложения и умножения вероятностей, формулы

Последние 2 утверждения называются теоремами сложения и умножения вероятностей.

Не всегда подсчет числа исходов является столь простым. В ряде случаев необходимо использовать формулы комбинаторики. При этом наиболее важным является подсчет числа событий, удовлетворяющих определенным условиям. Иногда такого рода подсчеты могут становиться самостоятельными заданиями.

Рассмотрим теперь другой случай с нашими учениками. Сколькими способами можно усадить 2 учеников на 6 свободных мест? Первый ученик займет любое из 6 мест. Каждому из этих вариантов соответствует 5 способов занять место второму ученику. Чтобы найти число всех вариантов, надо найти произведение .

В общем случае ответ на этот вопрос дает формула для числа размещений из n элементов по k элементам.

Источник: https://repetitor-mathematics.ru/teoriya-veroyatnosti-formulyi-i-primeryi-resheniya-zadach/

Теория вероятности — формулы нахождения с примерами и решениями

Развитие науки

Изучение вероятности наступления того или иного события берёт своё начало со Средних веков. Первоначально наблюдаемые закономерности не имели математического описания и основывались на различных эмпирических фактах. Ранние работы были непосредственно связаны с азартными играми. Французские учёные Паскаль и Ферма пытались выявить и рассчитать закономерности при бросании костей.

Независимо от них этим вопросом занимался и голландский физик Гюйгенс. В своей работе он оперировал такими понятиями, как величина шанса, математическое ожидание, цена случайности. Он первый, кто попробовал применить теоремы сложения и умножения в описание вероятности.

Фундаментальное значение для развития науки имели труды Бернулли, Байеса, Лапласа и Пуассона. Их стараниями были сформулированы и доказаны предельные теоремы, предложены первые формулы и примеры. В теории вероятности начали использовать анализ ошибочного наблюдения. Но лишь Карл Гаусс детально смог разобраться в нормальном распределении случайной величины.

В XIX веке русские и европейские учёные смогли доказать сделанные ранее предложения. В первую очередь это касалось закона больших чисел и центральной предельной теоремы. Формальная система для описания теории была принята в 1933 году.

Предложил её академик СССР Андрей Колмогоров. Руководствуясь идеями теории множеств, меры и интегрирования, он смог систематизировать аксиомы и с их помощью описать классическую теорию вероятности.

На основании его работ была создана новая теория — случайных процессов.

В его систему входит:

• алгебра событий — состоит из множества подмножеств, называемых событиями и их пространства;
• существование возможности появления событий — каждому случаю приписывается в соответствие вещественная вероятность наступления;
• нормировка — состояние, при котором вещественное число имеет вероятность свершения равное единице;
• аддитивность — если 2 события не пересекаются, их вероятность находится суммированием.

Объекты, удовлетворяющие системе, были названы полем вероятности (вероятностным пространством). Было принято, что аксиомы не могут противоречить друг другу. Аксиоматизация позволила привести все предположения к строгому математическому виду и стала восприниматься как один из разделов математического вычисления.

Предметом изучения науки являются закономерности, появляющиеся в случайных событиях, результат которых нельзя установить заранее. Но не все эксперименты можно изучать с помощью теории, а лишь те, что повторяются при одних и тех же условиях. Существует понятие «статистической устойчивости».

Если существует некоторое событие «А», которое может наступить в результате события или не произойти, то часть экспериментов должна стабилизироваться.

При этом с увеличением числа экспериментов вероятность повторения стремится к определённому числу Р(А). Оно и является характеристикой, определяющей степень возможности наступления события «А».

Объяснить основы теории вероятности для чайников можно с помощью классических понятий:

1. Вероятность, что событие «А» сможет произойти описывается выражением: Р (А) = m/n, где: n — общее количество исходов эксперимента, имеющих равные возможности; m — число исходов, соответствующих событию «А».
2. Для геометрического определения вместо чисел используется мера. В числитель формулы подставляется показатель, выражающий количество благоприятных исходов наступления рассматриваемого события, а в знаменатель — геометрическая мера. Например, ширина, плотность, объём.
3. При расчётах принимается, что полная группа событий образует вероятность равную единице: P (A1) + P (A2) + + P (An) = 1, при этом сумма противоположных событий также будет равна одному.
4. Шанс, что одно из двух несовместимых событий обязательно случится, определяется сложением этих вероятностей. Это формулировка справедлива и к любому количеству ожидаемых исходов: P (C +B +A) = Р(С) + Р (B) +P (A).
5. Исход, что любое из двух событий сбудется, равен вероятности суммы без учёта возможного их совместного появления: P (А+В) = Р (А) + Р (B) — P (АВ).

Основополагающими формулами являются выражения Байеса и Бернулли.

Согласно первому, если существует гипотеза «Вн», а событие уже наступило, вероятность её правдивости определяется как Pа (Вн) = Р (Вн) * Рв (А) / Р (А). Это выражение ещё называют формулой полной вероятности. Равенство же Бернулли помогает оценить вероятность, что конкретное событие «А» случится n количество раз при m вариантах: P = C n * p n * qn — m.

Алгоритм решения

Теория вероятностей используется, когда необходимо сделать прогноз на выпадение того или иного шанса в эксперименте. Случайность является основным понятием предмета.

Она обозначает явление, для которого невозможно точно вычислить периодичность наступления, поэтому в задачах находят именно число возможностей.

По своей сути вероятность — функция, способная принимать 3 значения:

• ноль — ожидание никогда не выполнится;
• единица — событие произойдёт при любых условиях;
• паритет — существует равная возможность выполнения или невыполнения ожидания.

Чтобы высчитать случайность, рекомендуется придерживаться разработанного алгоритма. Следует внимательно изучить задание и определить, вероятность чего необходимо вычислить, а также события, от которых случайность будет изменяться.

Определив схему задачи, подобрать формулу и, подставив в неё все имеющиеся данные, рассчитать шанс.

Чтобы правильно определиться с нужной схемой, необходимо знать о количестве экспериментов, существовании между ними зависимости, возможности применения нескольких гипотез.

Для понятия принципа нахождения случайности часто предлагается к решению следующая задача. В закрытом ящике лежит 6 разноцветных перемешанных между собой шаров. Из них 2 красного цвета, 3 зелёного и 1 белый. Нужно посчитать, насколько шансов достать белый шар меньше, чем цветной.

Случайность доставания цветного шара обозначают как событие «А». Согласно определению вероятность «А» определяется отношением благоприятствующих шансов к общему числу исходов.

Существует 6 различных возможностей вытянуть шар, из них 5 относятся к благоприятным, поэтому эксперимент покажет, что вероятность достать из ящика цветной шар будет составлять P = 5 / 6 = 0,83(3).

Это и есть показатель оценки степени случайности.

Таким способом можно узнать различную вероятность любого исхода, не прибегая к собиранию статистики и её анализу, то есть решить задачу математически, как, например, следующую.

В таксопарке используется 2 синих, 9 красных и 4 чёрных машины. Нужно определить, какая существует возможность приезда по вызову красного автомобиля. Решение простое.

Так как всего имеется 15 машин, вероятность приезда именно красной составит Р = 9/15 или 0,6.

Теорема Муавра — Лапласа

Это предельное определение, предложенное Лапласом в 1812 году. В основе теоремы используется формула Бернулли, но применяется она к довольно большому количеству экспериментов.

Суть её в следующем: если при независимых экспериментах n существует вероятность свершения случайного события N равная нулю или единице, при этом число испытаний равняется m, искомое значение близко к интегральной функции Лапласа.

Стандартные значения, соответствующие нормальному распределению, сведены в статистические таблицы. Взять их можно в решебниках задач по теории. Под приведёнными значениями понимается площадь кривой от нуля до числа x. Например, если придумать какую-либо величину площади между числами 0 и 2,34, согласно таблице она составит 0,49036.

При рассмотрении свершения m событий в n экспериментах существует вероятность, заключённая в определённом отрезке между значениями a и b, поэтому выражение для нахождения можно найти из формулы: Р(m) = (n! * pm * qn-m) / m!(n-m)!.

Уравнение требует сложных и громоздких расчётов, поэтому, чтобы найти вероятность, в математике из формулы используют асимптотическое распределение.

Но возможно это только при условии, что Р(m) неизменное, а число экспериментов будет стремиться к бесконечности.

Реальная формула, описывающая теорему сложна, поэтому используется приближённая:

Р(m) = 1 / ((2p*n*p*q)1/2) exp (-X2m/2).

Использовать её рекомендуют только при значениях событий больше 20, а экспериментов 100. Например, брак выпускаемых изделий составляет 15%. Поступает товар в упаковках по 100 штук. Нужно найти вероятность, что случайно взятая коробка будет укомплектована 13 бракованными изделиями. При этом число товара низкого качества в упаковке не превысит 20.

За испытание необходимо принять изготовление. Вероятность появления события, которое необходимо искать составит p = 0,15. Далее, находится случайность: n * p = 15 и n * p * q = 12,75. Таким образом, примерно 9,5% упаковок от общего количества содержат 13 товаров плохого качества, а в 92% случаях число изделий с браком не превышает 20.

Сочетание взаимных событий

При рассмотрении задач может возникнуть вопрос, как различные события могут зависеть друг от друга. Для характеристики их взаимосвязи вводится понятие условная вероятность. Например, имеются 2 случайных исхода одного эксперимента «А» и «В». Тогда условной вероятностью первого события «А» при условии, что второе произошло, называется отношение P (AB) / P (B).

Необходимо определить, с какой вероятностью в семье с ребёнком-девочкой родится мальчик. За вероятность появления в семье двух мальчиков нужно взять «А», а за ребёнка противоположного пола событие «В».

Существует 4 возможных исхода, поэтому справедливо будет записать: P (AB) = 1/4, P(B) = 3/4. Подставив эти значения в формулу можно рассчитать вероятность: P (A/B) = (1/4) / (3/4) = 0,3.

Первый исход считается независимым от второго, если наступление события «В» не оказывает влияние.

Если же события взаимны, они влияют друг на друга. В этом случае используется их перемножение: P(AB) = P(A) *PB (А). Например, в пачке 26 лотерей, из которых 3 призовых. Нужно определить шанс, что первый билет будет призовой и вероятность, что второй билет также будет с выигрышем, но при условии, что первый билет уже убрали.

Для решения задачи вначале нужно найти шанс, что первый билет будет с выигрышем: P (A) = 3/26 = 0,115. Затем рассчитать вероятность двух выигрышей подряд: P(AB) = P(A) * P(B) = (3/26) * (2/25) = 0,009.

Это довольно простые задачи, но существуют задания, для решения которых понадобится применять несколько формул. Такой расчёт вероятности наступления того или иного события может быть трудным, требующим повышенного внимания.

Источник: https://nauka.club/matematika/algebra/teoriya-veroyatnosti.html

Основные формулы теории вероятности / Теория вероятности [Калинин В.М., Тихомиров С.Р.] / 3dstroyproekt.ru

№№ п/п	Понятия, обозначения	Содержание, формула
1	Множество	Множество $A-$ совокупность каких-либо объектов $a$, называемых элементами множества: $a\in A$
2	Дополнение $\overline A $  { не $A$ }	$\overline A $ содержит все элементы, не принадлежащие $A$
3	Равенство множеств $A=B$	Два множества $A$ и $B$ равны между собой, если они состоят из одних и тех же элементов
4	Объединение { сумма } множеств $C=A+B$	Множество $C$ состоит из всех элементов, принадлежащих или множеству $A$, или множеству $B$ или и $A$ и $B$ одновременно
5	Пересечение { произведение } множеств $C=A\cdot B$	Множество $C$ состоит из элементов, принадлежащих одновременно и множеству $A$ и множеству $B$
6	Разность двух множеств $C=A-B$	$C$ состоит из элементов множества $A$, которые не являются элементами множества $B$
7	Эквивалентные множества	Два множества называются эквивалентными, если между ними установлено взаимно-однозначное соответствие.
8	Счетные множества	Бесконечные множества, эквивалентные множеству натуральных чисел $\mathbb { N } $
9	Перестановки. Число перестановок	Соединения, отличающиеся только порядком элементов, называются перестановками. Число перестановок из $n$ элементов $P_n =n!$, где $n!=1\cdot 2\cdot 3\cdot 4\cdot \ldots \cdot n$ $0!=1$
10	Размещения. Число размещений	Соединения из $n$ различных элементов по $m$, отличающихся друг от друга составом элементов либо их порядком, называются размещениями. Число размещений из $n$ по $m$ $A_n^m =\frac { n! } { (n-m)! } $
11	Сочетания. Число сочетаний	Соединения из $n$ различных элементов по $m$, отличающихся друг от друга хотя бы одним элементом, называются сочетаниями. Число сочетаний из $n$ по $m$ $C_n^m =\frac { n! } { (n-m)!m! } $ $C_n^m =C_n^ { n-m } ;$ $C_n^0 =1; C_ { n+1 } ^ { m+1 } =C_n^m +C_n^ { m+1 } ;$  $C_n^0 +C_n^1 +C_n^2 +\ldots +C_n^ { n-1 } +C_n^n =2^n$
12	Стохастический эксперимент	Это опыт { испытание } , результат которого заранее не определен
13	Достоверное событие	Результат, который обязательно наступает при осуществлении данного комплекса условий { опыта, эксперимента } называется достоверным событием
14	Случайное событие	Это событие, которое может произойти, а может и не произойти в данном испытании
15	Невозможное событие	Это событие, которое не может произойти при данном комплексе условий
16	Относительная частота события $A$	Отношение $\nu (A)=\frac { m } { n } $ числа экспериментов $m$, завершившихся событием $A$, к общему числу $n$ проведенных экспериментов
17	Статистическое определение вероятности	Если при неограниченном увеличении числа экспериментов относительная частота события $\nu (A)$ стремится к некоторому фиксированному числу, то событие $A$ стохастически устойчиво и это число $p(A)$ называют вероятностью события $A$
18	Определение вероятности в классической схеме	$P(A)=\frac { m } { n } $, где $m$ – число исходов стохастического эксперимента, благоприятствующих наступлению события $A$, $n$ – общее число всех равновозможных исходов
19	Вероятность суммы { объединения } , двух событий $A$ и $B$	$P(A+B)=P(A)+P(B)-P(AB)$
20	Вероятность произведения двух зависимых событий $A$ и $B$	$P(AB)=P(A)\cdot P(B/A)=P(B)\cdot P(A\vert B)$, где $P(B\vert A)$ – условная вероятность события $B$ при условии, что событие $A$ с ненулевой вероятностью произошло
21	Независимые события $A$ и $B$	Это такие события, для которых $P(B\vert A)=P(B)$ и $P(A\vert B)=P(A)$. Следовательно, $P(AB)=P(A)\cdot P(B)$
22	Схема Бернулли	Стохастический эксперимент состоит из последовательности $n$ независимых и одинаковых испытаний, в каждом из которых может произойти событие $A$ или событие, ему противоположное $\overline A $  с вероятностями соответственно равными $p$ и $q=1-p$
23	Формула Бернулли	Вероятность того, что в серии из $n$ испытаний событие $A$ появится ровно $m$ раз $P_n (m)=C_n^m \cdot p^m\cdot q^ { n-m } $
		Вероятность того, что при $n$ испытаниях $A$ появляется не менее $m_1 $ и не более $m_2 $  раз вычисляется по формуле: $P_n (m_1 \leqslant m\leqslant m_2 )=\sum\limits_ { m=m_1 } ^ { m_2 } { C_n^m \cdot p^m\cdot q^ { n-m } } $
24	Формула Пуассона	При достаточно большом $n$ и малом $p$, если $a=np\lt 10\rightarrow P_n (m)\approx \frac { a^m } { m! } e^ { -a } $  { таблица 1 }
		$P_n (m\leqslant k)\approx e^ { -a } \sum\limits_ { m=0 } ^k { \frac { a^m } { m! } } $  { таблица 2)
25	Локальная формула Муавра-Лапласа	При достаточно большом $n$ и не слишком малых $p$ и $q$ $P_n (m)\approx \frac { 1 } { \sqrt { npq } } \phi (x)$, где $\varphi (x)=\frac { 1 } { \sqrt { 2\pi } } e^ { \frac { -x^2 } { 2 } } $ и $x=\frac { m-np } { \sqrt { npq } } $; $\phi (-x)=\phi (x)$  { таблица 3)
26	Интегральная формула Муавра – Лапласа	$P_n (m_1 \leqslant m\leqslant m_2 )=\Phi (x_2 )-\Phi (x_1 )$, где $x_1 =\frac { m_1 -np } { \sqrt { npq } } $; $x_2 =\frac { m_2 -np } { \sqrt { npq } } $; $\Phi (x)=\frac { 1 } { \sqrt { 2\pi } } \int\limits_0^x { e^ { \frac { -t^2 } { 2 } } } dt$; $\Phi (-x)=-\Phi (x)$  { таблица 4 }
27	Понятие случайной величины	Случайной величиной называют переменную величину, которая принимает числовые значения в зависимости от исходов испытания случайным образом.
28	Понятие дискретной случайной величины { ДСВ $X$ }	ДСВ $X$ – случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, то есть численные значения которой образуют конечное или счетное множество.
29	Закон распределения дискретной случайной величины	Соответствие между значениями $x_1, x_2, \cdots $ дискретной случайной величины и их вероятностями $p_1, p_2, \cdots $ называется законом распределения и может быть задан таблично или аналитически { то есть с помощью формул } . Если ДСВ $X$ принимает конечное множество значений $x_1 ,x_2 ,x_3 …$  соответственно с вероятностями $p_1 ,p_2 ,…,p_n $, то ее закон распределения  определяется формулами $P(X=x_k )=p_k , ~k=1,2,…,n$ и $\sum\limits_ { k=1 } ^n { p_k =1 } $ Если ДСВ $X$ принимает бесконечную последовательность значений $x_1 ,x_2 ,x_3 …$ соответственно с вероятностями $p_1 ,p_2 ,p_3 ,…$, то ее закон распределения определяется формулами $P(X=x_k )=p_k, ~k=1,2,…,n$ и $\sum\limits_ { k=1 } ^\infty { p_k =1 } $
30	Понятие непрерывной случайной величины { НСВ $X$ }	НСВ $X$ – случайная величина, которая может принимать любые значения из некоторого промежутка, то есть множество значений непрерывной случайной величины несчетно.
31	Функция распределения. Свойства функции распределения	Функцией распределения случайной величины $X$ называется функция действительного переменного $x$, определяемая равенством $F(x)=P(X\lt x)$, где $P(X\lt x)$ — вероятность того, что случайная величина $X$ принимает значение, меньше $x$ Функция распределения $F(x)$ для ДСВ $X$, которая может принимать значения $x_1 ,x_2 ,…x_n $ c соответствующими вероятностями $p_1 ,p_2 ,…,p_n$  имеет вид $F(x)=\sum\limits_ { x_k \lt x } { P(X\lt x_k ) } $, где символ $x_k \lt x$ означает, что суммируются вероятности $p_k $ тех значений, которые меньше $x$. Функция является разрывной. Случайная величина $X$ называется непрерывной, если ее функция распределения $F(x)$ является непрерывно дифференцируемой. Вероятность того, что СВХ примет значение из промежутка $\left[ { \alpha ;\beta }\right)$, равна разности значений ее функции распределения на концах этого полуинтервала: $P(\alpha \leqslant X\lt \beta )=F(\beta )-F(\alpha )$ Свойства функции распределения 1. $0\leqslant F(x)\leqslant 1$  2. Если $x_1 \lt x_2 $, то $F(x_1 )\leqslant F(x_2 )$, то есть функция распределения является неубывающей.
31	Функция распределения. Свойства функции распределения	3. Функция $F(x)$ в точке $x_0 $  непрерывна слева, то есть $\mathop { \lim } \limits_ { x\to x_0 -0 } F(x)=F(x_0 )$; $F(x_0 -0)=F(x_0 )$ 4. Если все возможные значения  СВХ принадлежат интервалу $(a;b)$, то $F(x)=0$ при $x\leqslant a$, $F(x)=1$ при $x\geqslant b$  5. Если все возможные значения СВХ принадлежат бесконечному интервалу $\left( { -\infty ;+\infty }\right)$, то $\mathop { \lim } \limits_ { x\to -\infty } F(x)=0;\mathop { \lim } \limits_ { x\to +\infty } F(x)=1;$ Если $X$ – непрерывная случайная величина, то вероятность того, что она примет одно заданное определенное значение, равна нулю: $P(X=\alpha )=0$ Отсюда следует, что для непрерывной случайной величины выполняются равенства: $P(\alpha \lt X\lt \beta )=P(\alpha \leqslant X\leqslant \beta )=P(\alpha \leqslant X\lt \beta )=$ $=P(\alpha \lt X\leqslant \beta )=F(\beta )-F(\alpha )$
32	Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения.	Плотностью распределения { дифференциальной функцией распределения } вероятностей НСВ $X$ в точке $x$ называют предел отношения вероятности попадания значений этой величины в интервал $\left( { x;x+\Delta x }\right)$ к длине $\Delta x$ этого интервала, когда последняя стремится к нулю: $f(x)=\mathop { \lim } \limits_ { \Delta x\to 0 } \frac { P(x\lt X\lt x+\Delta x) } { \Delta x } $ Следовательно, $f(x)= { F } ‘(x)$, то есть плотность распределения есть первая производная от функции распределения НСВХ. Вероятность того, что НСВХ примет значение, принадлежащее интервалу $(a;b)$, определяется равенством $P(a\lt X\lt b)=\int\limits_a^b { f(x)dx } $
32	Плотность распределения вероятностей непрерывной случайной величины. Свойства функции плотности распределения.	Зная плотность распределения, можно найти функцию распределения $F(x)=\int\limits_ { -\infty } ^x { f(x)dx } $ Свойства функции плотности 1. Плотность распределения $f(x)$ — неотрицательная функция, то есть $f(x)\geqslant 0$  2. Несобственный интеграл по бесконечному промежутку $\left( { -\infty ;+\infty }\right)$ от функции плотности вероятностей равен единице: $\int\limits_ { -\infty } ^ { +\infty } { f(x)dx=1 } $ 3. Если все возможные значения случайной величины принадлежат отрезку $\left[ { \alpha ;\beta }\right]$, то $\int\limits_\alpha ^\beta { f(x)dx=1 } $, так как вне этого промежутка $f(x)=0$
33	Математическое ожидание	Для ДСВ $X$ равно сумме произведений всех ее значений на соответствующие вероятности: $M(X)=\sum\limits_ { i=1 } ^n { x_i p_i } $ Для НСВ $X:\;M(X)=\int\limits_ { -\infty } ^ { +\infty } { xf(x)dx } $, где $f(x)=F'(x)$ – функция плотности распределения вероятности.
34	Свойства математического ожидания	1. $M(C)=C$, если $C=const,$ 2. $M(CX)=CM(X),$ 3. $M(X+Y)=M(X)+M(Y),$ 4. Если $X$ и $Y$ – независимые случайные величины, то $M(XY)=M(X)\cdot M(Y)$
35	Дисперсия случайной величины	Разность $X-M(X)$ называется отклонением случайной величины $X$ от ее математического ожидания $M(X)=a$. Математическое ожидание отклонения равно нулю: $M(X-a)=0$  Дисперсией, или рассеянием случайной величины $X$ называется математическое ожидание квадрата ее отклонения: $D(X)=M((X-a)^2)$ Следовательно, для любой случайной величины $X:\;\;D(X)\geqslant 0$
36	Свойства дисперсии	1. $D(C)=0$, $C=const,$ 2. $D(CX)=C^2D(X)$, $C=const,$ 3. Если случайные величины $X$ и $Y$ независимы, то $D(X\pm Y)=D(X)+D(Y),$ 4. $D(XY)=D(X)\cdot D(Y),$  5. $D(X)=M(X^2)-(M(X))^2.$
37	Среднее квадратическое отклонение	Среднеквадратическим отклонением, или стандартным отклонением, случайной величины $X$ называется корень квадратный из ее дисперсии: $\sigma (X)=\sqrt { D(X) } \Leftrightarrow D(X)=\sigma ^2.$
38	Биномиальное распределение	Закон распределения дискретной случайной величины, определяемой формулой Бернулли $p_k =P_n (k)=C_n^k \cdot p^k\cdot q^ { n-k } (k=0,1,2,…,n)$ называется биномиальным. Постоянные $n,~p$ называются параметрами биномиального распределения $\left( { q=1-p }\right)$. $M(X)=np;\;D(X)=npq;\;\sigma (X)=\sqrt { npq } $
39	Распределение Пуассона	Распределением Пуассона называется  распределение вероятностей дискретной случайной величины, определяемое формулой Пуассона $P_n (k)=\frac { a^ke^ { -a } } { k! } $, где $a=np$ – параметр распределения. $M(X)=a;D(X)=a$
40	Равномерное распределение на интервале $\left( { a;b }\right)$	Если значения случайной величины, которые она принимает в конечном промежутке $(a;b)$, возможны в одинаковой степени, то плотность распределения вероятностей этой величины постоянна на данном промежутке и равна нулю вне этого промежутка, то есть $f(x)=\left\{ { \begin{array} { l } C\;\mbox { на } \;\left[ { a,b }\right], \\ 0\;\mbox { вне } \;(a,b). \\ \end{array} }\right.$ Доказано, что $C=\frac { 1 } { b-a } .$  $M(X)=\frac { a+b } { 2 } ; ~ D(X)=\frac { (b-a)^2 } { 12 } ; ~ \sigma (X)=\frac { b-a } { 2\sqrt 3 } $
41	Геометрическое распределение	Геометрическим называется распределение дискретной случайной величины $X$, определяемое формулой $P(X=m)=(1-p)^ { m-1 } \cdot p,$, где $0\lt p\lt 1$, и $m=1,2,3…$  { Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем $q=1-p$ } . $M(X)=\frac { 1 } { p } ; ~ D(X)=\frac { 1-p } { p^2 } $
42	Показательное распределение	Показательным называется распределение с плотностью вероятностей, определяемой по формуле  $f(x)=\left\{ { \begin{array} { l } 0\mbox { при } \;x\lt 0, \\ \lambda e^ { -\lambda x } \mbox { } \;\mbox { при } \;x\geqslant 0, \\ \end{array} }\right.$ где  $\lambda >0$ — параметр распределения. $M(X)=\frac { 1 } { \lambda } ; ~ D(X)=\frac { 1 } { \lambda ^2 } \quad ; ~ \sigma (X)=\frac { 1 } { \lambda } .$  Замечание. Если $T$ – время безотказной работы элемента, $\lambda $ — интенсивность отказов, то случайная величина $T$ распределена по экспоненциальному закону с функцией распределения $F(t)=P(T\lt t)=1-e^ { -\lambda t } ,_ { } $ где $\lambda \gt 0$. $F(t)$ определяет вероятность отказа элемента за время $t$. Вероятность безотказной работы элемента за время $t$ равна $e^ { -\lambda t } $. Функция $R(t)=e^ { -\lambda t } $ называется функцией надежности.
43	Нормальное распределение $N(a;\sigma )$	Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей  $f(x)=\frac { 1 } { \sigma \sqrt { 2\pi } } e^ { \frac { -(x-a)^2 } { 2\sigma ^2 } } $ Постоянные $a$ и $\sigma \quad (\sigma \gt 0)$  называются параметрами нормального распределения. $M(X)=a; ~ D(X)=\sigma ^2; ~ \sigma =\sqrt { D(X) } $ Вероятность попадания значений нормальной случайной величины $X$ в интервале $(\alpha ;\beta )$  определяется формулой $P(\alpha \lt X\lt \beta )=\Phi (\frac { \beta -\alpha } { \sigma } )-\Phi (\frac { \alpha -a } { \sigma } ),$ где $\Phi (x)$ – функция Лапласа. $M(X)=a; D(X)=\sigma ^2.$
44	Нормированное распределение $N(0;1)$	Нормированным или стандартным называется такое нормальное распределение непрерывной случайной величины, когда функция плотности вероятностей $f(x)=\frac { 1 } { \sqrt { 2\pi } } e^ { \frac { -x^2 } { 2 } } .$ $M(X)=a=0; ~ \sigma (X)=\sigma =1.$
45	Мода случайной величины $\overline M $	Модой ДСВ $X$ называется ее наиболее вероятное значение. Модой НСВ $X$ называется то ее значение, при котором плотность распределения вероятностей максимальна.
46	Медиана $M_e $	Медианой непрерывной случайной величины $X$ называется такое ее значение $M_e $, для которого одинаково вероятно, окажется ли случайная величина меньше или больше $M_e $, то есть $P(x\lt M_e )=P(x>M_e )=0,5$. Если прямая $x=a$ является осью симметрии кривой распределения $f(x)$, то $\overline M =M_e =M(X)=a$.
47	Начальные моменты $\nu _k $	Начальным моментом $\nu _k ~ k$ -го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени этой случайной величины: $\nu _k =M(X^k)$. Для ДСВ $X:_ { } \nu _k =\sum\limits_ { i=1 } ^n { x_i^k \cdot p_i } $,  где $\sum\limits_ { i=1 } ^\infty { p_i =1 } $. Начальный момент $k$-го порядка НСВ $X$ с плотностью распределения $f(x)$ определяется формулой : $\nu _k =\int\limits_ { -\infty } ^ { +\infty } { x^kf(x)dx } $,   где $\int\limits_ { -\infty } ^ { +\infty } { f(x)dx=1 } $.
48	Центральные моменты  $\mu _k $	Центральным моментом $\mu _k ~ k$-го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени отклонения этой величины от ее математического ожидания. Если обозначить $M(X)=a$, то $\mu _k =M((X-a)^k)$  Для ДСВ $X: \quad \mu _k =\sum\limits_ { i=1 } ^n { (x_i -a)^k\cdot p_i } $, если множество этой величины конечно, а если – счетно, то $\mu _k =\sum\limits_ { i=1 } ^\infty { (x_i -a)^k\cdot p_i } .$ Для НСВ $X$ с плотностью распределения $f(x)$ центральный момент $k$-го порядка определяется формулой: $\mu _k =\int\limits_ { -\infty } ^ { +\infty } { (x_i -a)^k\cdot f(x)dx } .$
49	Некоторые свойства начальных и центральных моментов	$\nu _0 =1;~ \nu _1 =M(X),$  $\mu _0 =1;~ \mu _1 =0;~ ~ \mu _2 =D\left( X \right),$ $\mu _2 =\nu _2 -\nu _1^2 ,$ $\mu _3 =\nu _3 -3\nu _1 \nu _2 +2\nu _1^3 ,$ $\mu _4 =\nu _4 -4\nu _1 \nu _3 +6\nu _1^2 \nu _2 -3\nu _1^4 .$
50	Асимметрия	Отношение центрального момента 3-го порядка к кубу среднеквадратического отклонения случайной величины называется асимметрией: $A(X)=\frac { \mu _3 } { \sigma ^3 } $. Если распределение случайной величины симметрично относительно ее математического ожидания, то асимметрия равна нулю.
51	Эксцесс	Эксцессом случайной величины называется величина $Э_x =\frac { \mu _4 } { \sigma ^4 } -3.$ Для нормального распределения $Э_x =0$. Кривые, более островершинные по сравнению с нормальной кривой Гаусса, имеют $Э_x \gt 0$. У более плосковершинных кривых $Э_x \lt 0.$

Теория вероятности простыми словами, как рассчитать вероятность событий

Теория вероятностей (тервер) – раздел математики, который изучает случайные события и их свойства. Ознакомиться с ней нужно, чтобы понимать, как принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно «предсказать» исход события.

Я не станут грузить вас сложными формулами – желающие углубленно заняться тервером могут сделать это по книге В. Е. Гмурмана «Теория вероятностей и математическая статистика». В статье покажу простые примеры для понимания зависимых и независимых событий, расскажу о состоянии неопределенности и интуитивном знании.

Материал полезен широкому кругу читателей.

Коротко о теории вероятностей

Вероятность в зависимых событиях

Вы решаете отправить в подарок другу балык. Знаете номер дома, подъезд, этаж. Курьер просит называть номер квартиры. С мучительными усилиями вспоминаете, что в доме по три двери на площадку, но дальше – туман. Давайте рассчитаем, сможет ли курьер попасть в нужную квартиру с первого раза.

Имеем три варианта развития событий:

1. Курьер звонит в первую (1) дверь.
2. Курьер звонит во вторую (2) дверь.
3. Курьер звонит в третью (3) дверь.

Но в истории участвует еще один человек: ваш друг. И событийность в его случае выглядит так:

• Друг за первой (1) дверью.
• Друг за второй (2) дверью.
• Друг за третьей (3) дверью.

Прежде чем пойти дальше, введем определение вероятности – количество благоприятных исходов к вероятному числу событий.

Теперь соберем данные в таблицу (таблица 1). Всего — 9 исходов. Отметим положительные (курьеру откроет друг) – их 3. Получается, что вероятность с первого раза позвонить в дверь к нужному человеку – 3/9 или 1/3. Если вам нравится видеть вероятность в процентах, умножьте результат на 100%.

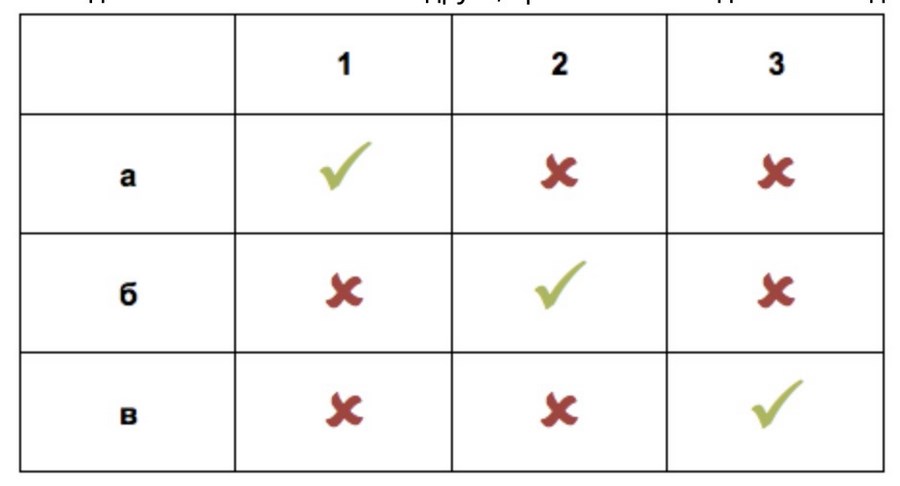Таблица 1 – Девять исходов, три благоприятных

Представим, что курьер ошибся, и за дверью оказалась сногсшибательная блондинка в коротком халате. Для курьера исход положительный, для вас – нет. Поэтому считаем новую вероятность:

1. Курьер звонит в первую (1) квартиру.
2. Курьер звонит во вторую (2) квартиру.

То же самое с другом:

• Друг ждет в первой (1) квартире.
• Друг ждет во второй (2) квартире.

Теперь у нас 4 варианта и 2 – выигрышные (таблица 2). Вероятность со второго раза попасть в квартиру друга – 1/2. Она уменьшилась из-за зависимости событий: мы уже исключили неблагоприятный исход и расчёт нужно производить заново. Если курьер настолько невезуч, что промахнется во второй раз, вероятность попасть по адресу в третий раз – 100%. Опытным путем мы проверили, что за двумя предыдущими дверьми балык никто не ждет.

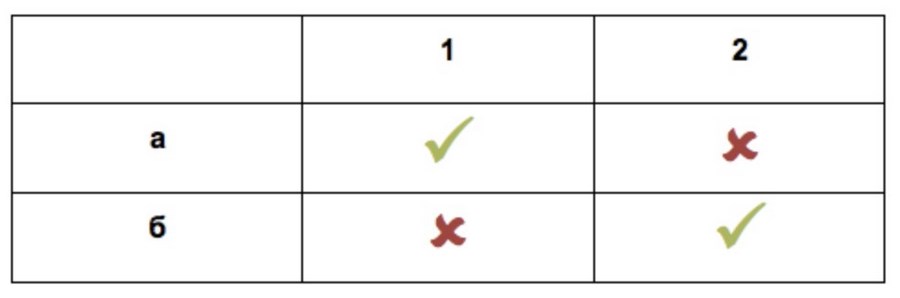Таблица 2 Четыре исхода, два благоприятных

Пример с курьером — начальный уровень тервера. Он применим для бытовых нужд: предугадать вероятность побочного эффекта от антибиотиков, выбрать из разнообразия бабушкиных пирожков пирожок с повидлом и др.

На экзамене по теории вероятности советский математик и автор учебника Елена Вентцель спросила:

— Кому все понятно? Поднимите руки.

В аудитории живо взметнулся лес рук.

— Отлично! Остальные свободны, оценка – пять баллов! Поднявшие руки – останьтесь. За годы преподавания я так и не поняла большей части тервера. Рада, что вы мне все сейчас объясните.

Байка с математического факультета

Вероятность в независимых событиях

Независимые события не влияют друг на друга: количество благоприятных исходов в каждом новом событии не меняется.

Регина Тодоренко и Леся Никитюк в рамках программы «Орел и Решка» приехали в США. Обе хотят провести уик-энд «по богатому» и кидают монетку. Леся поставила на орла, Регина – на решку. Вероятность уехать на собственном авто у девушек одинакова: 1/2. На это раз повезло Лесе. Впрочем, как в следующей поездке тоже.

Регина негодует, почему тервер работает не в ее сторону

Теперь определим, могут ли независимые события происходить подряд с одним и тем же исходом. Лесе везло уже два раза и выпадал «орел». Повезет ли в третий раз? Составим список возможных исходов:

1. Орел, орел, орел.
2. Орел, орел, решка.
3. Орел, решка, орел.
4. Орел, решка, решка.
5. Решка, орел, орел.
6. Решка, орел, решка.
7. Решка, решка, орел.
8. Решка, решка, решка.

По результату видно: вероятность определенной последовательности каждый раз меньше на вероятность одного события. То есть вероятность определенной последовательности – произведение вероятностей каждого события. Если в одном событии вероятность 1/2, то в трех: 1/2*1/2*1/2=1/8.

Как человек принимает решения в состоянии неопределённости

Часть мозга, которая ответственна за оценку ситуации связана с медиаторной системой — центром мотивационных и эмоциональных процессов. Логика и эмоции часто конфликтуют между собой, поэтому решение принимается случайным образом.

У моей подруги аллергия на виноград. Но в студенчестве она не могла отказаться от бокала вина на вечеринке. Часто ее дерзость оставалась безнаказанной и организм нормально воспринимал аллерген. Реже протестовал: у подруги появлялись отеки на лице и в горле. В эти моменты ее левое полушарие отчаянно искало закономерность и просчитывало вероятность наступления аллергической реакции, правое же шептало: «Не пей, лицо распухнет!». Она могла вывести количество благоприятных исходов математическим путем и пить вино без опасений, но эмоции оказались сильней. Подруга раз и навсегда отказалась от любых продуктов с виноградом.

Хороший пример принятия решений описан в книге Млодинова «(Не) совершенная случайность». Допустим, вы отправили рассказ в четыре издательства. От каждого получили отказ. На эмоциях вы придете к мысли: рассказ ужасный! Хотя, если изучить биографии популярных писателей, может оказаться, что дело не в вас. Отказы в публикации получали Стивен Кинг, Джоан Роулинг, Виктор Франкл. Такие истории случались вовсе не из-за отсутствия у них дара: просто в одном издательстве редактор не понял тонкую философию автора, в другом – спешил домой и проставил визу не читая.

Почему интуитивное знание всегда противоречит статистике

Моя бабушка считает: в Албании убивают на каждом шагу. Хотя в стране она не была и новостей о не слышала: ей так кажется интуитивно. Наверняка и вы не раз испытывали подобное чувство. Оно называется интуитивное знание – внутреннее убеждение, что собственная оценка более правдива, чем официальные источники и статистика.

Всего 127 убийств на 100 000 человек

Классическое исследование на тему интуитивного знания провели Даниэль Канеман и Амос Тверский. Они дали задание группе студентов: на основании портрета, оценить утверждения с таблицы как более (1 балл) и менее (8 баллов) вероятные (таблица 3).

Портрет выглядел так: «Линда, возраст – немного за 30. Умная, говорит, что думает. В колледже изучала философию. Тогда же выступала против социального неравенства, дискриминации и использования ядерного оружия. Не замужем».

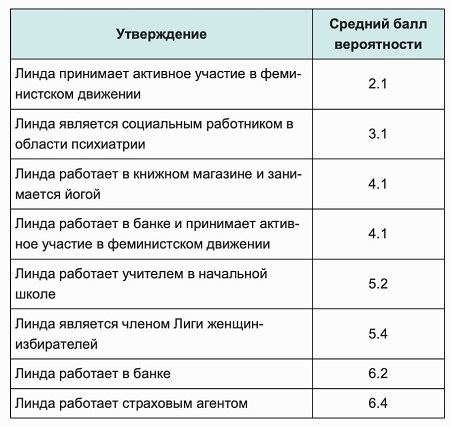Таблица 3

По портрету логично предположить, что Линда участвует в феминистском движении. Но студенты принимали решения интуитивно, что привело к ошибке. Вероятность, что Линда работает в банке и принимает участие в феминистском движении больше вероятности работы в банке.

Посмотрите на таблицу: вероятность работы в банке и увлечение феминистским движением – 4,1 балл. Но первое (работа в банке) и второе (феминистское движение) в сумме дают 8,3 балла. Согласно терверу, вероятность, что произойдут оба события не может быть выше, чем вероятность каждого события по отдельности. Главное утверждение (4,1 балла) содержит 2 события и является единым. В интуитивном решения правило тервера нарушено. Это доказывает — наши убеждения часто являются ложными.

В дальнейшем проводились множественные эксперименты, которые подтвердили догадку Канемана.

Вместо заключения

Теория вероятностей почти всегда разбивается о «случай», продиктованный убеждением или эмоцией отдельного человека. Поэтому использование ее в повседневной жизни может не оправдать ожиданий. Но выбирать вам! Хорошего дня!

Теория вероятности ℹ️ формула и примеры для чайников, задачи с решениями, как найти классическую вероятность в математике, как обозначается и в чем выражается вероятность

Развитие науки

Изучение вероятности наступления того или иного события берёт своё начало со Средних веков. Первоначально наблюдаемые закономерности не имели математического описания и основывались на различных эмпирических фактах. Ранние работы были непосредственно связаны с азартными играми. Французские учёные Паскаль и Ферма пытались выявить и рассчитать закономерности при бросании костей.

Независимо от них этим вопросом занимался и голландский физик Гюйгенс. В своей работе он оперировал такими понятиями, как величина шанса, математическое ожидание, цена случайности. Он первый, кто попробовал применить теоремы сложения и умножения в описание вероятности.

Фундаментальное значение для развития науки имели труды Бернулли, Байеса, Лапласа и Пуассона. Их стараниями были сформулированы и доказаны предельные теоремы, предложены первые формулы и примеры. В теории вероятности начали использовать анализ ошибочного наблюдения. Но лишь Карл Гаусс детально смог разобраться в нормальном распределении случайной величины.

В XIX веке русские и европейские учёные смогли доказать сделанные ранее предложения. В первую очередь это касалось закона больших чисел и центральной предельной теоремы. Формальная система для описания теории была принята в 1933 году. Предложил её академик СССР Андрей Колмогоров. Руководствуясь идеями теории множеств, меры и интегрирования, он смог систематизировать аксиомы и с их помощью описать классическую теорию вероятности. На основании его работ была создана новая теория — случайных процессов.

В его систему входит:

• алгебра событий — состоит из множества подмножеств, называемых событиями и их пространства;
• существование возможности появления событий — каждому случаю приписывается в соответствие вещественная вероятность наступления;
• нормировка — состояние, при котором вещественное число имеет вероятность свершения равное единице;
• аддитивность — если 2 события не пересекаются, их вероятность находится суммированием.

Объекты, удовлетворяющие системе, были названы полем вероятности (вероятностным пространством). Было принято, что аксиомы не могут противоречить друг другу. Аксиоматизация позволила привести все предположения к строгому математическому виду и стала восприниматься как один из разделов математического вычисления.

Предметом изучения науки являются закономерности, появляющиеся в случайных событиях, результат которых нельзя установить заранее. Но не все эксперименты можно изучать с помощью теории, а лишь те, что повторяются при одних и тех же условиях.

Существует понятие «статистической устойчивости». Если существует некоторое событие «А», которое может наступить в результате события или не произойти, то часть экспериментов должна стабилизироваться. При этом с увеличением числа экспериментов вероятность повторения стремится к определённому числу Р(А). Оно и является характеристикой, определяющей степень возможности наступления события «А».

Объяснить основы теории вероятности для чайников можно с помощью классических понятий:

1. Вероятность, что событие «А» сможет произойти описывается выражением: Р (А) = m/n, где: n — общее количество исходов эксперимента, имеющих равные возможности; m — число исходов, соответствующих событию «А».
2. Для геометрического определения вместо чисел используется мера. В числитель формулы подставляется показатель, выражающий количество благоприятных исходов наступления рассматриваемого события, а в знаменатель — геометрическая мера. Например, ширина, плотность, объём.
3. При расчётах принимается, что полная группа событий образует вероятность равную единице: P (A1) + P (A2) + + P (An) = 1, при этом сумма противоположных событий также будет равна одному.
4. Шанс, что одно из двух несовместимых событий обязательно случится, определяется сложением этих вероятностей. Это формулировка справедлива и к любому количеству ожидаемых исходов: P (C +B +A) = Р(С) + Р (B) +P (A).
5. Исход, что любое из двух событий сбудется, равен вероятности суммы без учёта возможного их совместного появления: P (А+В) = Р (А) + Р (B) — P (АВ).

Основополагающими формулами являются выражения Байеса и Бернулли.

Согласно первому, если существует гипотеза «Вн», а событие уже наступило, вероятность её правдивости определяется как Pа (Вн) = Р (Вн) * Рв (А) / Р (А). Это выражение ещё называют формулой полной вероятности. Равенство же Бернулли помогает оценить вероятность, что конкретное событие «А» случится n количество раз при m вариантах: P = C ⁿ * p ⁿ * q^{n — m}.

Алгоритм решения

Теория вероятностей используется, когда необходимо сделать прогноз на выпадение того или иного шанса в эксперименте. Случайность является основным понятием предмета. Она обозначает явление, для которого невозможно точно вычислить периодичность наступления, поэтому в задачах находят именно число возможностей. По своей сути вероятность — функция, способная принимать 3 значения:

• ноль — ожидание никогда не выполнится;
• единица — событие произойдёт при любых условиях;
• паритет — существует равная возможность выполнения или невыполнения ожидания.

Чтобы высчитать случайность, рекомендуется придерживаться разработанного алгоритма. Следует внимательно изучить задание и определить, вероятность чего необходимо вычислить, а также события, от которых случайность будет изменяться. Определив схему задачи, подобрать формулу и, подставив в неё все имеющиеся данные, рассчитать шанс. Чтобы правильно определиться с нужной схемой, необходимо знать о количестве экспериментов, существовании между ними зависимости, возможности применения нескольких гипотез.

Для понятия принципа нахождения случайности часто предлагается к решению следующая задача. В закрытом ящике лежит 6 разноцветных перемешанных между собой шаров. Из них 2 красного цвета, 3 зелёного и 1 белый. Нужно посчитать, насколько шансов достать белый шар меньше, чем цветной.

Случайность доставания цветного шара обозначают как событие «А». Согласно определению вероятность «А» определяется отношением благоприятствующих шансов к общему числу исходов. Существует 6 различных возможностей вытянуть шар, из них 5 относятся к благоприятным, поэтому эксперимент покажет, что вероятность достать из ящика цветной шар будет составлять P = 5 / 6 = 0,83(3). Это и есть показатель оценки степени случайности.

Таким способом можно узнать различную вероятность любого исхода, не прибегая к собиранию статистики и её анализу, то есть решить задачу математически, как, например, следующую. В таксопарке используется 2 синих, 9 красных и 4 чёрных машины. Нужно определить, какая существует возможность приезда по вызову красного автомобиля. Решение простое. Так как всего имеется 15 машин, вероятность приезда именно красной составит Р = 9/15 или 0,6.

Теорема Муавра — Лапласа

Это предельное определение, предложенное Лапласом в 1812 году. В основе теоремы используется формула Бернулли, но применяется она к довольно большому количеству экспериментов. Суть её в следующем: если при независимых экспериментах n существует вероятность свершения случайного события N равная нулю или единице, при этом число испытаний равняется m, искомое значение близко к интегральной функции Лапласа.

Стандартные значения, соответствующие нормальному распределению, сведены в статистические таблицы. Взять их можно в решебниках задач по теории. Под приведёнными значениями понимается площадь кривой от нуля до числа x. Например, если придумать какую-либо величину площади между числами 0 и 2,34, согласно таблице она составит 0,49036.

При рассмотрении свершения m событий в n экспериментах существует вероятность, заключённая в определённом отрезке между значениями a и b, поэтому выражение для нахождения можно найти из формулы: Р(m) = (n! * pm * qn-m) / m!(n-m)!. Уравнение требует сложных и громоздких расчётов, поэтому, чтобы найти вероятность, в математике из формулы используют асимптотическое распределение. Но возможно это только при условии, что Р(m) неизменное, а число экспериментов будет стремиться к бесконечности.

Реальная формула, описывающая теорему сложна, поэтому используется приближённая:

Р(m) = 1 / ((2p*n*p*q)1/2) exp (-X2m/2).

Использовать её рекомендуют только при значениях событий больше 20, а экспериментов 100. Например, брак выпускаемых изделий составляет 15%. Поступает товар в упаковках по 100 штук. Нужно найти вероятность, что случайно взятая коробка будет укомплектована 13 бракованными изделиями. При этом число товара низкого качества в упаковке не превысит 20.

За испытание необходимо принять изготовление. Вероятность появления события, которое необходимо искать составит p = 0,15. Далее, находится случайность: n * p = 15 и n * p * q = 12,75. Исходные данные подставляют в формулу Лапласа:

Таким образом, примерно 9,5% упаковок от общего количества содержат 13 товаров плохого качества, а в 92% случаях число изделий с браком не превышает 20.

Сочетание взаимных событий

При рассмотрении задач может возникнуть вопрос, как различные события могут зависеть друг от друга. Для характеристики их взаимосвязи вводится понятие условная вероятность. Например, имеются 2 случайных исхода одного эксперимента «А» и «В». Тогда условной вероятностью первого события «А» при условии, что второе произошло, называется отношение P (AB) / P (B).

Необходимо определить, с какой вероятностью в семье с ребёнком-девочкой родится мальчик. За вероятность появления в семье двух мальчиков нужно взять «А», а за ребёнка противоположного пола событие «В». Существует 4 возможных исхода, поэтому справедливо будет записать: P (AB) = 1/4, P(B) = 3/4. Подставив эти значения в формулу можно рассчитать вероятность: P (A/B) = (1/4) / (3/4) = 0,3. Первый исход считается независимым от второго, если наступление события «В» не оказывает влияние.

Если же события взаимны, они влияют друг на друга. В этом случае используется их перемножение: P(AB) = P(A) *PB (А). Например, в пачке 26 лотерей, из которых 3 призовых. Нужно определить шанс, что первый билет будет призовой и вероятность, что второй билет также будет с выигрышем, но при условии, что первый билет уже убрали.

Для решения задачи вначале нужно найти шанс, что первый билет будет с выигрышем: P (A) = 3/26 = 0,115. Затем рассчитать вероятность двух выигрышей подряд: P(AB) = P(A) * P(B) = (3/26) * (2/25) = 0,009.

Это довольно простые задачи, но существуют задания, для решения которых понадобится применять несколько формул. Такой расчёт вероятности наступления того или иного события может быть трудным, требующим повышенного внимания. Для облегчения вычислений существуют специальные интернет-порталы. Они предлагают рассчитать исход события даже тем, кто и вовсе не разбирается в теории. Например, allcalc.ru, kontrolnaya-rabota.ru, matburo.ru, math.semestr.ru.

На этих сайтах от пользователей требуется лишь заполнить предлагаемые формы исходными данными и нажать кнопку «Рассчитать». Все калькуляторы совмещают в себе быстроту нахождения ответа и ознакомление с подробным описанием решения.

формулы и примеры решения задач :: SYL.ru

«Случайности не случайны»… Звучит так, словно сказал философ, но на деле изучать случайности удел великой науки математики. В математике случайностями занимается теория вероятности. Формулы и примеры заданий, а также основные определения этой науки будут представлены в статье.

Что такое теория вероятности?

Теория вероятности – это одна из математических дисциплин, которая изучает случайные события.

Чтобы было немного понятнее, приведем небольшой пример: если подкинуть вверх монету, она может упасть «орлом» или «решкой». Пока монета находится в воздухе, обе эти вероятности возможны. То есть вероятность возможных последствий соотносится 1:1. Если из колоды с 36-ю картами вытащить одну, тогда вероятность будет обозначаться как 1:36. Казалось бы, что здесь нечего исследовать и предугадывать, тем более при помощи математических формул. Тем не менее, если повторять определенное действие много раз, то можно выявить некую закономерность и на ее основе спрогнозировать исход событий в других условиях.

Если обобщить все вышесказанное, теория вероятности в классическом понимании изучает возможность возникновения одного из возможных событий в числовом значении.

Со страниц истории

Теория вероятности, формулы и примеры первых заданий появились еще в далеком Средневековье, когда впервые возникли попытки спрогнозировать исход карточных игр.

Изначально теория вероятности не имела ничего общего с математикой. Она обосновывалась эмпирическими фактами или свойствами события, которое можно было воспроизвести на практике. Первые работы в этой сфере как в математической дисциплине появились в XVII веке. Родоначальниками стали Блез Паскаль и Пьер Ферма. Длительное время они изучали азартные игры и увидели определенные закономерности, о которых и решили рассказать обществу.

Такую же методику изобрел Христиан Гюйгенс, хотя он не был знаком с результатами исследований Паскаля и Ферма. Понятие «теория вероятности», формулы и примеры, что считаются первыми в истории дисциплины, были введены именно им.

Немаловажное значение имеют и работы Якоба Бернулли, теоремы Лапласа и Пуассона. Они сделали теорию вероятности больше похожей на математическую дисциплину. Свой теперешний вид теория вероятностей, формулы и примеры основных заданий получили благодаря аксиомам Колмогорова. В результате всех изменений теория вероятности стала одним из математических разделов.

Базовые понятия теории вероятностей. События

Главным понятием этой дисциплины является «событие». События бывают трех видов:

• Достоверные. Те, которые произойдут в любом случае (монета упадет).
• Невозможные. События, что не произойдут ни при каком раскладе (монета останется висеть в воздухе).
• Случайные. Те, что произойдут или не произойдут. На них могут повлиять разные факторы, которые предугадать очень трудно. Если говорить о монете, то случайные факторы, что могут повлиять на результат: физические характеристики монеты, ее форма, исходное положение, сила броска и т. д.

Все события в примерах обозначаются заглавными латинскими буквами, за исключением Р, которой отведена другая роль. Например:

• А = «студенты пришли на лекцию».
• Ā = «студенты не пришли на лекцию».

В практических заданиях события принято записывать словами.

Одна из важнейших характеристик событий — их равновозможность. То есть, если подбросить монету, все варианты исходного падения возможны, пока она не упала. Но также события бывают и не равновозможными. Это происходит, когда кто-то специально воздействует на исход. Например, «меченые» игральные карты или игральные кости, в которых смещен центр тяжести.

Еще события бывают совместимыми и несовместимыми. Совместимые события не исключают появления друг друга. Например:

• А = «студентка пришла на лекцию».
• В = «студент пришел на лекцию».

Эти события независимы друг от друга, и появление одного из них не влияет на появление другого. Несовместимые события определяются тем, что появление одного исключает появление другого. Если говорить о той же монете, то выпадение «решки» делает невозможным появление «орла» в этом же эксперименте.

Действия над событиями

События можно умножать и складывать, соответственно, в дисциплине вводятся логические связки «И» и «ИЛИ».

Сумма определяется тем, что может появиться или событие А, или В, или два одновременно. В случае когда они несовместимы, последний вариант невозможен, выпадет или А, или В.

Умножение событий заключается в появлении А и В одновременно.

Теперь можно привести несколько примеров, чтобы лучше запомнились основы, теория вероятности и формулы. Примеры решения задач далее.

Задание 1: Фирма принимает участие в конкурсе на получение контрактов на три разновидности работы. Возможные события, которые могут произойти:

• А = «фирма получит первый контракт».
• А₁ = «фирма не получит первый контракт».
• В = «фирма получит второй контракт».
• В₁ = «фирма не получит второй контракт»
• С = «фирма получит третий контракт».
• С₁ = «фирма не получит третий контракт».

С помощью действий над событиями попробуем выразить следующие ситуации:

• К = «фирма получит все контракты».

В математическом виде уравнение будет иметь следующий вид: К = АВС.

• М = «фирма не получит ни одного контракта».

М = А₁В₁С₁.

Усложняем задание: H = «фирма получит один контракт». Поскольку не известно, какой именно контракт получит фирма (первый, второй или третий), необходимо записать весь ряд возможных событий:

Н = А₁ВС₁υ АВ₁С₁ υ А₁В₁С.

А₁ВС₁ – это ряд событий, где фирма не получает первый и третий контракт, но получает второй. Соответственным методом записаны и другие возможные события. Символ υ в дисциплине обозначает связку «ИЛИ». Если перевести приведенный пример на человеческий язык, то фирма получит или третий контракт, или второй, или первый. Подобным образом можно записывать и другие условия в дисциплине «Теория вероятности». Формулы и примеры решения задач, представленные выше, помогут сделать это самостоятельно.

Собственно, вероятность

Пожалуй, в этой математической дисциплине вероятность события – это центральное понятие. Существует 3 определения вероятности:

• классическое;
• статистическое;
• геометрическое.

Каждое имеет свое место в изучении вероятностей. Теория вероятности, формулы и примеры (9 класс) в основном используют классическое определение, которое звучит так:

• Вероятность ситуации А равняется отношению числа исходов, что благоприятствуют ее появлению, к числу всех возможных исходов.

Формула выглядит так: Р(А)=m/n.

Р обозначает вероятность события А.

А – собственно, событие. Если появляется случай, противоположный А, его можно записывать как Ā или А₁.

m – количество возможных благоприятных случаев.

n – все события, которые могут произойти.

Например, А = «вытащить карту червовой масти». В стандартной колоде 36 карт, 9 из них червовой масти. Соответственно, формула решения задания будет иметь вид:

Р(А)=9/36=0,25.

В итоге вероятность того, что из колоды вытянут карту червовой масти, составит 0,25.

К высшей математике

Теперь стало немного известно, что такое теория вероятности, формулы и примеры решения заданий, которые попадаются в школьной программе. Однако теория вероятностей встречается и в высшей математике, которая преподается в вузах. Чаще всего там оперируют геометрическими и статистическими определениями теории и сложными формулами.

Очень интересна теория вероятности. Формулы и примеры (высшая математика) лучше начинать изучать с малого — со статистического (или частотного) определения вероятности.

Статистический подход не противоречит классическому, а немного расширяет его. Если в первом случае нужно было определить, с какой долей вероятности произойдет событие, то в этом методе необходимо указать, как часто оно будет происходить. Здесь вводится новое понятие «относительная частота», которую можно обозначить W_n(A). Формула ничем не отличается от классической:

W_n(A)=m/n.

Если классическая формула вычисляется для прогнозирования, то статистическая – согласно результатам эксперимента. Возьмем, к примеру, небольшое задание.

Отдел технологического контроля проверяет изделия на качество. Среди 100 изделий нашли 3 некачественных. Как найти вероятность частоты качественного товара?

А = «появление качественного товара».

W_n(A)=97/100=0,97

Таким образом, частота качественного товара составляет 0,97. Откуда взяли 97? Из 100 товаров, которые проверили, 3 оказались некачественными. От 100 отнимаем 3, получаем 97, это количество качественного товара.

Немного о комбинаторике

Еще один метод теории вероятности называют комбинаторикой. Его основной принцип состоит в том, что если определенный выбор А можно осуществить m разными способами, а выбор В — n разными способами, то выбор А и В можно осуществить путем умножения.

Например, из города А в город В ведет 5 дорог. Из города В в город С ведет 4 пути. Сколькими способами можно доехать из города А в город С?

Все просто: 5х4=20, то есть двадцатью разными способами можно добраться из точки А в точку С.

Усложним задание. Сколько существует способов раскладывания карт в пасьянсе? В колоде 36 карт – это исходная точка. Чтобы узнать количество способов, нужно от исходной точки «отнимать» по одной карте и умножать.

То есть 36х35х34х33х32…х2х1= результат не вмещается на экран калькулятора, поэтому его можно просто обозначить 36!. Знак «!» возле числа указывает на то, что весь ряд чисел перемножается между собой.

В комбинаторике присутствуют такие понятия, как перестановка, размещение и сочетание. Каждое из них имеет свою формулу.

Упорядоченный набор элементов множества называют размещением. Размещения могут быть с повторениями, то есть один элемент можно использовать несколько раз. И без повторений, когда элементы не повторяются. n — это все элементы, m – элементы, которые участвуют в размещении. Формула для размещения без повторений будет иметь вид:

A_n^m=n!/(n-m)!

Соединения из n элементов, которые отличаются только порядком размещения, называют перестановкой. В математике это имеет вид: Р_n = n!

Сочетаниями из n элементов по m называют такие соединения, в которых важно, какие это были элементы и каково их общее количество. Формула будет иметь вид:

A_n^m=n!/m!(n-m)!

Формула Бернулли

В теории вероятности, так же как и в каждой дисциплине, имеются труды выдающихся в своей области исследователей, которые вывели ее на новый уровень. Один из таких трудов — формула Бернулли, что позволяет определять вероятность появления определенного события при независимых условиях. Это говорит о том, что появление А в эксперименте не зависит от появления или не появления того же события в ранее проведенных или последующих испытаниях.

Уравнение Бернулли:

P_n(m)=C_n^m×p^m×q^n-m.

Вероятность (р) появления события (А) неизменна для каждого испытания. Вероятность того, что ситуация произойдет ровно m раз в n количестве экспериментов, будет вычисляться формулой, что представлена выше. Соответственно, возникает вопрос о том, как узнать число q.

q=1-p

Если событие А наступает р количество раз, соответственно, оно может и не наступить. Единица – это число, которым принято обозначать все исходы ситуации в дисциплине. Поэтому q – число, которое обозначает возможность ненаступления события.

Теперь вам известна формула Бернулли (теория вероятности). Примеры решения задач (первый уровень) рассмотрим далее.

Задание 2: Посетитель магазина сделает покупку с вероятностью 0,2. В магазин зашли независимым образом 6 посетителей. Какова вероятность того, что посетитель сделает покупку?

Решение: Поскольку неизвестно, сколько посетителей должны сделать покупку, один или все шесть, необходимо просчитать все возможные вероятности, пользуясь формулой Бернулли.

А = «посетитель совершит покупку».

В этом случае: р = 0,2 (как указано в задании). Соответственно, q=1-0,2 = 0,8.

n = 6 (поскольку в магазине 6 посетителей). Число m будет меняться от 0 (ни один покупатель не совершит покупку) до 6 (все посетители магазина что-то приобретут). В итоге получим решение:

P₆(0)=C₀⁶×p⁰×q⁶=q⁶=(0,8)⁶=0,2621.

Ни один из покупателей не совершит покупку с вероятностью 0,2621.

Как еще используется формула Бернулли (теория вероятности)? Примеры решения задач (второй уровень) далее.

После вышеприведенного примера возникают вопросы о том, куда делись С и р. Относительно р число в степени 0 будет равно единице. Что касается С, то его можно найти формулой:

C_n^m=n!/m!(n-m)!

Поскольку в первом примере m = 0, соответственно, С=1, что в принципе не влияет на результат. Используя новую формулу, попробуем узнать, какова вероятность покупки товаров двумя посетителями.

P₆(2)=C₆²×p²×q⁴ = (6×5×4×3×2×1)/(2×1×4×3×2×1)×(0,2)²×(0,8)⁴=15×0,04×0,4096=0,246.

Не так уж и сложна теория вероятности. Формула Бернулли, примеры которой представлены выше, прямое тому доказательство.

Формула Пуассона

Уравнение Пуассона используется для вычисления маловероятных случайных ситуаций.

Основная формула:

P_n(m)=λ^m/m!×e^(-λ).

При этом λ = n х p. Вот такая несложная формула Пуассона (теория вероятности). Примеры решения задач рассмотрим далее.

Задание 3: На заводе изготовили детали в количестве 100000 штук. Появление бракованной детали = 0,0001. Какова вероятность, что в партии будет 5 бракованных деталей?

Как видим, брак — это маловероятное событие, в связи с чем для вычисления используется формула Пуассона (теория вероятности). Примеры решения задач подобного рода ничем не отличаются от других заданий дисциплины, в приведенную формулу подставляем необходимые данные:

А = «случайно выбранная деталь будет бракованной».

р = 0,0001 (согласно условию задания).

n = 100000 (количество деталей).

m = 5 (бракованные детали). Подставляем данные в формулу и получаем:

Р₁₀₀₀₀₀(5) = 10⁵/5! Х е^-10 = 0,0375.

Так же как и формула Бернулли (теория вероятности), примеры решений с помощью которой написаны выше, уравнение Пуассона имеет неизвестное е. По сути его можно найти формулой:

е^-λ= lim _n->∞(1-λ/n)ⁿ.

Однако есть специальные таблицы, в которых находятся практически все значения е.

Теорема Муавра-Лапласа

Если в схеме Бернулли количество испытаний достаточно велико, а вероятность появления события А во всех схемах одинакова, то вероятность появления события А определенное количество раз в серии испытаний можно найти формулой Лапласа:

Р_n(m)= 1/√npq x ϕ(X_m).

X_m = m-np/√npq.

Чтобы лучше запомнилась формула Лапласа (теория вероятности), примеры задач в помощь ниже.

Задание 4: Рекламный агент раздает 800 листовок. Согласно статистическим исследованиям, каждая третья листовка находит своего потребителя. Какова вероятность того, что сработает ровно 267 рекламных листовок?

n = 800;

m = 267;

p = 1/3;

q = 2/3.

Сначала найдем X_m, подставляем данные (они все указаны выше) в формулу и получим 0,025. При помощи таблиц находим число ϕ(0,025), значение которого 0,3988. Теперь можно подставлять все данные в формулу:

Р₈₀₀(267) = 1/√(800 х 1/3 х 2/3) х 0,3988 = 3/40 х 0,3988 = 0,03.

Таким образом, вероятность того, что рекламная листовка сработает ровно 267 раз, составляет 0,03.

Формула Байеса

Формула Байеса (теория вероятности), примеры решения заданий с помощью которой будут приведены ниже, представляет собой уравнение, которое описывает вероятность события, опираясь на обстоятельства, которые могли быть связаны с ним. Основная формула имеет следующий вид:

Р (А|B) = Р (В|А) х Р (А) / Р (В).

А и В являются определенными событиями.

Р(А|B) – условная вероятность, то есть может произойти событие А при условии, что событие В истинно.

Р (В|А) – условная вероятность события В.

Итак, заключительная часть небольшого курса «Теория вероятности» — формула Байеса, примеры решений задач с которой ниже.

Задание 5: На склад привезли телефоны от трех компаний. При этом часть телефонов, которые изготавливаются на первом заводе, составляет 25%, на втором – 60%, на третьем – 15%. Известно также, что средний процент бракованных изделий у первой фабрики составляет 2%, у второй – 4%, и у третьей – 1%. Необходимо найти вероятность того, что случайно выбранный телефон окажется бракованным.

А = «случайно взятый телефон».

В₁ – телефон, который изготовила первая фабрика. Соответственно, появятся вводные В₂ и В₃ (для второй и третьей фабрик).

В итоге получим:

Р (В₁) = 25%/100% = 0,25; Р(В₂) = 0,6; Р (В₃) = 0,15 – таким образом мы нашли вероятность каждого варианта.

Теперь нужно найти условные вероятности искомого события, то есть вероятность бракованной продукции в фирмах:

Р (А/В₁) = 2%/100% = 0,02;

Р(А/В₂) = 0,04;

Р (А/В₃) = 0,01.

Теперь подставим данные в формулу Байеса и получим:

Р (А) = 0,25 х 0,2 + 0,6 х 0,4 + 0,15 х 0,01= 0,0305.

В статье представлена теория вероятности, формулы и примеры решения задач, но это только вершина айсберга обширной дисциплины. И после всего написанного логично будет задаться вопросом о том, нужна ли теория вероятности в жизни. Простому человеку сложно ответить, лучше спросить об этом у того, кто с ее помощью не единожды срывал джек-пот.

Теория вероятностей

Основы теории вероятностей

В этой статье мы расскажем кратко о том, что такое вероятность события. Дадим определение вероятности, введем понятия зависимых и независимых, совместных и несовместных событий. Объясним, что такое сумма событий и произведение событий.

Больше задач – в статье «Задание 4 Профильного ЕГЭ по математике. Теория вероятностей».

Случайным называется событие, которое невозможно точно предсказать заранее. Оно может либо произойти, либо нет. Теория вероятностей изучает случайные события и их закономерности, а также случайные величины и действия над ними.

Благоприятным мы называем исход, способствующий наступлению данного события.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность – величина положительная и не может быть больше единицы.

Например, перед экзаменом вы выучили 3 билета из 20. Вероятность вытянуть счастливый билет равна

Вот две простых задачи из вариантов ЕГЭ, где применяется определение вероятности:

1. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Иванов высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Иванову достанется удобное место, если всего в самолёте 300 мест.

В самолете 21+18=30 мест, удобных для Иванова. Всего в самолете 400 мест. Поэтому вероятность того, что пассажир Иванов получит удобное место, равна 30 : 300 = 0,1.

Просто применили определение вероятности.

2. В группе туристов 32 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист К. полетит пятым рейсом вертолёта.

Каждый рейс, в том числе и пятый, перевозит 4 человек из 32. Вероятность полететь пятым рейсом:

Ответ: 0,125.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Например, вы бросаете монету. «Выпал орел» и «выпала решка» — несовместные события.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.

Вы бросаете игральную кость. Вероятность выпадения «тройки» равна Вероятность выпадения «шестерки» также равна
Вероятность выпадения числа, которое делится на 3,

Произведение двух событий – термин, означающий, что произошло и одно, и другое событие.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

3. Говорят, что в старину каждый десятый на Руси был Иван, а каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?

Можно по-разному решать эту задачу, и вероятностный подход здесь тоже применим. Посчитаем вероятности двух событий
Событие А. Случайно выбранного мужчину зовут Иван Петрович
Событие В. Мужчину зовут Петр Иванович.

Вероятность быть Иваном Петровичем для жившего в старину россиянина равна Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр.
А вероятность оказаться Петром Ивановичем точно такая же:

4. (ЕГЭ) Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с ве-роятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Шахматист А. играет две партии, одну – белыми фигурами, другую – черными. События «выиграть белыми» и «выиграть черными фигурами» независимы. Вероятность того, что шахматист А. выиграет оба раза, равна произведению вероятностей выигрышей в каждой партии: 0,5 · 0,32 = 0,16.

5. (ЕГЭ) В классе 26 человек, среди них два друга — Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Пусть Андрей первым занял место в группе (неважно, в какой). И, кроме него, осталось еще 25 человек, среди которых его друг Сергей. Сколько у Сергея шансов оказаться в той же группе, что и Андрей? В группе должно быть 13 человек, то есть Андрей и еще 12. Значит, вероятность того, что Сергей окажется в той же группе, что и Андрей, равна , то есть 0,48.

Следующую задачу можно решить методами комбинаторики – например, с помощью формулы Бернулли. Однако в обычной школе не изучают комбинаторику, и тем не менее эта задача появилась в сборниках для подготовки к ЕГЭ.

6. Монету бросают 10 раз. Во сколько раз событие «Орел выпадет ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?

Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два – орел или решка.
Бросим монету два раза (или две монеты одновременно, все равно). И вот уже 4 возможных исхода:
ОО
ОР
РО
РР
(буквой О обозначен выпавший «орел», буквой «р» — решка.
Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка).
Для 10 бросков монеты количество возможных исходов, очевидно, равно

По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.

Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала ровно 1 раз.

Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки ровно 1 раз из 10 бросков

Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза.

Пронумеруем броски: 1,2,3…10.

Решка могла выпасть в первый и во второй раз. Обозначим эту комбинацию 12.

Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14…

Пронумеруем таким образом все благоприятные исходы.

12, 13, 14, 15, 16, 17, 18, 19, 1 10

23, 24, 25, 26, 27, 28, 29, 2 10

34, 35, 36, 37, 38, 39, 3 10

45, 46, 47, 48, 49, 4 10

56, 57, 58, 59, 5 10

67, 68, 69, 6 10

78, 79, 7 10

89, 8 10

9 10
Количество благоприятных исходов равно 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45.

Поделив на , получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:

Ответ: 4,5.

Разберем какую-нибудь типовую задачу ЕГЭ по теме «Теория вероятностей». Такую, в которой мы рисуем «дерево» возможных исходов.

7. (ЕГЭ) Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим все возможные исходы.

По условию, купленное в магазине стекло для автомобильной фары оказалось бракованным. Как это могло получиться?

Стекло сделано либо на первой фабрике, либо на второй. Эти события несовместны.

Вероятность того, что стекло с первой фабрики, равна 0,45.

Вероятность того, что стекло сделано на второй фабрике, равна 0,55.

Первая фабрика выпускает 3% бракованных стекол. Значит, с вероятностью 0,03 стекло, произведенное на первой фабрике, бракованное.

Вторая фабрика выпускает 1% бракованных стекол. Значит, с вероятностью 0,01 сделанное на ней стекло бракованное.

Покупатель купил бракованное стекло. Оно могло быть сделано на первой фабрике и оказалось бракованным. Это означает одновременное наступление, или произведение, двух независимых случайных событий – «стекло сделано на первой фабрике» и «стекло бракованное». Вероятность произведения этих двух событий равна

Или другой случай. Стекло могло быть со второй фабрики и также бракованное. Вероятность одновременного наступления этих двух событий равна События «стекло с первой фабрики» и «стекло со второй фабрики» несовместны – они не могут случиться одновременно.
Вероятность суммы несовместных событий равна сумме вероятностей.

Значит, вероятность купить бракованное стекло равна:

Ответ: 0,019.

Следующая задача будет интересна и старшеклассникам, и студентам. В самом деле – как быть, если вы пришли на экзамен, выучив всего 20 билетов из 30? Идти отвечать первым? Или вторым? Или предпоследним? В каком случае вероятность вытянуть билет, который ты выучил, будет наибольшей?

8. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?

Назовем билеты, которые студент выучил, «счастливыми».
Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна

Если идти отвечать вторым, возможны два случая:

1) Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.

2) Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.

Нарисуем схему возможных исходов, как всегда делаем в подобных задачах:

Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.

Конечно, это были самые простые задачи по теории вероятностей. Такие, которые встречаются на ЕГЭ по математике.

Продолжение:
Задание 4 Профильного ЕГЭ по математике. Теория вероятностей
Теория вероятностей. Парадокс Монти Холла

Формулы вероятности — список основных формул вероятности с примерами

• • Классы
    • Класс 1-3
    • Класс 4-5
    • Класс 6-10
    • Класс 11-12
  • КОНКУРСНЫЙ ЭКЗАМЕН
    • BNAT 000 NC
      • 000 NC Книги
        • Книги NCERT для класса 5
        • Книги NCERT для класса 6
        • Книги NCERT для класса 7
        • Книги NCERT для класса 8
        • Книги NCERT для класса 9
        • Книги NCERT для класса 10
        • Книги NCERT для класса 11
        • Книги NCERT для класса 12
      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT 9000 9000
        • NCERT Exemplar Class
          • Решения RS Aggarwal, класс 12
          • Решения RS Aggarwal, класс 11
          • Решения RS Aggarwal, класс 10
          90 003 Решения RS Aggarwal класса 9
          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • RD Sharma Class 6 Решения
          • Решения RD Sharma
          Решения RD Sharma Class 8
          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12
        • PHYSICS
          • Механика
          • Оптика
          • Термодинамика Электромагнетизм
        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица
        • MATHS
          • Теорема Пифагора
          0004
          • 000300030004
          • Простые числа
          • Взаимосвязи и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Деление фракций
        • 000
        • 000
        • 000
        • 000
        • 000
        • 000 Microology
        • 000
        • 000 Microology
        • 000 BIOG3000
          FORMULAS
          • Математические формулы
          • Алгебраические формулы
          • Тригонометрические формулы
          • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы
            • 0003000 PBS4000
            • 000300030002 Примеры калькуляторов химии
            Класс 6
            • Образцы бумаги CBSE для класса 7
            • Образцы бумаги CBSE для класса 8
            • Образцы бумаги CBSE для класса 9
            • Образцы бумаги CBSE для класса 10
            • Образцы бумаги CBSE для класса 11
            • Образцы бумаги CBSE чел для класса 12
          • CBSE Контрольный документ за предыдущий год
            • CBSE Контрольный документ за предыдущий год Класс 10
            • Контрольный документ за предыдущий год CBSE, класс 12
          • HC Verma Solutions
            • HC Verma Solutions Class 11 Physics
            • Решения HC Verma, класс 12, физика
          • Решения Лакмира Сингха
            • Решения Лакмира Сингха, класс 9
            • Решения Лакмира Сингха, класс 10
            • Решения Лакмира Сингха, класс 8
          • Заметки CBSE
          • , класс
            CBSE Notes
            Примечания CBSE класса 7
            • Примечания CBSE класса 8
            • Примечания CBSE класса 9
            • Примечания CBSE класса 10
            • Примечания CBSE класса 11
            • Примечания CBSE класса 12
            • Примечания к редакции CBSE
              • Примечания к редакции
              • CBSE
              • Примечания к редакции класса 10 CBSE
              • Примечания к редакции класса 11 CBSE 9000 4
              • Примечания к редакции класса 12 CBSE
            • Дополнительные вопросы CBSE
              • Дополнительные вопросы по математике класса 8 CBSE
              • Дополнительные вопросы по науке 8 класса CBSE
              • Дополнительные вопросы по математике класса 9 CBSE
              • Дополнительные вопросы по науке класса 9 CBSE
              Дополнительные вопросы по математике для класса 10
              • Дополнительные вопросы по науке, класс 10 по CBSE
            • CBSE, класс
              • , класс 3
              • , класс 4
              • , класс 5
              • , класс 6
              • , класс 7
              • , класс 8
              • , класс 9 Класс 10
              • Класс 11
              • Класс 12
            • Учебные решения
          • Решения NCERT
            • Решения NCERT для класса 11
              • Решения NCERT для класса 11 по физике
              • Решения NCERT для класса 11 Химия
              Решения для биологии класса 11
              • Решения NCERT для математики класса 11
              9 0003 NCERT Solutions Class 11 Accountancy
              • NCERT Solutions Class 11 Business Studies
              • NCERT Solutions Class 11 Economics
              • NCERT Solutions Class 11 Statistics
              • NCERT Solutions Class 11 Commerce
            • NCERT Solutions For Class 12
              • NCERT Solutions For Класс 12 по физике
              • Решения NCERT для химии класса 12
              • Решения NCERT для класса 12 по биологии
              • Решения NCERT для класса 12 по математике
              • Решения NCERT Класс 12 Бухгалтерия
              • Решения NCERT, класс 12, бизнес-исследования
              • Решения NCERT, класс 12 Экономика
              • NCERT Solutions Class 12 Accountancy Part 1
              • NCERT Solutions Class 12 Accountancy Part 2
              • NCERT Solutions Class 12 Micro-Economics
              • NCERT Solutions Class 12 Commerce
              • NCERT Solutions Class 12 Macro-Economics
            • NCERT Solutions For Класс 4
              • Решения NCERT для математики класса 4
              • Решения NCERT для класса 4 EVS
            • Решения NCERT для класса 5
              • Решения NCERT для математики класса 5
              • Решения NCERT для класса 5 EVS
            • Решения NCERT для класса 6
              • Решения NCERT для математики класса 6
              • Решения NCERT для науки класса 6
              • Решения NCERT для социальных наук класса 6
              • Решения NCERT для класса 6 Английский
            • Решения NCERT для класса 7
              • Решения NCERT для класса 7 Математика
              • Решения NCERT для класса 7 Наука
              • Решения NCERT для класса 7 по социальным наукам
              • Решения NCERT для класса 7 Английский
            • Решения NCERT для класса 8
              • Решения NCERT для класса 8 Математика
              • Решения NCERT для класса 8 Science
              • Решения NCERT для социальных наук 8 класса
              • Решение NCERT ns для класса 8 Английский
            • Решения NCERT для класса 9
              • Решения NCERT для социальных наук класса 9
            • Решения NCERT для математики класса 9
              • Решения NCERT для математики класса 9 Глава 1
              • Решения NCERT для Математика класса 9 Глава 2
              • Решения NCERT для математики класса 9 Глава 3
              • Решения NCERT для математики класса 9 Глава 4
              Решения NCERT
              • для математики класса 9 Глава 5
              • Решения NCERT для математики класса 9 Глава 6
              • Решения NCERT для Математика класса 9 Глава 7
              • Решения NCERT для математики класса 9 Глава 8
              Решения NCERT
              • для математики класса 9 Глава 9
              Решения NCERT
              • для математики класса 9 Глава 10
              • Решения NCERT для математики класса 9 Глава 11
              • Решения NCERT для Математика класса 9 Глава 12
              • Решения NCERT для математики класса 9 Глава 13
              Решения
              • NCERT для математики класса 9 Глава 14
              • Решения NCERT для математики класса 9 Глава 15
            • Решения NCERT для науки класса 9
              • Решения NCERT для науки класса 9 Глава 1
              • Решения NCERT для науки класса 9 Глава 2
              • Решения NCERT для класса 9 Наука Глава 3
              • Решения NCERT для Науки Класса 9 Глава 4
              • Решения NCERT для Науки Класса 9 Глава 5
              • Решения NCERT для Науки Класса 9 Глава 6
              • Решения NCERT для Науки Класса 9 Глава 7
              • Решения NCERT для Класса 9 Наука Глава 8
              • Решения NCERT для Науки Класса 9 Глава 9
              • Решения NCERT для Науки Класса 9 Глава 10
              • Решения NCERT для Науки Класса 9 Глава 12
              • Решения NCERT для Науки Класса 9 Глава 11
              • Решения NCERT для Класса 9 Наука Глава 13
              • Решения NCERT для класса 9 Наука Глава 14
              • Решения NCERT для класса 9 по науке Глава 15
            • Решения NCERT для класса 10
              • Решения NCERT для класса 10 по социальным наукам
            • Решения NCERT для математики класса 10
              • Решения NCERT для математики класса 10 Глава 1
              • Решения NCERT для математики класса 10 Глава 2
              • Решения NCERT для математики класса 10 Глава 3
              • Решения NCERT для математики класса 10 Глава 4
              • Решения NCERT для математики класса 10 Глава 5
              • Решения NCERT для математики класса 10 Глава 6
              • Решения NCERT для математики класса 10 Глава 7
              • Решения NCERT для математики класса 10 Глава 8
              • Решения NCERT для математики класса 10 Глава 9
              Решения NCERT
              • для математики класса 10 Глава 10
              Решения
              • NCERT для математики класса 10 Глава 11
              • Решения NCERT для математики класса 10 Глава 12
              • Решения NCERT для математики класса 10 Глава 13
              • NCERT Sol Решения NCERT для математики класса 10 Глава 14
              • Решения NCERT для математики класса 10 Глава 15
            • Решения NCERT для науки класса 10
              • Решения NCERT для науки класса 10 Глава 1
              • Решения NCERT для науки класса 10 Глава 2
              • Решения NCERT для науки класса 10, глава 3
              • Решения NCERT для науки класса 10, глава 4
              • Решения NCERT для науки класса 10, глава 5
              • Решения NCERT для науки класса 10, глава 6
              • Решения NCERT для науки класса 10, глава 7
              • Решения NCERT для науки 10 класса, глава 8
              • Решения NCERT для науки класса 10 Глава 9
              • Решения NCERT для науки класса 10 Глава 10
              • Решения NCERT для науки класса 10 Глава 11
              • Решения NCERT для науки класса 10 Глава 12
              • Решения NCERT для науки 10 класса Глава 13
              • Решения NCERT для науки 10 класса Глава 14
              • Решения NCERT для науки 10 класса Глава 15
              • Решения NCERT для науки 10 класса Глава 16
            • Учебный план NCERT
            • NCERT
          • Commerce
            • Class 11 Commerce Syllabus
              ancy Account
      .

      Вероятность

      Как вероятно что-то должно произойти.

      Многие события невозможно предсказать с полной уверенностью. Лучшее, что мы можем сказать, — это насколько вероятных они должны произойти, используя идею вероятности.

      Подбрасывание монеты

      Когда монета подбрасывается, возможны два исхода:

      Мы говорим, что вероятность выпадения монеты H равна ½

      А вероятность выпадения монеты T составляет ½

      Игра в кости

      Когда бросается один кубик, есть шесть возможных результатов: 1, 2, 3, 4, 5, 6 .

      Вероятность любого из них — 1 6

      Вероятность

      Всего:

      Вероятность наступления события = Количество способов, которыми это может случиться Общее количество исходов

      Пример: вероятность выпадения «4» на кубике

      Количество способов, которыми это может произойти: 1 (есть только 1 грань с цифрой «4»)

      Всего исходов: 6 (всего 6 граней)

      Таким образом, вероятность = 1 6

      Пример: в сумке 5 шариков: 4 синих и 1 красный.Какова вероятность, что синий шарик будет сорван?

      Количество способов, которыми это может случиться: 4 (всего 4 голубых)

      Всего исходов: 5 (всего 5 шариков)

      Таким образом, вероятность = 4 5 = 0,8

      Линия вероятности

      Мы можем показать вероятность на линии вероятности:

      Вероятность всегда от 0 до 1

      Вероятность — всего лишь ориентир

      Вероятность не говорит нам, что именно произойдет, это всего лишь ориентир

      Пример: подбросьте монету 100 раз, сколько выпадет орлов?

      Вероятность говорит, что у орла ½ шанса, так что можно ожидать 50 голов .

      Но , когда мы на самом деле попробуем его, мы можем получить 48 или 55 голов … или что-то еще, но в большинстве случаев это будет число около 50.

      Узнайте больше на сайте Probability Index.

      слов

      Некоторые слова имеют особое значение в Вероятности:

      Эксперимент: повторяемая процедура с набором возможных результатов.

      Пример: бросание кости

      Мы можем бросать кости снова и снова, так что это повторяется.

      Набор возможных результатов любого одиночного броска: {1, 2, 3, 4, 5, 6}

      Результат: Возможный результат эксперимента.

      Пример: получение «6»

      Sample Space: всех возможных результатов эксперимента.

      Пример: выбор карты из колоды

      В колоде 52 карты (не считая Джокеров)

      Таким образом, пробел — это все 52 возможных карты : {Туз червей, 2 червей и т. Д…}

      Пробное пространство состоит из контрольных точек:

      Точка выборки: только один из возможных исходов

      Пример: колода карт

      • пятерка треф — пробная точка
      • Король червей — точка отсчета

      «Король» не является точкой отбора проб. Всего 4 короля, так что это 4 различных точек выборки.

      Пример: бросание кости

      В пространстве выборки имеется 6 различных точек выборки.

      Событие: один или более результатов эксперимента

      Пример событий:

      У события может быть только один исход:

      • Получение хвоста при подбрасывании монеты
      • Прокатка «5»

      Событие может включать более одного результата:

      • Выбор «короля» из колоды карт (любой из 4 королей)
      • Выпадение «четного числа» (2, 4 или 6)

      Эй, давайте использовать эти слова, чтобы вы к ним привыкли:

      Пример: Алекс хочет посмотреть, сколько раз выпадет «дубль» при бросании 2 кубиков.

      Пространство выборки — все возможные Результаты (36 точек выборки):

      {1,1} {1,2} {1,3} {1,4} … {6,3} {6,4} {6,5} {6,6}

      Событие , которое ищет Алекс, — это «дабл», где оба кубика имеют одинаковое число. Он состоит из этих 6 точек выборки :

      {1,1} {2,2} {3,3} {4,4} {5,5} и {6,6}

      Это результаты Алекса:

      Эксперимент	Это дубль?
      {3,4}	№
      {5,1}	№
      {2,2}	Есть
      {6,3}	№
      …	…

      После 100 экспериментов , у Алекса есть 19 двойных событий … это близко к тому, что вы ожидали?

      ,Формула вероятности

      | Введение в формулы вероятности с примерами

      Вы, должно быть, слышали, что термин «вероятность» был придуман для предсказания прогноза погоды в новостных телеканалах на следующие несколько дней для некоторых частей страны. Для расчета вероятности различных типов ситуаций используется формула вероятности и связанные с ней основные понятия. Вероятность — это способ измерить неопределенность того, насколько вероятно событие произошло или должно произойти.

      Есть несколько важных терминов, которые связаны с формулой всех вероятностей .

      
      

    • • Эксперимент : любая ситуация или явление, такое как подбрасывание монеты, бросание кубиков и т. Д.
    
    
    • • Результат : Результат события после проведения эксперимента, подобный стороне монета после подбрасывания, число, выпадающее на кости после броска, и карта вытаскивается из колоды хорошо перемешанных карт и т.
    
    
    • • Событие : комбинация всех возможных результатов эксперимента, таких как выпадение орла или решки на подброшенной монете, получение четного или нечетного числа на кубиках и т. Д.
    
    
    • • Sample Space : Набор всех возможных результатов или исходов.
    
    
    • • Функция вероятности : функция помогает получить вероятность каждого исхода.
    
    Probabili ty Формулы с примерами
    Формула вероятности обеспечивает отношение количества благоприятных исходов к общему количеству возможных исходов
    
    Вероятность события = (Количество благоприятных исходов). исходов) / (Общее количество возможных исходов)
    P (A) = n (E) / n (S)
    P (A) Здесь P (A) означает нахождение вероятности события A, n (E) означает количество благоприятных исходов события, а n (S) означает множество всех возможных исходов события.

    Если вероятность наступления события равна P (A), то вероятность того, что событие не произойдет, равна
    
    

    Vedantu обеспечивает лучшее понимание основных формул вероятности на примере

    Пример 01: Вероятность выпадения нечетного числа при бросании кубиков хоть раз.
    
    

    Решение: Пространство выборки = {1, 2, 3, 4, 5, 6}
    n (S) = 6
    Благоприятные исходы = {1, 3, 5}
    n (E) = 3
    Используя формулу вероятности,
    
    

    P (Получение нечетного числа) = 3/6 = ½ = 0.5

    Важный список формул вероятности
    
    

    Событие (A OR B)
    P (AUB) = P (A) + P (B) — P (A ∩ B)
    
    

    Событие (A И B)
    P (A ∩ B) = P (A). P (B)
    
    

    Событие (A НЕ B)
    P (A NOT B) = A — B
    
    

    Событие (B NOT A)
    P (B NOT A) = B — A
    
    

    Вероятность возникновения события равна P (A) Вероятность того, что такое же событие не произойдет, равна P (A ‘).

    Примерно важных для вероятности формул , основанных на них, следующие:

    
    

    • • P (A.A ‘) = 0
    
    
    • • P (AB) + P (A’.B’) = 1
    
    
    • • P (A’B) = P (B) — P (AB)
    
    
    • • P (A.B ‘) = P (A) — P (AB)
    
    
    • • P (A + B) = P (AB ‘) + P (A’B) + P (AB)
    
    Пример 01: Два кубика бросаются одновременно. Вычислите вероятность того, что сумма чисел на двух кубиках равна 6.
    
    
    Решение: Пробел образца = [{(1, 1), (1, 2), (1,3), ( 1,4), (1,5), (1, 6)} {(2, 1), (2, 2), (2,3), (2,4), (2,5), (2 , 6)} {(3, 1), (3, 2), (3,3), (3,4), (3,5), (3, 6)} {(4, 1), (4 , 2), (4,3), (4,4), (4,5), (4, 6)} {(5, 1), (5,2), (5,3), (5, 4), (5,5), (5, 6)} {(6, 1), (6, 2), (6,3), (6,4), (6,5), (6, 6 )}] п (S) = 36 Благоприятные исходы = {(1, 5), (2, 4), (3, 3), (4, 2) и (5, 1)} n (E) = 5 Использование, P (A) = n (E) / n (S)

    P (Получение суммы чисел на двух кубиках 6) = 5/36
    
    

    Чего ожидать от Vedantu ?
    
    

    В Веданту есть список базовых и расширенных формул вероятности , необходимых в каждой программе для 6-12 классов

    
    
    • • Студенты могут получить доступ к бесплатным формулам в любое время.
    
    
    • • Математические формулы по главам могут быть загружены в формате PDF для учащихся 6-12 классов.
    
    
    • • Студенты могут получить доступ к важным примечаниям к пересмотру, образцам работ, учебным материалам и вопросам для практики.
    
    
    • • Веданту использует уникальную методологию для решения различных математических задач. Таким образом, учащиеся смогут легко понять основы проблемы и решения без каких-либо затруднений.
    
    Студенты могут получить доступ к основным учебным материалам от Vedantu, таким как решения RS Aggarwal, решения RD Sharma, решения NCERT и т. Д.Эти решения могут быть полезны в расширении представлений о вероятности и применении каждой формулы.

    Для практики

    Два кубика бросаются одновременно. Вероятность выпадения четных чисел на обеих костях равна
    a. $ \ Гидроразрыва {1} {4} $ б. $ \ Гидроразрыва {3} {4} $ с. $ \ Гидроразрыва {2} {{35}} $ д. $ \ frac {{11}} {{36}}
    долларов США

    ,

    Теоретическое определение вероятности, формула и пример.

    • • Классы
        • Класс 1-3
        • Класс 4-5
        • Класс 6-10
        • Класс 11-12
      • КОНКУРСНЫЙ ЭКЗАМЕН
        • BNAT 000 NC
          • 000 NC Книги
            • Книги NCERT для класса 5
            • Книги NCERT для класса 6
            • Книги NCERT для класса 7
            • Книги NCERT для класса 8
            • Книги NCERT для класса 9
            • Книги NCERT для класса 10
            • Книги NCERT для класса 11
            • Книги NCERT для класса 12
          • NCERT Exemplar
            • NCERT Exemplar Class 8
            • NCERT Exemplar Class 9
            • NCERT Exemplar Class 10
            • NCERT Exemplar Class 11
            • NCERT 9000 9000
            • NCERT Exemplar Class
              • Решения RS Aggarwal, класс 12
              • Решения RS Aggarwal, класс 11
              • Решения RS Aggarwal, класс 10
              90 003 Решения RS Aggarwal класса 9
              • Решения RS Aggarwal класса 8
              • Решения RS Aggarwal класса 7
              • Решения RS Aggarwal класса 6
            • Решения RD Sharma
              • RD Sharma Class 6 Решения
              • Решения RD Sharma
              Решения RD Sharma Class 8
              • Решения RD Sharma Class 9
              • Решения RD Sharma Class 10
              • Решения RD Sharma Class 11
              • Решения RD Sharma Class 12
            • PHYSICS
              • Механика
              • Оптика
              • Термодинамика Электромагнетизм
            • ХИМИЯ
              • Органическая химия
              • Неорганическая химия
              • Периодическая таблица
            • MATHS
              • Теорема Пифагора
              0004
              • 000300030004
              • Простые числа
              • Взаимосвязи и функции
              • Последовательности и серии
              • Таблицы умножения
              • Детерминанты и матрицы
              • Прибыль и убыток
              • Полиномиальные уравнения
              • Деление фракций
            • 000
            • 000
            • 000
            • 000
            • 000
            • 000 Microology
            • 000
            • 000 Microology
            • 000 BIOG3000
              FORMULAS
              • Математические формулы
              • Алгебраические формулы
              • Тригонометрические формулы
              • Геометрические формулы
              • КАЛЬКУЛЯТОРЫ
                • Математические калькуляторы
                • 0003000 PBS4000
                • 000300030002 Примеры калькуляторов химии
                Класс 6
                • Образцы бумаги CBSE для класса 7
                • Образцы бумаги CBSE для класса 8
                • Образцы бумаги CBSE для класса 9
                • Образцы бумаги CBSE для класса 10
                • Образцы бумаги CBSE для класса 11
                • Образцы бумаги CBSE чел для класса 12
              • CBSE Контрольный документ за предыдущий год
                • CBSE Контрольный документ за предыдущий год Класс 10
                • Контрольный документ за предыдущий год CBSE, класс 12
              • HC Verma Solutions
                • HC Verma Solutions Class 11 Physics
                • Решения HC Verma, класс 12, физика
              • Решения Лакмира Сингха
                • Решения Лакмира Сингха, класс 9
                • Решения Лакмира Сингха, класс 10
                • Решения Лакмира Сингха, класс 8
              • Заметки CBSE
              • , класс
                CBSE Notes
                Примечания CBSE класса 7
                • Примечания CBSE класса 8
                • Примечания CBSE класса 9
                • Примечания CBSE класса 10
                • Примечания CBSE класса 11
                • Примечания CBSE класса 12
                • Примечания к редакции CBSE
                  • Примечания к редакции
                  • CBSE
                  • Примечания к редакции класса 10 CBSE
                  • Примечания к редакции класса 11 CBSE 9000 4
                  • Примечания к редакции класса 12 CBSE
                • Дополнительные вопросы CBSE
                  • Дополнительные вопросы по математике класса 8 CBSE
                  • Дополнительные вопросы по науке 8 класса CBSE
                  • Дополнительные вопросы по математике класса 9 CBSE
                  • Дополнительные вопросы по науке класса 9 CBSE
                  Дополнительные вопросы по математике для класса 10
                  • Дополнительные вопросы по науке, класс 10 по CBSE
                • CBSE, класс
                  • , класс 3
                  • , класс 4
                  • , класс 5
                  • , класс 6
                  • , класс 7
                  • , класс 8
                  • , класс 9 Класс 10
                  • Класс 11
                  • Класс 12
                • Учебные решения
              • Решения NCERT
                • Решения NCERT для класса 11
                  • Решения NCERT для класса 11 по физике
                  • Решения NCERT для класса 11 Химия
                  Решения для биологии класса 11
                  • Решения NCERT для математики класса 11
                  9 0003 NCERT Solutions Class 11 Accountancy
                  • NCERT Solutions Class 11 Business Studies
                  • NCERT Solutions Class 11 Economics
                  • NCERT Solutions Class 11 Statistics
                  • NCERT Solutions Class 11 Commerce
                • NCERT Solutions For Class 12
                  • NCERT Solutions For Класс 12 по физике
                  • Решения NCERT для химии класса 12
                  • Решения NCERT для класса 12 по биологии
                  • Решения NCERT для класса 12 по математике
                  • Решения NCERT Класс 12 Бухгалтерия
                  • Решения NCERT, класс 12, бизнес-исследования
                  • Решения NCERT, класс 12 Экономика
                  • NCERT Solutions Class 12 Accountancy Part 1
                  • NCERT Solutions Class 12 Accountancy Part 2
                  • NCERT Solutions Class 12 Micro-Economics
                  • NCERT Solutions Class 12 Commerce
                  • NCERT Solutions Class 12 Macro-Economics
                • NCERT Solutions For Класс 4
                  • Решения NCERT для математики класса 4
                  • Решения NCERT для класса 4 EVS
                • Решения NCERT для класса 5
                  • Решения NCERT для математики класса 5
                  • Решения NCERT для класса 5 EVS
                • Решения NCERT для класса 6
                  • Решения NCERT для математики класса 6
                  • Решения NCERT для науки класса 6
                  • Решения NCERT для социальных наук класса 6
                  • Решения NCERT для класса 6 Английский
                • Решения NCERT для класса 7
                  • Решения NCERT для класса 7 Математика
                  • Решения NCERT для класса 7 Наука
                  • Решения NCERT для класса 7 по социальным наукам
                  • Решения NCERT для класса 7 Английский
                • Решения NCERT для класса 8
                  • Решения NCERT для класса 8 Математика
                  • Решения NCERT для класса 8 Science
                  • Решения NCERT для социальных наук 8 класса
                  • Решение NCERT ns для класса 8 Английский
                • Решения NCERT для класса 9
                  • Решения NCERT для социальных наук класса 9
                • Решения NCERT для математики класса 9
                  • Решения NCERT для математики класса 9 Глава 1
                  • Решения NCERT для Математика класса 9 Глава 2
                  • Решения NCERT для математики класса 9 Глава 3
                  • Решения NCERT для математики класса 9 Глава 4
                  Решения NCERT
                  • для математики класса 9 Глава 5
                  • Решения NCERT для математики класса 9 Глава 6
                  • Решения NCERT для Математика класса 9 Глава 7
                  • Решения NCERT для математики класса 9 Глава 8
                  Решения NCERT
                  • для математики класса 9 Глава 9
                  Решения NCERT
                  • для математики класса 9 Глава 10
                  • Решения NCERT для математики класса 9 Глава 11
                  • Решения NCERT для Математика класса 9 Глава 12
                  • Решения NCERT для математики класса 9 Глава 13
                  Решения
                  • NCERT для математики класса 9 Глава 14
                  • Решения NCERT для математики класса 9 Глава 15
                • Решения NCERT для науки класса 9
                  • Решения NCERT для науки класса 9 Глава 1
                  • Решения NCERT для науки класса 9 Глава 2
                  • Решения NCERT для класса 9 Наука Глава 3
                  • Решения NCERT для Науки Класса 9 Глава 4
                  • Решения NCERT для Науки Класса 9 Глава 5
                  • Решения NCERT для Науки Класса 9 Глава 6
                  • Решения NCERT для Науки Класса 9 Глава 7
                  • Решения NCERT для Класса 9 Наука Глава 8
                  • Решения NCERT для Науки Класса 9 Глава 9
                  • Решения NCERT для Науки Класса 9 Глава 10
                  • Решения NCERT для Науки Класса 9 Глава 12
                  • Решения NCERT для Науки Класса 9 Глава 11
                  • Решения NCERT для Класса 9 Наука Глава 13
                  • Решения NCERT для класса 9 Наука Глава 14
                  • Решения NCERT для класса 9 по науке Глава 15
                • Решения NCERT для класса 10
                  • Решения NCERT для класса 10 по социальным наукам
                • Решения NCERT для математики класса 10
                  • Решения NCERT для математики класса 10 Глава 1
                  • Решения NCERT для математики класса 10 Глава 2
                  • Решения NCERT для математики класса 10 Глава 3
                  • Решения NCERT для математики класса 10 Глава 4
                  • Решения NCERT для математики класса 10 Глава 5
                  • Решения NCERT для математики класса 10 Глава 6
                  • Решения NCERT для математики класса 10 Глава 7
                  • Решения NCERT для математики класса 10 Глава 8
                  • Решения NCERT для математики класса 10 Глава 9
                  Решения NCERT
                  • для математики класса 10 Глава 10
                  Решения
                  • NCERT для математики класса 10 Глава 11
                  • Решения NCERT для математики класса 10 Глава 12
                  • Решения NCERT для математики класса 10 Глава 13
                  • NCERT Sol Решения NCERT для математики класса 10 Глава 14
                  • Решения NCERT для математики класса 10 Глава 15
                • Решения NCERT для науки класса 10
                  • Решения NCERT для науки класса 10 Глава 1
                  • Решения NCERT для науки класса 10 Глава 2
                  • Решения NCERT для науки класса 10, глава 3
                  • Решения NCERT для науки класса 10, глава 4
                  • Решения NCERT для науки класса 10, глава 5
                  • Решения NCERT для науки класса 10, глава 6
                  • Решения NCERT для науки класса 10, глава 7
                  • Решения NCERT для науки 10 класса, глава 8
                  • Решения NCERT для науки класса 10 Глава 9
                  • Решения NCERT для науки класса 10 Глава 10
                  • Решения NCERT для науки класса 10 Глава 11
                  • Решения NCERT для науки класса 10 Глава 12
                  • Решения NCERT для науки 10 класса Глава 13
                  • Решения NCERT для науки 10 класса Глава 14
                  • Решения NCERT для науки 10 класса Глава 15
                  • Решения NCERT для науки 10 класса Глава 16
                • Учебный план NCERT
                • NCERT
              • Commerce
                • Class 11 Commerce Syllabus
                  ancy Account
                  • Программа бизнес-исследований 11 класса
                  • Учебная программа по экономике 11 класса
                • Учебная программа по коммерции 12 класса
                  • Учебная программа по бухгалтерии 12 класса
                  • Учебная программа по бизнесу 12 класса
                  • Учебная программа по экономике
                  • 9000 9000
                    • Образцы документов по коммерции класса 11
                    • Образцы документов по коммерции класса 12
                    • TS Grewal Solutions
                      • TS Grewal Solutions Class 12 Accountancy
                      • TS Grewal Solutions Class 11 Accountancy
                    • Отчет о движении денежных средств
                    • Что такое Entry eurship
                    • Защита прав потребителей
                    • Что такое основной актив
                    • Что такое баланс
                    • Формат баланса
                    • Что такое акции
                    • Разница между продажами и маркетингом
                  • ICSE
                    • Документы
                    • ICSE
                    • Вопросы ICSE
                    • ML Aggarwal Solutions
                      • ML Aggarwal Solutions Class 10 Maths
                      • ML Aggarwal Solutions Class 9 Maths
                      • ML Aggarwal Solutions Class 8 Maths
                      • ML Aggarwal Solutions Class 7 Maths
                      • ML 6 Maths
                      • ML 6 Maths
                    • Selina Solutions
                      • Selina Solutions для класса 8
                      • Selina Solutions для Class 10
                      • Selina Solutions для Class 9
                    • Frank Solutions
                      • Frank Solutions для математики класса 10
                      • Frank Solutions для математики класса 9
                    • Класс ICSE 9000 2
                    • ICSE Class 6
                    • ICSE Class 7
                    • ICSE Class 8
                    • ICSE Class 9
                    • ICSE Class 10
                    • ISC Class 11
                    • ISC Class 12
                • IAS
                  Exam
                  • IAS
                  • Civil
                  • Сервисный экзамен
                  • Программа UPSC
                  • Бесплатная подготовка к IAS
                  • Текущие события
                  • Список статей IAS
                  • Пробный тест IAS 2019
                    • Пробный тест IAS 2019 1
                    • Пробный тест IAS 2019 2
                • Экзамен KPSC KAS
                • Экзамен UPPSC PCS
                • Экзамен MPSC
                • Экзамен RPSC RAS ​​
                • TNPSC Group 1
                • APPSC Group 1
                • Экзамен BPSC
                • WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
                • Вопросник UPSC 2019
                  • Ключ ответов UPSC 2019
                • Коучинг IAS
                  • IA S Coaching Бангалор
                  • IAS Coaching Дели
                  • IAS Coaching Ченнаи
                  • IAS Coaching Хайдарабад
                  • IAS Coaching Mumbai
              • JEE
                • BYJU’SEE
                • 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
                • Вопросник JEE
                • Биномиальная теорема
                • Статьи JEE
                • Квадратичное уравнение
              • NEET
                • Программа BYJU NEET
                • NEET 2020
                • NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
                • Поддержка
                  • Разрешение жалоб
                  • Служба поддержки
                  • Центр поддержки
              • Государственные советы
                • GSEB
                  • GSEB Syllabus
                  • GSEB4
                  • GSEB3 Образец статьи
                  GSEB3 004
                  • MSBSHSE
                    • MSBSHSE Syllabus
                    • MSBSHSE Учебники
                    • Образцы статей MSBSHSE
                    • Вопросники MSBSHSE
                  • AP Board
                    • APSCERT
                    • Syll
                    • AP 9000SC4
                    • Syll
                    • AP
                    • Syll 9000SC4
                    • Syll
                    • Syll
                  • MP Board
                    • MP Board Syllabus
                    • MP Board Образцы документов
                    • Учебники MP Board
                  • Assam Board
                    • Assam Board Syllabus
                    • Assam Board Учебники 9000 9000 Board4 BSEB
                      • Bihar Board Syllabus
                      • Bihar Board Учебники
                      • Bihar Board Question Papers
                      • Bihar Board Model Papers
                    • BSE Odisha
                      • Odisha Board Syllabus
                      • Odisha Board Syllabus
                      • Odisha Board Syllabus
                      • Программа PSEB
                      • Учебники PSEB
                      • Вопросы PSEB
                    • RBSE
                      • Rajasthan Board Syllabus
                      • RBSE Учебники
                      • RBSE Question Papers
                    • HPBOSE
                    • HPBOSE
                    • HPBOSE
                    • JKBOSE
                      • Программа обучения JKBOSE
                      • Образцы документов JKBOSE
                      • Шаблон экзамена JKBOSE
                    • TN Board
                      • TN Board Syllabus
                      • TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
                        • Программа JAC
                        • Учебники JAC
                        • Вопросники JAC
                      • Telangana Board
                        • Telangana Board Syllabus
                        • Telangana Board Учебники
                        • Papers Telangana Board Учебники
                        • Учебный план KSEEB
                        • Типовой вопросник KSEEB
                      • KBPE
                        • Учебный план KBPE
                        • Учебники KBPE
                        • Документы по KBPE
                      • 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000
                    • Совет по Западной Бенгалии
                      • Учебный план Совета по Западной Бенгалии
                      • Учебники для Совета по Западной Бенгалии
                      • Вопросы для Совета по Западной Бенгалии
                    • UBSE
                    • TBSE
                    • Гоа Совет
                    • 000
                    • NBSE0003 Board
                    • Manipur Board
                    • Haryana Board
                  • Государственные экзамены
                    • Банковские экзамены
                      • Экзамены SBI
                      • Экзамены IBPS
                      • Экзамены RBI
                      • IBPS

                        03

                        Экзамены SSC

                        9SC2

                      • SSC GD
                      • SSC CPO 900 04
                      • SSC CHSL
                      • SSC CGL
                    • Экзамены RRB
                      • RRB JE
                      • RRB NTPC
                      • RRB ALP
                    • O Экзамены на страхование
                    • LIC4
                    • LIC4
              .

              No related posts.