Методы расчета сложных электрических цепей постоянного тока — Начало. Основы. — Справочник
Методы расчета сложных электрических цепей постоянного тока
1. Метод узловых и контурных уравнений
В основе расчета лежат первый и второй законы Кирхгофа.
∑I=0
∑E=∑IR
Порядок расчета
- Произвольно выбираем направление тока в ветвях.
- Произвольно выбираем направление обхода контуров.
- Зная полярность источников, проставляем направление ЭДС.
- Составляем уравнения по первому закону Кирхгофа. Их должно быть но одно меньше, чем узлов.
- Составляем уравнения по второму закону Кирхгофа из расчета, что общее число уравнений должно быть равно числу неизвестных токов.
- Решаем систему уравнений и определяем неизвестные токи. Если в результате решения какой-либо ток окажется со знаком «-», то направление его противоположно выбранному.
Приведем пример.
Дано:
- 1=r2=0;
- 1=0,3 Ом;
- 2=1 Ом;
- 3=24 Ом;
Е1=246 В;
Е2=230В
Найти:
I1,I2,I3.
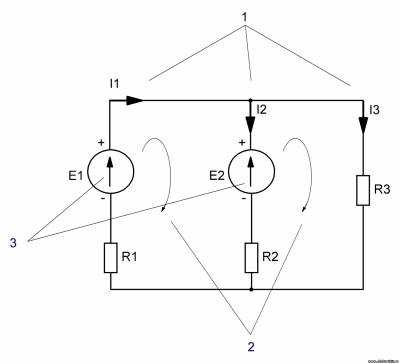
Решение:
Итак, на схеме рисуем направления токов (1), согласно этим направлениям рисуем направления обхода контуров (2), согласно полярности источников питания ставим направления ЭДС (3).
Согласно первому закону Кирхгофа:
I1-I2-I3=0 → -I2=I3-I1
Теперь составляем уравнения по второму закону Кирхгофа:
E1=I1R1+I3R3
Е2=-I2R2+I3R3
Получили систему из трех уравнений. Решаем.
E2=(I3-I1)R2+I3R3
230=I3(1+R3)-I1=25I3-I1 → I1= 25I3-230
E1=I1R1+I3R3=(25I3-230)R1+I3R3
246=0,3(25I3-230)+24I3
246=7,5I3-69+24I3
31,5I
I3=10A
I1=25∙10-230=20A
I2=I1-I3=20-10=10A
2. Метод контурных токов
Этот метод основан на втором законе Кирхгофа
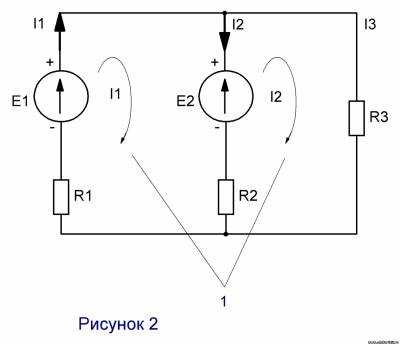
- Произвольно выбираем направления контурных токов (рис.2)
- Составляем уравнения по второму закону Кирхгофа.
E1-E2=I1(R1+R2)-I2R2
E2
=I2(R2+R3)-I1R2
246-230=I1(0,3+1)-I2 → 16=1,3I1-I2 → I2=1,3I1-16
230=25(1,3I1-16)-I1
31,5I1=630
I1=20A
I2=1,3∙20-16=10A
3. Определяем истинные токи.
I1=I1=20A
I2=I1-I2=10A
I3=I2=10A
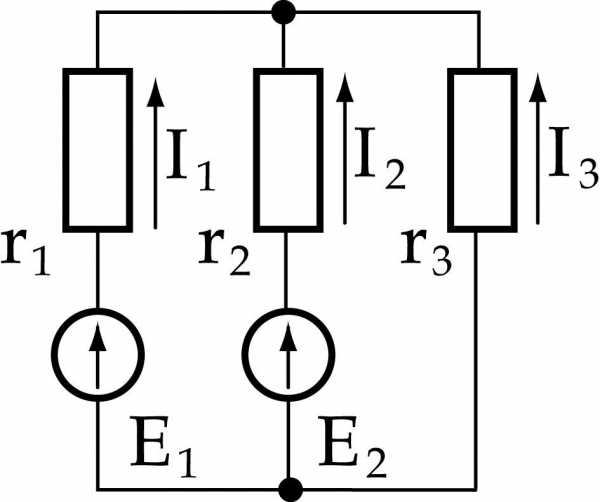
3. Метод двух узлов
Этот метод применим для схем, имеющих два узла
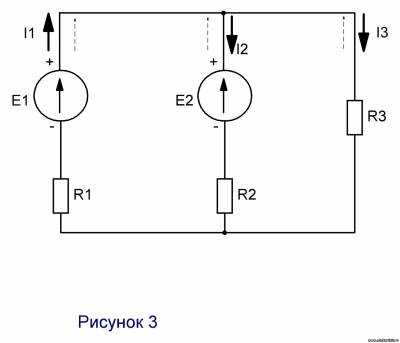
- Выбираем произвольно направления токов в ветвях в одну и ту-же сторону (см. рис.3 – стрелки со штрихами).
- Определяем проводимости ветвей:
q1=1/R1=1/0,3=3,33 Сим.
q2=1/R2=1 Сим.
q3=1/R3=1/24=0,0416 Сим.
- Определяем напряжение между двумя узлами по формуле:
U=∑Eq/∑arq=(E1+E2q2)/(q1+q2+q3)=(246∙3,31+230)/4,3716=240 В
- Определяем токи в ветвях
I=(E-U)q
I1=(E1-U)q1=(246-240)3,33=20A
I2=(E2-U)q2=230-240=-10A
I3=-Uq3=240∙0,0416=-10А
Так как, значения I2 и I3 получились отрицательными, то эти токи будут противоположными по направлению (на рисунке показаны жирные сплошные стрелки).
4. Метод наложения или метод суперпозиции
Метод основан на том, что любой ток в цепи создается совместным действием всех источников питания. Поэтому можно рассчитать частичные токи от действия каждого источника питания отдельно, а затем, найти истинные токи как арифметическую составляющую частичных.
Решение
1. Рис. 4. Е2=0; r2≠0
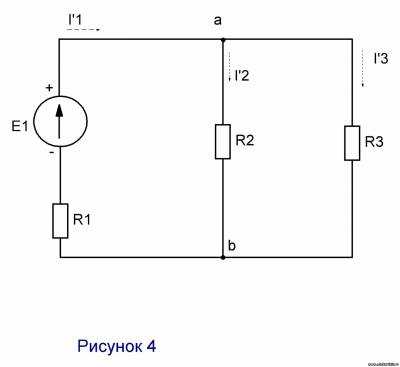
Rэ=R2R3/(R2+R3)+R1=24/25+0,3=0,96+0,3=1,26 Ом
I’1=E1/Rэ=246/1,26=195,23 Ом
Uab=I’1R23=195,23∙0,96=187,42 В
I’2=Uab/R2=187,42 A
I’3= Uab/R3=187,42/24=7,8 A
2. Рис. 5. E1=0; R1≠0
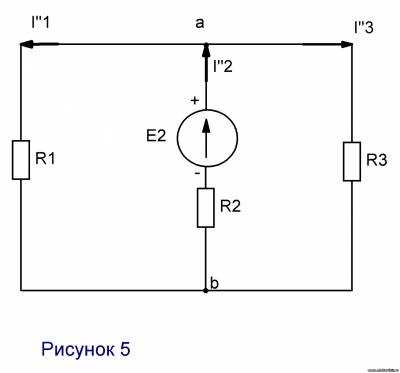
Rэ=R1R3/(R1+R3)+R2=0,3∙24/24,3+1=0,29+1=1,29 Ом
I”2=E2/Rэ=230/1,29=178,29 A
Uab=I”2R13=178,29∙0,29=51,7 В
I”1=Uab/R1=51,7/0,3=172,4 A
I”3=Uab/R3=51,7/24=2,15 A
3. Определяем истинные токи.
I1=I’1-I”1=195,23-172,4=22,83 A
I2=I’2-I”2=187,42-178,29=9,13 A
I3=I’3-I”3=7,8-2,15=5,65 A
www.elektrikii.ru
Задание №1 — Расчет сложной электрической цепи постоянного тока
Задание №1 — Расчет сложной электрической цепи постоянного тока 3
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа. 4
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов 8
Задание № 2 — Расчет электрической цепи переменного синусоидального тока 17
Активная мощность. Единица измерения — ватт (W, Вт). 26
Реактивная мощность. Единица измерения — вольт-ампер реактивный (var, вар) 26
Указания к выбору варианта задания
Электрические схемы, предлагаемые для расчета, пронумерованы. Соответствие варианта и расчетной схемы обозначено в таблице №1 и одинаково для обеих групп. Значения сопротивлений резисторов для студентов групп, номера которых заканчиваются цифрой 1 и 2 приведены в таблицах №3 и №4 соответственно. Значения ЭДС, действующих в ветвях, приведены в таблице №2 (первая строка для всех студентов группы, номер которой заканчивается цифрой 1, вторая строка – для группы, номер которой заканчивается цифрой 2). Внутренними сопротивлениями источников ЭДС следует пренебречь.
Содержание работы
1. Рассчитать токи во всех ветвях электрической цепи
а) методом непосредственного применения правил Кирхгофа;
б) методом контурных токов;
в) методом узловых потенциалов.
Результаты расчетов свести в таблицу.
2. Составить и решить уравнение баланса мощностей.
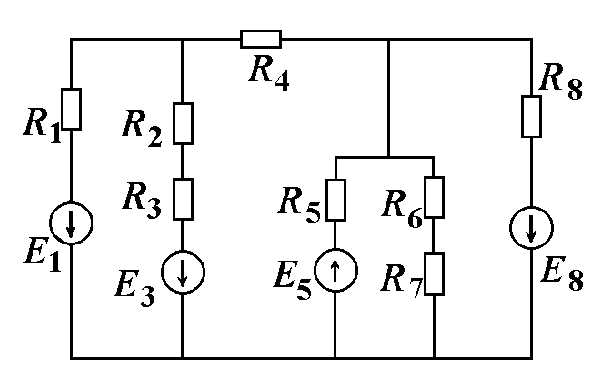
Рисунок 1.1
Таблица 1.1 – Значения параметров, вариант 10
R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | R7, Ом | R8, Ом | Е1, В | Е3, В | Е5, В | Е8, В |
15 | 29 | 8 | 22 | 39 | 19 | 25 | 30 | 10 | 36 | 27 | 26 |
1.1 Расчёт токов в исследуемой электрической цепи путём непосредственного применения законов Кирхгофа.
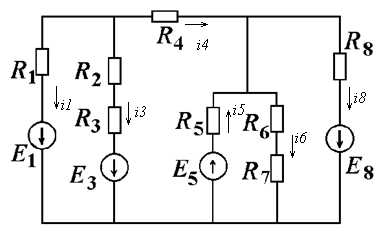
Рисунок 1.2 – Исследуемая схема цепи
Составим систему уравнений, согласно законам Кирхгофа для цепи (рисунок 1.2):
(1)
Решим систему матричным методом:
Находим токи в ветвях:
(2)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.2 Расчёт токов в ветвях методом контурных токов.
Для схемы (1.2 обход по часовой стрелке) составим систему уравнений:
(3)
Решая систему, получаем:
Находим токи в контурах:
(4)
Рассчитаем токи в ветвях:
(5)
(6)
(7)
(8)
(9)
(10)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A), i8 = 0,656(A),
1.3 Расчёт токов во всех ветвях схемы методом узловых потенциалов
Найдём проводимости ветвей схемы.
g1 = 0,067(См), g23 = 0,027 (См), g4 = 0,045 (См),
g5 = 0,026(См), g67= 0,023 (См), g8 = 0,033 (См).
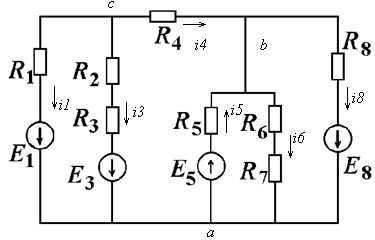
Рисунок 1.3
Запишем уравнения в матричной форме (φа=0):
(11)
Решая систему, получаем:
Находим токи в контурах:
(12)
Рассчитаем токи в ветвях:
(13)
(14)
(15)
(16)
(17)
(18)
i1 = -0,257(A), i3 = 0,599(A), i4 = -0,342(A), i5 = 0,854(A), i6 = -0,144(A),
i8 = 0,656(A),
Таблица 1.2 – Результаты расчётов
i1 | i3 | i4 | i5 | i6 | i8 | |
Законы Кирхгофа | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
Метод контурных токов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
Метод двух узлов | -0,257 | 0,599 | -0,342 | 0,854 | -0,144 | 0,656 |
1.4 Баланс мощностей.
Уравнение баланса мощностей:
(19)
Суммарная мощность источников:
(20)
Суммарная мощность приёмников:
(21)
Контрольные вопросы по теме
«Расчет электрических цепей постоянного тока»
Дайте определение электрической цепи и ее схемы замещения.
Электрическая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитных процессов, в которых могут быть описаны с помощью понятий сила тока и напряжение.
Схема замещения — электрическая схема, в которой все реальные элементы заменены максимально близкими по функциональности цепями из идеальных элементов.
Какими моделями пользуются при описании свойств идеальных и реальных источников электродвижущей силы (Э.Д.С.)?
Источник напряжения — идеализированный элемент ЭЦ, напряжение на зажимах которого не зависит от протекающего через него тока.
Какими моделями пользуются при описании свойств идеальных и реальных источников тока?
Источник тока – это идеализированный элемент ЭЦ, ток которого не зависит от напряжения на его зажимах.
Чем отличаются линейные и нелинейные элементы электрических цепей?
Элементы, ВАХ которых являются прямыми линиями, называются линейными. Электрические цепи, имеющие только линейные элементы, называются линейными электрическими цепями.
Элементы, ВАХ которых не являются прямыми линиями, называются нелинейными. Электрические цепи, имеющие хотя бы один нелинейный элемент, называются нелинейными.
Какие электрические цепи называются линейными электрическими цепями постоянного тока?
Элементы электрической цепи, ВАХ которых представляют собой прямые линии, называются линейными элементами, а цепи, состоящие из таких элементов, работающие от источника постоянного тока – линейными электрическими цепями постоянного тока.
Дайте определения ветви, узла и контура электрической цепи.
Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.
Узел цепи в электронике — точка, в которой соединяются три (или более) проводника электрической цепи. Узел (наряду с контуром) является базовым понятием, необходимым при анализе электрических цепей.
Контур — это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи, и есть замкнутый контур.
Сформулируйте первое правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается в первом правиле Кирхгофа?
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным.
Сформулируйте второе правило (закон) Кирхгофа. Какой принцип электромагнетизма утверждается во втором правиле Кирхгофа?
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю.
Докажите, что при последовательном соединении элементов в электрической цепи эквивалентное сопротивление равно сумме их сопротивлений.
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи: .
Так как ток в цепи один:
Докажите, что при параллельном соединении элементов в электрической цепи эквивалентная проводимость равна сумме их проводимостей.
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора).
Для двух параллельно соединённых резисторов их общее сопротивление равно: .
Если , то общее сопротивление равно:, то естьэквивалентная проводимость равна сумме проводимостей.
Приведите пример расчета электрической цепи методом непосредственного применения правил Кирхгофа.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом контурных токов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом узловых потенциалов.
Пример приведён в работе.
Приведите пример расчета электрической цепи методом эквивалентного генератора.
Метод эквивалентного генератора используется при расчёте сложных схем, в которых одна ветвь выделяется в качестве сопротивления нагрузки, и требуется исследовать и получить зависимость токов в цепи от величины сопротивления нагрузки. В соответствии с данным методом неизменная часть схемы преобразовывается к одной ветви, содержащей ЭДС и внутреннее сопротивление эквивалентного генератора.
ЭДС эквивалентного генератора определяется по формуле:
где: —проводимость участка цепи, равная
Для определения эквивалентного сопротивления генератора применяется расчет последовательно и параллельно соединённых сопротивлений, а также, в случае более сложных схем, применяют преобразование треугольник-звезда.
После определения параметров эквивалентного генератора можно определить ток в нагрузке при любом значении сопротивления нагрузки по формуле:
Параметры иможно так же определить по исходной схеме из опытовхолостого хода икороткого замыкания .
По опыту холостого хода Для определенияв исходной схеме убирают сопротивление нагрузки и полученную схему рассчитываютметодом узловых потенциалов. Через полученные значения потенциалов определяют
Значение обычно определяется из опыта короткого замыкания, для этого в исходной схеме сопротивление нагрузки заменяют проводом и пометоду контурных токов определяют ток в проводе. После этого эквивалентное сопротивление генератора определяется по формуле:
Приведите пример расчета электрической цепи методом эквивалентных преобразований.
Метод эквивалентных преобразований заключается в том, что электрическую цепь или ее часть заменяют более простой по структуре электрической цепью. При этом токи и напряжения в непреобразованной части цепи должны оставаться неизменными, т.е. такими, каким они были до преобразования. В результате преобразований расчет цепи упрощается и часто сводится к элементарным арифметическим операциям.
Одним из наиболее часто встречающихся случаев смешанного соединения сопротивлений.
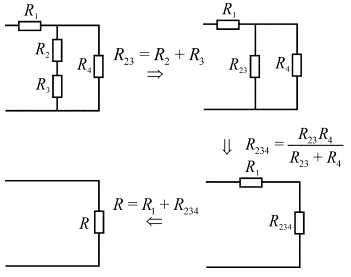
Исходная схема содержит параллельное соединение ветвей, содержащих и, т.е.. И этот участок с параллельным соединением включен последовательно с.
Поэтапным преобразованием эта цепь сводится к эквивалентному сопротивлению
.
Как и для чего составляется уравнение баланса мощностей при расчете электрической цепи? Приведите пример его составления.
Для проверки правильности расчёта электрической цепи. Пример приведён в работе.
studfiles.net
Примеры расчета сложных цепей постоянного тока
Расчет по законам Кирхгофа
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.
Параметры элементов схемы. |
| |
r1 = 5, Ом r2 = 20, Ом r3 = 0, Ом r4 = 10, Ом r5 = 5, Ом r6 = 15, Ом | E1= 40, В E2= 15, В E3= 5, В | |
Уравнения по первому закону Кирхгофа.
Уравнения по второму закону Кирхгофа.
Решаем систему линейных уравнений матричным методом относитель- но неизвестных токов.
Для чего составляем две матрицы. Матрицу A, состоящую из коэфи- циентов, стоящих в правой части системы. И матрицу B, состоящую из коэфициентов, стоящих в левой части системы. После умножения транс- портированной матрицы A на B получим матрицу C.
I1=C0 I1= 4.508, A
I2=C1 I2= 0.864, A
I3=C2 I3=-1.017, A
I4=C3 I4= 1.017, A
I5=C4 I5= 3.492, A
I6=C5 I6=-0.153, A
Все источники э.д.с. работают как источники энергии, так как действительные направления токов в них совпадают с направлениями э.д.с.
Проверка баланса:
Pn=188.22, Вт
Pi =188.22, Вт
Баланс сошелся.
Расчет методом контурных токов
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.
Параметры элементов схемы. |
| |
r1= 5, Ом r2= 5, Ом r3=15, Ом r4=15, Ом r5=10, Ом r6=10, Ом | E1=15, В E2=20, В E3=30, В | |
Составим уравнения по второму закону Кирхгофа для контурных токов.
Решаем систему уравнений матричным методом (см. предыдущий пример).
Находим контурные токи.
Контурные токи найдены:
Ik1=C0 Ik1=-0.722, A
Ik2=C1 Ik2= 2.713, A
Ik3=C2 Ik3= 1.948, A
Находим реальные токи.
Токи найдены:
I1= 1.991, A
I2= 2.713, A
I3= 1.948, A
I4= 0.765, A
I5= 1.226, A
I6=-0.722, A
Проверка баланса.
Pi =142.565, Вт
Pn=142.565, Вт
Баланс сошелся.
Потенциальные диаграммы.
Контур 1
| Ф0=0, В Ф1=-12.261, В Ф2=-5.043, В Ф3=-15.000, В Ф4=0, В | R0= 0, Ом R1=10, Ом R2=20, Ом R3=25, Ом R4=25, Ом |
Контур 2
| Ф0=0, В Ф1=-11.478, В Ф2=8.522, В Ф3=-5.043, В Ф4=-15, В Ф5=0, В | R0= 0, Ом R1=15, Ом R2=15, Ом R3=20, Ом R4=25, Ом R5=25, Ом |
Контур 3
| Ф0=0, В Ф1=-12.261, В Ф2=17.739, В Ф3=-11.478, В Ф4=0, В | R0= 0, Ом R1=10, Ом R2=20, Ом R3=25, Ом R4=40, Ом |
Примечание: Построение потенциальных диаграмм можно выполнить либо в программе MathCAD, либо в ручную. При построении указать на диаграммах значению сопротивлений и потенциалов узлов.
3. Расчет методом узловых напряжений (потенциалов)
В соответствии с заданием из таблиц 1.1 и 1.2 выбираем схему и ее параметры.
Параметры элементов схемы. |
| |
r1= 0, Ом r2=10, Ом r3=15, Ом r4= 5, Ом r5=10, Ом r6=15, Ом | E1=15, В E2=25, В E3=30, В | |
Проводимости.
g2=0.100, См | |||
g3=0.067, См | g4=0.200, См | ||
g5=0.100, См | g6=0.067, См |
Уравнения по I закону Кирхгофа:
Выразим неизвестные токи ветвей через «условно известные» потенциалы узлов:
Подставим токи в уравнения по I закону Кирхгофа и перегруппируем:
Решаем полученную систему уравнений относительно потенциалов узлов, с помощью определителей.
d = 0.084 | |
d1 = -0.733 | |
d2 = 0.133 |
Узловые потенциалы.
Ф1=-8.684, В | |
Ф3= 1.579, В |
Подставляем полученные потенциалы в уравнении токов.
I2= 0.842, A I3= 2.421, A I4=-1.737, A I5=-0.158, A I6= 0.684, A I1=-1.579, A | |
Проверка баланса.
Pn=117.386, Вт
Pi =117.386, Вт
Баланс сошелся.
studfiles.net
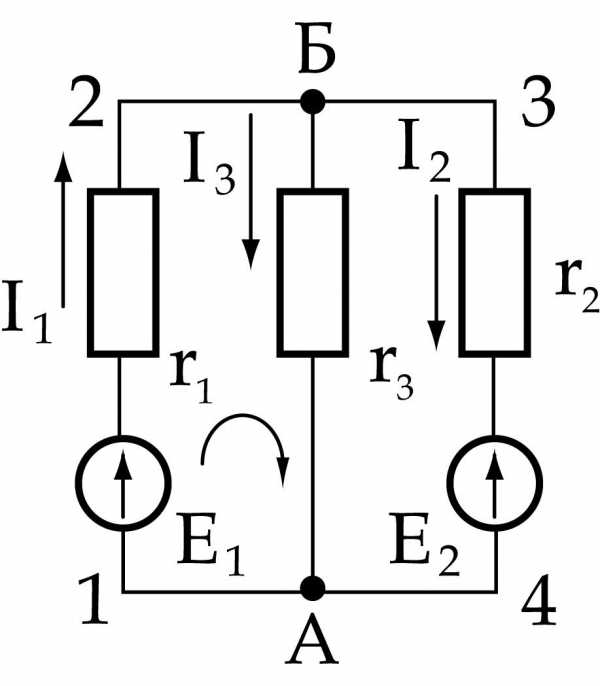
Сложные электрические цепи постоянного тока
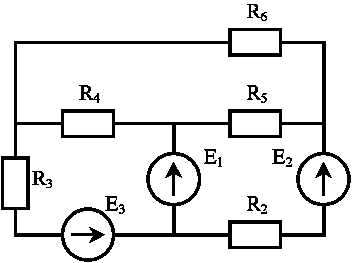
Сложными цепями называют разветвленные цепи, имеющие несколько контуров с произвольным размещением потребителей и источников питания.
Расчет сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа):
| Обычно расчет сложных цепей сводится к определению токов в ветвях по заданным величинам ЭДС и сопротивления. |
Порядок расчета
1. Произвольно выбираем направление токов в ветвях. Количество токов равно количеству ветвей. Если в результате расчета ток окажется отрицательным, то направление тока выбрано неверно.
2. Составляем уравнение по 1 и 2 правилу Кирхгофа. Количество уравнений должно быть равно количеству неизвестных токов.
3. Число уравнений,
составленных по 1 закону Кирхгофа, должно
быть равно 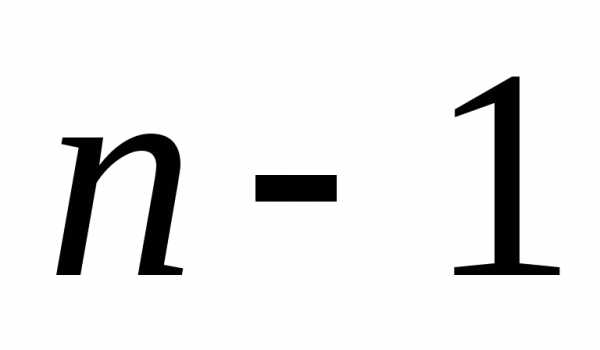 ,
где
,
где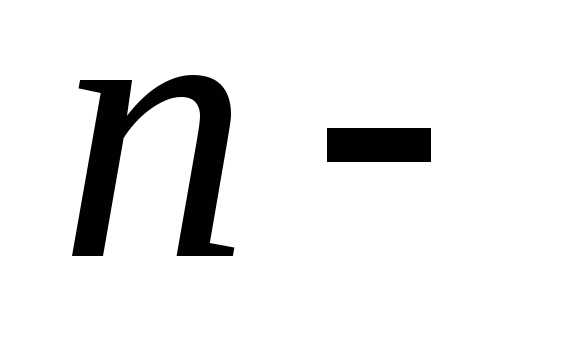 количество
узловых точек.
количество
узловых точек.
Остальные недостающие уравнения составляют по 2-му закону Кирхгофа. При этом произвольно выбирают положительное направление обхода контура. Если оно совпадает с направлением ЭДС, то его берут со знаком «+» и наоборот.
Если направление тока контура совпадает с направлением тока через резистор, то падение напряжения на резисторе берут со знаком «+» и наоборот.
Получаем систему из 5 уравнений:
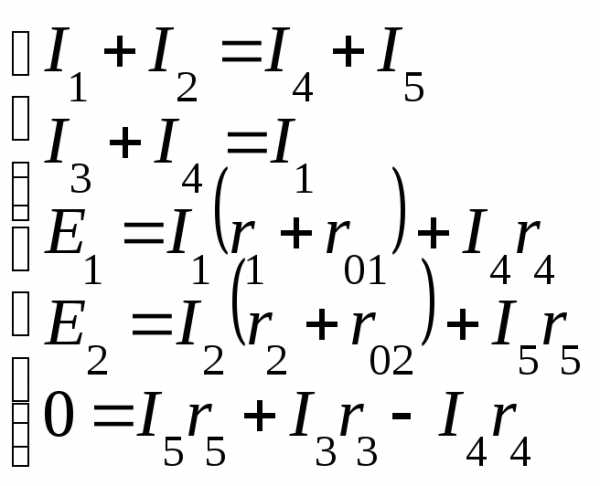
Задача
Дано:
| Решение: | |
|
| |
| ||
| ||
Метод узлового напряжения
Этот метод дает возможность более просто определить токи в ветвях.
| Примем за положительное направление токов направление от т.Б до т.А. Определим разность потенциалов между точками А и Б (узловое напряжение)
|
По Iзакону Кирхгофа для точки А получаем, что: | |
Раскроем скобки и определим U:
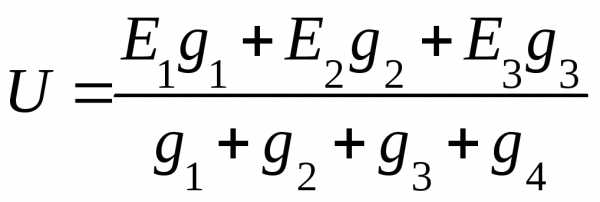
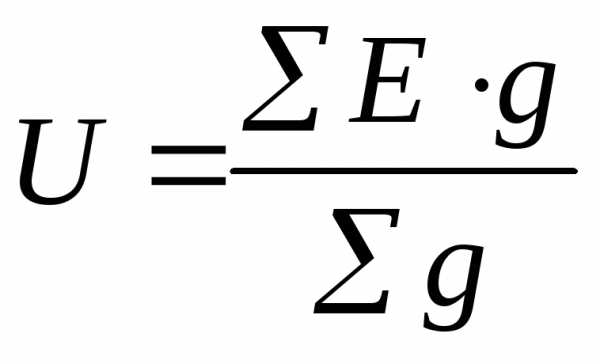
Если какая-либо ЭДС будет иметь противоположное направление, то в формулу она войдет со знаком «-».
Нагрузка
электростанции с течении суток сильно
изменяется, поэтому при малой нагрузке
работает один генератор, а при большой
– несколько. При параллельной работе
генераторов их токи будут одинаковы,
если одинаковы их ЭДС и rон.
Узловое напряжение (напряжение
на шинах) практически мало отличается
от ЭДС, т.е. разность
(напряжение
на шинах) практически мало отличается
от ЭДС, т.е. разность составляет несколько % от
составляет несколько % от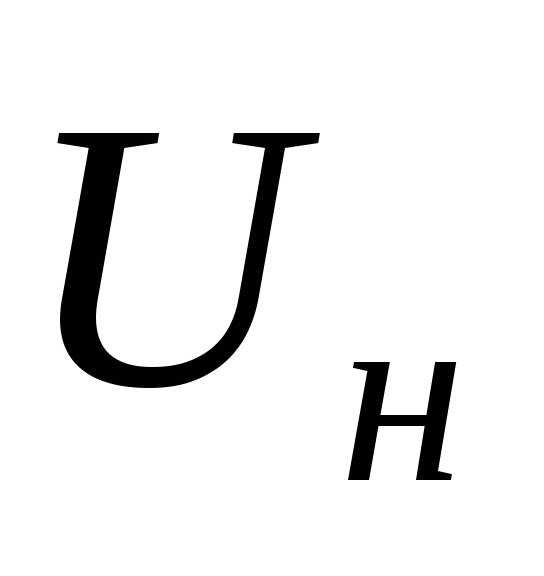 .
Поэтому, если ЭДС увеличить на 1%, то
разность увеличится на 40%. На столько
же увеличится ток нагрузки генератора,
т.к.
.
Поэтому, если ЭДС увеличить на 1%, то
разность увеличится на 40%. На столько
же увеличится ток нагрузки генератора,
т.к.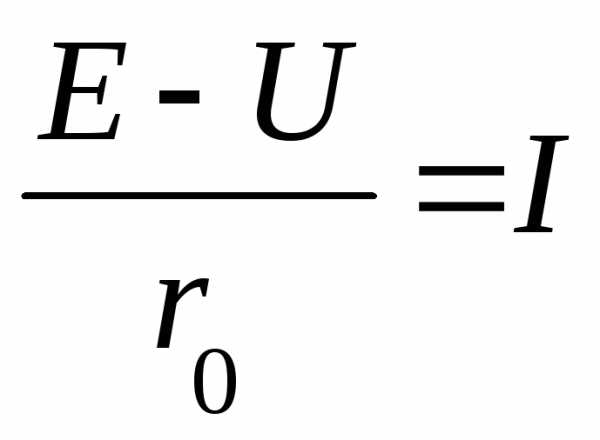 .
.
Для того, чтобы разгрузить генератор, достаточно его ЭДС уменьшить до значения узлового напряжения, при этом ток будет равен 0.
Если продолжать уменьшать ЭДС, Естанет меньшеU, ток будет меньше 0, генератор перейдет в двигательный режим работы.
Метод наложения (суперпозиции)
| Сущность метода заключается в том, что ток в какой-либо ветви является алгебраической суммой частичных токов, создаваемых каждым источником ЭДС в отдельности. Поэтому для каждой ветви получается столько частичных токов, сколько источников ЭДС. |
При алгебраическом суммировании частичных токов считают, что если направление частичного тока и реального тока совпадают, то он берется со знаком «+», если не совпадают – со знаком«-».
studfiles.net
Расчет сложных электрических цепей постоянного тока
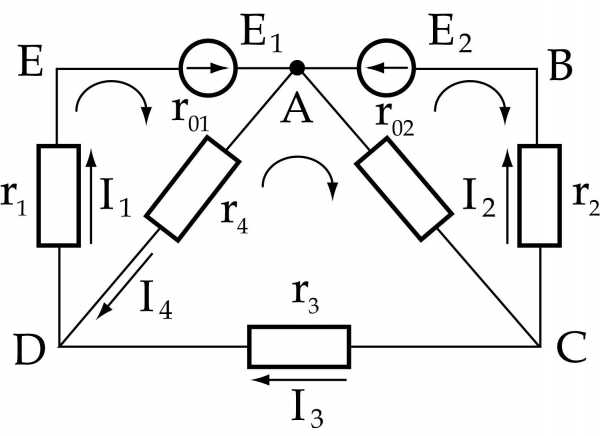
1.3.1. Метод уравнений Кирхгофа
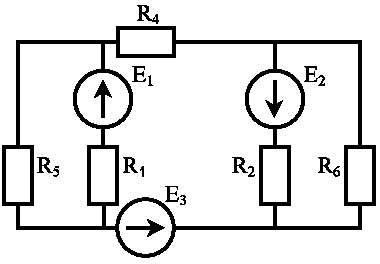
Этот метод сводится к решению системы уравнений, количество которых равно числу неизвестных токов (числу ветвей). Покажем его применение на примере схемы, изображенной на рис. 1.9.
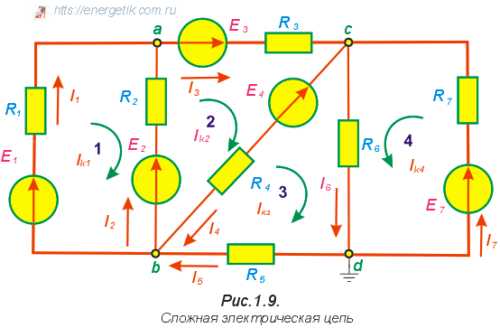
Первый закон Кирхгофа: в узле электрической цепи алгебраическая сумма токов равна нулю.
Произвольно задавшись направлениями токов в ветвях и принимая токи, подтекающие к узлу, положительными, а оттекающие от узла – отрицательными, записываем:
(1,6)
Число независимых уравнений в первом законе Кирхгофа – на единицу меньше числа узлов, поэтому для последнего узла d уравнение не пишем.
В заданной схеме семь ветвей, семь неизвестных токов. Система (1.6) содержит только три уравнения. Недостающие четыре записываем по второму закону Кирхгофа.
Второй закон Кирхгофа: в замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на всех сопротивлениях контура.
Число уравнений, составляемых по этому закону, равно числу взаимно независимых контуров. При рассмотрении схемы каждый последующий контур является независимым относительно предыдущих, если он отличается от них хотя бы одной новой ветвью. В заданной схеме таких контуров четыре. Они отмечены пронумерованными дугообразными стрелками. Любой другой контур новых ветвей не содержит, поэтому не является независимым. Дугообразные стрелки показывают произвольно выбранные направления обхода контуров. Если направления ЭДС и токов совпадают с направлением обхода контура, то они записываются с плюсом, если не совпадают – то с минусом.
(1.7)
Системы (1.6) и (1.7) дают достаточное количество уравнений для отыскания всех неизвестных токов.
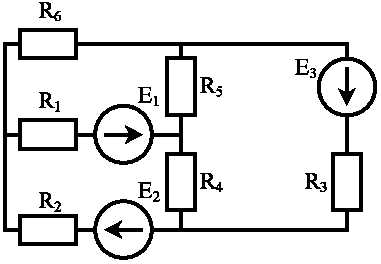
1.3.2. Метод узловых потенциалов
Уравнения, составляемые по этому методу, называются узловыми уравнениями. В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю. Пусть таким узлом будет узел d: φ d = 0. Равенство нулю какой-то точки схемы обычно показывается как ее заземление.
Запишем для каждой ветви выражение закона Ома:
(1.8)
Подставляя формулы (1.8) в систему (1.6) после несложных преобразований получаем следующие уравнения, количество которых на единицу меньше числа узлов:
(1.9)
При решении практических задач указанный вывод не делают, а узловые уравнения записывают сразу, пользуясь следующим правилом.
Потенциал узла, для которого составляется уравнение (например, в первом уравнении последней системы – это узел а), умножается на сумму проводимостей ветвей, присоединенных к этому узлу: φ а (G1+G2+G3).Это произведение записывается в левой части уравнения со знаком плюс. Потенциал каждого соседнего узла (b и с) умножается на проводимости ветвей, лежащих между этим (соседним) узлом и узлом, для которого составляется уравнение.
Эти произведения φ b (G1 + G2) и j сG3 записываются со знаком минус. В правой части уравнения стоит алгебраическая сумма произведений ЭДС на проводимости тех ветвей, которые присоединены к рассматриваемому узлу: E1G1, E2G2 и E3G3. Эти произведения записываются с плюсом, если ЭДС направлены к узлу, и с минусом, если от узла.
Найдя из (1.9) потенциалы узлов и подставляя их в (1.8), определяем токи ветвей.
Далее: 1.3.3. Метод контурных токов
energetik.com.ru
Расчет сложной электрической цепи постоянного тока
ГОУ ВПО «Дальневосточный государственный
университет путей сообщения»
Кафедра: «Электротехника,
электроника и электромеханика»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
на тему: «Расчет сложной электрической
цепи постоянного тока»
1904 001 225
выполнил: ст. 225 гр.
Парфута А.А.
проверил: Бузмакова Л.В.
Хабаровск
2009
Исходные данные:
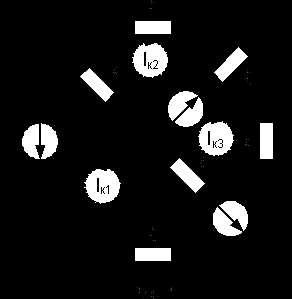
E1 = 40 В R1 = 20 Ом
E2 = 80 В R2 = 40 Ом
E3 = 75 В R3 = 25 Ом
R4 = 20 Ом
R5 = 25 Ом
R6 = 10 Ом
Задание №1
1.1. Уравнения по законам Кирхгофа.
1.2. Определение токов во всех ветвях методом узловых потенциалов.
Пусть φ4 = 0 В, тогда
где
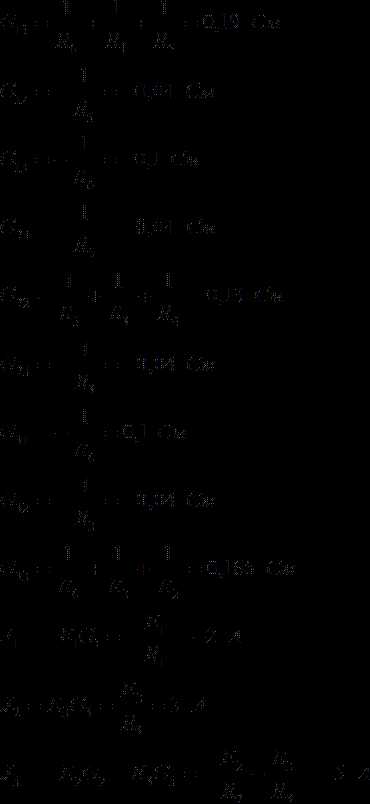
Общий вид матрицы, составленной из коэффициентов:
Откуда находим, что
А следовательно
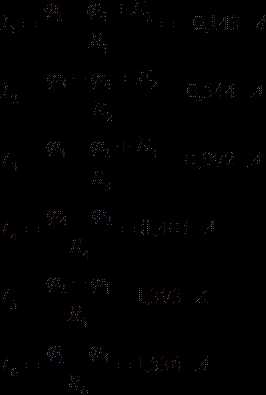
Проверка найденных значений токов по первому закону Кирхгофа:
Погрешности токов сходящихся в узлах составляют
1.3. Расчет мощностей. Баланс мощностей.
Для ветвей:

Для ЭДС:
Закон сохранения энергии:
Отсюда:
Погрешность мощности составляет
1.4. Метод контурных токов
Система уравнений для нахождения контурных токов
Подставив значения имеем
Далее
Откуда находим, что
А следовательно
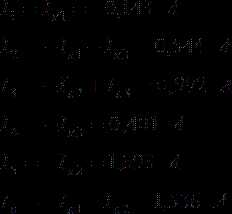
1.5. Значения токов, рассчитанных двумя разными способами:
Задание №2
2. Определение тока в ветви № 1 методом эквивалентного генератора
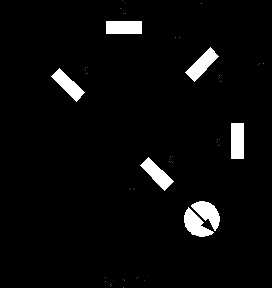
2.1. Определение внутреннего сопротивления эквивалентного генератора из режимов холостого хода и короткого замыкания (метод наложения)
 Замена части электрической цепи эквивалентным генератором
Замена части электрической цепи эквивалентным генераторомРасчет параметров холостого хода двухполюсника и короткого замыкания
Напряжение холостого хода
Определение
 Упрощенная схема
Упрощенная схемаОбщее сопротивление цепи
Откуда
Из уравнения
следует, что Определение
Определение Упрощенная схема
Общее сопротивление цепи
Откуда
Из уравнения
следует, чтоЗначит,
Ток короткого замыкания
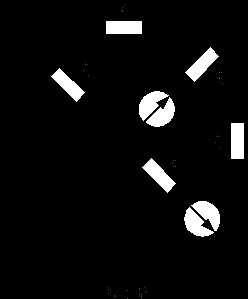
 Определение
Определение 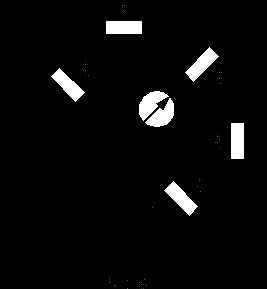 Упрощенная схема
Упрощенная схемаОбщее сопротивление цепи
Откуда
Так как ток
является частью тока , тоТак как ток
является частью тока , тоТогда по I закону Кирхгофа
Откуда
Определение
 Упрощенная схема
Упрощенная схемаОбщее сопротивление цепи
Откуда
Так как ток
является частью тока , тоТак как ток
является частью тока , тоТак как ток
является частью тока , тоmirznanii.com
РАСЧЕТ СЛОЖНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА
“РАСЧЕТ СЛОЖНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА”
Начертить схему согласно заданному варианту (источники тока включать параллельно заданной
ветви).
Преобразовать схему к двухконтурной.
Рассчитать двухконтурную схему, используя метод двух узлов.
Разворачивая схему в обратном порядке найти токи в исходной схеме.
Составить уравнения по законам Кирхгофа для исходной схемы и, подставив в них ранее найденные токи,
проверить уравнения.
Найти напряжение между точками Unn (согласно варианту).
Определить суммарную мощность всех источников энергии Рист=РE+РI и суммарную мощность всех приёмников энергии
Рпр=I2R. Проверить баланс мощностей Рист=Рпр.
Записать в общем виде уравнения по методам контурных токов и узловых потенциалов для исходной схемы.
Определить ток в заданной ветви методом эквивалентного генератора напряжения
(согласно варианту), при расчете напряжения холостого хода необходимо использовать метод контурных токов.
Для выбранного замкнутого контура схемы, включающего не менее 2-х источников ЭДС, построить в масштабе
потенциальную диаграмму (контур для построения потенциальной диаграммы выбирается студентом самостоятельно).
Представить ответы в виде таблицы:
I1 | I2 | I3 | I4 | I5 | I6 | I7 | I8 | Unn | Uхх | Rген | P |
0 | 0,331 | 3,436 | 6,564 | 3,436 | 0,647 | 0,315 | 2,7789 | 82,862 | 579,291 | 445,534 | 30524,099 |
Задание должно быть сдано на проверку не позднее ______________________
Ветви Направление Сопротивление Источники ЭДС Источники тока
1 42 250 0 0
2 26 110 510 0
3 63 310 0 0
4 31 470 0 -10
5 15 320 0 0
6 54 450 0 0
7 46 410 500 0
8 65 330 0 0
Найти токи в ветвях МКТ и напряжение U24
Составить баланс мощностей.
МЭГ найти ток в сопротивлении R6
Решение:
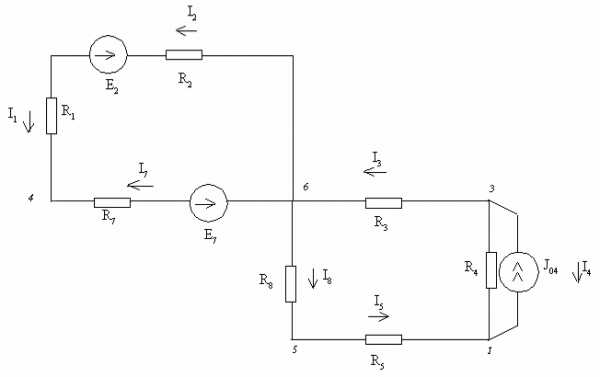
1) Начертим схему согласно заданному варианту (источники тока включим параллельно заданной ветви).
Для этого выполним следующую последовательность действий:
1. Расположим шесть узлов цепи в указанном порядке и в соответствии с вариантом задания соединим их ветвями (рис.1).
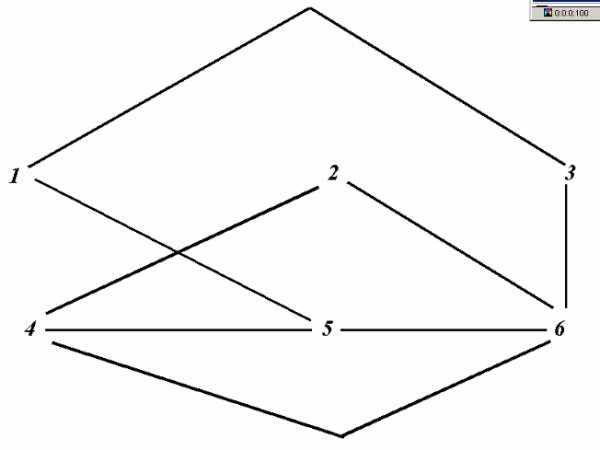
Рисунок 1
Перерисуем полученный граф схемы, изменив расположение узлов таким образом, чтобы ветви не пересекались (рис.2).
Рисунок 2
Включим в ветви сопротивления и заданные ЭДС. Источники тока подключим параллельно соответствующим ветвям. Придадим элементам схемы удобное расположение. Обозначим положительные направления источников ЭДС, источников тока и токов ветвей. Положительные направления определим индексами начального и конечного узлов, к которым присоединена ветвь. Всем сопротивлениям, источникам и токам ветвей присвоим номера соответствующих ветвей (рис.3).
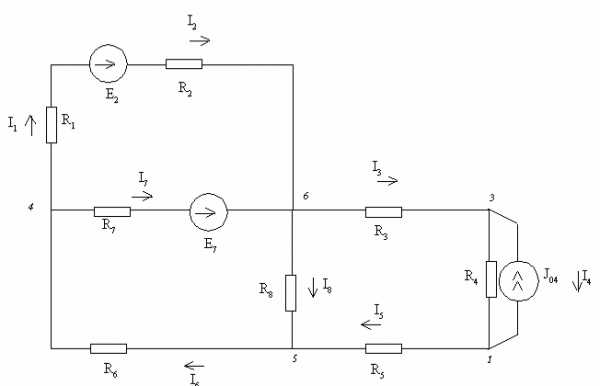
Рисунок 3
2) Преобразуем схему (рис.1) к двухконтурной.
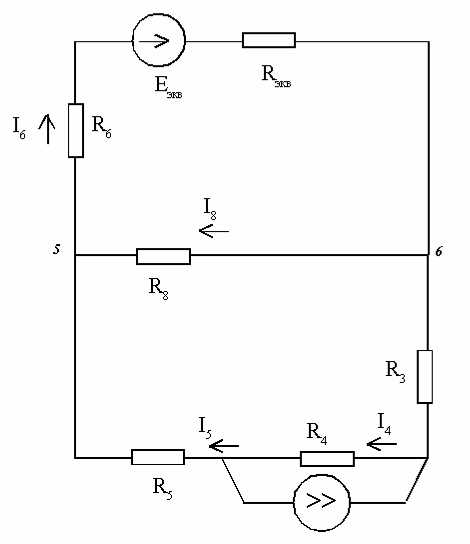
Рисунок 4
Для этого выполним эквивалентные преобразования:
Ом
3) Далее для расчета используем метод двух узлов:
Определим токи в цепи согласно рисунку 4 и эквивалентным преобразованиям:
4) Разворачивая цепь в обратном направлении, найдем остальные токи:
Заменим направление токов с отрицательными значениями на противоположные, изобразим модифицированную цепь на рис.5
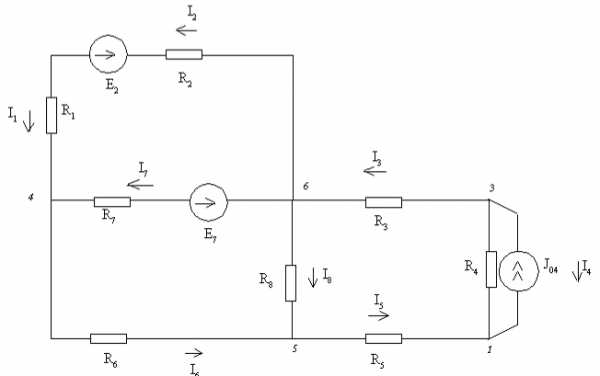
I11
I22
I33
Рисунок 5
Заполним таблицу.
5) Составим уравнения по первому закону Кирхгофа для цепи рис.5:
узел 1: I4–J04+I5=3,436+6,564–10=0
узел 3: J04–I4–I3=10-6,564–3,436=0
узел 4: I1+I7-I6=0,331+0,315–0,647=0
узел 5: I6+I8-I5=0,647+2,789–3,436=0
узел 6: I3–I8–I2–I7=3,436–2,789–0,331–0,315=0
Составим уравнения по второму закону Кирхгофа для цепи на рис.5:
I: I2R2+I1R1-I7R7=E7–E2
0,331×110+0,331×250–0,315×410=500–510
-10=-10
II: I8×R8–I6×R6–I1×R1–I2×R2=E2
2,789×330–0,647×450–0,331×250–0,331×110=510
510=510
III: I8×R8+I5×R5–I4×R4+I3×R3=0
2,789×330+3,436×320–6,564×470+3,436×310=0
0=0
6) Определим напряжение U24:
U24=φ2–φ4
Заземлим узел 2.
U24=0–(–I1R1)=0,331×250=82,862 (B)
7) Проверим правильность расчетов с помощью баланса мощностей.
Определим мощность, отдаваемую источниками энергии:
Pист= – E2×I2 – E7×I7 + I4×R4×J04 = – 510×3,436 – 500×0,315 + 6,564×470×10 = = 30524,099 (Вт)
Определим мощность, потребляемую нагрузкой:
Рн=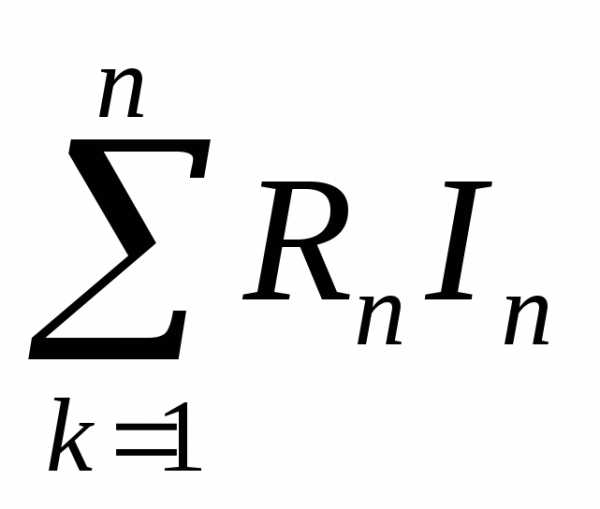 =250×0,3312 + 110×0,3312+ 310×3,4362+ 470×6,5642+ 320×3,4362+ 450×0,6472+ 410×0,3152+ 330×2,7892= 30524,099 (Вт)
=250×0,3312 + 110×0,3312+ 310×3,4362+ 470×6,5642+ 320×3,4362+ 450×0,6472+ 410×0,3152+ 330×2,7892= 30524,099 (Вт)
Таким образом Pист= Рн
8) Записать в общем виде уравнения по методам контурных токов и узловых потенциалов для схемы на рис.5:
Запишем в общем виде уравнения по методу узловых потенциалов для схемы на рис.5 с заземлением узла 6:
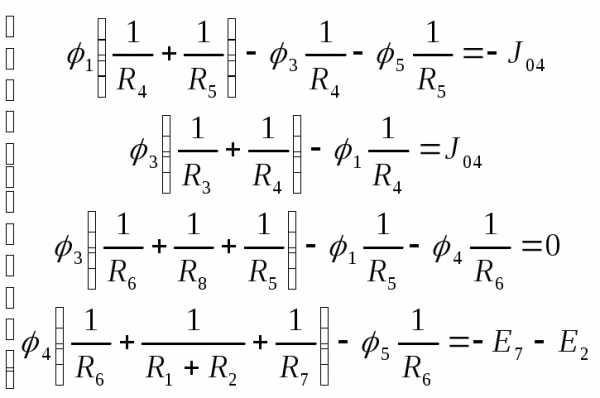
9) Методом эквивалентного генератора найдем ток в сопротивлении R6. Разорвем ветвь с сопротивлениемR6 . Схема примет вид (рис.6)
I11
I22
Uxx
Рисунок 6
Определим напряжение холостого хода по методу контурных токов:
Далее определим напряжение холостого хода по найденным контурным токам:
Uxx=R8×I22+I11(R1+R2)–E2=330 × 3,287+(250+110)0,013–510=579,291 (B)
Определим внутреннее сопротивление эквивалентного генератора согласно рисунку 7.
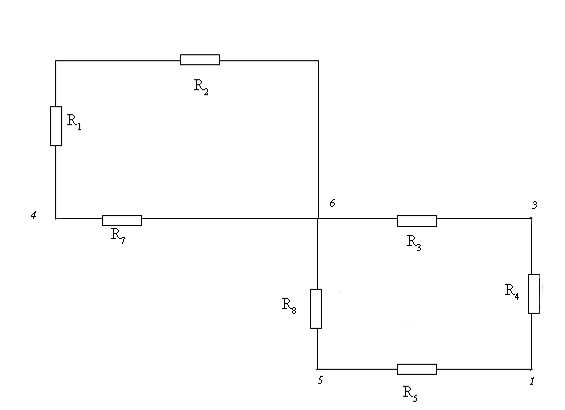
Рисунок 7.
(Ом)
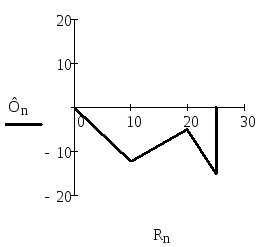
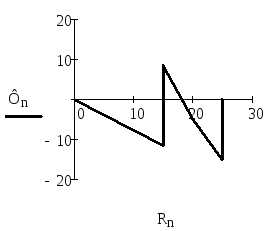
(А)
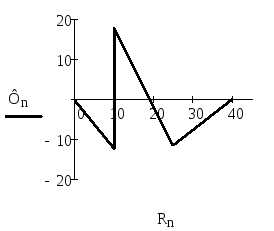
10) Выберем контур для построения потенциальной диаграммы 6-2-4-6. Данный контур содержит 2 источника ЭДС.
φ6=0 В
φ2=φ6 – I2×R2–E2=0 – 0,331×110–510= –546,459 (B)
φ4=φ2 – I1×R1=-546,459 – 0,331×250–510= –629,321 (B)
φ6=φ4 + I7×R7+E7= –629,321+500+0,315×410= 0 (B)
Построим диаграмму (рис.8).
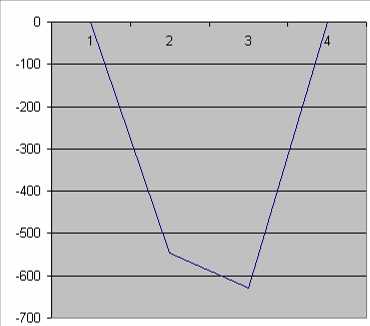
Рисунок 8.
7
studfiles.net

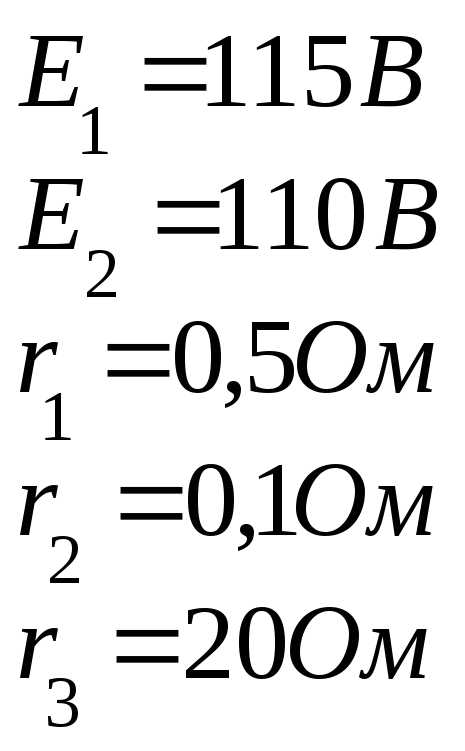
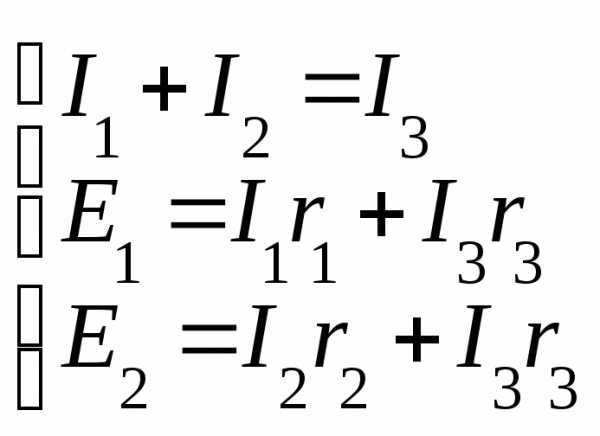
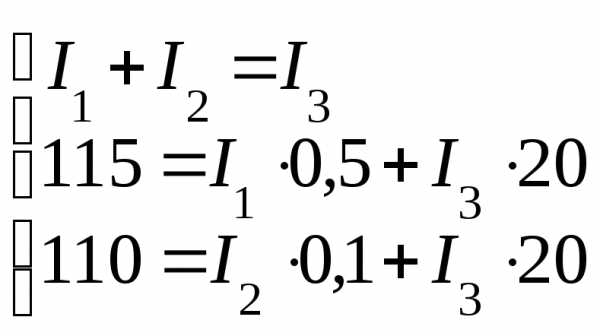
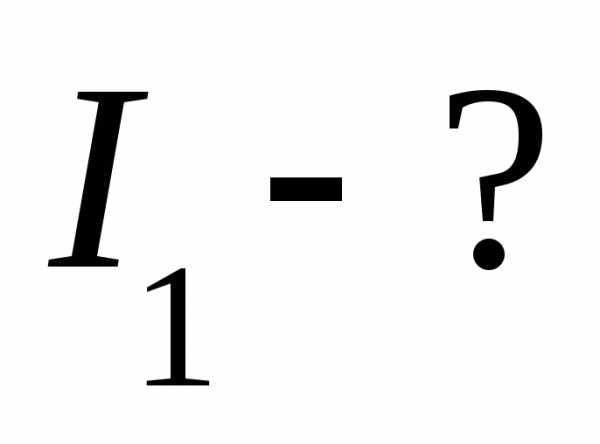
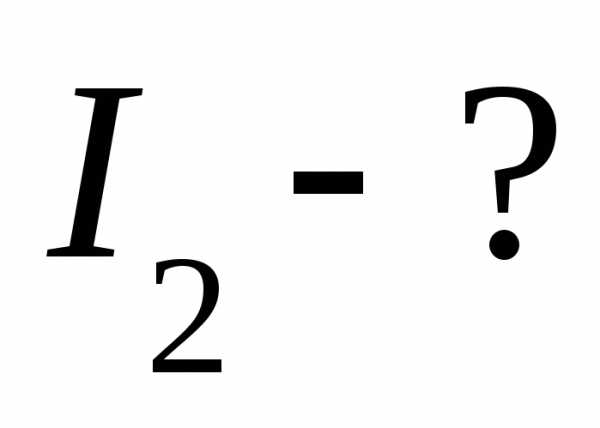
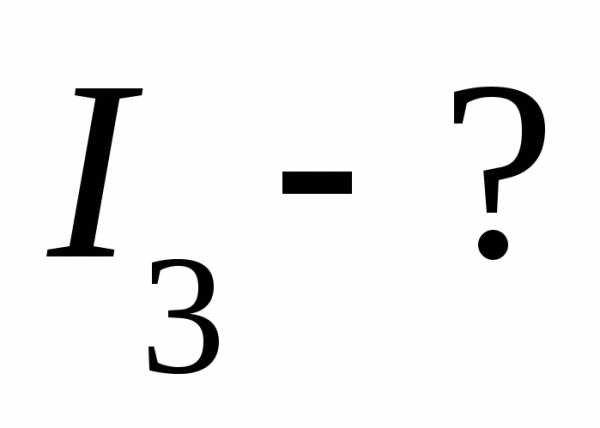
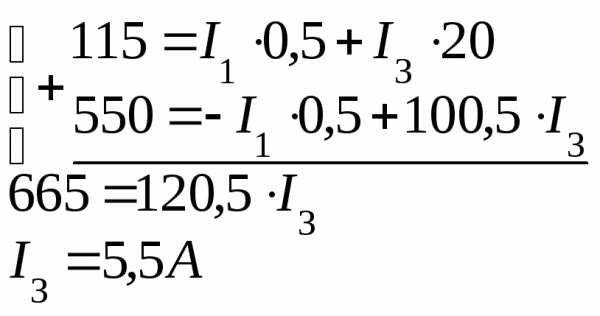
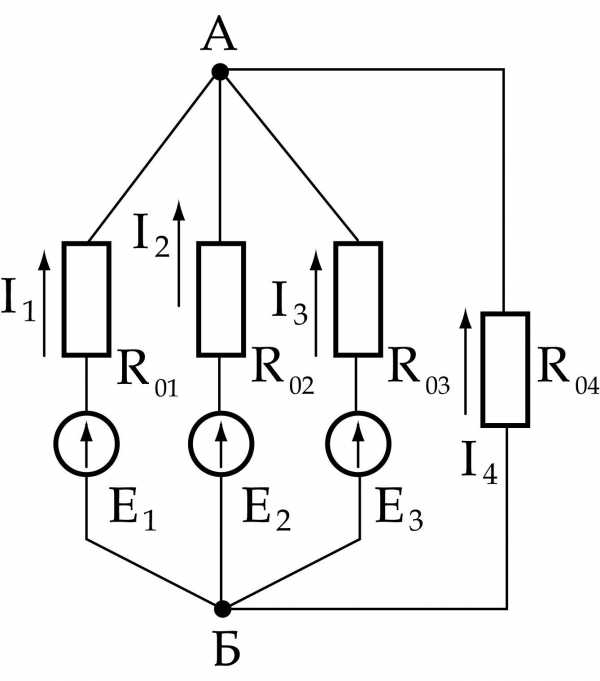
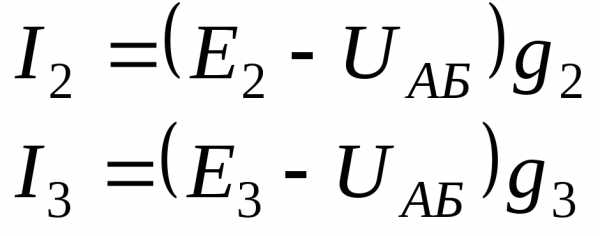
 ,331
,331