Разложение вектора по базису, формулы и примеры
Определение и формулы разложения вектора по базису
Если для произвольного вектора и произвольной системы векторов выполняется равенство
то говорят, что вектор является линейной комбинации указанной системы векторов.
Если система векторов является базисом некоторого векторного пространства (то есть векторы – упорядоченная линейно независимая система векторов, и добавление к ней хотя бы одного вектора делает ее линейно зависимой), тогда разложение (1) называется разложением вектора по базису .
Коэффициенты линейной комбинации (1) называются координатами вектора в базисе .
Примеры разложения вектора по базису
ТЕОРЕМА(О разложении вектора по базису). Любой вектор некоторого пространства можно разложить по его базису, причем такое разложение единственно.
Таким образом, чтобы разложить некоторый вектор по базису , необходимо найти такие коэффициенты , при которых линейная комбинация базисных векторов равна вектору :
ПРИМЕР
| Задание | Написать разложение вектора по векторам , , |
| Решение |
Векторы заданы в одном базисе. Пусть искомое разложение имеет вид:
Запишем это равенство в векторной форме:
При умножении вектора на число надо каждую координату этого вектора умножить на указанное число:
Чтобы найти сумму векторов, заданных своими координатами, необходимо просуммировать соответствующие координаты:
Два вектора равны, если равны их соответствующие координаты, то есть получаем следующую систему относительно неизвестных коэффициентов разложения:
Найдем решение полученной системы, например, методом Крамера. Основной определитель системы: Вычислим теперь вспомогательные определители системы:
Тогда
Следовательно, искомое разложение
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Базис системы векторов. Аффинные координаты
Определение 3. Векторное пространство называется
Базисом n-мерного пространства называется любая система из n независимых векторов этого пространства.
Пример 1. Доказать, что векторы
образуют базис в четырёхмерном пространстве.
Решение. Система векторов образует базис, если: 1) количество векторов равно размерности пространства; 2) эти векторы линейно независимы. Первое требование выполнено, остаётся доказать, что эти векторы линейно независимы. Попытаемся составить из них линейную нулевую комбинацию:
Подставим в это равенство вместо данных векторов их выражения в координатах и преобразуем левую часть:
или
Но вектор является нулевым, когда все его проекции равны нулю, т.е.
Таким образом, из данных векторов невозможно составить нулевую линейную комбинацию, у которой хотя бы один коэффициент был отличен от нуля. Поэтому векторы
линейно независимы и, следовательно, образуют базис в четырёхмерном пространстве.
Аналогичным образом определяется разложение вектора по базису на плоскости: базис образуется двумя векторами, а координат разложенного по базису вектора также две.
Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными линейными операциями над числами — координатами этих векторов.
Пример 2 Разложить вектор
по базису где
Решение. Рассматриваемые векторы принадлежат двумерному пространству: базис в этом пространстве должен состоять из двух векторов. В примере 7 установлено, что векторы
и
линейно независимы и, следовательно, образуют базис. Запишем разложение вектора по этому базису:
Чтобы найти значения и , подставим в это разложение выражения векторов , и через координаты:
Выполнив преобразования в правой части равенства, получим
или
Равенство векторов означает равенство их соответствующих координат, т.е.
откуда
Следовательно, разложение вектора по базису , имеет вид
Замечание.
В каждом векторном пространстве существует бесконечное множество различных базисов и в различных базисах один и тот же вектор имеет различные разложения (подобно тому, как точка имеет различные координаты в различных системах коорднат).Аффинные координаты в пространстве определяются заданием базиса , , и некоторой точки O, называемой началом координат.
Аффинными координатами любой точки M называются координаты вектора (относительно базиса , , .)
Поделиться с друзьями
Начало темы «Векторы»
Продолжение темы «Векторы»
function-x.ru
Разложение вектора по базису
Вектор
вида
,
где 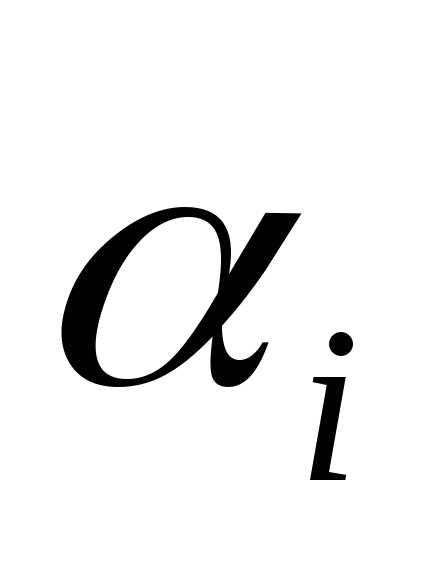
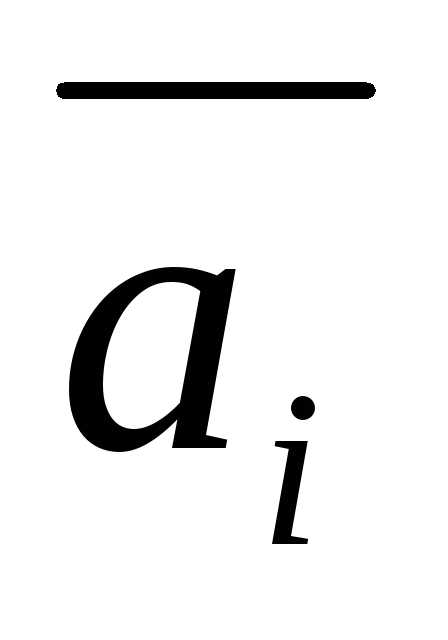 .
. 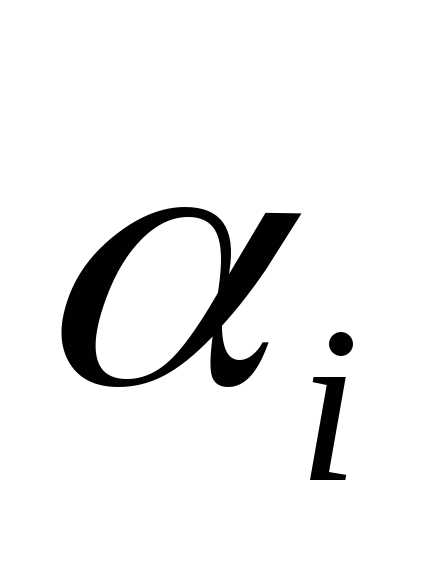 –
коэффициенты линейной комбинации. Если вектор
представлен как линейная комбинация
некоторых векторов, то говорят, что он разложен по этим
векторам.
–
коэффициенты линейной комбинации. Если вектор
представлен как линейная комбинация
некоторых векторов, то говорят, что он разложен по этим
векторам.Справедливы следующие теоремы
Т
е о р е м а 1. Пусть даны два неколлинеарных
вектора 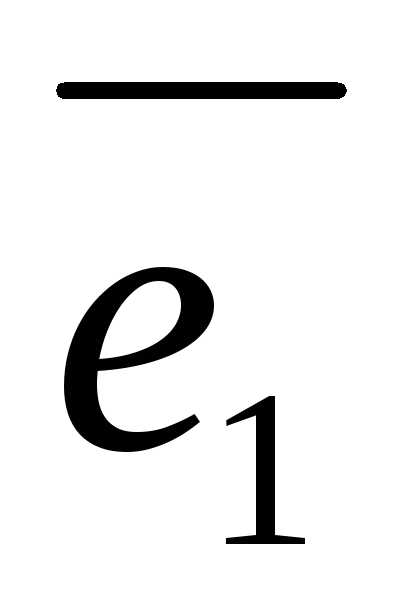 и
и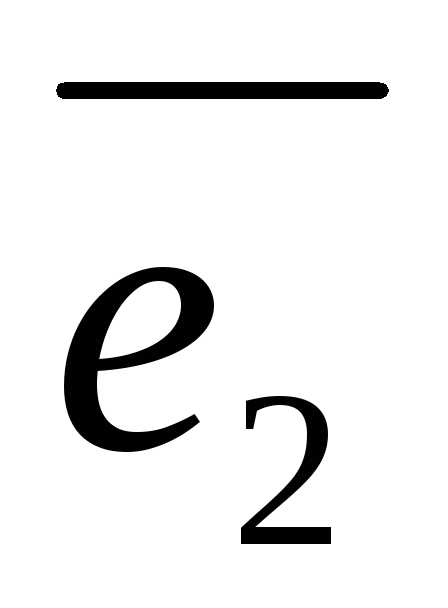 .
Любой компланарный с ними вектор
.
Любой компланарный с ними вектор раскладывается по ним и такое разложение
единственно. Т. е.,
раскладывается по ним и такое разложение
единственно. Т. е., =
=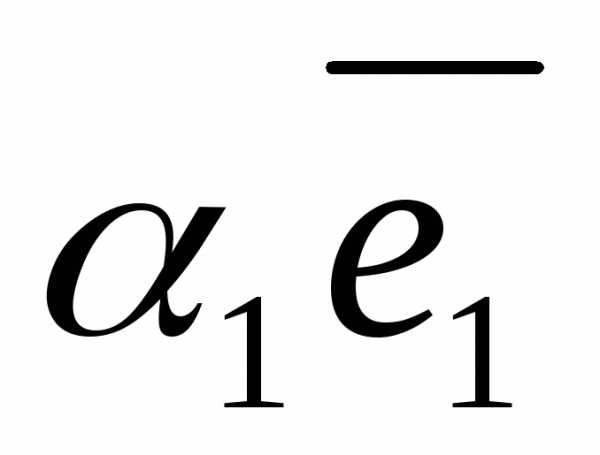
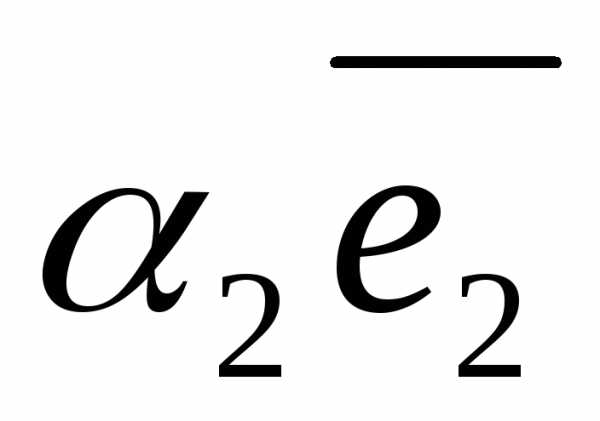 ,
где
,
где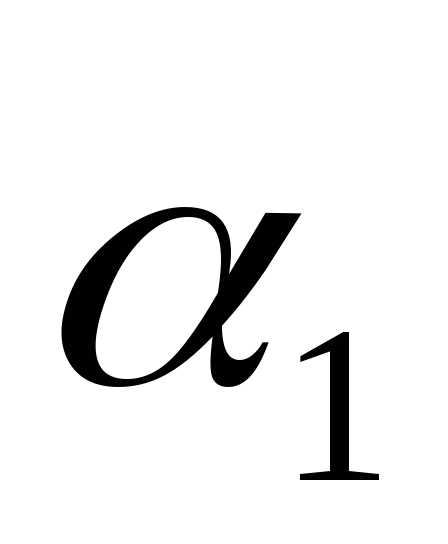 и
и единственные для этого вектора
единственные для этого вектора вполне определенные числа.
вполне определенные числа. Т
е о р е м а 2. Пусть даны три некомпланарных
вектора 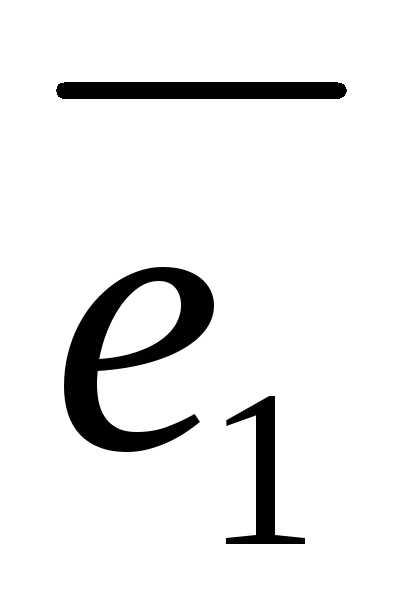 ,
,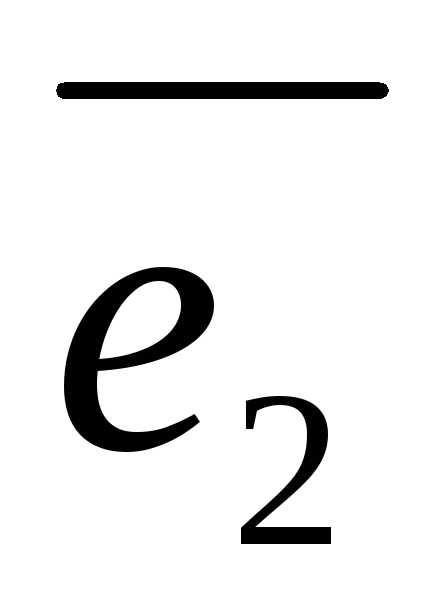 и
и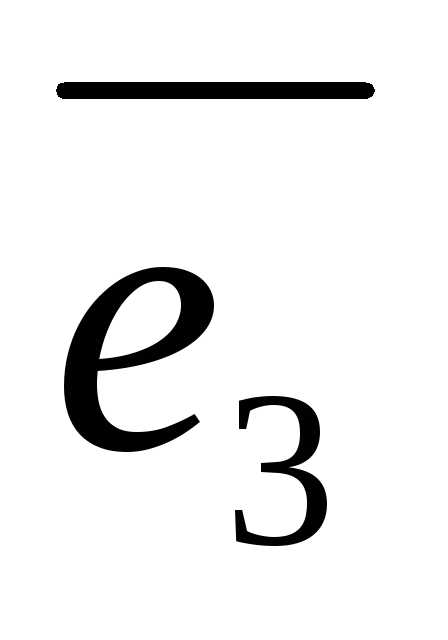 .
Любой вектор
.
Любой вектор раскладывается по ним и такое разложение
единственно. Т. е.,
раскладывается по ним и такое разложение
единственно. Т. е., =
=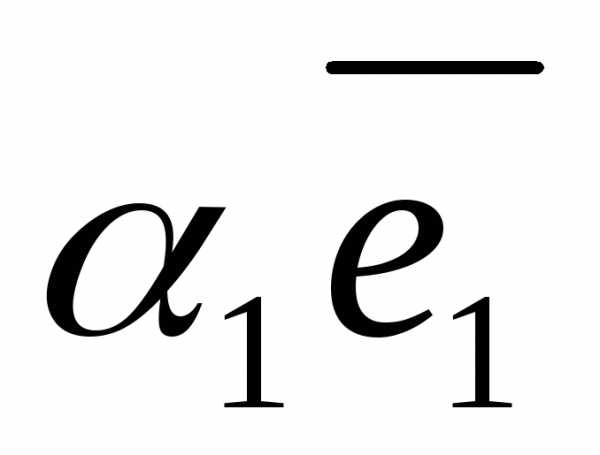 +
+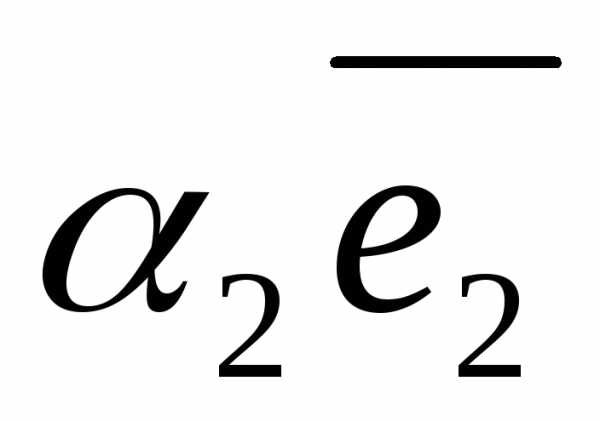
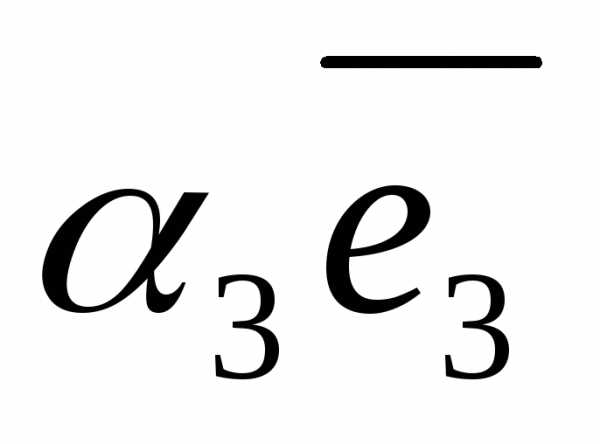 .
. Базисом в пространстве
называются три некомпланарных вектора,
взятых в определенном порядке. Базис
позволяет однозначно сопоставить
вектору упорядоченную тройку чисел 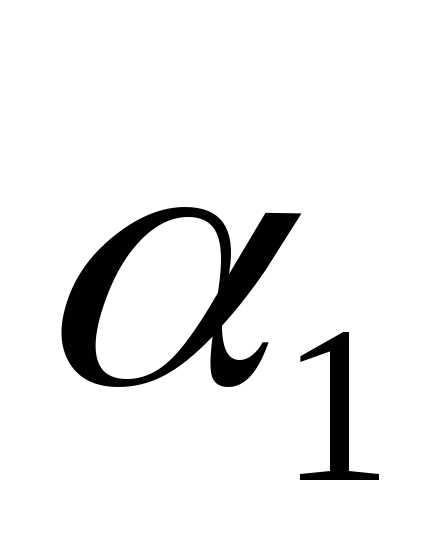 ,
,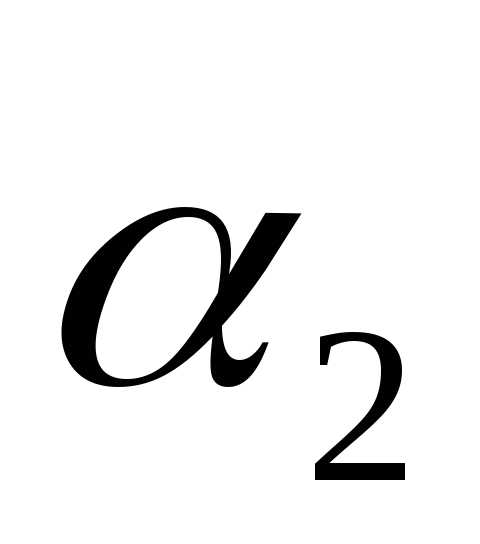 ,
,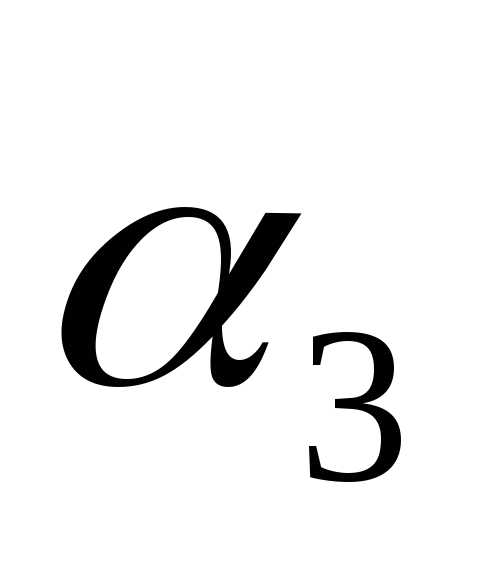 —
коэффициентов разложения этого вектора
по векторам базиса. С другой стороны,
каждой упорядоченной тройке чисел при
помощи базиса сопоставляется единственный
вектор. Если
—
коэффициентов разложения этого вектора
по векторам базиса. С другой стороны,
каждой упорядоченной тройке чисел при
помощи базиса сопоставляется единственный
вектор. Если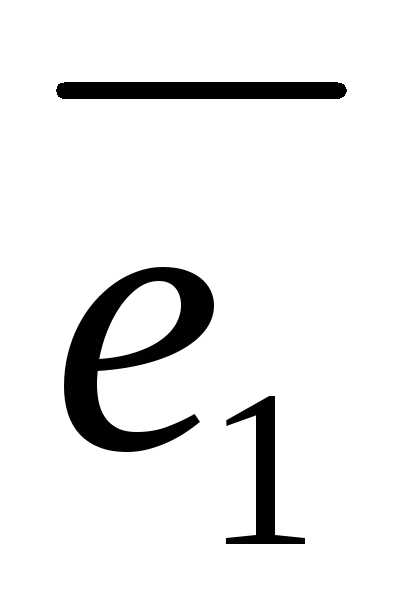 ,
,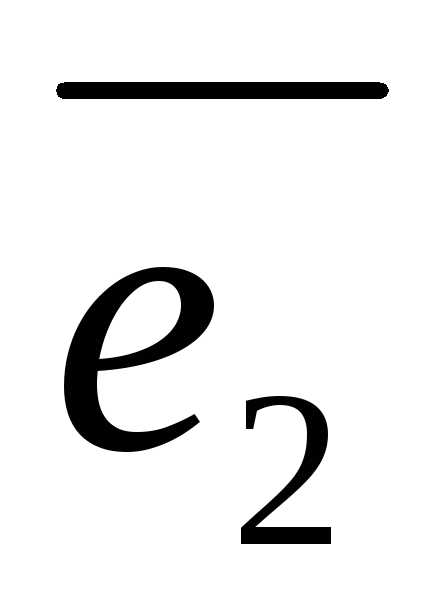 ,
,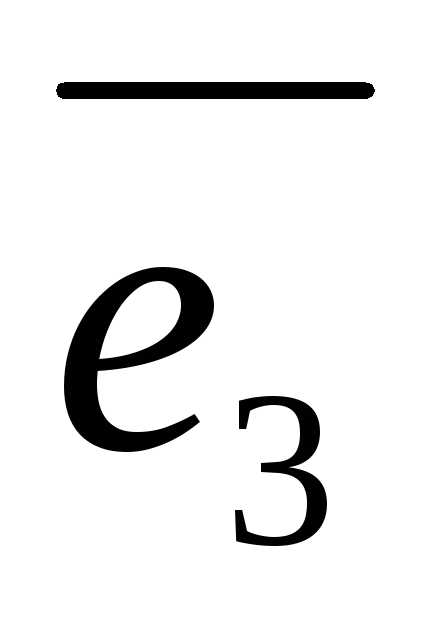 — базис и
— базис и
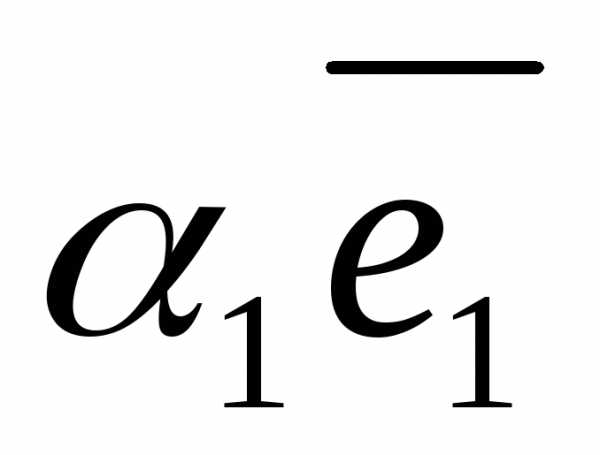 +
+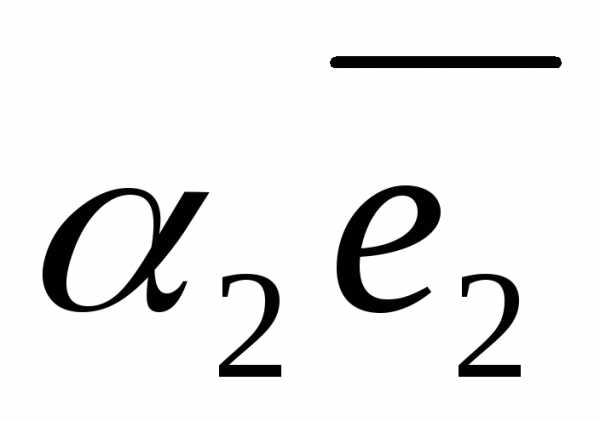 +
+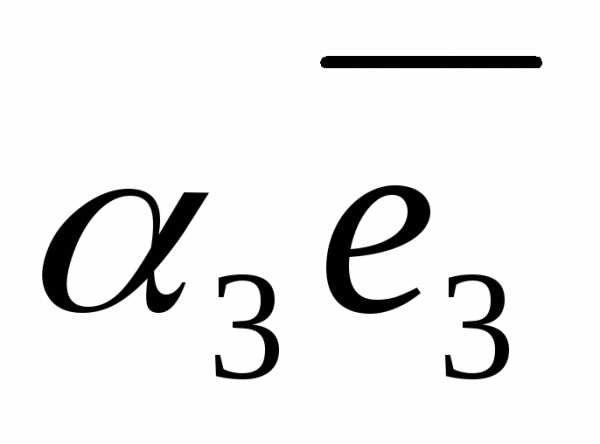 ,
то числа
,
то числа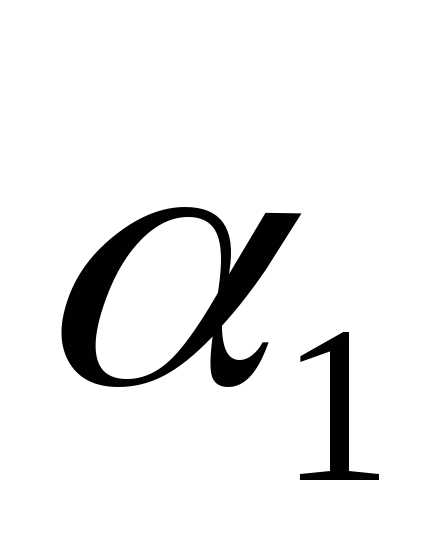 ,
,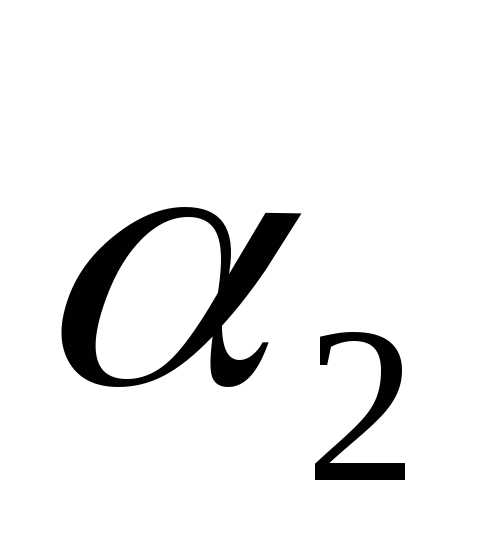 ,
,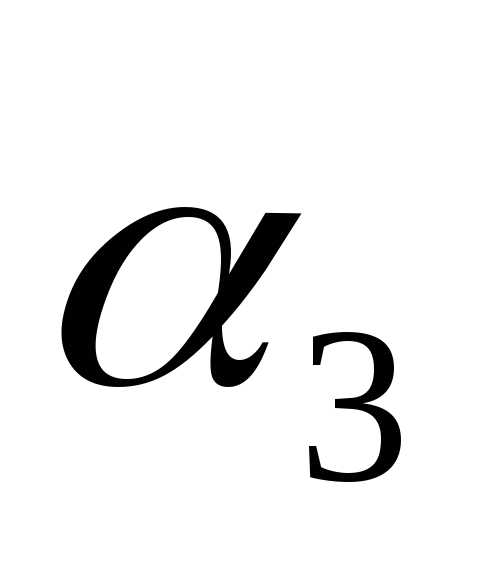 называютсякоординатами вектора
называютсякоординатами вектора  в данном базисе, при этом пишут. Аналогично
дается определение базиса на плоскости,
когда вектор имеет две координаты
в данном базисе, при этом пишут. Аналогично
дается определение базиса на плоскости,
когда вектор имеет две координаты .
.Действия над векторами, заданными своими координатами:
1.При умножении вектора на число все его координаты умножаются
на
это число. Т.е., 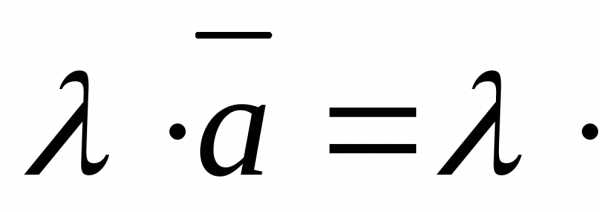
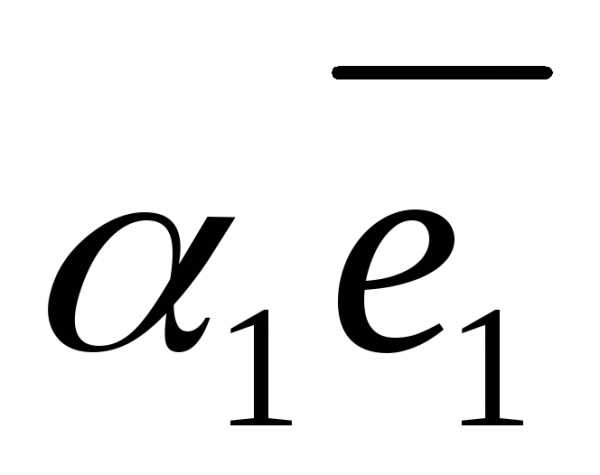 +
+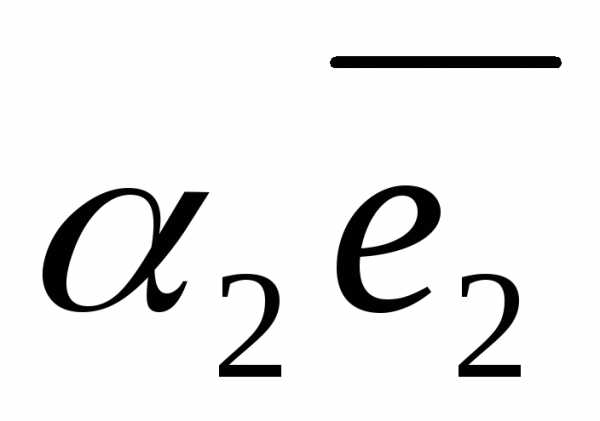 +
+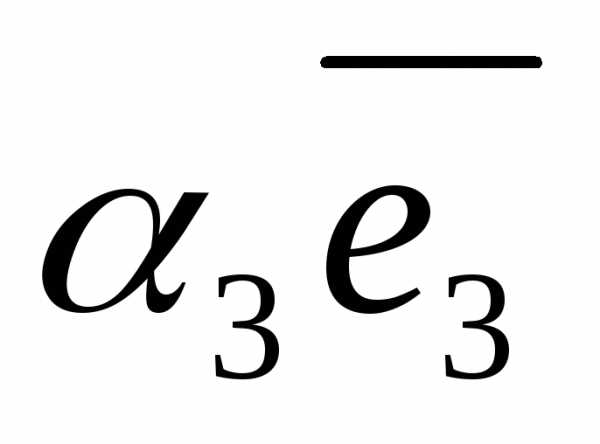 )=
)=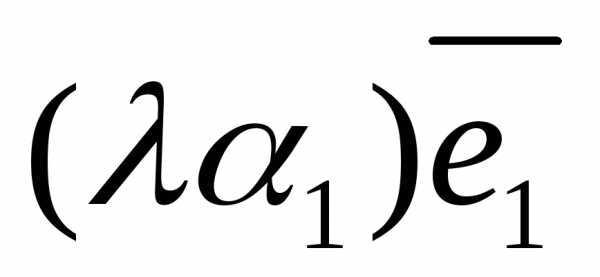 +
+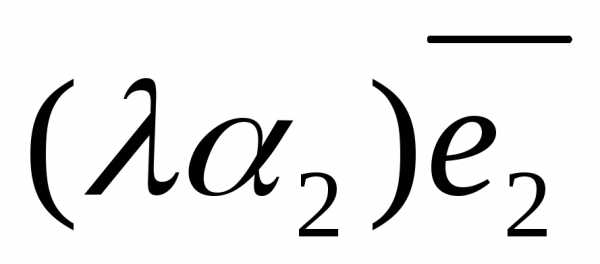 +
+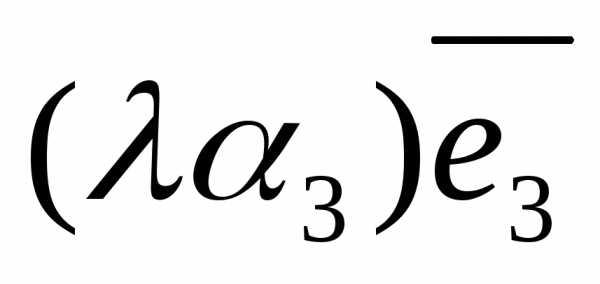 и
и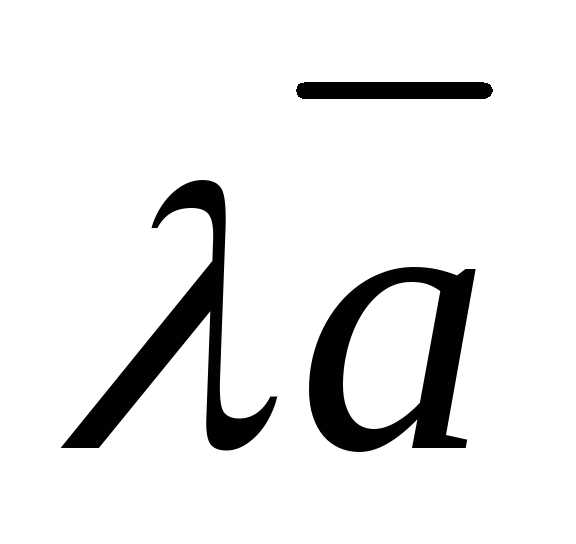 {,
{,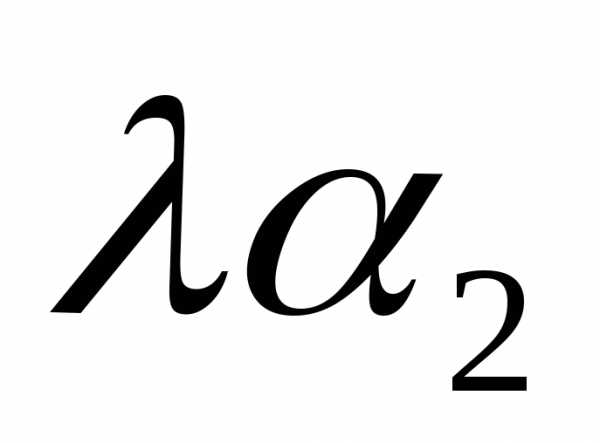 ,
,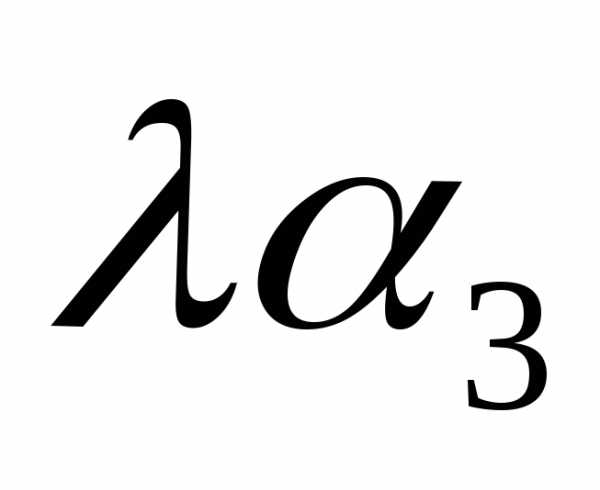 }.
}.2. При сложении векторов складываются их соответствующие координаты. Т. е., если в выбранном базисе ,, то.
Аффинные координаты
 Аффинные
координаты в пространстве
определяются (рис. 4) заданием базиса
Аффинные
координаты в пространстве
определяются (рис. 4) заданием базиса 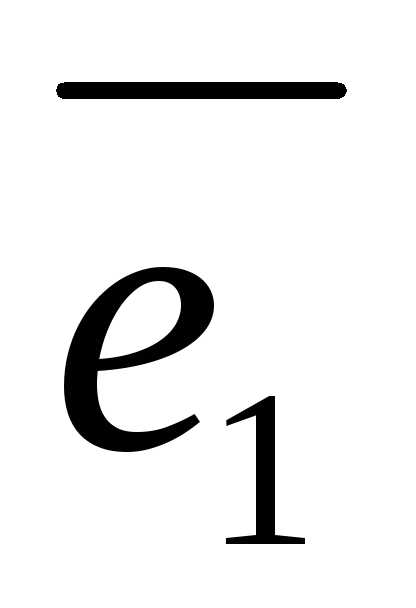 ,
,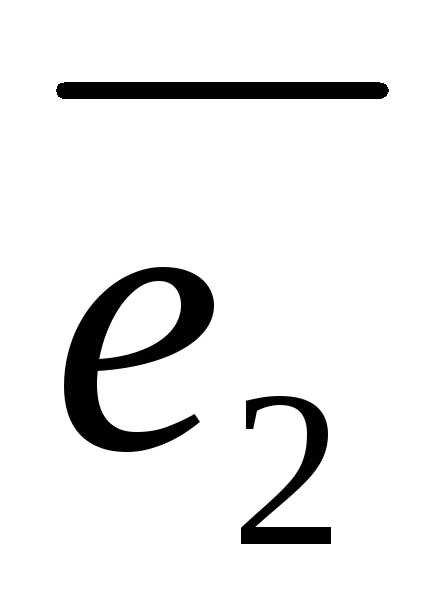 ,
,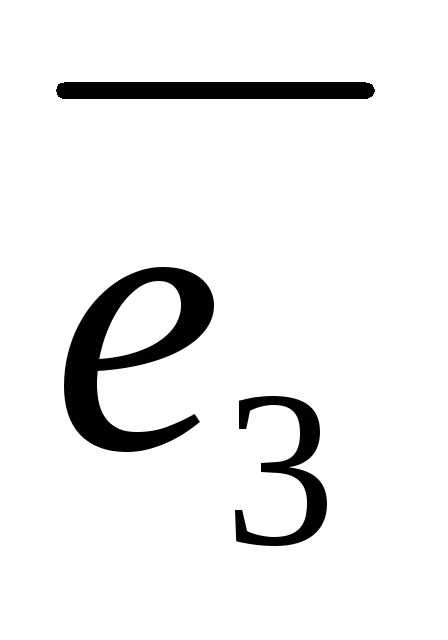 и точкиО –
начала координат (affinis – смежный,
соседний).
и точкиО –
начала координат (affinis – смежный,
соседний).
Рис. 4
Прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат: первая – ось абсцисс; вторая – ось ординат; третья – ось аппликат. Плоскости, проходящие через оси координат – координатные плоскости.
Пусть
в пространстве задана точка М. 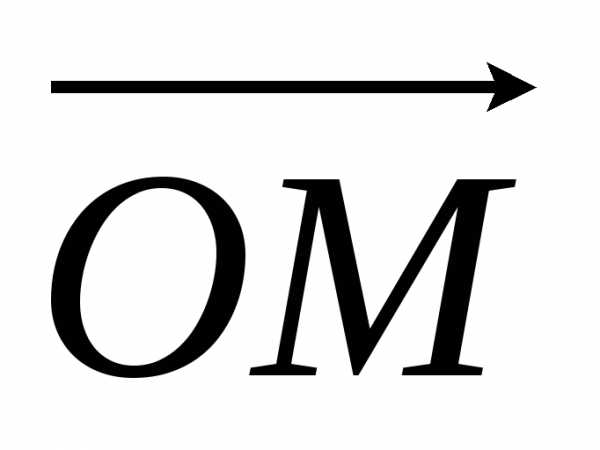 —радиус-вектор точки М.
Тогда разложение по векторам базиса
—радиус-вектор точки М.
Тогда разложение по векторам базиса 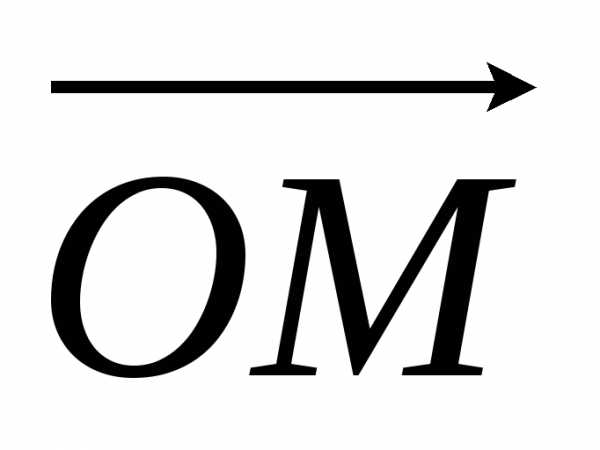 =
=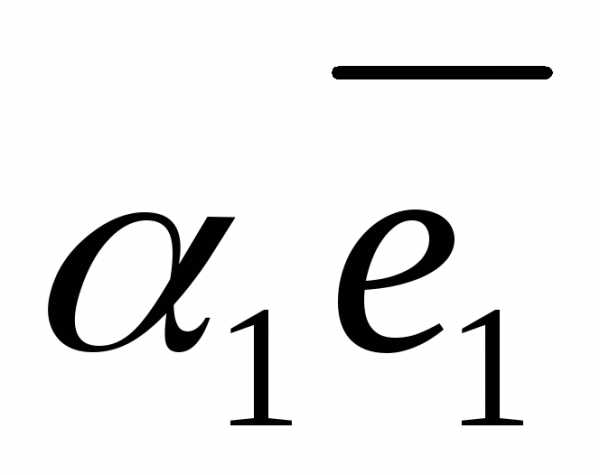 +
+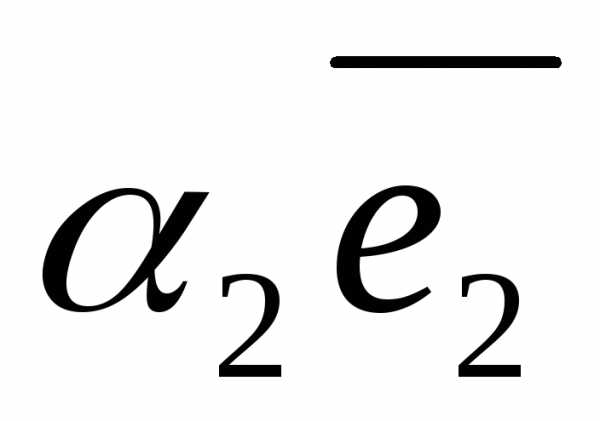 +
+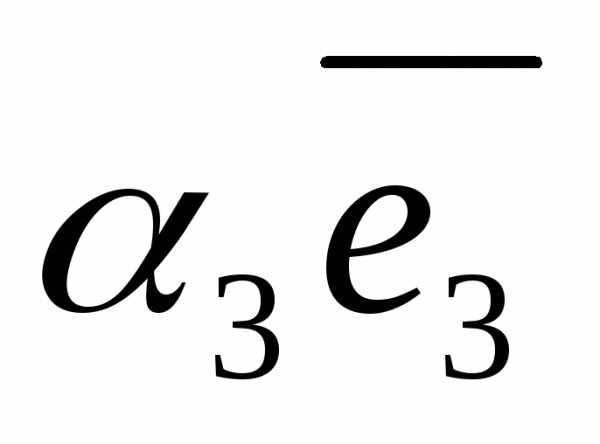 .Аффинными
координатами точки М называются координаты — радиус-вектора
.Аффинными
координатами точки М называются координаты — радиус-вектора
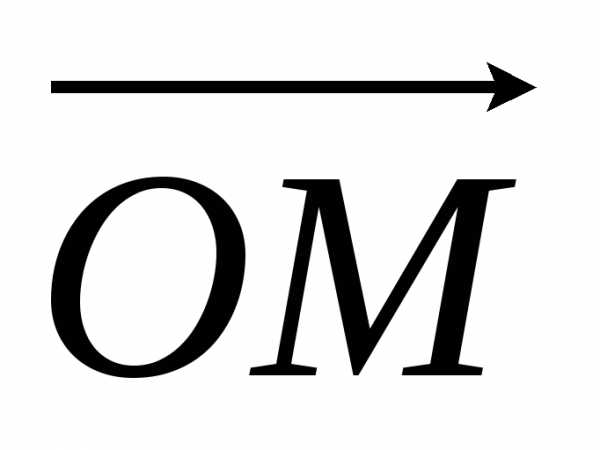 в
рассматриваемой системе координат,
пишут
,
где
в
рассматриваемой системе координат,
пишут
,
где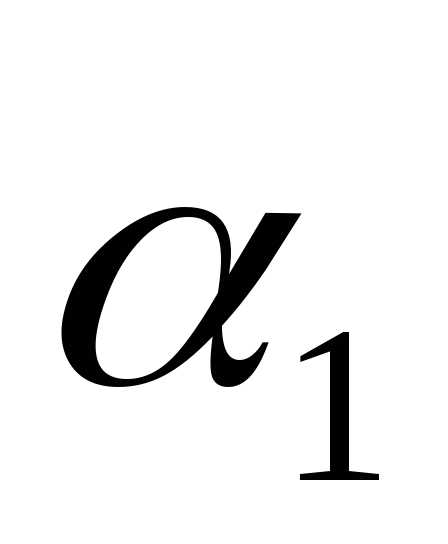 — абсцисса,
— абсцисса,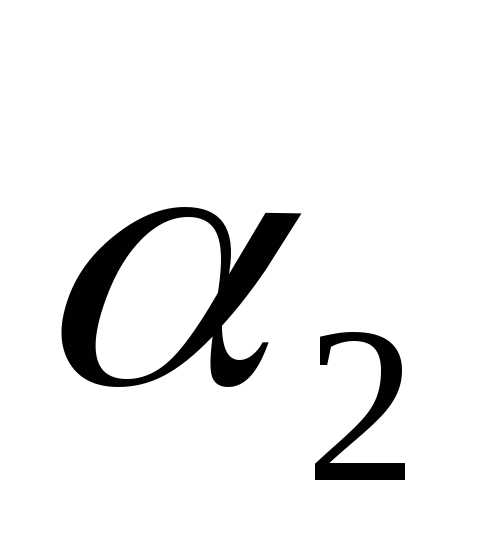 — ордината,
— ордината,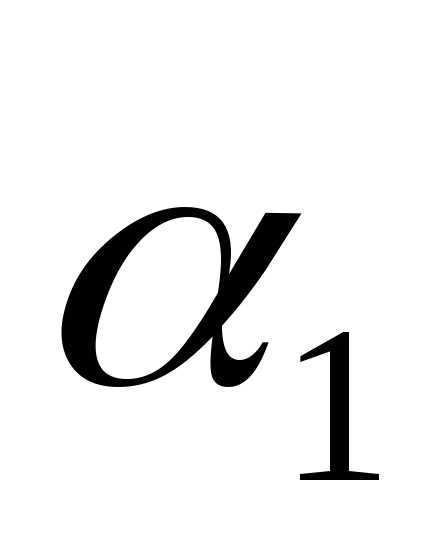 — аппликата точкиМ. В заданной
аффинной системе координат координаты
фиксированной точки определяются однозначно. С другой стороны, если задана система
координат, то в ней каждой упорядоченной
тройке чисел
ставится в соответствие единственная
точка.
Аффинная система координат на плоскости
— аппликата точкиМ. В заданной
аффинной системе координат координаты
фиксированной точки определяются однозначно. С другой стороны, если задана система
координат, то в ней каждой упорядоченной
тройке чисел
ставится в соответствие единственная
точка.
Аффинная система координат на плоскости 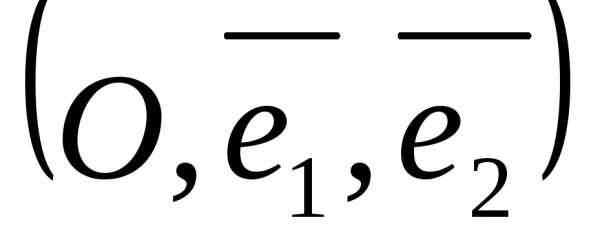 определяет такое же соответствие между
точками и упорядоченными парами чисел.
определяет такое же соответствие между
точками и упорядоченными парами чисел.
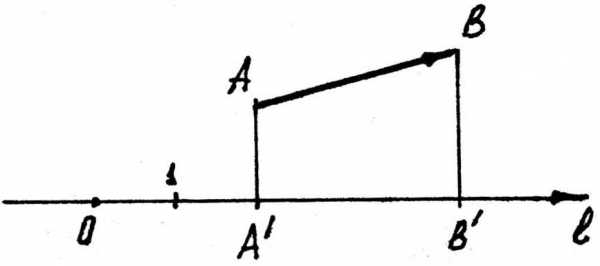
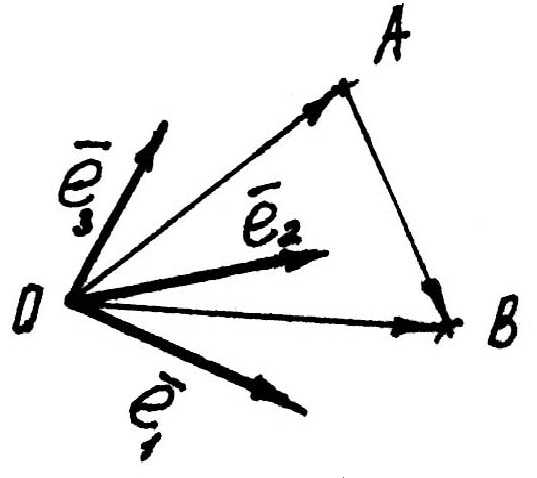 З
а д а ч а. Пусть в заданной аффинной
системеи.
Требуется найти координаты вектора
З
а д а ч а. Пусть в заданной аффинной
системеи.
Требуется найти координаты вектора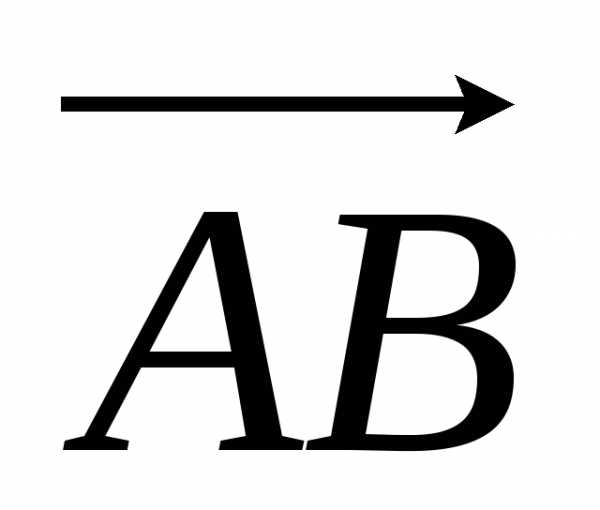 .
.
Рис. 5
Р е ш е н и е . Из чертежа (рис. 5) видно , тогда
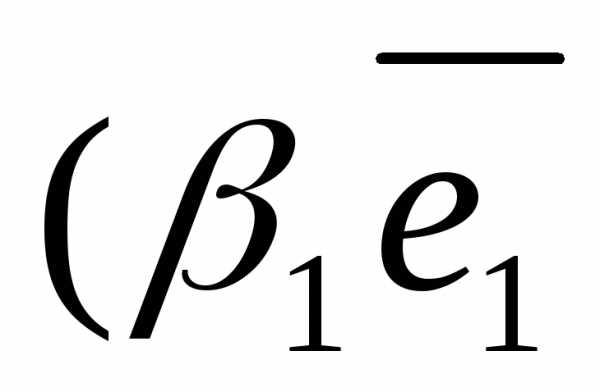 +
+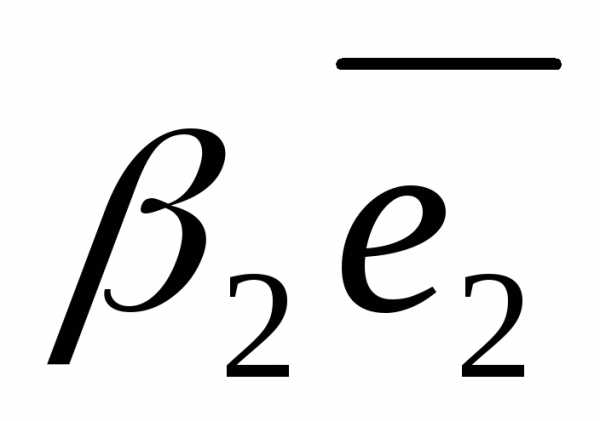 +
+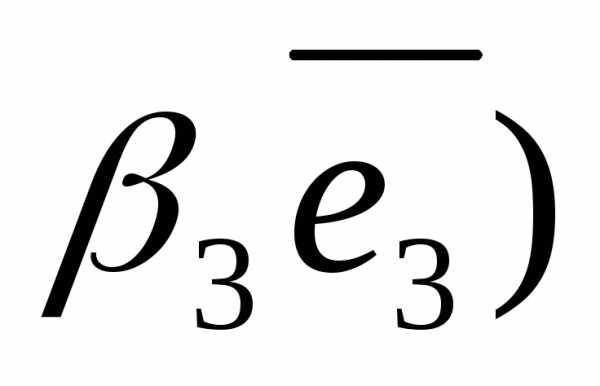
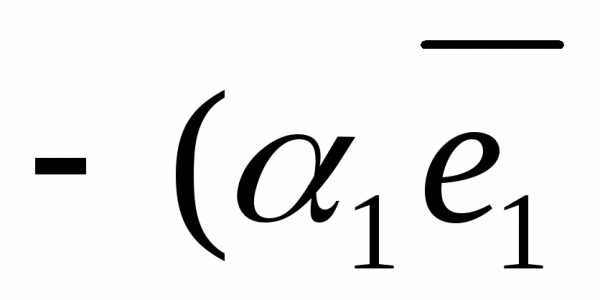 +
+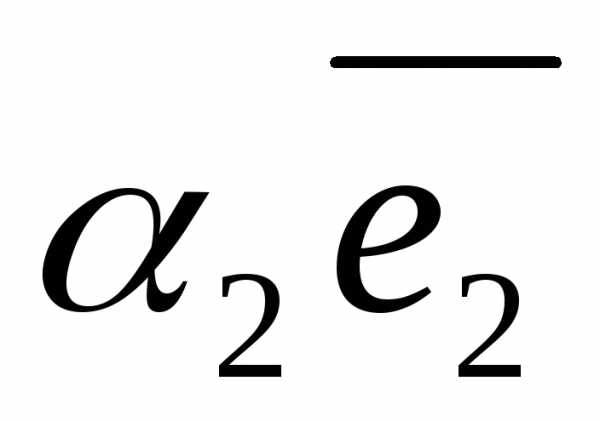 +
+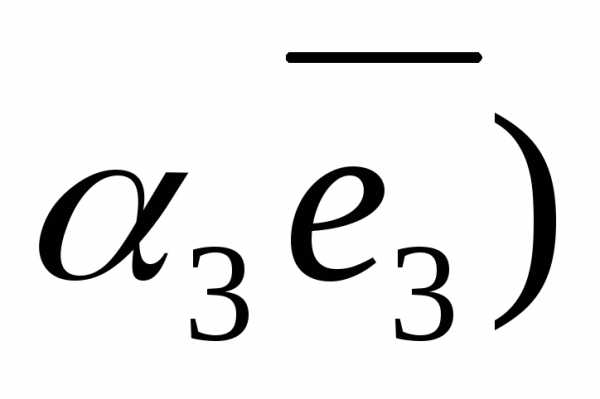 =
=
=.
Таким образом, , то есть, координаты вектора равны разности соответствующих координат конца и начала вектора.
Проекция вектора на ось
 Ориентированной
осью называется
прямая, на которой закреплена точка —
начало отсчета, выбрана единица длины
и направление отсчета.
Ориентированной
осью называется
прямая, на которой закреплена точка —
начало отсчета, выбрана единица длины
и направление отсчета.
Рис. 6
Проекцией
вектора 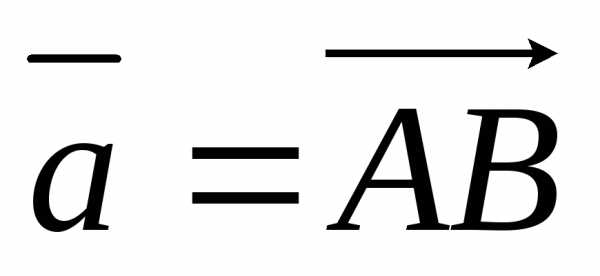 на ось
на ось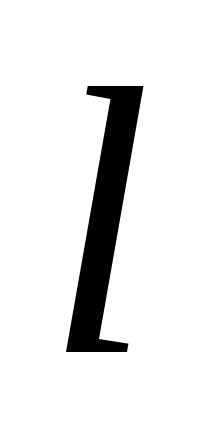
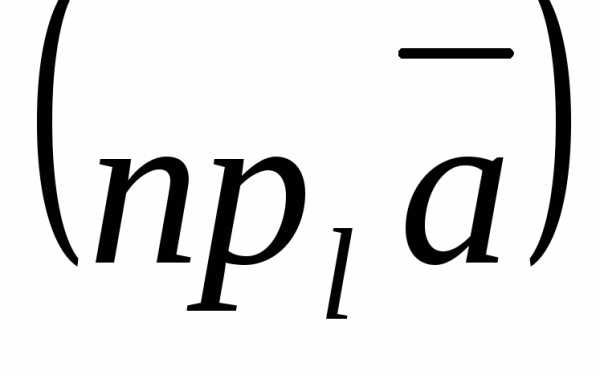 называется величина, численно равная
длине отрезка
называется величина, численно равная
длине отрезка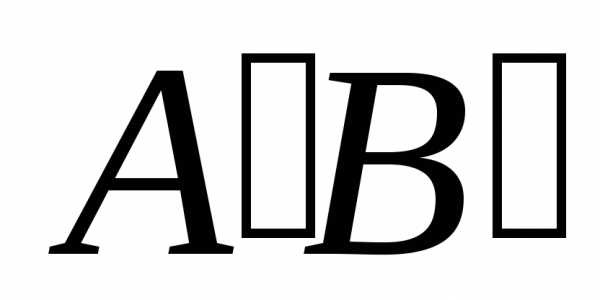 между основаниями перпендикуляров,
опущенных из точекА и В на l.
Эта длина берется со знаком плюс,
если направление от
между основаниями перпендикуляров,
опущенных из точекА и В на l.
Эта длина берется со знаком плюс,
если направление от  к
к совпадает с направлением осиl и минус в противном
случае (рис. 6). Аналогично определяется
проекция одного вектора на другой.
совпадает с направлением осиl и минус в противном
случае (рис. 6). Аналогично определяется
проекция одного вектора на другой.
Углом
между осью и вектором называется угол,  на который
нужно повернуть ось до совмещения с
вектором кратчайшим образом (так чтобы
их стрелки совпали). Из такого определения
следует, что
.
на который
нужно повернуть ось до совмещения с
вектором кратчайшим образом (так чтобы
их стрелки совпали). Из такого определения
следует, что
.
Свойства проекции вектора на ось.
1. Проекция равна нулю тогда и только тогда, когда вектор перпендикулярен оси (говорят, вектор ортогонален оси).
2. При параллельном переносе вектора его проекция не меняется.
3. Проекция вектора на ось равна произведению длины вектора на
косинус угла между вектором и осью.
.
Рис. 7 Рис. 8
В этой формуле знак проекции регулируется знаком косинуса:
—
если  острый угол (рис. 7), тои
острый угол (рис. 7), тои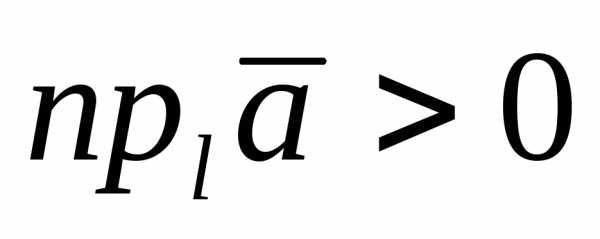 ;
;
—
если  тупой угол (рис. 8), тои
тупой угол (рис. 8), тои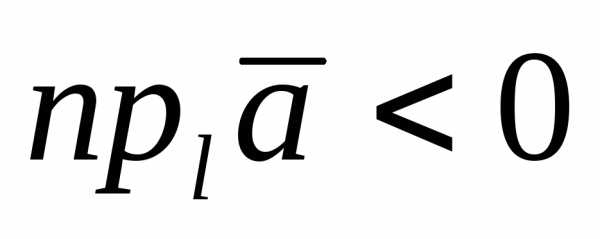 .
.
4. Скалярный множитель можно выносить за знак проекции
.
5. Проекция суммы векторов равна сумме проекций слагаемых
.
studfiles.net
Разложение вектора по базису » Аналитическая геометрия f(x)dx.Ru
п.2. Разложение вектора по базису.
Определение. Пусть – произвольный вектор, – произвольная система векторов. Если выполняется равенство
, (1)
то говорят, что вектор представлен в виде линейной комбинации данной системы векторов. Если данная система векторов является базисом векторного пространства, то равенство (1) называется разложением вектора по базису . Коэффициенты линейной комбинации называются в этом случае координатами вектора относительно базиса .
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство. 1) Пусть L произвольная прямая (или ось) и – базис . Возьмем произвольный вектор . Так как оба вектора и коллинеарные одной и той же прямой L, то . Воспользуемся теоремой о коллинеарности двух векторов. Так как , то найдется (существует) такое число , что и тем самым мы получили разложение вектора по базису векторного пространства .
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и , где . Тогда и используя закон дистрибутивности, получаем:
.
Так как , то из последнего равенства следует, что , ч.т.д.
2) Пусть теперь Р произвольная плоскость и – базис . Пусть произвольный вектор этой плоскости. Отложим все три вектора от какой-нибудь одной точки этой плоскости. Построим 4 прямых. Проведем прямую , на которой лежит вектор , прямую , на которой лежит вектор . Через конец вектора проведем прямую параллельную вектору и прямую параллельную вектору . Эти 4 прямые высекают параллелограмм. См. ниже рис. 3. По правилу параллелограмма , и , , – базис , – базис .
Теперь, по уже доказанному в первой части этого доказательства, существуют такие числа , что
и . Отсюда получаем:
и возможность разложения по базису доказана.
рис.3.
Теперь докажем единственность разложения по базису. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства : и . Получаем равенство
, откуда следует . Если , то , а т.к. , то и коэффициенты разложения равны: , . Пусть теперь . Тогда , где . По теореме о коллинеарности двух векторов отсюда следует, что . Получили противоречие условию теоремы. Следовательно, и , ч.т.д.
3) Пусть – базис и пусть произвольный вектор. Проведем следующие построения.
Отложим все три базисных вектора и вектор от одной точки и построим 6 плоскостей: плоскость, в которой лежат базисные векторы , плоскость и плоскость ; далее через конец вектора проведем три плоскости параллельно только что построенным трем плоскостям. Эти 6 плоскостей высекают параллелепипед:
рис.4.
По правилу сложения векторов получаем равенство:
. (1)
По построению . Отсюда, по теореме о коллинеарности двух векторов, следует, что существует число , такое что . Аналогично, и , где . Теперь, подставляя эти равенства в (1), получаем:
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и . Тогда
. (3)
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
. (4)
Из равенства (4) следует, что вектор раскладывается по базису , т.е. вектор лежит в плоскости векторов и, следовательно, векторы компланарные, что противоречит условию.
б) Остается случай , т.е. . Тогда из равенства (3) получаем или
. (5)
Так как – базис пространства векторов лежащих в плоскости, а мы уже доказали единственность разложения по базису векторов плоскости, то из равенства (5) следует, что и , ч.т.д.
Теорема доказана.
Возможно найдутся ответы здесь:
fxdx.ru
33. Единственность разложения векторов по базису. Координаты. Действия над векторами в координатной форме.
Пусть произвольные векторы являются базисом n-мерного векторного пространства. Если к ним добавить некоторый n-мерный вектор x, то полученная система векторов будет линейно зависимой. Из свойств линейной зависимости мы знаем, что хотя бы один вектор линейно зависимой системы линейно выражается через остальные. Иными словами, хотя бы один из векторов линейно зависимой системы раскладывается по остальным векторам.
Так мы подошли к очень важной теореме.
Теорема.
Любой вектор n-мерного векторного пространства единственным образом раскладывается по базису.
Доказательство.
Пусть — базис n-мерного векторного пространства. Добавим к этим векторам n-мерный вектор x. Тогда полученная система векторов будет линейно зависимой и вектор x может быть линейно выражен через векторы : , где — некоторые числа. Так мы получили разложение вектора x по базису. Осталось доказать, что это разложение единственно.
Предположим, что существует еще одно разложение , где — некоторые числа. Отнимем от левой и правой частей последнего равенства соответственно левую и правую части равенства :
Так как система базисных векторов линейно независима, то поопределению линейной независимости системы векторов полученное равенство возможно только тогда, когда все коэффициенты равны нулю. Поэтому, , что доказывает единственность разложения вектора по базису.
Определение.
Коэффициенты называются координатами вектора x в базисе .
После знакомства с теоремой о разложении вектора по базису, мы начинаем понимать суть выражения «нам задан n-мерный вектор ». Это выражение означает, что мы рассматриваем вектор x n-мерного векторного пространства, координаты которого заданы в некотором базисе. При этом мы понимаем, что этот же вектор x в другом базисе n-мерного векторного пространства будет иметь координаты, отличные от .
Рассмотрим следующую задачу.
Пусть в некотором базисе n-мерного векторного пространства нам задана система из nлинейно независимых векторов и вектор . Тогда векторы также являются базисом этого векторного пространства.
Пусть нам требуется найти координаты вектора x в базисе . Обозначим эти координаты как .
Вектор x в базисе имеет представление . Запишем это равенство в координатной форме: Это равенство равносильно системе из n линейных алгебраических уравнений с nнеизвестными переменными : Основная матрица этой системы имеет вид Обозначим ее буквой А. Строки матрицы А представляют собой векторы линейно независимой системы векторов , поэтому ранг этой матрицы равен n, следовательно, ее определитель отличен от нуля. Этот факт указывает на то, что система уравнений имеет единственное решение, которое может быть найдено любым методом, например, методом Крамера или матричным методом.
Так будут найдены искомые координаты вектора x в базисе .
Разберем теорию на примерах.
Пример.
В некотором базисе трехмерного векторного пространства заданы векторы Убедитесь, что система векторов также является базисом этого пространства и найдите координаты вектора x в этом базисе.
Решение.
Чтобы система векторов была базисом трехмерного векторного пространства нужно, чтобы она была линейно независима. Выясним это, определив ранг матрицы A, строками которой являются векторы . Ранг найдем методом Гаусса следовательно, Rank(A) = 3, что показывает линейную независимость системы векторов.
Итак,
векторы являются
базисом. Пусть в этом базисе вектор x имеет
координаты .
Тогда, как мы показали выше, связь
координат этого вектора задается
системой уравнений
Подставив
в нее известные из условия значения,
получим
Решим
ее методом Крамера:  Таким
образом, вектор x в
базисе имеет
координаты .
Таким
образом, вектор x в
базисе имеет
координаты .
Ответ:
.
Пример.
В некотором базисе четырехмерного векторного пространства задана линейно независимая система векторов Известно, что . Найдите координаты вектора x в базисе .
Решение.
Так как система векторов линейно независима по условию, то она является базисом четырехмерного пространства. Тогда равенство означает, что вектор x в базисе имеет координаты . Обозначим координаты вектора x в базисе как .
Система уравнений, задающая связь координат вектора x в базисах и имеет вид Подставляем в нее известные значения и находим искомые координаты :
Ответ:
.
studfiles.net
12.3. Разложение вектора по базису Представление вектора в произвольном базисе
Пусть система векторов
является базисом,
а вектор  — их
линейной комбинацией. Имеет место
следующая теорема.
— их
линейной комбинацией. Имеет место
следующая теорема.
ТЕОРЕМА 2. Разложение любого вектора в базисе, если оно существует, является единственным.
Доказательство.
Предположим, что вектор 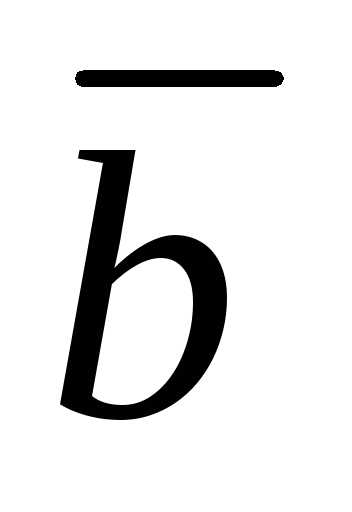 может быть представлен в виде линейной
комбинации векторов (12.9) двумя способами:
может быть представлен в виде линейной
комбинации векторов (12.9) двумя способами:
где наборы чисел αi и βi, среди которых обязательно есть ненулевые значения, не совпадают. Вычитая одно равенство из другого, имеем
Мы получили, что линейная комбинация векторов системы (12.9), в которой не все коэффициенты равны нулю (в силу несовпадения αi и βi), равна нулю, т.е. данная система оказалась линейно зависимой, что противоречит условию теоремы. Полученное противоречие доказывает теорему.
Стало быть, в произвольном базисе пространства Rn
любой вектор этого пространства обязательно представим в виде разложения по базисным векторам:
причем это разложение является единственным для данного базиса. Коэффициенты разложения
называются координатами вектора 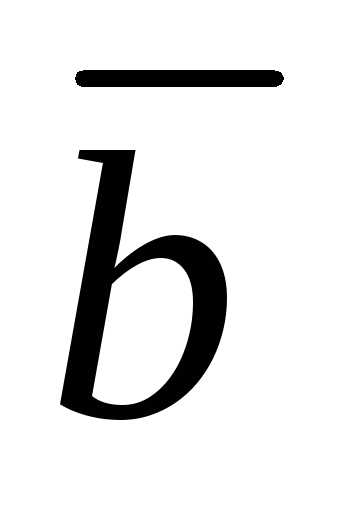 в базисе (12.10), и, как следует из сказанного,
этот набор единственный для любого
вектора из Rn в данном
базисе.
в базисе (12.10), и, как следует из сказанного,
этот набор единственный для любого
вектора из Rn в данном
базисе.
Задача нахождения
коэффициентов разложения в случае
произвольного базиса (12.10) является,
вообще говоря, непростой. Нужно
приравнять соответствующие координаты
линейной комбинации векторов слева
и координаты вектора 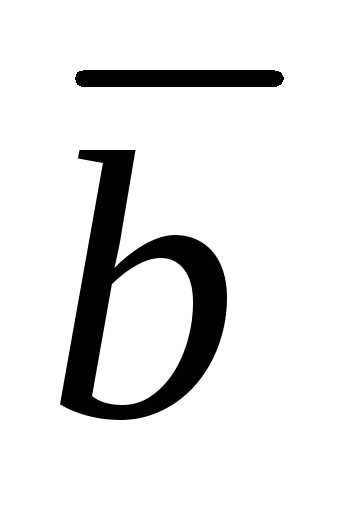 в (12.11). Пусть базисные векторы и вектор
в (12.11). Пусть базисные векторы и вектор 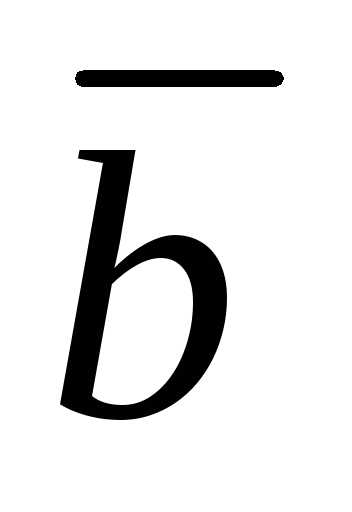 заданы в следующей координатной форме:
заданы в следующей координатной форме:
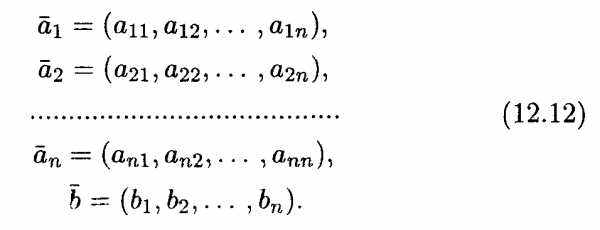
Выполнение
процедуры, описанной выше, приводит к системе п
линейных уравнений относительно п неизвестных координат разложения
вектора 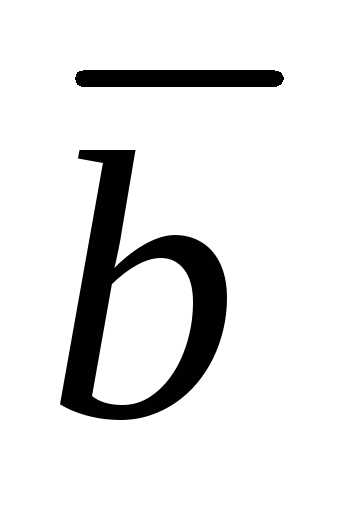 в базисе (12.10):
в базисе (12.10):
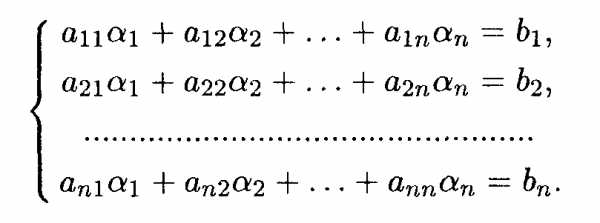
Такие системы уравнений и методы их решения представляют отдельные разделы линейной алгебры; они будут рассмотрены в следующих главах.
Разложение вектора в ортогональном базисе
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса:
Ортогональные базисы хорошо известны и широко используются на плоскости и в пространстве (рис. 12.2). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются по весьма простой процедуре, не требующей трудоемких вычислений.
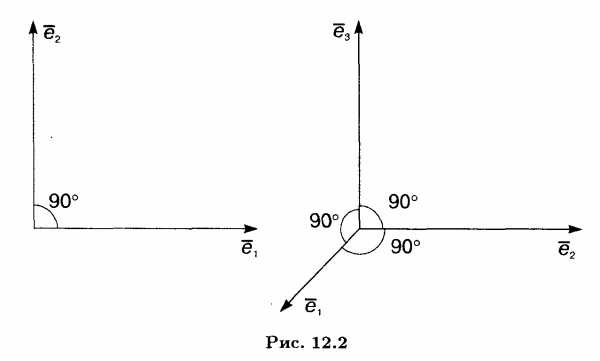
Действительно,
пусть требуется найти разложение
произвольного вектора 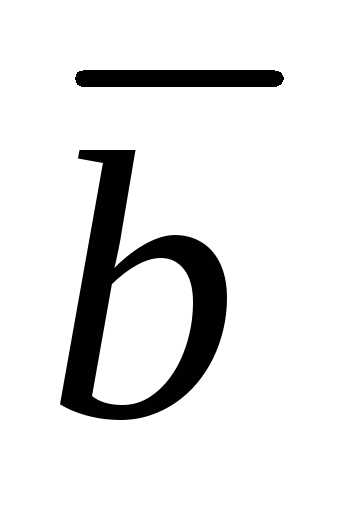 в ортогональном базисе (12.13). Составим
разложение
этого вектора с неизвестными пока
координатами разложения в данном базисе:
в ортогональном базисе (12.13). Составим
разложение
этого вектора с неизвестными пока
координатами разложения в данном базисе:
Умножим обе части
этого равенства, представляющие собой
векторы, на вектор  1.
В силу свойств 2 и 3 скалярного произведения
векторов имеем
1.
В силу свойств 2 и 3 скалярного произведения
векторов имеем
Однако в силу взаимной ортогональности векторов базиса (12.13) все скалярные произведения векторов базиса, за исключением первого, равны нулю, т.е. коэффициент α1 определяется по формуле
Умножая поочередно
равенство (12.14) на другие базисные
векторы, мы получаем простую формулу
для вычисления коэффициентов
разложения вектора 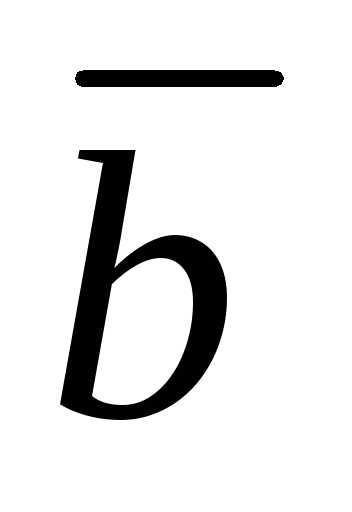 :
:
Нетрудно видеть,
что соотношения (12.15) имеют смысл,
поскольку | i| ≠
0.
i| ≠
0.
Отметим особо
частный случай ортогонального базиса,
когда все векторы в (12.13) имеют единичную
длину (| i| = 1),
или
нормированы по своей длине. В таком
случае базис называют ортонормированным и координаты разложения (12.15) имеют
наиболее простой вид:
i| = 1),
или
нормированы по своей длине. В таком
случае базис называют ортонормированным и координаты разложения (12.15) имеют
наиболее простой вид:
studfiles.net
Разложение вектора по базисным векторам. — КиберПедия
Пусть заданапрямоуг. с-ма координат. Введем в рассмотрение единичные векторы, коорд. осей . -базисные вектора с-мы координат или орты. -произвольный вектор пр-ва. Отложим из начала координат вектор . По св-вам координат . Пусть числу на оси Ох соотв-ет точка , на . Тогда , ,
— ф-ла разложения по базисным векторам.
Пр. (1;2;3)
(1;0;0)+2(0;1;0)+3(0;0;1)=
Скалярное произведение векторов.
О.Скалярное произведение двух векторов и – число, равное произведению их модулей на угла между ними.
Св-ва:
ü
ü
ü тогда и только тогда, когда
ü угла между векторами вычисляется по ф-ле:
ü
ü
Т. Если векторы имеют координаты ; , тогда
Док-во:
Разложим исходные вертора по базисным векторам:а=a1*i+a2*j+a3*k;b=b1*i+b2*j+b3*k,перемножим
a*b=(a1*i+a2*j+a3*k)*( b1*i+b2*j+b3*k)={i*i=1,i*j=j*i=0,j*k=0,j*j=1,k*k=1}=
следствие:
1)cosf= /корень(а1^2+a2^2+a3^2)*(b1^2+b2^2+b3^2)
2)верторы ортогональны тогда и только тогда,когда =0
Правые и левые с-мы координат.
Три некомпланарных вектора в указанном порядке наз-ют тройкой векторов.
Пусть отложены из одной точки, будем смотреть из конца вектора на плоскость, содержащую и . Если кратчайший поворот от к осуществляется против часовой стрелки, то тройка векторов наз-тсяправой тройкой, если по часовой-то левой.
Векторное произведение векторов.
О. Векторным произведением на наз-тся , к-рый удовлетворяет след.условиям:
1.
2. каждому из векторов и
3.тройка векторов ,является правой
Св-ва:
ü
ü и -коллинеарны только тогда, когда =0
ü площадь параллелограмма, построенного на векторах и = модулю векторного произведения
ü
ü
ü
Т. Пусть , , тогда
Разложим и по базисным векторам
=
Пр.
тогда Смешанное произведение
О. Пусть даны 3 вектора . Умножим векторно, а полученный р-т скалярно на . В р-те получим число , называемое смешанным произведением векторов .
Смешанное произведение 3-х некомпланарных векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «+», если тройка правая и со знаком «-» — если левая.
Док-во:
Рассмотрим паралнлогрампостроенный на этих векторах.
16)Функции нескольких переменных.
Рассм. арифметическое -мерное пр-во ú
Пусть подмнож-во множ-ва . –нек-рое множ-во элементов , если каждому элементу ставится в соотв-е единственный элемент , то говорят, что на множ-ве задана ф-я
О. Пусть имеется переменных величин и каждому значению из некоторогомнож-ва соотв-ет одно, вполне определенное значение переменной . Тогда говорят, что задана ф-я нескольких переменных .
Ф-ла задает объем цилиндра, как ф-ю двух переменных . переменные величины называют независимыми переменными или аргументами. –зависимая переменная. Символ обозначает з-н соотв-я, множ-во – область определения.
Рассм. нек-рые примеры ф-и нескольких переменных. Ф-я 1) , -называется линейной; 2) —квадратичная ф-я.
Предел.
Множ-во точек , координаты к-рых удовлетворяют нер-ву <dназ-сяd -окрестностью точки .
О. Пусть нек-рая ф-я определена в нек-рой окрестности точки кроме самой точки . Число А наз-тся пределом ф-и при , или . Если для любого существует , такое что для всех и из -окрестности точки вып-тсянер-во <e.
, <e
Предел ф-и двух переменных обладает св-вами, аналогичнымисв-вам предела ф-и одной переменной. О.Ф-я наз-тсянепрерывной в точке если:
1.она определена в
2.имеет конечный предел при ,
3.этот предел = значению ф-и, т.е. .
cyberpedia.su
