Квадратное уравнение с комплексными корнями
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Определение 1
Двучленным называется уравнение вида $x^{n} =A$.
Рассмотрим три случая:
- В случае если $A$ — это положительное действительное число, то корни уравнения находятся по формуле \[x_{k} =\sqrt[{n}]{A} \cdot \left(\cos \frac{2k\pi }{n} +i\cdot \sin \frac{2k\pi }{n} \right),\, \, \, k=0,..,n-1.\]
- В случае если $A$ — это отрицательное действительное число, то корни уравнения находятся по формуле \[x_{k} =\sqrt[{n}]{|A|} \cdot \left(\cos \frac{\pi +2k\pi }{n} +i\cdot \sin \frac{\pi +2k\pi }{n} \right),\, \, \, k=0,..,n-1.\]
- В случае если $A$ — это комплексное число, то корни уравнения находятся по формуле \[x_{k} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]
Пример 1
Решить уравнение: $x^{3} =8$.
Решение:
Так как $A>0$, то $x_{k} =\sqrt[{3}]{8} \cdot \left(\cos \frac{2k\pi }{3} +i\cdot \sin \frac{2k\pi }{3} \right),\, \, \, k=0,..,2$.
При $k=0$ получаем $x_{0} =\sqrt[{3}]{8} \cdot \left(\cos 0+i\cdot \sin 0\right)=\sqrt[{3}]{8} =2$.
При $k=1$ получаем
\[x_{1} =\sqrt[{3}]{8} \cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)=\sqrt[{3}]{8} \cdot (-\frac{1}{2} +\frac{\sqrt{3} }{2} \cdot i)=2\cdot (-\frac{1}{2} +\frac{\sqrt{3} }{2} \cdot i)=-1+\sqrt{3} \cdot i.\]При $k=2$ получаем
\[x_{2} =\sqrt[{3}]{8} \cdot \left(\cos \frac{4\pi }{3} +i\cdot \sin \frac{4\pi }{3} \right)=\sqrt[{3}]{8} \cdot (-\frac{1}{2} -\frac{\sqrt{3} }{2} \cdot i)=2\cdot (-\frac{1}{2} -\frac{\sqrt{3} }{2} \cdot i)=-1-\sqrt{3} \cdot i.\]Пример 2
Решить уравнение: $x^{3} =1+i$.
Решение:
Так как $A$ — комплексное число, то
\[x_{k} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1,\, \, \, k=0,..,2.\]Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
\[r=\sqrt{1^{2} +1^{2} } =\sqrt{1+1} =\sqrt{2} \]Вычислим аргумент исходного комплексного числа:
\[\varphi =\arg z=arctg\frac{1}{1} =arctg1=\frac{\pi }{4} \]Подставим полученные значения и получим:
\[A=\sqrt{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} )\]Уравнение перепишем в виде:
\[x^{3} =\sqrt{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} )\]При $k=0$ получаем $x_{0} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4}{3} +i\cdot \sin \frac{\pi /4}{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)=\sqrt[{6}]{2} \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.
При $k=1$ получаем
\[\begin{array}{l} {x_{1} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+2\pi }{3} +i\cdot \sin \frac{\pi /4+2\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right)} \end{array}\]При $k=2$ получаем
\[\begin{array}{l} {x_{2} =\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{\pi /4+4\pi }{3} +i\cdot \sin \frac{\pi /4+4\pi }{3} \right)=\sqrt[{3}]{\sqrt{2} } \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)=} \\ {=\sqrt[{6}]{2} \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right)} \end{array}\]Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом
\[x_{1,2} =\frac{-b\pm \sqrt{D} }{2a} .\]Примечание 1
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Пример 3
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
\[D=2^{2} -4\cdot 1\cdot 5=4-20=-16.\]Так как $D \[x_{1,2} =\frac{-2\pm \sqrt{-16} }{2} =\frac{-2\pm i\cdot \sqrt{16} }{2} =\frac{-2\pm i\cdot 4}{2} =-1\pm 2i.\]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
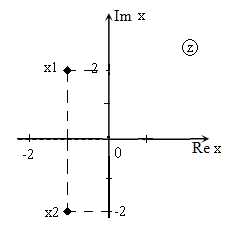
Рис. 1
Примечание 2
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Определение 3
Комплексное число вида $\overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Примечание 3
Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.
Пример 4
Зная корни уравнения $x_{1,2} =1\pm 2i$, записать исходное уравнение.
Решение:
Запишем уравнение следующим образом:
\[(x-(1-2i))\cdot (x-(1+2i))=0.\]Выполним умножение комплексных чисел
\[x^{2} -(1-2i)\cdot x-x\cdot (1+2i)+(1-2i)\cdot (1+2i)=0\]\[x^{2} -x+2i\cdot x-x-2i\cdot x+1-4i^{2} =0\] \[x^{2} -2x+1+4=0\] \[x^{2} -2x+5=0\]Следовательно, $x^{2} -2x+5=0$ — искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Пример 5
Решить уравнение: $z^{2} +(1-2i)\cdot z-(1+i)=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
\[D=(1-2i)^{2} +4\cdot 1\cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.\]Так как $D>0$, уравнение имеет два корня:
\[x_{1} =\frac{-(1-2i))-\sqrt{1} }{2} =\frac{-1+2i-1}{2} =\frac{-2+2i}{2} =-1+i.\] \[x_{2} =\frac{-(1-2i))+\sqrt{1} }{2} =\frac{-1+2i+1}{2} =\frac{2i}{2} =i.\]Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
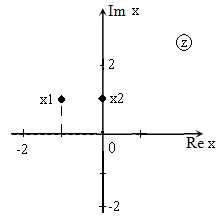
Рис. 2
Примечание 4
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
spravochnick.ru
Решение квадратных уравнений в поле комплексных чисел » Аналитическая геометрия f(x)dx.Ru
п.7. Решение квадратных уравнений в поле комплексных чисел.
Вывод формулы корней квадратного уравнения в поле комплексных чисел ничем не отличается от такового в поле действительных чисел (как, впрочем, и в любом поле, в том числе и в конечном). Вспомним этот вывод.
Теорема. Пусть , z – комплексная переменная. Тогда квадратное уравнение имеет ровно два корня (они могут быть равными), которые можно найти по формуле: .
Доказательство. Выделим полный квадрат в левой части квадратного уравнения:
.
Теперь квадратное уравнение можно записать в виде:
. Здесь мы применили следствие из п.6. Доказываемая формула очевидно следует из последнего равенства.
Теорема доказана.
Пример. Решить уравнение .
Решение. Вычисляем дискриминант
. Вычисляем корни из дискриминанта по формуле квадратных корней из комплексного числа:
.
Вычисляем корни уравнения по формуле корней квадратного уравнения:
или ; .
Ответ: .
Замечание. Аналогично решаются квадратные уравнения с действительными коэффициентами, но с отрицательным дискриминантом.
Пример. Решить уравнение .
Решение. Вычислим дискриминант. . Отсюда следует, что действительных корней квадратное уравнение не имеет, но, согласно теореме, оно имеет два корня в поле комплексных чисел. Для вычисления корня из дискриминанта применяем следствие из предыдущего п.6, смотри там же пример. Получаем:
. Теперь подставляем в формулу корней квадратного уравнения: .
Ответ: .
Возможно найдутся ответы здесь:
fxdx.ru
Решение комплексных квадратных уравнений
Задание. Составить квадратное уравнение, которое имеет корни и . Решить его.
Решение. Известно, что если — корни квадратного уравнения , то указанное уравнение можно записать в виде . А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:
Раскрываем скобки и выполняем операции над комплексными числами:
— искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде . То есть
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений и :
решив которую, имеем, что , или , . Рассматривая любую из полученных пар, например, первую, получаем, что , а тогда
Ответ.
www.webmath.ru
Конспект урока по математике на тему «Решение квадратных уравнений с помощью комплексных чисел» 1 курс профессия «Мастер по лесному хозяйству»
Урок на тему: «Решение квадратных уравнений с помощью комплексных чисел».
Цели:
Образовательные: расширить понятие числа, ввести понятие комплексного числа, действия над комплексными числами, заданными в алгебраической форме.
Воспитательные: прививать интерес к математике, ознакомить учащихся с историей развития комплексных чисел, воспитывать
Развивающие: развивать творческое мышление, пространственное мышление, научить применять теоретические знания при решении практических задач, формировать активность и самостоятельность при работе в группах.
Используемые технологии и методы: 1) проблемный диалог; 2) информационно- коммуникационные технологии.
Тип занятия: комбинированный.
План урока:
Организационный момент.
Повторение материала предыдущего занятия.
Изучение нового материала.
Закрепление нового материала.
Рефлексия.
1.Организационный момент (2 мин).
2. Повторение материала предыдущего занятия (10 мин).
Множество действительных чисел;
Множество комплексных чисел;
Определение и форма записи комплексного числа;
Изображение комплексного числа на комплексной оси;
Степени мнимой единицы;
3. Изучение нового материала.

Вопрос группе:
-Как называется картинка, которую вы видите на экране? (Мем).
-Что мы знаем об извлечении корня из отрицательных чисел? (что корень из отрицательных чисел не извлекается).
-А что, если я докажу вам сегодня на уроке, что не так уж этот корень и нереален? А помогут мне в этом числа, с которыми мы познакомились на предыдущем занятии — комплексные числа!
Верно, что во множестве действительных чисел корней из отрицательных чисел быть не может. Об этом нам всем говорили в школе. НО, введение понятия «комплексное число» продвинуло вперед современную математику, а с ней и другие естественные науки.
Так вот, в множестве комплексных чисел корень из -1 извлекается и очень хорошо! Вспомним знакомую нам формулу . Корень из -1= i,
Исследование алгебраических уравнений является одним из важнейших вопросов в математике. Например, действительных корней не имеет квадратное уравнение с отрицательным дискриминантом. Простейшим таким уравнением является уравнение
.
Для того чтобы это уравнение имело решение, необходимо расширить множество действительных чисел путем присоединения к нему корня уравнения
.
Обозначим этот корень через . Таким образом, по определению
, или
,
следовательно,
.
Таким образом, действительных чисел явно недостаточно, чтобы построить такую теорию квадратных уравнений, в рамках которой каждое квадратное уравнение было бы разрешимо. Это приводит к необходимости расширять множество действительных чисел до множества, в котором было бы разрешимо любое квадратное уравнение. Такое множество называется множеством комплексных чисел и обозначается С.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
, ,
,
,
Решим квадратное уравнение .
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:
– сопряженные комплексные корни
Т.о., у уравнения есть 2 сопряженных комплексных корня:
,
Найти корни квадратного уравнения
Решение: на первом месте расположена мнимая единица, и, в принципе, от неё можно избавиться (умножая обе части на ), однако, в этом нет особой надобности.
Для удобства выпишем коэффициенты:
Не теряем «минус» у свободного члена. Уравнение в стандартном виде :
Вычислим дискриминант:
А вот и главное препятствие:
Применение общей формулы извлечения корня осложняется серьёзными затруднениями, связанными с аргументом подкоренного комплексного числа (убедитесь сами). Но существует и другой, «алгебраический» путь! Корень будем искать в виде:
Возведём обе части в квадрат:
Два комплексных числа равны, если равны их действительные и их мнимые части. Таким образом, получаем следующую систему:
Систему проще решить подбором (более основательный путь – выразить из 2-го уравнения – подставить в 1-е, получить и решить биквадратное уравнение). Из 1-го уравнения следуют, что «икс» по модулю больше, чем «игрек». Кроме того, положительное произведение сообщает нам, что неизвестные одного знака. Исходя из вышесказанного, и ориентируясь на 2-е уравнение, запишем все подходящие ему пары:
Очевидно, что 1-му уравнению системы удовлетворяют две последние пары, таким образом:
Не помешает промежуточная проверка:
что и требовалось проверить.
Находим корни, не забывая, кстати, что :
Ответ:
Проверим, удовлетворяют ли найденные корни уравнению :
1) Подставим :
верное равенство.
2)Подставим
:
верное равенство.
Таким образом, решение найдено правильно.
4. Закрепление нового материала
Решить уравнения:
1. х2 + (5 – 2i) x + 5(1– i) = 0;
2. х2 + (1 – 2i) х – 2i = 0;
3.
5. Рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
6. Домашнее задание
Составить конспект на тему «Тригонометрическая форма записи комплексного числа»;
Решить уравнения:
z^2-2z+5=0
z^2+3z+6=0
z^2-4z+25=0
3z^2-3z+3=0
infourok.ru
Как решать комплексные уравнения. Примеры
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:
где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = {0, 1, 2, 3, …n-1 }.
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Ответ:
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:
Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
Найдем корни уравнения:
Ответ:
Пример 3. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = {0, 1, 2, 3}. Найдем модуль комплексного числа:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
Ответ:
Пример 4. Найти корни уравнения
Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
Ответ:
Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
matematyka.ru
Решение квадратных уравнений на множестве комплексных чисел; алгоритм извлечения квадратного корня из комплексного числа; полезные следствия для формулы корней квадратного уравнения
Решение квадратных уравнений на множестве комплексных чисел; алгоритм извлечения квадратного корня из комплексного числа; полезные следствия для формулы корней квадратного уравнения
|
Похожие:
| Общий вид квадратного уравнения: Общий вид квадратного уравнения Графически квадратное уравнение можно рассмотреть как график квадратичной функции (параболу). В этом случае корнями квадратного уравнения… | Сформулируйте определение квадратного уравнения. Сформулируйте определение квадратного уравнения Объясните, в чём заключается смысл ограничения в определении квадратного уравнения (а ≠ 0) | ||
| Ввести определения квадратного уравнения, неполных квадратных уравнений Учебное пособие-справочник для учителей и учащихся 6 класса по литературе(информация из Википедии) | План урока сформулируйте определение квадратного уравнения. Перечислите виды квадратных уравнений Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения… | ||
| Франсуа Виет не только записал в об-щем виде формулы для корней квадратного уравнения, но и нашёл выражение для коэффи-циентов уравнения через его корни, которое сейчас называ-ется теоремой Виета Виет франсуа (1540-1603), французский математик. Разработал почти всю элементар-ную алгебру. Известны «формулы Виета», дающие зависимость… | Еще одна формула корней квадратного уравнения (1 урок) 8 класс Учитель моу лицея №35 г. Ставрополя Данченко О. В. Цель урока Вы отметили, что a, b, c некоторые числа, причем a≠0, а что произойдет, если b=0 или c=0, вдруг они оба станут равны 0? | ||
| Решение квадратных уравнений 10-ю способами Элективный курс «10 способов решения квадратных уравнений» Цель Повысить уровень знаний по истории о квадратных уравнениях и различных способах решения квадратных уравнений | Урока: Повторить определение арифметического квадратного корня. Ввести и доказать теорему о квадратном корне из произведения Корень из произведения неотрицательных множителей равен произведению корней из этих множителей | ||
| Инструкция по подключению Интернета… Алгоритм содержит несколько шагов. Шаг отдельное законченное действие Алгоритм это чёткое описание последовательности действий, которые должен выполнить исполнитель для достижения конкретной цели. Примеры:… | Азбука квадратного уравнения Неполные квадратные уравнения |
rpp.nashaucheba.ru rpp.nashaucheba.ru
rpp.nashaucheba.ru
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 | program kvadratnoe_uravnenie;
var a, b, c, D, x, x1, x2, z: real;
begin
writeln('Ввели коэффициенты a, b и c для квадратного уравнения вида (ax^2+bx+c=0) :');
write('a= ');
read (a);
write('b= ');
read (b);
write('c= ');
read (c);
writeln('Решение:');
D:=b*b-4*a*c;
if D<0 then
begin
z:=-4*a*c;
if z<0 then
begin
writeln( );
writeln('Нет корней,т.к. дискриминант меньше 0');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,z);
writeln('D=',D);
writeln('D<0');
end
else
begin
writeln( );
writeln('Нет корней,т.к. дискриминант меньше 0');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,'+',z);
writeln('D=',D);
writeln('D<0');
end
end
else
if D=0 then
begin
x:=(-b)/2*a;
z:=-4*a*c;
if z<0 then
begin
writeln( );
writeln('Есть лишь один корень');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,z);
writeln('D=',D);
writeln( );
writeln('x=',-b,'/',2*a);
end
else
begin
writeln( );
writeln('Есть лишь один корень');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,'+',z);
writeln('D=',D);
writeln( );
writeln('x=',-b,'/',2*a);
end
end
else
begin
x1:=(-b-sqrt(D))/2*a;
x2:=(-b+sqrt(D))/2*a;
z:=-4*a*c;
if z<0 then
begin
writeln( );
writeln('Есть два корня');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,z);
writeln('D=',D);
writeln( );
writeln('x1=',-b,'-',sqrt(D),'/',2*a);
writeln('x2=',-b,'+',sqrt(D),'/',2*a);
writeln( );
writeln('x1=',x1);
writeln('x2=',x2);
end
else
begin
writeln( );
writeln('Есть два корня');
writeln( );
writeln(a,'x^2+',b,'x+',c,'=0');
writeln( );
writeln('D=',b,'^2-4*',a,'*',c);
writeln('D=',b*b,'+',z);
writeln('D=',D);
writeln( );
writeln('x1=',-b,'-',sqrt(D),'/',2*a);
writeln('x2=',-b,'+',sqrt(D),'/',2*a);
writeln( );
writeln('x1=',x1);
writeln('x2=',x2);
end
end
end. |
forundex.ru
