Решение тригонометрических уравнений онлайн
В общем виде, тригонометрическое уравнение можно записать следующим образом:
f(trig(x)) = 0
где f — некоторая произвольная функция, trig(x) — некоторая тригонометрическая функция.
Как правило, метод решения тригонометрических уравнений заключается в преобразовании исходного уравнения к более простому, решение которого известно. Преобразования осуществляются при помощи различных тригонометрических формул.
Например, рассмотрим решение тригонометрического уравнения:
Используя формулу косинуса двойного угла, преобразуем данное уравнение:
Полученное уравнение является простейшим и легко решается. Наш онлайн калькулятор, построенный на системе Wolfram Alpha способен решить более сложные тригонометрические уравнения с описанием подробного хода решения.
www.mathforyou.net
Решение тригонометрических уравнений онлайн — Ответ Прост!
Решение тригонометрических уравнений онлайн
Предлагаем вашему вниманию калькулятор нового поколения
для пошагового решения любых тригонометрических уравнений.
Для решения любого тригонометрического уравнения вам достаточно ввести свое уравнение в окошко калькулятора и нажать кнопку «ответ». Калькулятор выдаст решение тригонометрического уравнения бесплатно.
Способ ввода уравнения как на обычном калькуляторе.
Правила набора уравнений | |
Уравнение | Синтаксис |
tg^2 (x) + 3tg( x) =0 | |
4sin^4 (x) + cos (4x) = 1 + 12cos^4 (x) | |
6cos^2( x) + cos (3x )= cos(x) | |
2cos (x)cos(2x)= cos(x ) | |
sin(2x)/(1-cos(2x))=(1+cos(2x))/(2cos(x)) | |
3sin ^2( x) + sin( x )cos (x) = 2cos^ 2( x) | |
23,729 просмотров всего, 9 просмотров сегодня
otvet-prost.ru
Решить тригонометрическое уравнение онлайн
Главной задачей при решении тригонометрических уравнений является его преобразование до более простого уравнения основного вида, которое решаются стандартными методами. Для решения данного рода уравнений можно использовать один из семи методов:
— алгебраический;
— разложения на множители;
— преобразования к одному уравнению;
— перехода к половинному углу;
— вспомогательного угла;
— преобразования произведения в сумму;
— подстановки.
Так же читайте нашу статью «Решить систему тригонометрических уравнений онлайн решателем»
Выбор метода определяется исходя из самого уравнения. Одно уравнение можно решить несколькоми способами, однако при правильном выборе метода вы решите его за меньшее количество математических операций.
Допустим, нам дано уравнение такого вида:
\[\sin x + \cos x = 1\]
Чтобы решить данное уравнение необходимо воспользоватся 2м методом и выполнить перенос всех членов влево:
\[\sin x +\ cos x — 1 = 0\]
Теперь преобразуем и разложим на множители левую часть уравнения:
\[\sin x -2 sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot\cos(\frac {x}{2})-2\sin^2(\frac {x}{2})=0\]
\[2\sin(\frac {x}{2})\cdot[\cos(\frac {x}{2}) — \sin(\frac {x}{2})]=0\]
1)
\[\sin (\frac {x}{2})=0\]
\[\frac{x}{2}\pi k\]
\[x_1=2\pi k\]
2)
\[\cos(\frac {x}{2})-\sin(\frac {x}{2})=0\]
\[\tan\frac {x}{2}=1\]
\[\frac {x}{2}=\arctan 1 +\pi n\]
\[\frac {x}{2} = \frac {\pi}{4}+\pi n\]
\[x_2 = \frac {\pi}{2}2\pi n\]
Где можно решить тригонометрическое уравнение онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
| Функция | Описание | Пример ввода | Результат ввода |
|---|---|---|---|
| pi | Число \(\pi\) | pi | $$ \pi $$ |
| e | Число \(e\) | e | $$ e $$ |
| e^x | Степень числа \(e\) | e^(2x) | $$ e^{2x} $$ |
| exp(x) | Степень числа \(e\) | exp(1/3) | $$ \sqrt[3]{e} $$ |
| |x| abs(x) |
Модуль (абсолютное значение) числа \(x\) | |x-1| abs(cos(x)) |
\( |x-1| \) \( |\cos(x)| \) |
| sin(x) | Синус | sin(x-1) | $$ sin(x-1) $$ |
| cos(x) | Косинус | 1/(cos(x))^2 | $$ \frac{1}{cos^2(x)} $$ |
| tg(x) | Тангенс | x*tg(x) | $$ x \cdot tg(x) $$ |
| ctg(x) | Котангенс | 3ctg(1/x) | $$ 3 ctg \left( \frac{1}{x} \right) $$ |
| arcsin(x) | Арксинус | arcsin(x) | $$ arcsin(x) $$ |
| arccos(x) | Арккосинус | arccos(x) | $$ arccos(x) $$ |
| arctg(x) | Арктангенс | arctg(x) | $$ arctg(x) $$ |
| arcctg(x) | Арккотангенс | arcctg(x) | $$ arcctg(x) $$ |
| sqrt(x) | Квадратный корень | sqrt(1/x) | $$ \sqrt{\frac{1}{x}} $$ |
| x^(1/n) | Корень произвольной числовой целой степени >= 2 x^(1/2) эквивалентно sqrt(x) |
(cos(x))^(1/3) | $$ \sqrt[\Large 3 \normalsize]{cos(x)} $$ |
| ln(x) | Натуральный логарифм (основание — число e) |
1/ln(3-x) | $$ \frac{1}{ln(3-x)} $$ |
| log(a,x) | Логарифм x по основанию a | log(3,cos(x)) | $$ log_3(cos(x)) $$ |
| sh(x) | Гиперболический синус | sh(x-1) | $$ sh(x-1) $$ |
| ch(x) | Гиперболический косинус | ch(x) | $$ ch(x) $$ |
| th(x) | Гиперболический тангенс | th(x) | $$ th(x) $$ |
| cth(x) | Гиперболический котангенс | cth(x) | $$ cth(x) $$ |
| Вывод | Перевод, пояснение | ||
| Solve for x over the real numbers | Решить относительно х в действительных числах (бывают ещё комплексные) | ||
| Multiply both sides by … | Умножаем обе части на … | ||
| Simplify and substitute … | Упрощаем и делаем подстановку … | ||
| Simplify trigonometric functions | Упрощаем тригонометрические функции | ||
| Bring … together using the commom denominator … | Приводим … к общему знаменателю … | ||
| The left hand side factors into a product with two terms | Левая часть разбивается на множители как два многочлена | ||
| Split into two equations | Разделяем на два уравнения | ||
| Take the square root of both sides | Извлекаем квадратный корень из обоих частей | ||
| Subtract … from both sides | Вычитаем … из обеих частей уравнения | ||
| Add … to both sides | Прибавляем … к обоим частям уравнения | ||
| Multiply both sides by … | Умножаем обе части уравнения на … | ||
| Divide both sides by … | Делим обе части уравнения на … | ||
| Substitute … Then … | Делаем подстановку … Тогда … | ||
| Substitute back for … | Обратная подстановка для … | ||
| … has no solution since for all … | … не имеет решения для всех … | ||
| Take the inverse sine of both sides | Извлекаем обратный синус (арксинус) из обоих частей | ||
| Simplify the expression | Упрощаем выражение | ||
| Answer | Ответ | ||
| \(log(x)\) | Натуральный логарифм, основание — число e. У нас пишут \(ln(x)\) | ||
| \(arccos(x)\) или \(cos^{-1}(x)\) | Арккосинус. У нас пишут \( arccos(x) \) | ||
| \(arcsin(x)\) или \(sin^{-1}(x)\) | Арксинус. У нас пишут \( arcsin(x) \) | ||
| \(tan(x)\) | Тангенс. У нас пишут \(tg(x) = \frac{sin(x)}{cos(x)}\) | ||
| \(arctan(x)\) или \(tan^{-1}(x)\) | Арктангенс. У нас пишут \(arctg(x)\) | ||
| \(cot(x)\) | Котангенс. У нас пишут \(ctg(x) = \frac{cos(x)}{sin(x)}\) | ||
| \(arccot(x)\) или \(cot^{-1}(x)\) | Арккотангенс. У нас пишут \(arcctg(x)\) | ||
| \(sec(x)\) | Секанс. У нас пишут также \(sec(x) = \frac{1}{cos(x)}\) | ||
| \(csc(x)\) | Косеканс. У нас пишут \(cosec(x) = \frac{1}{sin(x)}\) | ||
| \(cosh(x)\) | Гиперболический косинус. У нас пишут \(ch(x) = \frac{e^x+e^{-x}}{2} \) | ||
| \(sinh(x)\) | Гиперболический синус. У нас пишут \(sh(x) = \frac{e^x-e^{-x}}{2} \) | ||
| \(tanh(x)\) | Гиперболический тангенс. У нас пишут \(th(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}} \) | ||
| \(coth(x)\) | Гиперболический котангенс. У нас пишут \(cth(x) = \frac{1}{th(x)} \) |
www.math-solution.ru
Решить систему тригонометрических уравнений онлайн
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Тригонометрическими уравнениями именуются все уравнения, в состав которых входит переменная, находящаяся под знаком тригонометрической функции. Например: \[\sin x= a, \cos x = b\]. Решение тригонометрических уравнений сводится к таким подзадачам:
* решение уравнения;
* отбор корней.

Так же читайте нашу статью «Решить нелинейное уравнение онлайн решателем»
Ответ в таких уравнениях записывается в:
— градусах;
— радианах.
Чтобы решить данного рода уравнения необходимо преобразовать уравнение в одно/несколько основных тригонометрических уравнений: \[\sin x = a; \cos x = a: \tan x = a; \cot x = a.\] А решение уже основных таких уравнений заключается в использовании таблицы преобразования или поиске положений \[х\] на единичной окружности.
Например, дано тригонометрические уравнения, решаемые с помощью таблицы преобразования, следующего вида:
\[\tan (x — \pi/4) = 0\]
Ответ: \[x = \pi /4 + \pi n\]
\[\cot2x = 1,732\]
Ответ: x = \[\pi /12 + \pi n\]
\[\sin x = 0,866\]
Ответ: \[ x = \pi/3 \]
Где можно решить систему тригонометрических уравнений онлайн бесплатно?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Решение тригонометрических функций в онлайн калькуляторе
Онлайн калькулятор на нашем сайте легко и быстро решает тригонометрические функции, вам не понадобится таблица тригонометрических функций. С нашим калькулятором можно навсегда забыть, что такое таблица Брадиса! Наш бесплатный калькулятор позволяет решать и самые простые задачи (например, найти косинус или синус угла), и сложные выражения с использованием обратных и гиперболических функций тригонометрии.
Кнопки калькулятора для решения тригонометрических функций:
Наш тригонометрический калькулятор может осуществлять вычисления как в градусах, так и в радианах. Таким образом, найти косинус угла можно вне зависимости от единицы измерения, в которой он задан. Это очень удобно и экономит массу времени при емких расчетах. Прежде чем приступить к вычислениям, нужно на панели управления указать, какая единица измерения углов будет использоваться: градусы (Deg) или радианы (Rad).
Выбор единицы измерения угла:
Обратите внимание, что в одной операции нельзя использовать разные единицы измерения углов, другими словами выражение «сумма синус 30 градусов и косинус пи =» — будет посчитано неверно!
Ниже перечислены способы решений различных тригонометрических функций в нашем онлайн калькуляторе.
Простые тригонометрические функции
Простые тригонометрические функции: синус — sin(α), косинус — cos(β) и тангенс — tan(y). Рядом указаны их обозначения так, как они используются в калькуляторе (в зарубежной литературе тангенс сокращенно обозначается tan, в русской — tg).
Кнопки калькулятора, отвечающие за простые тригонометрические функции:
Функция косинуса является четной, поэтому ее значение для отрицательного угла будет положительным. Синус, тангенс и котангенс — нечетные тригонометрические функции, соответственно, значения тригонометрических функции для отрицательных углов также будут отрицательными. Онлайн калькулятор сам учитывает четность тригонометрических функций при умножении и делении. Вам не потребуется постоянно обращать внимание на соблюдение правила знаков.
Пример вычислений с простыми тригонометрическими функциями:
Обратные тригонометрические функции
Кнопки калькулятора, отвечающие за обратные тригонометрические функции:
Если не вдаваться в формулы и подробности относительно единичной окружности, то обратные тригонометрические функции можно объяснить на простом примере: арккосинус x — это угол, косинус которого равен x. Обратные тригонометрические функции являются многозначными, и одному значению аргумента принадлежит множество значений самой функции.
Пример выражения с обратными тригонометрическими функциями:
Гиперболические функции
Гиперболические функции: гиперболический синус — sinh(), гиперболический косинус — cosh() и гиперболический тангенс tanh(). Гиперболические (круговые) функции — семейство элементарных тригонометрических функций, выраженных через экспоненту.
Кнопки калькулятора, отвечающие за гиперболические функции:
Пример решения гиперболической функции:
Обратные гиперболические функции: гиперболический арксинус — asinh(), гиперболический арккосинус — acosh() и гиперболический арктангенс — atanh().
Кнопки калькулятора, отвечающие за обратные гиперболические функции:
Пример решения обратной гиперболической функции:
Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>
Решение тригонометрических функций was last modified: Март 3rd, 2016 by Admin
compuzilla.ru
Таблица прямых и обратных тригонометрических функций, онлайн калькулятор
В данной таблице тригонометрических функций углов представлены значения, которые используются в большинстве геометрических задач.
Для решения математических задач часто используют тригонометрические функции, которые, обычно, выражают зависимость величины сторон треугольника от его углов. В этом списке:
- синус (sin)
- косинус (cos)
- тангенс (tg)
- котангенс (ctg)
Для того чтобы найти их значение предлагаем Вам воспользоваться нашей таблицей тригонометрических функций основных углов:
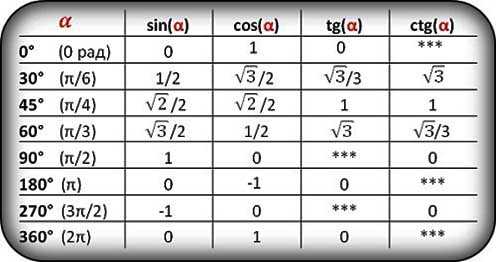
Как пользоваться таблицей
Алгоритм работы с таблицей довольно прост:
- В первом столбце выбираем значение угла (например, 30 градусов).
- В первой строке выбираем необходимую функцию (например, cos).
- Находим место их пересечение (в данном случае, 3/2).
Если Вам надо узнать значение обратных тригонометрических функций угла (arcsin, arccos, arctg, arcctg) необходимо совершить действия в обратном порядке:
- В первой строке выбираем функцию (если Вам известен arccos, то берем cos).
- Выбираем значение угла (например, -1).
- В первом столбце определяем угол, которому соответствует значение (в данном случае, 180 градусов).
Обратите внимание на то, что в таблице представлены стандартные тригонометрические углы (30, 60, 90, 180, 270 и 360 градусов). В ситуации, когда Вам дано другое значение (например, 87 градусов), рекомендуем воспользоваться нашими онлайн-калькуляторами.
Калькулятор расчета тригонометрических функций
Алгоритм работы с нашим калькулятором очень прост. Из выпадающего списка Тригонометрическая функция необходимо выбрать подходящую, например: косинус. В поле Угол, градусов необходимо ввести значение угла в градусах. Можно ввести дробное значение угла, разделяя дробную часть запятой или точкой, например: 78,14 или 78.14. Обратите внимание: после запятой идут не минуты (или секунды), а дробная часть угла! То есть 45,5 это 45 градусов и 30 минут.
После того как Вы ввели значение угла и выбрали функцию нажмите на кнопку Вычислить значение
Калькулятор расчета обратных тригонометрических функций
Для вычисления обратных тригонометрических функций (arcsin, arcos, arctg, arcctg) Вам необходимо выбрать саму функцию из выпадающего списка. Далее в поле Значение триг. функции угла: ввести целое или дробное ее значение, например: 1 или 0.57(0,57). Нажать на кнопку Вычислить значение. Результатом будет величина угла в градусах.
Обратите внимание: значения arcsin и arcсos не могут быть больше 1 и меньше -1!
Понравилась статья, расскажите о ней друзьям:
Скорее всего, Вам будет интересно:
people-ask.ru
