Действия с рациональными числами
Сложение
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму 2,5 + 3,2.
Решение. Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7
Пример 2. Найти сумму (-2,5) + (-3,2).
Решение. Сначала надо сложить модули слагаемых:
2,5 + 3,2 = 5,7
Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:
(-2,5) + (-3,2) = -5,7
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший, в результате ставится знак того числа, у которого модуль больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4,7) + (+12) = 7,3, так как 12 — 4,7 = 7,3
9 + (-15) = -6, так как 15 — 9 = 6
Из данных примеров следует, что в результате сложения двух чисел с разными знаками может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю:
(-7) + 7 = 0
Вычитание
Вычитание одного рационального числа из другого можно заменить сложением, при этом уменьшаемое берётся со своим знаком, а вычитаемое с противоположным:
(+10) — (+3,4) = (+10) + (-3,4) = 6,6
(+10) — (-3,4) = (+10) + (+3,4) = 13,4
(-10) — (-3,4) = (-10) + (+3,4) = -6,6
(-10) — (+3,4) = (-10) + (-3,4) = -13,4
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные:
3 · 5 = 15
3 · (-5) = -15
-3 · 5 = -15
-3 · (-5) = 15
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | — | = | — |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное
При умножении любого числа на -1 получится число противоположное данному:
-1,5 · (-1) = 1,5
2,5 · (-1) = -2,5
Деление
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные:
15 : 5 = 3
15 : (-5) = -3
-15 : 5 = -3
-15 : (-5) = 3
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число противоположное данному:
-1,5 : (-1) = 1,5
2,5 : (-1) = -2,5
naobumium.info
Рациональные числа
Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.
Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.
Что такое рациональное число
Рациональное число — это число, которое может быть представлено в виде дроби , где
К рациональным числам относятся следующие категории чисел:
- целые числа (например −2, −1, 0 1, 2 и т.д.)
- обыкновенные дроби (например , , и т.п.)
- смешанные числа (например , , и т.п.)
- десятичные дроби (например 0,2 и т.п.)
- бесконечные периодические дроби (например 0,(3) и т.п.)
Каждое число из этой категории может быть представлено в виде дроби .
Примеры:
Пример 1. Целое число 2 может быть представлено в виде дроби . Значит число 2 относится не только к целым числам, но и к рациональным.
Пример 2. Смешанное число может быть представлено в виде дроби . Данная дробь получается путём перевода смешанного числа в неправильную дробь
Значит смешанное число относится к рациональным числам.
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей.
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби . Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби.
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием —
Рациональные числа на координатной прямой
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество точек. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей
Попробуем понять, почему дробь вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь , а эта дробь также как и равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь
Пример 2.
Значение дроби равно 1,5
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю
Значение дроби равно 0,02
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3
это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь
Значение дроби равно 2,5
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 2,5
Минус перед рациональным числом
В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.
Рассмотрим простейшее выражение
(−6) : 2 = −3
В данном выражении делимое (−6) является отрицательным числом.
Теперь рассмотрим второе выражение
6 : (−2) = −3
Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.
Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:
А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью
Поэтому между выражениями и и можно поставить знак равенства, потому что они несут одно и то же значение
В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.
Противоположные рациональные числа
Как и целое число, рациональное число имеет своё противоположное число.
Например, для рационального числа противоположным числом является . Располагается оно на координатной прямой симметрично расположению относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат
Перевод смешанных чисел в неправильные дроби
Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..
Например, переведём смешанное число в неправильную дробь
Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:
(2 × 2) + 1
Вычислим данное выражение:
(2 × 2) + 1 = 4 + 1 = 5
Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:
Полностью данная процедура записывается следующим образом:
Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби
Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.
Рассмотрим дробь . Выделим в этой дроби целую часть. Получим
Чтобы вернуть изначальную дробь нужно перевести смешанное число в неправильную дробь. Но если мы воспользуемся старым правилом, а именно умножим целую часть на знаменатель дробной части и к полученному числу прибавим числитель дробной части, то получим следующее противоречие:
Мы получили дробь , а должны были получить дробь .
Делаем вывод, что смешанное число в неправильную дробь переведено неправильно:
Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть числитель дробной части. В этом случае у нас всё встанет на свои места
Отрицательное смешанное число является противоположным для смешанного числа . Если положительное смешанное число располагается в правой части и выглядит так
то отрицательное смешанное число будет располагаться в левой части симметрично относительное начала координат
И если читается как «две целых и одна вторая», то читается как «минус две целых и минус одна вторая». Поскольку числа −2 и располагаются в левой части координатной прямой — они оба являются отрицательными.
Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число в развёрнутом виде записывается как .
А отрицательное смешанное число записывается как
Теперь мы можем понять, почему смешанное число расположилось в левой части координатной прямой. Минус перед двойкой указывает, что мы сдвинулись от нуля на два шага влево, в результате оказались в точке, где находится число −2
Затем, начиная от числа −2 сдвинулись ещё влево на шага. А поскольку значение равно −0,5 то наш шаг будет половиной от полного шага.
В итоге, мы окажемся посередине между числами −3 и −2
Пример 2. Выделить в неправильной дроби целую часть, затем полученное смешанное число обратно перевести в неправильную дробь
Выполним первую часть задания, а именно выделим в неправильной дроби целую часть
Выполним вторую часть задания, а именно переведём полученное смешанное число в неправильную дробь. Для этого умножим целую часть на знаменатель дробной части и из полученного числа вычтем числитель дробной части:
Если нет желания путаться и привыкать к новому правилу, то можно смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.
Выполним предыдущее задание этим способом, а именно переведём смешанное число в неправильную дробь
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Навигация по записям
spacemath.xyz
Рациональные числа, понятие и примеры.
Рациональные числа вы с ними уже знакомы, осталось только обобщить и сформулировать правила. Так какие числа называются рациональными числами? Рассмотрим подробно в этой теме урока.
Понятие рациональных чисел.
Определение:
Рациональные числа – это числа, которые можно представить в виде дроби \(\frac{m}{n}\), где m – целое число, а n – натуральное число.
Другими словами, можно сказать:
Рациональные числа – это все натуральные числа, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Разберем каждый пункт подробно.
- Любое натуральное число можно представить в виде дроби, например, число 5=\(\frac{5}{1}\).
- Любое целое число можно представить в виде дроби, например, числа 4, 0 и -2. Получаем 4=\(\frac{4}{1}\), 0=\(\frac{0}{1}\) и -2=\(\frac{-2}{1}\).
- Обыкновенные дроби уже записаны в рациональном виде, например, \(\frac{6}{11}\) и \(\frac{9}{2}\).
- Бесконечные периодические дроби, например, 0,8(3)=\(\frac{5}{6}\).
- Конечные десятичные дроби, например, 0,5=\(\frac{5}{10}=\frac{1}{2}\).
Множество рациональных чисел.
Вспомним, что множество натуральны чисел обозначается латинской буквой N.
Множество целых чисел обозначается латинской буквой Z.
А множество рациональных чисел обозначается латинской буквой Q.
Во множество рациональных чисел входит множество целых и натуральных чисел в этом и заключается смысл рациональных чисел.
На рисунке можно показать множество рациональных чисел.
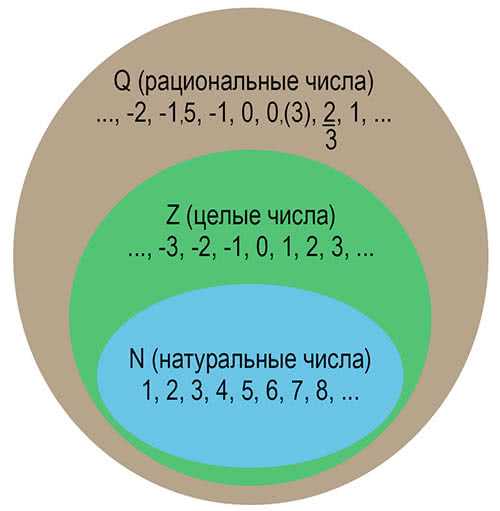
Но не все числа являются рациональными. Бывают еще множества различных чисел, которые в дальнейшем вы будите изучать.
Бесконечные непрериодические дроби не принадлежат множеству рациональных чисел.
Например, число е, \(\sqrt{3}\) или число \(\pi\) (читается число пи) не являются рациональными числами.
Вопросы по теме «Рациональные числа»:
Какое выражение является рациональным числом из чисел \(\sqrt{5}, -0.(3), 15, \frac{34}{1569}, \sqrt{6}\) ?
Ответ:
Корень из 5 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Бесконечная десятичная периодическая дробь -0,(3)=\(-\frac{3}{10}\) можно представить в виде дроби, поэтому это рациональное число.
Число 15 можно представить в виде дроби \(\frac{15}{1}\), поэтому это рациональное число.
Дробь \(\frac{34}{1569}\) это рациональное число.
Корень из 6 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
Записать число 1 в виде рационального числа?
Ответ: чтобы записать в виде рационального число 1 нужно представить его в виде дроби 1=\(\frac{1}{1}\).
Докажите, что число \(\sqrt{0,0049}\) является рациональным?
Доказательство: \(\sqrt{0,0049}=0,07\)
Является ли простое число под корнем рациональным числом?
Ответ: нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому не является рациональным числом.
tutomath.ru
Рациональные числа
Название рациональных числе произошло от латинского «ratio» (что в переводе значит «отношение»). Конечно же вы зададитесь вопросом: почему именно отношение? Все достаточно просто: рациональные числа с момента своего появления обозначаются, как отношение двух целых чисел, например 3 и 7 (3:7 или 3/7).
Другое название рациональных чисел – дроби. Дроби – это числа, которыми можно обозначит нецелое количество определенных предметов (например, полстакана, три четверти пятого, треть лимона и т.д.). Под дробью также понимают те рациональные числа, которые к целым отнести нельзя.
Понятное дело, что появление рациональных чисел позволило решить огромное количество прикладных задач, которые ранее решить было, к сожалению, невозможно (причем, не только из области математики, а и из области других наук).
В отличии от множества целых числе, во множестве рациональных числе всегда присутствует деление (конечно же, это не касается деления на ноль). Довольно интересным является тот факт, что исторически, проблема деления была решена намного раньше, нежели проблема вычитания. Именно поэтому множество натуральных чисел (куда входит и ноль) сначала расширили до множества неотрицательных рациональных чисел, а уж потом появилось множество отрицательных чисел. И на самом-то деле, ведь дроби действительно намного «реальнее», чем отрицательные числа? Почему же? Все очень просто, ведь дроби намного легче ощутить на реальных, жизненных примерах, чего не скажешь об отрицательных числах. Но, согласитесь, с точки зрения математики, логичнее и естественнее было бы сначала сформировать множество отрицательных чисел, так как они целые, а уж потом формировать рациональные положительные и отрицательные числа. Но, как видим, в школьной программе пользуются историческим подходом, ведь учеников сначала знакомят с дробями, а уж потом с отрицательными числами.
Правила действий с рациональными | ||||||||||||||||||||
|
mateshka.ru
Свойства действий с рациональными числами. Видеоурок. Математика 6 Класс
На этом уроке мы вспомним основные свойства действий с числами. Мы не только повторим основные свойства, но и научимся применять их к рациональным числам. Все полученные знания закрепим с помощью решения примеров.
Основные свойства действий с числами:
Первые два свойства – это свойства сложения, следующие два – умножения. Пятое свойство относится к обеим операциям.
Ничего нового в этих свойствах нет. Они были справедливы и для натуральных, и для целых чисел. Они также верны для рациональных чисел и будут верны для чисел, которые мы будем изучать дальше (например, иррациональных).
Перестановочные свойства:
От перестановки слагаемых или множителей результат не меняется.
Сочетательные свойства: , .
Сложение или умножение нескольких чисел можно делать в любом порядке.
Распределительное свойство: .
Свойство связывает обе операции – сложение и умножение. Также если его читать слева направо, то его называют правилом раскрытия скобок, а если в обратную сторону – правилом вынесения общего множителя за скобки.
Следующие два свойства описывают нейтральные элементы для сложения и умножения: прибавление нуля и умножение на единицу не меняют исходного числа.
Еще два свойства, которые описывают симметричные элементы для сложения и умножения, сумма противоположных чисел равна нулю; произведение обратных чисел равно единице.
Следующее свойство: . Если число умножить на ноль, в результате всегда будет ноль.
Последнее свойство, которое мы рассмотрим: .
Умножив число на , получаем противоположное число. У этого свойства есть особенность. Все остальные рассмотренные свойства нельзя было доказать, используя остальные. Это же свойство можно доказать, используя предыдущие.
Умножение на
Докажем, что если умножить число на , то получим противоположное число. Используем для этого распределительное свойство:
interneturok.ru
Деление рациональных чисел | Формулы с примерами
Деление рациональных чисел 6 класс
Формула, правилоЕсли значение a меньше 0, а значение b больше 0, то деление a на b равно делению их модулей.
Пример ( — 6 ) : ( — 2 ) = 6 : 2 = 3;( -12 ) : ( — 4 ) = 12 : 4 = 3;
( -2,4 ) : ( — 12 ) = 4,8.
Деление чисел с разными знаками
Формула, правило! На ноль ( 0 ) делеие запрещено.
Пример2 : ( 5 ) = -2 : 5 = 0,4;
12 : ( -3 ) = -12 : 3 = -4;
( -2,5 ) : 0,5 = -2,5 : 0,5 = 5.
Свойства деления
Свойство, пример 1. a : 1 = a.2 : 1 = 2;
( — 1,3 ) : 1 = -1,3;
( — 12,4 ) : 1 = -12,4.
Свойство, пример 2. a : a = 1.10 : 10 = 1;
121 : 121 = 1;
( — 32,4 ) : ( -32,4 ) = 1.
Свойство, пример 3. a : ( -1 ) = -a.14 : ( -1 ) = -14;
421 : ( -1 ) = -421;
432,54 : ( — 1 ) = -432, 54.
Свойство, пример 4. 0 : a = 0.0 : 4 = 0;
0 : 12,4 = 0;
0 : 221,5 = 0.
Свойство, пример 5. a : ( b • c ) = ( a : b ) : c = ( a : c ) : b.2 : ( 5 • 4 ) = ( 2 : 5 ) : 4 = ( 2 : 4 ) : 5 = 0,1;
5 : ( 5 • 8 ) = ( 5 : 5 ) : 8 = ( 5 : 8 ) : 5 = 0,125;
8 : ( 2 • 20 ) = ( 8 : 2 ) : 20 = ( 8 : 20 ) : 2 = 0,2.
Свойство, пример 6. a : ( b : c ) = ( a : b ) • c = ( a • c ) : b.( -2,4 ) : ( -1,8 : ( -3)) = (( -2,4) : 1,8) • ( -3 ) = (( -2,4) • (-3)) : 1,8 = 4.
formula-xyz.ru
Действия с рациональными числами. Решение уравнений
Урок № 132
Тема: «Действия с рациональными числами. Решение уравнений»
Тип урока: обобщения и систематизации знаний
Цель урока: закрепить, обобщить умения и навыки в действиях с положительными и отрицательными числами; подготовить учащихся к контрольной работе по теме «Умножение и деление положительных и отрицательных чисел»; тренировать
Задачи урока:
Предметная: Систематизировать упрочить и углубить знания по данной теме.
Личностная: Воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Метапредметная: Повышение познавательной активности учащихся в учебном процессе, логического мышления.
Планируемые результаты:
Предметные: знать, свойства действий с рациональными числами и уметь применять данные свойства,
вычислять числовое значение буквенного выражения при заданных значениях букв
Личностные: умение ясно, точно, грамотно излагать свои мысли; способность к самооценке на основе критерия успешности учебной деятельности. проявление положительного отношения к урокам математики, доброжелательного отношения к сверстникам; ориентация на понимание причин успеха в учебной деятельности;
Метапредметные:
Р – уметь определять и формулировать цель на уроке с помощью учителя;
П – уметь ориентироваться в своей системе знаний; добывать новые знания;
К – организовывают и планируют учебное сотрудничество с учителем и сверстниками.
Оборудование: мультимедийный проектор, компьютер, интерактивная доска.
Методы обучения: фронтальный опрос, практическая тренировка.
Структура урока:
Ход урока
Приветствую учащихся. Сажаю их на места. | Приветствуют учителя. | К: следовать правилам поведения |
| ||
— Какие вопросы по Д/З? Разбираем, если есть вопросы. № 1226 (в,г), 1227 (в,г ), 1228, 1230
| Спрашивают. | К: Умение слушать и вступать в диалог. |
| ||
Устный счет
| Отвечают на вопросы -Формулируют, записывают в тетрадях число, кл/р, тема урока | Р: прогнозирование своей деятельности; К: Умение слушать и вступать в диалог. Л: Умение выделять нравственный аспект поведения |
4. Воспроизведение изученного и его применение в стандартных ситуациях | ||
№ 1224 (2)
№ 1219 а) -|x|, x=0 б) 2 -|x|, x=0 2-|0|=2 в) -|x-1|, x=1 -|1-1|=0 г) –(x-1)2, x=1 –(1-1)2=0 № 1222
№ 1221
| Один ученик у доски, а остальные в тетрадях. Один ученик у доски, а остальные в тетрадях. Один ученик у доски, а остальные в тетрадях | П: уметь ориентироваться в своей системе знаний К: уметь слушать и понимать речь других, оформлять мысли в устной речи Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение |
5. Физкультминутка | ||
А теперь, ребята, встали. Быстро руки вверх подняли, В стороны, вперед, назад. Повернулись вправо, влево, Тихо сели, вновь за дело. | Выполняют | |
6. Усвоение ведущих идей и основных теорий на основе широкой системы знаний. | ||
№ 1203
№ 1211 а) >0 б) <0 № 1225
Подготовка к контрольной работе.
| Один ученик у доски, а остальные в тетрадях. Один ученик у доски, а остальные в тетрадях. | Р – формируют способность к мобилизации сил и энергии; способность к волевому усилию в преодолении препятствий. П – произвольно и осознанно владеют общим приемом решения задач. К – управляют своим поведением (контроль, самокоррекция, оценка своего действия) |
8. Рефлексия | ||
| Поднимают руки. | Р: уметь оценивать правильность выполнения действий |
9. Постановка Д/З | ||
№ 1226 (д-е), 1227 (д-е), 1229 (г-е), 1232 | записывают. | |
infourok.ru











