Методы оптимальных решений. Транспортная задача в MS Excel
В этой статье мы пошагово рассмотрим, как решить транспортную задачу посредством функций MS Excel. Задачи данного типа изучаются студентами на таких дисциплинах, как исследование операций и методы оптимальных решений.
Условие
Есть некие предприятия и склады с грузом. Каждое предприятие, нуждается в определённом объёме нашего груза. Каждый склад доставляет тонну груза по собственному тарифу. Таким образом, нужно составить маршрут, по которому мы развезём объём груза, удовлетворяющий каждое предприятие, и при этом затратим меньше всего средств.
Так транспортная задача выглядит в своём наиболее общем и типовом виде.
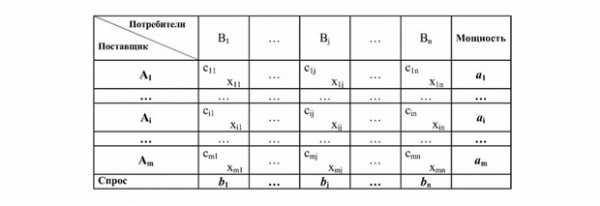
С – это цена за тонну. X – это то, сколько мы привезём тонн со склада на предприятие. Например, если мы примем X11 равным 5, это будет значить, что со склада А1 к потребителю B1 мы повезём 5 тонн по цене C11. Вот нам и нужно как-то распределить всё так, чтобы потратить меньше всего денег.

Варианты решения
Транспортную задачу можно решить «вручную». Существует несколько подходов к её решению на бумаге. Среди них:
- Метод опорного плана;
- Метод минимального элемента;
- Метод Фогеля.
Как правило, решая задачу одним из этих способов, вы получаете решение, находите потенциалы для него и понимаете, что в числе потенциалов есть положительные значения. Соответственно, это говорит о том, что вы нашли неверное решение. Далее вам нужно действовать, что называется, наугад. Вы переставляете различные цифры в таблице, пробуете разные варианты, словом, ищите решение методом «научного тыка». Далее снова пересчитываете потенциалы, и снова ничего не срастается.
Однозначного алгоритма, работающего безотказно в любых условиях, к сожалению, пока не придумали.
Транспортная задача в Экселе
Для решения нам потребуется надстройка «Поиск решения». Возможно, она не будет активирована в вашем редакторе по умолчанию, поэтому, проделываем следующую очередность действий:
- Жмём «Файл»;
- В появившемся меню нажимаем по предпоследней кнопке «Параметры»;
- Вновь находим предпоследний пункт «Надстройки» и переходим в «Управление»:
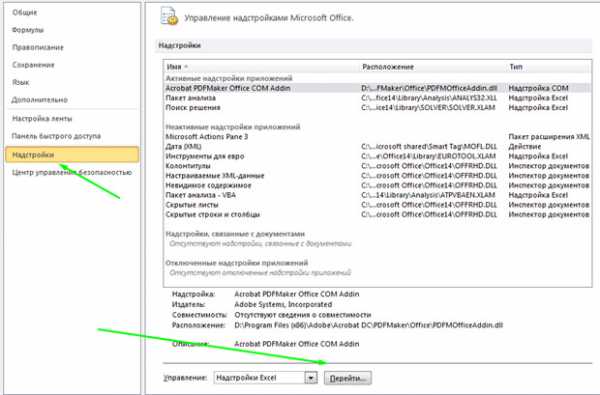
- Ставим галочку в появившемся окне рядом с пунктов «Поиск решения» и жмём «ОК».
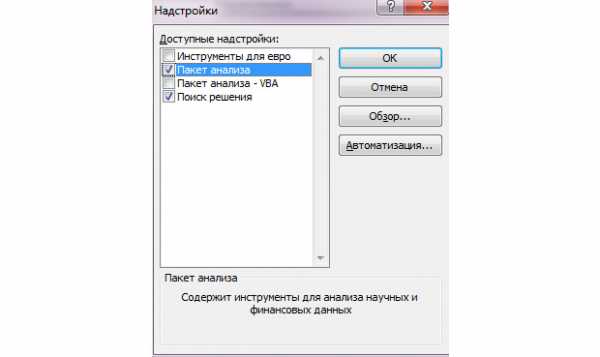
Поиск решения активирован. Далее он будет нами использован.
Пример задачи
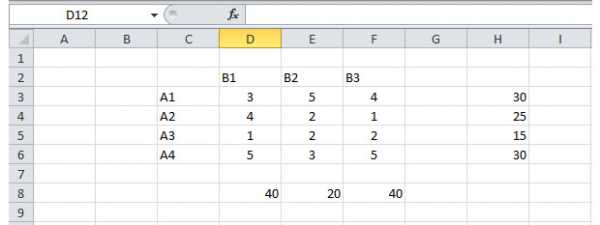
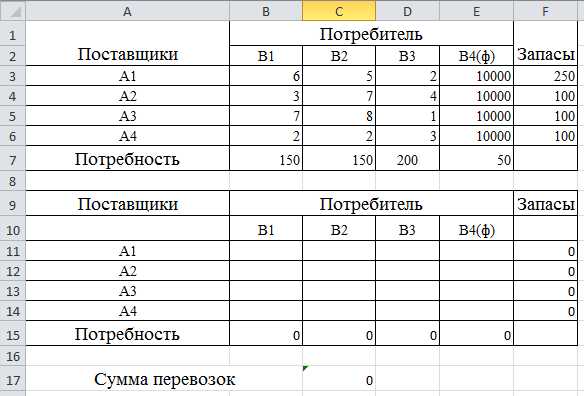
На складах A1 — A4 есть суммарно 100 тонн зерна, и их нужно развести по текущим расценкам в пункты B1 – B3, потратив как можно меньше средств на доставку. Тарифы на доставку указаны в центре таблицы.
Шаг 1
Дублируем нашу таблицу в Excel.
Шаг 2
Рисуем другую таблицу.
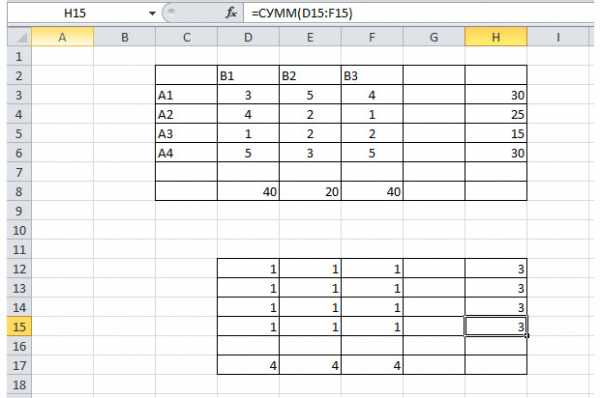
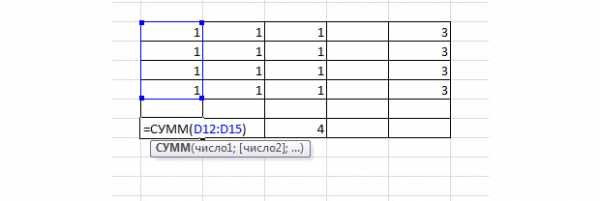
Диапазон ячеек D12 – F15 заполняем единицами. Эти значения мы впоследствии будем изменять, чтобы найти самый дешёвый вариант перевозки. В диапазоне h22 – h25 должна быть сумма трёх единиц таблицы в строке D12 – F12, а в D17 – F17 – сумма четырёх единиц в столбце. Так напротив каждой строки и каждого столбца
Шаг 3
Рисуем третью таблицу, которая перемножит соответствующие ячейки первых двух таблиц.
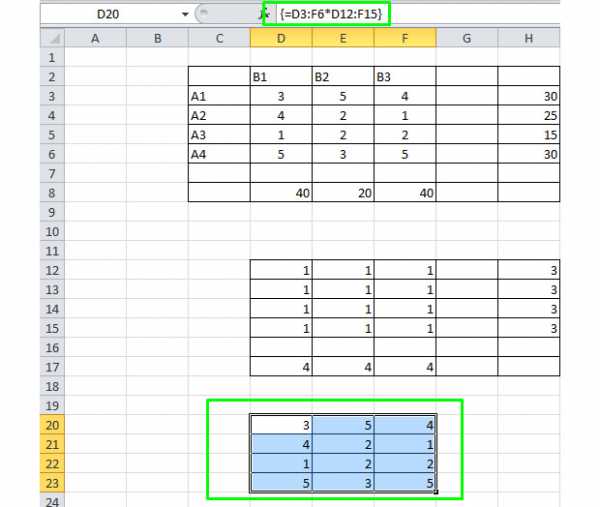
Для этого выделяем диапазон 3 на 4 клетки, жмём на кнопку « = », выделяем диапазон D3-F6, жмём на клавиатуре « * », выделяем D12 – F15 и зажимаем сочетание клавиш Ctrl + Shift + Enter. Всё, вы перемножили значения.
Шаг 4
Теперь суммируем все значения последней таблицы. Для этого просто выберите произвольную свободную ячейку в MS Excel. Введите в неё « =СУММ( » и выделите третью таблицу. Нажмите Enter.
Шаг 5
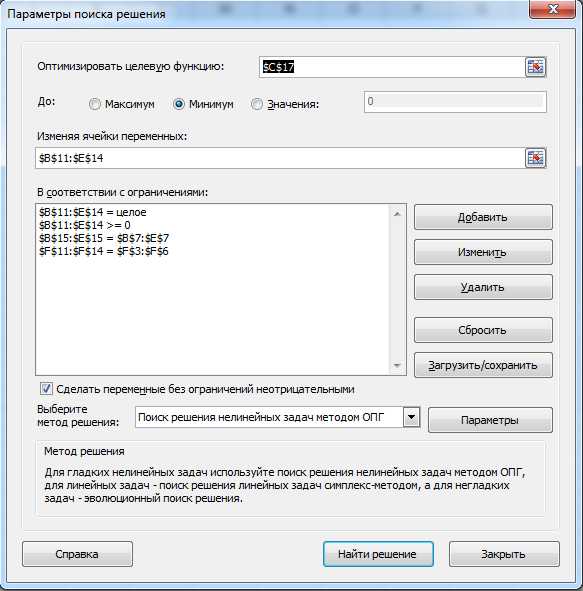
Переходим во вкладку «Данные» и находим там «Поиск решения».
Щелкаем по данной кнопке. Далее всё делаем, как представлено на рисунке.
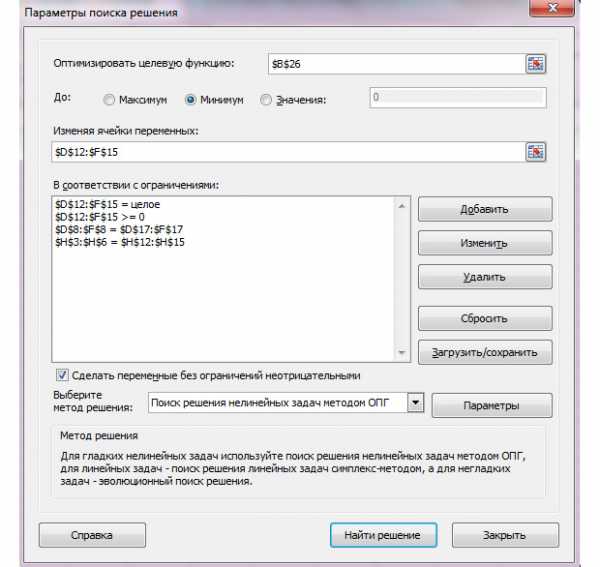
Описываю сверху вниз всё окно. Выберите целевую ячейку ту, которую мы сделали в 4-ом шаге нашего решения. Далее выберите минимум. В поле «Изменяя ячейки переменных» выберите диапазон, где мы проставили единицы. Выставляем ограничения. Значения, которые будут находиться вместо единиц, должны быть больше нуля и целыми, а потребности не должны превысить запасов. Жмём «Найти решение».
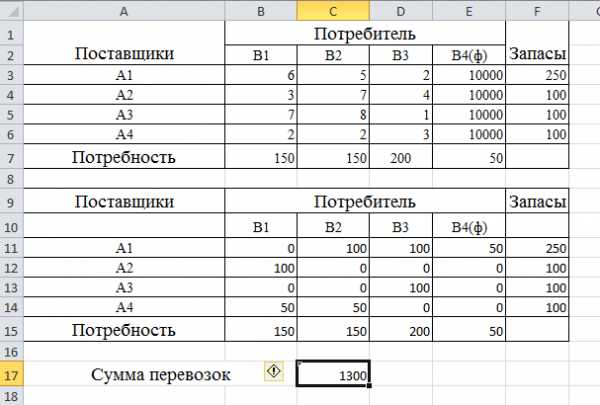
Получаем следующий результат.
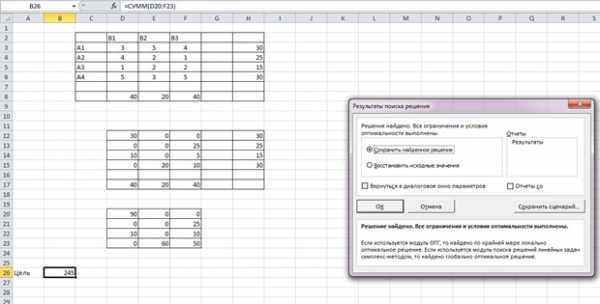
Если вы всё сделали правильно, то у вас должно быть всё точно так же.
Заключение
По второй таблице сверху вы видите, сколько тонн и куда мы повезём. В третьей таблице вы видите, сколько это будет стоить. Например, мы повезём 30 тонн в B1 со склада A1 и 10 тонн со склада A3, так как спрос у пункта B1 равен 40. Аналогично и с другими пунктами.
reshatel.org
Поиск решения MS EXCEL (1.8). Транспортная задача. Примеры и методы
Создадим модель для решения Транспортной задачи (Transportation Problem, Shipping Routes). Решение Транспортной задачи позволяет определить самые недорогие маршруты для перевозки товаров от производителей на склад. Расчет будем проводить с помощью надстройки Поиск решения.
Рассмотрим Транспортную задачу на основе примера из файла solvsamp.xls (при установленном MS EXCEL 2010 файл находится в папке C:\Program Files\Microsoft Office\Office14\SAMPLES).
Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь.
Задача
Компания доставляет товары с трех заводов на пять региональных складов. Товары могут доставляться с любого завода на любой склад, однако, очевидно, что стоимость доставки на большее расстояние будет большей.
Требуется определить объемы перевозок между заводами и складами, в соответствии с потребностями складов и производственными возможностями (мощностями) заводов, при которых транспортные расходы минимальны.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера).
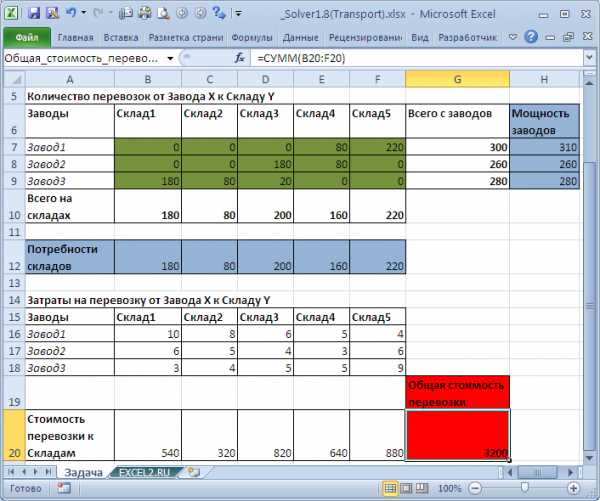
Переменные (выделено зеленым). В качестве переменных модели следует взять объемы перевозок между заводами и складами.
Ограничения (выделено синим). Потребности складов должны быть удовлетворены (т.е. суммарные поставки на склад должны быть больше или равны потребности). Суммарные объемы перевозок с завода не должны превосходить его мощности.
Целевая функция (выделено красным). Суммарные транспортные расходы должны быть минимальны.
Убедитесь, что метод решения соответствует линейной задаче.
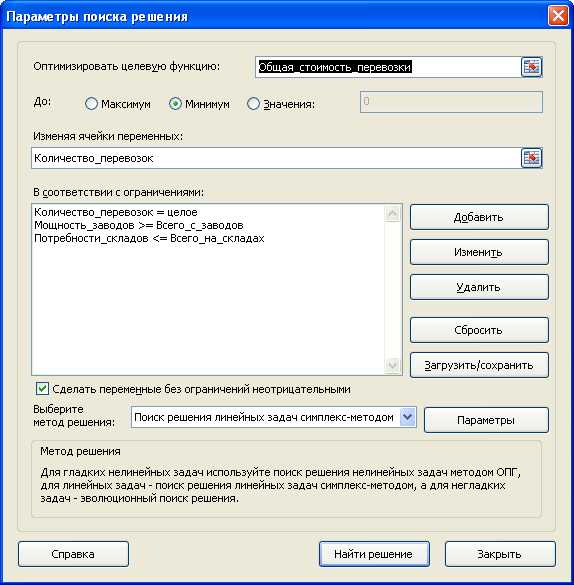
Теперь в диалоговом окне можно нажать кнопку Найти решение.
excel2.ru
Решение транспортной задачи в Excel (задача с обязательными поставками)
Решение задачи
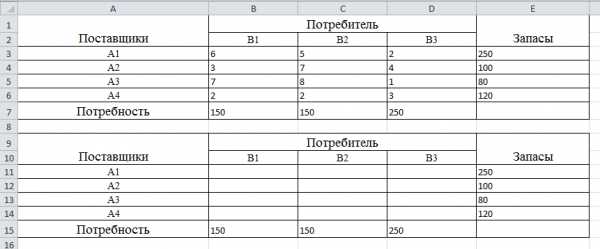
Для решения данной задачи в табличном процессоре необходимо составить две таблицы, приведенные выше, но вторую таблицу не заполнять данными.
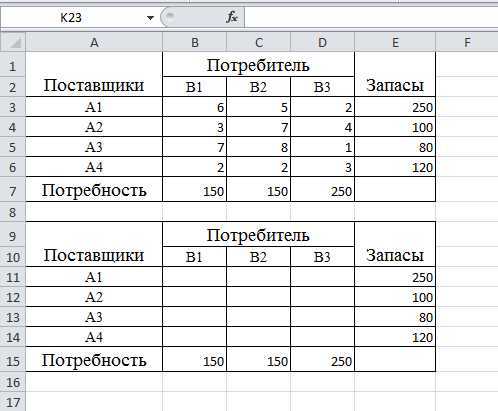
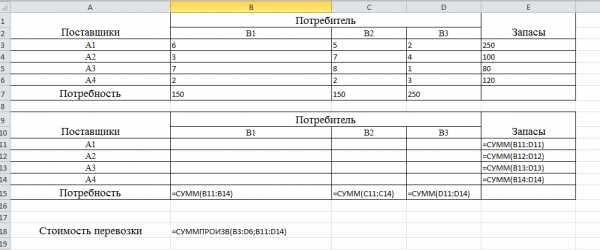
Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».
Для отображения формул необходимо на вкладке «Формулы» в группе «Зависимости формул» выбрать «Показать формулы» либо горячее сочетание клавиш «Ctrl+` (тильда)».
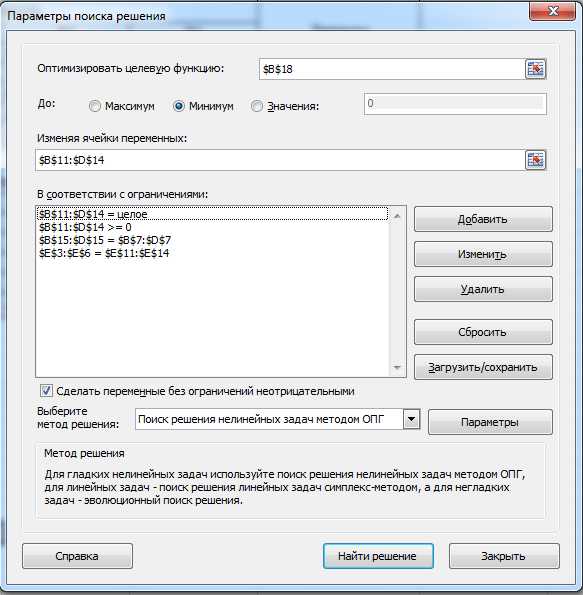
Дальше выбираем команду «Поиск решения» на вкладке «Данные» (Файл – Параметры – Надстройки – Управление – Поиск решений).
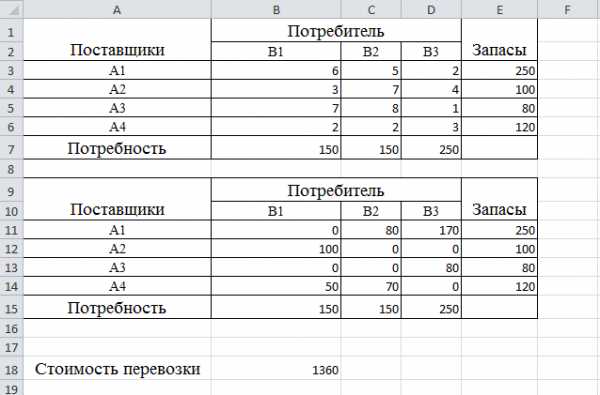
Решение поставленной задачи
Решение транспортной задачи в MS Excel (фиктивный поставщик или потребитель)
Постановка задачи
Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.
Существует потребность в этой продукции B1, B2, B3
Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.
Необходимо составить такой план перевозок, который бы удовлетворил все потребности и имел минимальную стоимость.
Решение задачи
Если просуммировать запасы и потребности, то получиться, что запасов меньше потребностей на 40. Для того, чтобы решить задачу в Excel, необходимо сбалансировать сумму потребностей и поставок. Для этого следует добавить фиктивного поставщика. При этом, цену на перевозки можно поставить значительно больше той, которая установлена для реальных поставщиков. Таким образом, балансировка по фиктивному поставщику будет проходить в последнюю очередь, главное потом не забыть вычесть фиктивные поставки из суммы поставок.
Однако, можно цену поставок оставить равной нулевой, в этом случае, вычитать из суммы перевозок ничего не придется поскольку умножение на ноль дает ноль.
Для последующего решения задачи выберем вариант с ненулевой ценой перевозки.
Сбалансировав саму задачи решаем ее стандартным способом. Для начал составим две таблицы: одна с данными, вторая – без.
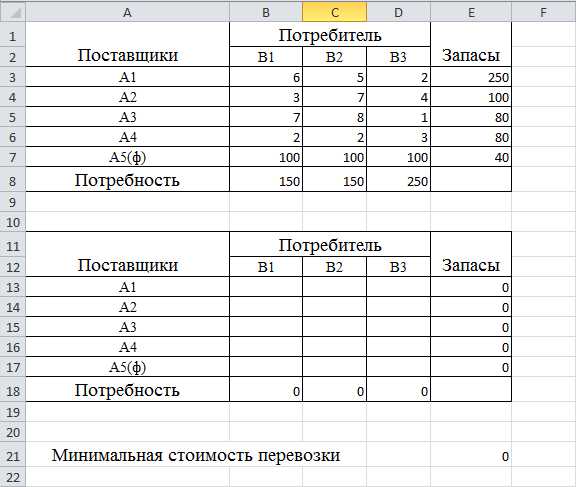
Для решения транспортной задачи потребуются функции: СУММПРОИЗВ, СУММ и надстройка «Поиск решения».
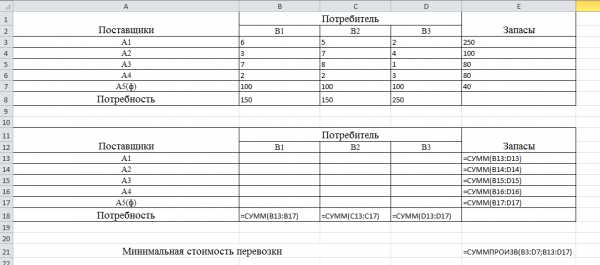
На рисунке выше, обратите внимание, курсор находится ф ячейке с функцией, которую следует минимизировать. В самой функции уже отнимается цена фиктивных перевозок. Цену перевозок можно отнять отдельно, важно просто не забыть это сделать.
=СУММПРОИЗВ(B3:D7;B13:D17)-СУММПРОИЗВ(B7:D7;B17:D17)
Дальше выбираем команду «Поиск решения» на вкладке «Данные».
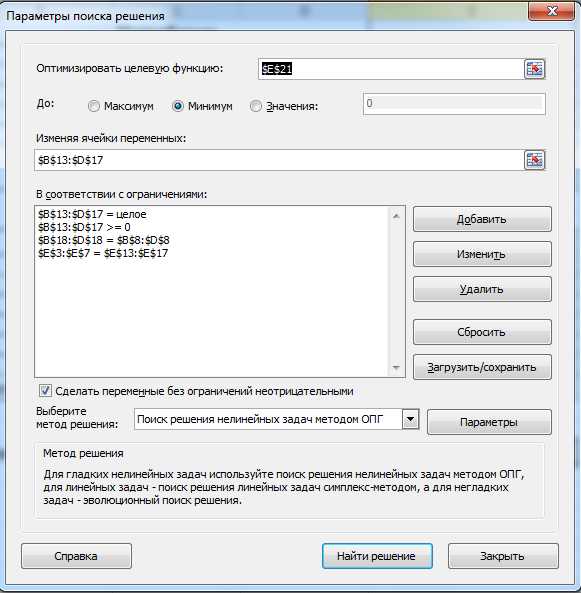
Решение поставленной задачи
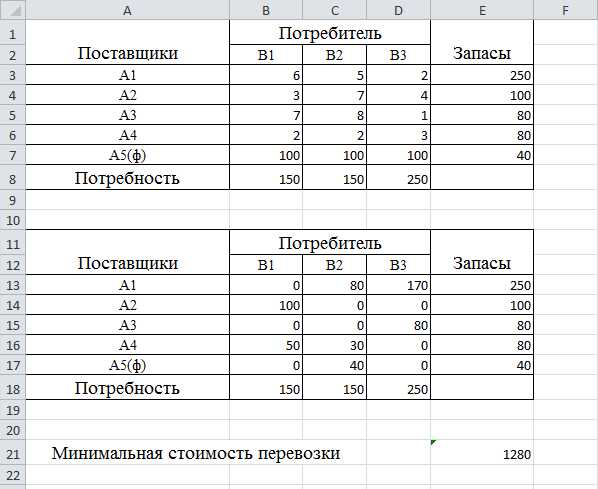
Как видно из решения все фиктивные поставки пришлись на потребителя В1, именно у него будет недопоставка в 40 единиц товара.
Если задача будет несбалансированная по потребителям, тогда вводится фиктивный потребитель, чтобы сбалансировать потребности и запасы.
Решение транспортной задачи в Excel (задача с обязательными поставками)
Продолжая тему решения транспортных задач средствами MS Excel, рассмотрим вариант, когда количество запасов меньше потребностей и у поставщиков есть обязательства перед потребителями. Другими словами, решаем несбалансированную транспортную задачу с обязательными поставками.
В основном, задача с обязательными поставками повторяет условие задачи с дисбалансом между спросом и предложением.
Постановка задачи
Есть запасы однотипной продукции у поставщиков A1, A2, A3, A4.
Существует потребность в этой продукции B1, B2, B3
Стоимость доставки единицы продукции от поставщиков к потребителям представлена в таблице.
Необходимо составить такой план перевозок, который бы удовлетворил все потребности и имел минимальную стоимость.
Решение задачи
Запасов меньше потребностей на 40 единиц, соответственно необходимо ввести фиктивного поставщика, сбалансировать задачу и решить ее в Excel. Вся процедура была описана ранее, здесь повторяться не будем, а остановимся на тех отличиях, которые появляются в связи с обязательными поставками.
Допустим, у первого поставщика есть обязательство перед потребителем B3 в обязательной поставке 200 единиц товара, а у второго – перед потребителем B2, в обязательной поставке 80 единиц товара.
Записанное условие в таблицах MS Excel выглядит следующим образом:
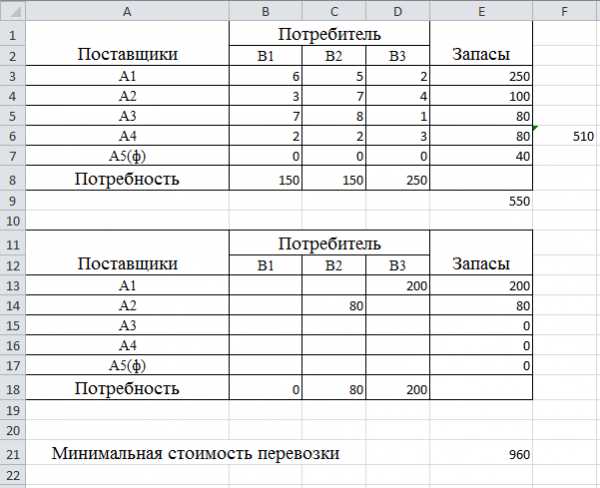
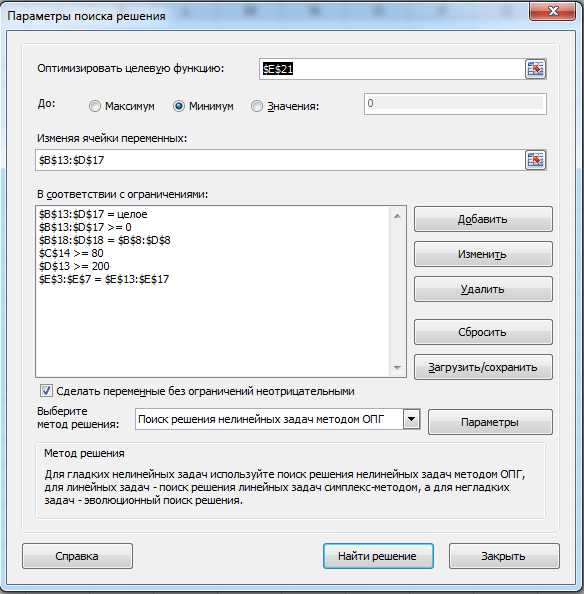
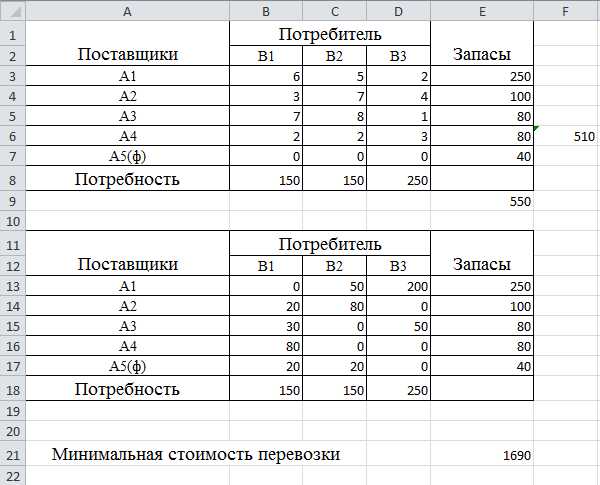
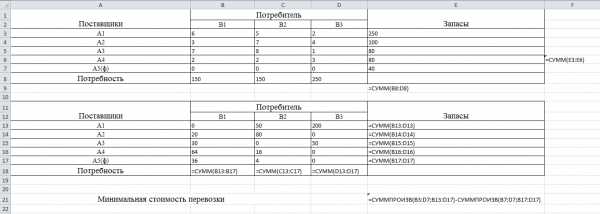
Как видим, минимальная стоимость перевозки несколько больше предыдущей задачи (1690 против 1280), поскольку контракты на обязательную поставку снизили общую эффективность перевозки.
megaobuchalka.ru
Решение транспортной задачи методом потенциалов в Excel с примером
Решим транспортную задачу методом потенциалов. Нам известны торговые запасы, потребительские запросы и стоимость доставки за единицу продукции. Сделаем три исходные таблицы.
Построим опорный план транспортной задачи с помощью инструмента «Поиск решений». Рядом составим такие же по объему таблицы с пустыми ячейками. Таблица А – аналог стоимостной, Б – «запасов», В – «спроса».
Элементы таблицы Б – сумма соответствующих строк в таблице А. Элементы таблицы В – сумма соответствующих столбцов в таблице А.
Отдельно составим результирующую таблицу Г. В ней отразятся оптимальные транспортные расходы. Каждый элемент таблицы Г – произведение элемента А и соответствующего элемента стоимостной таблицы.
В отдельном месте листа введем формулу функции: =СУММПРОИЗВ(A1:C3;G1:I3)
Первый массив – стоимостная таблица, второй – диапазон А.
Ставим курсор в ячейку со значением функции. Вызываем инструмент «Поиск решения». Заполняем диалоговое окно:
- Целевая ячейка – ссылка на ячейку со значением функции.
- Она должна быть равна «максимальному значению», как наиболее выгодному для перевозчика.
- Команда изменяет значения ячеек в таблице А. Значения – целые числа.
- Диапазон таблицы Б = «Запасам».
- Диапазон В = «Потребительскому спросу».
В открытом диалоговом окне нажимаем кнопку «Параметры» и устанавливаем следующие настройки:
Жмем ОК – «Выполнить». Получаем опорный план транспортной задачи:
Он залит бледно-зеленым цветом. Ячейки со значениями выше нуля называются «базисными», «занятыми». Ячейки со значением 0 – «свободными».
Далее действуем по плану:
Посчитаем число занятых клеток с помощью функции СЧЕТЕСЛИ.
Так как результат равен 5, опорный план является не вырожденным. Проверим оптимальность опорного плана – найдем потенциалы по занятым клеткам.
Нужно составить систему уравнений. Предполагается, что αj = 0, а αi + βj = сij (стоимость доставки единицы груза). Вызываем команду «Поиск решения». Вносим условия системы уравнений в качестве ограничений.
Заполненное диалоговое окно:
Результат работы инструмента «Поиск решения»:
Посчитаем оценки свободных клеток. Формула: сij – (αi + βj). Берем свободную клетку из таблицы А. Смотрим ее значение в стоимостной таблице. Это будет сij. Далее смотрим, какие потенциалы соответствуют данной клетке. Вставляем их значения в формулу.
В программе Excel найдем оценки с помощью математических операторов и ссылок на соответствующие ячейки.
План считается оптимальным, если оценки больше или равны 0. В нашем случае получились отрицательные значения – план не является оптимальным. Поэтому двигаемся дальше.
Находим, какой клетке в таблице А соответствует минимальная оценка. Строим для этой клетки цикл – замкнутую ломаную линию. Условия: обязательно чередование вертикального и горизонтального направления, только по базисным клеткам.
В исходной клетке (с минимальной оценкой) ставим знак «+». Далее чередуем: «-», «+» и т.д.
В таблице стоимости находим минимальное значение со знаком «-».
В нашем примере – это «5», ячейка В1. Эту клетку нужно убрать из базиса. А ячейку с минимальной оценкой сделать базисной.
С учетом изменившихся данных вновь строим опорный план транспортной задачи. Применяем инструмент «Поиск решения». Пересчитанный план перевозок выглядит так:
Обратите внимание: ячейка I1 (где была минимальная оценка) стала базисной, занятой.
Скачать пример решения транспортной задачи
Проводим те же расчеты для нового плана (с пункта №1): находим потенциалы, оценки свободных клеток для проверки оптимальности. И так до тех пор, пока оценки свободных клеток не будут больше или равны 0.
exceltable.com
Решение транспортной задачи в Excel (задача с обязательными поставками)
- Курсы
- Новости
- Статьи
- Excel
- PowerPoint
- Windows
- Word
- Заметки
- Excel
- PowerPoint
- Windows
- Word
- Другие заметки
- Видео
- Excel
- PowerPoint
- Windows
- Word
- Другие видео
- Блог
- Shop
- Доступ к курсам
- Услуги
Поиск
- Главная
- Центр обучения
- Справочник
- Поддержка
- Контакт
- Курсы
- Новости
msoffice-prowork.com
Лабораторная работа 2. Решение транспортной задачи в пакете ms Excel.
Транспортная задача – это задача о минимизации транспортных расходов, связанных с обеспечением пунктов потребления определенным количеством однородной продукции, производимой в нескольких пунктах производства [1, 3, 7]. В общем виде задача может быть сформулирована следующим образом.
Однородный
продукт, сосредоточенный в 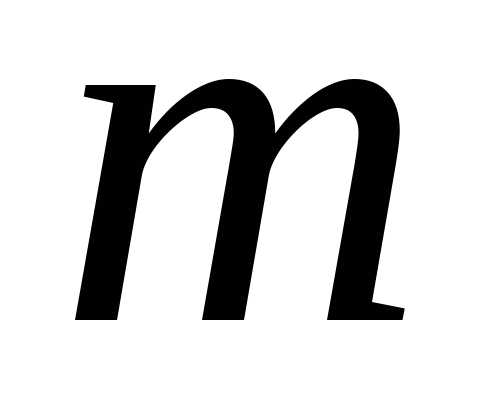 пунктах производства, необходимо
распределить между
пунктах производства, необходимо
распределить между 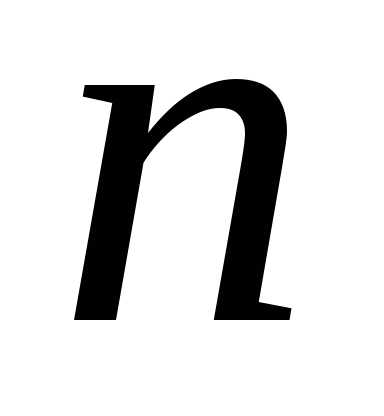 пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.
пунктами потребления. Стоимость перевозки
единицы продукции известна для всех
маршрутов. Необходимо составить такой
план перевозок, при котором запросы
всех пунктов потребления были бы
удовлетворены за счет имеющихся продуктов
в пунктах производства и общие транспортные
расходы по доставке продуктов были бы
минимальными.
Примем
следующие обозначения: i
– номер пункта производства, j
–номер пункта потребления, 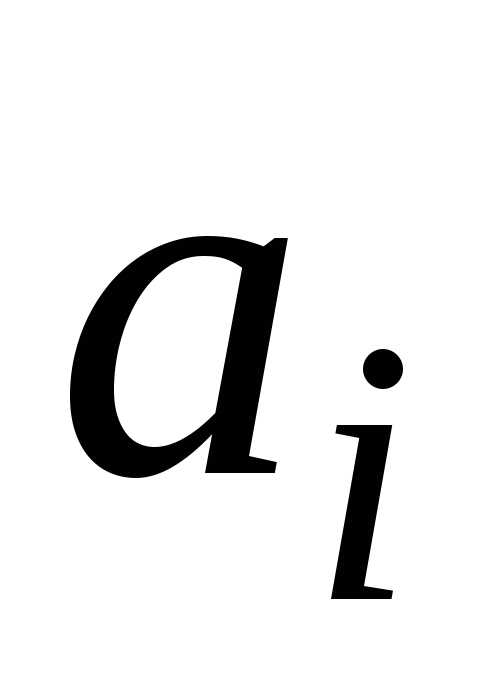 –
количество продукта, имеющееся в i-ом
пункте производства,
–
количество продукта, имеющееся в i-ом
пункте производства, 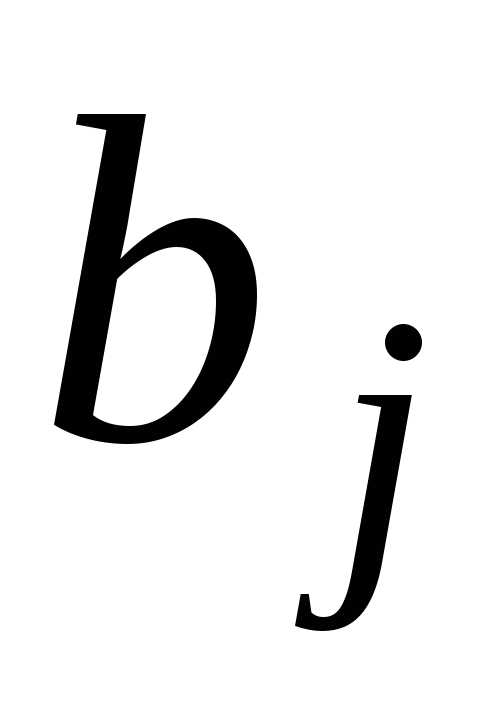 – количество продукта, необходимое для
j-го
пункта потребления,
– количество продукта, необходимое для
j-го
пункта потребления, 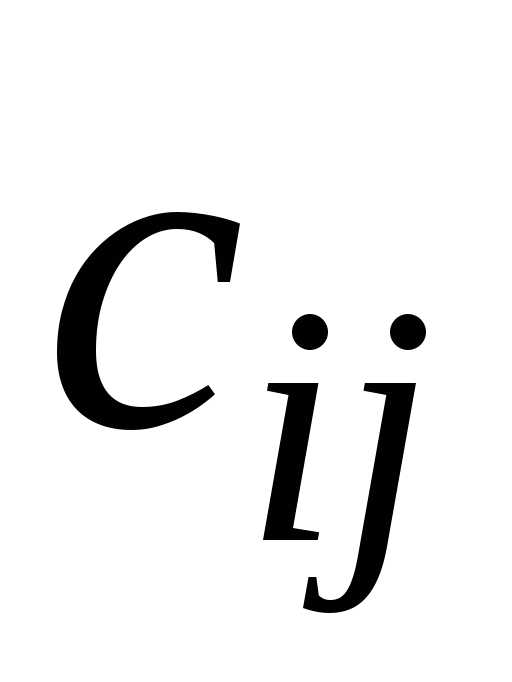 – стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления,
– стоимость перевозки единицы продукта
из i-го
пункта производства в j-й
пункт потребления, 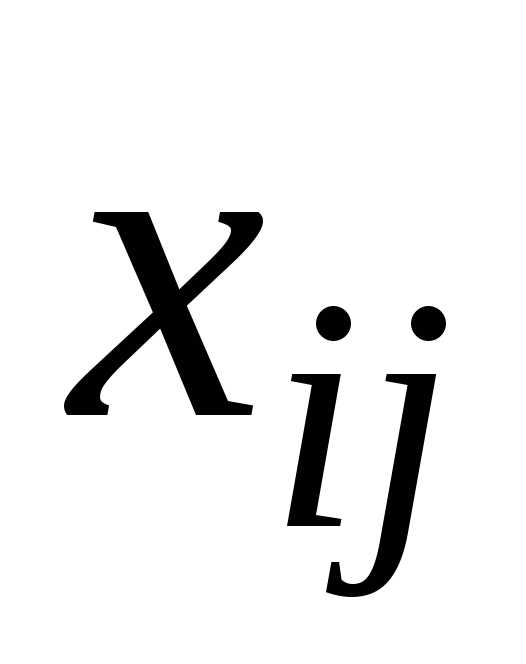 – количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:
– количество груза, планируемого к
перевозке из i-го
пункта производства в j-й
пункт потребления, i=1,2,…,m;
j=1,2,…,n.
Математическая модель транспортной
задачи будет выглядеть следующим
образом:
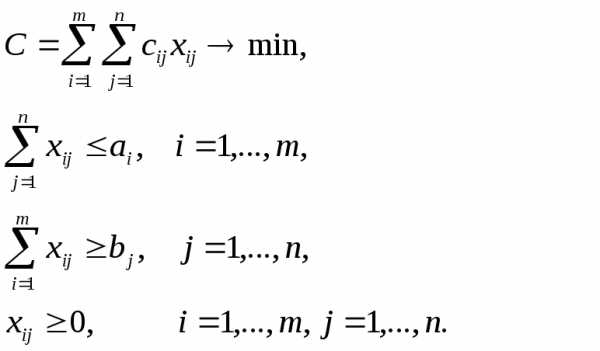
Условия задачи удобно записывать в виде таблицы, которая называется матрицей планирования:
с11 с12 … с1n
. . .
сm1 сm2 … сmn
a1
…
am
b1 b2… bn
Рассмотрим решение транспортной задачи в табличном процессоре MS Excel. Так как транспортная задача является частным случаем задачи линейного программирования, то эту задачу можно решать так, как описано выше. Однако благодаря свойствам задачи, ее можно записать в более компактной форме.
Рассмотрим транспортную задачу, матрица планирования которой имеет вид:
Bj
Ai
B1
B2
B3
B4
B5
A1
14
25
18
19
23
33
A2
2
17
16
24
2
25
A3
29
3
7
15
22
25
A4
5
20
17
23
10
17
33
11
11
11
34
bj ai
Для решения транспортной задачи введем данные, как показано на рис.6.
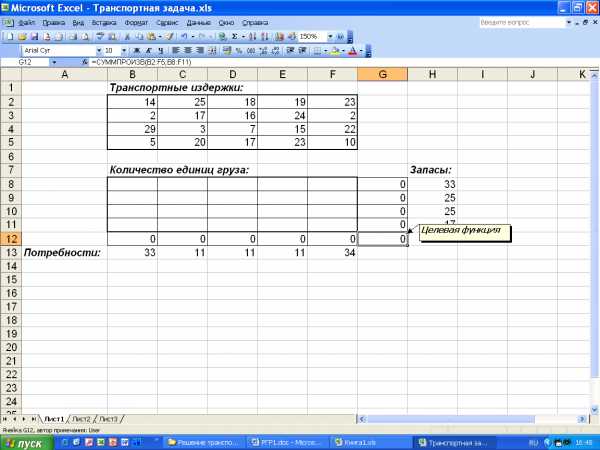
Рис.6. Исходные данные транспортной задачи.
В ячейки B2 : F5 введем стоимость перевозок. Ячейки B8 : F11 отведены под значения объемов перевозок, пока неизвестные. В ячейки H8 : h21 введены объемы производства, а в ячейки B13 : F13 — потребности (спрос) в продукции в пунктах потребления.
В ячейку G12 вводится целевая функция
= СУММПРОИЗВ (B2 : F5; B8 : F11) .
В ячейки B12 : F12 вводятся формулы
= СУММ (B8 : B11),
= СУММ (C8 : C11),
= СУММ (D8 : D11),
= СУММ (E8 : E11),
= СУММ (F8 : F11),
определяющие объем продукции, ввозимой в пункты потребления. В ячейки
G8 : G11 введены формулы
= СУММ (B8 : F8),
= СУММ (B9 : F9),
= СУММ (B10 : F10),
= СУММ (B11 : F11),
характеризующие объем продукции, вывозимой из пунктов производства.
Далее выбираем команду Сервис, Поиск решения и заполняем открывшееся диалоговое окно Поиск решения, как показано на рис.7.
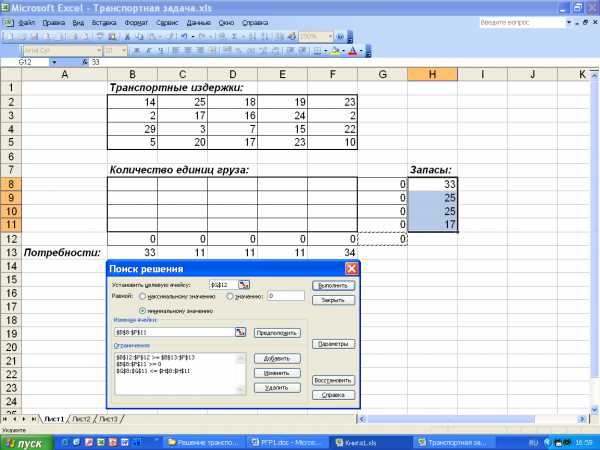
Рис.7. Диалоговое окно Поиск решения для транспортной задачи.
В диалоговом окне Параметры поиска решения установить флажок Линейная модель (рис.8).
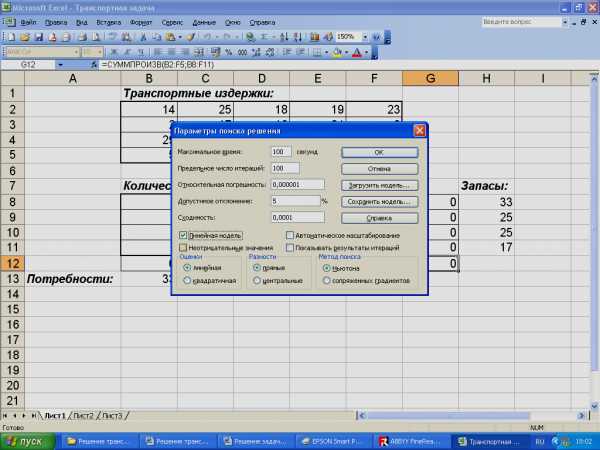
Рис.8. Диалоговое окно Параметры поиска решений.
После нажатия кнопки Выполнить получаем оптимальный план поставок продукции и соответствующие ему транспортные расходы (рис. 9).
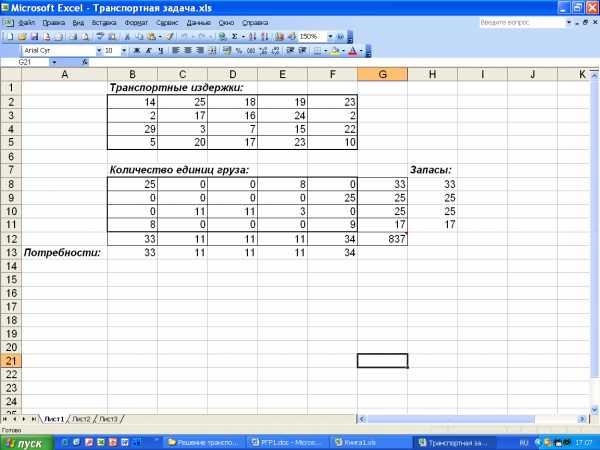
Рис.9. Оптимальное решение транспортной задачи.
studfiles.net
Решение транспортной задачи с промежуточными пунктами в Excel
Государственное образовательное учреждение
средняя общеобразовательная школа № 218
Фрунзенского административного района Санкт-Петербурга
Реферат
Транспортные задачи в Excel
Выполнили: ученики 10 А класса
Фёдоров Артём
Верещагин Михаил
Научные руководители:
учитель математики Сеферян К.О.,
учитель информатики Махаева Е.П.
Санкт-Петербург, 2011 год
Содержание
Введение……………………………………………………………3
Глава 1.
Классическая транспортная задача……………………………………4
1.1. Решение классической сбалансированной транспортной задачи в Excel……………………………………………………………………5
1.2. Решение классической несбалансированной транспортной задачи в Excel………………………..…………………………………..…….10
Глава 2.
Транспортная задача с промежуточными пунктами………………….13
2.1. Решение транспортной задачи с промежуточными пунктами в Excel………………………………………………………………….14
Заключение……………………………………………………….19
Список литературы………………………………………………20
Введение
В настоящее время в условиях жесткой конкуренции автомобильным компаниям приходится бороться за каждый рубль прибыли, поэтому вопрос об уменьшении издержек производства становится первостепенным. И, конечно же, рациональное размещение производственных объектов играет здесь ключевую роль [2].
Так, например, перед ООО «MG Auto» стоит реальная задача: стоит ли изменить действующую на сегодняшний день схему транспортировки автомобилей с заводов до распределительных центрах в Денвере и Майами или же действующая схема наиболее эффективна? Таким образом, в этой работе делается попытка показать пути снижения общих затрат предприятия путем снижения транспортных издержек.
На практике при планировании различных экономических процессов, в частности при решении вопросов рационализации поставок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта широко применяется транспортная задача линейного программирования. Поэтому в данном проекте будет рассмотрена сама транспортная задача, ее постановка и способы решения, а также особенности постановки задачи развития и размещения объектов автомобильной промышленности. Конечной целью является экономическая оценка эффективности транспортировки автомобилей до конечного пункта.
Глава 1
Классическая транспортная задача
Транспортная задача является частным видом линейной оптимизационной задачи. Наиболее часто транспортная задача представляется следующим образом: имеются n пунктов производства и m пунктов распределения продукции. Стоимость перевозки единицы продукции с i-гo пункта производства в j-й центр распределения cji приведена в таблице, где под строкой понимается пункт производства, а под столбцом — пункт распределения. Кроме того, в этой таблице в i-той строке указан объем производства в i-м пункте производства, а в j-м столбце указан спрос в j-м центре распределения[6]. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.
Для
математического описания транспортной
задачи введем переменные xij,
обозначающие объемы поставок товара
от i-го
источника к j-му
стоку. В этом случае xi1+xi2+…+xin — общий объем поставок товара от i-го
источника, т.е. мощность этого источника; x1j+x2j+…+xmj — общий объем поставок товара к j-му
стоку, т.е. мощность этого стока; c11x11+c12x12+…+cmnxmn — суммарная стоимость перевозок товара
от источников к стокам[7]. С учетом этого
рассматриваемая задача может быть
представлена в следующем виде: 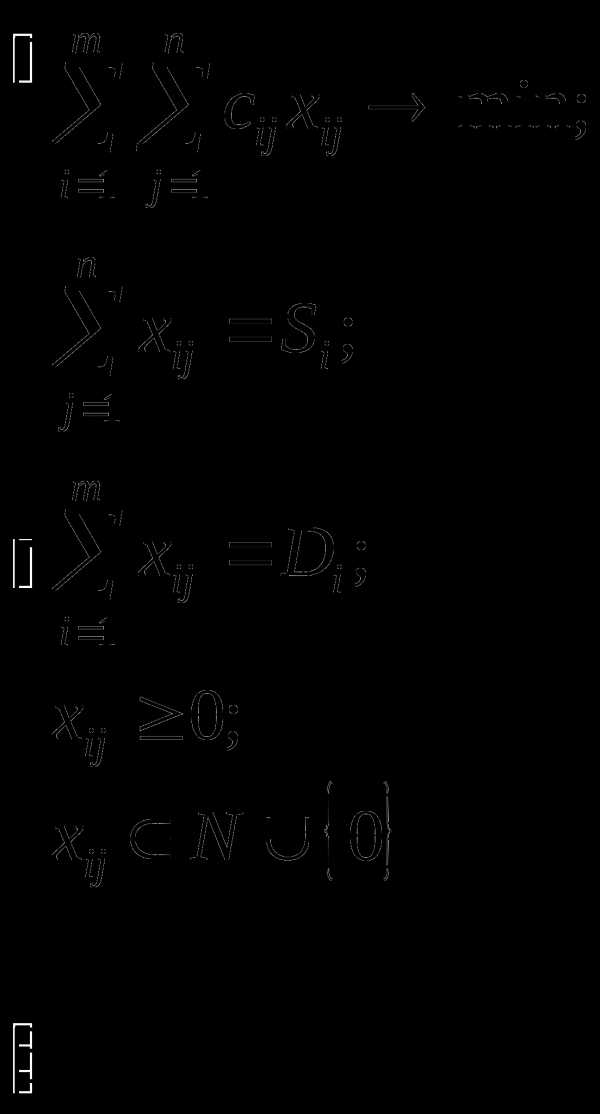
Задача состоит в определении неизвестных величин xij, минимизирующих суммарные транспортные расходы и удовлетворяющих ограничениям, накладываемым на объемы грузов в пунктах отправления (предложение) и пунктах назначения (спрос).
1.1. Решение классической сбалансированной транспортной задачи в Excel
Рассмотрим решение классической транспортной задачи.
Автомобильная компания MG Auto имеет три завода в Лос-Анджелесе, Детройте и Новом Орлеане и два распределительных центра в Денвере и Майами. Объемы производства заводов компании в следующем квартале составят соответственно 1000, 1500 и 1200 автомобилей. Ежеквартальная потребность распределительных центров составляет 2300 и 1400 автомобилей. Расстояние (в милях) между заводами и распределительными центрами приведены в .
Таблица 1
Поставщики
Потребители
Денвер
Майами
Лос-Анджелес
1000
2690
Детройт
1250
1350
Новый Орлеан
1275
850
Транспортная компания оценивает свои услуги в 8 центов за перевозку одного автомобиля на одну милю. В результате получаем, представленную в , стоимость перевозок (с округлением до доллара) по каждому маршруту.
Таблица 2
Поставщики | Потребители | |
Денвер | Майами | |
Лос-Анджелес | $80 | $215 |
Детройт | $100 | $108 |
Новый Орлеан | $102 | $68 |
Решение:
В данной задаче общий объем произведенных автомобилей (S=1000+1500+1200=3700) равен суммарному спросу распределительных центров (D=2300+1400=3700).
Задачу можно решить с помощью транспортной таблицы. Исходные данные для решения классической транспортной задачи целесообразно представить в виде двух таблиц, в первой из которых представлены значения стоимости перевозок единицы товара cij от i-го поставщика к j-му потребителю (см. Рисунок 1).
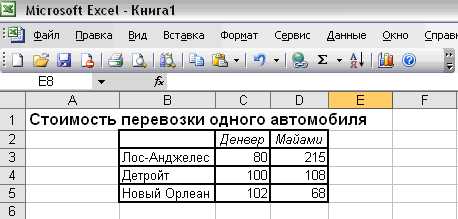
Рисунок 1
Во второй таблице представлены: значения Si предложения каждого i-го поставщика; значения Dj спроса каждого j-го потребителя; переменные xij, первоначально принимающие нулевые значения; вспомогательная строка и вспомогательный столбец «Сумма» (см. Рисунок 2).
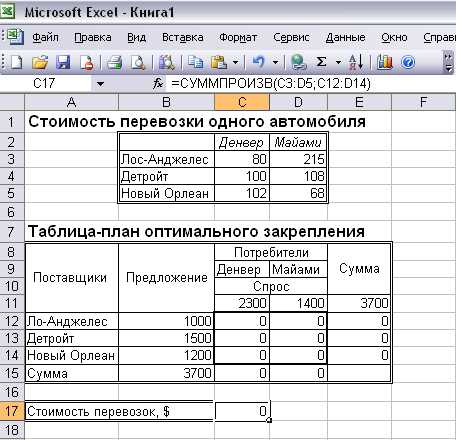
Рисунок 2
Целевая ячейка C17 должна содержать формулу, выражающую целевую функцию: = СУММПРОИЗВ(C3:D5; C12:D14). (Рисунок 3)
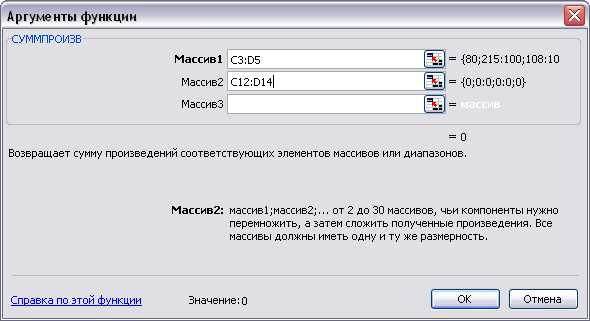
Рисунок 3
Используя меню СервисПоиск решения открываем диалоговое окно Поиск решения (см. Рисунок 4), в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить [3].
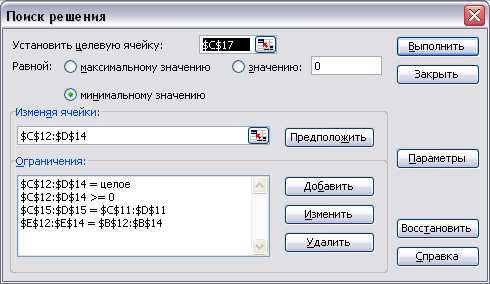
Рисунок 4
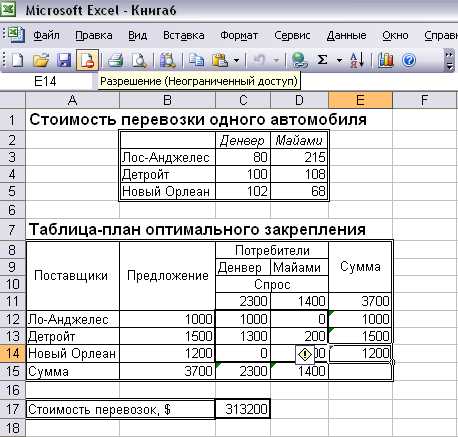
Рисунок 5
Оптимальное решение задачи (Рисунок 5). Оно предполагает перевозку 1000 автомобилей из Лос-Анджелеса в Детройт, 1300 автомобилей – из Детройта в Денвер, 200 автомобилей – из Детройта в Майами и 1200 – из Нового Орлеана в Майами. Минимальная стоимость перевозок составляет 313200 долларов.
1.2. Решение классической несбалансированной транспортной задачи в Excel
Несбалансированная классическая транспортная задача – это когда суммарный объем предложений (грузов, имеющихся в пунктах отправления) не равен общему объему спроса на товары (грузы), запрашиваемые пунктами назначения. В этом случае, при решении классической транспортной задачи вводят фиктивные пункты назначения или отправления [4]. В Excel несбалансированная транспортная задача решается путем изменения ограничений по спросу (если спрос превышает предложение) или по предложению (если предложение превышает спрос), т.е. система ограничений будет иметь вид:
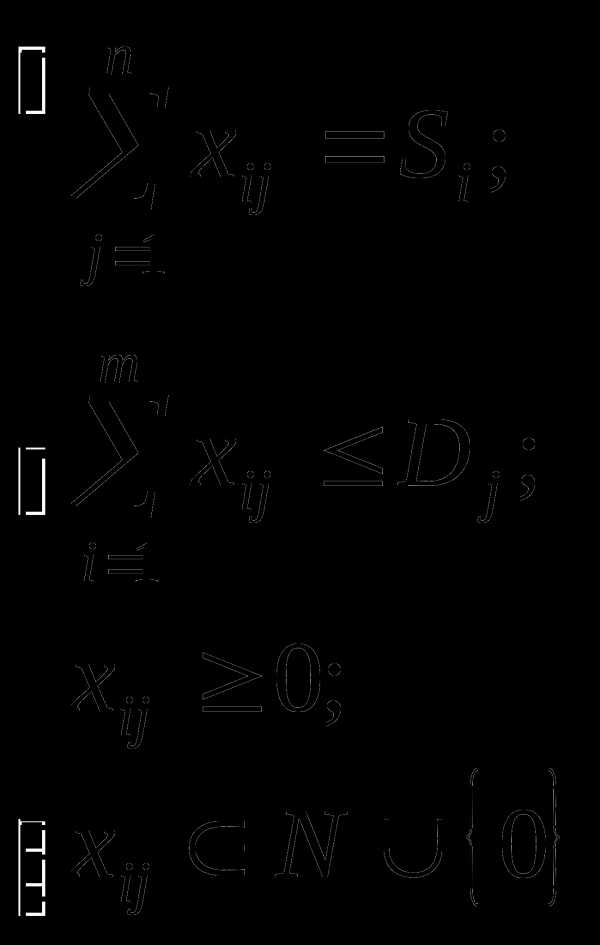 или
или 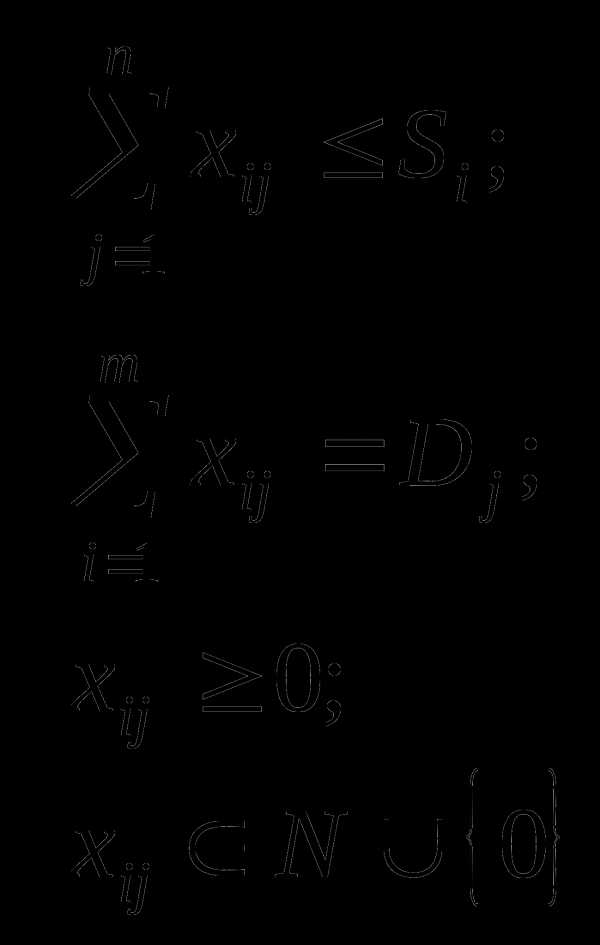
Рассмотрим решение несбалансированной транспортной задачи в Excel
В рамках модели компании MG Auto предположим, что завод в Детройте уменьшил выпуск продукции до 1300 автомобилей (вместо 1500, как было ранее). В этом случае общее количество произведенных автомобилей (=3500) меньше общего количества заказанных (=3700) автомобилей. Таким образом, очевидно, что часть заказов распределительных центров Денвера и Майами не будет выполнена.
Решение: Представлено на Рисунок 6 – Рисунок 8 (аналогично предыдущему).
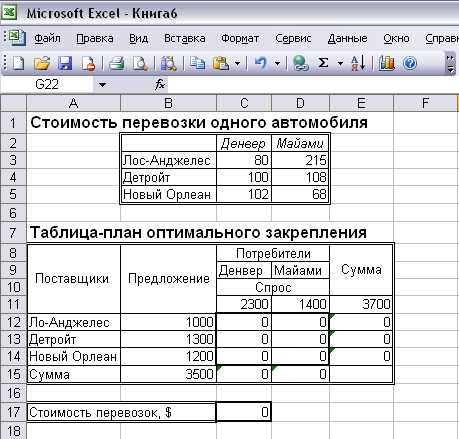
Рисунок 6
Изменения имеют место в ограничениях (выделенная строка):
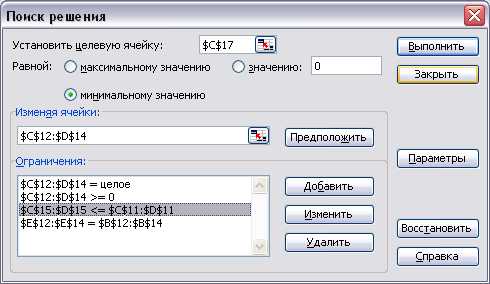
Рисунок 7
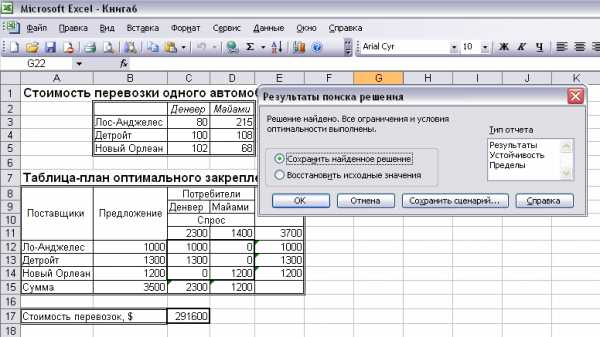
Рисунок 8
В таблице-плане оптимального закрепления на Рисунок 8 представлено оптимальное решение. Решение показывает, что спрос распределительного центра Денвера будет удовлетворен полностью, а в распределительный центр Майами из заказа в 1400 автомобилей не будет поставлено 200 автомобилей.
Глава 2.
Транспортная задача с промежуточными пунктами
Одно практически важное обобщение классической транспортной задачи связано с учетом возможности доставки товара от i-го источника к j-му стоку по маршруту, проходящему через некоторый промежуточный пункт (склад) [6]. Так, например, промежуточные пункты являются составной частью распределительной системы любой крупной компании, имеющей сеть универсальных магазинов во многих городах. Такая компания обычно имеет зональные оптовые базы (источники), снабжающие товарами более мелкие региональные склады (промежуточные пункты), откуда эти товары поступают в розничную торговую сеть (стоки). При этом товар для каждого фиксированного стока в общем случае может быть доставлен не из любого источника и по маршрутам, не обязательно проходящим через все промежуточные пункты. Кроме того, промежуточные пункты могут обладать вполне определенной спецификой. Так, например, при транспортировке товара от источника к стоку по маршруту, проходящему через склад, часть товара может быть использована для создания неприкосновенного запаса на складе.
Задачу выбора плана перевозок товаров от источников стокам с учетом промежуточных пунктов, обеспечивающего минимальные транспортные затраты и потребности стоков, в исследовании операций называют транспортной задачей с промежуточными пунктами [7].
Пусть J — множество номеров складов, на которые товар может быть доставлен с k-го склада, а I — множество номеров складов, с которых товар может быть доставлен на k-й склад. Tk — величина чистого запаса товара, равная объему исходного предложения или исходного спроса. Тогда математическую модель данной задачи можно представить следующим образом:
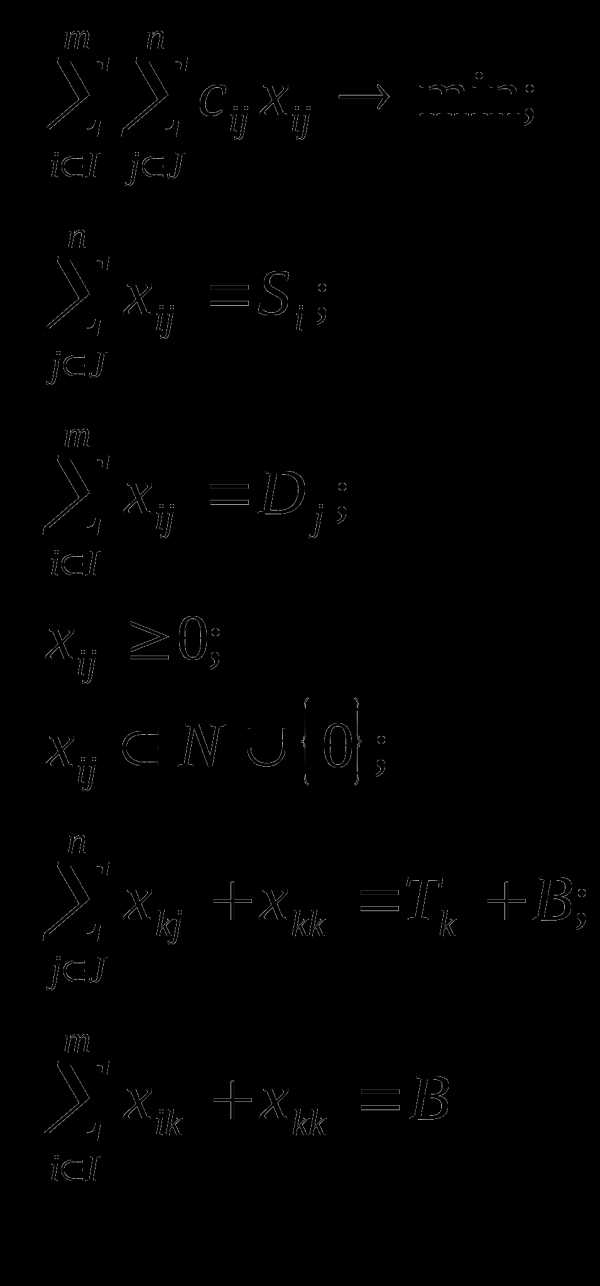
2.1. Решение транспортной задачи с промежуточными пунктами в Excel
Торговая фирма имеет восемь складов, на которых сосредоточены все имеющиеся в наличии запасы товара. Перед началом рекламной компании решено перераспределить часть запасов товара между складами в соответствии с прогнозами сбыта в районах их размещения. Требуется разработать план перевозок товара между складами, который позволит при минимальных транспортных затратах создать на каждом складе необходимый запас товара.
Найти решение транспортной задачи с промежуточными пунктами, в рассмотренном выше примере, если стоимость перевозки единицы товара составляет: c12=3 у.е., c23=7 у.е., c25=3 у.е., c43=6 у.е., c45=4 у.е., c47=5 у.е., c54=5 у.е., c56=3 у.е., c67=5 у.е., c78=2 у.е.
Решение:
На Рисунок 9 представлены таблицы Стоимость перевозки единицы товара и План перевозок товара между складами, сформированные на рабочем листе Excel. Здесь в таблице Стоимость перевозки единицы товара мы видим, что если между отдельными складами отсутствует возможность перевозки товара, то в соответствующие ячейки таблицы (выделенные темным фоном) заносится любое большое число (в данном случае 100). Для того, чтобы найти в таблице Плана перевозок товара между складами объем предложения и объем спроса, определим объем буфера B по следующему правилу:
B = общий объем предложения = S1+S4= 10+2 = 12 ед.
или
B = общий объем спроса = D3+D6+D8= 3+1+8 = 12 ед.
Для остальных промежуточных пунктов объемы предложения Si или объемы спроса Dj равны нулю.
В целевую ячейку, в данном случае C23, необходимо занести формулу: =СУММПРОИЗВ(C4:I9;C15:I20).
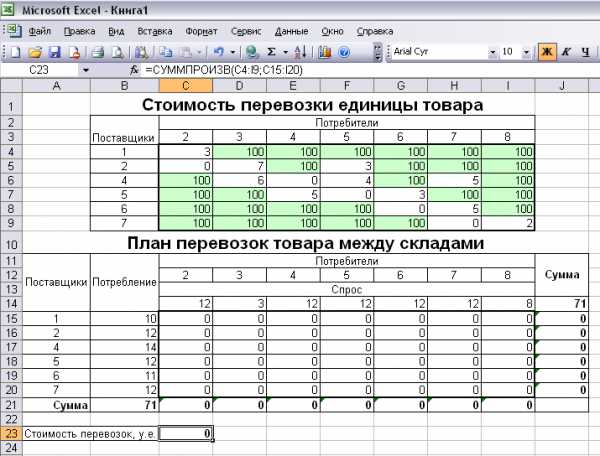
Рисунок 9
Используя меню Сервис Поиск решения открываем диалоговое окно Поиск решения (см. Рисунок 10), в котором устанавливаем целевую ячейку равной минимальному значению, определяем диапазон изменяемых ячеек и ограничения и запускаем процедуру вычисления, щелкнув по кнопке Выполнить [2].
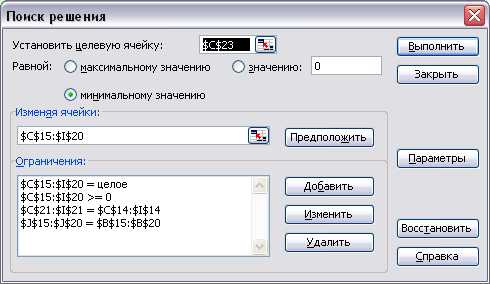
Рисунок 10
Результат решения данной задачи представлен на Рисунок 11.
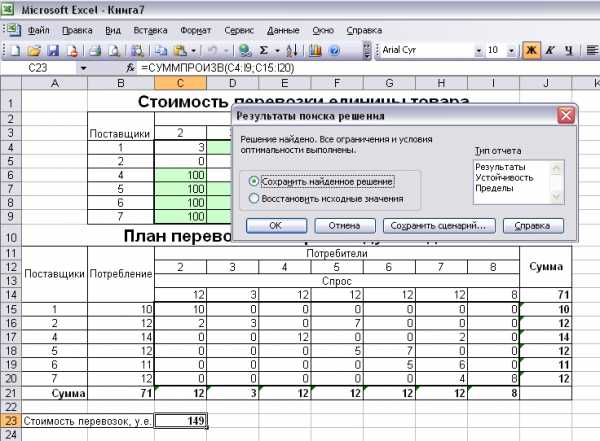
Рисунок 11
Здесь мы видим, что оптимальный план перевозок товара между складами следующий:
со склада 1 товар в количестве трех единиц транзитом через склад 2 отправлен на склад 3, который является истинным пунктом назначения;
со склада 1 товар в количестве семи единиц транзитом через склады 2 и 5 отправлен на склад 6, где одна единица товара используется для пополнения запаса на этом складе;
со склада 6 товар в количестве шести единиц транзитом через склад 7 отправлен на склад 8, который также является истинным пунктом назначения;
со склада 4 избыток товара в количестве четырех единиц отправлен на склад 8 транзитом через склад 7.
Стоимость перевозок при этом минимальна и составляет 149 условных денежных единиц.
Заключение
Таким образом, в данном проекте на основе транспортной задачи линейного программирования были выявлены пути составления плана перевозок по доставке требуемой продукции в пункты распределения, минимизирующего суммарные транспортные расходы.
Была найдена минимальная стоимость перевозок автомобилей в указанные города, которая составила 313200 долларов.
Отсюда следует, что воспользовавшись новой схемой транспортировки автомобилей можно сэкономить до 40% транспортных расходов. Таким образом, сэкономленными средствами можно поступить по-разному:
1) за счет этих средств увеличить прибыль предприятия, и воспользоваться ею для каких-либо нужд предприятия;
2) либо снизить стоимость автомобилей на заводах, что может принести еще больше прибыли.
В заключение можно сделать вывод, что в настоящее время рациональное размещение производственных сил имеет очень большое значение, потому что таким образом можно существенно снизить транспортные затраты предприятия, а значит и увеличить его прибыль. А как известно, увеличение прибыли – залог успеха предприятия [1].
Список литературы
1. Дубина А.Г. Excel для экономистов и менеджеров/ А.Г. Дубина, С.С. Орлова, И.Ю. Шубина, А.В. Хромов. – СПб.: Питер, 2004. – 295 с.
2. Кузьмин В. Microsoft Office Excel 2003. Учебный курс/ В. Кузьмин. – СПб.: Питер, 2004. – 493 с.
3. Мур Д. Экономическое моделирование в Microsoft Excel/ Д. Мур, Ларри Р. Уэдерфорд и др. – М.: Издательский дом «Вильямс», 2004. – 1024 с.
4. /lp_on_line.htm
5. /text/method/usl_razresh.htm
6. /book/preview/BDAC41E5C58241D6949C90F37E3F4AC
7. /Решение_транспортной_задачи
gigabaza.ru
