тригонометрические неравенства | математика-повторение
Записи с меткой «тригонометрические неравенства»
На предыдущих трех занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели неравенства вида:
Рассмотрим тригонометрические неравенства вида: cost>a.
Используем алгоритм решения, как в предыдущем уроке 10.2.3. Решение тригонометрических неравенств. Часть 3.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=cost и y=a.
3. Находим такие две соседние точки пересечения графиков
4. Записываем двойное неравенство для аргумента t, учитывая период косинуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду. (График функции y=cosx также называют синусоидой!) Построение синусоиды y=cosx рассматривается подробно в предыдущем уроке 10.2.3. Решение тригонометрических неравенств. Часть 3.
Пример 1.
Далее, по алгоритму, определяем те значения аргумента t, при которых синусоида располагается выше прямой. Выпишем эти значения в виде двойного неравенства, учитывая периодичность функции косинуса, а затем вернемся к первоначальному аргументу х.
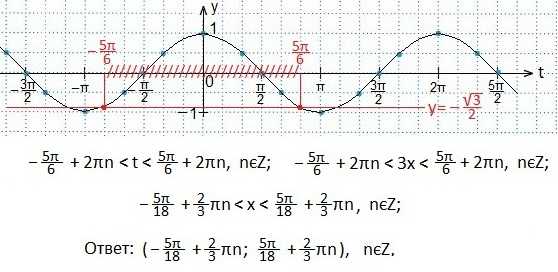
Пример 2.
Выделяем промежуток значений t, при которых синусоида находится выше прямой.

Записываем в виде двойного неравенства значения t, удовлетворяющих условию. Не забываем, что наименьший период функции y=cost равен 2π. Возвращаемся к переменной х, постепенно упрощая все части двойного неравенства.
Ответ записываем в виде закрытого числового промежутка, так как неравенство было нестрогое.
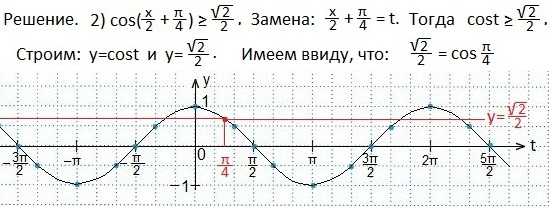
Пример 3.
Нас будет интересовать промежуток значений t, при которых точки синусоиды будут лежать выше прямой.
Значения t запишем в виде двойного неравенства, перезапишем эти же значения для 2х и выразим х. Ответ запишем в виде числового промежутка.
Смотрите видео: «10.2.4. Решение тригонометрических неравенств. Часть 4.»
И снова формула, которой вам следует воспользоваться на экзамене ЕНТ или ЕГЭ при решении тригонометрического неравенства вида cost>a.
Если cost>a, (-1≤а≤1), то — arccos a + 2πn < t < arccos a + 2πn, nєZ.
Применяйте формулы для решения тригонометрических неравенств, и вы сэкономите время на экзаменационном тестировании.
На предыдущих двух занятиях по решению тригонометрических неравенств графическим способом мы рассмотрели решения неравенств вида:
Продолжаем решать тригонометрические неравенства графическим способом. Рассмотрим неравенства вида cost<a:
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=cost и y=a.
3. Находим такие две соседние точки пересечения графиков, между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период косинуса Т=2π (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду. (График функции y=cosx также называют синусоидой!)
Первое неравенство.
Преобразуем левую часть неравенства по формуле косинуса двойного аргумента:
Координатную плоскость готовим так же, как готовили для построения графика функции y=sinx. (10.2.1. Решение тригонометрических неравенств. Часть 1), т.е. единичный отрезок берем равным двум клеткам, тогда значение π изображаем равным шести клеткам и т.д. Вот так должна выглядеть координатная плоскость для построения синусоид:
Воспользуемся таблицей значений косинусов некоторых углов:
а также свойствами: графиков четных функций, непрерывностью и периодичностью функции косинуса. Отмечаем точки:
Проводим через эти точки кривую — график функции y=cosx.
Определяем промежуток значений х, при которых точки синусоиды лежат ниже точек прямой.
Учтем периодичность функции косинуса и запишем в виде двойного неравенства решение данного неравенства:
Второе неравенство.
Находим абсциссы точек пересечения графиков, между которыми график косинуса лежит ниже прямой.

Концы этого промежутка тоже являются решениями неравенства, так как неравенство нестрогое.
Запишем решение в виде двойного неравенства для переменной t.
Подставим вместо t первоначальное значение аргумента.
Выразим х.
Ответ запишем в виде промежутка.
Третье неравенство.
Смотрите видео: «10.2.3. Решение тригонометрических неравенств. Часть 3.»
А теперь формула, которой вам следует воспользоваться на экзамене ЕНТ или ЕГЭ при решении тригонометрического неравенства вида cost<a.
Если cost<a, (-1≤а≤1), то arccos a + 2πn < t < 2π — arccos a + 2πn, nєZ.
Примените эту формулу для решения рассмотренных в этой статье неравенств, и вы получите ответ гораздо быстрее и безо всяких графиков!
На прошлом занятии «10.2.1. Решение тригонометрических неравенств. Часть 1» мы решили три неравенства вида sint<a. На этом уроке мы рассмотрим три неравенства вида sint>a, где -1≤а≤1
.Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается выше прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решаем первое неравенство:
Построение графика синуса мы рассмотрели подробно в занятии «10.2.1. Решение тригонометрических неравенств. Часть 1».
Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющий последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х. Ответ запишем в виде промежутка.
Решаем второе неравенство:
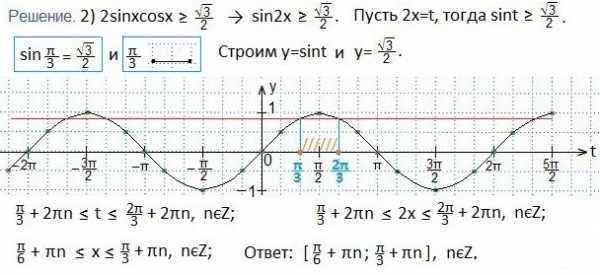
При решении второго неравенства нам пришлось преобразовать левую часть данного неравенства по формуле синуса двойного аргумента, чтобы получить неравенство вида: sint≥a. Далее мы следовали алгоритму.
Решаем третье неравенство:

Смотрите видео: «10.2.2. Решение тригонометрических неравенств. Часть 2.»
Дорогие выпускники и абитуриенты! Имейте ввиду, что такие способы решения тригонометрических неравенств, как приведенный выше графический способ и, наверняка, вам известный, способ решения с помощью единичной тригонометрической окружности (тригонометрического круга) применимы лишь на первых этапах изучения раздела тригонометрии «Решение тригонометрических уравнений и неравенств». Думаю, вы припомните, что и простейшие тригонометрические уравнения вы вначале решали с помощью графиков или круга. Однако, сейчас вам не придет в голову решать таким образом тригонометрические уравнения. А как вы их решаете? Правильно, по формулам. Вот и тригонометрические неравенства следует решать по формулам, тем более, на тестировании, когда дорога каждая минута. Итак, решите три неравенства этого урока по соответствующей формуле.
Если sint>a, где -1≤a≤1, то arcsin a + 2πn < t < π — arcsin a + 2πn, nєZ.
Учите формулы!
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается ниже прямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решение тригонометрических неравенств с помощью графиков надежно страхует нас от ошибок только в том случае, если мы грамотно построим синусоиду.
Для построения графика функции y=sinx выберем единичный отрезок, равный двум клеткам. Тогда по горизонтальной оси Ох значение π (≈3,14) составит шесть клеток. Рассчитываем остальные значения аргументов (в клетках).
Вот как будет выглядеть координатная плоскость.
Эти точки мы взяли из таблицы значений синуса. Также используем свойство нечетности функции y=sinx (sin (-x)=-sinx), периодичность синуса (наименьший период Т=2π) и известное равенство: sin (π-x)=sinx. Проводим синусоиду
. Проводим прямую.
Теперь нам предстоит определить такие две точки пересечения синусоиды и прямой, между которыми синусоида располагается ниже, чем прямая. Крайняя точка справа определена, абсцисса ближайшей искомой отстоит от начала отсчета влево на 8 клеток. Построим ее и определим.
Между этими (выделенными) значениями аргумента и находится та часть синусоиды, которая лежит ниже данной прямой, а значит, промежуток между этими выделенными точками удовлетворяет данному неравенству. Учтем период синуса, запишем результат в виде двойного неравенства, а ответ в виде числового промежутка.
Решим второе неравенство.
Синусоиду строим так же, а прямая будет параллельна оси Оt и отстоять от нее на 1 клетку вниз.
Определяем промежуток, внутри которого точки синусоиды лежат ниже прямой.
Записываем промежуток значений введенной переменной t. Возвращаемся к первоначальному значению аргумента (2х). Все части двойного неравенства делим на 2 и определяем промежуток значений х. Записываем ответ в виде числового промежутка.
Аналогично решаем и третье неравенство.
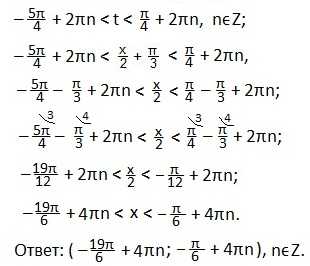 В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместо t подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.
В выделенном промежутке синусоида располагается ниже прямой, поэтому, учитывая периодичность функции синуса, запишем в виде двойного неравенства значения t. Затем вместо t подставим первоначальный аргумент синуса и будем выражать х из полученного двойного неравенства.
Ответ запишем в виде числового промежутка.
Смотрите видео: 10.2.1. Решение тригонометрических неравенств вида: sinx<a графическим способом.
И, напоследок: знаете ли вы, что математика — это определения, правила и ФОРМУЛЫ?!
Конечно, знаете! И самые любознательные, изучив эту статью и просмотрев видео, воскликнули: «Как долго и сложно! А нет ли формулы, позволяющей решать такие неравенства безо всяких графиков и окружностей?» Да, разумеется, есть!
ДЛЯ РЕШЕНИЯ НЕРАВЕНСТВ ВИДА: sint<a (-1≤а≤1) справедлива формула:
— π — arcsin a + 2πn < t < arcsin a + 2πn, nєZ.
Примените ее к рассмотренным примерам и вы получите ответ гораздо быстрее!
Вывод: УЧИТЕ ФОРМУЛЫ, ДРУЗЬЯ!
Страница 1 из 11
www.mathematics-repetition.com
Тригонометрические уравнения и неравенства
Тригонометрические уравнения и неравенстваРешение простейших тригонометрических уравнений
Простейшими тригонометрическими уравнениями называют уравнения cos x = a, sin x = a, tg x = a, ctg x = a.
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
Уравнение cos x = a
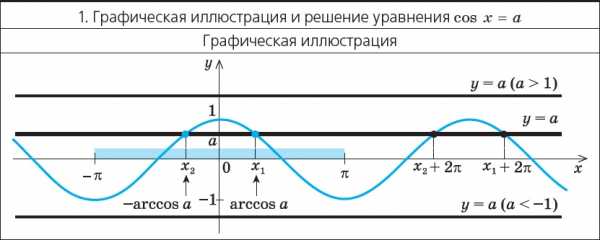
Примеры решения задач


Уравнение sin x = a



Примеры решения задач

Уравнение tg x = a и ctg x = a


Примеры решения задач


Решение тригонометрических уравнений, отличающихся от простейших
Как правило, решение тригонометрических уравнений сводится к решению простейших уравнений с помощью преобразований тригонометрических выражений, разложения на множители и замены переменных.
Замена переменных при решении тригонометрических уравнений
Если в уравнение, неравенство или тождество переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).

При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:
-
Пробуем привести все тригонометрические функции к одному аргументу.
-
Если удалось привести к одному аргументу, то пробуем все тригонометрические выражения привести к одной функции.
-
Если к одному аргументу удалось привести, а к одной функции — нет, тогда пробуем привести уравнение к однородному.
-
В других случаях переносим все члены в одну сторону и пробуем получить произведение ил используем специальные приемы решения.
Решение тригонометрических уравнений приведением к одной функции

Решение простейших тригонометрических неравенств









ya-znau.ru
Тригонометрические неравенства. Разбор и примеры решения
Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими — ‹, › и нестрогими — ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.
Простейшие тригонометрические неравенства
Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.
Способ 1 — Решение неравенств с помощью построения графика функции
Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.
Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:
Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки — [ ]. Ответ задачи можно также записать в виде очередного неравенства:
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения
Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.
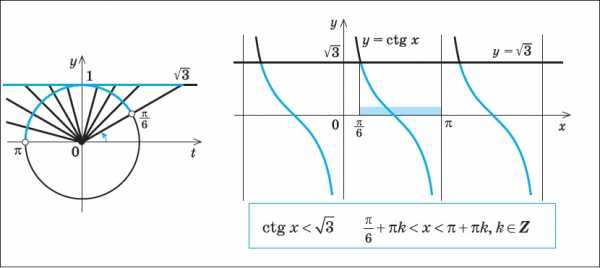
Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.
Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы
являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Сложные тригонометрические неравенства
Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:
Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:
В результате должна получиться красивая кривая.
Для простоты поиска решения заменим сложный аргумент функции
Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.
Найденный отрезок является решением для переменной t:
Однако, цель задания найти все возможные варианты неизвестной x:
Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:
Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.
Похожие статьи
Рекомендуем почитать:
karate-ege.ru
Простейшие тригонометрические неравенства | Формулы с примерами
sin x > a, | a |Множество решений неравенства : x (arcsin a + 2?n; ? — arcsin a + 2?n), n Z
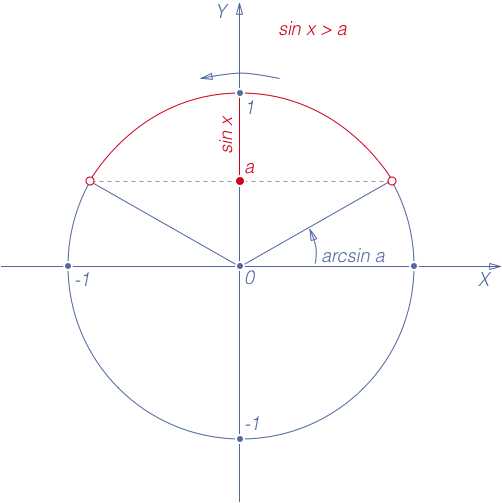
2. sin x
Множество решений неравенства: x (-? — arcsin a + 2?n; arcsin a + 2?n), n Z

3. cos x > a, | a |
Множество решений неравенства: x (-arccos a + 2?n; arccos a + 2?n), n Z

4. cos x
Множество решений неравенства: x (arccos a + 2?n; 2? — arccos a + 2?n), n Z
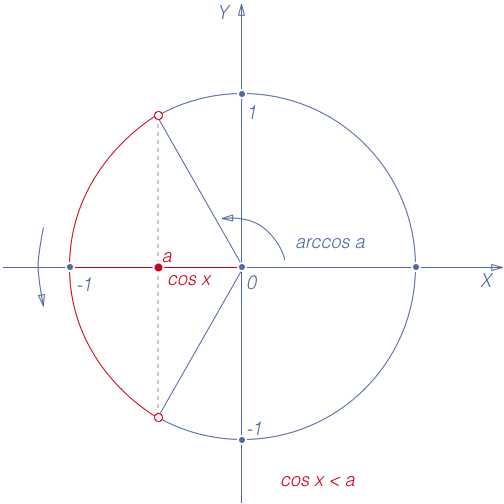
5. tg x > a, a R
Множество решений неравенства: x (arctg a + ?n; ?2 + ?n), n Z
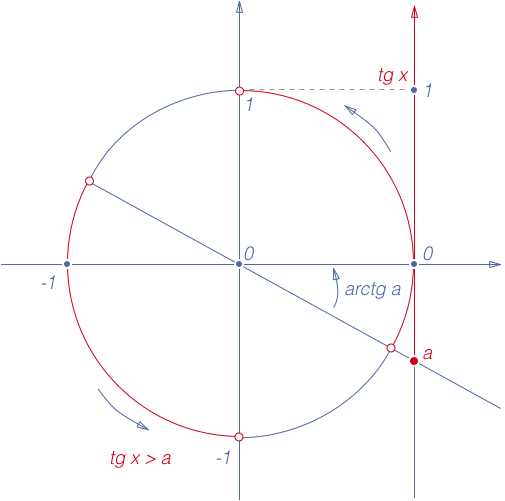
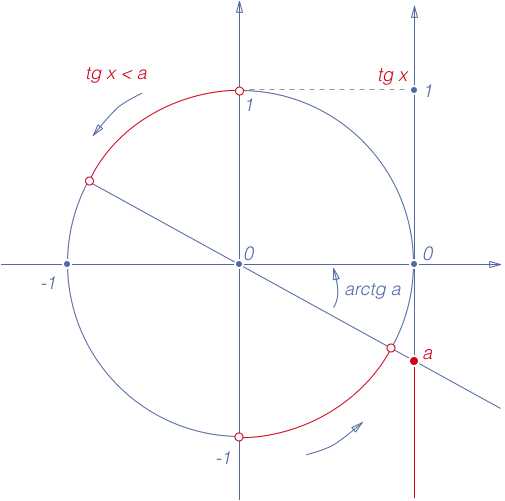
6. tg x R
Множество решений неравенства: x (- ?2 + ?n; arctg a + ?n), n Z
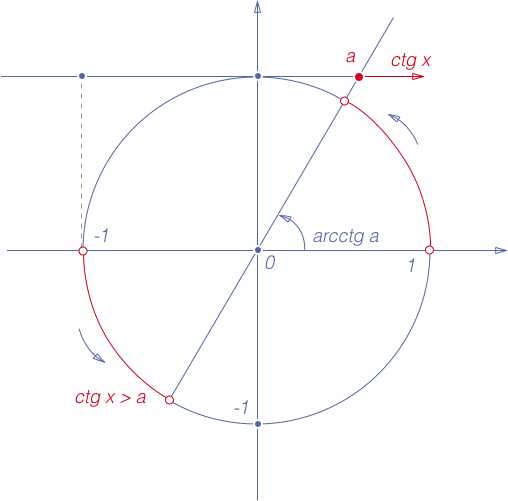
7. ctg x > a, a R
Множество решений неравенства: x (?n; arcctg a + ?n), n Z
 8. ctg x R
8. ctg x R
Множество решений неравенства: x (arcctg a + ?n; ? + ?n), n Z

formula-xyz.ru
Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике
Часть 1.
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
,
,
,
,
где – один из знаков , .
Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).

Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.
Пример 1.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , меньшие – левее точки на оси косинусов.
Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше
Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .
Обратите внимание, многие, назвав первую точку вместо второй точки указывают точку , что неверно!
Становится видно, что неравенству удовлетворяют следующие значения
Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:
Пример 2.
Решить неравенство:
Решение:
Отмечаем на оси косинусов
Все значения , большие или равные – правее точки , включая саму точку.
Тогда выделенные красной дугой аргументы отвечают тому условию, что .
Пример 3.
Решить неравенство:
Решение:
Отмечаем на оси синусов
Все значения , большие или равные – выше точки , включая саму точку.
«Транслируем» выделенные точки на тригонометрический круг:

Пример 4.
Решить неравенство:
Решение:
Кратко:
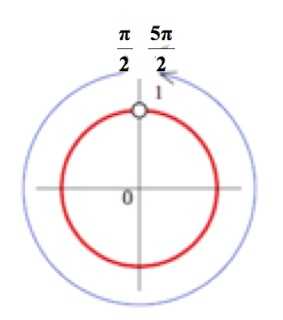
или все , кроме
Пример 5.
Решить неравенство:
Решение:
Неравенство равносильно уравнению , так как область значений функции –
Пример 6.
Решить неравенство:
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.
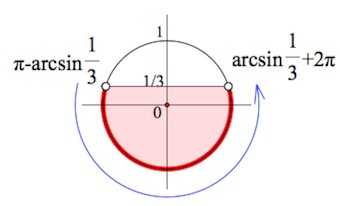
Если не очень понятно, загляните сюда –>+ показать
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен
А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому

Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:
1. Решить неравенство:
Ответ: + показать
2. Решить неравенство:
Ответ: + показать
3. Решить неравенство:
Ответ: + показать
4. Решить неравенство:
Ответ: + показать
5. Решить неравенство:
Ответ: + показать
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!
egemaximum.ru
Вывод формул для решения тригонометрических неравенств. 10-й класс
Разделы: Математика
Тип урока: комбинированный урок.
Цели урока:
- образовательные — научить учащихся решать тригонометрические неравенства с помощью графиков тригонометрических функций, вывести формулы для решения этих неравенств
- развивающие — развивать речь учащихся через обогащение и усложнение её словарного запаса, развивать мышление учащихся через умение анализировать, обобщать и систематизировать материал
- воспитательные — формирование гуманного отношения у учащихся к участникам образовательного процесса
Оборудование урока:
- интерактивная доска
- плакаты с графиками тригонометрических функций
Структура урока
| № | Основные фрагменты урока | Время |
| 1 | Организационный момент, вводная часть | 2 мин |
| 2 | Повторение | 5 мин |
| 3 | Изучение нового материала | 19 мин |
| 4 | Закрепление нового материала | 10 мин |
| 5 | Самостоятельная работа с последующей взаимопроверкой | 6 мин |
| 6 | Подведение итогов урока. Разбор домашнего задания | 3 мин |
Организационный момент, вводная часть.
Учитель объявляет тему урока, цели урока и основные моменты урока. Проверяет готовность класса к работе.
Повторение.
На доске вывешены плакаты с графиками тригонометрических функций y = sin x, y = cos x, y = tg x, y = ctg x. Рядом написаны вопросы для повторения.
Вопросы:
- Назовите область определения функции.
- Назовите область значений функции.
- Определите чётность функции (вид симметричности графика функции)
- Определите периодичность функции .
- Найдите наибольшее и наименьшее значение функции. В каких точках они достигаются?
- Найдите асимптоты для графика функции.
Изучение нового материала.
На интерактивную доску выводится <Рисунок1>. Разбирается вывод формулы для решения неравенства cos ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. cos t >a.
На интерактивную доску выводится <Рисунок2>. Разбирается вывод формулы для решения неравенства cos ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. cos t <a.
На интерактивную доску выводится <Рисунок3>. Разбирается вывод формулы для решения неравенства sin ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. sin t >a.
На интерактивную доску выводится <Рисунок4>. Разбирается вывод формулы для решения неравенства sin ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. sin t <a.
На интерактивную доску выводится <Рисунок5>. Разбирается вывод формулы для решения неравенства tg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. tg t >a.
На интерактивную доску выводится <Рисунок6>. Разбирается вывод формулы для решения неравенства tg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. tg t <a.
На интерактивную доску выводится <Рисунок7>. Разбирается вывод формулы для решения неравенства ctg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. ctg t >a.
На интерактивную доску выводится <Рисунок8>. Разбирается вывод формулы для решения неравенства сtg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е.сtg t <a.
IV. Закрепление нового материала.
Решите неравенства.
Решение неравенств.
V. Самостоятельная работа.
Решите неравенство.
1 вариант:
2 вариант:
Решение самостоятельной работы показывается на интерактивной доске.
VI. Подведение итогов урока.
Во время подведения итогов урока ещё раз следует обратить внимание учащихся на строгие и нестрогие тригонометрические неравенства. Особо следует отметить неравенства с тангенсом и котангенсом.
3.07.2011
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Тригонометрические неравенства и их решения — энциклопедический справочник и словарь для студента от А до Я
ОПРЕДЕЛЕНИЕ
Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида:
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла есть ординатой точки единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Рис. 1
Примеры решения тригонометрических неравенств
ПРИМЕР 1
Решить неравенство
Поскольку
, то это неравенство имеет решение и его можно решить двумя способами
.Первый способ. Решим это неравенство графически. Для этого построим в одной системе координат график синуса (рис. 2) и прямой
Рис. 2
Выделим промежутки, на которых синусоида расположена ниже графика прямой . Найдем абсциссы и точек пересечения этих графиков:
Получили интервал но так как функцию периодическая и имеет период , то ответом будет объединение интервалов:
Второй способ. Построим единичную окружность и прямую , точки их пересечения обозначим и (рис. 3). Решением исходного неравенства будет множество точек ординаты, которых меньше . Найдем значение и , совершая обход против часовой стрелки, ^
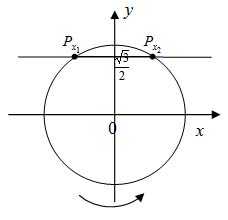
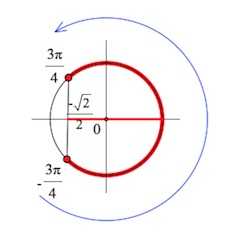
Рис. 3
Учитывая периодичность функции синус, окончательно получим интервалы
Решить неравенство
Синус – функция ограниченная: , а правая часть данного неравенства больше единицы, поэтому решений нет.
ПРИМЕР 3
Решить неравенство
Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть и . Выделим промежутки, на которых график функции косинус расположен выше графика прямой (рис. 4).
Рис. 4
Найдем абсциссы точек и – точек пересечения графиков функций и , которые являются концами одного из промежутков, на котором выполняется указанное неравенство.
Учитывая, что косинус – функция периодическая, с периодом , ответом будет значения x из промежутков 
Рис. 5
Второй способ. Построим единичную окружность и прямую (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим и (рис. 5) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше . Найдем значение и , совершая обход против часовой стрелки так, чтобы :
Учитывая периодичность косинуса, окончательно получим интервалы
ПРИМЕР 4
Решить неравенство
Построим в одной системе координат графики функций
Выделим промежутки, на которых график функции расположен не выше графика прямой (рис. 6). 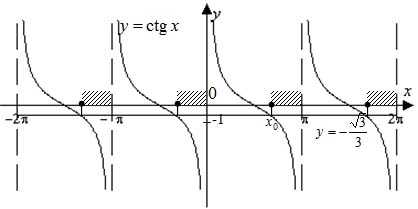
Рис. 6
Найдем абсциссу точки , которая является концом одного из промежутков, на котором неравенство
Другим концом этого промежутка есть точка , а функция в этой точке неопределенна. Таким образом, одним из решением данного неравенства является промежуток . Учитывая, что котангенс функция периодическая, с периодом , то окончательно получим
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
ПРИМЕР 5
Решить неравенство
Выразим в правой части данного неравенства косинус:
Ведем замену , после чего данное неравенство преобразуется к простейшему неравенству 
Рис. 7
Решим его, используя единичную окружность. Построим единичный круг и прямую . Обозначим и – точки пересечения прямой и единичной окружности (рис. 7).
Решением исходного неравенства будет множество точек абсциссы, которых не больше . Точке соответствует угол , а точке . Таким образом, учитывая период косинуса, получим
Сделаем обратную замену
Выразим x, для сначала этого из каждой части неравенства вычтем
а затем, разделим на 2
Двойные тригонометрические неравенства
ПРИМЕР 6
Решить двойное тригонометрическое неравенство
Введем замену , тогда исходное неравенство примет вид

Рис. 8
Решим его, используя единичную окружность. Так как на единичной окружности синусу соответствует ось ординат, выделим на ней множество ординаты которых больше и меньше или равно . На рисунке 8 эти точки будут расположены на дугах и . Найдем значение , совершая обход против часовой стрелки, причем :
Таким образом, получаем два интервала, которые, учитывая периодичность функции синус, можно записать следующим образом
Сделаем обратную замену
Выразим x, для этого умножим все стороны обои неравенств на 2, получим
sciterm.ru
