Ряды фурье
Напомним некоторые сведения из предыдущих разделов математики.
Функция называется кусочно-монотонной
на отрезке 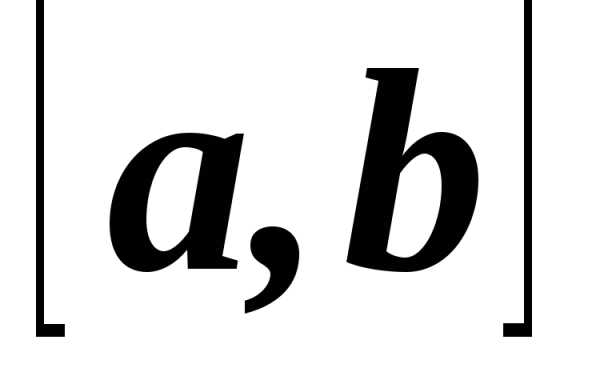 ,
если этот отрезок можно разбить на
конечное число интервалов таким образом,
чтобы в каждом из них функция была
монотонной, т.е. либо не возрастающей,
либо не убывающей.
,
если этот отрезок можно разбить на
конечное число интервалов таким образом,
чтобы в каждом из них функция была
монотонной, т.е. либо не возрастающей,
либо не убывающей.
Функция  называется периодической с периодом ,
если для любого значения аргумента из
области определения функции имеет место
равенство
называется периодической с периодом ,
если для любого значения аргумента из
области определения функции имеет место
равенство
.
Для таких функций
результат интегрирования в пределах,
отличающихся на 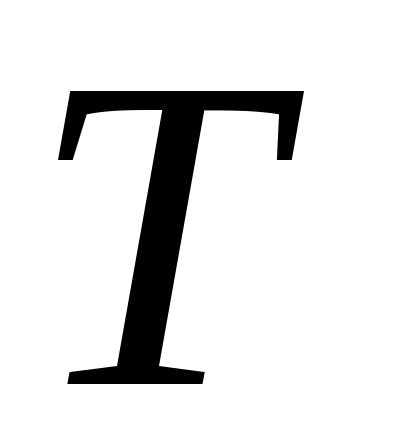 ,
не зависит от выбора нижнего предела
интегрирования, т.е. для любого
,
не зависит от выбора нижнего предела
интегрирования, т.е. для любого 
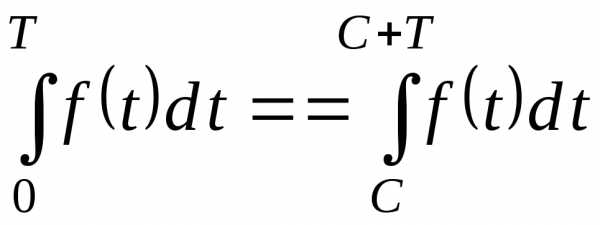 (23)
(23)
Функция ,
описывающая гармоническое колебание,
имеет период 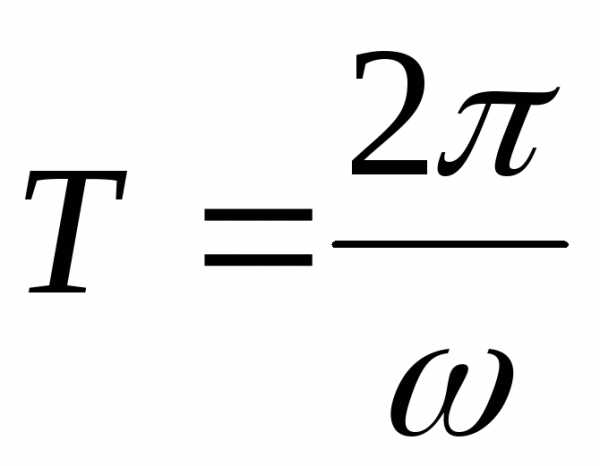 .
.
Функции будем называть гармониками. Их можно представить также в виде
,
где ; .
Сумма гармоник 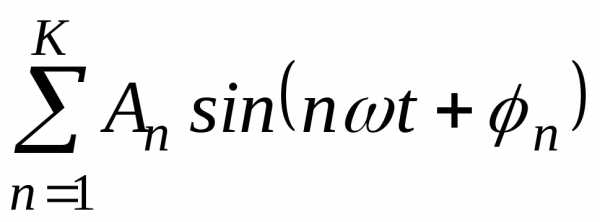 ,
являясь периодической, уже не будет
гармоникой. Можно поставить обратную
задачу. Можно ли периодическую функцию
,
являясь периодической, уже не будет
гармоникой. Можно поставить обратную
задачу. Можно ли периодическую функцию 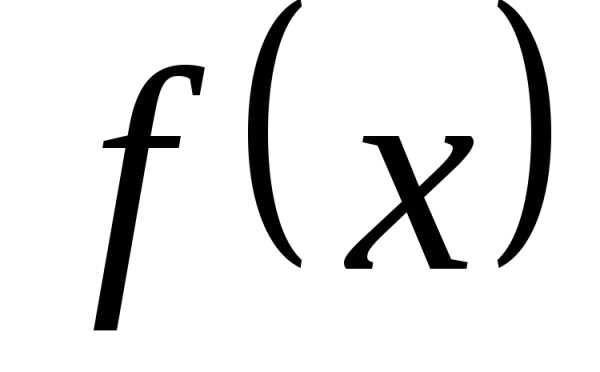 представить в виде такой суммы?. Оказалось,
что при определенных условиях,
сформулированных в теореме Дирихле
(см. ниже), периодическую функцию с
периодом
представить в виде такой суммы?. Оказалось,
что при определенных условиях,
сформулированных в теореме Дирихле
(см. ниже), периодическую функцию с
периодом 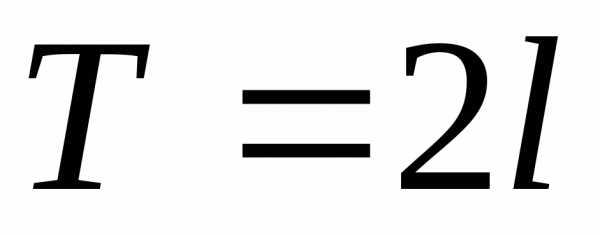 можно представить в виде суммы бесконечного
числа гармоник, называемой тригонометрическим
рядом.
можно представить в виде суммы бесконечного
числа гармоник, называемой тригонометрическим
рядом.
. (24)
Если коэффициенты ряда (24) определяются по формулам
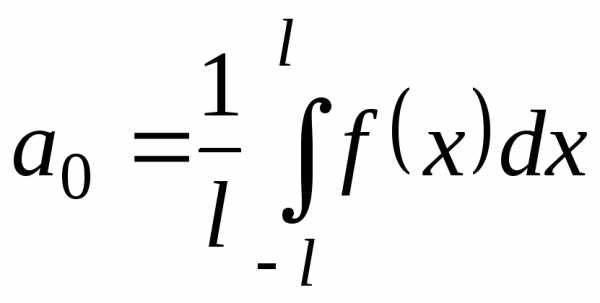 ,
,
, (25)
,
то их называют коэффициентами Фурье, а сам ряд рядом Фурье.
Говорят, что функция удовлетворяет условиям Дирихле, если она непрерывна на отрезке за исключением, быть может, конечного числа точек разрыва первого рода, а также кусочно-монотонна на этом отрезке.
ТЕОРЕМА 12.(Теорема Дирихле)
Если периодическая
функция 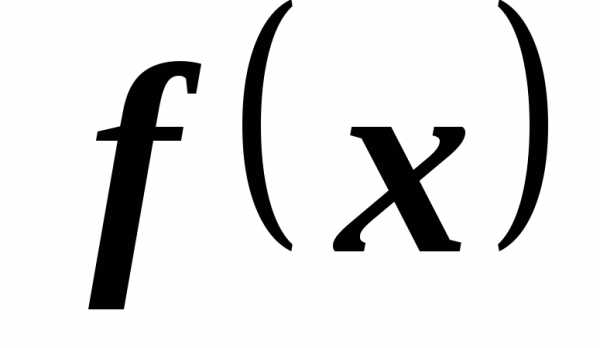 с периодом
с периодом 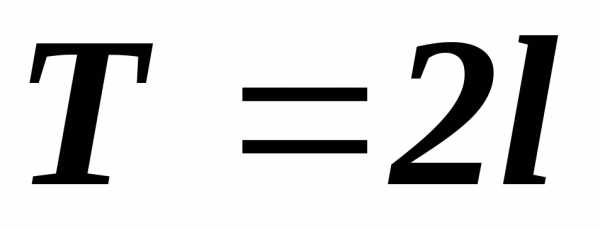 удовлетворяет на отрезке
удовлетворяет на отрезке 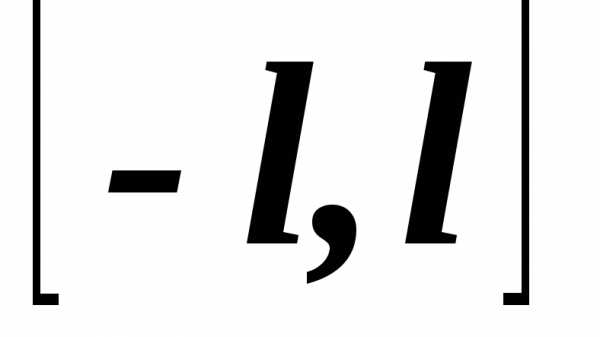 условиям Дирихле, то ряд Фурье этой
функции сходится во всем отрезке
условиям Дирихле, то ряд Фурье этой
функции сходится во всем отрезке
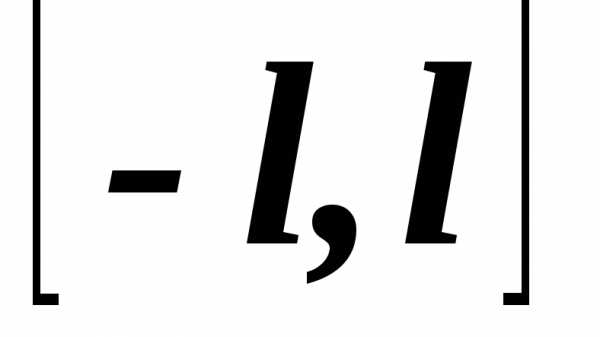 и сумма этого ряда
и сумма этого ряда  равна:
равна:1) Во всех точках непрерывности функции ;
2) Полусумме пределов функции слева и справа, т.Е., если является точкой разрыва первого рода, то .
.
Из теорем (11) и (12) следует, что класс функций представляемых в виде ряда Фурье шире класса функций, разлагаемых в ряд Тейлора, так как для последнего необходимо существование производных функций любого порядка.
В ряде практических
задач электросвязи рассматриваются
периодические функции с 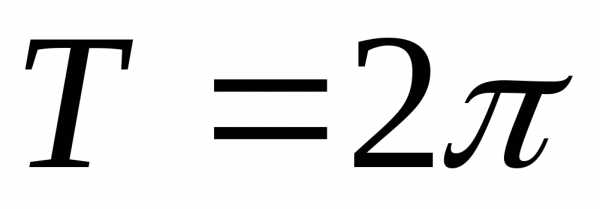 .
Тогда
.
Тогда 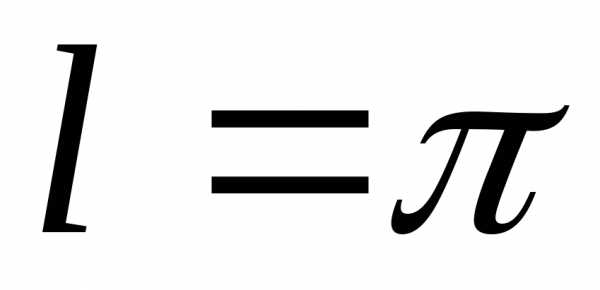 и формулы 24-25 упрощаются
и формулы 24-25 упрощаются
(26)
 ,
,
, (27)
.
Замечания:
-
Учитывая формулу (23), при нахождении коэффициентов Фурье целесообразно в качестве пределов интегрирования использовать границы области задания функции. Например, если
 —
периодическая функция задана на отрезке
—
периодическая функция задана на отрезке  ,
в формулах (27) следует интегрировать
от нуля до
,
в формулах (27) следует интегрировать
от нуля до  .
.
Если функция
 четная,
то коэффициенты
четная,
то коэффициенты  =0,
а остальные коэффициенты можно найти
по формулам
=0,
а остальные коэффициенты можно найти
по формулам
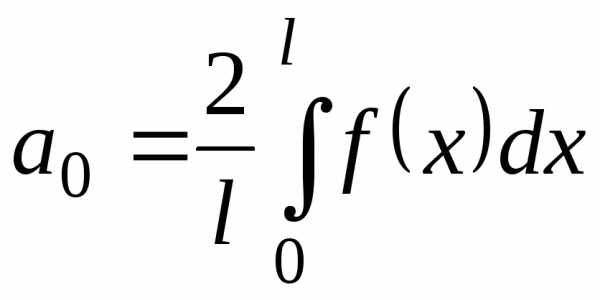 , . (28)
, . (28)
Если же
функция нечетная,
то 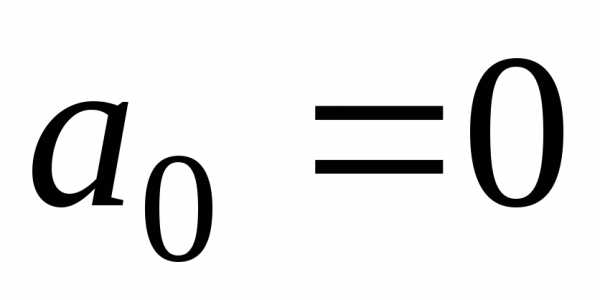 и
и 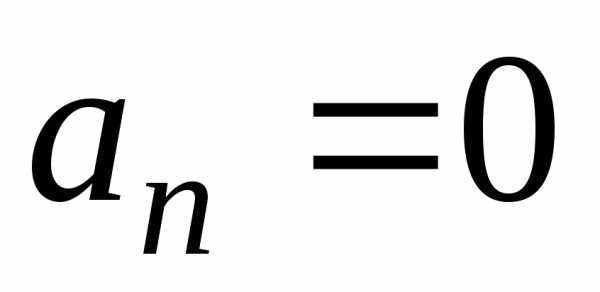
. (29)
Ряд Фурье можно представить в амплитудно — фазовой форме. Пусть
, ,
Тогда , ,  .
.
, (30)
где 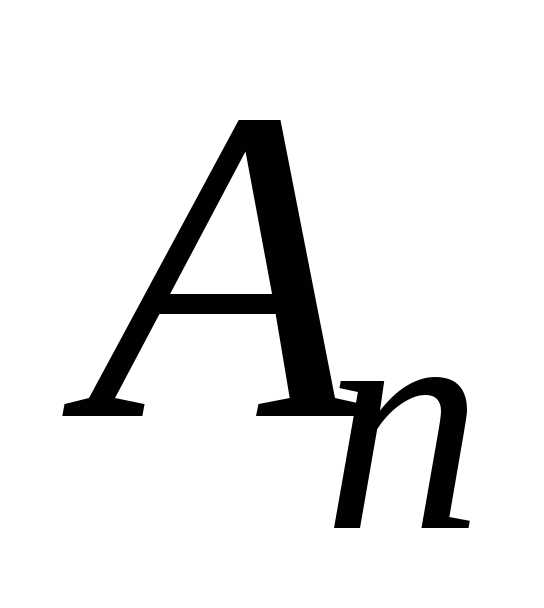 — амплитуда, а
— амплитуда, а 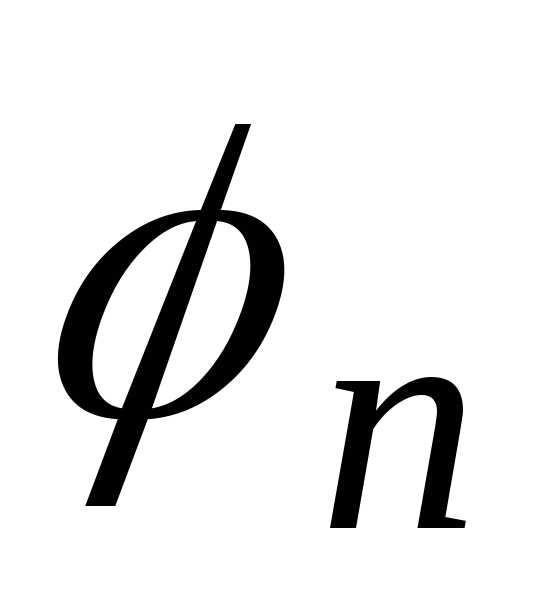 — начальная фаза
— начальная фаза 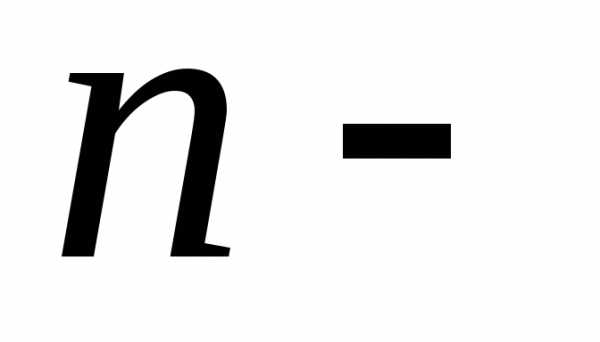 гармоники.
гармоники.
Пример 31. Разложить в ряд Фурье функцию f(x), заданную на промежутке длиной, равной периоду

Изобразить диаграмму спектра амплитуд.
Решение.
Рис. 1. График функции
По формулам (25) находим коэффициенты ряда.

Если n — четное 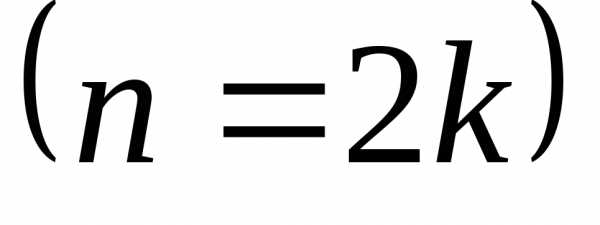 ,
, 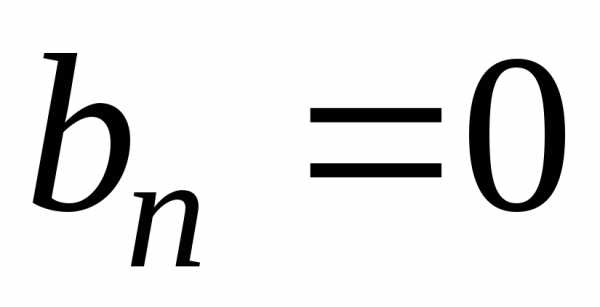 .
При нечетном n
.
При нечетном n 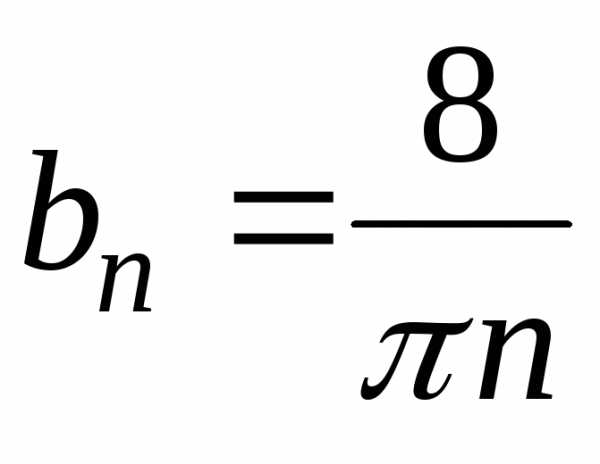 ,
.
,
.
Ряд Фурье имеет вид
Рис. 2. иллюстрирует
представления функции 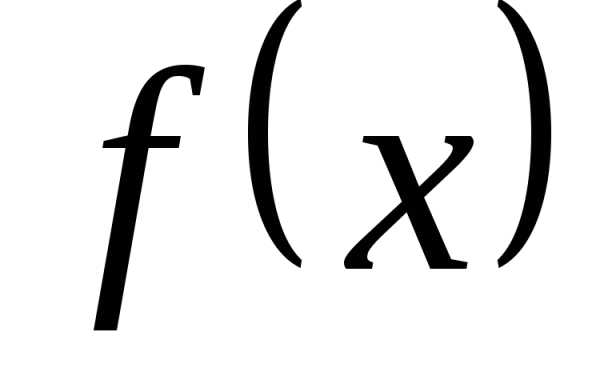 ,
описывающей периодический сигнал
прямоугольной формы, через сумму
нескольких первых членов ряда. Видно,
что с ростом
,
описывающей периодический сигнал
прямоугольной формы, через сумму
нескольких первых членов ряда. Видно,
что с ростом 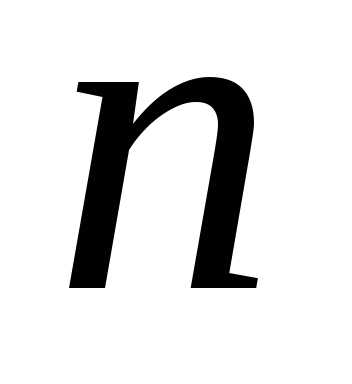 частичные суммы все точнее представляют
частичные суммы все точнее представляют  .
.
а)
б)
в)
Рис. 2. Графики суммы двух(а), трех (б) и пяти(в) членов ряда
График суммы ряда 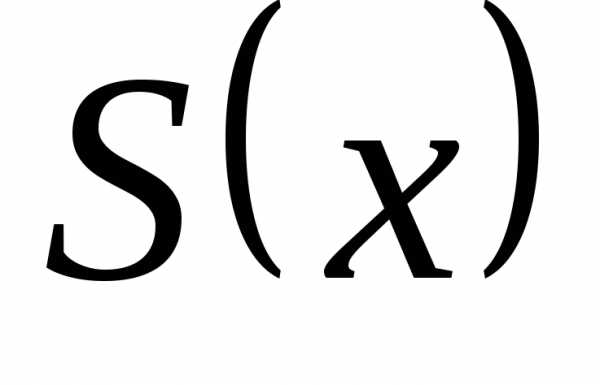
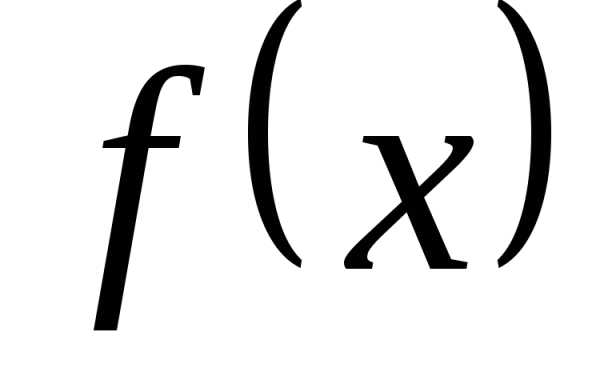 (рис. 1), а в точках разрыва
(рис. 1), а в точках разрыва 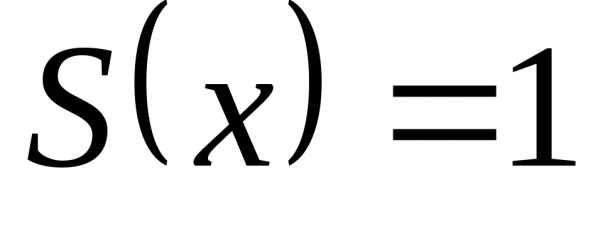 (см. теорему Дирихле). Так как
(см. теорему Дирихле). Так как 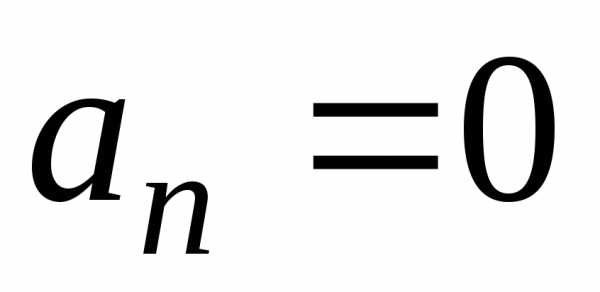 ,
то
,
то 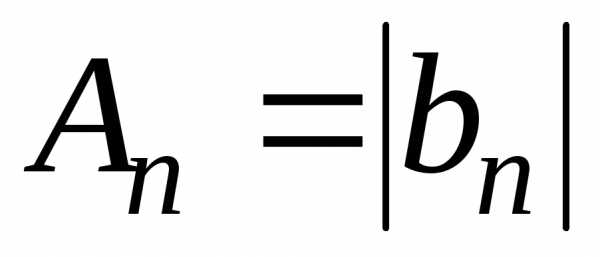 .
. 
1 2 3 4 5 6 
Рис.3. Спектр амплитуд
Пример 32. Разложить функцию f(x) в ряд Фурье по косинусам, продолжив в симметричный интервал. Нарисовать график суммы ряда S(x). Найти значения суммы

Решение. Продолжив
функцию на интервале (-1,0) четным образом,
и далее с периодом 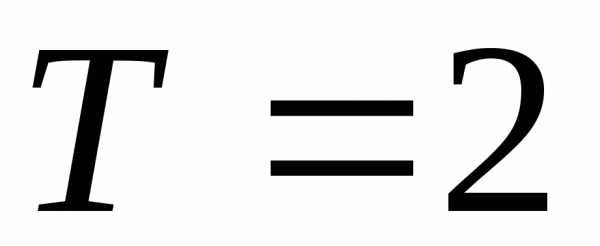
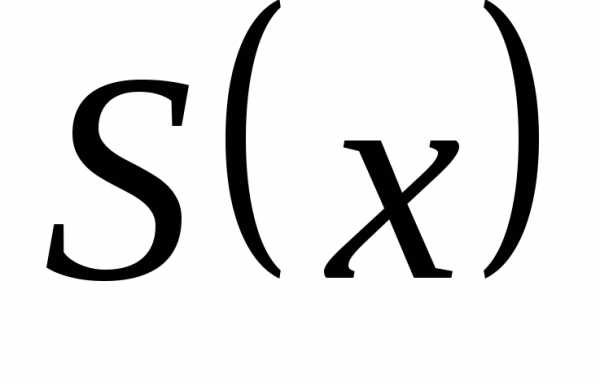 .
. 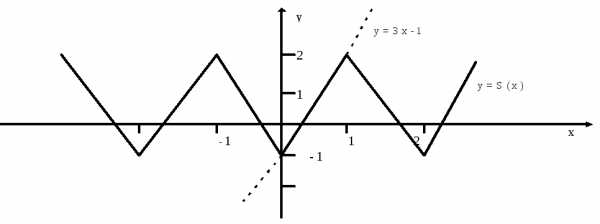
Рис. 4. Графики
функций и 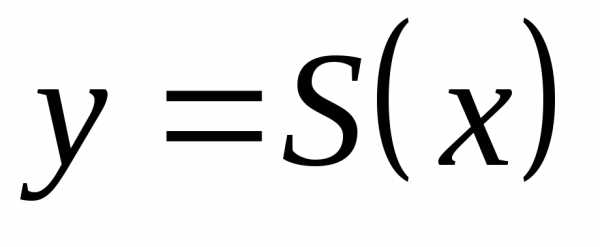
Определим
коэффициенты Фурье  и
и 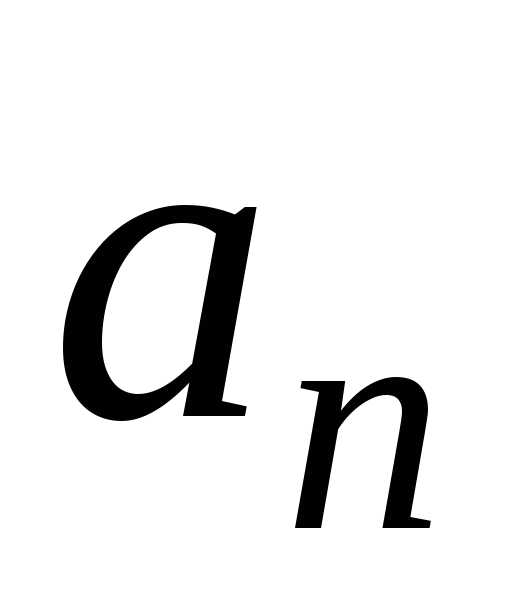 .
.
.
Вычислим
эти интегралы отдельно, используя для
первого интеграла формулу интегрирования
по частям 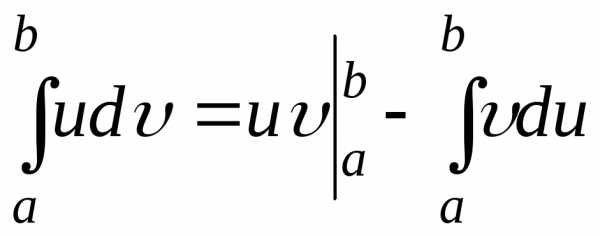 .
.
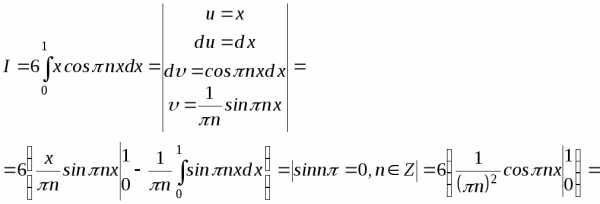
.
Получаем ряд Фурье:
Найдем значение
суммы в точках .
На отрезке 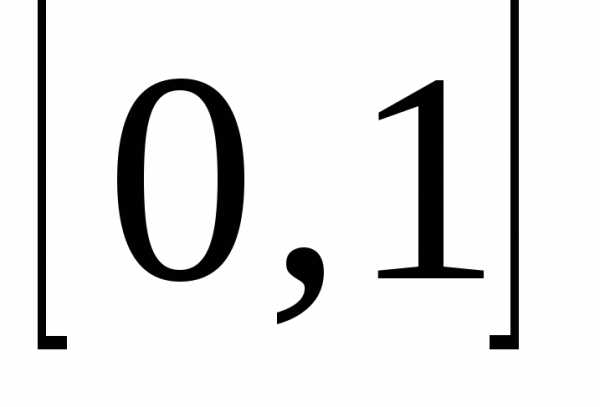
.
.
Для вычисления 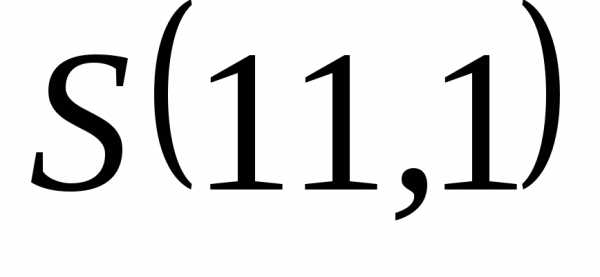
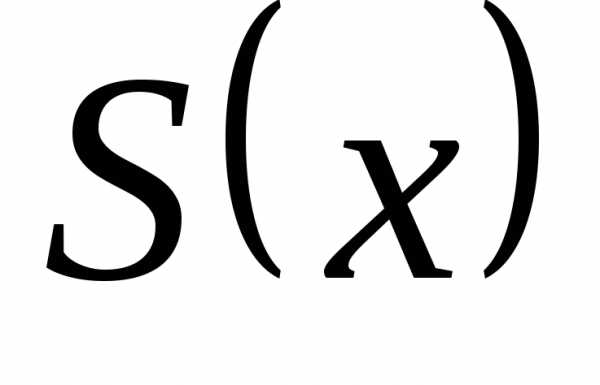 .
..
studfiles.net
Ряды фурье
Напомним некоторые сведения из предыдущих разделов математики.
Функция называется кусочно-монотонной
на отрезке 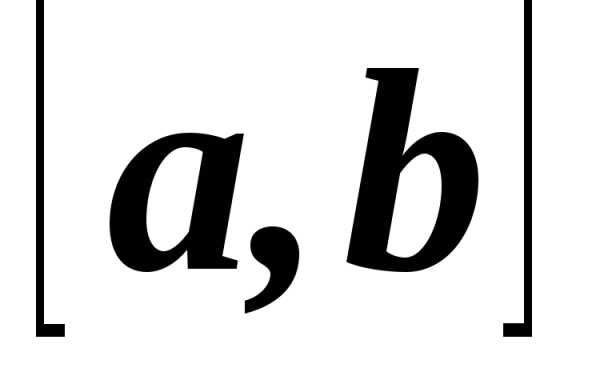 ,
если этот отрезок можно разбить на
конечное число интервалов таким образом,
чтобы в каждом из них функция была
монотонной, т.е. либо не возрастающей,
либо не убывающей.
,
если этот отрезок можно разбить на
конечное число интервалов таким образом,
чтобы в каждом из них функция была
монотонной, т.е. либо не возрастающей,
либо не убывающей.
Функция 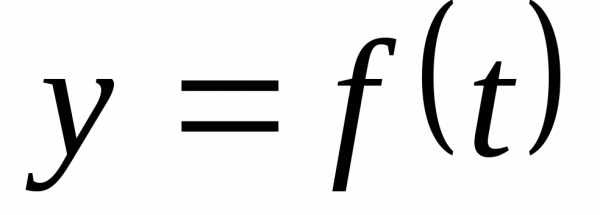 называется периодической с периодом ,
если для любого значения аргумента из
области определения функции имеет место
равенство
называется периодической с периодом ,
если для любого значения аргумента из
области определения функции имеет место
равенство
.
Для таких функций
результат интегрирования в пределах,
отличающихся на 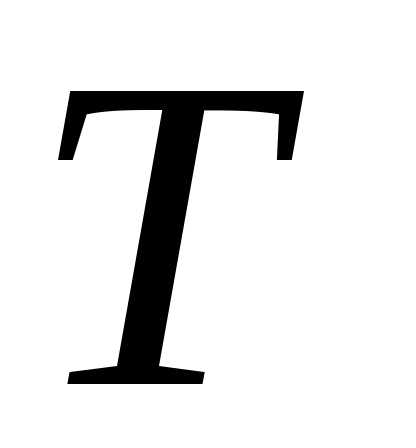 ,
не зависит от выбора нижнего предела
интегрирования, т.е. для любого
,
не зависит от выбора нижнего предела
интегрирования, т.е. для любого 
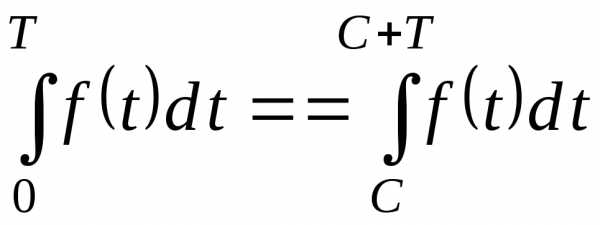 (23)
(23)
Функция ,
описывающая гармоническое колебание,
имеет период  .
.
Функции будем называть гармониками. Их можно представить также в виде
,
где ; .
Сумма гармоник 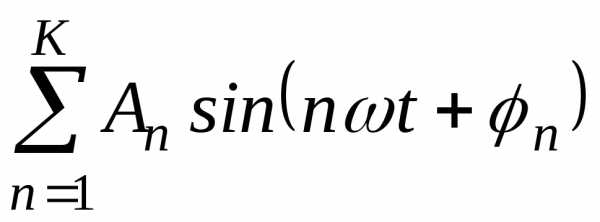 ,
являясь периодической, уже не будет
гармоникой. Можно поставить обратную
задачу. Можно ли периодическую функцию
,
являясь периодической, уже не будет
гармоникой. Можно поставить обратную
задачу. Можно ли периодическую функцию 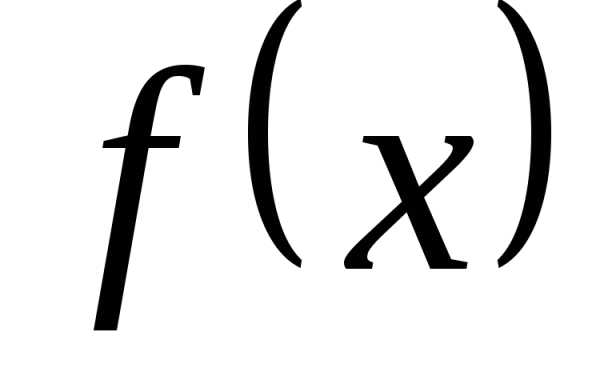 представить в виде такой суммы?. Оказалось,
что при определенных условиях,
сформулированных в теореме Дирихле
(см. ниже), периодическую функцию с
периодом
представить в виде такой суммы?. Оказалось,
что при определенных условиях,
сформулированных в теореме Дирихле
(см. ниже), периодическую функцию с
периодом 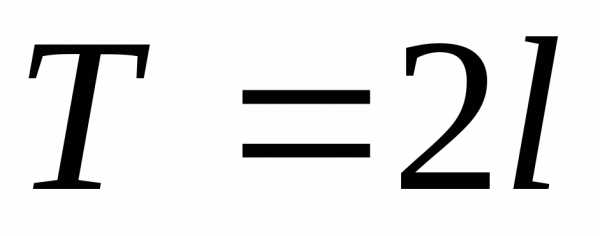
. (24)
Если коэффициенты ряда (24) определяются по формулам
 ,
,
, (25)
,
то их называют коэффициентами Фурье, а сам ряд рядом Фурье.
Говорят, что
функция удовлетворяет условиям
Дирихле,
если она непрерывна на отрезке 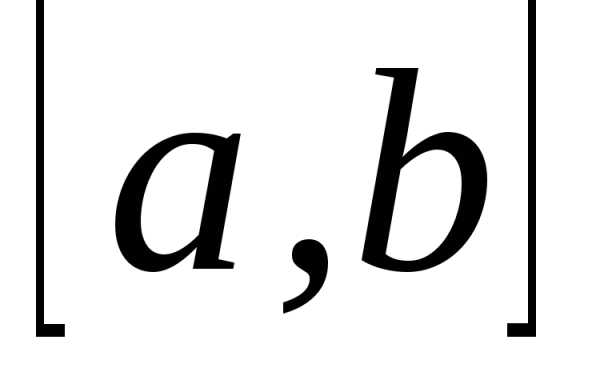 за исключением, быть может, конечного
числа точек разрыва первого рода, а
также кусочно-монотонна на этом отрезке.
за исключением, быть может, конечного
числа точек разрыва первого рода, а
также кусочно-монотонна на этом отрезке.
ТЕОРЕМА 12.(Теорема Дирихле)
Если периодическая
функция 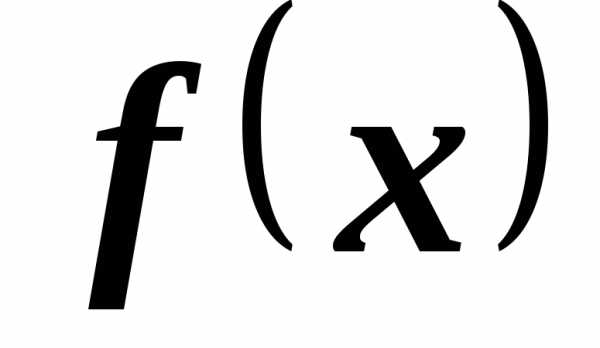 с периодом
с периодом  удовлетворяет на отрезке
удовлетворяет на отрезке 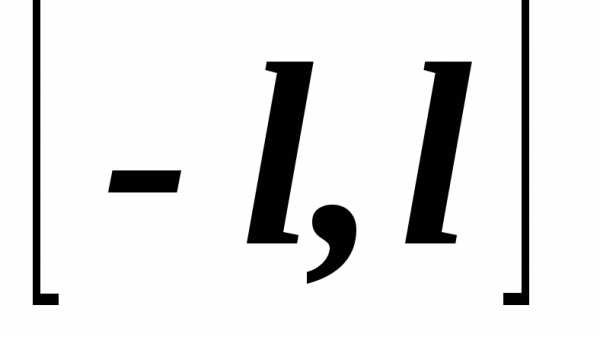 условиям Дирихле, то ряд Фурье этой
функции сходится во всем отрезке
условиям Дирихле, то ряд Фурье этой
функции сходится во всем отрезке  и сумма этого ряда
и сумма этого ряда 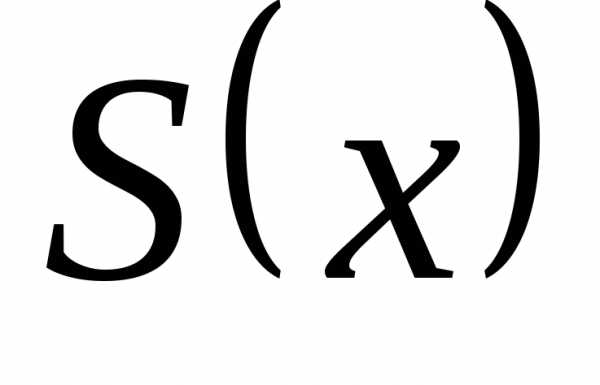 равна:
равна:
1) Во всех точках непрерывности функции ;
2) Полусумме пределов функции слева и справа, т.Е., если является точкой разрыва первого рода, то .
.
Из теорем (11) и (12) следует, что класс функций представляемых в виде ряда Фурье шире класса функций, разлагаемых в ряд Тейлора, так как для последнего необходимо существование производных функций любого порядка.
В ряде практических
задач электросвязи рассматриваются
периодические функции с  .
Тогда
.
Тогда  и формулы 24-25 упрощаются
и формулы 24-25 упрощаются
(26)
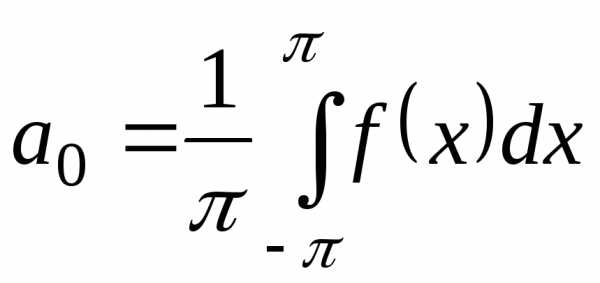 ,
,
, (27)
.
Замечания:
Учитывая формулу (23), при нахождении коэффициентов Фурье целесообразно в качестве пределов интегрирования использовать границы области задания функции. Например, если
 —
периодическая функция задана на отрезке
—
периодическая функция задана на отрезке  ,
в формулах (27) следует интегрировать
от нуля до
,
в формулах (27) следует интегрировать
от нуля до  .
.
Если функция
 четная,
то коэффициенты
четная,
то коэффициенты  =0,
а остальные коэффициенты можно найти
по формулам
=0,
а остальные коэффициенты можно найти
по формулам
 , . (28)
, . (28)
Если же
функция нечетная,
то 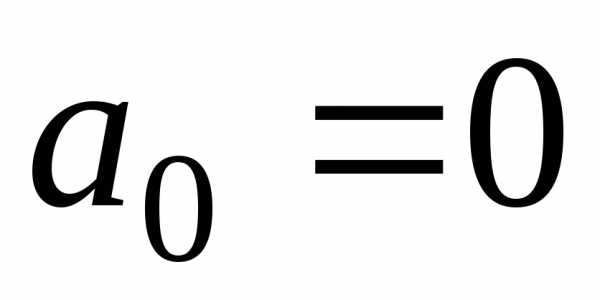 и
и 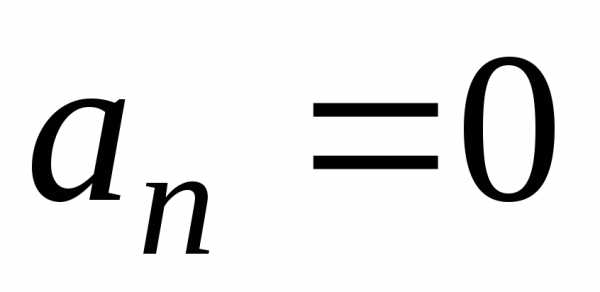 ,
а
,
а
. (29)
Ряд Фурье можно представить в амплитудно — фазовой форме. Пусть
, ,
Тогда , 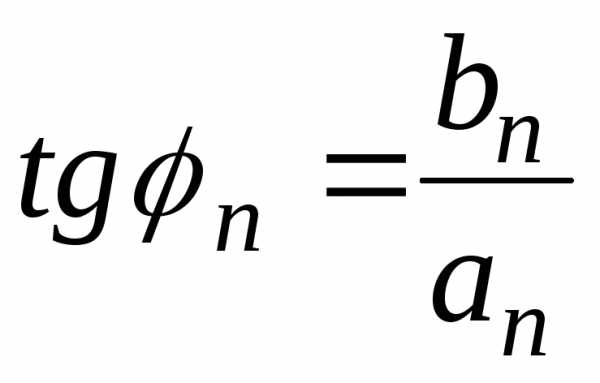 ,
, 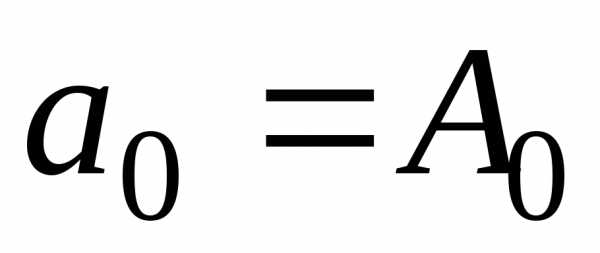 .
.
, (30)
где 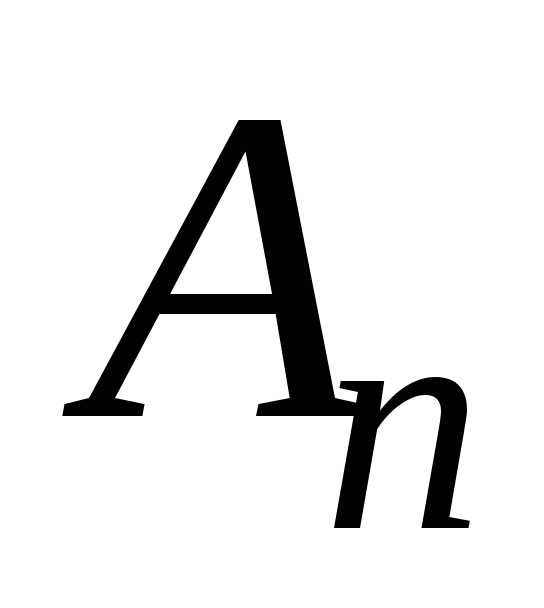 — амплитуда, а
— амплитуда, а 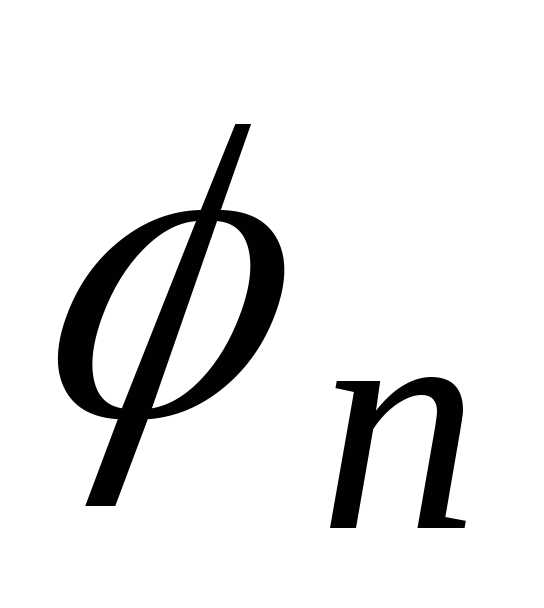 — начальная фаза
— начальная фаза  гармоники.
гармоники.
Пример 31. Разложить в ряд Фурье функцию f(x), заданную на промежутке длиной, равной периоду

Изобразить диаграмму спектра амплитуд.
Решение.
Рис. 1. График функции
По формулам (25) находим коэффициенты ряда.
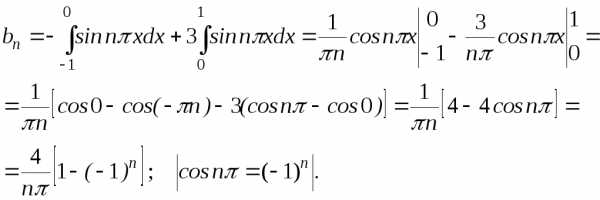
Если n — четное 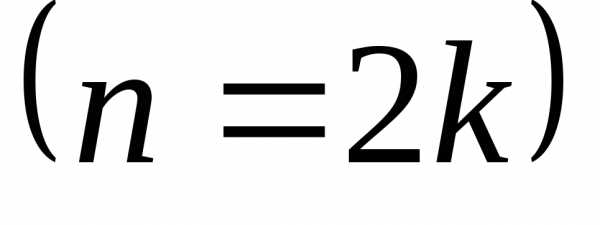 ,
, 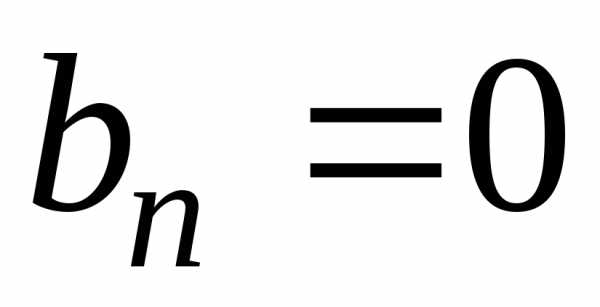 .
При нечетном n
.
При нечетном n 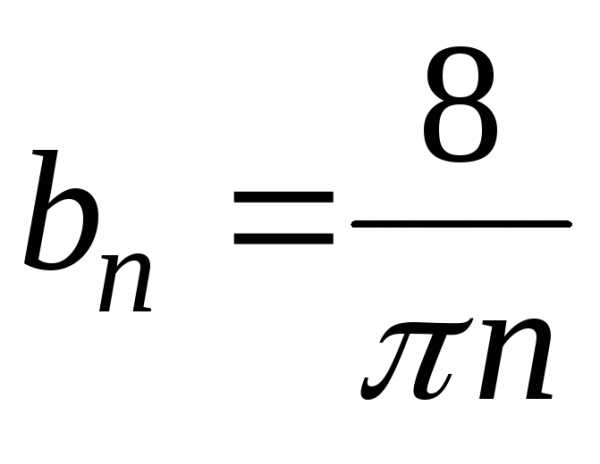 ,
.
,
.
Ряд Фурье имеет вид
Рис. 2. иллюстрирует
представления функции 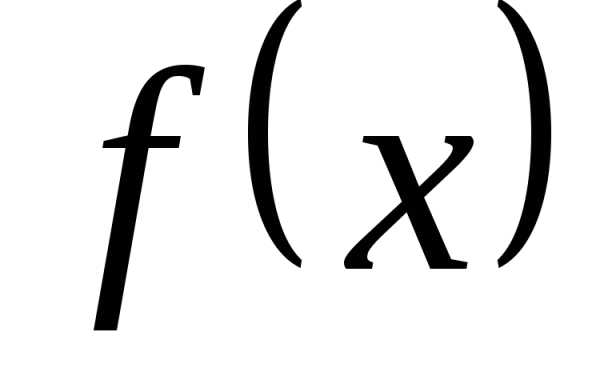 ,
описывающей периодический сигнал
прямоугольной формы, через сумму
нескольких первых членов ряда. Видно,
что с ростом
,
описывающей периодический сигнал
прямоугольной формы, через сумму
нескольких первых членов ряда. Видно,
что с ростом 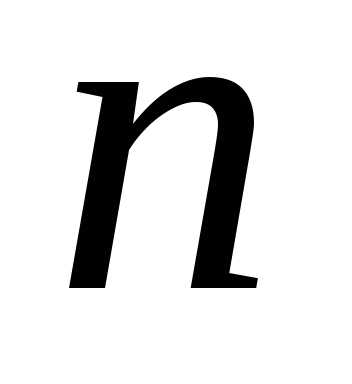 частичные суммы все точнее представляют
частичные суммы все точнее представляют 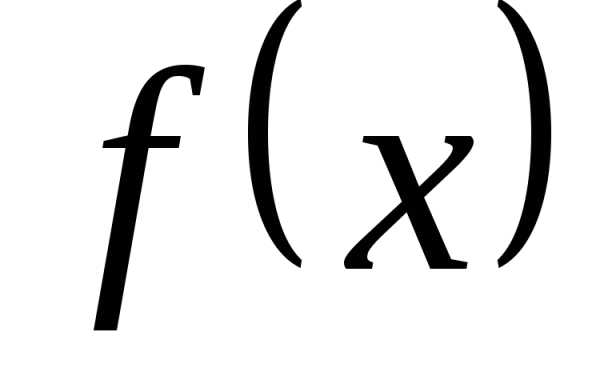 .
.
а)
б)
в)
Рис. 2. Графики суммы двух(а), трех (б) и пяти(в) членов ряда
График суммы ряда 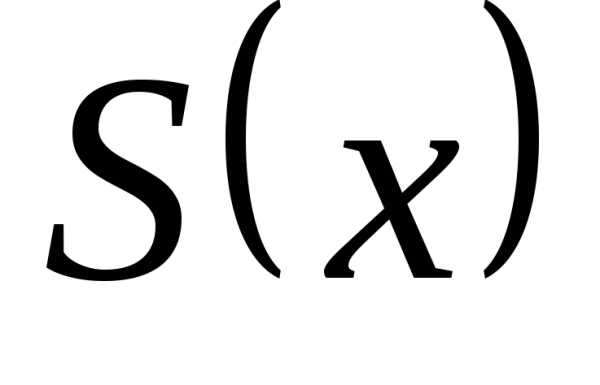 в точках непрерывности функции совпадает
с графиком
в точках непрерывности функции совпадает
с графиком 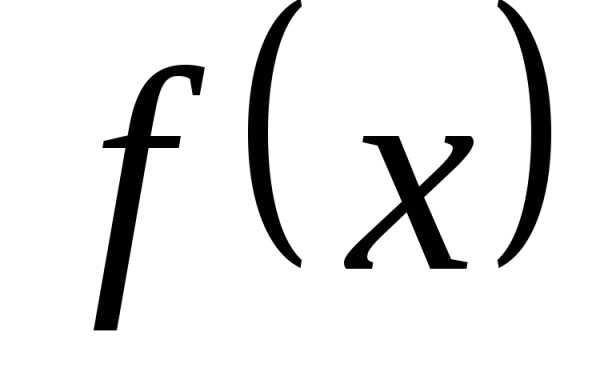 (рис. 1), а в точках разрыва
(рис. 1), а в точках разрыва 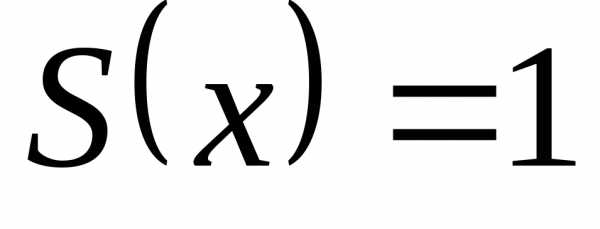 (см. теорему Дирихле). Так как
(см. теорему Дирихле). Так как 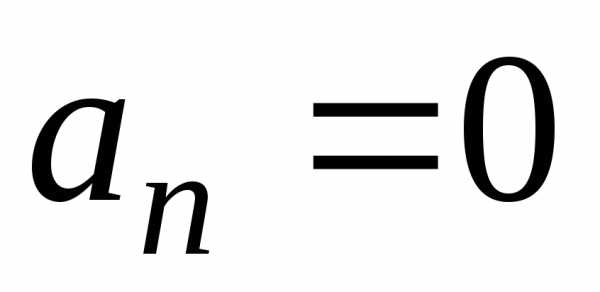 ,
то
,
то 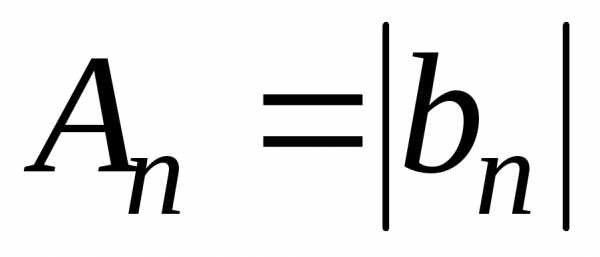 .
.
1 2 3 4 5 6 
Рис.3. Спектр амплитуд
Пример 32. Разложить функцию f(x) в ряд Фурье по косинусам, продолжив в симметричный интервал. Нарисовать график суммы ряда S(x). Найти значения суммы

Решение. Продолжив
функцию на интервале (-1,0) четным образом,
и далее с периодом  ,
получим сумму ряда
,
получим сумму ряда 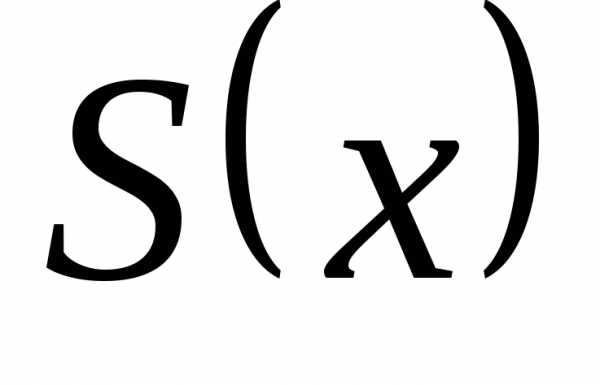 .
.
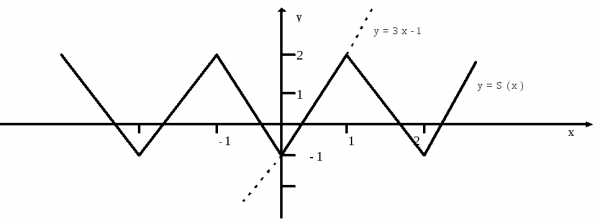
Рис. 4. Графики
функций и 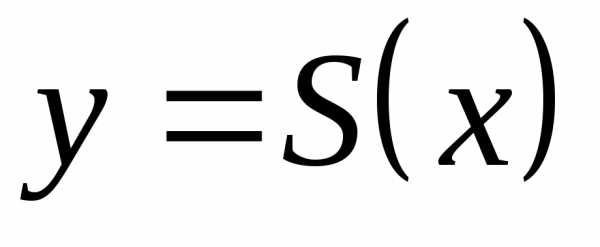
Определим
коэффициенты Фурье  и
и 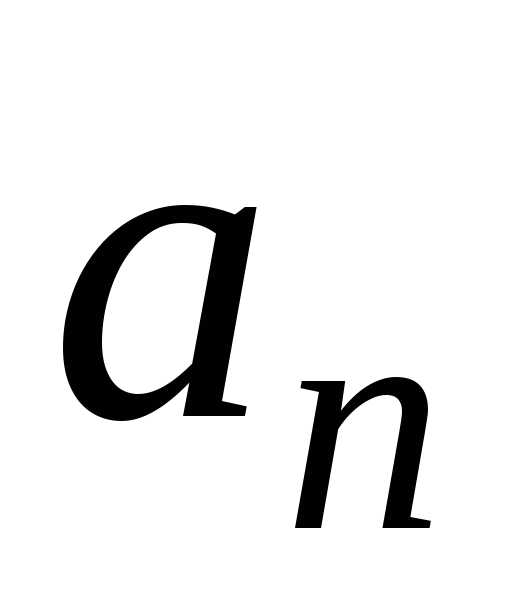 .
.
.
Вычислим
эти интегралы отдельно, используя для
первого интеграла формулу интегрирования
по частям 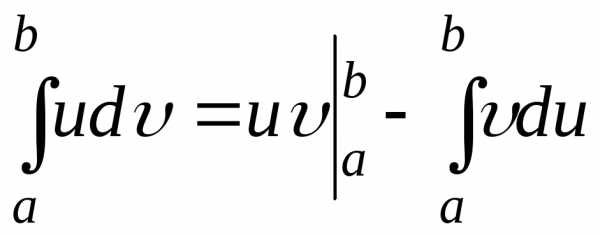 .
.

.
Получаем ряд Фурье:
Найдем значение
суммы в точках .
На отрезке 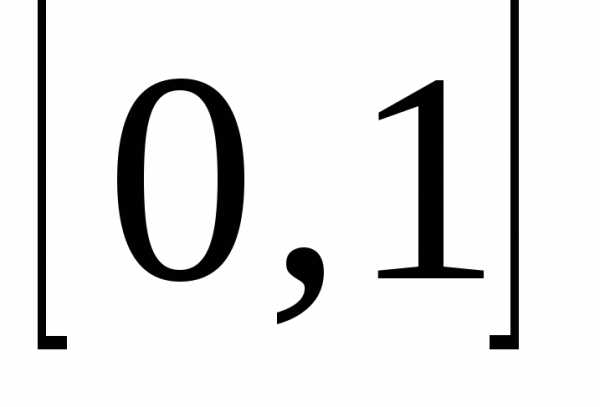
.
.
Для вычисления 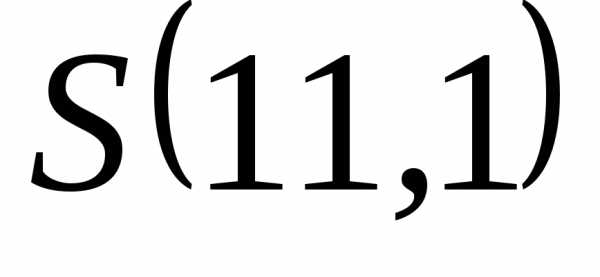 используем свойства четности и
периодичности
используем свойства четности и
периодичности 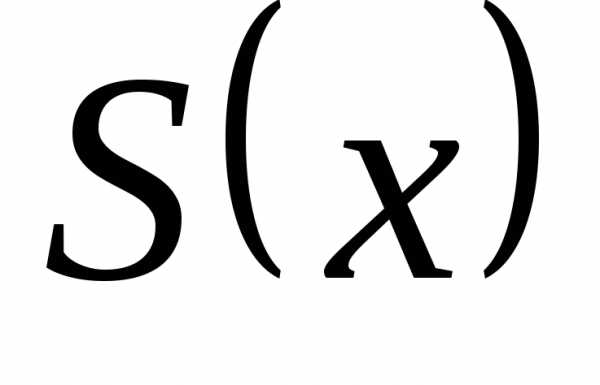 .
.
.
studfiles.net
3. Ряды Фурье
3.1. Периодические функции
Многие процессы, происходящие в природе и технике, обладают свойством повторяться через определенные промежутки времени. Такие процессы называются периодическими и математически описываются периодическими функциями. К таким функциям относятся sin(x), cos(x), sin(wx), cos(wx). Сумма двух периодических функций, например, функция вида , вообще говоря, уже не является периодической. Но можно доказать, что если отношение w1/w2– число рациональное, то эта сумма есть периодическая функция.
Простейшие периодические процессы – гармонические колебания – описываются периодическими функциями sin(wx) и cos(wx). Более сложные периодические процессы описываются функциями, составными либо из конечного, либо из бесконечного числа слагаемых вида sin(wx) и cos(wx).
3.2. Тригонометрический ряд. Коэффициенты Фурье
Рассмотрим функциональный ряд вида:
. (1)
Этот ряд называется тригонометрическим; числа а0,b0,a1,b1,а2,b2…,an,bn,… называются коэффициентами тригонометрического ряда. Ряд (1) часто записывается следующим образом:
. (2)
Так как члены
тригонометрического ряда (2) имеют общий
период 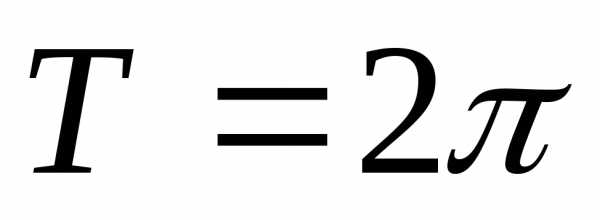 ,
то и сумма ряда, если он сходится, также
является периодической функцией с
периодом
,
то и сумма ряда, если он сходится, также
является периодической функцией с
периодом .
.
Допустим, что функция f(x) есть сумма этого ряда:
. (3)
В таком случае
говорят, что функция f(x) раскладывается в тригонометрический
ряд. Предполагая, что этот ряд сходится
равномерно на промежутке 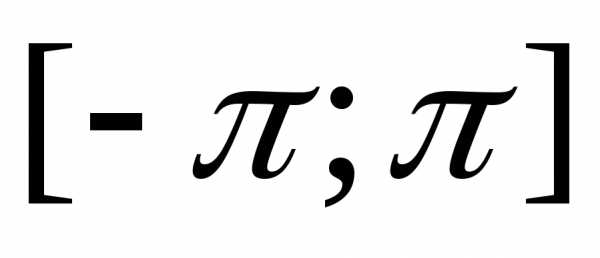 ,
можно определить его коэффициенты по
формулам:
,
можно определить его коэффициенты по
формулам:
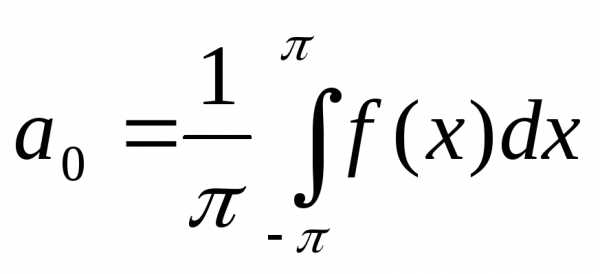 , ,.
(4)
, ,.
(4)
Коэффициенты ряда, определенные по этим формулам, называются коэффициентами Фурье.
Тригонометрический ряд (2), коэффициенты которого определяются по формулам Фурье (4), называются рядом Фурье, соответствующим функции f(x).
Таким образом, если периодическая функция f(x) является суммой сходящегося тригонометрического ряда, то этот ряд является ее рядом Фурье.
3.3. Сходимость ряда Фурье
Формулы (4) показывают,
что коэффициенты Фурье могут быть
вычислены для любой интегрируемой на
промежутке 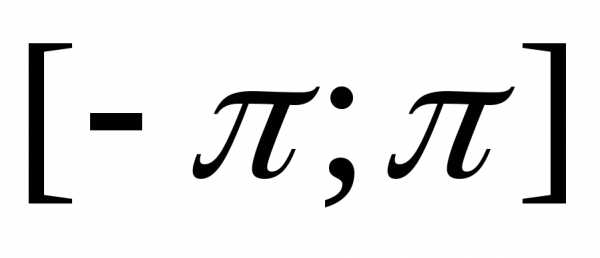
 -периодической
функции, т.е. для такой функции всегда
можно составить ряд Фурье. Но будет ли
этот ряд сходиться к функцииf(x) и при каких условиях?
-периодической
функции, т.е. для такой функции всегда
можно составить ряд Фурье. Но будет ли
этот ряд сходиться к функцииf(x) и при каких условиях?
Напомним, что функция f(x), определенная на отрезке [a;b], называется кусочно-гладкой, если она и ее производная имеют не более конечного числа точек разрыва первого рода.
Следующая теорема дает достаточные условия разложимости функции в ряд Фурье.
Теорема Дирихле. Пусть  -периодическая
функцияf(x) является кусочно-гладкой на
-периодическая
функцияf(x) является кусочно-гладкой на 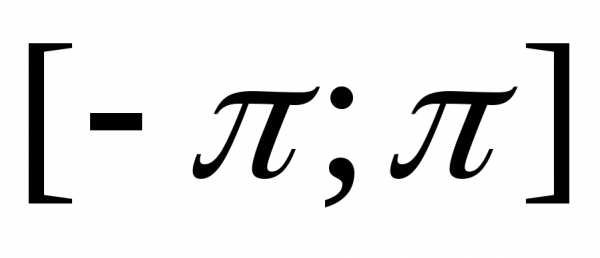 .
Тогда ее ряд Фурье сходится кf(x) в каждой ее точке непрерывности и к
значению 0,5(f(x+0)+f(x-0)) в точке
разрыва.
.
Тогда ее ряд Фурье сходится кf(x) в каждой ее точке непрерывности и к
значению 0,5(f(x+0)+f(x-0)) в точке
разрыва.
Пример1.
Разложить в ряд
Фурье функцию f(x)=x,
заданную на интервале  .
.
Решение. Эта функция удовлетворяет условиям Дирихле и, следовательно, может быть разложена в ряд Фурье. Применяя формулы (4) и метод интегрирования по частям , найдем коэффициенты Фурье:
Т.к. .
Таким образом, ряд Фурье для функции f(x) имеет вид:
.
studfiles.net
история и влияние математического механизма на развитие науки
Ряды Фурье – это представление произвольно взятой функции с конкретным периодом в виде ряда. В общем виде данное решение называют разложением элемента по ортогональному базису. Разложение функций в ряд Фурье является довольно мощным инструментарием при решении разнообразных задач благодаря свойствам данного преобразования при интегрировании, дифференцировании, а также сдвиге выражения по аргументу и свертке.
Человек, не знакомый с высшей математикой, а также с трудами французского ученого Фурье, скорее всего, не поймет, что это за «ряды» и для чего они нужны. А между тем данное преобразование довольно плотно вошло в нашу жизнь. Им пользуются не только математики, но и физики, химики, медики, астрономы, сейсмологи, океанографы и многие другие. Давайте и мы поближе познакомимся с трудами великого французского ученого, сделавшего открытие, опередившее свое время.
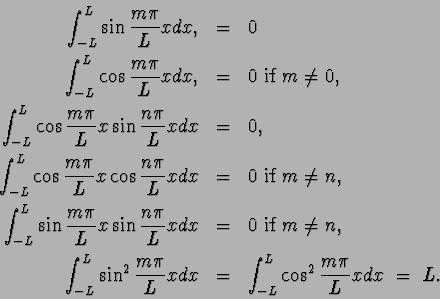
Человек и преобразование Фурье
Ряды Фурье являются одним из методов (наряду с анализом и другими) преобразования Фурье. Данный процесс происходит каждый раз, когда человек слышит какой-либо звук. Наше ухо в автоматическом режиме производит преобразование звуковой волны. Колебательные движения элементарных частиц в упругой среде раскладываются в ряды (по спектру) последовательных значений уровня громкости для тонов разной высоты. Далее мозг превращает эти данные в привычные для нас звуки. Все это происходит помимо нашего желания или сознания, само по себе, а вот для того чтобы понять эти процессы, понадобится несколько лет изучать высшую математику.
Подробнее о преобразовании Фурье
Преобразование Фурье можно проводить аналитическими, числительными и другими методами. Ряды Фурье относятся к числительному способу разложения любых колебательных процессов – от океанских приливов и световых волн до циклов солнечной (и других астрономических объектов) активности. Используя эти математические приемы, можно разбирать функции, представляя любые колебательные процессы в качестве ряда синусоидальных составляющих, которые переходят от минимума к максимуму и обратно. Преобразование Фурье является функцией, описывающей фазу и амплитуду синусоид, соответствующих определенной частоте. Данный процесс можно использовать для решения весьма сложных уравнений, которые описывают динамические процессы, возникающие под действием тепловой, световой или электрической энергии. Также ряды Фурье позволяют выделять постоянные составляющие в сложных колебательных сигналах, благодаря чему стало возможным правильно интерпретировать полученные экспериментальные наблюдения в медицине, химии и астрономии.

Историческая справка
Отцом-основателем этой теории является французский математик Жан Батист Жозеф Фурье. Его именем впоследствии и было названо данное преобразование. Изначально ученый применил свой метод для изучения и объяснения механизмов теплопроводности – распространения тепла в твердых телах. Фурье предположил, что изначальное нерегулярное распределение тепловой волны можно разложить на простейшие синусоиды, каждая из которых будет иметь свой температурный минимум и максимум, а также свою фазу. При этом каждая такая компонента будет измеряться от минимума к максимуму и обратно. Математическая функция, которая описывает верхние и нижние пики кривой, а также фазу каждой из гармоник, назвали преобразованием Фурье от выражения распределения температуры. Автор теории свел общую функцию распределения, которая трудно поддается математическому описанию, к весьма удобному в обращении ряду периодических функций косинуса и синуса, в сумме дающих исходное распределение.
Принцип преобразования и взгляды современников
Современники ученого — ведущие математики начала девятнадцатого века — не приняли данную теорию. Основным возражением послужило утверждение Фурье о том, что разрывную функцию, описывающую прямую линию или разрывающуюся кривую, можно представить в виде суммы синусоидальных выражений, которые являются непрерывными. В качестве примера можно рассмотреть «ступеньку» Хевисайда: ее значение равно нулю слева от разрыва и единице справа. Данная функция описывает зависимость электрического тока от временной переменной при замыкании цепи. Современники теории на тот момент никогда не сталкивались с подобной ситуацией, когда разрывное выражение описывалось бы комбинацией непрерывных, обычных функций, таких как экспонента, синусоида, линейная или квадратичная.
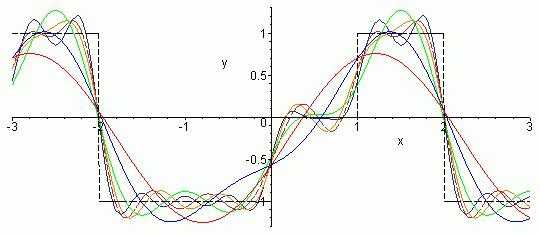
Что смущало французских математиков в теории Фурье?
Ведь если математик был в прав в своих утверждениях, то, суммируя бесконечный тригонометрический ряд Фурье, можно получить точное представление ступенчатого выражения даже в том случае, если оно имеет множество подобных ступеней. В начале девятнадцатого века подобное утверждение казалось абсурдным. Но несмотря на все сомнения, многие математики расширили сферу изучения данного феномена, выведя его за пределы исследований теплопроводности. Однако большинство ученых продолжали мучиться вопросом: «Может ли сумма синусоидального ряда сходиться к точному значению разрывной функции?»
Сходимость рядов Фурье: пример
Вопрос о сходимости поднимается всякий раз при необходимости суммирования бесконечных рядов чисел. Для понимания данного феномена рассмотрим классический пример. Сможете ли вы когда-либо достигнуть стены, если каждый последующий шаг будет вдвое меньше предыдущего? Предположим, что вы находитесь в двух метрах от цели, первый же шаг приближает к отметке на половине пути, следующий – к отметке в три четверти, а после пятого вы преодолеете почти 97 процентов пути. Однако сколько бы вы шагов ни сделали, намеченной цели вы не достигните в строгом математическом смысле. Используя числовые расчеты, можно доказать, что в конце концов можно приблизиться на сколь угодно малое заданное расстояние. Данное доказательство является эквивалентным демонстрации того, что суммарное значение одной второй, одной четвертой и т. д. будет стремиться к единице.
Вопрос сходимости: второе пришествие, или Прибор лорда Кельвина
Повторно данный вопрос поднялся в конце девятнадцатого века, когда ряды Фурье попробовали применить для предсказания интенсивности отливов и приливов. В это время лордом Кельвином был изобретен прибор, представляющий собой аналоговое вычислительное устройство, которое позволяло морякам военного и торгового флота отслеживать это природное явление. Данный механизм определял наборы фаз и амплитуд по таблице высоты приливов и соответствующих им временных моментов, тщательно замеренных в данной гавани в течение года. Каждый параметр представлял собой синусоидальную компоненту выражения высоты прилива и являлся одной из регулярных составляющих. Результаты измерений вводились в вычислительный прибор лорда Кельвина, синтезирующий кривую, которая предсказывала высоту воды как временную функцию на следующий год. Очень скоро подобные кривые были составлены для всех гаваней мира.
А если процесс будет нарушен разрывной функцией?
В то время представлялось очевидным, что прибор, предсказывающий приливную волну, с большим количеством элементов счета может вычислить большое количество фаз и амплитуд и так обеспечить более точные предсказания. Тем не менее оказалось, что данная закономерность не соблюдается в тех случаях, когда приливное выражение, которое следует синтезировать, содержало резкий скачок, то есть являлось разрывным. В том случае, если в устройство вводятся данные из таблицы временных моментов, то оно производит вычисления нескольких коэффициентов Фурье. Исходная функция восстанавливается благодаря синусоидальным компонентам (в соответствии с найденными коэффициентами). Расхождение между исходным и восстановленным выражением можно измерять в любой точке. При проведении повторных вычислений и сравнений видно, что значение наибольшей ошибки не уменьшается. Однако они локализируются в области, соответствующей точке разрыва, а в любой иной точке стремятся к нулю. В 1899 году этот результат был теоретически подтвержден Джошуа Уиллардом Гиббсом из Йельского университета.

Сходимость рядов Фурье и развитие математики в целом
Анализ Фурье неприменим к выражениям, содержащим бесконечное количество всплесков на определенном интервале. В общем и целом ряды Фурье, если изначальная функция представлена результатом реального физического измерения, всегда сходятся. Вопросы сходимости данного процесса для конкретных классов функций привели к появлению новых разделов в математике, например теории обобщенных функций. Она связана с такими именами, как Л. Шварц, Дж. Микусинский и Дж. Темпл. В рамках данной теории была создана четкая и точная теоретическая основа под такие выражения, как дельта-функция Дирака (она описывает область единой площади, сконцентрированной в бесконечно малой окрестности точки) и «ступень» Хевисайда. Благодаря этой работе ряды Фурье стали применимы для решения уравнений и задач, в которых фигурируют интуитивные понятия: точечный заряд, точечная масса, магнитные диполи, а также сосредоточенная нагрузка на балке.
Метод Фурье
Ряды Фурье, в соответствии с принципами интерференции, начинаются с разложения сложных форм на более простые. Например, изменение теплового потока объясняется его прохождением сквозь различные препятствия из теплоизолирующего материала неправильной формы или изменением поверхности земли – землетрясением, изменением орбиты небесного тела – влиянием планет. Как правило, подобные уравнения, описывающие простые классические системы, элементарно решаются для каждой отдельной волны. Фурье показал, что простые решения также можно суммировать для получения решения более сложных задач. Выражаясь языком математики, ряды Фурье – это методика представления выражения суммой гармоник – косинусоид и синусоид. Поэтому данный анализ известен также под именем «гармонический анализ».
Ряд Фурье – идеальная методика до «компьютерной эпохи»
До создания компьютерной техники методика Фурье являлась лучшим оружием в арсенале ученых при работе с волновой природой нашего мира. Ряд Фурье в комплексной форме позволяет решать не только простые задачи, которые поддаются прямому применению законов механики Ньютона, но и фундаментальные уравнения. Большинство открытий ньютоновской науки девятнадцатого века стали возможны только благодаря методике Фурье.

Ряды Фурье сегодня
С развитием компьютеров преобразования Фурье поднялись на качественно новый уровень. Данная методика прочно закрепилась практически во всех сферах науки и техники. В качестве примера можно привести цифровой аудио- и видеосигнал. Его реализация стала возможной только благодаря теории, разработанной французским математиком в начале девятнадцатого века. Так, ряд Фурье в комплексной форме позволил совершить прорыв в изучении космического пространства. Кроме того, это повлияло на изучение физики полупроводниковых материалов и плазмы, микроволновой акустики, океанографии, радиолокации, сейсмологии.
Тригонометрический ряд Фурье
В математике ряд Фурье является способом представления произвольных сложных функций суммой более простых. В общих случаях количество таких выражений может быть бесконечным. При этом чем больше их число учитывается при расчете, тем точнее получается конечный результат. Чаще всего в качестве простейших используют тригонометрические функции косинуса или синуса. В таком случае ряды Фурье называют тригонометрическими, а решение таких выражений – разложением гармоники. Этот метод играет важную роль в математике. Прежде всего, тригонометрический ряд дает средства для изображения, а также изучения функций, он является основным аппаратом теории. Кроме того, он позволяет решать ряд задач математической физики. Наконец, данная теория способствовала развитию математического анализа, вызвала к жизни целый ряд весьма важных разделов математической науки (теорию интегралов, теорию периодических функций). Кроме того, послужила отправным пунктом для развития следующих теорий: множеств, функций действительного переменного, функционального анализа, а также положила начало гармоническому анализу.
fb.ru
1.2. Ряды Фурье для чётных и нечётных
функций с периодом T = 2π
Если функция f(x) является чётной, то есть f(–x) = f(x), то её график симметричен относительно оси ординат и
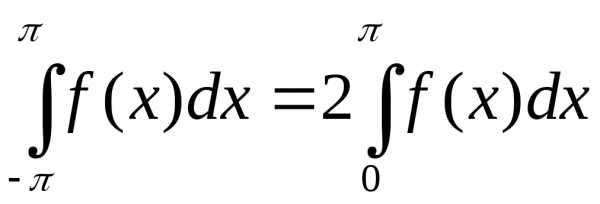 ,
,
тогда формулы (1.3) упрощаются. Действительно, подынтегральная функция является нечётной, иbn = 0 как интеграл от нечётной функции в симметричных пределах, а коэффициент an будет равен
, (1.4)
так как подынтегральная функция является чётной.
Таким образом, ряд Фурье для чётной функции, удовлетворяющей условиям Дирихле, не содержит синусов и имеет вид
, (1.5)
причëм
(1.6)
Если функция f(x) является нечётной, то есть f(–x) = –f(x), то её график симметричен относительно начала координат. Тогда a0 = 0, и так как функция является нечётной, тоan = 0 как интеграл от нечётной функции в симметричных пределах, а коэффициент bn будет
(1.7)
Поэтому ряд Фурье для нечётной функции, удовлетворяющей условиям Дирихле, содержит только синусы и имеет вид
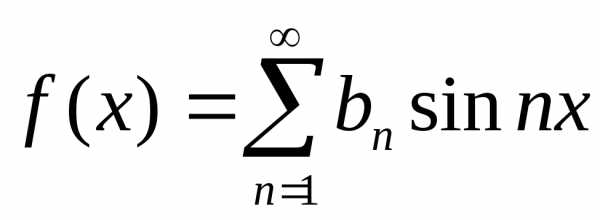 ,
(1.8)
,
(1.8)
причём
(1.9)
1.3. Ряд Фурье для функций с произвольным периодом T = 2l
Если f(x)
– периодическая функция с периодом T = 2l,
удовлетворяющая условиям Дирихле,
то, выполняя замену переменной по
формуле  ,
получим функцию переменнойt с периодом 2π.
Её можно разложить в ряд Фурье на отрезке
,
получим функцию переменнойt с периодом 2π.
Её можно разложить в ряд Фурье на отрезке 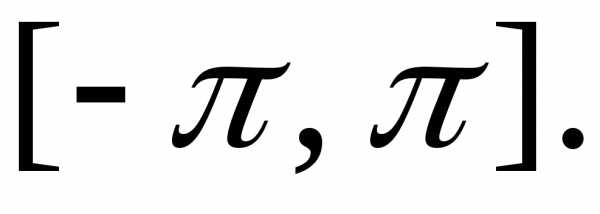 Возвращаясь далее к старой переменной,
получим разложение функцииf(x)
с произвольным периодом T = 2l в ряд Фурье вида
Возвращаясь далее к старой переменной,
получим разложение функцииf(x)
с произвольным периодом T = 2l в ряд Фурье вида
, (1.10)
где
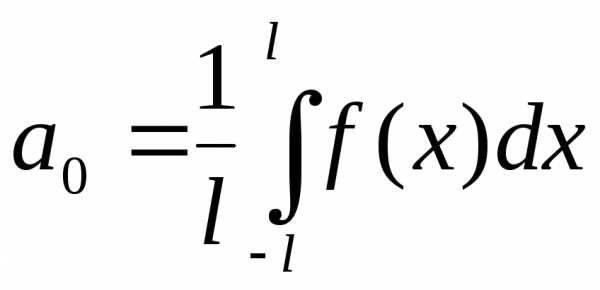 ,
,
, (1.11)
.
Аналогично (1.5–1.6) и (1.8–1.9) получим ряд Фурье для чётной функции с периодом T = 2l:
, (1.12)
(1.13)
и ряд Фурье для нечётной функции с периодом T = 2l:
(1.14)
(1.15)
1.4. Разложение в ряд Фурье непериодических функций
Пусть f(x) – непериодическая, кусочно-монотонная и ограниченная функция, заданная на конечном промежутке [–l, l]. Присоединим к графику заданной функции все его горизонтальные смещения на расстояния, кратные 2l (на рис.1.2 они показаны пунктиром). Тогда получим периодическое продолжение заданной функции на всю числовую ось. Получившаяся периодическая вспомогательная функция f*(x), определённая на всей числовой оси, в соответствии с теоремой о разложимости может быть представлена в виде ряда Фурье (1.10–1.11).
Рис.1.2.
Но для всех
,
кроме точек разрыва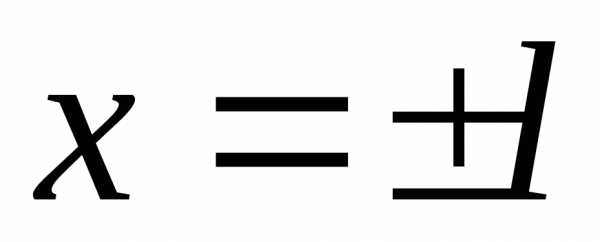 ,
значения вспомогательной функции
совпадают с заданной:f*(x)
= f(x).
Следовательно, сумма членов ряда Фурье
для вспомогательной функции во всех
точках
,
кроме точек разрыва, даст значения
заданной функции. Поэтому разложение
непериодической функции в ряд Фурье, в
действительности, осуществляется без
привлечения вспомогательной функции
непосредственно по формулам (1.10–1.11).
,
значения вспомогательной функции
совпадают с заданной:f*(x)
= f(x).
Следовательно, сумма членов ряда Фурье
для вспомогательной функции во всех
точках
,
кроме точек разрыва, даст значения
заданной функции. Поэтому разложение
непериодической функции в ряд Фурье, в
действительности, осуществляется без
привлечения вспомогательной функции
непосредственно по формулам (1.10–1.11).
Пример. Разложить в ряд Фурье функцию y = f(x), заданную на отрезке [-4,4]:

Решение. График функции представлен на рис.1.3.
Рис.1.3.
Как видно из рисунка, функция y = f(x) удовлетворяет условиям теоремы Дирихле. Ряд Фурье для этой функции на промежутке примет вид
. (1.16)
Коэффициенты ряда находим по формулам (1.11) при l = 4:
 .
(1.17)
.
(1.17)
Так как функция f(x) имеет разные выражения на трёх участках промежутка [–4, 4], то интеграл в (1.17) разбиваем на сумму трёх интегралов:
,
.
Коэффициент bn определяется аналогично:
.
Таким образом, ряд Фурье для заданной функции примет вид
.
Во всех точках непрерывности функции f(x) сумма ряда S(x) совпадает с еë значениями, а в точках разрыва она будет равна:
.
studfiles.net
3. Определение ряда Фурье.
Если Lконечномерное
евклидово пространство с базисом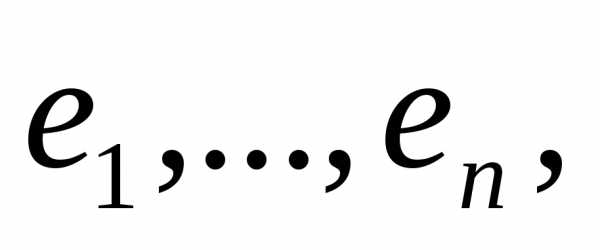 то любой элемент
то любой элемент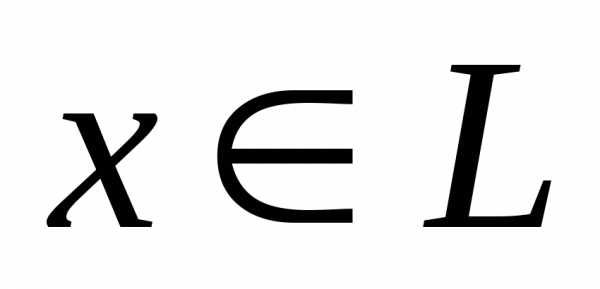 можно разложить по этому базису, то есть
можно разложить по этому базису, то есть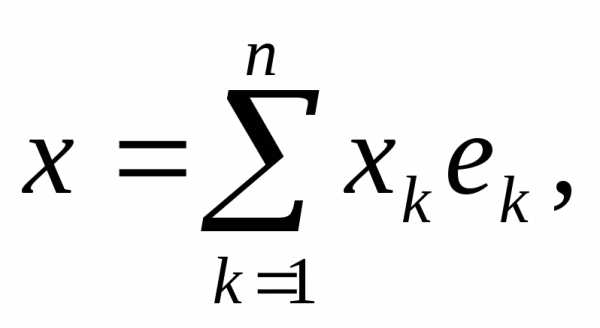 где.
где.
В случае бесконечномерного евклидова
пространства Е разложение элемента 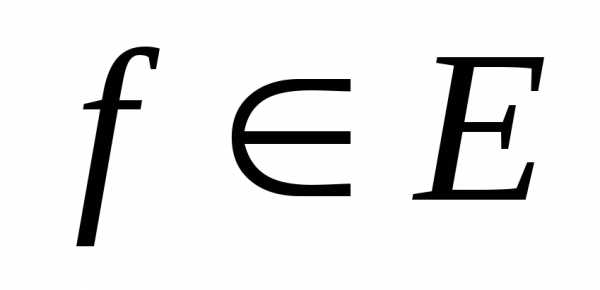 по бесконечной ортонормированной
системе называется рядом Фурье.
по бесконечной ортонормированной
системе называется рядом Фурье.
Пусть (1.2) является ортонормированной системой в евклидовом пространстве Е.
Определение 3.2. Рядом
Фурье элемента по ортонормированной системе (1.2)
называется ряд
по ортонормированной системе (1.2)
называется ряд
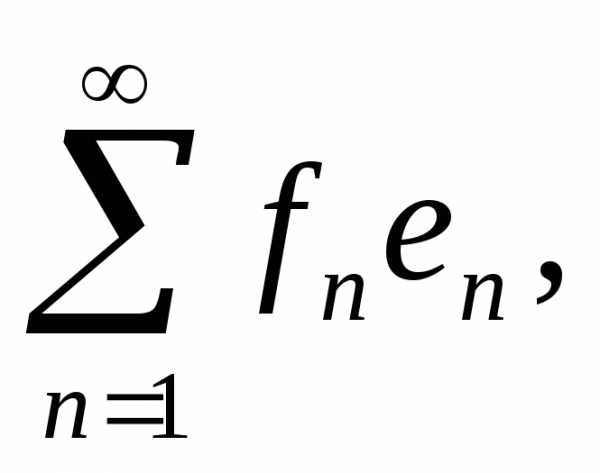 (5.2)
(5.2)
где
Числа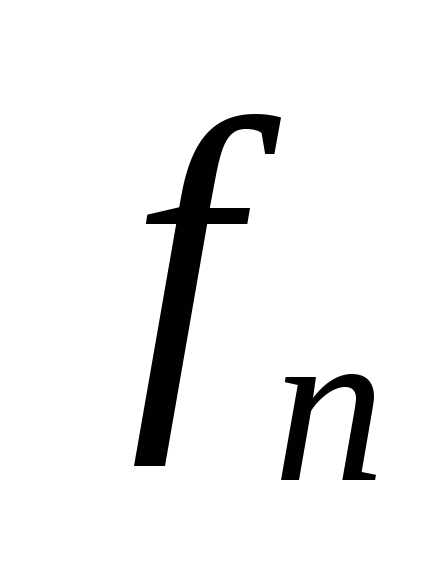 называются коэффициентами Фурье или
координатами элемента
называются коэффициентами Фурье или
координатами элемента в системе (1.2). Выражение
в системе (1.2). Выражение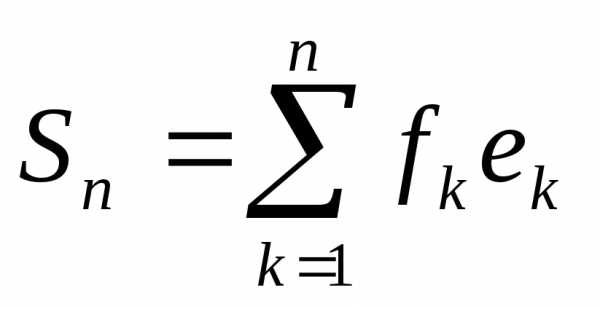 называетсяn-й частичной
(или просто частичной) суммой ряда Фурье
(5.2).
называетсяn-й частичной
(или просто частичной) суммой ряда Фурье
(5.2).
Определение 4.2. Говорят,
что ряд Фурье (5.2) сходится в среднем
(или по норме Е), если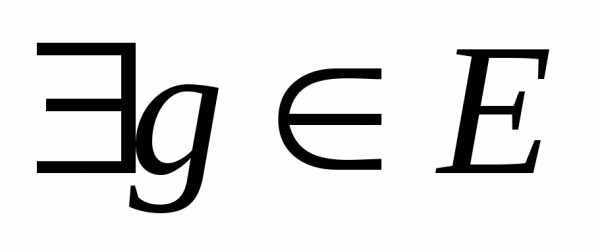 такая, что
такая, что
(6.2)
Если выполнено равенство (6.2), то будем
говорить, что ряд (5.2) сходится в среднем
к элементу 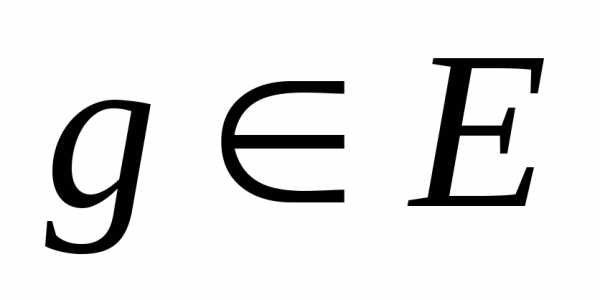 и писать
и писать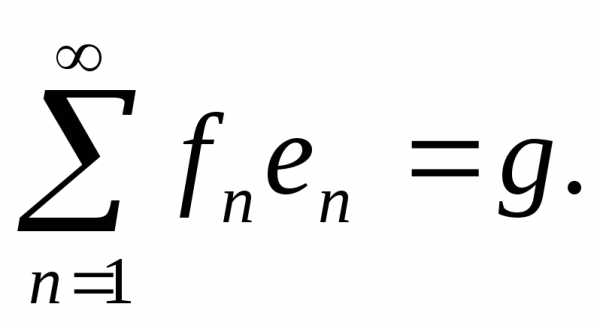
Основной целью параграфа является
изучение вопроса о том, в каких случаях
ряд Фурье элемента  сходится к
сходится к в среднем.
в среднем.
Исследуем для начала вопрос о просто сходимости ряда Фурье.
Теорема 1.2. Если Е-гильбертово
пространство, то ряд Фурье (5.2) элемента сходится для любой ортонормированной
системы (1.2).
сходится для любой ортонормированной
системы (1.2).
Для доказательства теоремы нам потребуется вспомогательное утверждение относительно свойств ортонормированных систем в евклидовых пространствах.
Лемма 1.2. Если Е-евклидово
пространство и (1.2) ортонормированная
система в Е, то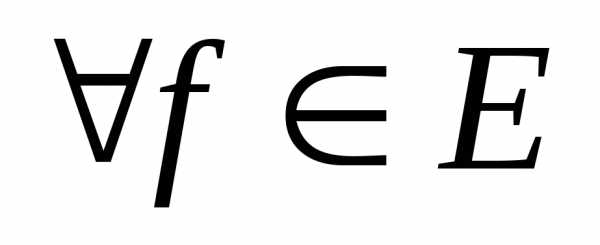 имеет место соотношение (равенство
Бесселя):
имеет место соотношение (равенство
Бесселя):
(7.2)
а также равенство
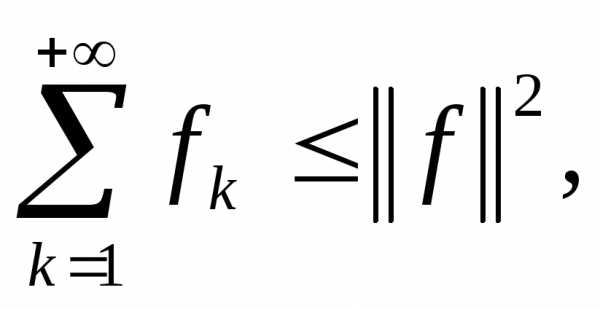 (8.2)
(8.2)
которое называется неравенством Бесселя.
Здесь
— коэффициенты Фурье элемента .
.
Доказательство.
поскольку система {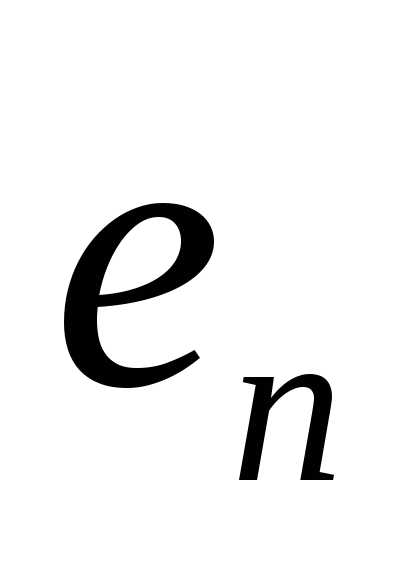 }
– ортонормированна.
}
– ортонормированна.
Равенство Бесселя (7.2) доказано. Из него, в частности, следует, что
Следовательно, все частичные суммы ряда в (8.2) ограничены. Поэтому этот ряд сходится. Переходя в последнем неравенстве к пределу при , получим неравенство (8.2) . Лемма доказана.
Замечание 3.2. Из неравенства Бесселя, в частности следует, что ряд слева в (8.2) сходится и, значит, коэффициенты Фурьедля любого элемента.
Доказательство теоремы 1.2.
Докажем, что последовательность  фундаментальна в Е. Имеем при
фундаментальна в Е. Имеем при
где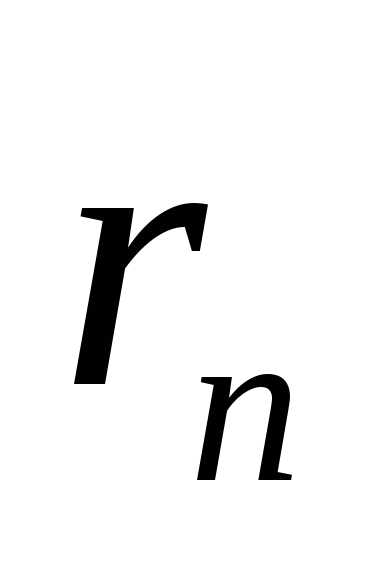 остаток ряда
остаток ряда Из неравенства Бесселя следует, что
этот ряд сходится и, значит,
Из неравенства Бесселя следует, что
этот ряд сходится и, значит, Поэтому
Поэтому
Следовательно, 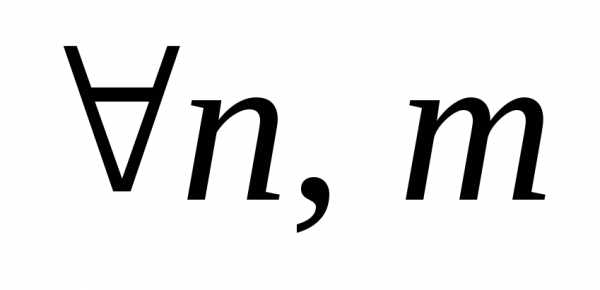 таких, что.
Таким образом, {
таких, что.
Таким образом, {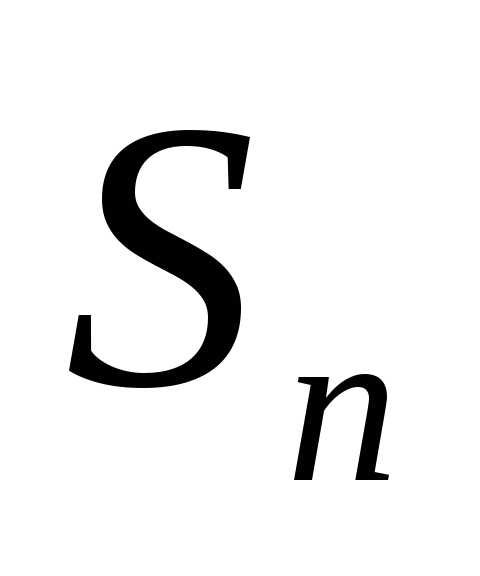 }
фундаментальная последовательность.
А так как Е полное пространство, то
}
фундаментальная последовательность.
А так как Е полное пространство, то
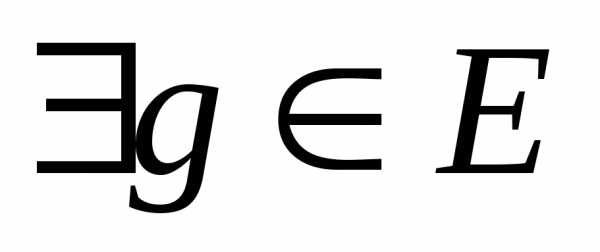 такая, что.
Теорема доказана.
такая, что.
Теорема доказана.
4. Замкнутые системы в евклидовых пространствах.
Рассмотрим еще одно важное свойство ряда Фурье.
Теорема 3.2. Если (1.2) есть
ортонормированная система в пространстве
Е, то иимеет место неравенство
иимеет место неравенство
(9.2)
где  есть
есть -я
частичная сумма ряда Фурье функции
-я
частичная сумма ряда Фурье функции .
.
Доказательство.
Так как система 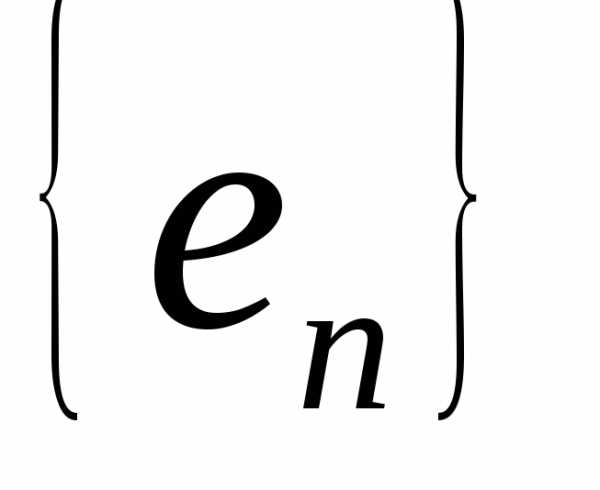 ортонормированна, то
ортонормированна, то
согласно равенству Бесселя. Теорема доказана.
Замечание 4.2. Неравенство (9.2)
называется минимальным свойством
коэффициентов Фурье. Оно означает, что
частичные суммы ряда Фурье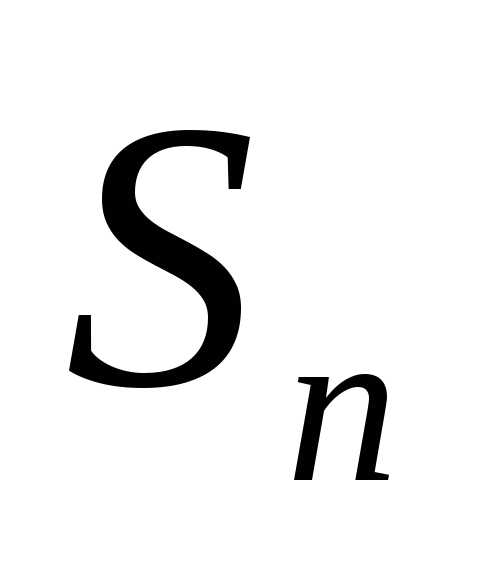 наилучшим образом приближают в среднем
элемент
наилучшим образом приближают в среднем
элемент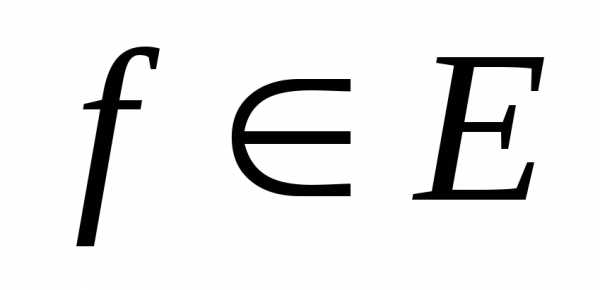 в линейной оболочке первых
в линейной оболочке первых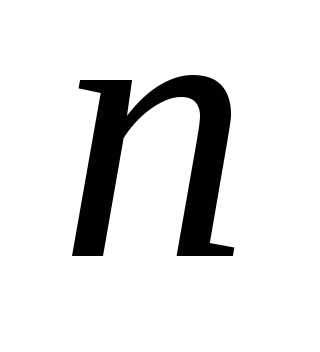 векторов системы (1.2).
векторов системы (1.2).
Определение 5.2.Система
векторов (1.2) называется замкнутой в
нормированном пространстве Е, если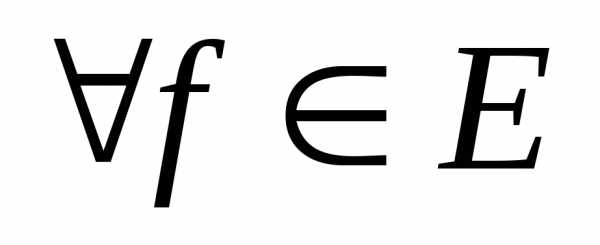 и
и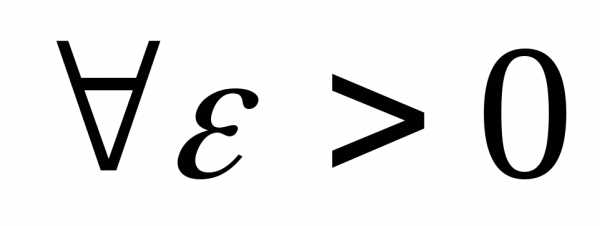 существует конечный набор чисел
существует конечный набор чисел такой, что
такой, что
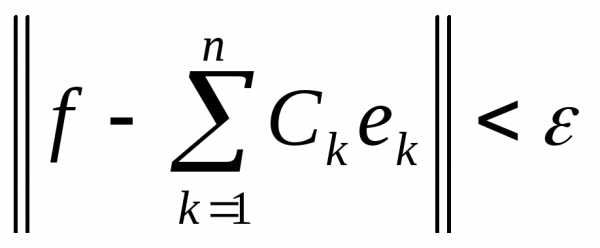 .
(10.2)
.
(10.2)
Если через 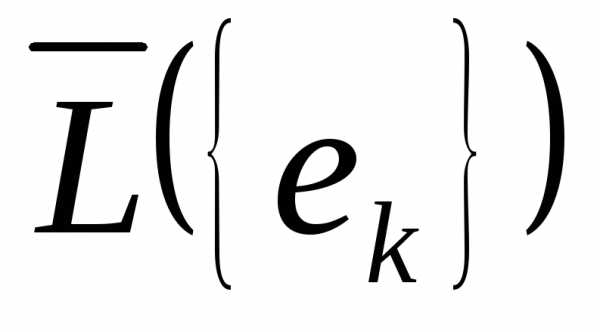 обозначить замыкание по норме Е множества
всех конечных линейных комбинаций
системы (1.2) (линейной оболочки
обозначить замыкание по норме Е множества
всех конечных линейных комбинаций
системы (1.2) (линейной оболочки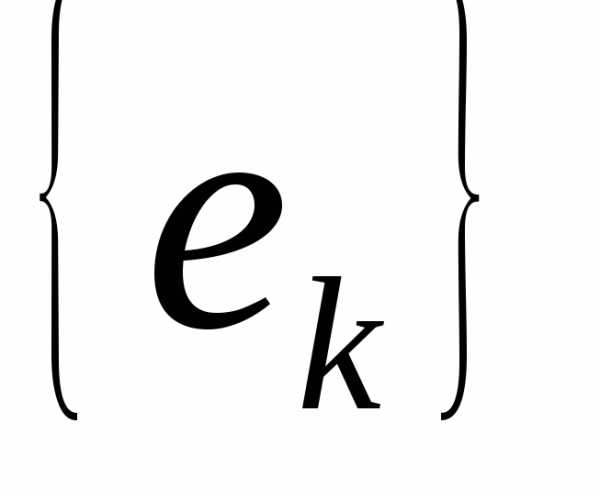 ),
то определение (5.2) можно переформулировать
так: система
),
то определение (5.2) можно переформулировать
так: система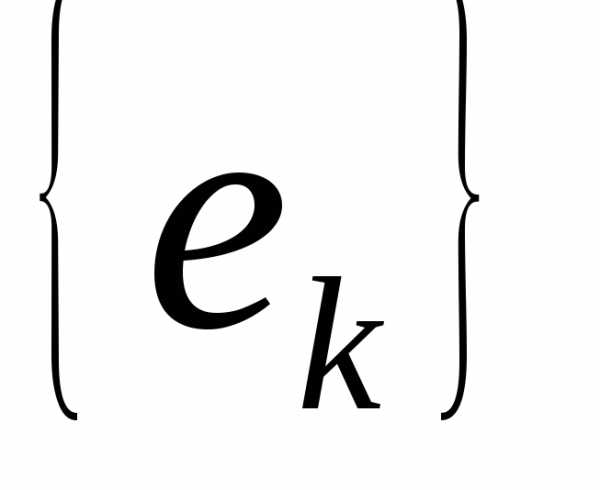 замкнута в Е, если Е
замкнута в Е, если Е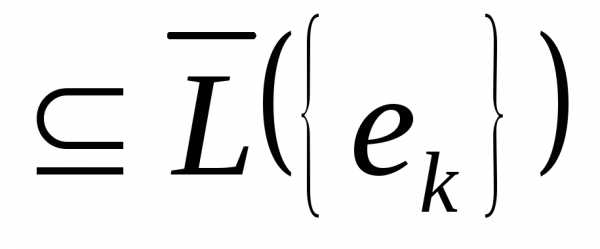 .
.
Следующие теоремы описывают свойства замкнутых систем.
Теорема 4.2. Если (1.2) ортонормированная система в евклидовом пространстве Е, то следующие условия эквивалентны:
1. Система (1.2) замкнута в Е;
Для
 неравенство Бесселя превращается в
неравенство (Парсеваля)
неравенство Бесселя превращается в
неравенство (Парсеваля)
 где(11.2)
где(11.2)
Для
 ряд Фурье элемента
ряд Фурье элемента сходится в среднем к
сходится в среднем к ,
то есть
,
то есть
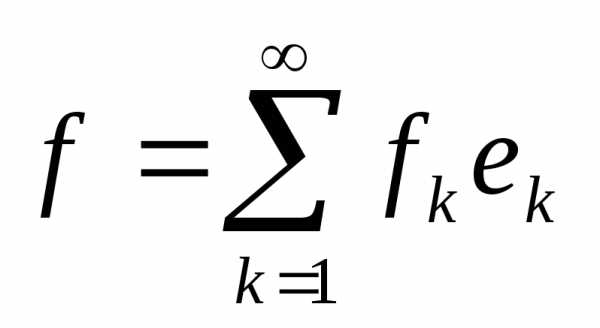 в среднем. (12.2)
в среднем. (12.2)
Доказательство.
1. 2.
Возьмем
2.
Возьмем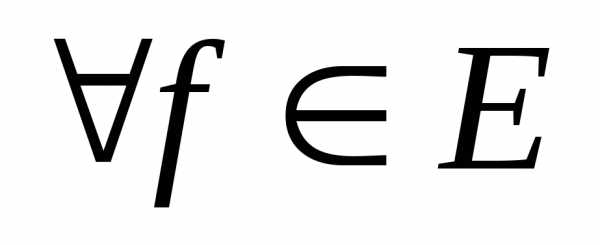 и
и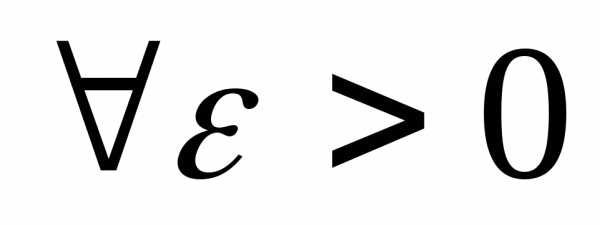 .
Так как система (1.2) замкнута, тотакие, что
.
Так как система (1.2) замкнута, тотакие, что .
.
Используя равенство Бесселя, и минимальное свойство коэффициентов ряда Фурье (9.2), выведем:
Если в этом неравенстве перейти к пределу при и воспользоваться неравенством Бесселя, то получим
Отсюда следует равенство Парсеваля (11.2).
2. 3.
Для
3.
Для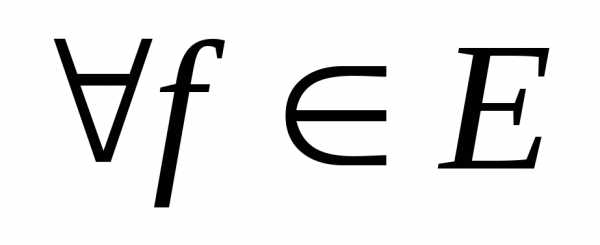 ,
воспользовавшись равенством Парсеваля,
получим
,
воспользовавшись равенством Парсеваля,
получим

А это и означает (12.2).
3. 1.
Из (12.2) следует
1.
Из (12.2) следует
Поэтому система (1.2) замкнута. Теорема доказана.
Замечание 5.2. Из теоремы 4.2 следует, что замкнутая ортонормированная система в бесконечномерном пространстве.
Задача 2.2. Если (1.2) есть замкнутая
ортонормированная система в евклидовом
пространстве ,
тоимеет место равенство (обобщённое
равенство Парсеваля)
,
тоимеет место равенство (обобщённое
равенство Парсеваля)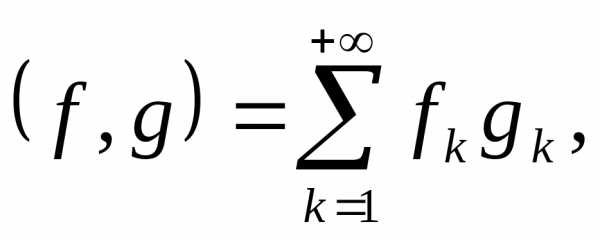 где
где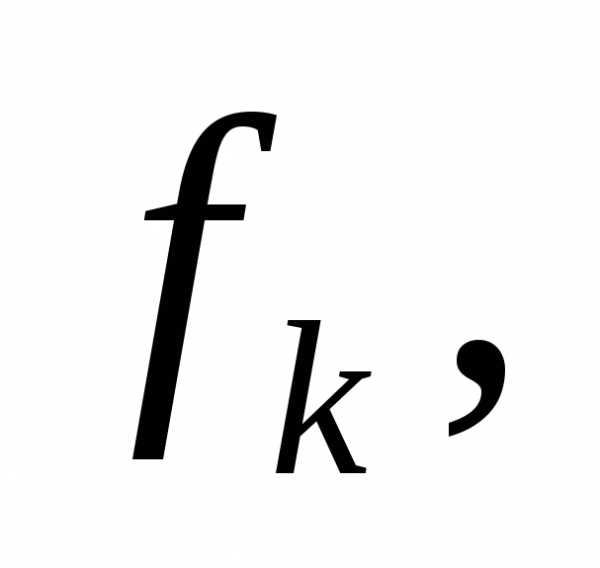
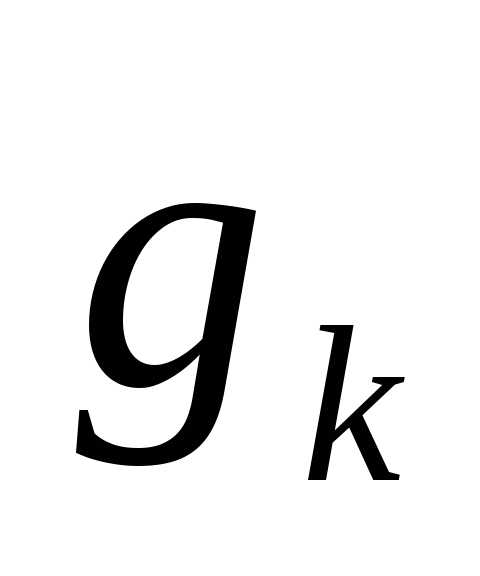 есть коэффициенты Фурье элементов
есть коэффициенты Фурье элементов и
и соответственно.
соответственно.
Утверждение 2.2.Если (1.2)
замкнутая ортонормированная система
в ,
то в
,
то в не
существует ненулевого элемента, у
которого все коэффициенты Фурье равны
0. (системы с таким свойством называются
полными).
не
существует ненулевого элемента, у
которого все коэффициенты Фурье равны
0. (системы с таким свойством называются
полными).
Доказательство.
Действительно, если 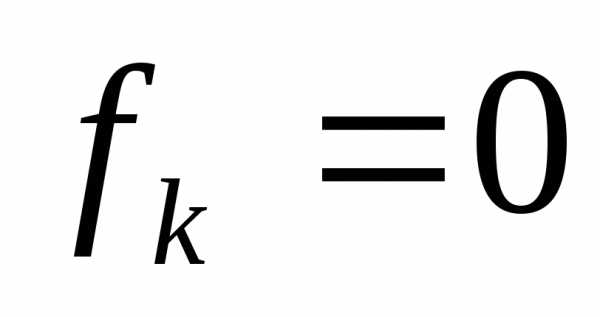 при всех
при всех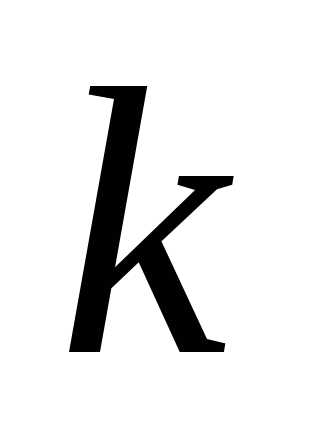 ,
то из равенства Парсеваля следует
,
то из равенства Парсеваля следует .
Утверждение доказано.
.
Утверждение доказано.
Следствие 1.2.Для всякой замкнутой
ортонормированной системы в два различных элемента не могут иметь
одинаковые ряды Фурье.
два различных элемента не могут иметь
одинаковые ряды Фурье.
Действительно, если элементы  и
и имеют одинаковые ряды Фурье, то у разности
имеют одинаковые ряды Фурье, то у разности все коэффициенты Фурье равны 0.
Следовательно,.
все коэффициенты Фурье равны 0.
Следовательно,.
Следствие 2.2. Если (1.2) есть
замкнутая ортонормированная система
в и для элемента
и для элемента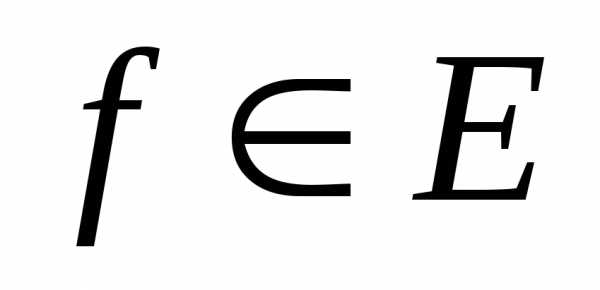 в смысле сходимости в среднем имеет
место равенство
в смысле сходимости в среднем имеет
место равенство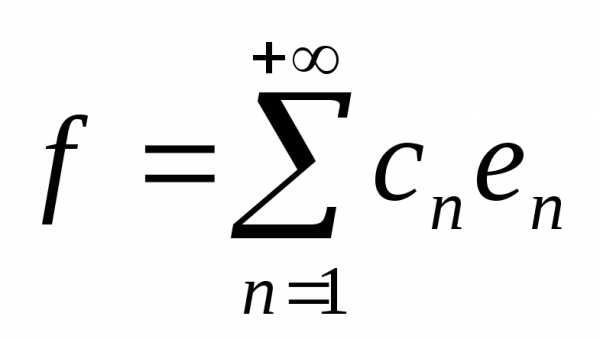 ,
то
,
то есть коэффициенты Фурье функции
есть коэффициенты Фурье функции ,
то есть.
,
то есть.
Доказательство.
Пусть
есть коэффициенты Фурье .
Тогда из условия и утвержденияIIIтеоремы 4.2 следует:.
Учитывая ортонормированность системы
(1.2), отсюда выведем.
Это означает, что
.
Тогда из условия и утвержденияIIIтеоремы 4.2 следует:.
Учитывая ортонормированность системы
(1.2), отсюда выведем.
Это означает, что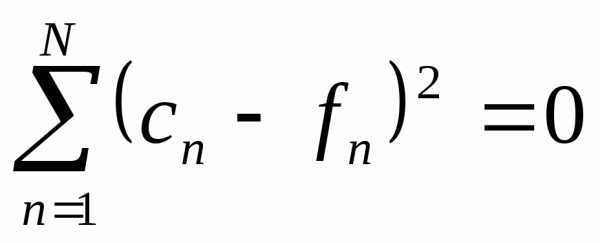 и
и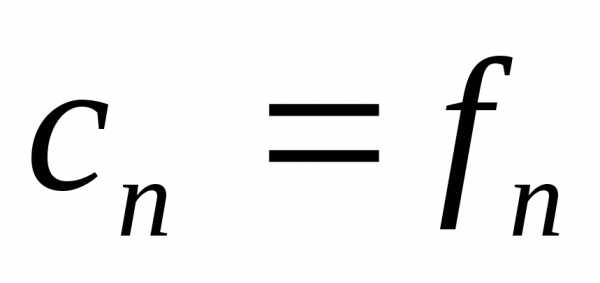
 .
Следствие доказано.
.
Следствие доказано.
Мы рассмотрели вопрос о разложении векторов в ряд Фурье в произвольном бесконечномерном Евклидовом пространстве. Ряды Фурье являются эффективным аппаратом при решении различных задач математической физики и математики. При этом в качестве евклидовых пространств берутся функциональные пространства с соответствующими ортонормированными системами. Примерами таких систем являются полиномы Лежандра, полиномы Чебышева, система Хаара, система Радемахера, функция Бесселя и другие.
В следующем параграфе мы подробно рассмотрим вопрос о разложении функций в ряд Фурье по тригонометрической системе.
studfiles.net
Ряды Фурье и их приложения
Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181)
При выводе формул (4), (17), (18) мы заранее предполагали, что функция ƒ(x) разлагается в правильно сходящийся тригонометрический ряд (1). Если же такого предположения не делать, а допустить, что для функции ƒ(x) существуют все интервалы, стоящие в правых частях формул (4), (17), (18), то по этим формулам можно вычислить коэффициенты a0, ak и bk и составить тригонометрический ряд (1), который представляет собой ряд Фурье, соответствующий данной функции.
Является ли построенный таким образом ряд Фурье сходящимся и если он сходится, то имеем ли мы право утверждать, что он сходится именно к функции ƒ(x), с помощью которой вычислялись коэффициенты ряда?
Оказывается, что сходимость ряда Фурье к заданной функции имеет место для довольно широкого класса функций. Достаточные условия сходимости ряда Фурье, и, следовательно, возможность разложения функций в ряд Фурье даются теоремой Дирихле. Прежде чем формулировать эту теорему, введем два определения.
Функция ƒ(x) называется кусочно-монотонной на сегменте [a, b], если этот сегмент можно разделить на конечное число сегментов, внутри каждого, из которых функция либо только возрастает, либо только убывает, либо постоянна.
Основное определение. Функция ƒ(x) называется удовлетворяющей условиям Дирихле на сегменте [ a, b], если:
1)функция непрерывна на сегменте [ a, b] или же имеет
на нем конечное число точек разрыва 1 рода;
2) функция кусочно-монотонна на сегменте [ a, b].
3.1. Примеры разложения функций в ряды Фурье.
Пример 1. Периодическая функция ƒ(x) с периодом 2π определяется следующим образом: ƒ(x) = х , -π < x ≤ π.
Эта функция – кусочно монотонная и ограниченная. Следовательно, её можно разложить в ряд Фурье.
По формуле (4) находим:
Применяя формулам (17), (18) и интегрируя по частям, получим:
.Таким образом, получаем ряд:
.Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. нулю.
Пример 2. Периодическая функция ƒ(x) с периодом 2π определена следующим образом:
ƒ(x) = -1 при –π < x < 0,
ƒ(x) = 1 при 0 ≤ x ≤ π.
Эта функция кусочно монотонна и ограничена на отрезке [-π, π]. Вычислим ее коэффициенты Фурье:
,(Нарисовать: рис. 377 , стр. 334 , Пискунов)
Следовательно, для рассматриваемой функции ряд Фурье имеет вид:
.Это равенство справедливо во всех точках, кроме точек разрыва.
4. Замечание о разложении периодической функции в ряд Фурье.
Отметим следующее свойство периодической функции ψ(x) с периодом 2π:
, каково бы ни было число λ.Действительно, так как ψ(ξ — 2π) = ψ (ξ) , то, полагая x = ξ — π, можем написать при любых c и d:
.В частности, принимая с = — π, d = λ, получим:
поэтому
Указанное свойство означает, что интеграл от периодической функции ψ(x) по любому отрезку, длина которого равна периоду, имеет всегда одно и тоже значение.
Из доказанного свойства вытекает, что при вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования (-π, π) промежутком интегрирования (λ, λ +2π), т. е. можем положить
 (20)
(20)где λ – любое число.
Это следует из того, что функция ƒ(x) является, по условию, периодической с периодом 2π; следовательно и функция ƒ(x)·cоsnx, и ƒ(x)·sinnx являются периодическими функциями с периодом 2π. В некоторых случаях доказанное свойство упрощает процесс нахождения коэффициентов.
Пример.
Пусть требуется разложить в ряд Фурье функцию ƒ(x) с периодом 2π, которая на отрезке 0 < x ≤ 2π задана равенством ƒ(x)= х.
(Пискунов, рис. 382, стр. 339 )
Эта функция на отрезке [-π, π] задается двумя формулами:
ƒ(x) = х + 2π на отрезке [-π, 0]
ƒ(x) = х на отрезке [0, π].
В то же время на отрезке [0, 2π] гораздо проще она задается одной формулой ƒ(x) = х. Поэтому для разложения этой функции в ряд Фурье выгоднее воспользоваться формулами (20), приравняв λ=0.

Следовательно,
5. Ряды Фурье для чётных и нечётных функций.
Из определения четной и нечетной функции следует, что если ψ(x) – четная функция, то
.Действительно,
так как по определению четной функции ψ(- x) = ψ(x).
Аналогично можно доказать, что если ψ(x) – нечетная функция, то
Если в ряд Фурье разлагается нечетная функция ƒ(x), то произведение ƒ(x) ·coskx есть функция также нечетная, а ƒ(x) · sinkx – четная; следовательно,
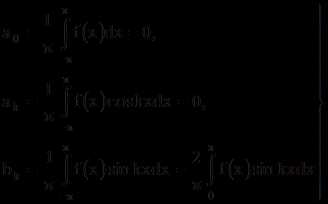 (21)
(21)т. е. ряд Фурье нечетной функции содержит «только синусы».
Если в ряд Фурье разлагается четная функция, то произведение ƒ(x) · sinkx есть функция нечетная, а ƒ(x) · coskx – четная, то:
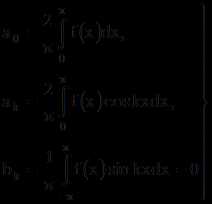 (22)
(22)т. е. ряд Фурье четной функции содержит «только косинусы».
Полученные формулы позволяют упрощать вычисления при разыскании коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной. Очевидно, что не всякая периодическая функция является четной или нечетной.
6. Ряд Фурье для функции с периодом 2 l .
Пусть функция ƒ(x) есть периодическая функция с периодом 2 l , вообще говоря, отличным от 2π. Разложим её в ряд Фурье.
Сделаем замену переменной по формуле
х = lt / π.Тогда функция ƒ(lt / π) будет периодичной функцией от t с периодом 2π. Её можно разложить в ряд Фурье на отрезке –π ≤ x ≤ π:
где (Пискунов, стр. 341 – дописывать не надо)
Возвратимся к старой переменной x:
Тогда будем иметь:
(24)Формула (23) получит вид
, (25)где коэффициенты a0, ak, bk вычисляются по формулам (24). Это и есть ряд Фурье для периодической функции с периодом 2 l.
Заметим, что все теоремы, которые имели место для рядов Фурье от периодических функций с периодом 2π, сохраняются и для рядов Фурье от периодических функций с каким-либо другим периодом 2 l .
Пример.
Разложить в ряд Фурье функцию ƒ(x) с периодом 2 l , которая на отрезке [-l , l ] задается равенством ƒ(x) = | x |.
(Пискунов, стр. 342, рис. 383 )
Решение. Так как рассматриваемая функция – четная, то
Следовательно, разложение имеет вид
7. Разложение в ряд Фурье непериодической функции.
Пусть на некотором отрезке [a, b] задана кусочно монотонная функция ƒ(x). Покажем, что данную функцию ƒ(x) в точках её непрерывности можно представить в виде суммы ряда Фурье. Для этого рассмотрим произвольную периодическую кусочно монотонную функцию ƒ1 (x) с периодом 2μ ≥ a — b, совпадающую с функцией ƒ(x) на отрезке [a, b]. Таким образом, дополнили определение функции ƒ(x).
Разложим функцию ƒ1 (x) в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] (кроме точек разрыва) совпадает с заданной функцией ƒ(x), т. е. мы разложили функцию ƒ(x) в ряд Фурье на отрезке [a, b].
mirznanii.com

 —
периодическая функция задана на отрезке
—
периодическая функция задана на отрезке 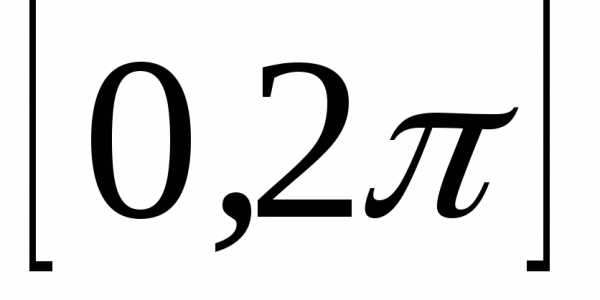 ,
в формулах (27) следует интегрировать
от нуля до
,
в формулах (27) следует интегрировать
от нуля до 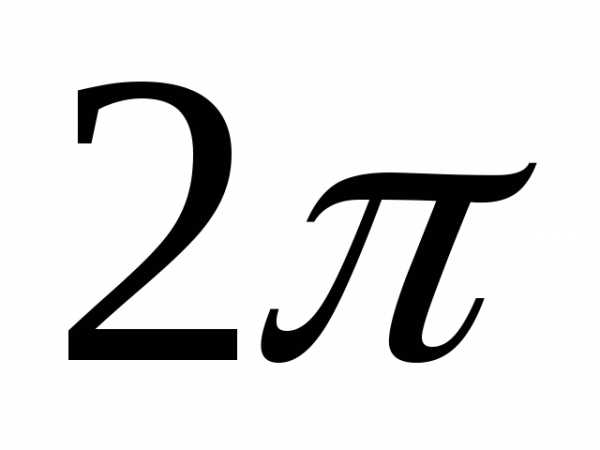 .
.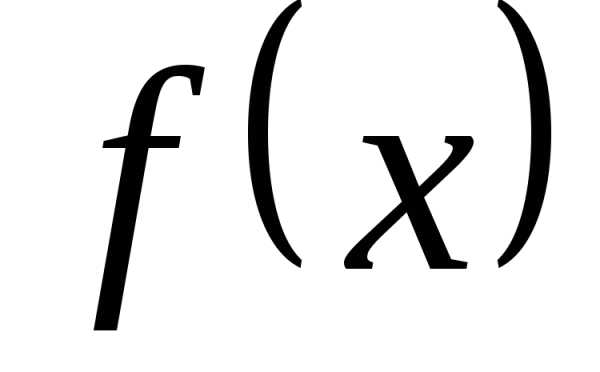 четная,
то коэффициенты
четная,
то коэффициенты  =0,
а остальные коэффициенты можно найти
по формулам
=0,
а остальные коэффициенты можно найти
по формулам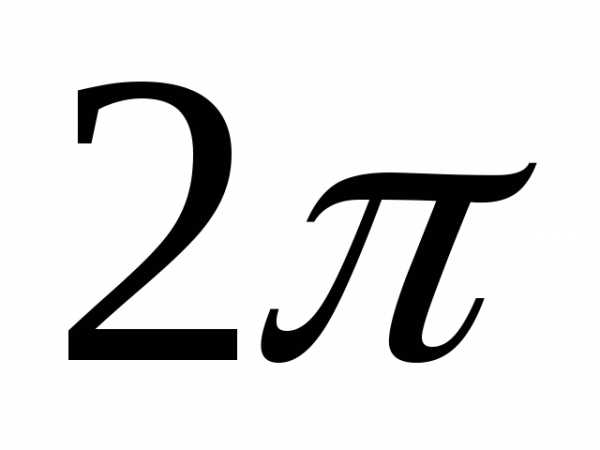 —
периодическая функция задана на отрезке
—
периодическая функция задана на отрезке 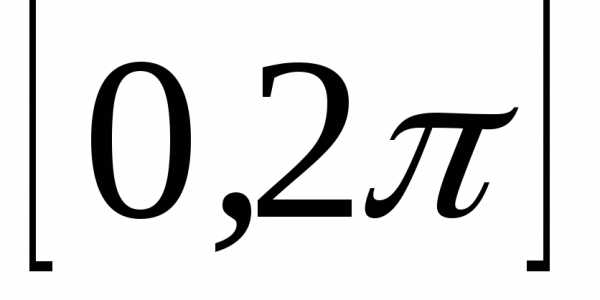 ,
в формулах (27) следует интегрировать
от нуля до
,
в формулах (27) следует интегрировать
от нуля до 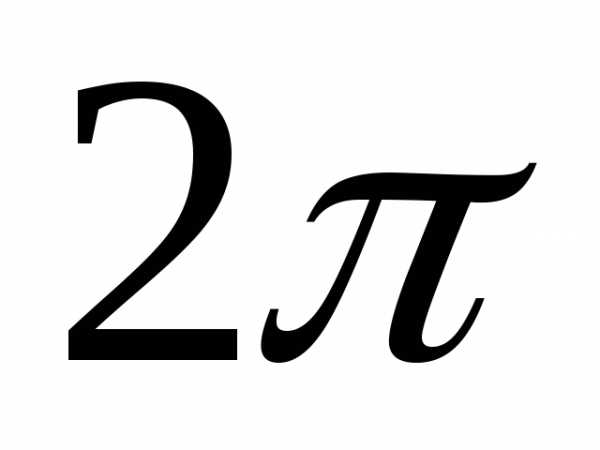 .
.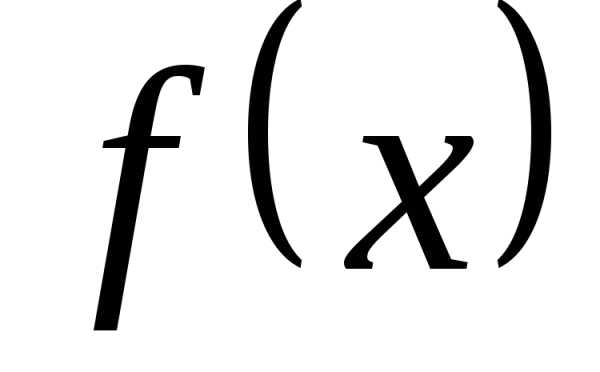 четная,
то коэффициенты
четная,
то коэффициенты 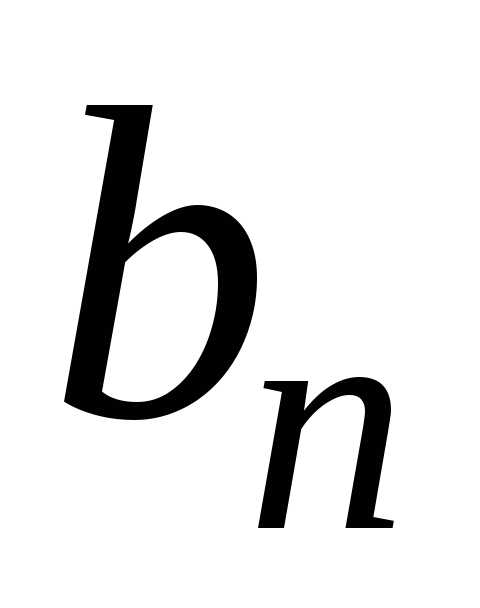 =0,
а остальные коэффициенты можно найти
по формулам
=0,
а остальные коэффициенты можно найти
по формулам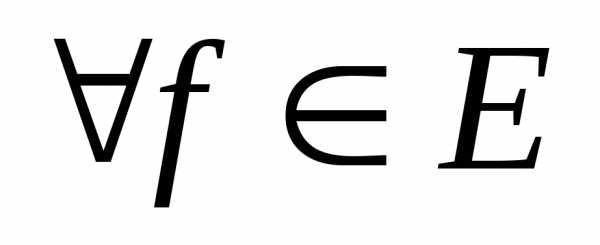 неравенство Бесселя превращается в
неравенство (Парсеваля)
неравенство Бесселя превращается в
неравенство (Парсеваля) ряд Фурье элемента
ряд Фурье элемента сходится в среднем к
сходится в среднем к ,
то есть
,
то есть