Тригонометрические функции: свойства и их графики
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).
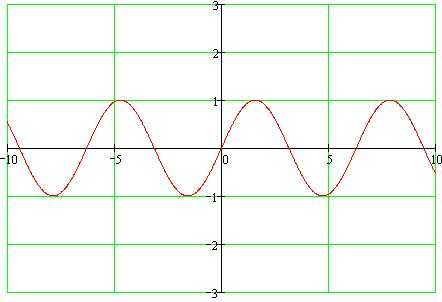
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = cos(x)
График функции y=cos(x).
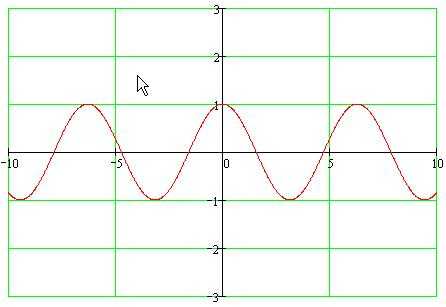
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
Y = tg(x)
График функции y=tg(x).
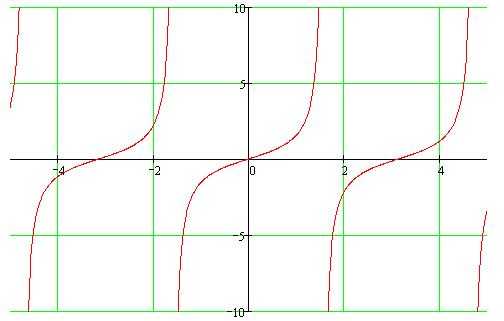
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
График функции y=ctg(x).

Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Нужна помощь в учебе?
Предыдущая тема: Электронный учебник по физике: все темы школьной программы
Следующая тема:   Периодичность тригонометрических функций: четные и нечетные
Все неприличные комментарии будут удаляться.
www.nado5.ru
Гра фик функ ции. Как построить график функции в Microsoft Excel
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Изучение свойств функций и их графиков занимает значительное место как в школьной математике, так и в последующих курсах. Причем не только в курсах математического и функционального анализа, и даже не только в других разделах высшей математики, но и в большинстве узко профессиональных предметов. Например, в экономике — функции полезности, издержек, функции спроса, предложения и потребления…, в радиотехнике — функции управления и функции отклика, в статистике — функции распределения… Чтобы облегчить дальнейшее изучение специальных функций, нужно научиться свободно оперировать графиками элементарных функций. Для этого после изучения следующей таблицы рекомендую пройти по ссылке «Преобразования графиков функций».
prontapizza.ru
y = 1/2*sin(2*x-pi/3)+1
Дано$$f{\left (x \right )} = \frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1$$
График функции
Точки пересечения с осью координат X
График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$\frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1 = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X
Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в sin(2*x — pi/3)/2 + 1.
$$\frac{1}{2} \sin{\left (- \frac{\pi}{3} + 0 \cdot 2 \right )} + 1$$
Результат:
$$f{\left (0 \right )} = — \frac{\sqrt{3}}{4} + 1$$
(0, 1 — sqrt(3)/4)
Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение$$\frac{d}{d x} f{\left (x \right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$\frac{d}{d x} f{\left (x \right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = — \frac{\pi}{12}$$
$$x_{2} = \frac{5 \pi}{12}$$
Зн. экстремумы в точках:
-pi
(—-, 1/2)
12
/pi pi
cos|— — —|
5*pi 3 3 /
(—-, 1 + ————)
12 2
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
$$x_{2} = — \frac{\pi}{12}$$
Максимумы функции в точках:
$$x_{2} = \frac{5 \pi}{12}$$
Убывает на промежутках
[-pi/12, 5*pi/12]
Возрастает на промежутках
Точки перегибов Найдем точки перегибов, для этого надо решить уравнение(-oo, -pi/12] U [5*pi/12, oo)
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = 0$$
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$\frac{d^{2}}{d x^{2}} f{\left (x \right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = \frac{\pi}{6}$$
$$x_{2} = \frac{2 \pi}{3}$$
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
(-oo, pi/6] U [2*pi/3, oo)
Выпуклая на промежутках
Горизонтальные асимптоты[pi/6, 2*pi/3]
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -\infty}\left(\frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1\right) = \langle \frac{1}{2}, \frac{3}{2}\rangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = \langle \frac{1}{2}, \frac{3}{2}\rangle$$
Наклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции sin(2*x — pi/3)/2 + 1, делённой на x при x->+oo и x ->-oo$$lim_{x to -\infty}\left(\frac{1}{x} \left(\frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1\right)\right) = 0$$
Возьмём предел
значит,
наклонная совпадает с горизонтальной асимптотой слева
Чётность и нечётность функции
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$\frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1 = — \frac{1}{2} \sin{\left (2 x + \frac{\pi}{3} \right )} + 1$$
— Нет
$$\frac{1}{2} \sin{\left (2 x — \frac{\pi}{3} \right )} + 1 = — \frac{1}{2} \left(-1 \sin{\left (2 x + \frac{\pi}{3} \right )}\right) — 1$$
— Нет
значит, функция
не является
ни чётной ни нечётной
uchimatchast.ru
