Синус и косинус числового аргумента, знаки значений функций. Тест
Тестирование онлайн
Единичная окружность
Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1.
Каждой точке на единичной окружности соответствует угол, координата х и координата y.
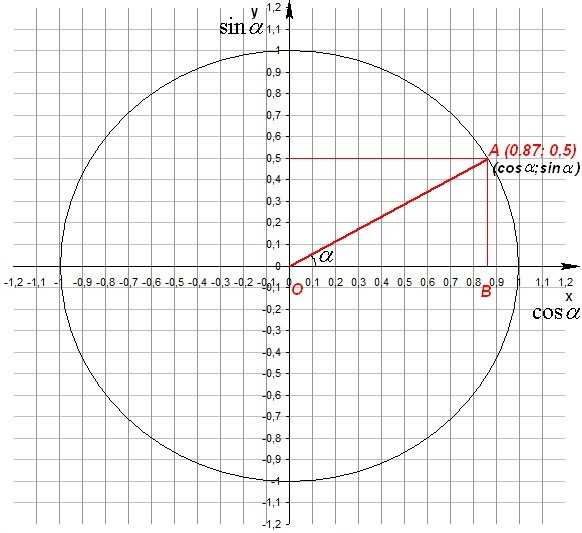
Точке А соответствует угол ?=300, координата х=0,87, координата y=0,5. Рассмотрим треугольник ОАВ: ; . Таким образом, координата х точки А — косинус угла ?, а координата y точки А — синус угла ?.
Для любой точки на окружности, соответствующей любому углу, можно определить значения косинуса и синуса этого угла.

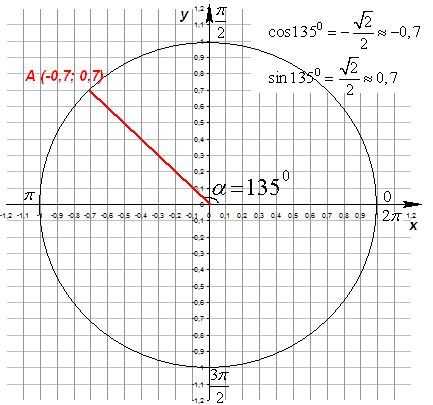
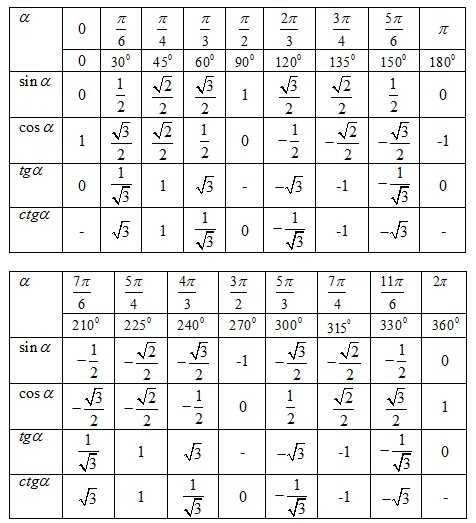
Табличные значения углов
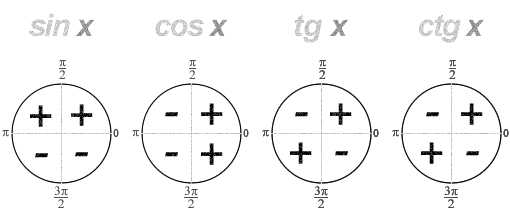
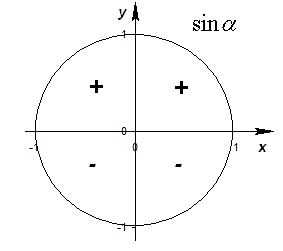
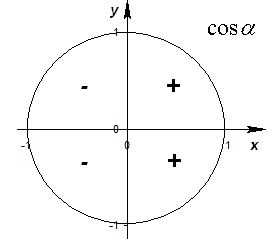
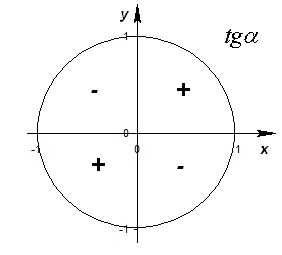
Знаки функций

В соответствующей четверти синус, косинус, тангенс, котангенс принимают положительное или отрицательное значения.

Значение угла на тригонометрической окружности
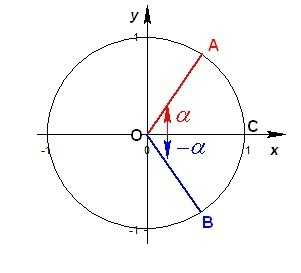
При прохождении окружности против часовой стрелки, начиная с точки С (1;0), угол положительный, при прохождении по часовой стрелки — отрицательный.
В точку А можно попасть при повороте ОС на угол или на угол, отличающийся от на любое целое число оборотов. Например, или , или и т.д. Поэтому для описания угла, соответствующего точке А на окружности, применяют общую запись
В точку В можно попасть при повороте ОС на угол или, в общем виде, . Если угол, соответствующий точке В, описывать, используя положительное направление отсчета, получим эквивалентную запись .
fizmat.by
Единичная окружность | Треугольники
Что такое единичная окружность и как с ее помощью вводятся определения синуса, косинуса, тангенса и котангенса?
Рассмотрим в прямоугольной декартовой системе координат окружность с центром в начале координат — точке O.
Отметим на окружности точку P, лежащую на оси абсцисс справа от точки O.
Осуществим поворот радиуса OP около точки O на угол α в верхнюю полуплоскость.
При этом радиус OP займет положение OA. Говорят, что при повороте на угол альфа радиус OP переходит в радиус OA, а точка P переходит в точку точку A(x;y).
Опустив перпендикуляр AB из точки A на ось Оx, получим прямоугольный треугольник OAB, в котором гипотенуза OA равна радиусу окружности, катеты AB и OB — ординате и абсциссе точки A: OA=R, AB=y, OB=x.
Катет AB — противолежащий углу AOB, равному α, катет OB — прилежащий.
По определению косинуса острого угла в прямоугольном треугольнике,
Таким образом, на окружности косинус угла α — это отношение абсциссы точки A окружности к радиусу этой окружности.
Аналогично, по определению синуса острого угла в прямоугольном треугольнике,
Значит, синус угла α — это отношение ординаты точки A окружности к радиусу этой окружности.
Для окружности любого радиуса отношения x/R и y/R не зависят от величины радиуса, а зависят только от угла альфа. Поэтому удобно взять R=1. Для окружности единичного радиуса определение синуса и косинуса упрощаются:
Определение.
Окружность с центром в начале координат и радиусом, равным единице, называется единичной окружностью.
Отсюда получаем определения синуса и косинуса на единичной окружности.
Определение.
Синусом угла α называется ордината точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.
Косинусом угла α называется абсцисса точки A единичной окружности, полученной при повороте точки P(1;0) на угол α.
Применив определения тангенса и котангенса острого угла в прямоугольном треугольнике в ∆AOB, получаем:
откуда
Приходим к определению тангенса и котангенса на единичной окружности.
Определение.
Тангенсом угла α называется отношение ординаты точки A единичной окружности к абсциссе этой точки.
Котангенсом угла α называется отношение абсциссы точки A единичной окружности к ординате этой точки.
Тригонометрия окружность со всеми значениями: ось синусов
Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…» )
Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.
Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.
Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику. Сходите по ссылке, кто ещё не был. Тогда и здесь всё ясно будет.
Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность. Это я расскажу прямо здесь и сейчас.
Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов. Это будет в следующих уроках.
Всё. Разобравшись с этими тремя китами, получим надёжную, безотказную и совершенно законную шпаргалку для всей тригонометрии сразу.
А то в школьных учебниках с этой самым тригонометрическим кругом как-то не очень…
Начнём, помаленьку.
В предыдущем уроке вы усвоили, что синус, косинус, тангенс и котангенс (т.е.
тригонометрические функции) зависят только от угла. И не зависят от длин сторон в прямоугольном треугольнике. Отсюда интересный вопрос. Пусть у нас есть вот такой угол. Назовём его угол β. Буква красивая.)
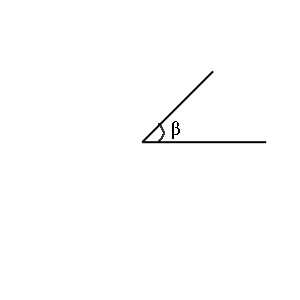
Раз есть угол, у него должны быть тригонометрические функции! Синус, скажем, или котангенс… А где их взять? Нет ни гипотенузы, ни катетов…
Как определить тригонометрические функции угла без прямоугольного треугольника? Задачка… Придётся опять лезть в сокровищницу мировых знаний. К средневековым людям. Те всё умели…
Первым делом возьмём координатную плоскость. Это самые обычные координатные оси, ОХ – по горизонтали, ОY – по вертикали. И… прибьём одну сторону угла к положительной полуоси ОХ. Вершина угла, естественно, в точке О. Крепко прибьём, чтобы не оторвать! Вторую сторону оставим подвижной, чтобы угол менять можно было. Раздвижной у нас угол будет. Конец неприбитой стороны угла обозначим точкой А. Получим вот такую картинку:
Так, угол пристроили. А где его синус, где косинус? Спокойно! Сейчас всё будет.
Отметим координаты точки А на осях. Наведите курсор мышки на картинку и всё увидите. На ОХ это будет точка В, на ОY — точка С. Понятно, что В и С — это какие-то числа. Координаты точки А.
Так вот, число В будет косинусом угла β, а число С – его синусом!
С чего бы это? Древние люди учили нас, что синус и косинус – это отношения сторон! Которые от длин сторон не зависят. А мы тут координаты точки придумали… Но! Посмотрите на треугольник ОАВ. Прямоугольный, кстати… По древнему определению косинус угла β равен отношению прилежащего катета к гипотенузе. Т.е. ОВ/ОА. Ладно, не возражаем. Причём косинус и синус не зависят от длин сторон.
Синус, косинус, тангенс и котангенс. Тригонометрический круг
А это вообще отлично! Это значит, что длины сторон можно брать какие угодно. Имеем полное право взять длину ОА за единицу! Неважно чего. Хоть метр, хоть километр, всё равно синус не меняется. А в этом случае
Вот так. Если провести такие же рассуждения для синуса, получим, что синус угла β равен АВ. Но АБ = ОС. Следовательно,
Нет, не обидели средневековые люди древних! Сберегли наследие! И отношение сторон сохранили, и возможности расширили чрезвычайно!
Однако, а где тригонометрический круг!? Где единичная окружность!? Ни слова про круги не было!
Верно. Но осталось всего ничего. Взять подвижную сторону ОА и повернуть её вокруг точки О на полный оборот. Как вы думаете, какую фигуру нарисует при этом точка А? Совершенно верно! Окружность! Вот она.
Вот это и будет тригонометрический круг.
Вот так. А почему круг — тригонометрический? Круг и круг… Вопрос резонный. Поясняю. Каждой точке окружности соответствуют два числа. Координата этой точки по Х и координата этой точки по Y. А координаты у нас что? Наведите курсор на рисунок. Координаты у нас — точки В и С. Т.е. косинус и синус угла β. Т.е. тригонометрические функции. Поэтому круг и называется тригонометрическим.
Вспомнив, что ОА = 1, а ОА – радиус, сообразим, что это же – и единичная окружность тоже.
А так как синус и косинус — просто какие-то числа — этот тригонометрический круг будет ещё и числовой окружностью.
Три термина в одном флаконе.)
В данной теме эти понятия: тригонометрический круг, единичная окружность и числовая окружность – одно и то же. В более широком смысле, единичная окружность – это любая окружность с радиусом, равным единице. Тригонометрический круг – практический термин, как раз для работы с единичной окружностью в тригонометрии. Чем мы сейчас и позанимаемся. Работой с тригонометрическим кругом.
Первую половину работы мы уже выполнили. Нарисовали тригонометрический круг с помощью угла (классно звучит, правда?).
Теперь выполним вторую половину работы. Сделаем то же самое, только наоборот. Пройдём путь от тригонометрического круга к углу.
Пусть нам дана единичная окружность. Т.е. просто окружность, нарисованная на координатной плоскости, с радиусом, равным единице. Возьмём произвольно точку А на окружности. Отметим её координаты точками В и С на осях. Как нам помнится, её координаты — это cosβ (по иксу) и sinβ (по игреку). И синус с косинусом отметим. Получим вот такую картинку:
Всё понятно? Внимание, вопрос!
Где β!? Где угол β, без которого синуса и косинуса не бывает!?
Наводим курсор на картинку, и… вот он, вот он угол β! Именно его синус и косинус являются координатами точки А.
Кстати, здесь не нарисована прибитая сторона угла. Она и в предыдущих рисунках не нужна, только так, для понимания… Угол всегда отсчитывается от положительного направления оси ОХ. От направления стрелки.
А если точку А взять в другом месте? Окружность — она круглая… Да пожалуйста! Где угодно! Поместим, к примеру, точку А во вторую четверть, отметим её координаты, синус, косинус, как полагается. Вот так:
Самые наблюдательные заметят, что синус угла β – положительный (точка С – на положительной полуоси OY), а вот косинус – отрицательный! Точка В лежит на отрицательной полуоси ОХ.
Наводим курсор на картинку и видим угол β. Угол β здесь – тупой. Чего, кстати, решительно не бывет в прямоугольном треугольнике. А зря, что ли, мы возможности расширяли?
Уловили суть тригонометрического круга? Если взять точку в любом месте окружности, её координатами будут косинус и синус угла. Угол отсчитывается от положительного направления оси ОХ и до прямой, соединяющей центр координат с этой самой точкой на окружности.
Вот и всё. Проще хотелось бы, да некуда. Кстати, мой вам совет. Работая с тригонометрическим кругом, рисуйте не только точки на окружности, но и сам угол! Как на этих рисунках. Понятнее будет.
Рисовать вам этот круг в тригонометрии постоянно придётся. Это не обязаловка, это и есть та легальная шпаргалка, которой пользуются умные люди. Сомневаетсь? Тогда назовите мне по памяти знаки вот таких выражений, к примеру: sin1300, cos1500, sin2500, cos3300? Я уж не спрашиваю про cos10500 или sin(-1450)… Про такие углы в следующем уроке написано.
И нигде-то вы подсказку не найдёте. Только на тригонометрическом круге. Рисуем примерный угол в правильной четверти и сразу видим, куда попадают его синус и косинус. На положительные полуоси, или отрицательные. Кстати, определение знаков тригонометрических функций постоянно требуется в самых различных заданиях…
Или ещё, чисто для примера… Надо вам, например, узнать, что больше, sin1300, или sin1550? Попробуй-ка, сообрази просто так…
А мы умные, мы нарисуем тригонометрический круг. И нарисуем на нём угол примерно 130 градусов. Исходя только из того, что он больше 90 и меньше 180 градусов. Ориентируемся на угол, а не на окружность! Уж где пересечёт подвижная сторона угла окружность, там и пересечёт. Отмечаем игрековую координату точки пересечения. Это будет sin1300. Как на этом рисунке:
А затем, здесь же, нарисуем угол 155 градусов. Примерно нарисуем, зная, что он больше 130 градусов. И меньше 180. Отметим и его синус. Наведите курсор на картинку, всё увидите. Ну и что, какой синус больше? Тут уж совсем трудно ошибиться! Конечно sin1300 больше, чем sin1550!
Долго? Да ну?! Никто не требует от вас тщательно прорисовывать картину и обеспечивать мультипликацию! Поработаете с этим сайтом, и по этой задаче будете за 10 секунд рисовать вот такую картинку:
Другой и не сообразит, что это за каракули, да… А вы спокойно и уверенно дадите правильный ответ! Хотя, аккуратность и не мешает… А то можно такую «окружность» нарисовать, что ответ обратный получится…
Эта задачка — только один пример широких возможностей тригонометрического круга. Освоить эти возможности вполне реально. Чем мы и займёмся далее.
Чаще всего вам придётся иметь с тригонометрическими функциями в обычной, алгебраической записи. Типа sin450, tg(-3), cos(x+y) и так далее. Безо всяких картинок и тригонометрических кругов! Рисовать этот самый круг надо самим. Руками. Если, конечно, хотите легко и правильно решать задания по тригонометрии. В том числе и самые продвинутые. Но особо не волнуйтесь. Уж на этом сайте, в тригонометрии, я вам обеспечу рисование кругов! И вы освоите этот крайне полезный приём. Однозначно.
Подведём итоги урока.
В этой теме мы плавно перешли от тригонометрических функций угла в прямоугольном треугольнике к тригонометрическим функциям любого угла. Для этого нам понадобилось освоить понятия «тригонометрический круг, единичная окружность, числовая окружность». Это очень полезно.)
Здесь я рассказывал о тригонометрическом круге в применении к синусу и косинусу. Но тангенс и котангенс тоже можно увидеть на круге! Одно движение ручкой, и вы легко и правильно определяете знак тангенса — котангенса любого угла, решаете тригонометрические неравенства и вообще потрясаете окружающих своими тригонометрическими способностями.)
Если вас интересуют такие перспективы — можно посетить урок «Тангенс и котангенс на тригонометрическом круге» в Особом разделе 555.
Далее мы разберёмся со следующими вопросами.
Как выглядят углы в 1000 градусов? Как выглядят отрицательные углы? Что за загадочное число «Пи», на которое неизбежно наталкиваешься в любом разделе тригонометрии? И каким боком это «Пи» к углам пристраивается? Всё это – в следующих уроках.
laservirta.ru
Числовая окружность на координатной плоскости. Синус и косинус
В ходе урока вы сможете самостоятельно изучить тему «Числовая окружность на координатной плоскости. Синус и косинус». В первой части урока рассматривается круг и его составные части. Разбираются примеры задач. Далее дается определения sinα и cosα, рассказывается о том, как вычислять эти значения и находить синусы и косинусы для основных реперных точек окружности
Мы уже знаем, что аргумент можно откладывать на числовой окружности. Рассмотрим круг и его основные части, которые нам будут нужны в дальнейшем.
Определение радиана. Углы могут измеряться разными единицами – градусами и радианами.
Радианом называется такой центральный угол, длина дуги которого равна радиусу (рис.1).
;
Ð
, т.к. длина хорды АВ меньше длины дуги .
Связь радиана и градуса.
Окружность разделили на 360 равных частей и угол, равный одной части, приняли за угол в
А сколько углов в 1рад можно получить в одной окружности?
Длина окружности , т.е. в окружности содержится штук радиусов R.
;
— связь градуса и радиана;
— иррациональное число.
Типовые задачи.
1. Дано: . Перевести в рад.
a) Дано: Перевести в рад.
2. Дано: 1рад. Перевести в градусы.
Через радианную меру угла удобно выражать площадь сектора круга и длину дуги окружности.
Имеем круг радиуса R. Найти площадь сектора AOB.
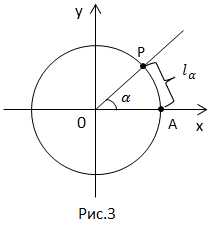
Длина дуги .
Если , то
Если окружность имеет , то, отложив длину дуги , мы получим центральный угол, который равен в радианном измерении.
Наша цель – тригонометрические функции. Аргументы тригонометрических функций откладывают либо на единичной окружности, либо на координатной прямой. Если окружность единичная, откладывать можно и числа, и углы.
Переходим к числовой окружности в координатной плоскости.
На окружности начало отсчета – т. А (рис.4).
Зададим . Отложим дугу , получим угол и т.В.
– уравнение окружности с центром в т. О(0;0).
Если ,то уравнение единичной окружности с центром в т.О(0;0).
Мы уже знаем, что любая точка на окружности описывает множество чисел, первое из них – число либо угол Важно уметь находить координаты этих точек.
Любая точка на координатной плоскости характеризуется двумя координатами —.
Определение. Если т. В соответствует числу , а значит и углу , то ее абсциссу называют косинусом этого числа или этого угла, а ее ординату – синусом этого числа или этого угла.
Как вычислять эти значения?
Мы имеем уравнение единичной окружности
И ранее были вычислены соответствующие значения для углов .
Пример:
Вычислить значения
Решение:
.
Необходимо найти
Изобразим т. М на единичной окружности (рис.5). Спроектируем ее на координатные оси и получим точки
координата т.координата т.
Т.е. нам необходимо найти
Рассмотрим прямоугольный (рис.6).
Но т.принадлежит отрицательной полуоси поэтому
Ответ:.
Найдем синусы и косинусы основных реперных точек. Реперные точки – это точки пересечения единичной окружности с осями координат (рис.7).
Т. А соответствует углу 0 рад.
По определению
Значит
Т .В соответствует углу
Значит
Т.С соответствует углу
Значит
Т. D соответствует углу .
Значит
Мы ввели числовую окружность и поместили ее в координатную плоскость, решили типовые задачи, определили, что такое синус и косинус угла, выяснили, что если в числовой окружностиR=1, то дуга , соответствующая центральн
interneturok.ru
Тригонометрия: определение тригонометрических функций
В этой статье мы рассмотрим тригонометрический круг и введем определения тригонометрических функций с помощью тригонометрического круга .
Впервые с определением синуса, косинуса, тангенса и котангенса школьники встречаются в восьмом классе в курсе геометрии. Напомню эти определения. Рассмотрим прямоугольный треугольник: Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе:
sin A=a/b; sin C=c/b
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
cos A=c/b; cos C= a/b
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
tg A=a/c; tg C=c/a.
Эти определения тригонометрических функций удобно использовать при решении геометрических задач, связанных с нахождением сторон и углов в прямоугольном треугольнике, однако они не улучшают понимания того, что из себя представляют тригонометрические функции именно как функции.
Часто во время занятий со школьниками я сталкиваюсь с тем, что они не понимают, откуда «взялись» тригонометрические функции, что они из себя представляют, и как их «готовить», чтобы легко решать уравнения и неравенства, содержащие тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, чтобы понять, что такое синус, косинус, тангенс и котангенс, как они между собой связаны, и как легко определять знаки тригонометрических функций без использования таблиц.
Итак.
Косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующеий данному углу α.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса (x), синус — ордината (y).
Поскольку радиус окружности равен 1, для любого угла и синус, и косинус находятся в пределах от −1 до 1:
−1 ≤ cos α ≤ 1, −1 ≤ sin α ≤ 1.
Основное тригонометрическое тождество является следствием теоремы Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
sin2 α+ cos2 α = 1
Чтобы узнать знаки синуса и косинуса какого-либо угла, находим на нашей окружности точку, соответствующую данному углу α, смотрим, положительны или отрицательны её координаты по x (это косинус угла α) и по y (это синус угла α).
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и 13»
ege-ok.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге.
| ||||||||||||||||||||||||||||||||||||
dpva.ru
Как запомнить значения косинусов и синусов основных точек числовой окружности
Пример 1.
Найти радианную меру угла равного а) 40° , б)120° , в)105°
Решение
а) 40° = 40·π / 180 = 2π/9
б) 120° = 120·π/180 = 2π/3
в) 105° = 105·π/180 = 7π/12
Пример 2.
Найти градусную меру угла выраженного в радианах а) π/6 , б) π/9, в) 2·π/3
Решение
а) π/6 = 180°/6 = 30°
б) π/9 = 180°/9 = 20°
в) 2π/3 = 2·180°/6 = 120°
Определение синуса, косинуса, тангенса и котангенса
— Синус острого угла t прямоугольного треугольника равен отношению противолежащего катета к гипотенузе (рис.1):
sin t = b/c.
— Косинус острого угла t прямоугольного треугольника равен отношению прилежащего катета к гипотенузе (рис.1):
cos t = a/c.
Эти определения относятся к прямоугольному треугольнику и являются частными случаями тех определений, которые представлены в данном разделе.
Поместим тот же прямоугольный треугольник в числовую окружность (рис.2).

Мы видим, что катет b равен определенной величине y на оси Y (оси ординат), катет а равен определенной величине x на оси X (оси абсцисс). А гипотенуза с равна радиусу окружности (R).
Таким образом, наши формулы обретают иной вид.
Так как b = y, a = x, c = R, то:
y x
sin t = —— , cos t = ——.
R R
Кстати, тогда иной вид обретают, естественно, и формулы тангенса и котангенса.
Так как tg t = b/a, ctg t = a/b, то, верны и другие уравнения:
tg t = y/x,
ctg = x/y.
Но вернемся к синусу и косинусу. Мы имеем дело с числовой окружностью, в которой радиус равен 1. Значит, получается:
y
sin t = —— = y,
1
x
cos t = —— = x.
1
Так мы приходим к третьему, более простому виду тригонометрических формул.
Эти формулы применимы не только к острому, но и к любому другому углу (тупому или развернутому).
Определения и формулы cos t, sin t, tg t, ctg t.
| Косинусом числа t числовой окружности называют абсциссу этого числа: cos t = x Синус числа t – это его ордината: sin t = y Тангенс числа t – это отношение синуса к косинусу: sin tπ tg t = ———,где t ≠ — + πk cos t2 Котангенс числа t – это отношение косинуса к синусу: cos t ctg t = ———,где t ≠ πk sin t |
Из формул тангенса и котангенса следует еще одна формула:
| sin t cos tπk tg t · ctg t = ——— · ——— = 1,при t ≠ —— cos t sin t2 |
Уравнения числовой окружности.
| Из предыдущего раздела мы знаем одно уравнение числовой окружности: x2 + y2 = 1 Но поскольку x = cos t, а y = sin t, то получается новое уравнение: cos2 t + sin2 t = 1 |
Знаки синуса, косинуса, тангенса и котангенса в четвертях окружности:
| 1-я четверть | 2-я четверть | 3-я четверть | 4-я четверть | |
| cos t | + | – | – | + |
| sin t | + | + | – | – |
| tg t, ctg t | + | – | + | – |
Косинус и синус основных точек числовой окружности:
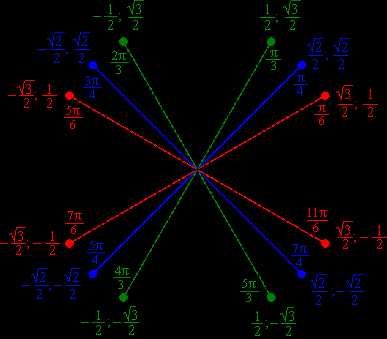
Как запомнить значения косинусов и синусов основных точек числовой окружности.
Прежде всего надо знать, что в каждой паре чисел значения косинуса стоят первыми, значения синуса – вторыми.
1) Обратите внимание: при всем множестве точек числовой окружности мы имеем дело лишь с пятью числами (в модуле):
1 √2 √3
0; —; ——; ——; 1.
2 2 2
Сделайте для себя это «открытие» — и вы снимете психологический страх перед обилием чисел: их на самом деле всего-то пять.
2) Начнем с целых чисел 0 и 1. Они находятся только на осях координат.
Не надо учить наизусть, где, к примеру, косинус в модуле имеет единицу, а где 0.
На концах оси косинусов (оси х), разумеется, косинусы равны модулю 1, а синусы равны 0.
На концах оси синусов (оси у) синусы равны модулю 1, а косинусы равны 0.
Теперь о знаках. Ноль знака не имеет. Что касается 1 – тут просто надо вспомнить самую простую вещь: из курса 7 класса вы знаете, что на оси х справа от центра координатной плоскости – положительные числа, слева – отрицательные; на оси у вверх от центра идут положительные числа, вниз – отрицательные. И тогда вы не ошибетесь со знаком 1.
3) Теперь перейдем к дробным значениям.
— Во всех знаменателях дробей – одно и то же число 2. Уже не ошибемся, что писать в знаменателе.
— В серединах четвертей косинус и синус имеют абсолютно одинаковое значение по модулю: √2/2. В каком случае они со знаком плюс или минус – см.таблицу выше. Но вряд ли вам нужна такая таблица: вы знаете это из того же курса 7 класса.
— Все ближайшие к оси х точки имеют абсолютно одинаковые по модулю значения косинуса и синуса: (√3/2; 1/2).
— Значения всех ближайших к оси у точек тоже абсолютно идентичны по модулю – причем в них те же числа, только они «поменялись» местами: (1/2; √3/2).
Теперь о знаках – тут свое интересное чередование (хотя со знаками, полагаем, вы должны легко разобраться и так).
Если в первой четверти значения и косинуса, и синуса со знаком плюс, то в диаметрально противоположной (третьей) они со знаком минус.
Если во второй четверти со знаком минус только косинусы, то в диаметрально противоположной (четвертой) – только синусы.
Осталось только напомнить, что в каждом сочетании значений косинуса и синуса первое число – это значение косинуса, второе число – значение синуса.
— Обратите внимание еще на одну закономерность: синус и косинус всех диаметрально противоположных точек окружности абсолютно равны по модулю. Возьмем, к примеру, противоположные точки π/3 и 4π/3:
cos π/3 = 1/2, sin π/3 = √3/2
cos 4π/3 = -1/2, sin 4π/3 = -√3/2
Различаются значения косинусов и синусов двух противоположных точек только по знаку. Но и здесь есть своя закономерность: синусы и косинусы диаметрально противоположных точек всегда имеют противоположные знаки.
Важно знать:
Значения косинусов и синусов точек числовой окружности последовательно возрастают или убывают в строго определенном порядке: от самого малого значения до самого большого и наоборот (см. раздел «Возрастание и убывание тригонометрических функций» — впрочем, в этом легко убедиться, лишь просто посмотрев на числовую окружность выше).
В порядке убывания получается такое чередование значений:
√3 √2 1 1 √2 √3
1; ——; ——; —; 0; – —; – ——; – ——; –1
2 2 2 2 2 2
Возрастают они строго в обратном порядке.
Поняв эту простую закономерность, вы научитесь довольно легко определять значения синуса и косинуса.
studopedya.ru