Комбинаторика. Размещения, перестановки, сочетания | Математика, которая мне нравится
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математики связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при >.
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки ладей
по определению!
Определение. Сочетаниями из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются хотя бы одним элементом (иначе говоря, -элементные подмножества данного множества из элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов по элементов в каждом обозначается (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два — .
.
Свойства чисел {\sf C}_n^k
1. .
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
2. .
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
.
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14. Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
hijos.ru
35 Элементы комбинаторики-перестановки,размещения, сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела математикисвязано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве—элементов. Тогда число всех различных пар, гдебудет равно.
Доказательство. Действительно, с одним элементом из множества мы можем составитьтаких различных пар, а всего в множествеэлементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два?.
Определение. Размещениями множества из различных элементов поэлементовназываются комбинации, которые составлены из данныхэлементов поэлементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов поэлементов обозначается через(от начальной буквы французского слова “arrangement”, что означает размещение), гдеи.
Теорема. Число размещений множества из элементов поэлементов равно
Доказательство. Пусть у нас есть элементы . Пусть— возможные размещения. Будем строить эти размещения последовательно. Сначала определим— первый элемент размещения. Из данной совокупностиэлементов его можно выбратьразличными способами. После выбора первого элементадля второго элементаостаетсяспособов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Очевидно, перестановки можно считать частным случаем размещений при .
Число всех перестановок из элементов обозначается(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. Сколькими способами можно расставить 8 ладей на шахматной доске так, чтобы они не били друг друга?
Решение. Искомое число расстановки 8 ладей
по определению!
Определение. Сочетаниями из различных элементов поэлементов называются комбинации, которые составлены из данныхэлементов поэлементов и отличаются хотя бы одним элементом (иначе говоря,-элементные подмножества данного множества изэлементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из элементов поэлементов в каждом обозначается(от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа
Все сочетания из множества по два —.
.
studfiles.net
Формулы комбинаторики
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N.
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4. Число различных перестановок без повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:
Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать способом. С каждым выбором конкретной пятерки можно произвестиперестановок местами. Согласно теореме умножения искомое число способов посадки равно.
Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как
б) Решение очевидно —
в)  — число выборов занимаемых стульев.
— число выборов занимаемых стульев.
 — число размещений
трех человек на трех выбранных стульях.
— число размещений
трех человек на трех выбранных стульях.
Общее число выборов равно .
Не трудно проверить
формулы  ;
;
;
— число всех подмножеств множества, состоящего из n элементов.
Размещения с повторением
Размещением с повторением из n элементов по m называется всякое упорядоченное подмножество множества N, состоящее из m элементов так, что любой элемент ожжет входить в это подмножество от 1 до m раз, либо вообще в нем отсутствовать.
Число
размещений с повторением обозначают  и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:
и вычисляют по формуле, представляющей
собой следствие из теоремы умножения:

Пример 2. Пусть дано множество из трех букв N = {a, b, c}. Назовем словом любой набор из букв, входящих в это множество. Найдем количество слов длиной 2, которые можно составить из этих букв: .
Замечание: Очевидно, размещения с повторением можно рассматривать и при .
Пример 3. Требуется из букв {a, b}, составить всевозможные слова длиной 3. Сколькими способами это можно сделать?
Ответ:
studfiles.net
Комбинаторика: основные правила и формулы.
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Решение
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:
.
Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»

ya-znau.ru
Размещения с повторениями
(mперестановки с неограниченными повторениями)
Пусть А = {a1,a2,…,an} , гдеa1,a2,…,an– “представители” 1-го, 2-го, …n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой. Рассмотрим следующую схему выбора упорядоченной последовательности изmэлементов: выбираем элемент на 1-е место, имеетсяnвариантов выбора. После этого элемент возвращается обратно и может быть выбран еще, т.е. на 2-е место имеетсяnпретендентов и т.д. Наm-е место также имеетсяnпретендентов.
Число различных размещений с повторениямиизnпо mравно
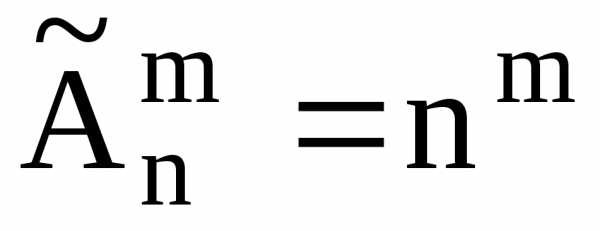 .
.
Здесь может быть m>n,m<n,m=n.
Например:
Сколько различных сигналов могут дать 4 светофора одновременно?
Решение:
Число различных сигналов на одном светофоре равно 3. Разные светофоры могут подавать одинаковые сигналы. Тогда, N- число различных сигналов, равно числу различных размещений с повторениями из 3 по 4:
.
Сочетания с повторениями
Пусть А = {a1,a2,…,an}, гдеa1,a2,…,an— “представители” 1-го, 2-го, …,n-го типа элементов. Объектов каждого типа имеется в неограниченном количестве, элементы одного типа неразличимы между собой.
Сочетания с повторениями отличаются составом элементов, входящих в выбираемое множество. Порядок элементов не имеет значения. Имеет значение, сколько элементов каждого типа вошло в сочетание. Рассмотрим определенное сочетание.
Пусть в него входят: r1объектов 1-го типа,
r2объектов 2-го типа,
. . . . . . . . . .
rnобъектовn-го типа;
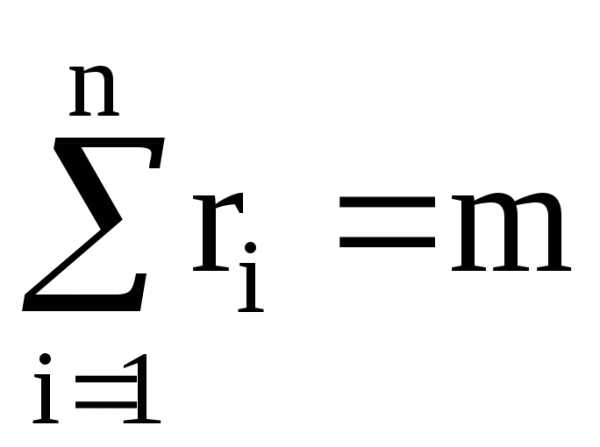 .
.
Некоторыеriмогут быть равны 0. Сочетанию можно поставить в соответствие следующую схему:
Вертикальные черточки отделяют элементы одного типа от элементов другого. Если элементов какого-либо типа нет, две черты будут рядом. Количество черточек равно (n-1). Каждому сочетанию с повторениями соответствует схема и наоборот, каждая подобная схема соответствует некоторому сочетанию с повторениями.
Количество сочетаний с повторениями из nпоmравно числу таких схем.
Всего в схеме (n– 1) +mобъектов, (n– 1) – черточек иm– нулей. Число схем равно числу различных перестановок из (n+m– 1) – элементов, среди которых (n– 1) – одинаковых “ | ” иm– одинаковых “0”.
Число различных сочетаний с повторениямиизnпоmравно:
Например:
1) В кондитерской продают 4 вида пирожных. Сколькими способами один человек может купить 8 пирожных?
2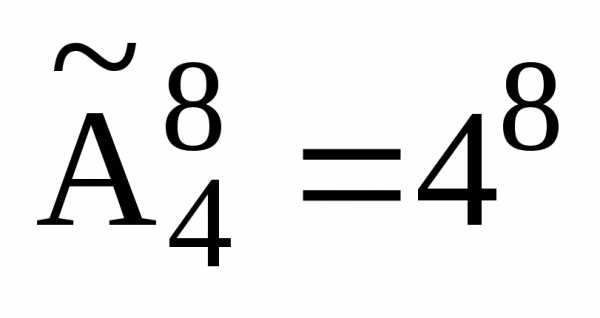 )
В кондитерской продают 4 вида пирожных.
Сколькими способами 8 различных человек
могут купить по 1 пирожному?
)
В кондитерской продают 4 вида пирожных.
Сколькими способами 8 различных человек
могут купить по 1 пирожному?
Формулы пересчета для основных видов комбинаторных соединений
Соединения | Без повторений элементов | С повторениями элементов |
Сочетания |
| |
Размещения |
|
|
Перестановки |
|
Принцип включения- исключения
Пусть имеется nобъектов
и множество свойств.
Каждый объект может обладать или не
обладать одним или несколькими свойствами .
.
Введем ряд обозначений.
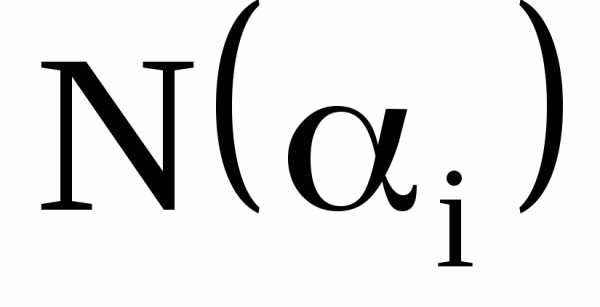 – количество объектов, обладающих
свойством
– количество объектов, обладающих
свойством .
.
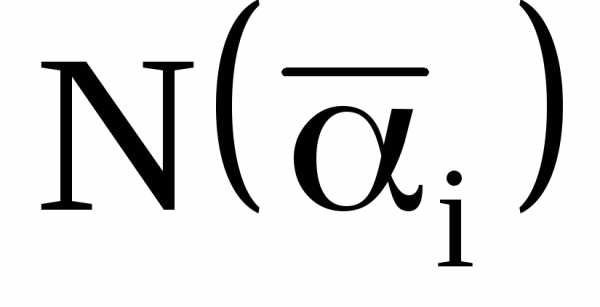 –
количество объектов, не обладающих
свойством
–
количество объектов, не обладающих
свойством .
.
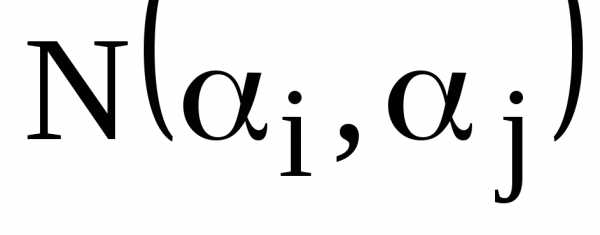 – количество объектов, обладающих
двумя свойствами
– количество объектов, обладающих
двумя свойствами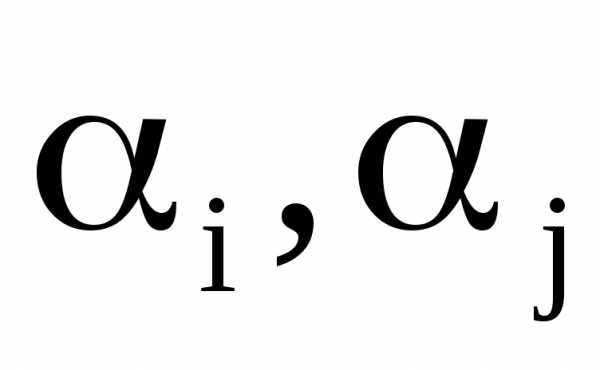 .
.
– количество объектов, обладающих
тремя свойствами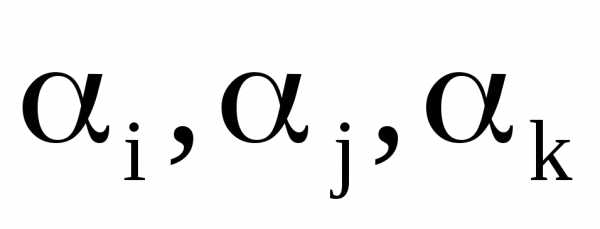 .
.
– количество объектов, обладающих всеми свойствами.
свойствами.
– количество объектов, не обладающих ни одним из n свойств.
Формула включений и исключений определяет
количество объектов, не обладающих ни
одним из  свойств, заданных множеством
свойств, заданных множеством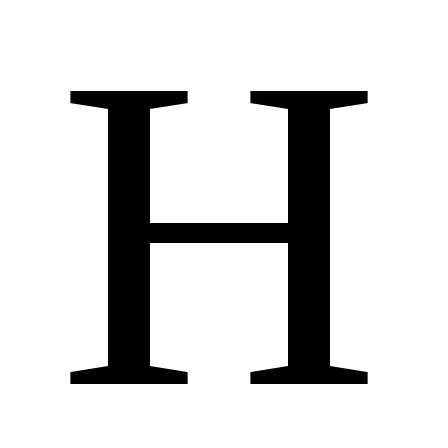 .
.
При произвольном |
Например:
На фирме работает 67 сотрудников. Из них 47 владеют английским языком, 35 -немецким, 20-французским; одновременно английским и немецким владеют – 23 человека, английским и французским-12, немецким и французским-11, тремя языками владеют 5сотрудников. Сколько человек не владеют ни одним языком?
Решение:
Определим следующие свойства:
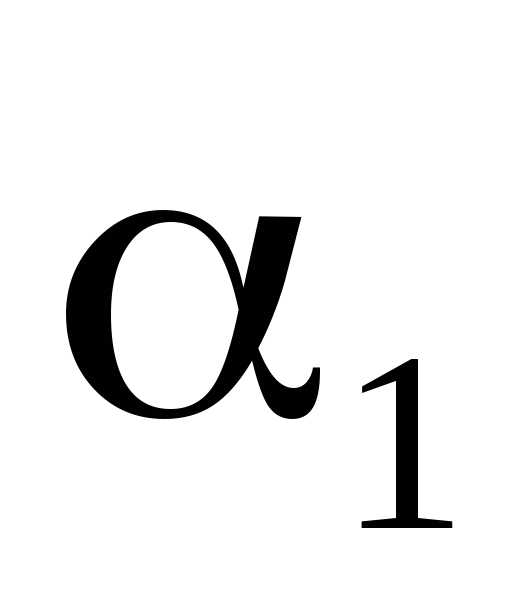 – “владеть английским языком”;
– “владеть английским языком”;
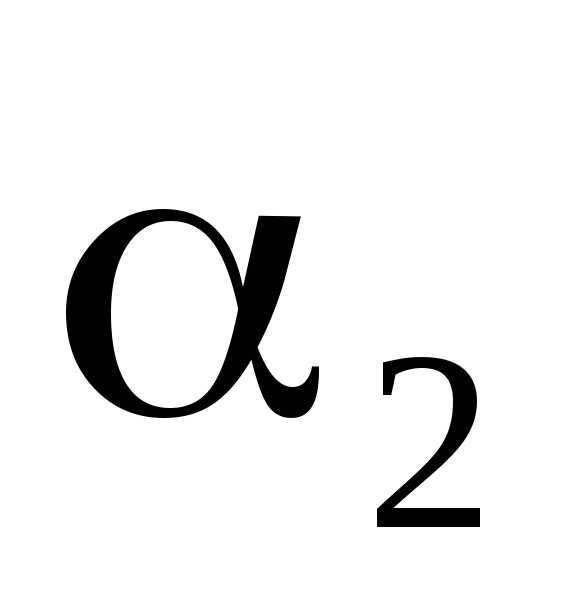 – “владеть немецким;
– “владеть немецким;
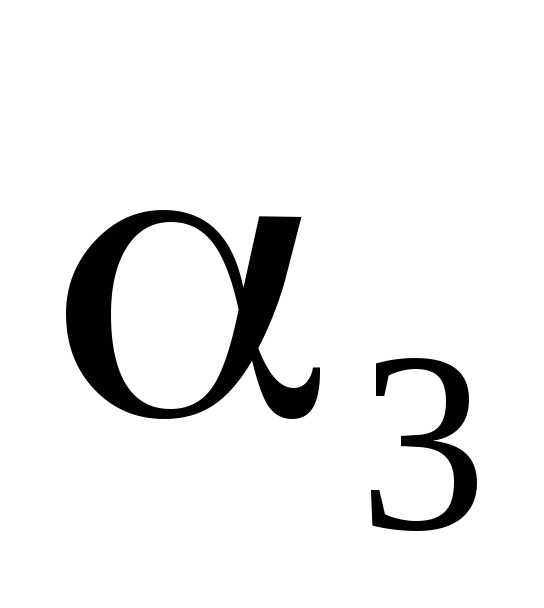 – “владеть французским”.
– “владеть французским”.
По формуле включений и исключений имеем:
Шесть человек не владеют ни одним из перечисленных языков.
studfiles.net
Комбинаторика. Основные формулы
Цель занятия: уметь применять основные формулы комбинаторики и знать условия применения этих формул; знать свойства биномиальных коэффициентов и уметь определять разложение бинома при конкретных значениях n.
План занятия:
1. Число размещений.
2. Число перестановок.
3. Число сочетаний.
4. Повторения.
5. Бином Ньютона. Треугольник Паскаля.
Методические указания по изучению темы
Во многих практических случаях возникает необходимость подсчитать количество возможных комбинаций объектов, удовлетворяющих определенным условиям. Такие задачи называются комбинаторными. Разнообразие комбинаторных задач не поддается исчерпывающему описанию, но среди них есть целый ряд особенно часто встречающихся, для которых известны способы подсчета.
Комбинаторика – область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих данному множеству. Термин «комбинаторика» происходит от латинского слова combina – сочетать, соединять.
Пусть есть некоторое множество из n элементов: x1, x2, x3, …, xn.
Из этого множества можно образовать различные подмножества, то есть выборки, каждая из которых содержит m элементов (0 ≤ m ≤ n). Различают упорядоченные выборки (размещения), перестановки и неупорядоченные выборки (сочетания).
Размещения
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком.
Число размещений из n элементов по m элементов обозначают (А – первая буква французского слова arrangement, что означает размещение, приведение в порядок) и вычисляют по формуле:
Понятие факториала
Произведение n натуральных чисел от 1 до n обозначается символом n! (n факториал), то есть
Например, 2!=
3!=
5!=
Заметим, что удобно рассчитывать 0!, полагая по определению, 0!=1.
Примеры:
Из последних двух формул следует, что
Пример.
В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки?
Решение: Так как порядок команд в призовой тройке важен, то мы имеем дело с размещениями. Тогда
(вариантов).
Пример.
Сколькими способами можно выбрать три лица на три различные должности из десяти кандидатов?
Решение:
(способов).
Пример.
Сколько можно составить телефонных номеров из 5 цифр так, чтобы в каждом отдельно взятом номере все цифры были различными?
Решение:
(телефонных номеров).
Перестановки
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Число всех возможных перестановок из n элементов обозначают Pn (P – первая буква французского слова permutation, что означает перестановка) и вычисляют по формуле:
Пример.
В финальном забеге на 100 метров участвуют 8 спортсменов. Сколько существует вариантов протокола забега?
Решение:
В данном случае речь идёт обо всех перестановках из 8 элементов. Тогда (вариантов)
Пример.
Сколькими различными способами могут разместиться на скамейке10 человек?
Решение:
(способов)
Пример.
Сколькими способами можно разместить 7 лиц за столом, на котором поставлено 7 столовых приборов?
Решение:
(способов).
Сочетания
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом.
Число сочетаний вычисляют по формуле: (С — первая буква французского слова combinasion).
Пример.
Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?
Решение:
(способов).
Пример.
Сколькими способами можно выбрать три детали из ящика, содержащего 15 деталей?
Решение:
(способов).
Другой вид формул числа размещений и числа сочетаний
; , то есть .
Свойства числа сочетаний:
1)
2)
3)
4)
5)
При решении задач комбинаторики используют следующие правила:
Правило суммы.Если некоторый объект А может быть выбран из совокупности объектов n способами, а другой объект В – k способами, то объект «либо А, либо В» можно выбрать n+k способами.
Правило произведения.Если некоторый объект А может быть выбран из совокупности объектов n способами и после каждого такого выбора другой объект В – k способами, то пара объектов (А, В) в указанном порядке может быть выбрана n×k способами.
Если некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.
Размещения с повторениями
Число размещений по m элементов с повторениями из n различных элементов равно nm,то есть
Пример.
Из цифр 1,2,3,4,5 можно составить 53 =125 трехзначных чисел, если в одном и том же числе могут попадаться и одинаковые цифры.
Перестановки с повторениями
Если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями
где
Пример.
Сколько различных перестановок букв можно сделать в слове «математика»?
Решение:
Сочетания с повторениями
Число сочетаний с повторениями из n различных элементов по m элементов равно числу сочетаний без повторений из (n+m-1) различных элементов по m элементов:
Пример.
Найти число сочетаний с повторениями из четырех элементов a, b, c, d по 3 элемента.
Решение:
Искомое число будет
Бином Ньютона
Для произвольного положительного целого числа n справедлива следующая формула:
.
Это бином Ньютона. Коэффициенты называются биномиальными коэффициентами.
При n = 2 получим формулу ;
При n = 3 получим формулу .
Пример. Определить разложение при n=4.
Решение:
.
Биномиальные коэффициенты обладают рядом свойств:
1. ;
2. ;
3. ;
4. .
Рассмотрим следующий треугольник:
………………………….
Строка под номером n содержит биномиальные коэффициенты разложения . Воспользовавшись свойством , можно заметить, что каждый внутренний элемент треугольника равен сумме двух элементов, расположенных над ним, а боковые элементы треугольника – единицы:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
……………………….
Это треугольник Паскаля. Он позволяет быстро найти значения биномиальных коэффициентов.
Решение примеров рекомендуется выполнять в среде табличного процессора MS Excel. При этом надо учитывать некоторую терминологическую путаницу.
В русскоязычной литературе перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются либо составом элементов, либо их порядком, обычно называют размещениями, а под перестановками понимают всю совокупность комбинаций, состоящих из одних и тех же n различных элементов и отличающихся только порядком их расположения. В этом смысле число всех возможных перестановок для множества из n различных элементов считается по формуле факториала Pn = n! или в Excel «=ФАКТР(N)» (см. рис. № 1)
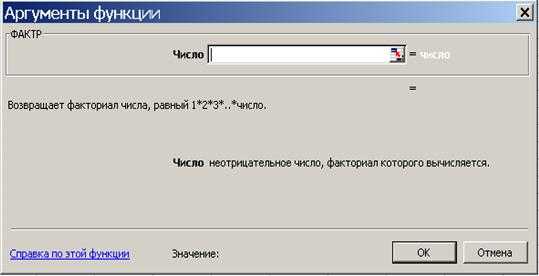
Рис. 1
В Excel считать «перестановки», т.е. размещения, очень удобно, не нужно даже вычислять факториалы (см. рис. №2 и №3): «=ПЕРЕСТ(N;K)». Вместо N и K задаются целые положительные числа, N≥K.
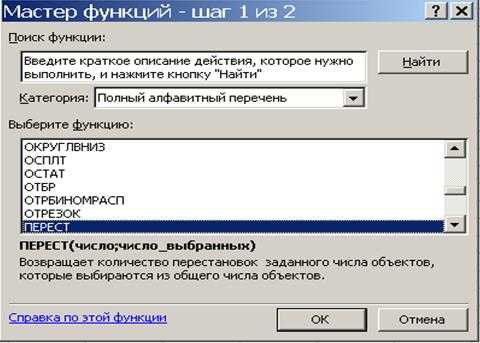
Рис. 2
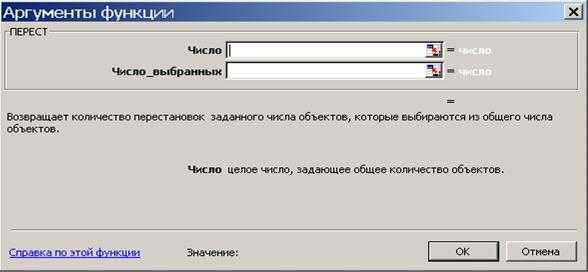
Рис. 3
Например, если ввести «=ПЕРЕСТ(3;2)», получим 6. Это 6 комбинации: (1,2), (2,1), (1,3), (3,1), (2,3), (3,2).
А вот встроенная функция «=ЧИСЛКОМБ(N;K)» выдает комбинаторную формулу, называемую у нас «Число сочетаний». В русскоязычной литературе так именуют перестановки, составленные из n различных элементов выбором по m элементов, которые отличаются только составом элементов, а порядок их выбора безразличен (см. рис, №4)
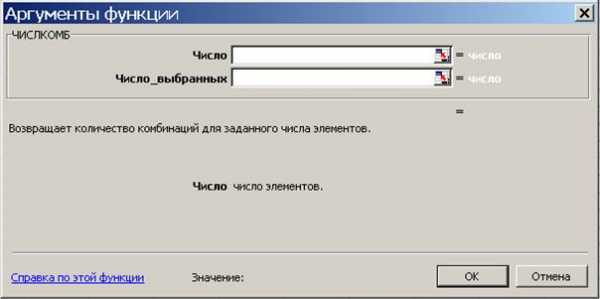
Рис. 4
При использовании встроенных функций пользуйтесь «Справкой по этой функции». Например:
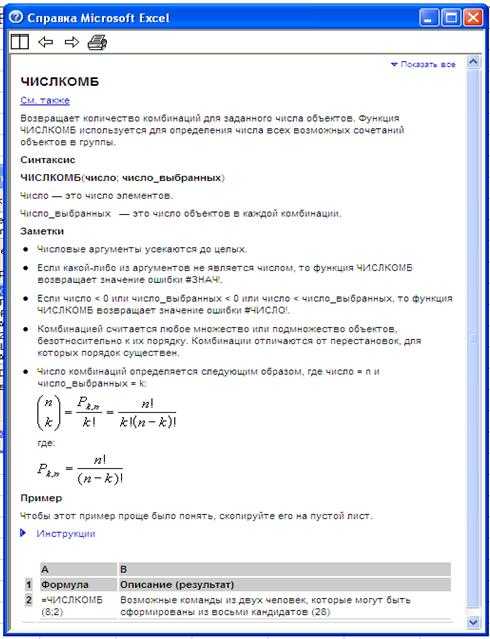
Задачи для самостоятельного решения
1. Вычислить:
2. Вычислить:
3. Вычислить:
4. Найти n, если 5Сn3 =
5. Найти n, если
6. Найти n, если
7. Найти n, если
8. Найти n, если , k n
9. Решить уравнение
10. Решить систему
11. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
12. Сколькими способами можно выбрать четыре лица на четыре различные должности из девяти кандидатов?
13. Сколько можно составить телефонных номеров из 6 цифр так, чтобы в каждом отдельно взятом номере все цифры были различны?
14. В классе 10 учебных предметов и 5 разных уроков в день. Сколькими способами могут быть распределены уроки в один день?
15. Сколько можно записать четырёхзначных чисел, используя без повторения все 10 цифр?
16. Фирма производит выбор из девяти кандидатов на три различные должности. Сколько существует способов такого выбора?
17. В восьмом классе изучается 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 уроков?
18. В высшей лиге чемпионата страны по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
19. Сколькими способами можно разместить 9 лиц за столом, на котором поставлено 9 приборов?
20. На собрании выступят 6 ораторов. Сколькими способами их фамилии можно расположить в списке?
21. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
22. Сколькими различными способами можно расставить 10 различных книг на полке, чтобы определённые 4 книги стояли рядом?
23. В однокруговом турнире по футболу участвуют 8 команд. Сколько всего матчей будет сыграно?
24. Из 25 студентов нужно выбрать трех делегатов на конференцию. Сколькими способами это можно сделать?
25. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
26. В колоде 36 карт, из них 4 туза. Сколькими способами можно извлечь 6 карт так, чтобы среди них было 2 туза?
27. Комплексная бригада состоит из двух маляров, трёх штукатуров и одного столяра. Сколько различных бригад можно создать из рабочего коллектива, в котором 15 маляров, 10 штукатуров и 5 столяров?
28. В отборочном турнире за 3 путёвки на чемпионат мира участвуют 10 команд. Сколько существует вариантов «счастливой тройки»?
29. Из 12 человек выбирают четверых для назначения на 4 одинаковые должности. Сколькими способами можно сделать такой выбор?
30. Сколькими различными способами можно составить разведывательную группу из 3-х солдат и одного командира, если имеется 12 солдат и 3 командира?
31. На плоскости дано n точек, из которых никакие три не лежат на одной прямой. Найти число прямых, которые можно получить, соединяя точки попарно.
32. Буквы азбуки Морзе образуются как последовательность точек и тире. Сколько различных букв можно образовать, если использовать 5 символов?
33. Сколько существует различных семизначных телефонных номеров?
34. Пусть буквы некоторой азбуки образуются как последовательность точек, тире и пробелов. Сколько различных букв можно образовать, если использовать 5 символов?
35. При игре в бридж между четырьмя игроками распределяется колода карт в 52 листа по 13 карт каждому игроку. Сколько существует различных способов раздать карты?
36. В почтовом отделении продаются открытки пяти видов. Определить число способов покупки семи открыток.
37. Два коллекционера обмениваются марками. Найти число способов обмена, если первый коллекционер обменивает 3 марки, а второй – 6 марок. ( Обмен происходит по одной марке ).
38. У одного студента 6 книг по математике, а у другого – 5. Сколькими способами они могут обменять 2 книги одного на 2 книги другого?
39. Сколько различных перестановок букв можно сделать в словах: «замок», «ротор», «обороноспособность», «колокол», «семинар»?
40. Сколькими различными способами можно разместить в 9 клетках следующие 9 букв: а, а, а, б, б, б, в, в, в?
41. В автомашине 6 мест. Сколькими способами 6 человек могут сесть в эту машину, если занять место водителя могут только двое из них?
42. Сколькими способами из колоды в 52 карты можно извлечь 6 карт, содержащих туза и короля одной масти?
43. Определить разложение при n=5.
44. Определить разложение при n=8.
45. Найти член разложения , не содержащий x (то есть содержащий x в нулевой степени).
46. Найти шестой член разложения , если биномиальный коэффициент третьего от конца члена равен 45.
47. В разложении коэффициент третьего члена на 44 больше коэффициента второго члена. Найти свободный член, то есть член разложения, не зависящий от x (членом, не зависящим от x, будет тот, который содержит x в нулевой степени).
48. В разложении бинома найти члены, не содержащие иррациональности.
49. Найти номер того члена разложения , который содержит a и b в одинаковых степенях.
Практическое занятие №2
(интерактивное занятие в малых группах)
Булевы функции
Цель занятия: уметь строить различные булевы функции, проверять эквивалентность булевых формул (используя таблицу истинности), определять существенные и фиктивные переменные.
План занятия:
1. Основные операции
2. Булевы функции от n переменных
3. Основные эквивалентности
4. Формулы
infopedia.su
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
При решении задач по комбинаторике используют следующие важные понятия
Размещения
Рассмотрим следующую задачу.
Задача. 9 карточек пронумерованы числами 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Из этих карточек четыре наугад взятых карточки выкладываем в ряд. Сколько при этом можно получить различных четырехзначных чисел?
Решение.Сначала слева направо пронумеруем места в ряду, куда выкладываем карточки: первое место, второе, третье, четвертое.
На первое место можно положить одну из 9 карточек. Для этого есть 9 способов. В каждом из этих 9 способов на второе место можно положить одну из оставшихся 8 карточек. Таким образом, существует
способа, чтобы положить карточки на первое и второе места. В каждом из этих 72 способов на третье место можно положить одну из оставшихся 7 карточек. Следовательно, существует
способа, чтобы положить карточки на первое, второе и третье места. В каждом из этих 504 способов на четвертое место можно положить одну из оставшихся 6 карточек. Отсюда вытекает, что существует
различных способа, чтобы выложить в ряд 4 карточки из набора, состоящего из 9 пронумерованных карточек. Таким образом, при выкладывании карточек можно получить 3024 различных четырехзначных числа.
Ответ: 3024.
При решении задачи мы провели подсчет числа способов раскладывания карточек, который является частным случаем общего метода подсчета числа размещений и заключается в следующем.
Определение 1. Рассмотрим множество, содержащее n элементов, и все его упорядоченные подмножества, содержащие k элементов. Каждое из этих подмножеств называют размещением из n элементов по k элементов.
Если обозначить символом число размещений из n элементов по k элементов, то будет справедлива формула:
| (1) |
В соответствии с определением факториала, формулу (1) можно также записать в виде:
В задаче множеством из n элементов является исходный набор из 9 пронумерованных карточек, а упорядоченным подмножеством из k элементов – 4 карточки, выложенные в ряд.
Таким образом, при решении задачи мы на частном примере подсчитали, чему равно число размещений из 9 элементов по 4 элемента, т.е. число
В соответствии с формулой (1),
что и было получено в задаче.
Замечание 1. Введенные в данном разделе размещения также называют размещениями без повторений.
Замечание 2. Из формул для числа перестановок и числа размещений вытекает формула
смысл которой заключается в следующем.
Утверждение. Размещение из n элементов по n элементов является перестановкой из n элементов.
Сочетания
Определение 2. Рассмотрим множество, состоящее из n элементов. Каждое его подмножество, содержащее k элементов, называют сочетанием из n элементов по k элементов.
Число сочетаний из n элементов по k элементов обозначается символом
Замечание 3. Важно отметить, что, в отличие от определения размещений, рассмотренные в определении сочетаний подмножества, содержащие k элементов, не являются упорядоченными. Поэтому, если в каждом подмножестве, содержащем k элементов (из определения 2), совершить всевозможные перестановки, количество которых равно k ! , то мы получим все размещения.
Таким образом, справедлива формула:
Следовательно,
откуда вытекает формула
| (2) |
Теперь рассмотрим несколько примеров подсчета числа сочетаний, которые непосредственно вытекают из формулы (2):
В заключение приведем часто используемое равенство, также непосредственно вытекающее из формулы (2):
Замечание 4. С разделом справочника «Сочетания» близко связан раздел «Бином Ньютона», где приведены и доказаны свойства чисел сочетаний.
С понятиями факториала числа n и перестановок из n элементов можно познакомиться в разделе «Комбинаторика: факториалы и перестановки» нашего справочника.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru

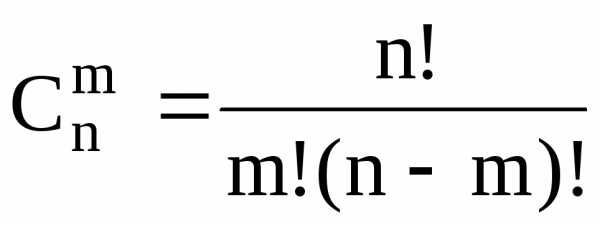
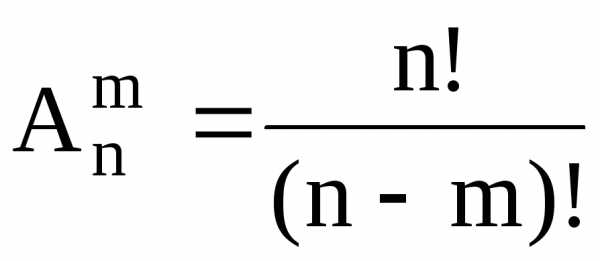
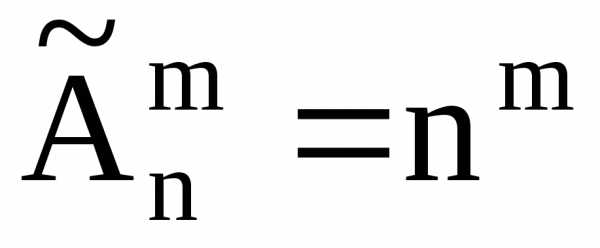
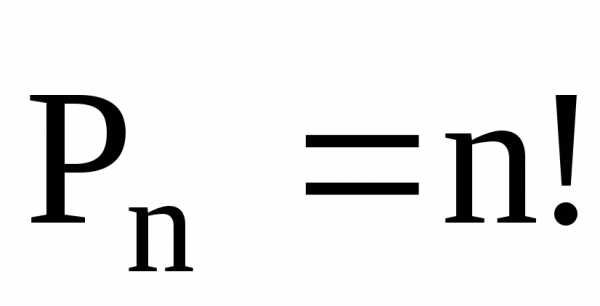
 справедлива следующая формула включений
и исключений:
справедлива следующая формула включений
и исключений: