Однородные дифференциальные уравнения первого порядка
Однородное дифференциальное уравнение первого порядка – это уравнение вида
, где f – функция.
Как определить однородное дифференциальное уравнение
Для того, чтобы определить, является ли дифференциальное уравнение первого порядка однородным, нужно ввести постоянную t и заменить y на ty и x на tx: y → ty, x → tx. Если t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется.
.
Пример
Определить, является ли данное уравнение однородным
Решение
Делаем замену y → ty, x → tx.
Делим на t 2.
.
Уравнение не содержит t. Следовательно, это однородное уравнение.
Метод решения однородного дифференциального уравнения
Однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными с помощью подстановки y = ux. Покажем это. Рассмотрим уравнение:
(i)
Делаем подстановку:
y = ux,
где u — функция от x. Дифференцируем по x:
y′ = (ux)′ = u′ x + u (x)′ = u′ x + u
Подставляем в исходное уравнение (i).
,
,
(ii) .
Разделяем переменные. Умножаем на dx и делим на x ( f(u) – u ).
При f(u) – u ≠ 0 и x ≠ 0 получаем:
Интегрируем:
Таким образом, мы получили общий интеграл уравнения (i) в квадратурах:
Заменим постоянную интегрирования C на ln C, тогда
Опустим знак модуля, поскольку нужный знак определяется выбором знака постоянной C. Тогда общий интеграл примет вид:
Далее следует рассмотреть случай f(u) – u = 0.
Если это уравнение имеет корни, то они являются решением уравнения (ii). Поскольку уравнение (ii) не совпадает с исходным уравнением, то следует убедиться, что дополнительные решения удовлетворяют исходному уравнению (i).
Всякий раз, когда мы, в процессе преобразований, делим какое либо уравнение на некоторую функцию, которую обозначим как g(x, y), то дальнейшие преобразования справедливы при g(x, y) ≠ 0. Поэтому следует отдельно рассматривать случай g(x, y) = 0.
Пример решения однородного дифференциального уравнения первого порядка
Решить уравнение
Решение
Проверим, является ли данное уравнение однородным. Делаем замену y → ty, x → tx. При этом y′ → y′.
,
,
.
Сокращаем на t.
Постоянная t сократилась. Поэтому уравнение является однородным.
Делаем подстановку y = ux, где u – функция от x.
y′ = (ux)′ = u′ x + u (x)′ = u′ x + u
Подставляем в исходное уравнение.
,
,
,
.
При x ≥ 0, |x| = x. При x ≤ 0, |x| = – x. Мы пишем |x| = ± x подразумевая, что верхний знак относится к значениям x ≥ 0, а нижний – к значениям x ≤ 0.
,
Умножаем на ± dx и делим на .
При u2 – 1 ≠ 0 имеем:
Интегрируем:
Интегралы табличные,
.
Применим формулу:
(a + b)(a – b) = a 2 – b 2.
Положим a = u, .
.
Возьмем обе части по модулю и логарифмируем,
.
Отсюда
.
Таким образом имеем:
,
.
Опускаем знак модуля, поскольку нужный знак обеспечивается выбором знака постоянной C.
Умножаем на x и подставляем ux = y.
,
.
Возводим в квадрат.
,
,
.
Теперь рассмотрим случай, u2 – 1 = 0.
Корни этого уравнения
.
Легко убедиться, что функции y = ± x удовлетворяют исходному уравнению.
Ответ
,
,
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Однородные дифференциальные уравнения первого порядка
Дифференциальное уравение первого порядка называется однородным, если и — однородные функции одной и то же степени.
Функция называется однородной функцией k-й степени, если для любого t выполняется равенство .
В частном случае, если однородная функция имеет нулевую степень, то выполняется равенство
Пример 1. Установить, являются ли однородными функции
1) ;
2) ;
Решение. Находим
Следовательно, — однородная функция третьей степени.
Аналогично устанавливается, что — однородная функция четвёртой степени:
Отношение двух однородных функций одинаковых степеней также есть однородная функция, но
нулевой степени. Пусть и
— однородные функции
Как решить однородное дифференциальное уравнение первого порядка?
Решение однородного дифференциального уравнения первого порядка сводится к решению дифференциального уравнения с разделяющимися переменными.
Для этого преобразуем уравнение к виду
или , (1)
где — однородная функция нулевой степени как отношение однородных функций одинаковых степеней. Это равенство справедливо при любом t. В частности, если , то , или , т. е. функция представлена в виде функции от .
Обозначим это отношение через z, т. е. , откуда . Тогда
и уравнение (1) преобразуется так:
Это уравнение с разделяющимися переменными. Разделив переменные и выполнив почленное интегрирование, затем следует заменить z на .
Пример 5. Решить однородное дифференциальное уравнение
Решение. Поделим почленно уравнение на dx и получим
или
.
Произведём подстановку , откуда . Тогда уравнение примет вид
.
Путём дальнейших преобразований получаем
Итак, или
.
Почленное интегрирование даёт
.
Заменяя z на , получим
Чтобы избавиться от дробности, умножим обе части выражения на
— общий интеграл данного уравнения.
Выводы. Чтобы решать однородные дифференциальные уравнения, необходимо хорошо владеть методами интегрирования — путём замены переменной и по частям. В практических задачах на этот вид дифференциальных уравнений нередко после преобразований получаются выражения, интегрируя которые, требуется применять как один, так и другой метод интегрирования дважды или даже трижды.
Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
function-x.ru
3. Однородные дифференциальные уравнения первого порядка
Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.
Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
. | (3.1) |
Например, функция — однородная функция первого измерения, так как
;
— однородная функция третьего измерения , так как
;
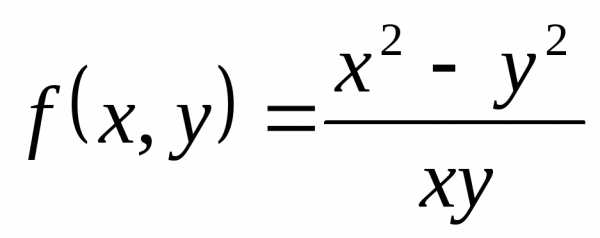 — однородная функция нулевого измерения,
так как
— однородная функция нулевого измерения,
так как
, т.е..
Определение 2.Дифференциальное уравнение первого порядкаy‘ = f(x,y) называется однородным, если функцияf(x,y) есть однородная функция нулевого измерения относительно
Его можно представить в виде
P (x, y) dx + Q (x, y) dy = 0, | (3.2) |
где P(x,y) иQ(x,y) – однородные функции одинакового измерения: отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения (см. третий из приведенных выше примеров).
Возможна следующая форма записи уравнения (3.2):
| (3.3) |
что позволяет определить однородное уравнение как такое дифференциальное, которое можно преобразовать к виду (3.3).
Замена 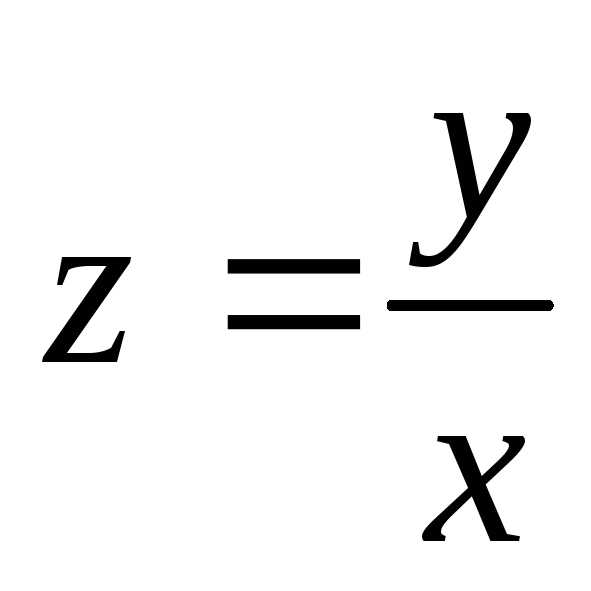 приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим
приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим ,
,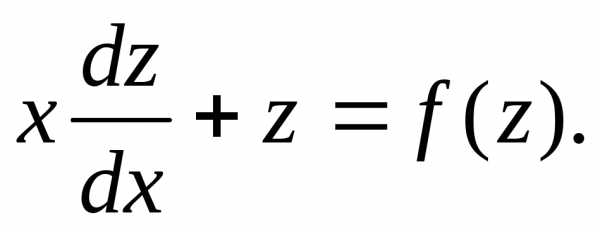 Разделяя переменные и интегрируя,
найдем:
Разделяя переменные и интегрируя,
найдем:
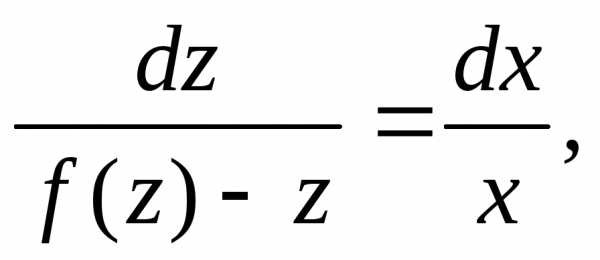 ,
,
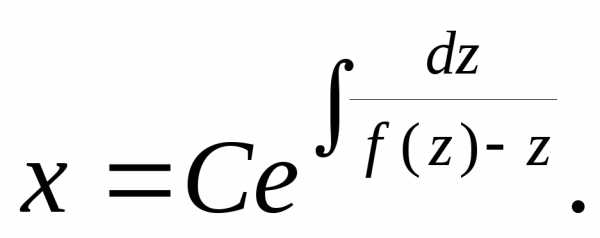
Пример 1.Решить уравнение .
Δ Полагаем у = zx, 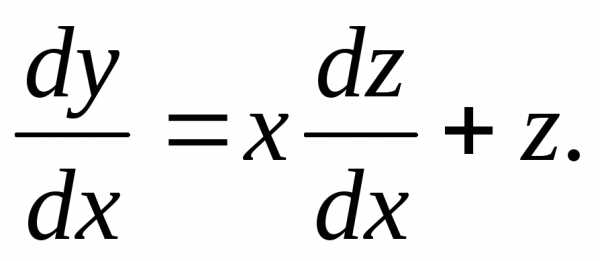 Подставляем
эти выраженияy иdyв данное уравнение:
Подставляем
эти выраженияy иdyв данное уравнение: или
или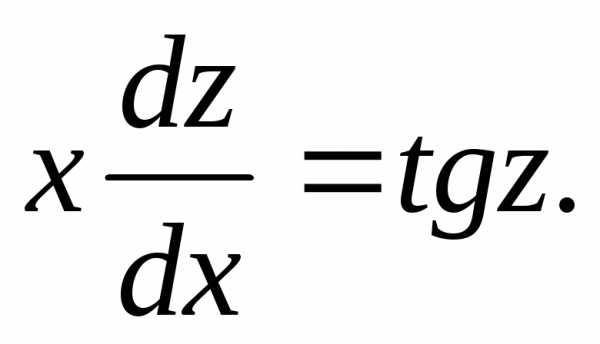 Разделяем переменные:
Разделяем переменные: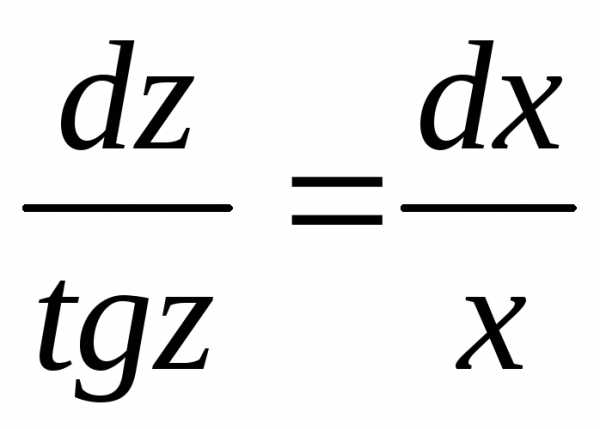 и интегрируем:
и интегрируем: ,
,
Заменяя zна ,
получим
,
получим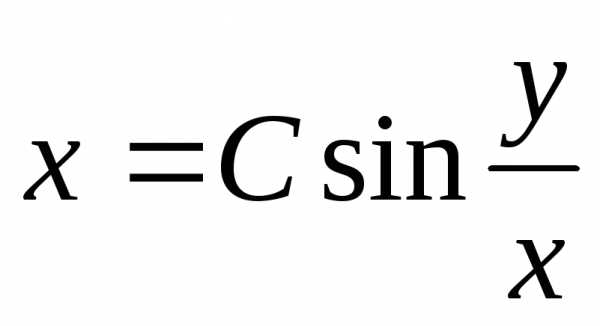 .
.
Δ В данном уравнении P (x,y)
=x2-2y2,Q(x,y)
=2xy– однородные
функции второго измерения, следовательно,
данное уравнение является однородным.
Его можно представить в виде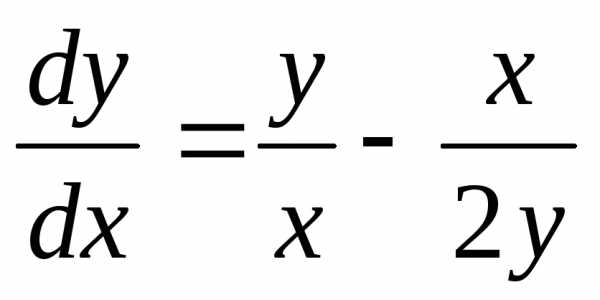 и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
,
то есть

или
dx+2
Разделяем переменные, считая 
 .
.
Интегрируем почленно это уравнение
 ,
откуда
,
откуда
то есть 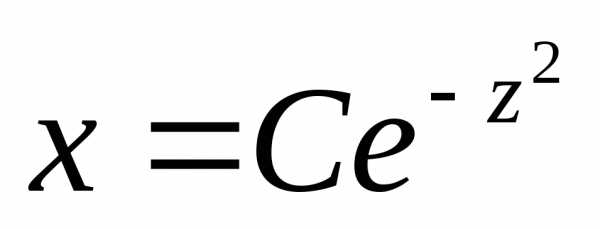 .
Возвращаясь к прежней функции
.
Возвращаясь к прежней функции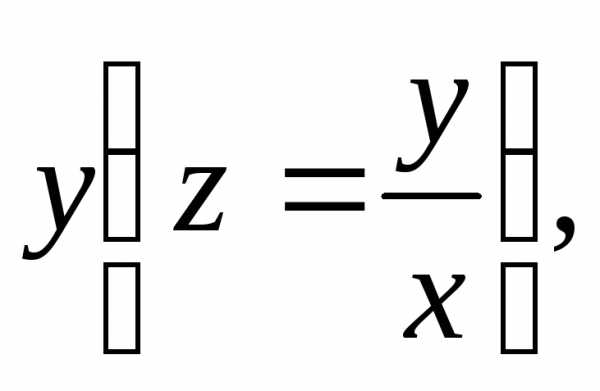 находим общее решение
находим общее решение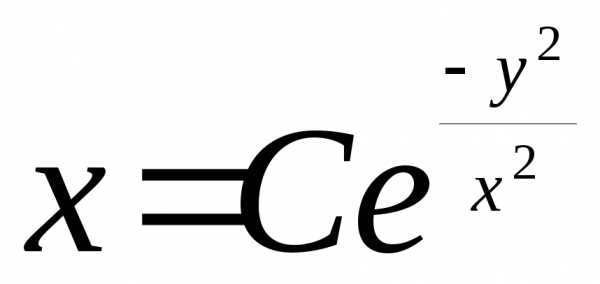
Пример 3. Найти общее
решение уравнения
Δ
Цепочка преобразований:  ,y = zx,,
,y = zx,,  ,
, 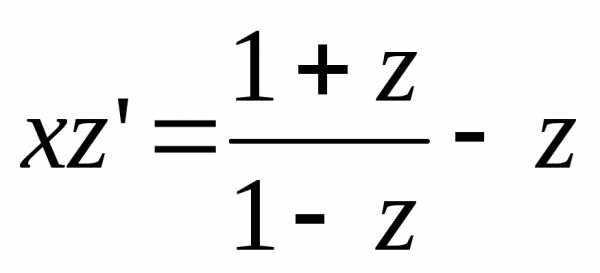 ,
,  ,
,  ,
,
, , , .
,
,
, , , .
Лекция 8.
4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
, | (4.1) |
 ,
, ,c(x) –
непрерывные функции.
,c(x) –
непрерывные функции. Если ,
то уравнение (4.1) можно записать в
приведённом виде
,
то уравнение (4.1) можно записать в
приведённом виде
(4.1a) |
Здесь – свободный член, называемый также правой частью уравнения. В этом виде будем рассматривать линейное уравнение в дальнейшем.
Если  0,
то уравнение (4.1а) называется линейным
неоднородным. Если же
0,
то уравнение (4.1а) называется линейным
неоднородным. Если же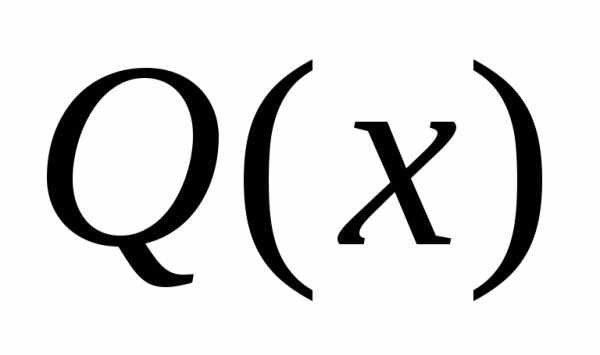 0, то уравнение принимает вид
0, то уравнение принимает вид
(4.2) |
и называется линейным однородным.
Название уравнения (4.1а) объясняется
тем, что неизвестная функция y и её производная входят в него линейно, т.е. в первой
степени.
входят в него линейно, т.е. в первой
степени.
В линейном однородном уравнении
переменные разделяются. Переписав его
в виде  откуда
откуда и интегрируя, получаем:,т.е.
и интегрируя, получаем:,т.е.
| (4.3) |
При делении на  теряем решение
теряем решение .
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
.
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций отх:
(4.4) |
Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).
Дифференцируя обе части равенства (4.4), находим .
Подставляя полученное выражение
производной  ,
а также значениеу в уравнение (4.1а), получаем,
или
,
а также значениеу в уравнение (4.1а), получаем,
или
. | (4.5) |
Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы
| (4.6) |
т.е. в качестве функции vвозьмём решение однородного линейного уравнения (4.6):
. | (4.3а) |
Ввиду произвольности в выборе v,мы можем не учитывать произвольную постояннуюС (точнее – можем приравнять её нулю). Подставляя найденное значениеv(x) в уравнение (4.5), получим, учитывая (4.6):
| (4.7) |
откуда
(4.8) |
(Здесь Cписать обязательно, иначе получится не общее, а частное решение).
Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).
Подставляя  иv(x) в
формулу (4.4), окончательно получаем
иv(x) в
формулу (4.4), окончательно получаем
,
или
. | (4.9) |
Пример 1.Найти общее решение
уравнения
Положим 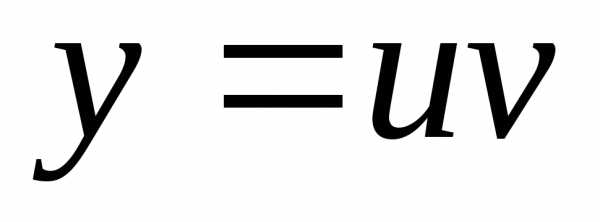 ,
тогда
,
тогда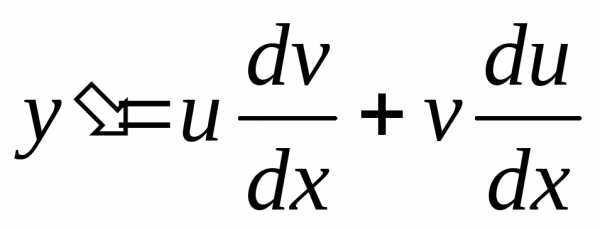 .
Подставляя выражения
.
Подставляя выражения и
и в
исходное уравнение, получимили(*)
в
исходное уравнение, получимили(*)
Приравняем нулю коэффициент при  :
: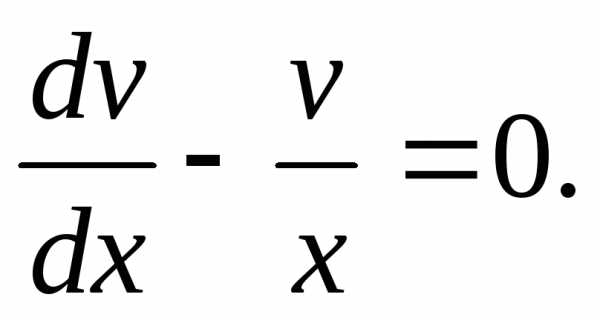
Разделяя переменные в полученном
уравнении, имеем 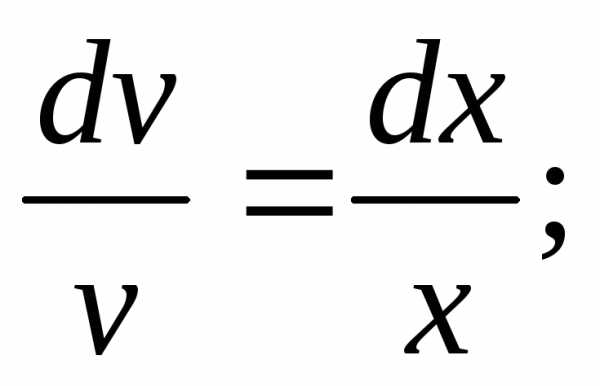

 (произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
(произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
 ,,
,,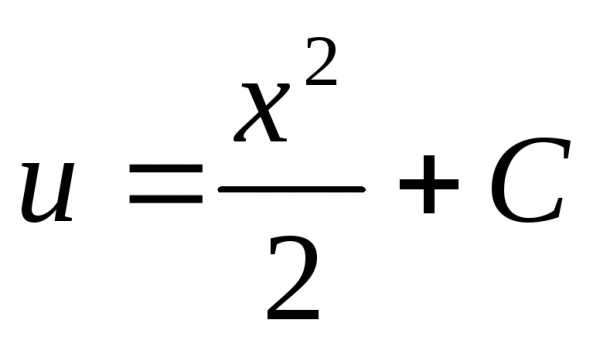 .
.
Следовательно, 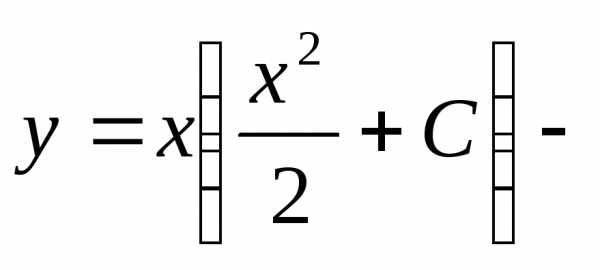 общее
решение исходного уравнения.
общее
решение исходного уравнения.
Отметим, что уравнение (*) можно было записать в эквивалентном виде:
.
Произвольно выбирая функцию u,
а неv, мы могли полагать .
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
.
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.
Приводим рассматриваемое уравнение к виду.
Используя подстановку
 ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.Группируем члены уравнения, выносим одну из функций uилиvза скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.
Записываем общее решение, подставив выражения для найденных функций u иvв равенство
 .
.Если требуется найти частное решение, то определяем Сиз начальных условий и подставляем в общее решение.
Отметим далее, что иногда уравнение первого порядка становится линейным, если усчитать независимой переменной, аx– зависимой, т.е. поменять ролиx иy. Это можно сделать при условии, чтоxиdxвходят в уравнение линейно.
Пример 2. Решить уравнение .
Однако если рассматривать xкак функцию оту, то, учитывая, что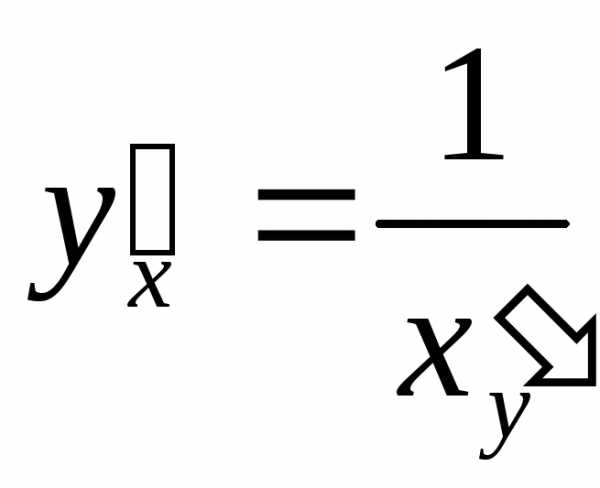 ,его
можно привести к виду
,его
можно привести к виду
| (4.1 б) |
Заменив  на
на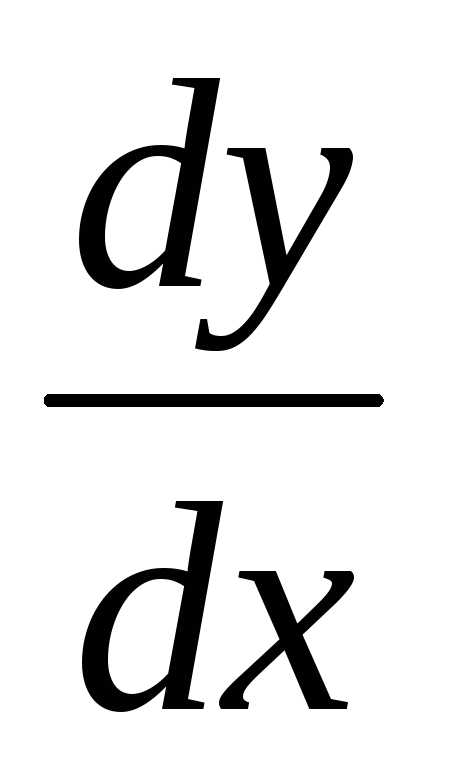 ,получим
,получим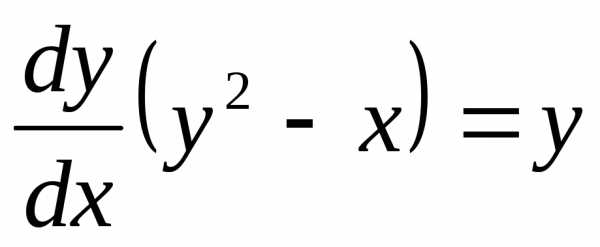 или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
 , или
, или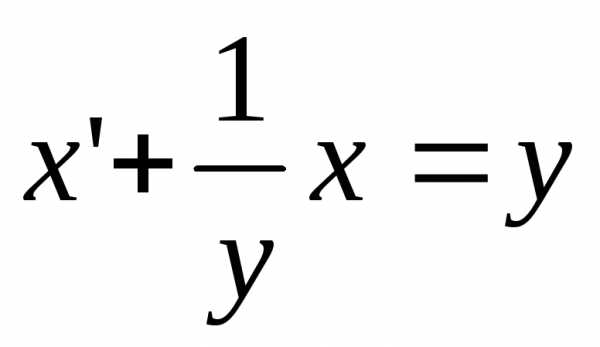 .
(**)
.
(**)
Здесь P(y)= ,
,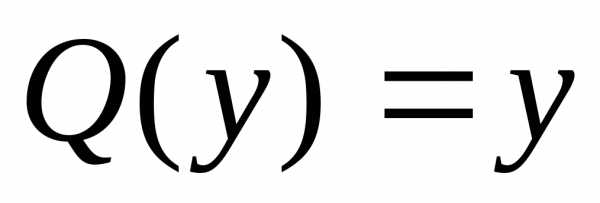 .
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
.
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
или.
Выберем vтак, чтобы ,
,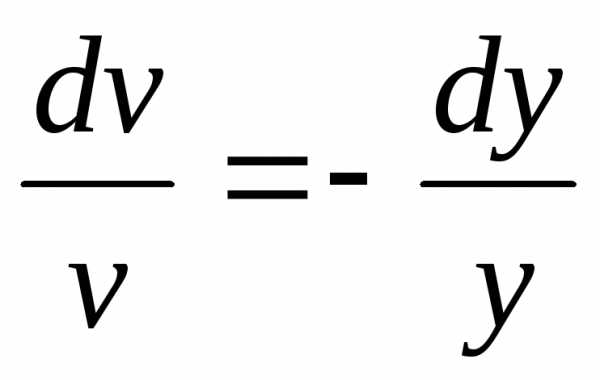 ,
откуда
,
откуда ;
;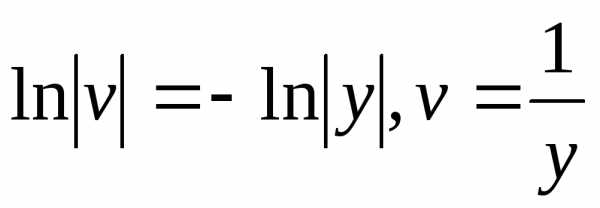 .
Далее имеем
.
Далее имеем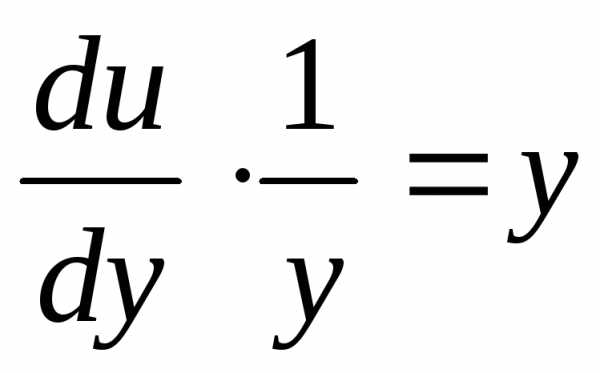 ,
, ,
,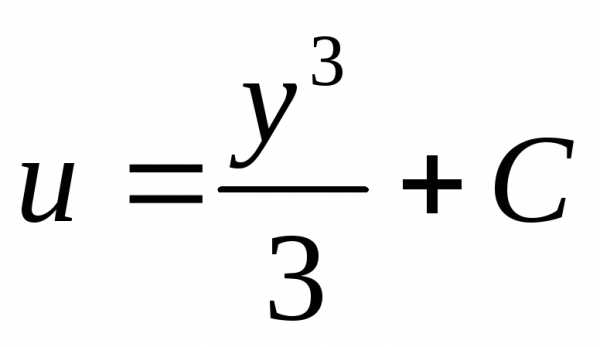 .
.
Т.к. , то приходим к общему решению данного уравнения в виде
 .
.
Отметим, что в уравнение (4.1а) P(x) иQ (x) могут входить не только в виде функций от x, но и констант:P=a,Q=b. Линейное уравнение
(4.10) |
можно решать и с помощью подстановки y=uv и разделением переменных:
 ;
; .
.
Отсюда  ;;;
где
;;;
где .
Освобождаясь от логарифма, получаем
общее решение уравнения
.
Освобождаясь от логарифма, получаем
общее решение уравнения
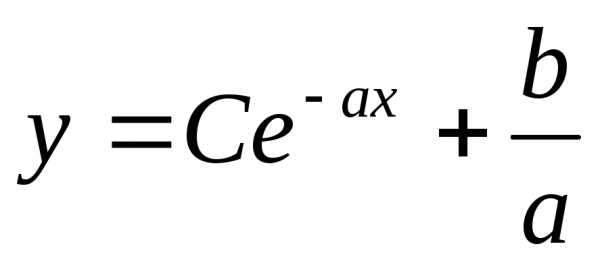 (здесь
(здесь ).
).
При b=0 приходим к решению уравнения
| (4.10а) |
в виде
| (4.11) |
(см. уравнение показательного роста
(2.4) при 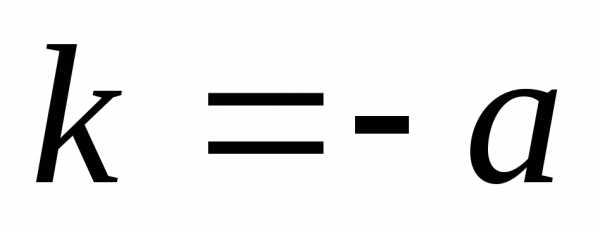 ).
).
Применим далее для интегрирования неоднородного линейного уравнения (4.1а) метод вариации произвольной постоянной (метод Лагранжа).
Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель Св (4.3) функцией отх, т.е. по существу делаем замену переменной
, | (4.3а) |
где C(x)-новая
неизвестная функцияx.
Подставляя производнуюв исходное неоднородное уравнение
(4.1а), получим: ,
или
,
или
, | (4.12) |
откуда, интегрируя, находим
dx+C1, | (4.13) |
где С1-постоянная. Следовательно,
. | (4.14) |
Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).
При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).
Применим метод Лагранжа к уравнению, рассмотренному в примере 1:
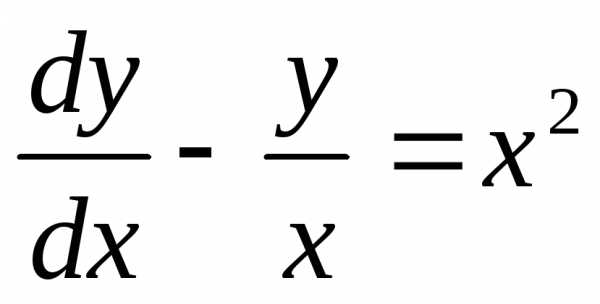 .
.
Интегрируем соответствующее однородное
уравнение  .
.
Разделяя переменные, получаем 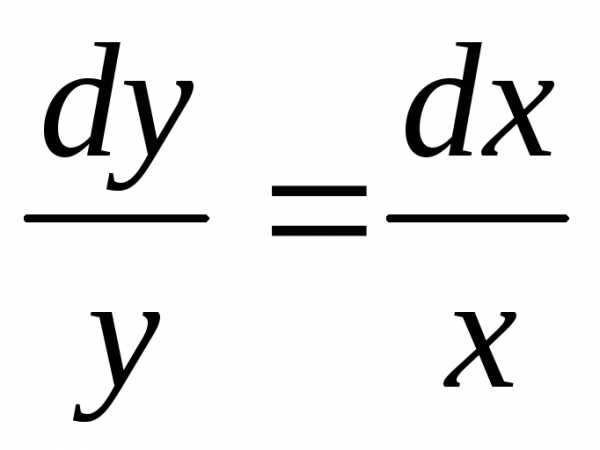 и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим;
и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим;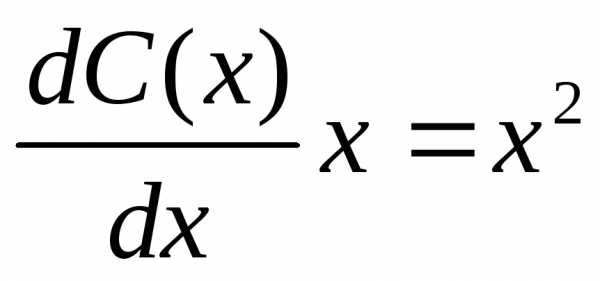 ;,
;, .
Общее решение исходного уравнения имеет
вид
.
Общее решение исходного уравнения имеет
вид
.
В заключение отметим, что к линейному уравнению приводится уравнение Бернулли
,
( | (4.15) |
которое можно записать в виде
. | (4.15а) |
Заменой  оно приводится к линейному уравнению:
оно приводится к линейному уравнению:
 ,
, ,.
,.
Уравнения Бернулли также решаются изложенными выше методами.
Пример 3. Найти общее решения уравнения.
Цепочка преобразований: 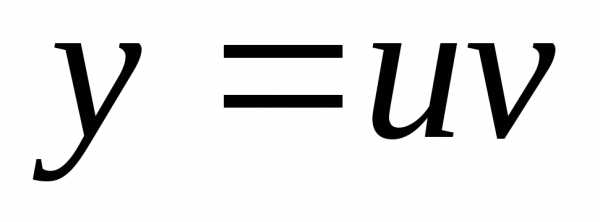 ,,,,
,,,, ,
, ,
,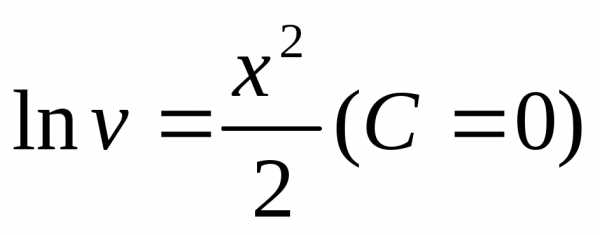 ,
, ,
, ,
, ,
,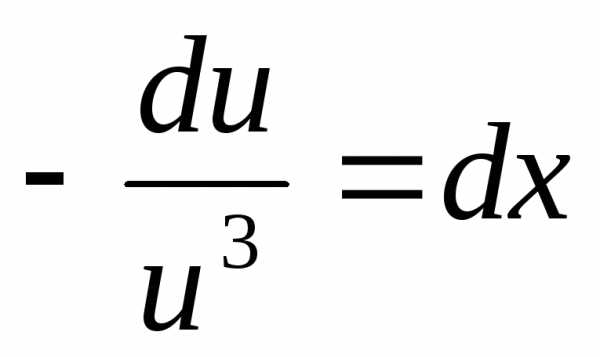 ,
, ,
,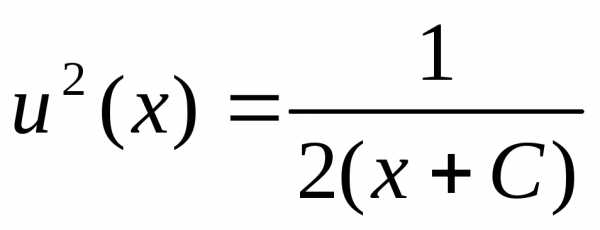 ,,
,,
studfiles.net
Однородные дифференциальные уравнения первого порядка
Легко можно убедиться в том, что дифференциальные уравнения
не являются уравнениями с разделяющимися переменными. Они являются однородными уравнениями.
Определение. Дифференциальное уравнение
называетсяоднородным
дифференциальным уравнением первого
порядка, если 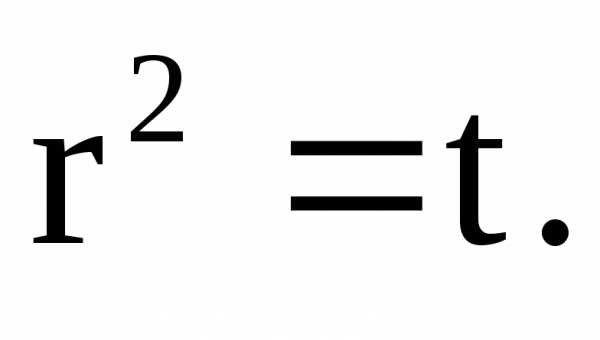 – однородная функция нулевого измерения.
– однородная функция нулевого измерения.
Дадим понятие однородной функции нулевого измерения.
Определение. Функция 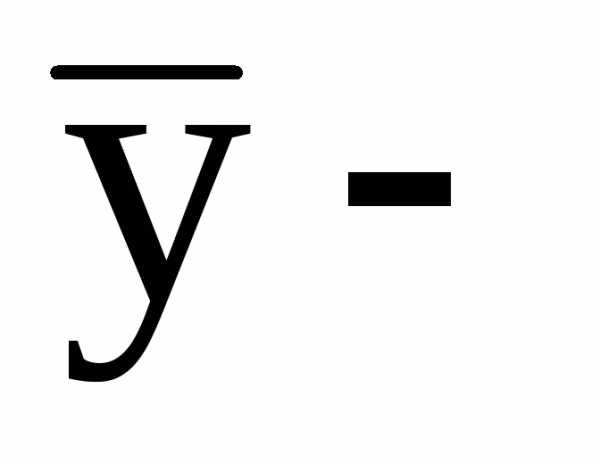 называетсяоднородной
функцией нулевого измерения, если при любом t
справедливо тождество
называетсяоднородной
функцией нулевого измерения, если при любом t
справедливо тождество
Так, функции 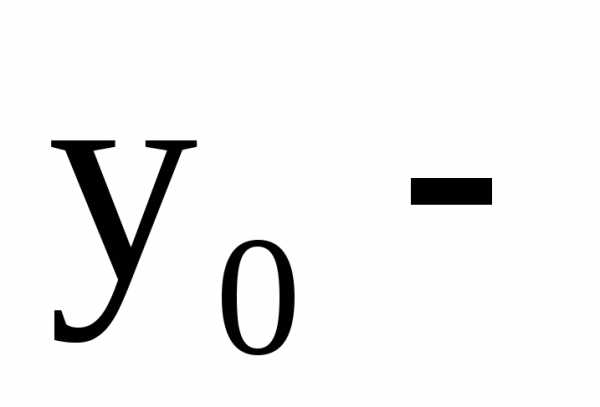 – однородные функции нулевого измерения,
т. к.
– однородные функции нулевого измерения,
т. к.
Чтобы проверить, является ли д. у.1 однородным уравнением, нужно в этом уравнении заменить Если после этогоt всюду сократится и получится первоначальное уравнение, то данное уравнение – однородное.
Поэтому уравнение является однородным. Действительно,
сократив уравнение на t, получим исходное уравнение.
Решение однородного дифференциального уравнения первого порядка
Так как функция  в правой части уравненияявляется однородной функцией нулевого
измерения, то, по определению,Положим в этом тождестве
в правой части уравненияявляется однородной функцией нулевого
измерения, то, по определению,Положим в этом тождестве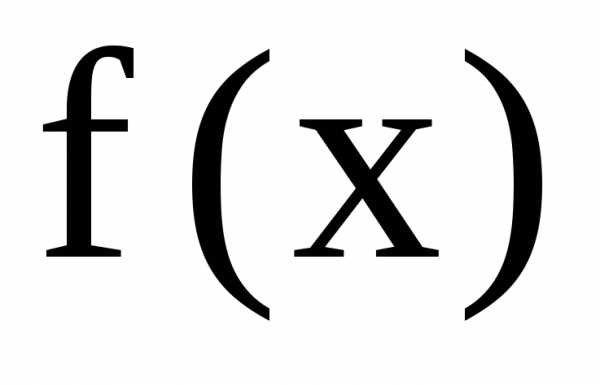 получим
получим 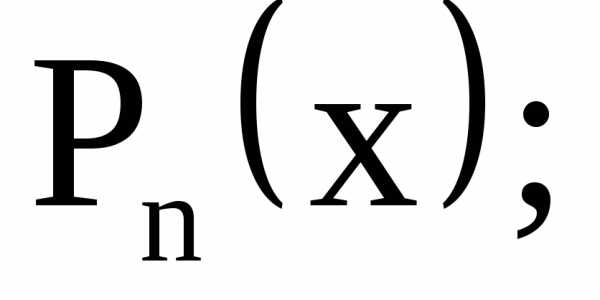 т. е. однородная функция нулевого
измерения зависит только от отношения у/х. Д.у.1 в этом случае примет вид
т. е. однородная функция нулевого
измерения зависит только от отношения у/х. Д.у.1 в этом случае примет вид

Сделаем подстановку y/x=u, т. е.
где неизвестная функция.
Тогда
Уравнение 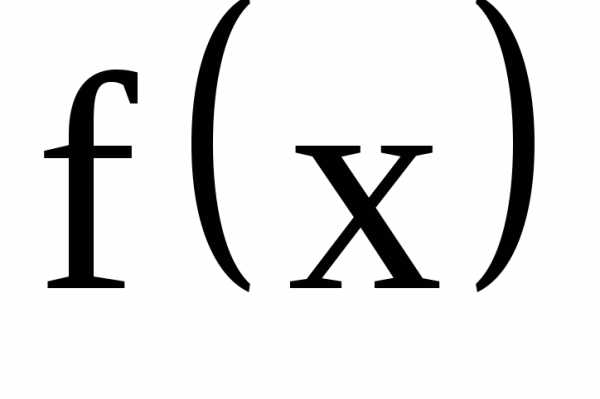 примет видилиили
примет видилиили – уравнение с разделяющимися переменными.
– уравнение с разделяющимися переменными.
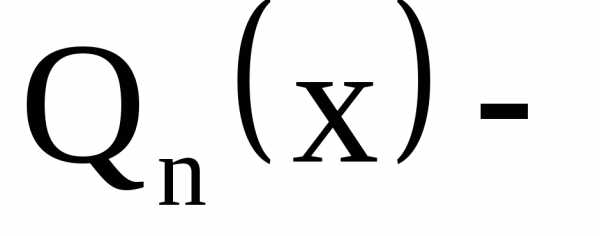
Интегрируя, находим
Найдя отсюда выражение u как функции от x, подставим его в равенство получим искомое общее решение однородного д.у.1. Чаще всего не уда-
ется найти явное
выражение функции  Тогда после интегрирования следует
Тогда после интегрирования следует
в левую часть
вместо u
подставить  В результате получим общий интеграл
(т. е. общее решение в неявном виде).
В результате получим общий интеграл
(т. е. общее решение в неявном виде).
Решим уравнения.
Пример 1. Найти общее решение дифференциального уравнения

Решаем уравнение
подстановкой Подставив  в данное уравнение, получим
в данное уравнение, получим
или 
Получили
дифференциальное уравнение с разделяющимися
переменными относительно вспомогательной
функции  Упростим правую часть:
Упростим правую часть:
 Умножив на
Умножив на  ,
получим уравнение с разделенными
переменными
,
получим уравнение с разделенными
переменными
Интегрируя, получим
или
или 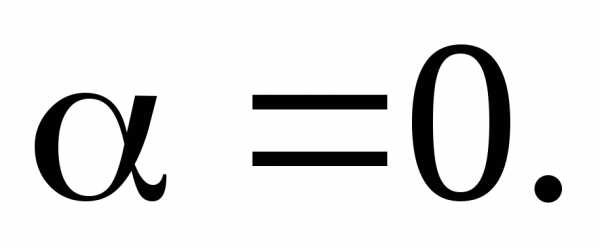
Потенцируем
Подставив 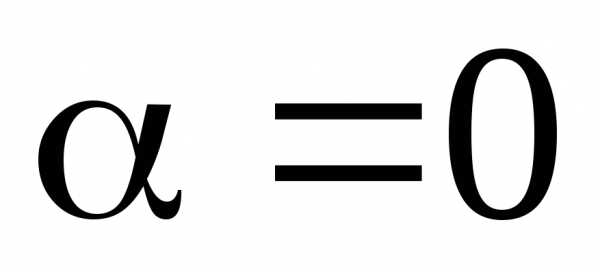 получим общий интеграл данного
дифференциального уравнения.
получим общий интеграл данного
дифференциального уравнения.
Проверка: 
или – искомое уравнение.
Пример 2. Найти частное решение дифференциального уравнения
при начальных
условиях 
Убедимся, что
данное дифференциальное уравнение
является однородным. Подставим в
уравнение вместо  соответственно
Получим
соответственно
Получим
Разделив на t обе части уравнения, получим данное уравнение. Решаем уравнение подстановкой
Поставим  в уравнение, получим
в уравнение, получим
Сгруппируем слагаемые с .
–это уравнение с разделяющимися переменными. Разделив обе части на получим
–уравнение с разделенными переменными. Интегрируя левую и правую части уравнения, получим
Подставив  получим общий интеграл данного
дифференциального уравнения:
получим общий интеграл данного
дифференциального уравнения:
Найдем частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям
Подставим в формулу общего интеграла
отсюда  и частный интеграл
и частный интеграл

studfiles.net
Однородные дифференциальные уравнения 1-ого порядка
Определение и формулы однородных ДУ первого порядка
Уравнение вида (1) заменой
(или ) сводится к уравнению с разделяющимися переменными относительно новой функции :
или
Общий интеграл уравнения:
Интеграл, стоящий в правой части, табличный, тогда:
Необходимо рассмотреть еще особый случай . Если это уравнение имеет корни, то они являются и решением уравнения . Но это уравнение не совпадает с исходным дифференциальным уравнением, поэтому надо убедиться, что решения уравнения удовлетворяют исходному уравнению (1).
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
как решить однородное дифференциальное уравнение
Чтобы решить однородное дифференциальное уравнение 1-го порядка, используют подстановку u=y/x, то есть u — новая неизвестная функция, зависящая от икса. Отсюда y=ux. Производную y’ находим с помощью правила дифференцирования произведения:y’=(ux)’=u’x+x’u=u’x+u (так как x’=1). Для другой формы записи: dy=udx+xdu.После подстановки уравнение упрощаем и приходим к уравнению с разделяющимися переменными.
Примеры решения однородных дифференциальных уравнений 1-го порядка.
1) Решить уравнение
Решение:
Проверяем, что это уравнение является однородным (см. Как определить однородное уравнение). Убедившись, делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем: u’x+u=u(1+ln(ux)-lnx). Так как логарифм произведения равен сумме логарифмов, ln(ux)=lnu+lnx. Отсюда
u’x+u=u(1+lnu+lnx-lnx). После приведения подобных слагаемых: u’x+u=u(1+lnu). Теперь раскрываем скобки
u’x+u=u+u·lnu. В обеих частях стоит u, отсюда u’x=u·lnu. Поскольку u — функция от икса, u’=du/dx. Подставляем,
Получили уравнение с разделяющимися переменными. Разделяем переменные, для чего обе части умножаем на dx и делим на x·u·lnu, при условии, что произведение x·u·lnu≠0
Интегрируем:
В левой части — табличный интеграл. В правой — делаем замену t=lnu, откуда dt=(lnu)’du=du/u
ln│t│=ln│x│+C. Но мы уже обсуждали, что в таких уравнениях вместо С удобнее взять ln│C│. Тогда
ln│t│=ln│x│+ln│C│. По свойству логарифмов: ln│t│=ln│Сx│. Отсюда t=Cx. ( по условию, x>0). Пора делать обратную замену: lnu=Cx. И еще одна обратная замена:
По свойству логарифмов:
Это — общий интеграл уравнения.
Вспоминаем условие произведение x·u·lnu≠0 (а значит, x≠0,u≠0, lnu≠0, откуда u≠1). Но x≠0 из условия, остается u≠1, откуда x≠y. Очевидно, что y=x ( x>0) входят в общее решение.
Ответ:
2) Найти частный интеграл уравнения y’=x/y+y/x, удовлетворяющий начальным условиям y(1)=2.
Решение:
Сначала проверяем, что это уравнение является однородным (хотя наличие слагаемых y/x и x/y уже косвенно указывает на это). Затем делаем замену u=y/x, откуда y=ux, y’=(ux)’=u’x+x’u=u’x+u. Подставляем полученные выражения в уравнение:
u’x+u=1/u+u. Упрощаем:
u’x=1/u. Так как u — функция от икса, u’=du/dx:
Получили уравнение с разделяющимися переменными. Чтобы разделить переменные, умножаем обе части на dx и u и делим на x (x≠0 по условию, отсюда u≠0 тоже, значит, потери решений при этом не происходит).
Интегрируем:
и поскольку в обеих частях стоят табличные интегралы, сразу же получаем
Выполняем обратную замену:
Это — общий интеграл уравнения. Используем начальное условие y(1)=2, то есть подставляем в полученное решение y=2, x=1:
Ответ:
3) Найти общий интеграл однородного уравнения:
(x²-y²)dy-2xydx=0.
Решение:
Замена u=y/x, откуда y=ux, dy=xdu+udx. Подставляем:
(x²-(ux)²)(xdu+udx)-2ux²dx=0. Выносим x² за скобки и делим на него обе части (при условии x≠0):
x²(1-u²)(xdu+udx)-2ux²dx=0
(1-u²)(xdu+udx)-2udx=0. Раскрываем скобки и упрощаем:
xdu-u²xdu+udx-u³dx-2udx=0,
xdu-u²xdu-u³dx-udx=0. Группируем слагаемые с du и dx:
(x-u²x)du-(u³+u)dx=0. Выносим общие множители за скобки:
x(1-u²)du-u(u²+1)dx=0. Разделяем переменные:
x(1-u²)du=u(u²+1)dx. Для этого обе части уравнения делим на xu(u²+1)≠0 (соответственно, добавляем требования x≠0 (уже отметили), u≠0):
Интегрируем:
В правой части уравнения — табличный интеграл, рациональную дробь в левой части раскладываем на простые множители:
(или во втором интеграле можно было вместо подведения под знак дифференциала сделать замену t=1+u², dt=2udu — кому какой способ больше нравится). Получаем:
По свойствам логарифмов:
Обратная замена
Вспоминаем условие u≠0. Отсюда y≠0. При С=0 y=0, значит, потери решений не происходит, и y=0 входит в общий интеграл.
Ответ:
Замечание
Можно получить запись решения в другом виде, если слева оставить слагаемое с x:
Геометрический смысл интегральной кривой в этом случае — семейство окружностей с центрами на оси Oy и проходящих через начало координат.
Задания для самопроверки:
1) (x²+y²)dx-xydy=0
2)
Показать решение
1) Проверяем, что уравнение является однородным, после чего делаем замену u=y/x, откуда y=ux, dy=xdu+udx. Подставляем в условие: (x²+x²u²)dx-x²u(xdu+udx)=0. Разделив обе части уравнения на x²≠0, получаем: (1+u²)dx-u(xdu+udx)=0. Отсюда dx+u²dx-xudu-u²dx=0. Упростив, имеем: dx-xudu=0. Отсюда xudu=dx, udu=dx/x. Интегрируем обе части:
где С=(С1)².
Так как u=y/x, u²=y²/x², то есть y²=u²x²,
Ответ:
2) Проверив, что данное уравнение является однородным, делаем замену y=ux, отсюда y’=u’x+u. Подставляем в условие:
Делим обе части уравнения на x:
Упрощаем:
Интегрируем обе части:
Так как u=y/x, то
и, умножив на x обе части уравнения, получаем:\
Ответ:
www.matematika.uznateshe.ru
Однородные уравнения первого порядка
Понятие однородного уравнения
Дифференциальное уравнение первого порядка, представленное в стандартном виде $y’=f\left(x,y\right)$, является однородным, если его правая часть зависит не просто от переменных $x$ и $y$, а от отношения функции $y$ к независимой переменной $x$, то есть $ f (x,y) = f (x/y)$.
Зависимость функции от отношения $\frac{y}{x} $ следует понимать так, что функция не изменяется при замене в ней данного отношення на любое другое, имеющее вид $\frac{t\cdot y}{t\cdot x} $. Например, именно такое свойство имеет функция $f\left(x,y\right)=\frac{y}{x} \cdot \cos \frac{y}{x} $. Действительно, $f\left(x,y\right)=\frac{y}{x} \cdot \cos \frac{y}{x} =\frac{t\cdot y}{t\cdot x} \cdot \cos \frac{t\cdot y}{t\cdot x} $. После замены переменных $x$ и $y$ на $t\cdot x$ и $t\cdot y$ соответственно и последующего сокращения на $t$ данная функция приобретает свой исходный вид. В этом и состоит основное свойство однородного дифференциального уравнения.
Общий метод решения
Однородное дифференциальное уравнение $y’=f (x/y)$ решают посредством применения замены $\frac{y}{x} =u$, где $u=u\left(x\right)$ — новая неизвестная функция. Идея состоит в том, что найдя функцию $u$ и умножив её на $x$, можно будет найти и нужную функцию $y$.
Представим замену в виде $y=u\cdot x$ и продифференцируем её: $\frac{dy}{dx} =\frac{du}{dx} \cdot x+u\cdot \frac{dx}{dx} =\frac{du}{dx} \cdot x+u$. Подставим $y$ и $\frac{dy}{dx} $ в данное дифференциальное уравнение: $\frac{du}{dx} \cdot x+u=f\left(u\right)$.
Полученное дифференциальное уравнение представляет собой уравнение с разделяющимися переменными. Действительно, после элементарных преобразований его можно представить в виде $\frac{du}{dx} =\frac{f\left(u\right)-u}{x} $, где $f_{1} \left(x\right)=\frac{1}{x} $ — функция, зависящая только от $x$, и $f_{2} \left(u\right)=f\left(u\right)-u$ — функция, зависящая только от $u$. Применим к этому дифференциальному уравнению метод решения дифференциальных уравнений с разделяющимися переменными.
Сначала вычисляем интеграл $I_{1} =\int f_{1} \left(x\right)\cdot dx $. Получаем: $I_{1} =\int \frac{1}{x} \cdot dx=\ln \left|x\right| $. Теперь записываем интеграл $I_{2} =\int \frac{du}{f_{2} \left(u\right)} $. Получаем: $I_{2} =\int \frac{du}{f\left(u\right)-u} $. Общее решение записываем в форме $I_{2} =I_{1} +C$, то есть $\int \frac{du}{f\left(u\right)-u} =\ln \left|x\right|+C$. Правую часть полученного решения можно упростить, если представить произвольную постоянну в более удобной форме $\ln \left|C\right|$. При этом получим: $\ln \left|x\right|+\ln \left|C\right|=\ln \left|x\cdot C\right|$.
Окончательно получаем: $\int \frac{du}{f\left(u\right)-u} =\ln \left|x\cdot C\right|$. После вычисления интеграла $\int \frac{du}{f\left(u\right)-u} $ и замены $u$ на $\frac{y}{x} $ общее решение данного однородного дифференциального уравнения будет найдено.
Общий метод решения можно представить в виде следующего алгоритма:
- В первую очередь убеждаемся, что решаемое дифференциальное уравнение является однородным. Для этого нужно представить его в стандартном виде $y’=f\left(x,y\right)$, после чего в функции $f\left(x,y\right)$ переменные $x$ и $y$ заменить на $t\cdot x$ и $t\cdot y$ соответственно. Если после элементарных тождественных преобразований удается вернуться к той же функции $f\left(x,y\right)$, то данное дифференциальное уравнение является однородным и $ f (x,y) = f (x/y)$. Если добиться этого оказалось невозможным, то данное дифференциальное уравнение должно решаться иным методом.
- Находим $f\left(u\right)$, выполнив для функции $f (x/y)$ замену $y=u\cdot x$, после чего записываем функцию $f\left(u\right)-u$.
- Находим интеграл $I=\int \frac{du}{f\left(u\right)-u} $ и записываем общее решение в виде $I=\ln \left|x\cdot C\right|$.
- Выполняем обратную замену $u=\frac{y}{x} $ и проводим упрощающие тождественные преобразования.
- Находим особые решения, которые могли быть утрачены при разделении переменных.
Решение типичных задач
Задача 1
Найти общее решение дифференциального уравнения $y’=2+\frac{y}{x} $.
По внешнему виду данного дифференциального уравнения его можно сразу отнести к однородному.
Для функции $f (x/y)=2+\frac{y}{x} $ выполняем замену $y=u\cdot x$ и находим $f\left(u\right)=2+\frac{u\cdot x}{x} =2+u$. Записываем функцию $f\left(u\right)-u=2+u-u=2$.
Находим интеграл $I=\int \frac{du}{f\left(u\right)-u} =\int \frac{du}{2} =\frac{u}{2} $.
Записываем общее решение в виде $\frac{u}{2} =\ln \left|x\cdot C\right|$.
Выполняем обратную замену $u=\frac{y}{x} $ и получаем $\frac{y}{2\cdot x} =\ln \left|x\cdot C\right|$ или $y=2\cdot x\cdot \ln \left|x\cdot C\right|$.
Так как $f\left(u\right)-u=2$, то особых решений данное дифференциальное уравнение не имеет.
Задача 2
Найти общее решение дифференциального уравнения $x\cdot y’=5\cdot y+x$.
Приводим данное дифференциальное уравнение к стандартному виду $y’=5\cdot \frac{y}{x} +1$, после чего можно сделать вывод, что оно является однородным.
Для функции $f (x/y)=5\cdot \frac{y}{x} +1$ выполняем замену $y=u\cdot x$ и находим $f\left(u\right)=5\cdot \frac{u\cdot x}{x} +1=5\cdot u+1$.
Записываем функцию $f\left(u\right)-u=5\cdot u+1-u=4\cdot u+1$.
Находим интеграл $I=\int \frac{du}{f\left(u\right)-u} =\int \frac{du}{4\cdot u+1} =\frac{1}{4} \cdot \ln \left|4\cdot u+1\right|$.
Записываем общее решение в виде $\frac{1}{4} \cdot \ln \left|4\cdot u+1\right|=\ln \left|x\cdot C\right|$, откуда $\ln \left|4\cdot u+1\right|=\ln \left|x\cdot C\right|^{4} $; $4\cdot u+1=x^{4} \cdot C^{4} $ или просто $4\cdot u+1=C\cdot x^{4} $.
Выполняем обратную замену $u=\frac{y}{x} $ и получаем $4\cdot \frac{y}{x} +1=C\cdot x^{4} $.
Таким образом, общее решение имеет вид: $4\cdot y+x=C\cdot x^{5} $.
Решая уравнение $f\left(u\right)-u=4\cdot u+1=0$ или $4\cdot \frac{y}{x} +1=0$, находим особое решение $y=-\frac{x}{4} $. Проверка подстановкой в данное дифференциальное уравнение $x\cdot \left(-\frac{1}{4} \right)=5\cdot \left(-\frac{x}{4} \right)+x$ показывает, что особое решение $y=-\frac{x}{4} $ удовлетворяет данному дифференциальному уравнению.
Однако это же решение можно получить из общего решения $4\cdot y+x=C\cdot x^{5} $, положив в нём $C=0$.
Таким образом, окончательный результат: $4\cdot y+x=C\cdot x^{5} $.
Уравнения, приводящиеся к однородным
При определенных условиях дифференциальное уравнение вида $y’=\frac{a_{1} \cdot x+b_{1} \cdot y+c_{1} }{a_{2} \cdot x+b_{2} \cdot y+c_{2} } $, в котором $a_{1} $, $b_{1} $, $c_{1} $, $a_{2} $, $b_{2} $, $c_{2} $ — постоянные коэффициенты, может быть приведено к однородному.
Если $\Delta \equiv \left|\begin{array}{cc} {a_{1} } & {b_{1} } \\ {a_{2} } & {b_{2} } \end{array}\right|\ne 0$, то приведение его к однородному достигается с помощью замен $x=m+\alpha $ и $y=n+\beta $, где постоянные $\alpha $ и $\beta $ следует выбрать как результат решения системы $\left\{\begin{array}{c} {a_{1} \cdot \alpha +b_{1} \cdot \beta =-c_{1} } \\ {a_{2} \cdot \alpha +b_{2} \cdot \beta =-c_{2} } \end{array}\right. $.
Так как $\Delta \ne 0$, то эта система имеет единственное решение, которое проще всего найти по формулам Крамера.
Используя найденные выражения для $x=m+\alpha $ и $y=n+\beta $, получим дифференциальное уравнение $\frac{dn}{dm} =\frac{a_{1} \cdot m+b_{1} \cdot n}{a_{2} \cdot m+b_{2} \cdot n} $, которое является однородным.
spravochnick.ru

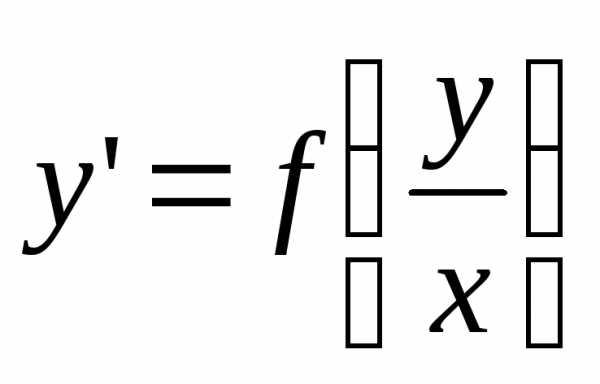

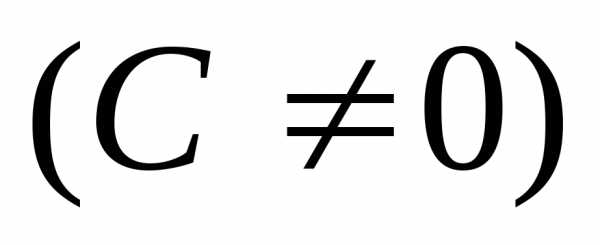
 ,
, ,
, ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.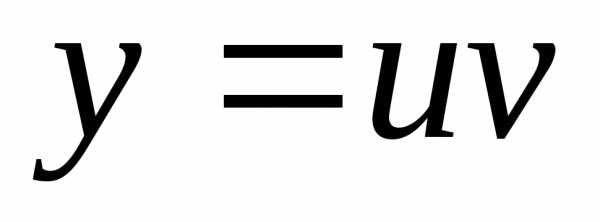 .
.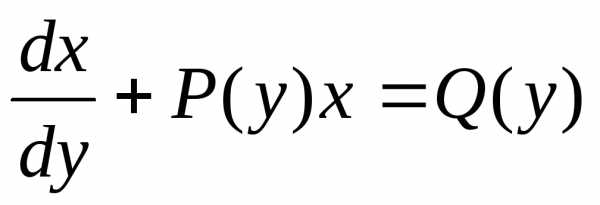

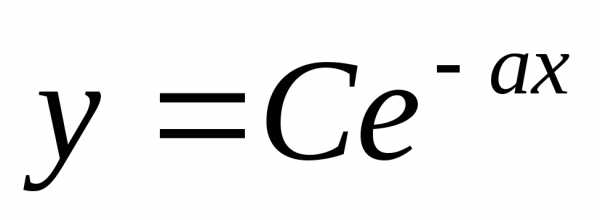
 )
)