Дробная степень | Алгебра
Какими свойствами обладает степень с дробным показателем (дробная степень)? Как выполнить возведение числа в дробную степень?
Определение.
1) Степенью числа a (a>0) с рациональным показателем r
где m — целое число, n — натуральное число (n>1), называется число
2) При a=0 и r>0
В частности,
При a<0 степень с дробным показателем не определяется.
Все свойства степеней из курса алгебры 7 класса выполняются и для степеней с рациональными показателями.
Для упрощения вычислений при возведении числа в дробную степень удобно использовать таблицу степеней и следующее свойство корня:
Примеры.
Выполнить возведение в дробную степень:
Если показатель степени — десятичная дробь, нужно предварительно перевести ее в обыкновенную.
Смешанное число нужно предварительно перевести в неправильную дробь:
www.algebraclass.ru
| 1. |
Произведение в виде степени (положительные числа)
Сложность: лёгкое |
3,5 |
| 2. |
Основание и показатель степени (числа)
Сложность: лёгкое |
3 |
| 3. |
Степень бинома
Сложность: лёгкое |
1,5 |
| 4. |
Основание и показатель степени (бином)
Сложность: лёгкое |
2 |
| 5. |
Произведение одинаковых множителей (одночлен)
Сложность: лёгкое |
1 |
| 6. |
Произведение одинаковых множителей (бином)
|
1 |
| 7. |
Степень числа (показатель степени — n)
Сложность: лёгкое |
2 |
| 8. |
Степень числа (основание)
Сложность: лёгкое |
2 |
| 9. | Сложность: лёгкое |
2 |
| 10. |
Площадь квадрата
Сложность: лёгкое |
2 |
| 11. |
Квадрат числа (минус перед числом)
Сложность: лёгкое |
2 |
|
Числовые неравенства, сравнение
Сложность: лёгкое |
1 | |
| 13. |
Возведение в степень десятичных дробей
Сложность: лёгкое |
1 |
| 14. |
Возведение в степень целых чисел
Сложность: лёгкое |
1 |
| 15. |
Возведение в степень дробей (смешанных чисел)
Сложность: среднее |
2 |
| 16. |
Произведение степеней и простых чисел
Сложность: среднее |
3 |
| 17. |
Произведение (целые числа)
Сложность: среднее |
3 |
| 18. |
Частное (чётная степень)
Сложность: среднее |
3 |
| 19. |
Дробь
Сложность: среднее |
3 |
| 20. |
Разность произведений
Сложность: среднее |
4 |
| 21. |
Сумма произведений
Сложность: среднее |
5 |
| 22. |
Уравнение
Сложность: среднее |
5 |
| 23. |
Убывание (возрастание) степеней
Сложность: среднее |
4 |
www.yaklass.ru
Таблица основных степеней. Видеоурок. Алгебра 7 Класс
На этом уроке мы рассмотрим таблицу основных степеней.
Вначале вспомним определение степени. Затем составим таблицу основных степеней чисел от 1 до 10 и решим ряд задач с ее использованием.
Тема: Степень с натуральным показателем и ее свойства
Урок: Таблица основных степеней
Напоминание определения:
Здесь a — основание степени,
n— показатель степени,
— n-ая степень числа.
Из определения степени получаем таблицу основных степеней, где основание – простые числа в пределах 10.
Таблица основных степеней:
|
|
|||
|
|
|
||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямая и обратная задачи
1) Вычислить Решение:
По определению степени:
2) Число 729 записать в виде степени.
Решение основано на основной теореме арифметики. Видим, что 729 делится на 3. Разложим число 729 по степеням 3.
|
729 |
3 |
|
243 |
3 |
|
81 |
3 |
|
27 |
3 |
|
9 |
3 |
|
3 |
3 |
|
1 |
|
Получаем, что.
3) Число 256 записать в виде степени.
Разлагаем данное число по степеням двойки по основной теореме арифметики.
|
256 |
2 |
|
128 |
2 |
|
64 |
2 |
|
32 |
2 |
|
16 |
2 |
|
8 |
2 |
|
4 |
2 |
|
2 |
2 |
|
1 |
|
Получаем, что.
Задача: дано . Сравнить n и k.
Решение:
По таблице или по основной теореме арифметики находим:
n = 7, k = 5
Ответ:
Для практических вычислений удобно продолжить таблицу для чисел 1, 0, -1, 10.
Продолжение таблицы для чисел 1; 0; — 1; 10
(сводка правил)
n – натуральное число.
Решим задачи на таблицу (или основную теорему арифметики).
Задача: Найти k, если:
а)
Разлагаем 512 по основной теореме арифметики либо используем таблицу степеней.
|
512 |
2 |
|
256 |
2 |
|
128 |
2 |
|
64 |
2 |
|
32 |
2 |
|
16 |
2 |
|
8 |
2 |
|
4 |
2 |
|
2 |
2 |
|
1 |
|
Ответ: .
б)
Разлагаем по основной теореме арифметики либо используем таблицу степеней.
|
625 |
5 |
|
125 |
5 |
|
25 |
5 |
|
5 |
5 |
|
1 |
|
Ответ: .
в)
Разлагаем по основной теореме арифметики либо используем таблицу степеней.
|
343 |
7 |
|
49 |
7 |
|
7 |
7 |
|
1 |
|
Ответ: .
г)
Разлагаем по основной теореме арифметики либо используем таблицу степеней. Видим, что делится на 3, так как сумма цифр 18 делится на 3.
|
3 |
|
|
243 |
3 |
|
81 |
3 |
|
27 |
3 |
|
9 |
3 |
|
3 |
3 |
|
1 |
|
Ответ: .
Задача: Вычислить.
а)
б)
Задача: Представить в виде куба некоторого числа.
а) 125.
. Значит, .
Ответ:
б)
. Значит, .
Ответ:
в)
. Значит, .
Ответ: .
Итак, мы рассмотрели таблицу основных степеней, правило ее формирования и использование в различных типовых задачах.
Список рекомендованной литературы
1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.
Рекомендованные ссылки на ресурсы интернет
1. Школьная математика (Источник).
2. Инженерный справочник. Таблицы DVPA.info (Источник).
3. Образовательный онлайн сервис Webmath.ru (Источник).
4. Интернет-портал 2mb.ru (Источник).
Рекомендованное домашнее задание
1. Вычислить:
interneturok.ru
Степень с целым показателем.
I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:
Примеры. Вычислить:
Решение.
II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
Примеры. Вычислить:
Решение.
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:
Решение.
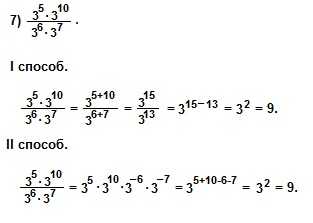При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
Пример 8 ) решаем так же, как решали пример 7) вторым способом.
В примере 9) представим 73как 72∙7, а степень 45как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
www.mathematics-repetition.com
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Пусть p – произвольное положительное рациональное число. Тогда это рациональное число можно представить в виде несократимой дроби
где m и n – натуральные числа. Предположим также, что a – произвольное положительное действительное число.
Теперь мы можем дать определение степени с рациональным показателем.
Определение. Степень, показатель которой есть положительное рациональное число, определяется по формуле:
Определение. Степень, показатель которой есть отрицательное рациональное число, определяется по формуле:
Определение. Степень с нулевым показателем определяется по формуле:
a0 = 1 .
Пример.
Свойства степеней с рациональными показателями
Для степеней с рациональными показателями выполняются следующие свойства:
Кроме того, если p и q – произвольные рациональные числа, то
Замечание. Желающие могут ознакомиться с нашей презентацией «Степень с рациональным показателем», содержание которой связано с данным разделом.
Понятие о степени с иррациональным показателем
Кроме степеней с рациональными показателями в математике и других точных науках большое значение имеют и степени с иррациональными показателями, однако их определение выходит за рамки курса средней школы. Упомянем лишь о том, что степень с иррациональным показателем строится с помощью предельного перехода по последовательностям степеней с рациональными показателями, которые являются приближениями иррационального показателя степени с недостатком и с избытком.
С понятиями степени с целочисленным показателем и арифметического корня можно ознакомиться в разделе «Степень с целочисленным показателем и арифметический корень» нашего справочника.
Графики степенных и показательных функций представлены в разделе «Графики степенных, показательных и логарифмических функций» нашего справочника.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Возведение в степень .
Комментарии преподавателя
На этом уроке мы изучим возведение степени в степень. Вначале вспомним определение степени и теоремы об умножении и делении степеней с одинаковым основанием. Далее будет сформулирована теорема о возведении степени в степень. Затем мы приведем примеры ее использования на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач и будем решать типичные примеры с помощью всех теорем.
Напоминание:
Основные определения:
Здесь a – основание степени,
n – показатель степени,
– n-ая степень числа.
Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:
При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.
Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:
При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.
На этом уроке будет рассмотрена следующая теорема.
Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:
Вывод: частные случаи подтвердили правильность формулы . Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.
По определению степени:
Применим теорему 1:
Итак, мы доказали: , где а – любое число, n и k – любые натуральные числа.
Другими словами, чтобы возвести степень в степень показатели нужно перемножить, а основание оставить неизменным.
Пример 1: Упростить.
Для решения следующи
www.kursoteka.ru
Степени чисел | Алгебра
Степени чисел, записанные на одной странице, пригодятся при решении многих заданий алгебры, содержащих степени и корни.
Любая степень единицы равна 1.
С помощью формулы это можно записать так:
Далее таблица первых десяти натуральных степеней чисел от 2 до 9 и степени 10.
Проще всего работать со степенями числа 10 — каков показатель степени, столько нулей после единицы:
www.algebraclass.ru