Свойства степени с натуральным показателем
I. Произведение степеней с одинаковыми основаниями.
Произведение двух степеней с одинаковыми основаниями всегда можно представить в виде степени с основанием х.
По определению степени х7 есть произведение семи множителей, каждый из которых равен х, а х9 – произведение девяти таких же множителей. Следовательно, х7 · х9 равно произведению 7 + 9 множителей. Каждый из которых равен х, то есть
х7 · х9 = х7+9 = х16
Получается, если основание степени а – произвольное число, а m и n – любые натуральные числа, то верно равенство:
am · an = am+n
Это равенство выражает одно из свойств степени.
Произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей этих степеней.
Это свойство имеет место и в случаях, когда число множителей больше двух.
Например, в случае трёх множителей имеем:
am · an · ak = (am · an)ak = am+n · ak = am+n+k
При выполнении преобразований удобно пользоваться правилом: при умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.
Рассмотрим примеры.
Пример 1.
х6 · х5 = х6+5 = х11
Пример 2.
а7 · а-8 = а-1
Пример 3.
61.7 · 6— 0.9 = 61.7+( — 0.9) = 61.7 — 0.9 = 60.8
II. Частное степеней с одинаковыми основаниями.
Частное двух степеней с одинаковыми показателями всегда можно представить в виде степени с тем же основанием.
Рассмотрим примеры.
Пример 1. Частное х17 : х5 можно представить виде степени с основанием х:
х17 : х5 = х12,
так как по определению частного и на основании свойства степени х5 · х12 = х17. Показатель степени частного (число 12) равен разности показателей делимого и делителя (17 – 5):
х17 : х5 = х17-5
Пример 2.
8 16 : 8 12 = 816-12 = 84
Пример 3.
а-8 : а6 = а -8-6 = а-14
Пример 4.
b5 : b-4 = b5-(-4) = b9
Пример 5.
91.5 : 9— 0.5 = 91.5 — (- 0.5) = 91.5 + 0.5 = 92
При выполнении преобразований удобно пользоваться правилом: при делении степеней с одинаковыми основаниями основания оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Пример 6.
а4 : а4 = а4-4 = а0
Значение выражения а0 при всяком а ≠ 0 равно 1.
III. Возведение степени в степень.
Пусть требуется седьмую степень выражения а2 представить в виде степени с основанием а.
По определению степени (а2)7 есть произведение семи множителей, каждый из которых равен а2, то есть
(а2)7 = а2 · а2 · а2 × а2 · а2 · а2 · а2.
Применяя свойство степени, получим:
а2 · а2 · а2 · а2 · а2 · а2
· а2 = а2+2+2+2+2+2+2 = a2·7. Получается, (а2)7 = а2·7 = а14.
Получается, (а2)7 = а2·7 = а14.
При возведении степени в степень основание оставляют тем же, а показатели перемножают:
(аm)n = аmn.
Рассмотрим примеры.
Пример 1.
(43)4 = 43·4 = 412
Пример 2.
((-2)2)5 = (-2)10 = 1024
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
ПРАВИЛА ДЕЙСТВИЙ СО СТЕПЕНЯМИ — МегаЛекции
Действия над степенями производятся по нижеследующим правилам:
(1)
(2)
(3)
(4)
(5)
11)Степенная функция,ее общий вид (уметь строить график и описать свойства степенной функции при n=1; 2,3; -1; -2;1/2;1/3.):
СТЕПЕННАЯ ФУНКЦИЯ
Степенная функция — функция вида , где — заданное число, называемое показателем степени. Иногда степенной функцией называется функция несколько более общего вида .
Многие функциональные зависимости выражаются через степенную функцию. Например, объем куба есть степенная функция от (длины его ребра): ; период колебаний математического маятника пропорционален длине маятника в степени , а именно . Если газ расширяется или сжимается без теплообмена с окружающей средой, то его давление и объем связаны формулой (для воздуха, например, ). Заметим, что в двух последних случаях показатель не является целым числом.
При любом показателе степени показательная функция определена во всяком случае на положительной полуоси. Свойства степенной функции различны в зависимости от значения показателя степени. Если — натуральное число , то функция определена на всей числовой оси, обращается в нуль при , четная при четном и нечетная при нечетном, неограниченно возрастает при безграничном возрастании аргумента . На рис. 1 и 2 приведены графики типичных степенных функций с целым положительным показателем: (кубическая парабола) и (парабола четвертой степени). При степенная функция является линейной функцией, при — квадратичной функцией .
Рис. 1
Рис. 2
Если — отрицательное целое число , то степенная функция определяется равенством . Она определена при всех отличных от нуля . Ее график состоит из двух частей (ветвей), имеющих асимптотами оси координат, к которым эти кривые неограниченно приближаются. Типичные представители — функции и их графики даны на рис. 3 и 4. При по определению . Если , то функция (обозначается также ) определяется как обратная функция для функции . При четном функция определена лишь для , а при нечетном — на всей оси. Графики таких функций и изображены на рис. 5 и 6.
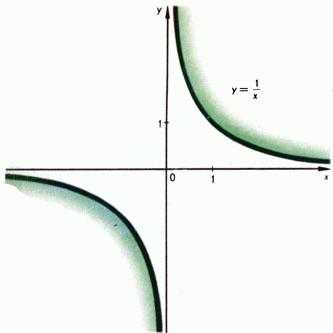
Рис. 3
Рис. 4
Рис. 5
Рис. 6
Для рационального показателя ( — несократимая дробь) степенная функция определяется формулой
.
Графики типичных степенных функций с рациональным показателем приведены на рис. 7, 8, 9.
Рис. 7
Рис. 8
Рис. 9
Степенная функция
Степенная функция – это функция видаy = xn (где x – независимая переменная, n – натуральное число).
Свойства степенной функции различаются в зависимости от того, четным или нечетным является значение n.
Свойства степенной функцииy = xnпри четном значенииn.
Графиком функции является парабола, расположенная в положительной полуплоскости координат (рис.1).
Свойства степенной функцииy = x Графиком функции является винтообразная кривая (рис.2).
|
12)Показательная функция,ее общий вид,график и свойства:
Функция вида называется показательной функцией.
Замечание. Исключение из числа значений основания a чисел 0; 1 и отрицательных значений a объясняется следующими обстоятельствами:
| a = 0 | Выражения вида 0x определено при x > 0 и в этом случае тождественно равно нулю. |
| a = 1 | Выражение 1x определено при всех x, имеет постоянное значение (тождественно единице). |
| a < 0 | Возможно возведение в целую степень или в рациональную степень с нечётным знаменателем. |
Само аналитическое выражение ax в указанных случаях сохраняет смысл и может встречаться в решении задач. Например, для выражения xy точка x = 1; y = 1 входит в область допустимых значений.
Построить графики функций: и .
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Степени правила действия со степенями
Тип урока: урок обобщения и систематизации знаний
Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация “Степени” для устного счета, карточки с заданиями, раздаточный материал.
I. Организационный момент
Сообщение темы и целей урока.
На предыдущих уроках вы открыли для себя удивительный мир степеней, научились умножать и делить степени, возводить их в степень. Сегодня мы должны закрепить полученные знания при решении примеров.
II. Повторение правил (устно)
III. Устный счет (по мультимедиа)
IV. Историческая справка
Все задачи из папируса Ахмеса, который записан около 1650 года до н. э. связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, здесь присутствует и возведение в разные степени, решение уравнений первой и второй степени с одним неизвестным.
Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.
V. Работа у доски
Найдите значение выражения рациональным способом:
Вычислите значение выражения:
VI. Физкультминутка
VII. Решение задач (с показом на интерактивной доске)
Является ли корень уравнения положительным числом?
xn--i1abbnckbmcl9fb.xn--p1ai
Формулы степеней и корней.
Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.
Число c является n-ной степенью числа a когда:
Операции со степенями.
1. Умножая степени с одинаковым основанием их показатели складываются:
2. В делении степеней с одинаковым основанием их показатели вычитаются:
3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:
(abc…) n = a n · b n · c n …
4. Степень дроби равняется отношению степеней делимого и делителя:
5. Возводя степень в степень, показатели степеней перемножают:
Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.
Операции с корнями.
1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:
2. Корень из отношения равен отношению делимого и делителя корней:
3. При возведении корня в степень довольно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:
5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:
Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:
Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4 :a 7 = a 4 — 7 = a -3 .
Чтобы формула a m :a n =a m — n стала справедливой при m=n, нужно присутствие нулевой степени.
Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.
Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:
Формулы степеней.
6. a — n = — деление степеней;
7. — деление степеней;
8. a 1/n = ;
www.calc.ru
Степени правила действия со степенями
1. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей (с тем же показателем):
(abc…) n = a n b n c n …
Пример 1. (7•2•10) 2 = 7 2 •2 2 •10 2 = 49•4•100 = 19600. Пример 2. (x 2 –a 2 ) 3 = [(x +a)(x — a)] 3 =(x +a) 3 (x — a) 3
Практически более важно обратное преобразование:
a n b n c n … = (abc…) n
т.е. произведение одинаковых степеней нескольких величин равно той же степени произведения этих величин.
Пример 3. Пример 4. (a +b) 2 (a 2 – ab +b 2 ) 2 =[(a +b)(a 2 – ab +b 2 )] 2 =(a 3 +b 3 ) 2
2. Степень частного (дроби) равна частному от деления той же степени делимого на ту же степень делителя:
Пример 5. Пример 6.
Обратное преобразование:. Пример 7.. Пример 8..
3. При умножении степеней с одинаковыми основаниями показатели степеней складываются:
Пример 9.2 2 •2 5 =2 2+5 =2 7 =128. Пример 10. (a – 4c +x) 2 (a – 4c +x) 3 =(a – 4c + x) 5 .
4. При делении степеней с одинаковыми основаниями показатель степени делителя вычитается из показателя степени делимого
Пример 11. 12 5 :12 3 =12 5-3 =12 2 =144. Пример 12. (x-y) 3 :(x-y) 2 =x-y.
5. При возведении степени в степень показатели степеней перемножаются:
Пример 13. (2 3 ) 2 =2 6 =64. Пример 14.
www.maths.yfa1.ru
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются :
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
( a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р . ( 2 · 3 · 5 / 15 ) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:
Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным, нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р . a 4 : a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы . 2 0 = 1, ( – 5 ) 0 = 1, ( – 3 / 5 ) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а :
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует .
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x, т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x, то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x, что и требовалось доказать.
Если считать, что правила действий со степенями распространяются и на степени с нулевым основанием, то
0 0 — любое число.
Р е ш е н и е . Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
www.bymath.net
Свойства степени
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1
Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8 : t = 3 4
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2 : 4 4m + 3 = 4 5m + 6 + m + 2 : 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2 ) на 4 1 . Это понятно, если посчитать (4 3 −4 2 ) = (64 − 16) = 48 , а 4 1 = 4
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n ) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.
По свойству возведения степени в степень известно, что при возведении в степень показатели перемножаются, значит:
При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.
(a · b) n = a n · b n , где « a », « b » — любые рациональные числа; « n » — любое натуральное число.
miassats.ru
Степень правила определения — Справочник химика 21
Правила определения степеней окисления [c.111]Правила определения степени окисления [c.409]
Весьма перспективно использование химических методов для изучения высших структур нуклеиновых кислот и нуклеопротеидов (фермент-субстратных комплексов, вирусов, рибосом и т. д.) в функционально активном состоянии. В этом направлении сделаны пока еще первые шаги, но полученные результаты дают все основания для оптимизма. Следует отметить, что при изучении первичной и высших структур нуклеиновых кислот добиваются, как правило, максимальной (в пределе — количественной) степени модификации определенного типа звеньев или изучают кинетику основной реакции. При этом механизм реакции, кинетика промежуточных стадий и строение промежуточных продуктов (а при изучении [c.18]
Описываемое таким способом оптимальное размещение сопл выражается почти через те же самые отношения и для круглых, и для щелевых сопл. С достаточной степенью точности можно использовать следующие правила определения оптимального размещения сопл, пригодные для обоих типов сопл [c.273]
Если же задаться определенным значением показателя степени правой части последнего уравнения, то можно получить формулу для вычисления Хв явном и простом виде. Весьма удобно принять ( 2 — 1)/( з — 2) = Ь т. е. пользоваться значениями ф при ь 2 и 3, отличающихся одно от другого в арифметической прогрессии. Тогда уравнение (2.68) приводится к удобной для практических расчетов формуле [87] [c.97]
Сахар, как правило, тщательно очищают до почти полной чистоты. Большая часть тростникового сахара, который мы покупаем в магазине, это почти 100-процентная сахароза. Такой сахар имеет чисто белый цвет и лишен какого бы то ни было привкуса, кроме сладкого вкуса. Кленовый же сахар нарочно не очищают до такой степени он слегка желтоватый и содержит небольшие количества веществ — примесей. Именно эти примеси и придают кленовому сахару своеобразный вкус. Можно так же не полностью очищать и тростниковый сахар. В продаже есть разные сорта такого сахара желтого или коричневого цвета, их нередко употребляют в кулинарии, потому что такой сахар имеет определенный вкус, а не просто сладость. [c.142]
Необходимо отметить, что данные об изменении степени упорядоченности, найденные рентгенографически и с использованием метода ИК-спектроскопии, в ряде случаев не совпадают. Степень упорядоченности, определенная рентгенографически, как правило, выше [c.78]
Методом подстановки получается уравнение четвертой степени для определения концентрации иона Na+ в растворе. Оно может быть решено обычными методами, в том числе приближенными. Расчет для нескольких экспериментальных определений показал, что найденные значения констант равновесия и уравнения дают достаточно точные результаты с расхождением, как правило, не более 5—6%. Большое число переменных, определяющих равновесие в статических условиях, не дает возможности простого графического представления связи между ними. [c.101]
Правила определения суммарного пятна контакта, его относительные размеры и расположение на сопряженных поверхностях зубьев назначаются конструктором передачи в зависимости от ее служебного назначения, степени нагруженности, жесткости и геометрических особенностей рабочих поверхностей зубьев зубчатых колес. [c.531]
Холодильная техника, естественно, сильно потеснила за последнее столетие древние способы охлаждения, основанные иа использовании природного холода. Заготовка природного льда свелась в наше время почти к нулю. Однако наивно было бы полагать, что холодильная техника, при всех ее достижениях, должна полностью вытеснять из низкотемпературной технологии холод, который дает природа. Отец невесты в Свадьбе» Чехова, который предпочитал натуральное — умственному , был в определенной степени прав. Оказалось, что по мере развития цивилизации, когда задачи организации ее рационального взаимодействия с живой природой (экологические) выходят на первый план, ситуация существенно меняется. Сокращение расходов материалов и энергии становится не только экономической задачей, но в полном смысле слова — вопросом жизни. Соответственно возрастает и значение экологически чистого естественного холода. [c.218]
С момента производства топлив до их применения в летательном аппарате проходит, как правило, продолжительное время. Это связано прежде всего с тем, что в аэропортах должен быть определенный запас топлив для бесперебойной работы. Кроме того, необходимо время на транспортировку, фильтрацию топлив и другие операции. Продолжительность времени, в течение которого топливо может использоваться по прямому назначению, регламентируется специальными документами. Ограничение сроков хранения топлив, а также строгие правила транспортировки и условий хранения вызваны тем, что все нефтяные топлива в той или иной степени изменяют свой первоначальный состав, а следовательно, и свойства. [c.41]
Склонность исследуемого бензина к детонации оценивается сравнением его с эталонными топливами, детонационная стойкость которых заранее известна. В качестве эталонных топлив используются, как правило, чистые индивидуальные углеводороды или другие соединения, названия которых применяют для обозначения соответствующего числа — толуоловое, бензольное, ксилольное, анилиновое, этиловое и т. п. [1 ]. В настоящее время наиболее широко для оценки детонационной стойкости пользуются так называемым октановым числом. При его определении эталонное топливо готовят смешением двух индивидуальных углеводородов. Один из них — изооктан (2,2,4-триметилпентан) — детонирует только при высокой степени сжатия и его детонационная стойкость принята равной 100 октановым единицам. Другой углеводород — н-гептан — обладает плохими антидетонационными свойствами и его октановое число принято за нуль. Смеси изооктана и гептана в различных соотношениях обладают разной детонационной стойкостью она характеризуется октановыми числами от нуля до 100. [c.92]
Периодическая ректификация с отбором дистиллята постоянного состава более экономична, но связана с трудностями непрерывного регулирования флегмового числа. Поэтому иногда процесс ведут при постоянном флегмовом числе, выбранном так, чтобы состав конечного суммарного дистиллята отвечал допустимой, в этих случаях невысокой, степени чистоты целевого продукта. Однако в общем случае для колонн с определенным числом тарелок нецелесообразно вести периодическую ректификацию при неизменном флегмовом числе как правило, вначале оно бывает небольшим, но постепенно возрастает к концу первой стадии процесса. Во второй стадии процесс ведется уже при закрепленном флегмовом числе и переменном составе верхнего продукта колонны. [c.220]
&e
www.chem21.info
