Степени двоичной системы счисления – . .

Двоичная система счисления

Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.

Сложение, вычитание и умножение двоичных чисел.

Таблица сложения

Пример: 1001 + 10 = 1011

Таблица вычитания

Пример: 1111101 — 10001 = 1101100

Таблица умножения

Пример: 1111 · 1001 = 10000111

Перевод чисел.

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

Пример: 73₁₀ = 1001001₂

Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.

Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

---

Другие заметки по информатике

edu.glavsprav.ru

Двоичная система счисления

Главная / Ассемблер / Для чайников / Системы счисления /

Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа. А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два состояния – вЫключено и включено (или

нет напряжения – есть напряжение). Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо, потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете почитать здесь: Структура процессора.

Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.

Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.

Каждая цифра в двоичном числе называется бит (или разряд). Четыре бита – это полубайт (или тетрада), 8 бит – байт, 16 бит – слово, 32 бита – двойное слово. Запомните эти термины, потому что в программировании они используются очень часто. Возможно, вам уже приходилось слышать фразы типа слово данных или байт данных. Теперь, я надеюсь, вы понимаете, что это такое.

Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит

(нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например,

101 – это десятичное число
101b – это двоичное число, которое эквивалентно десятичному числу 5.

А теперь попробуем понять, как формируется двоичное число.

Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду. Тетрада (или полубайт) имеет 4 бита.

Двоичное	Десятичное	Пояснения
0000	0	—
0001	1	В младший бит устанавливается 1.
0010	2	В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается.
0011	3	В младший бит устанавливается 1.
0100	4	В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются.
0101	5	В младший бит устанавливается 1.
0110	6	Продолжаем в том же духе…
0111	7	…
1000	8	…
1001	9	…
1010	10	…
1011	11	…
1100	12	…
1101	13	…
1110	14	…
1111	15	…

Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:

Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе:

0…9
10 – очищаем младший разряд, а в старший добавляем 1

Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).

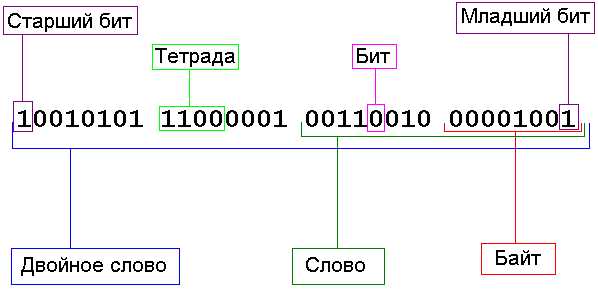
Рис. 2.2. Двоичное число.

av-assembler.ru

Иллюстрированный самоучитель по цифровой графике › Системы счисления › Основания и степени в системе счисления [страница — 43] | Самоучители по графическим программам

Основания и степени в системе счисления

Наконец, пришло время для итоговой таблицы всех рассмотренных систем счисления. В табл. 4.6 представлены числа в нескольких интересующих нас системах счисления, но не все числа, а только те, которые являются «круглыми» в одной из систем (они выделены полужирным шрифтом).

Таблица 4.6. «Круглые» числа в нескольких системах счисления.

Двоичная	Восьмеричная	Десятичная	Шестнадцатеричная
10 = 21	2	2	2
100 = 22	4	4	4
1010	12	10 = 101	А
1000 = 23	10 = 81	8	8
10000 = 24	20	16	10 = 161
1 00000 = 25	40	32	20
1000000 = 26	100 = 82	64	40
1100100	144	100 = 102	64
1 0000000 = 27	200	128	80
100000000 = 28	400	256	100 = 162
1000000000 = 29	1000 = 83	512	200
1111101000	1750	1000 = 103	ЗЕ8
1 0000000000 = 210	2000	1024	400
100000000000 = 211	4000	2048	800
1 00000000000 = 212	10000 = 84	4096	1000 = 163

Обратите внимание на одну интересную закономерность, заметную при рассмотрении этой таблицы. «Круглые» числа во всех системах счисления расположены там, где происходит добавление следующего разряда, а количество нулей соответствует степени числа на том же основании.

Пример

«Шестнадцатеричная тысяча» (три нуля) равна третьей степени основания системы счисления (16), «восьмеричные десять тысяч» (четыре нуля) равны четвертой степени основания системы счисления (8) и, наконец, «двоичный миллиард» (двенадцать нулей) равен двенадцатой степени основания системы счисления (2).

Это еще один аргумент в пользу мысли, что законы математики едины (законы арифметики также). Изменяется всего-навсего основание в каждой конкретной арифметике.

Тот факт, что нам до сих пор привычной представлялась только десятичная система счисления, не может служить препятствием для перехода к другим системам счисления: двоичной, восьмеричной и шестнадцатеричной, как того требуют компьютерные технологии.

• Коды пронизывают нашу жизнь. Код – это совокупность знаков и система определенных правил.
• В компьютерных технологиях все виды информации кодируются только цифрами или, точнее, числами, которые представляются в двоичной системе счисления – способе представления любых чисел с помощью двух знаков (цифр) по позиционному принципу.
• Позиционная система счисления состоит в использовании ограниченного числа цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры в числе на математическом языке называется разрядом.
• Основание позиционной системы счисления – это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе.
• Для того чтобы двоичные числа, отличающиеся довольно значительной длиной, было легче воспринимать и отображать, их сжимают в восьмеричную и шестнадцатеричную системы счисления.

Если данная тема понятна, следует обратить внимание еще на один аспект, ради которого, собственно, и был затеян этот длинный экскурс в элементарную математику, а именно связь двоичных разрядов и количества кодов, которые можно ему присвоить.

samoychiteli.ru

Двоичная система счисления, 0 и 1, двоичные числа

Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:

Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.

Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.

Общая форма записи двоичных чисел

Для целых двоичных чисел можно записать:

a_n−1a_n−2…a₁a₀=a_n−1⋅2ⁿ⁻¹+a_n−2⋅2ⁿ⁻²+…+a₀⋅2⁰

Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Правила сложения двоичных чисел

Основные правила сложения однобитовых чисел

0+0=0
0+1=1
1+0=1
1+1=10

Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел

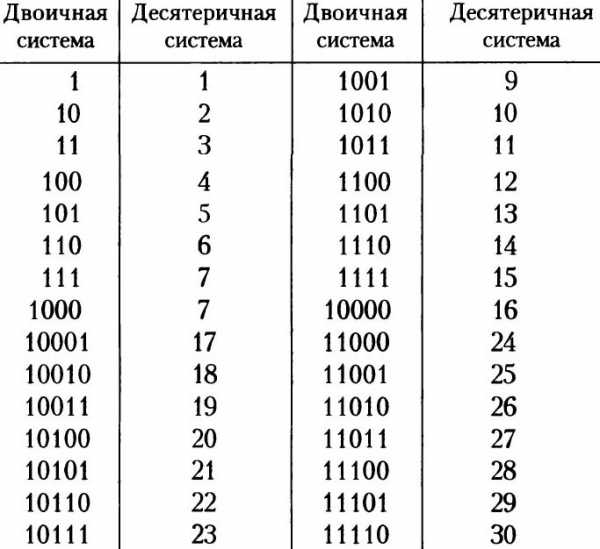
Правила вычитания двоичных чисел

0-0=0
1-0=0
10-1=1

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001

Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).

110 — 101 = ?

В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).

Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 1010 — 101 = ?
Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 101100 — 101 = ?
Вычтите цифры в правом столбце. В нашем примере:
101100 — 101 = ?
Правый столбец: 10 — 1 = 1.
102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).
12 = (1×1) = 110.

Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

101100 — 101 = __1 = _01 = 001 = 1.

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

Рассмотрим пример: 101100₂ — 11101₂= ?

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.

101100₂ — 011101₂= ?

В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

011101₂ → 100010₂.

На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

Теперь вместо вычитания сложите два двоичных числа.

101100₂ +100011₂= ?

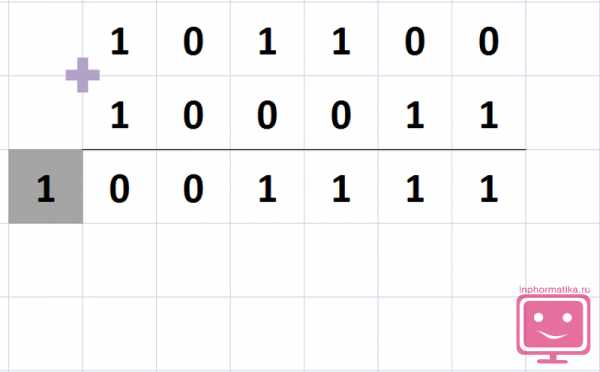
Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Разр.	6	5	4	3	2	1	0
A		1	0	1	1	0	1
B			1	1	0	1	1

 

4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.

Заем из текущего разряда Oi-1	Ai	Bi	Ci	Заем из следующего разряда Oi+1
	0	0	0
	0	1	1	1
	1	0	1
	1	1	0
1	0	0	1	1
1	0	1	0	1
1	1	0	0
1	1	1	1	1

 

Весь процесс сложения наших чисел выглядит следующим образом:

(красным шрифтом показаны заёмы из соответствующего разряда)

Получилось 101101₂ — 11011₂ = 10010₂
или в десятичной системе счисления: 45₁₀ — 27₁₀ = 18₁₀

Правила умножения двоичных чисел.

В целом эти правила очень просты и понятны.

0*0=0
0*1=0
1*0=0
1*1=1

Умножение многоразрядных двоичных чисел происходит точно также как и обычных. Каждое значащий разряд умножаем на верхнее число по приведенным правилам, соблюдая позиции. Умножать просто — так как умножение на единицу даёт одно и тоже число.

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

 

Система счисления Методы перевода десятичного числа в двоичное

inphormatika.ru

Особенности двоичной системы счисления

В повседневной жизни мы используем десятичную систему счисления, которая состоит всего лишь из десяти цифр от 0 до 9, а все остальные числа являются комбинацией этих чисел. Данная комбинация получила название позиционной системы. Суть данной системы заключается в том, что число разбивают на части, кратные десяти, и записывают каждую часть на соответствующем месте, считая справа налево. Разберем на примере 365. Эта запись будет иметь следующий вид:  где его разбивают на части и в такой же последовательности записывают множители при степенях десяти.

Если мы при построении счетчиков используем триггеры, то нам необходимо учитывать и то, что триггеры могут находится только в двух состояниях – либо единица, либо ноль. Поэтому любое число для них может быть записано только в двоичной системе счисления. По аналогии с десятичной системой, каждое число разбивают на части, которые будут кратны уже не десяти, а двум. Такое выражение будет иметь вид:

Давайте рассмотрим на примере все того же 365 и определим все степени двойки, которые в этом числе могут быть:

2⁰=1; 2¹=2; 2²=4; 2³=8; 2⁴=16; 2⁵=32; 2⁶=64; 2⁷= 128; 2⁸=256; 2⁹=512;

Поскольку 2⁹=512 – а это больше чем 365, то мы берем ближайшее меньшее к 365 – а это 2⁸=256. Последовательно отнимая от заданного числа степени двойки получим:

365 — 256(2⁸)=109; 109 — 64(2⁶)=45; 45 – 32(2⁵)=13; 13 – 8(2³) =5; 5 – 4(2²) =1; 1 – 1(2⁰)=0;

А это значит что:

365=256+64+32+8+4+1 = 

То есть запись в позиционной системе будет иметь вид:

101101101

Проще переход к двоичной системе можно произвести еще таким способом:

Заданное число делят на два. Если оно получается непарным, то от него отнимают единицу, которую записывают справа от числа за вертикальной чертой как показано выше. После того, как оно стало парным (365-1=364), его делят на два и результат записывают ниже заданного (364:2=182). Поскольку 182 парное, то справа записываем ноль и снова делим на два. Подобные действия проделывают до конца, а потом выписывают единицы и нули в направлении снизу вверх и получают 101101101.

Для перехода к десятичной системе счисления над каждой цифрой числа, записанного в двоичной системе, сверху надписывают справа налево степень двойки:

1    0    1     1    0    1     1    0   1

Подсчитывают степени соответствующие единице и суммируют результат:

2⁸+2⁶+2⁵+2³+2²+2⁰ = 256+ 64+32+8+4+1 =365

Каждый разряд двоичного числа называет «бит». В нашем случае использовано девять бит. Биты группируются в старшие разряды. Так, восемь битов составляют «байт». Число, состоящее из байтов и битов называют «словом». Для записи больших чисел удобно использовать так называемую двоично – десятичную систему. Для осуществления этого каждую цифру в десятичной системе записывают  в двоичном коде отдельно: 3 – 0011; 6 – 0110; 5 – 0101. Итак, 365 в двоично – десятичной системе будет иметь вид:

365 – 0011  0110  0101

При этом понадобится не девять бит, а двенадцать, но в таком виде гораздо удобней осуществлять перевод из одной системы в другую.

elenergi.ru

Двоичная система счисления

Рейтинг:   / 1

Подробности

Просмотров: 4414

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:

0 – это ноль

1 – это один (и это предел разряда)

10 – это два

11 – это три (и это снова предел)

100 – это четыре

101 – пять

110 – шесть

111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 10³ + 4 * 10² + 7 * 10¹ + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 137₁₀

Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания. 

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)

38 / 2 = 19 (0 остаток)

19 / 2 = 9 (1 остаток)

9 / 2 = 4 (1 остаток)

4 / 2 = 2 (0 остаток)

2 / 2 = 1 (0 остаток)

1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

• < Назад
• Вперёд >

palkins.ru

Двоичная система счисления. Правила двоичной арифметики.

В двоичнойсистеме счисления для записи чисел используется две цифры 0 и 1. Основание системы q=2 записывается как 10₂= [1*2¹+0*2⁰]₁₀. В данной СС любое число может быть представлено последовательностью двоичных цифр. Эта запись соответствует сумме степеней цифры 2, взятых с указанными в ней коэффициентами: X=a_m×2^m+a_m-1×2^m-1+…+a₁×2¹+a_0×2⁰+… . Например, двоичное число (10101101)₂=1×2⁷+0×2⁶+1×2⁵+0×2⁴+1×2³+1×2²+0×2¹+1×2⁰=173₁₀.

Арифметические операции над двоичными числами отличаются простотой и легкостью технического выполнения.

Правила двоичной арифметики:

Сложение:0+0=0 1+0=1

0+1=1 1+1=10

— перенос единицы в старший разряд.

Вычитание:0-0=0 1-1=0

1-0=1 10-1=1

— заем единицы в старшем разряде.

Умножение:0х0=0 1х0=0

0х1=0 1х1=1

Двоичная система счисления является основной для использо­вания в ЭВМ, удобной из-за простоты выполнения арифметических операций над двоичными числами. С точки зрения затрат оборудо­вания на создание ЭВМ эта система уступает только троичной систе­ме счисления.

В двоично-кодированных системах счисления, имеющих основа­нияq, отличные от 2 (q>2), каждая цифра числа представляется в двоичной системе счисления. Наибольшее применение в ЭВМ полу­чили шестнадцатеричная систе­ма счисления и десятичная двоично-кодированная систе­ма счисления.

2. Восьмеричная и шестнадцатеричная системы счисления.

Восьмеричная и шестнадцатеричная системы счисления являют­ся вспомогательными системами при подготовке задачи к решению. Удобство их использования состоит в том, что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему счисления и наобо­рот несложен и выполняется простым механическим способом.

Пример 2.1. Число 137,45₈ перевести в двоичную систему счисления. Перевод осуществляется заменой каждой восьмеричной цифры трехзнач­ным двоичным числом (триадой):

1	3	7,	4	5
001	011	111,	100	101

т,е 137,45₈ = 001011111,100101₂. И наоборот, заменой каждой триады слева и справа от запятой эквивалентным значением восьмеричной цифры обра­зуется восьмеричное число.

Если в крайней слева или справа триаде окажется меньше трех двоичных чисел, то эти тройки дополняют нулями.

Пример 2.2. Число 5F,94₁₆ перевести в двоичную систему счисления. Перевод осуществляется заменой каждой шестнадцатеричной цифры четырехзначным двоичным числом (тетрадой):

5	F,	9	4
0101	1111	1001	0100

т.e. 5F,94₁₆=01011111,10010100₂. Число 5F,94₁₆ в восьмеричной системе счис­ления имеет вид 137,45₈.

В десятичной двоично-кодированной системе счисления, часто называемой двоично-десятичной системой, используются десятичные числа. В ней каждую цифру десятичного числа (от 0 до 9) заменяют тетрадой.

Пример 2.3. Число 273,59₁₀ перевести в двоично-десятичную систему счисления. Перевод осуществим следующим образом:

2	7	3,	5	9
0010	0111	0011	0101	1001

т.е. 273,59₁₀ = 001001110011,01011001_2-10

Двоично-десятичную запись числа используют непосредственно или как промежуточную форму записи между обычной десятичной его записью и машинной двоичной. Вычислительная машина сама по специальной программе переводит двоично-десятичные числа в двоичные и обратно.

studfiles.net