Свойства непрерывных в точке функций (доказательства теорем)
Формулировки свойств и теорем
Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Доказательство ⇓
Теорема о сохранении знака непрерывной функции
Пусть функция f(x) непрерывна в точке x0. И пусть она имеет положительное (отрицательное) значение в этой точке:
f(x0) > 0 ( f(x0) < 0 ).
Тогда существует такая окрестность U(x0) точки x0, на которой функция имеет положительное (отрицательное) значение:
f(x) > 0 ( f(x) < 0 ) при x ∈ U(x0).
Доказательство ⇓
Арифметические свойства непрерывных функций
Пусть функции f(x) и g(x) непрерывны в точке x0.
Тогда сумма f(x) + g(x), разность f(x) – g(x) и произведение f(x) · g(x) функций непрерывны в точке x0.
Если g(x0) ≠ 0, то и частное функций f(x) / g(x) непрерывно в точке x0.
Доказательство ⇓
Свойство непрерывности слева и справа
Функция f непрерывна в точке x0 тогда и только тогда, когда она непрерывна в x0 слева и справа.
Доказательство ⇓
Доказательства свойств и теорем
Доказательство теоремы об ограниченности непрерывной функции
Формулировка ⇑ Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению имеется такая функция , что для любого ,
при .
Положим . Тогда при имеем:
.
Раскроем знак модуля и преобразуем неравенства.
;
.
Пусть M есть наибольшее из чисел: . Тогда
, или
.
Итак, мы нашли окрестность , на которой функция ограничена числом :
.
Теорема доказана.
Доказательство теоремы о сохранении знака непрерывной функции
Формулировка ⇑ Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению имеется такая функция , что для любого ,
при .
Положим . Тогда при имеем:
(1) .
Пусть . Раскроем в (1) знак модуля и преобразуем неравенства:
;
;
.
Итак, мы нашли окрестность , на которой функция ограничена снизу положительным числом:
.
Поэтому на этой окрестности функция имеет положительное значение:
.
Для случая теорема доказана.
Теперь рассмотрим случай . Также раскрываем в (1) знак модуля и преобразуем неравенства:
;
;
;
.
Тем самым мы нашли окрестность , на которой функция ограничена сверху отрицательным числом:
.
Поэтому на этой окрестности .
Теорема доказана.
Доказательство арифметических свойств непрерывных функций
Формулировка ⇑ Воспользуемся определением непрерывности функции в точке. Согласно этому определению, Функция называется непрерывной в точке , если она определена на некоторой окрестности этой точки, и если предел при стремящемся к существует и равен значению функции в :
.
Поскольку функции и непрерывны в точке , то они определены на некоторых окрестностях и , соответственно, этой точки. Пусть окрестность является пересечением окрестностей и . Тогда обе функции и определены на окрестности .
Поскольку функции и определены на окрестности , то они определены и на проколотой окрестности точки , которая получается из исключением точки .
Итак, функции и определены на некоторой проколотой окрестности конечной точки , и существуют пределы:
и .
Тогда, согласно арифметическим свойствам пределов функции, существуют пределы суммы, разности и произведения функций:
;
;
.
Если , то существует предел частного:
.
Свойства доказаны.
Доказательство свойства непрерывности слева и справа
Формулировка ⇑1) Пусть функция непрерывна в точке . Докажем, что она непрерывна в справа и слева.
Воспользуемся определением непрерывности функции в точке по Коши. Согласно этому определению, имеется такая функция , так что для любого ,
(2) при .
Поскольку неравенство выполняется для любых значений , принадлежащих окрестности , то наложим дополнительное ограничение: . Тогда
для любого , имеется , так что
при .
Это означает, что . То есть функция непрерывна в справа.
Теперь, в (2), наложим ограничение . Тогда
для любого , имеется , так что
при .
Это означает, что . То есть функция непрерывна в слева.
Первая часть свойства доказана.
2) Теперь пусть функция непрерывна в точке x0 слева и справа.
Поскольку функция непрерывна слева, то имеется такая функция , так что для любого ,
при .
Поскольку функция непрерывна в точке справа, то имеется такая функция , так что для любого ,
при .
Пусть . Тогда . Если принадлежит окрестности , то также принадлежит окрестности . Поэтому
при .
Аналогично, если , то . Поэтому
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
Это означает, что . То есть функция является непрерывной в точке .
Свойство доказано.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
11. Непрерывность функции в точке. Свойства функций, непрерывных в точке.
Непрерывная функция— функция без «скачков», то есть такая, у которой малые измененияаргументаприводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, навещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
ε-δ определение
Пусть и.
Функция непрерывна в точке, если для любогосуществуеттакое, что для любого
Функция непрерывна на множестве, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция классаи пишут:или, подробнее,.
Комментарии
Точки разрыва
Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция
Устранимые точки разрыва
Если предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка называетсяточкой устранимого разрывафункции(вкомплексном анализе—устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывнойилидоопределением функции по непрерывности, что и обосновывает название точки, как точкиустранимогоразрыва.
[Править] Точки разрыва первого и второго рода
Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Свойства Локальные
studfiles.net
Непрерывность функций (теоремы и свойства)
Определение непрерывности функции
Определение
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности этой точки, и если предел при x стремящемся к x0 равен значению функции в x0:
.
Используя определения предела функции по Коши и по Гейне, можно дать развернутые определения непрерывности функции в точке.
Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Тогда функция непрерывна в точке , если
.
Введем новую функцию:
.
Ее называют приращением функции в точке . Тогда функция непрерывна в точке , если
.
Определение непрерывности справа (слева)
Функция f(x) называется непрерывной справа (слева) в точке x0, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x0 равен значению функции в x0:
.
Более подробно, см. «Определение непрерывности функции в точке».
Свойства непрерывных в точке функций
Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Теорема о сохранении знака непрерывной функции
Пусть функция непрерывна в точке . И пусть она имеет положительное (отрицательное) значение в этой точке:
.
Тогда существует такая окрестность точки , на которой функция имеет положительное (отрицательное) значение:
при .
Арифметические свойства непрерывных функций
Пусть функции и непрерывны в точке .
Тогда функции , и непрерывны в точке .
Если , то и функция непрерывна в точке .
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Теорема о непрерывности сложной функции
Пусть функция непрерывна в точке . И пусть функция непрерывна в точке .
Тогда сложная функция непрерывна в точке .
Предел сложной функции
Теорема о пределе непрерывной функции от функции
Пусть существует предел функции при , и он равен :
.
Здесь точка t0 может быть конечной или бесконечно удаленной: .
И пусть функция непрерывна в точке .
Тогда существует предел сложной функции , и он равен :
.
Теорема о пределе сложной функции
Пусть функция имеет предел и отображает проколотую окрестность точки на проколотую окрестность точки . Пусть функция определена на этой окрестности и имеет на ней предел .
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Тогда существует предел сложной функции и он равен :
.
Подробнее, см. «Предел и непрерывность сложной функции».
Точки разрыва
Определение точки разрыва
Пусть функция определена на некоторой проколотой окрестности точки . Точка называется точкой разрыва функции , если выполняется одно из двух условий:
1) не определена в ;
2) определена в , но не является непрерывной ⇑ в этой точке.
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Подробнее, см. «Точки разрыва функции – определения, классификация и примеры».
Свойства функций, непрерывных на отрезке
Определение функции, непрерывной на отрезке
Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и непрерывна справа и слева ⇑ в точках a и b, соответственно.
Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке , то она ограничена на этом отрезке.
Определение достижимости максимума (минимума)
Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех .
Определение достижимости верхней (нижней) грани
Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Теорема Больцано – Коши о промежуточном значении
Пусть функция непрерывна на отрезке . И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой
.
Следствие 1
Пусть функция непрерывна на отрезке . И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
.
Следствие 2
Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:
при .
Подробнее, см. «Свойства функций, непрерывных на отрезке».
Обратные функции
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Для возрастающей функции . Для убывающей – .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Подробнее, см. «Обратные функции – определение и свойства».
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Показательная функция имеет следующие свойства:
(П.0) определена, при , для всех ;
(П.1) при a ≠ 1 имеет множество значений ;
(П.2) строго возрастает при , строго убывает при , является постоянной при ;
(П.3) ;
(П.3*) ;
(П.4) ;
(П.5) ;
(П.6) ;
(П.7) ;
(П.8) непрерывна для всех ;
(П.9) при ;
при .
Подробнее, см. «Определение и доказательство свойств показательной функции».
Логарифм
Логарифмическая функция, или логарифм, y = loga x, с основанием a – это функция, обратная к показательной функции с основанием a.
Теорема. Свойства логарифмаЛогарифмическая функция с основанием a, y = loga x, имеет следующие свойства:
(Л.1) определена и непрерывна, при и , для положительных значений аргумента,;
(Л.2) имеет множество значений ;
(Л.3) строго возрастает при , строго убывает при ;
(Л.4) при ;
при ;
(Л.5) ;
(Л.6) при ;
(Л.7) при ;
(Л.8) при ;
(Л.9) при .
Подробнее, см. «Определение и доказательство свойств логарифма».
Экспонента и натуральный логарифм
В определениях показательной функции и логарифма фигурирует постоянная a, которая называется основанием степени или основанием логарифма. В математическом анализе, в подавляющем большинстве случаев, получаются более простые вычисления, если в качестве основания использовать число e:
.
Показательную функцию с основанием e называют экспонентой: , а логарифм по основанию e – натуральным логарифмом: .
Свойства экспоненты и натурального логарифма изложены на страницах
«Экспонента, е в степени х»,
«Натуральный логарифм, функция ln x»
Степенная функция
Степенная функция с показателем степени p – это функция f(x) = x p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого, f(0) = 0 p = 0 при p > 0.
Здесь мы рассмотрим свойства степенной функции y = x p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».
Степенная функция, y = x p, с показателем p имеет следующие свойства:
(С.1) определена и непрерывна на множестве
при ,
при ;
(С.2) имеет множество значений
при ,
при ;
(С.3) строго возрастает при ,
строго убывает при ;
(С.4) при ;
при ;
(С.5) ;
(С.5*) ;
(С.6) ;
(С.7) ;
(С.8) ;
(С.9) .
Подробнее, см. «Непрерывность и свойства степенной функции».
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус (sin x), косинус (cos x), тангенс (tg x) и котангенс (ctg x), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x) и арккотангенс (arcctg x), непрерывны на своих областях определения.
Подробнее, см. «Доказательство непрерывности тригонометрических функций».
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Свойства функций непрерывных в точке — ПриМат
функции непрерывные в точке
Лимит времени: 0
Информация
Тест на тему «функции непрерывные в точке»:
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Задание 1 из 3
Количество баллов: 1Расставить в правильной последовательности:
Если функция f
непрерывна
в точке a, то она
- ограниченна
в некоторой окрестности этой
точки.
Правильно
Неправильно
Задание 2 из 3
Количество баллов: 2 Расставить в правильной последовательности:Если z=f(y) непрерывна
в точке
y,аy=φ(x),
непрерывна в точке x0 причем
-
y0=φ(x0),
то в некоторой окрестности x0
равная
f[φ(x)]
которая также непрерывна в точке x0
Правильно
Неправильно
Задание 3 из 3
Количество баллов: 2- ∃c>0∃Uδ(a):∀x∈Uδ(a):|f(x)|c
- ∃Uδ(a):∀x∈Uδ(a)→signf(x)=signf(a)
- limy→y0f(y)=f(y0)limx→x0φ(x)=φ(x0)}⇒limx→x0f[φ(x)]=f[φ(x0)]
Если функция f непрерывна в точке a, то она ограниченна в некоторой окрестности этой точки :
Если функция f непрерывна в точке a и f(a)≠0, то в некоторой окрестности точки a знак функции совпадает со знаком числа f(a):
Если z=f(y) непрерывна в точке y,аy=φ(x), непрерывна в точке x0 причем y0=φ(x0), то в некоторой окрестности x0 определена сложная функция равная f[φ(x)] которая также непрерывна в точке x0:
Правильно
Неправильно
ib.mazurok.com
Свойства непрерывных функций Свойства функций, непрерывных в точке:
1. Если функции f(x)иφ(x)непрерывны в точкех0, то
их суммаf(x)+φ(x), произведениеf(x)φ(x)и частное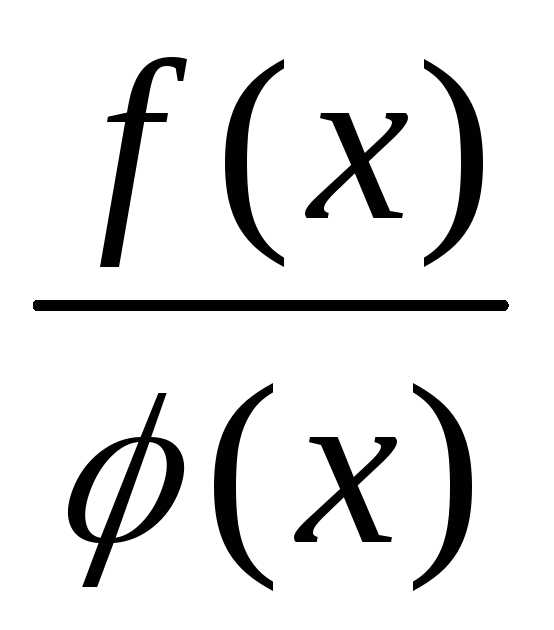 (при условии
(при условии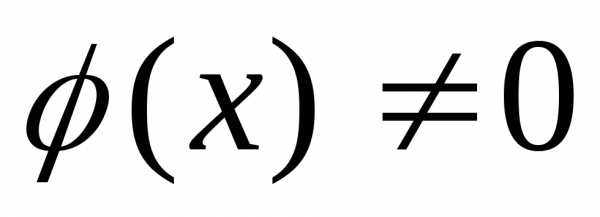 )
являются функциями, непрерывными в
точке х0.
)
являются функциями, непрерывными в
точке х0.
2. Если функция у=f(x)непрерывна в точкех0иf(х0)>0, то существует такая окрестность точких0, в которойf(х)>0.
3. Если функция f(и)>0 непрерывна в точкеи0, а функцияи= φ(x)непрерывна в точкеи0= φ(x0), то сложная функцияу= f(φ(x))непрерывна в точкех0.
Свойство 3 может быть записано в виде , т.е. под знаком непрерывной функции можно переходить к пределу.
Функция у=f(x)называется непрерывной на промежуткеХ, если она непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны в области их определения.
Свойства функций, непрерывных на отрезке:
1. Если функция у=f(x)непрерывна на отрезке [a,b], то она ограничена на этом отрезке.
2. Если функция у=f(x) непрерывна на отрезке [a,b], то она достигает на этом отрезке наименьшего значеният и наибольшего значенияМ (теорема Вейерштрасса).
3. Если функция у=f(x) непрерывна на отрезке [a,b]
и значения ее на концах отрезка f(а)и f(b) имеют противоположные знаки, то внутри
отрезка найдется точка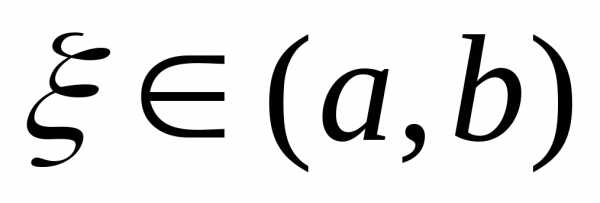 такая,f(ξ)=0(теорема
Больцано-Коши).
такая,f(ξ)=0(теорема
Больцано-Коши).
Вопросы для самопроверки
Что называется числовой последовательностью?
Что называется пределом числовой последовательности?
Что называется пределом функции непрерывного аргумента?
Сформулируйте основные теоремы о пределах функции.
Какая переменная величина называется бесконечно малой? бесконечно большой? Какова зависимость между ними?
Сформулируйте основные свойства бесконечно малых величин.
Как найти предел дробно рациональной функции
 при,
если
при,
если и
и ?
?Укажите приемы вычисления предела от простейших иррациональных функций.
Сформулируйте и напишите первый замечательный предел.
Сформулируйте и напишите второй замечательный предел.
Как сравнить между собой две бесконечно малые величины?
Какие две бесконечно малые величины называются эквивалентными, и каковы свойства эквивалентных бесконечно малых величин?
Что называется левосторонним пределом функции в данной точке? правосторонним пределом функции в данной точке?
Дайте определение непрерывности функции в точке; в интервале.
Какая точка называется точкой разрыва функции?
Что называется разрывом первого рода? второго рода?
Что называется скачком функции в точке разрыва?
Сформулируйте основные свойства функции непрерывной на отрезке.
Тема 4. Дифференциальное исчисление функции одной независимой переменной
Литература.[1], [2], [6], [7], [17].
Определение производной; ее механический и геометрический смысл
Производной функцииу = f(x)в точке называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю.
Обозначают одним из символов:
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю.
Обозначают одним из символов:
Итак, по определению
Производная функции  есть
некоторая функция
есть
некоторая функция .
.
Функция у= ,
имеющая производную в каждой точке
интервала (а;b),
называетсядифференцируемойв этом
интервале; операция нахождения производной
функции называетсядифференцированием.
,
имеющая производную в каждой точке
интервала (а;b),
называетсядифференцируемойв этом
интервале; операция нахождения производной
функции называетсядифференцированием.
Значение производной функции у=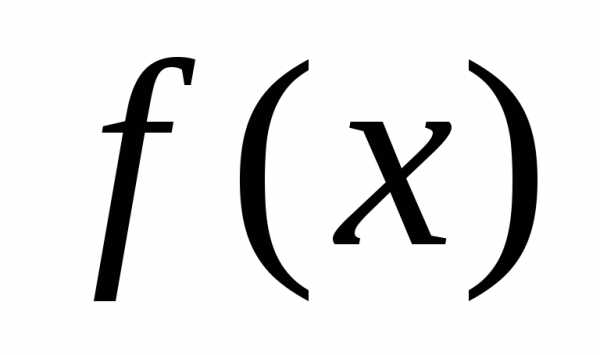 в точке
в точке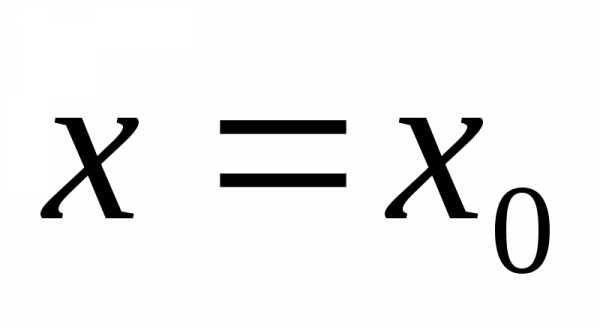 обозначается одним из символов:
обозначается одним из символов:

Пример 1. Найти производную функции у = с, с = const.
Решение: Значению 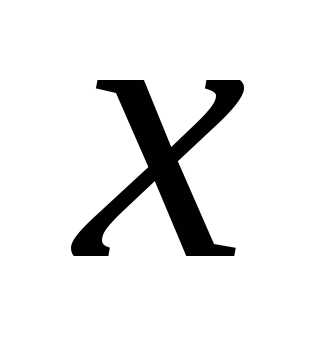 даем приращение
даем приращение ;
находим приращение функции;
значит,
;
находим приращение функции;
значит, 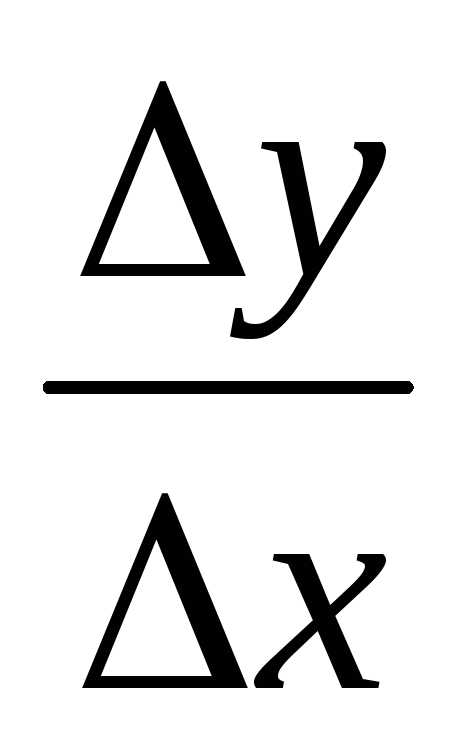 =
= 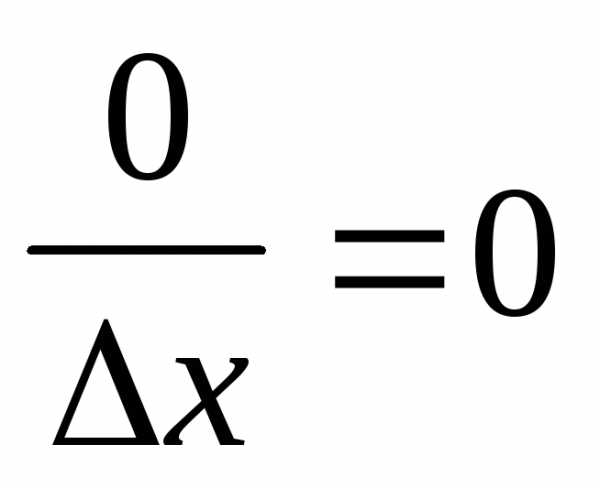 ;
;
следовательно, 
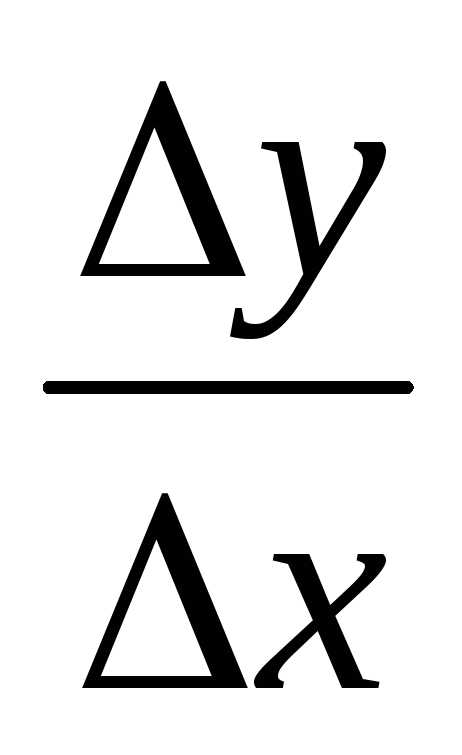 =
=
Пример 2. Найти производную функции у = х2.
Решение: Аргументу х даем
приращение 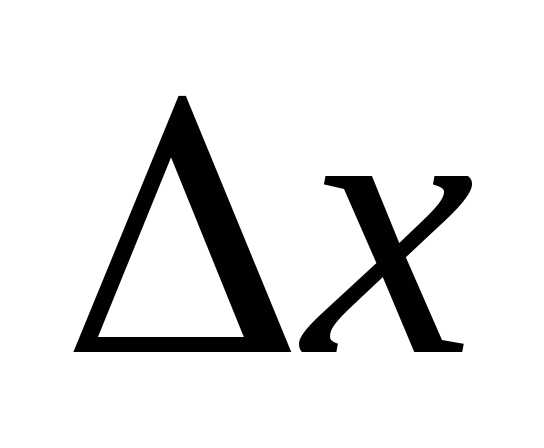 ;
находим
;
находим
;
составляем отношение 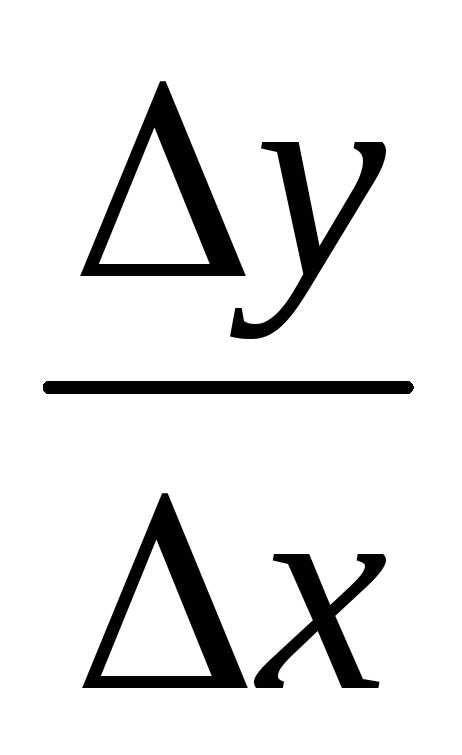 :
: 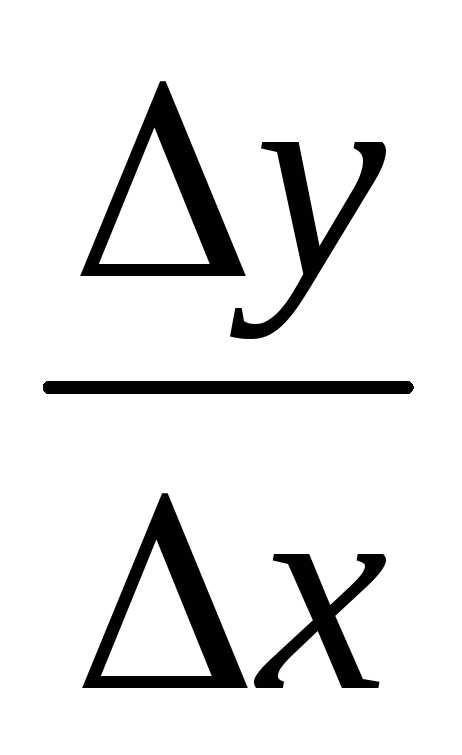 =;
находим предел этого отношения:
=;
находим предел этого отношения:
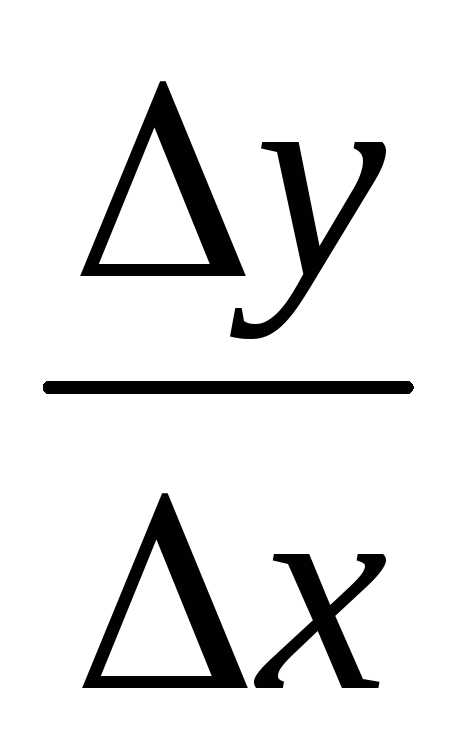 =
=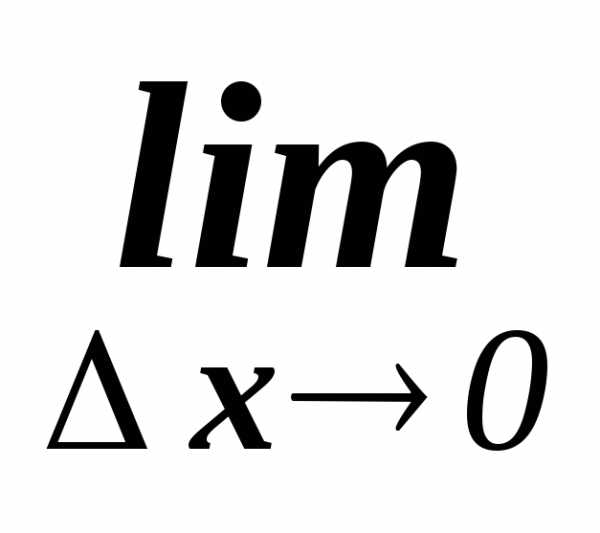
Таким образом,
Механический смысл производной:

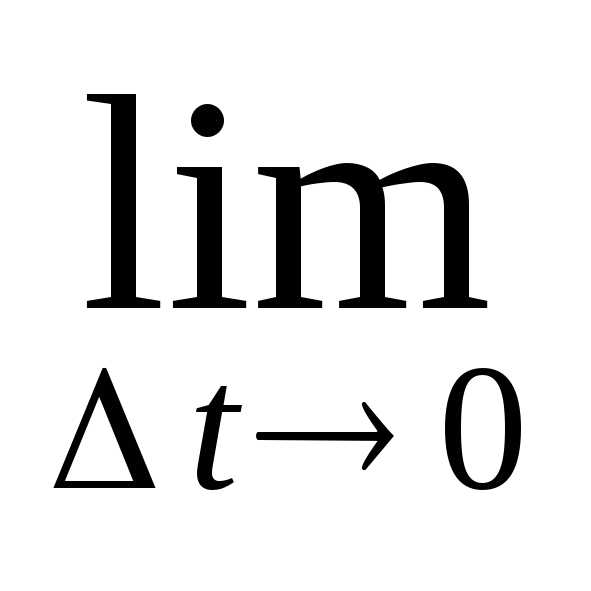
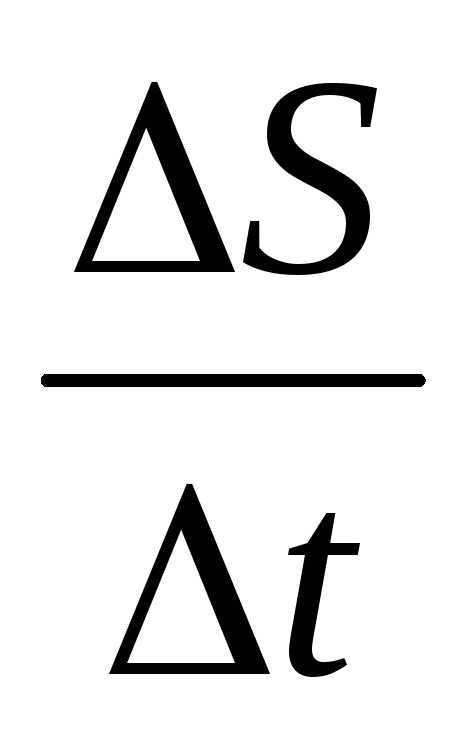 ,
,
или V = S¢t, т. е. скорость прямолинейного движения материальной точки в момент времениtесть производная от путиSпо времениt.
Обобщая, можно сказать, что если функция у = f(x) описывает какой-либо физический процесс, то производная у’ есть скорость протекания этого процесса. В этом состоит физический смысл производной.
Геометрический смысл производной:
Угловой коэффициент касательной 
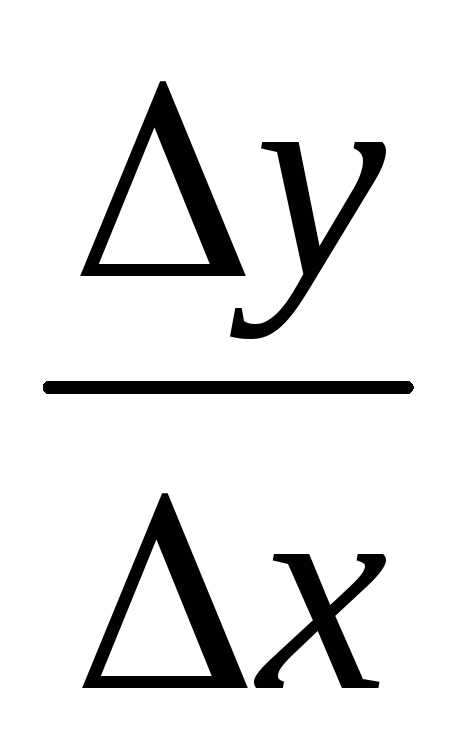 =
= ,
т.е. производная
,
т.е. производная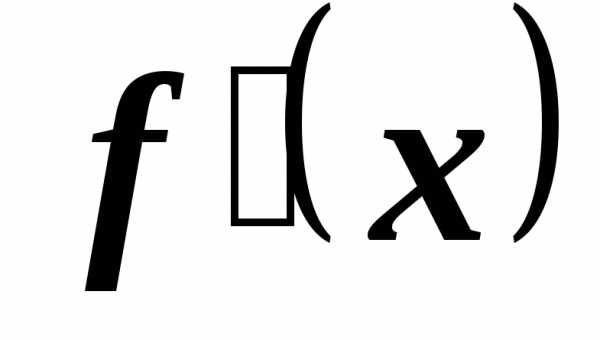 в точкеxравна угловому
коэффициенту касательной к графику
функции у =f(x)
в точке, абсцисса которой равна х.
в точкеxравна угловому
коэффициенту касательной к графику
функции у =f(x)
в точке, абсцисса которой равна х.
Уравнение касательной: у —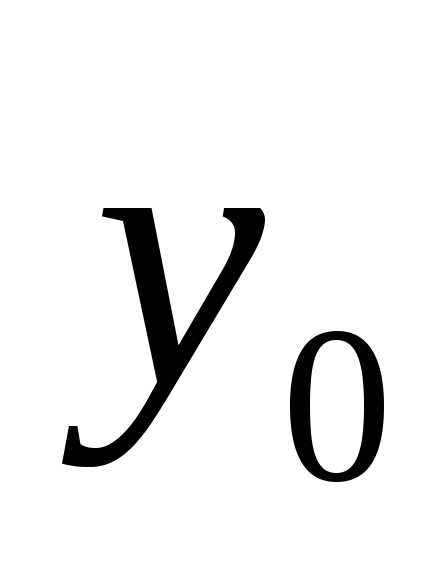 =
=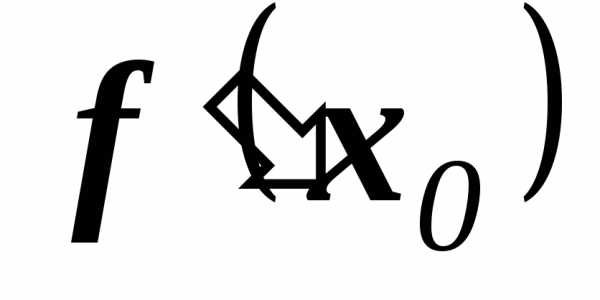 ×(x-х0).
×(x-х0).
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
Уравнение нормали:
(если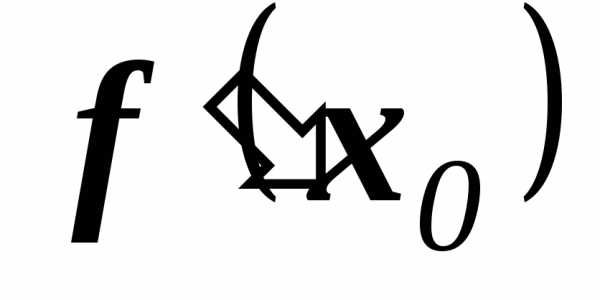
 .
.
studfiles.net
17. Свойства непрерывных функций.
1) Сумма, произведение и частное двух непрерывных функций есть функция непрерывная. (для частного кроме тех случаев, когда значение знаменателя равно нулю)
Пусть
функции 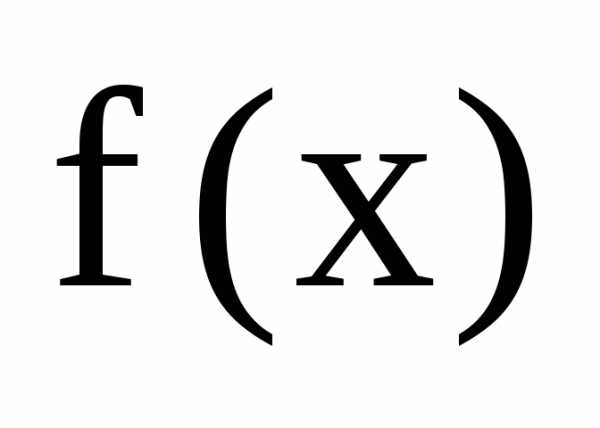 и
и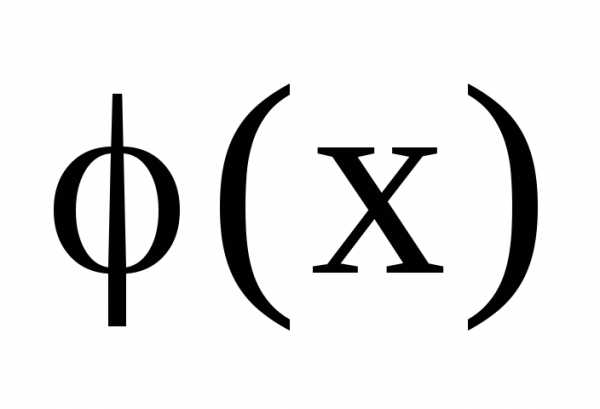 непрерывны на некотором множестве Х и
непрерывны на некотором множестве Х и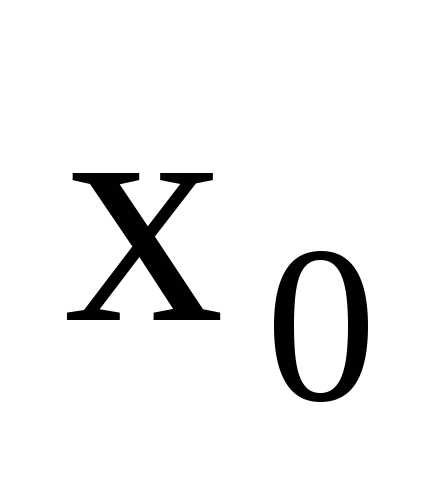 — любое значение из этого множества.
— любое значение из этого множества.
2) Пусть функции 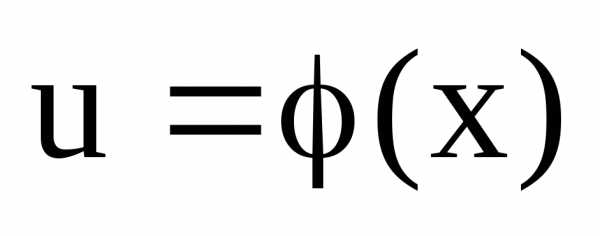 непрерывна в точке
непрерывна в точке ,
а функция
,
а функция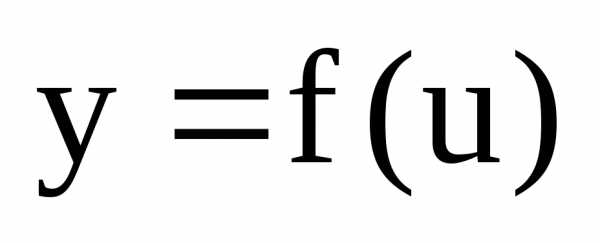 непрерывна в точке.
Тогдасложная
функция
непрерывна в точке.
Тогдасложная
функция 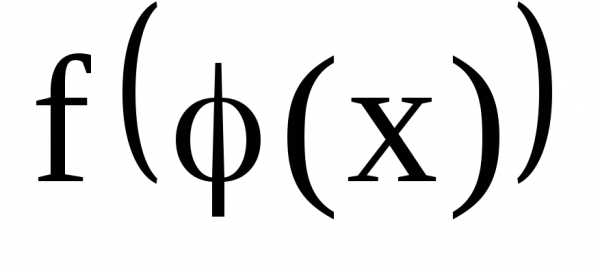 ,
состоящая из непрерывных функций,
непрерывна в точке
,
состоящая из непрерывных функций,
непрерывна в точке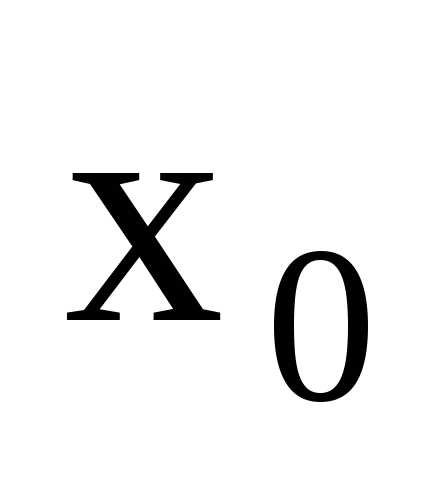 .
.
В силу непрерывности
функции 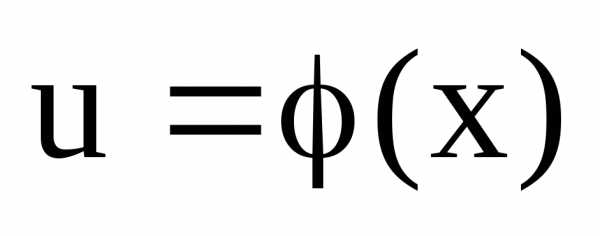 ,,
т.е. при
,,
т.е. при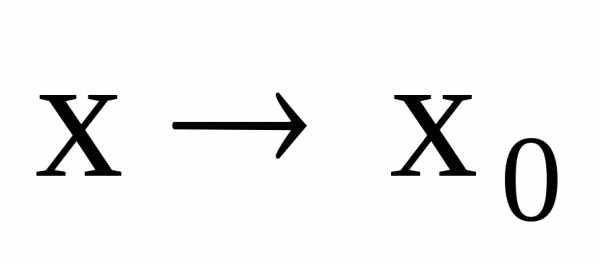 имеем
имеем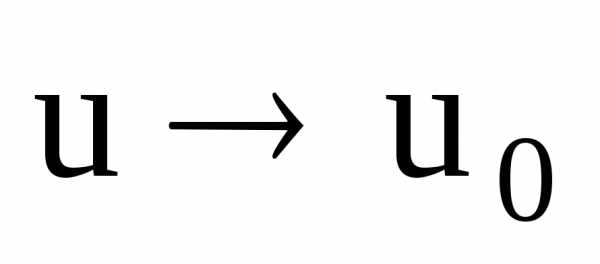 .
В следствии непрерывности функции
.
В следствии непрерывности функции имеем :
имеем :
3) Если функция  непрерывна и строго монотонна на [a;b]
оси Ох, то обратная функция
непрерывна и строго монотонна на [a;b]
оси Ох, то обратная функция  также непрерывна и монотонна на
соответствующем отрезке [c;d]
оси Oy.
также непрерывна и монотонна на
соответствующем отрезке [c;d]
оси Oy.
18. Точки разрыва и их классификация.
Точки,
в которых нарушается непрерывность
функции, называются точками
разрыва этой
функции. Если  — точка разрыва функции
— точка разрыва функции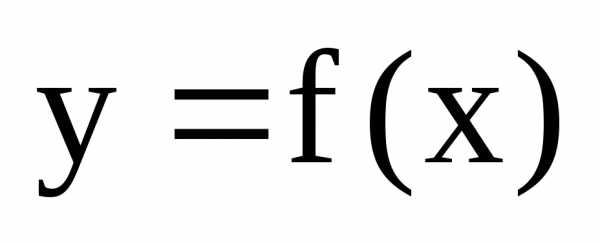 ,
то в ней не выполняется по крайней мере
одно из условий непрерывности функции.
,
то в ней не выполняется по крайней мере
одно из условий непрерывности функции.
Функция определена в окрестности точки
 ,
но не определена в самой точке
,
но не определена в самой точке .
.Функция
 определена в точке
определена в точке и в ее окрестности, но не существует
пределаf(x)
при
и в ее окрестности, но не существует
пределаf(x)
при 
Точка 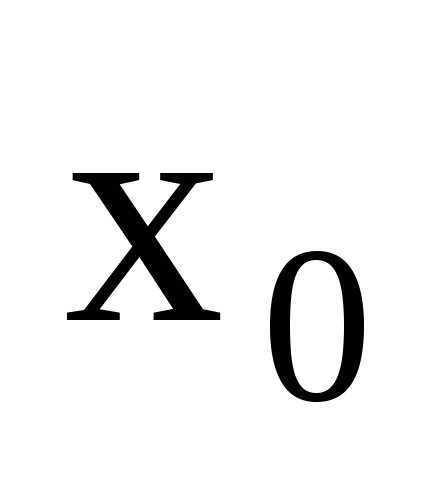 называетсяточкой
разрыва первого рода функции
,
если в этой точке существуют конечные
пределы слева и справа (односторонние
пределы), т.е.и.
При этом:
называетсяточкой
разрыва первого рода функции
,
если в этой точке существуют конечные
пределы слева и справа (односторонние
пределы), т.е.и.
При этом:
Если
 ,
то точка
,
то точка называетсяточкой
устранимого разрыва.
называетсяточкой
устранимого разрыва.Если
 ,
то точка
,
то точка называетсяточкой
конечного разрыва
называетсяточкой
конечного разрыва
Величину  называютскачком
функции в
точке разрыва первого рода.
называютскачком
функции в
точке разрыва первого рода.
Точка  называетсяточкой
разрыва второго рода функции
называетсяточкой
разрыва второго рода функции 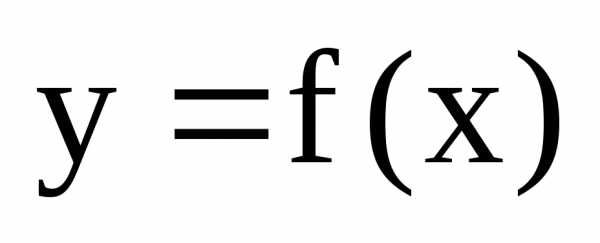 ,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
,
если по крайней мере один из односторонних
пределов не существует или равен
бесконечности.
19. Непрерывность функции на интервале и на отрезке.
Функция 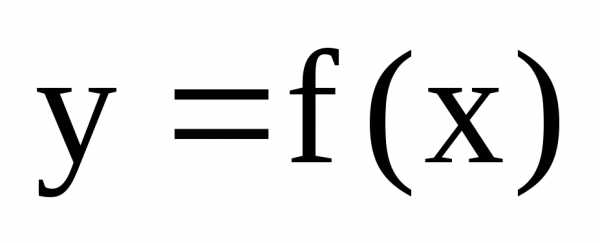 называетсянепрерывной
на интервале (a;b),
если она непрерывна в каждой точке
этого интервала.
называетсянепрерывной
на интервале (a;b),
если она непрерывна в каждой точке
этого интервала.
Функция называетсянепрерывной на отрезке [a;b], если она непрерывна на отрезке (a;b) и в точке x = a непрерывна справа , а в точкеx = b непрерывна слева .
20. Свойства функций, непрерывных на отрезке.
1) Теорема Вейрштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
1’) Следствие. Если функция непрерывна на отрезке, то она ограничена на этом отрезке.
2)
Теорема Больцано-Коши.
Если функция 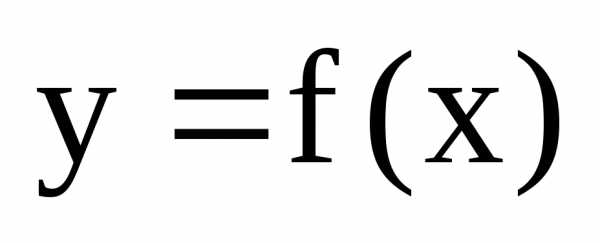 непрерывна на отрезке [a;b]
и принимает на его концах неравные
значения f(a)
= A
и f(b)
= B,
то на этом отрезке она принимает и все
промежуточные значения между А и В.
непрерывна на отрезке [a;b]
и принимает на его концах неравные
значения f(a)
= A
и f(b)
= B,
то на этом отрезке она принимает и все
промежуточные значения между А и В.
2’)
Следствие.
Если функция 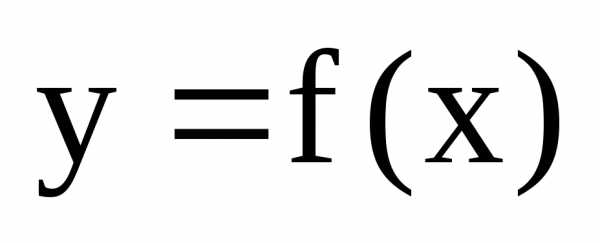 непрерывна на отрезке [a;b]
и принимает на его концах разные по
знаку значения, то внутри отрезка [a;b]
найдется хотя бы одна точка с, в которой
функция обращается в нуль. F(c)
= 0
непрерывна на отрезке [a;b]
и принимает на его концах разные по
знаку значения, то внутри отрезка [a;b]
найдется хотя бы одна точка с, в которой
функция обращается в нуль. F(c)
= 0
21. Дифференциальное исчисление функций одной переменной.
Производной
функции 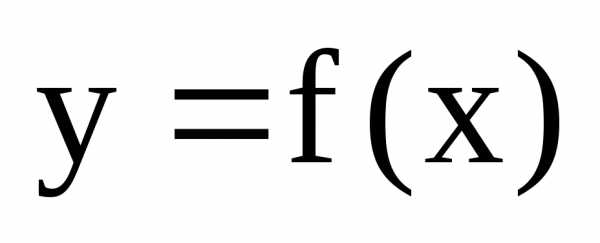 в точке
в точке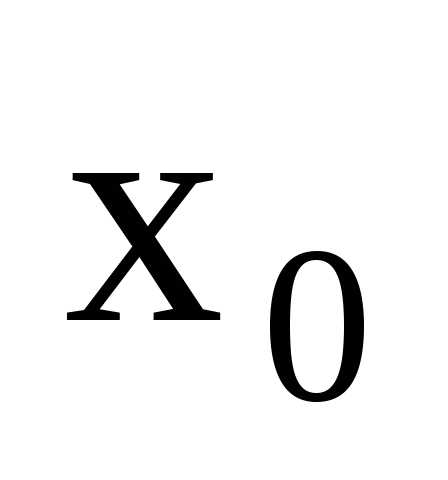 называется предел отношения приращения
функции к приращению аргумента, при
условии, что приращение аргумента
стремится к нулю.
называется предел отношения приращения
функции к приращению аргумента, при
условии, что приращение аргумента
стремится к нулю.
или
Функция 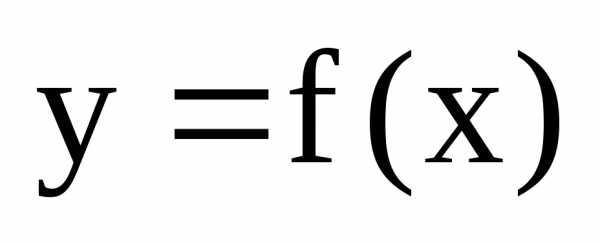 ,
имеющая производную в каждой точке
интервала (a;b),
называется дифференцируемой в этом интервале; операция нахождения
производной функции называется дифференцированием.
,
имеющая производную в каждой точке
интервала (a;b),
называется дифференцируемой в этом интервале; операция нахождения
производной функции называется дифференцированием.
22. Производная функции, ее геометрический и физический смысл.
Физический смысл. Производная – скорость протекания процесса.
Геометрический
смысл.
Производная  в точке х равна угловому коэффициенту
касательной (тангенсу угла наклона) к
графику функции
в точке х равна угловому коэффициенту
касательной (тангенсу угла наклона) к
графику функции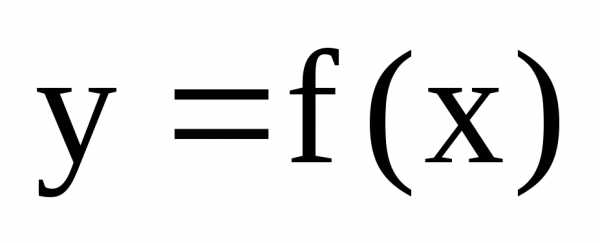 в точке, абсцисса которой равна х.
в точке, абсцисса которой равна х.
23. Уравнение касательной и нормали к кривой.
Уравнение касательной.
Уравнение нормали. 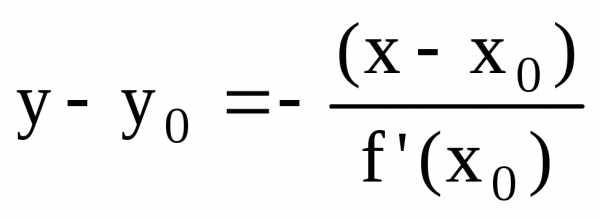
24. Односторонние производные функции в точке.
Возьмем
функцию y
= |x|
в точке х=0. 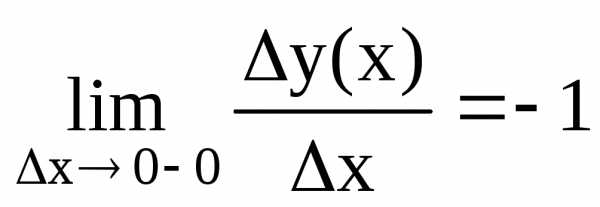 ,
,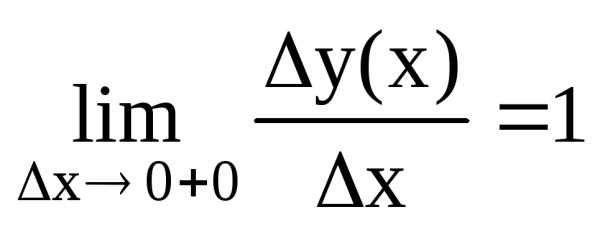 .
.
В
таких случаях говорят, что функция
имеет односторонние производные(или
«производные слева и справа»), и
обозначают соответственно  и
и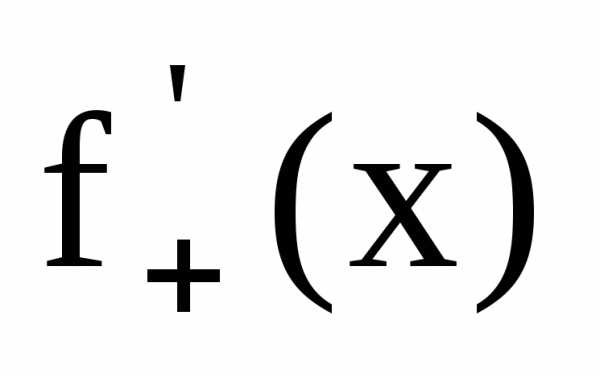 .
.
Если, значит, производная в точке не существует.
25. Основные правила дифференцирования.
Производная суммы (разности) двух функций равна сумме (разности) производных этих функций. .
Производная произведения двух функций равна произведению первого сомножителя на второй плюс произведение первого сомножителя на производную второго: .
Производная
частного двух функций равна дроби, числитель которой есть
разность произведения знаменателя
дроби на производную числителя и
числителя дроби на производную
знаменателя, а знаменатель есть квадрат
прежнего знаменателя:  .
Выполняется, когда
.
Выполняется, когда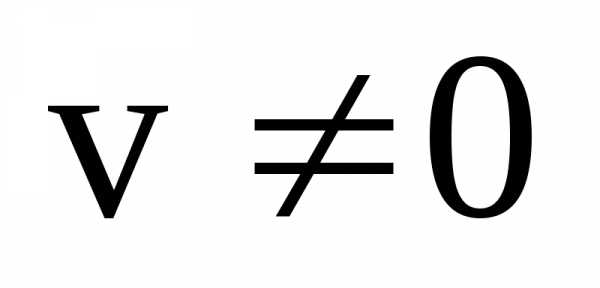 .
.
studfiles.net
Непрерывность функции в точке.
Определение. Функция f(x), определенная в окрестности некоторой точки х0, называется непрерывной в точке х0, если предел функции и ее значение в этой точке равны, т.е.
Тот же факт можно записать иначе:
Определение. Если функция f(x) определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Пример непрерывной функции:
y
f(x0)+
f(x0)
f(x0)-
0 x0- x0 x0+ x
Пример разрывной функции:
y
f(x0)+
f(x0)
f(x0)-
x0 x
Определение. Функция f(x) называется непрерывной в точке х0, если для любого положительного числа >0 существует такое число >0, что для любых х, удовлетворяющих условию

верно неравенство .
Определение. Функция f(x) называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
f(x) = f(x0) + (x)
где (х) – бесконечно малая при хх0.
Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2)
Частное двух непрерывных функций 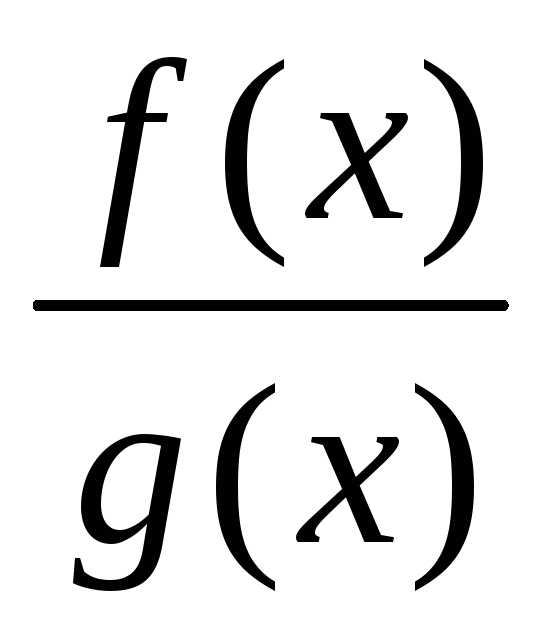 –
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
–
есть непрерывная функция при условии,
что g(x)
не равна нулю в точке х0.
3) Суперпозиция непрерывных функций – есть непрерывная функция.
Это свойство может быть записано следующим образом:
Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.
Справедливость приведенных выше свойств можно легко доказать, используя теоремы о пределах.
Непрерывность некоторых элементарных функций.
1) Функция f(x) = C, C = const – непрерывная функция на всей области определения.
2) Рациональная функция непрерывна для всех значений х, кроме тех, при которых знаменатель обращается в ноль. Таким образом, функция этого вида непрерывна на всей области определения.
3) Тригонометрические функции sinиcosнепрерывны на своей области определения.
Докажем свойство 3 для функции y = sinx.
Запишем приращение функции y = sin(x + x) – sinx, или после преобразования:
Действительно,
имеется предел произведения двух функций 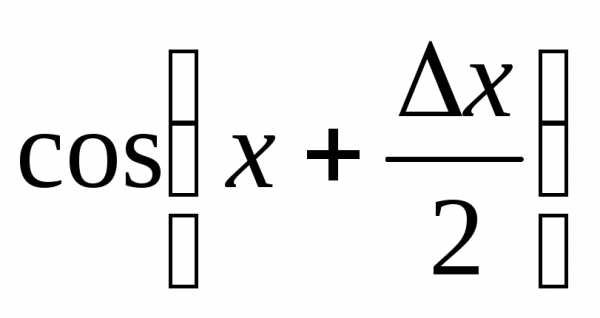 и
и .
При этом функция косинус – ограниченная
функция прих0
.
При этом функция косинус – ограниченная
функция прих0  ,
а т.к.
,
а т.к.
предел
функции синус 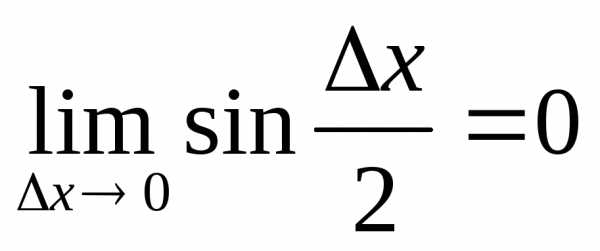 ,
то она является бесконечно малой прих0.
,
то она является бесконечно малой прих0.
Таким образом, имеется произведение ограниченной функции на бесконечно малую, следовательно это произведение, т.е. функция у – бесконечно малая. В соответствии с рассмотренными выше определениями, функция у = sinx – непрерывная функция для любого значения х = х0 из области определения, т.к. ее приращение в этой точке – бесконечно малая величина.
Точки разрыва и их классификация.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел (см. выше) , то функция называется непрерывной справа.
х0
Если односторонний предел (см. выше) , то функция называется непрерывной слева.
х0
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Из определения можно сделать вывод, что в точке разрыва 1 – го рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 – го рода еще иногда называют устранимой точкой разрыва, но подробнее об этом поговорим ниже.
Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Непрерывность функции на интервале и на отрезке.
Определение. Функция f(x) называется непрерывной на интервале (отрезке), если она непрерывна в любой точке интервала (отрезка).
При этом не требуется непрерывность функции на концах отрезка или интервала, необходима только односторонняя непрерывность на концах отрезка или интервала.
Свойства функций, непрерывных на отрезке.
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897)- немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке [a, b] выполняется условие –M f(x) M.
Доказательство этого свойства основано на том, что функция, непрерывная в точке х0, ограничена в некоторой ее окрестности, а если разбивать отрезок [a, b] на бесконечное количество отрезков, которые “стягиваются” к точке х0, то образуется некоторая окрестность точки х0.
Свойство 2: Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения х1 и х2, что f(x1) = m, f(x2) = M, причем
m f(x) M
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например – f(x) = sinx).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано – Коши). Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция f(x) непрерывна в точке х = х0, то существует некоторая окрестность точки х0, в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) – Коши). Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0.
Т.е. если sign(f(a)) sign(f(b)), то х0: f(x0) = 0.
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.


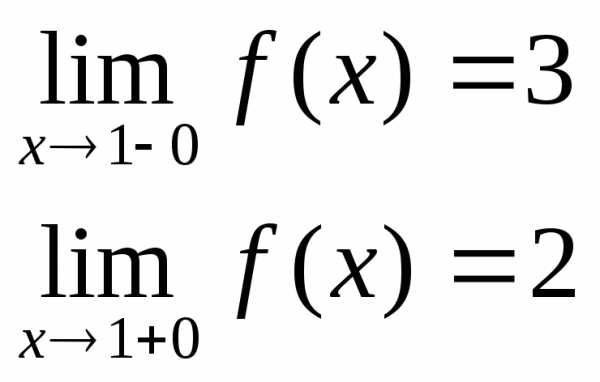
в точке х = -1 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
у
3
2
-4 -1 0 1 х
Пример. Исследовать на непрерывность функцию и определить тип точек разрыва, если они есть.
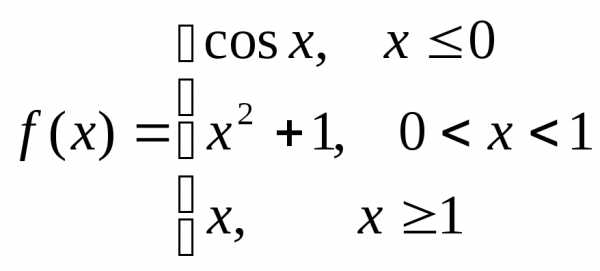

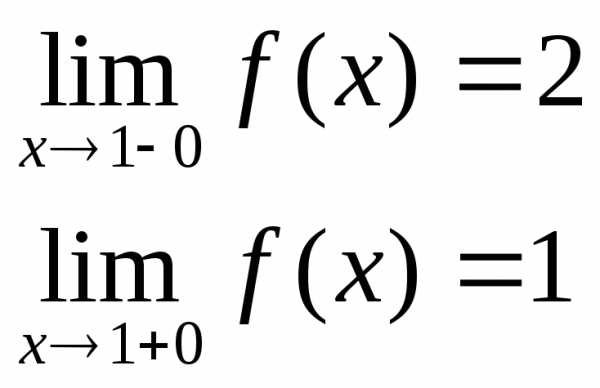
в точке х = 0 функция непрерывна в точке х = 1 точка разрыва 1 – го рода
у
2
1
- -/2 0 1 x
studfiles.net

 при,
если
при,
если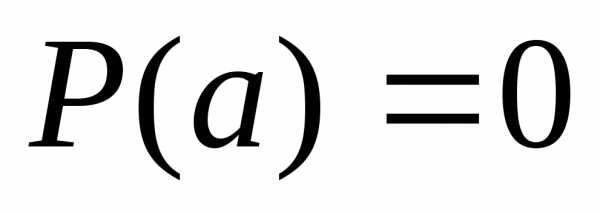 и
и ?
?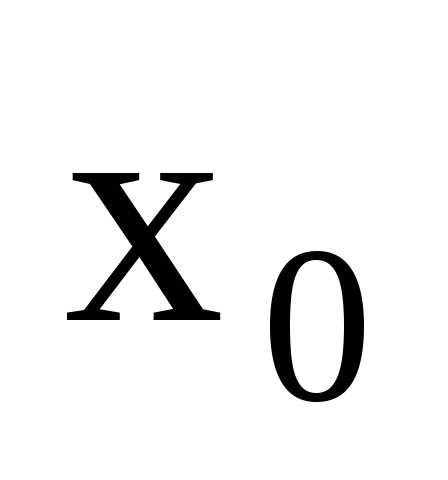 ,
но не определена в самой точке
,
но не определена в самой точке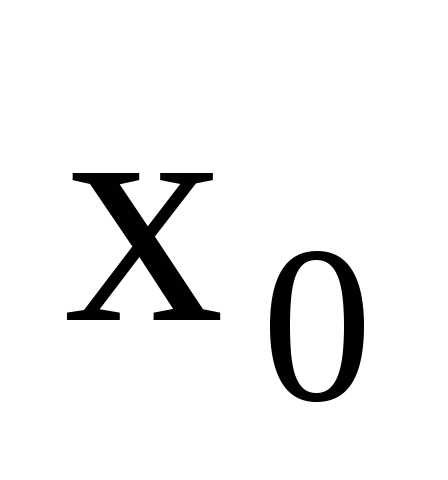 .
. определена в точке
определена в точке и в ее окрестности, но не существует
пределаf(x)
при
и в ее окрестности, но не существует
пределаf(x)
при 
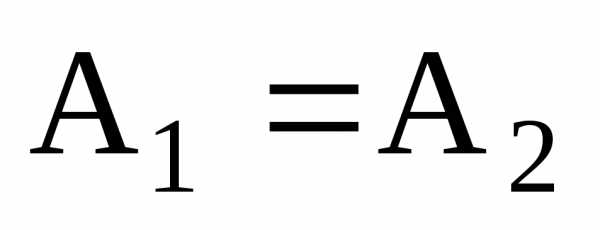 ,
то точка
,
то точка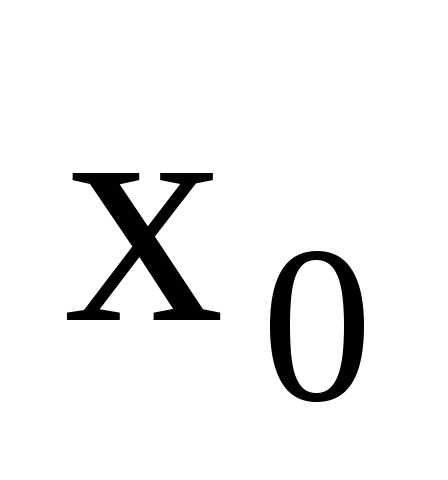 называетсяточкой
устранимого разрыва.
называетсяточкой
устранимого разрыва. ,
то точка
,
то точка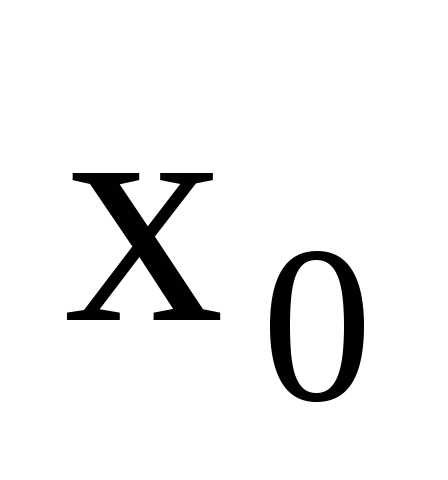 называетсяточкой
конечного разрыва
называетсяточкой
конечного разрыва