Таблица значений пи тригонометрия – синуса, косинуса, тангенса, котангенса. Как пользоваться

Таблица значений тригонометрических функций

Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».

См. также полезные материалы:

Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки  sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.

Синус пи, косинус пи, тангенс пи и других углов в радианах

Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых

задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.

Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. 

Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.

Примеры:
1. Синус пи. 
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.

2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.

3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.

Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)  

Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. 

Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
 0, 15, 30, 45, 60, 90 … 360 градусов  
(цифровые значения «как по таблицам Брадиса»)  

значение угла α (градусов)	значение угла α в радианах	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)
0	0	0	1	0	-
15	π/12	0,2588	0,9659	0,2679	3,7321
30	π/6	0,5000	0,8660	0,5774	1,7321
45	π/4	0,7071	0,7071	1	1
50	5π/18	0,7660	0,6428	1.1918	0,8391
60	π/3	0,8660	0,5000	1,7321	0,5774
65	13π/36	0,9063	0,4226	2,1445	0,4663
70	7π/18	0,9397	0,3420	2,7475	0,3640
75	5π/12	0,9659	0,2588	3,7321	0,2679
90	π/2	1	0	-	0
105	5π/12	0,9659	-0,2588	-3,7321	-0,2679
120	2π/3	0,8660	-0,5000	-1,7321	-0,5774
135	3π/4	0,7071	-0,7071	-1	-1
140	7π/9	0,6428	-0,7660	-0,8391	-1,1918
150	5π/6	0,5000	-0,8660	-0,5774	-1,7321
180	π	0	-1	0	-
270	3π/2	-1	0	-	0
360	2π	0	1	0	-

 Иногда для быстрых расчетов нужно не точное, а вычисляемое значение (число десятичной дробью), которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.

Содержание главы:
 Радианы и градусы. Радiани i градуси | Описание курса | Синус, ко синус, тангенс угла 15 градусов (sin 15 cos 15 tg 15) 

   

profmeter.com.ua

Таблица Брадиса — ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОТ АРГУМЕНТА В РАДИАНАХ

Тригонометрически функции от аргумента в радианах (Таблица Брадиса 12)

Таблица брадиса 12 не содержит тех готовых поправок, какие даны почти во всех других таблицах брадиса, а потому, чтобы получить значение тригоно­метрической функции для промежуточного значения аргумента, надо полностью про­вести операцию линейного интерполирования, о которой говорится ниже. Особой осторожности требует интерполирование значений тангенса: необходимо предварительно выяснить, законна ли на данном участке таблицы операция линей­ного интерполирования, т. е. имеется ли на этом участке достаточно равномерное из­менение функции; если не имеется, то значения функции надо округлить, чтобы их изменение стало почти равномерным. Так, при изменении х от 1,30 до 1,12 таблич­ные разности равны 2,0143 — 1,9648 — 0,0495 и 2,0660 — 2,0143 = 0,0517, линейная ин­терполяция недопустима, но становится допустимой, если предварительно округлить табличные значения до тысячных, так как 2,014 — 1,965 = 0,049 и 2,066 — 2,014 = 0,052, соседние табличные разности отличаются одна от другой меньше чем на 4 единицы разряда последней цифры.

 

X	sin х	cos x	tg x	X	sin x	cos x	tg x	X	sin x	cos x	tg x
0,00	0,0000	1,0000	0,0000	0,40	0,3894	0,9211	0,4228	0,80	0,7174	0,6967	1,0296
0,01	0100	1,0000	0100	0,41	3986	9171	4346	0,81	7243	6895	0505
0,02	0200	0,9998	0200	0,42	4078	9131	4466	0,82	7311	6822	0717
0,03	0300	9996	0300	0,43	4169	9090	4586	0,83	7379	6749	0934
0,04	0400	9992	0400	0,44	4259	9048	4708	0,84	7446	6675	1156
0,05	0500	9988	0500	0,45	4350	9004	4831	0,85	7513	6600	1383
0,06	0600	9982	0601	0,46	4439	8961	4954	0,86	7578	6524	1616
0,07	0699	9976	0701	0,47	4529	8916	5080	0,87	7643	6448	1853
0,08	0799	9968	0802	0,48	4618	8870	5206	0,88	7707	6372	2097
0,09	0899	9960	0902	0,49	4706	8823	5334	0,89	7771	6294	2346
0,10	0,0998	0,9950	0,1003	0,50	0,4794	0,8776	0,5463	0,90	0,7833	0,6216	1,2602
0,11	1098	9940	1105	0,51	4882	8727	5594	0,91	7895	6137	2864
0,12	1197	9928	1206	0,52	4969	8678	5726	0,92	7956	6058	3133
0,13	1296	9916	1307	0,53	5055	8628	5859	0,93	8016	5978	3409
0,14	1395	9902	1409	0,54	5141	8577	5994	0,94	8076	5898	3692
0,15	1494	9888	1511	o.sa	5227	8525	6131	0,95	8134	5817	3984
0,16	1593	9872	1614	0,56	5312	8473	6269	0,96	8192	5735	4284
0,17	1692	9856	1717	0,57	5396	8419	6410	0,97	8249	5653	4592
0,18	1790	9838	1820	0,58	5480	8365	6552	0,98	8305	5570	4910
0,19	1889	9820	1923	0,59	5564	8309	6696	0,99	8360	5487	5237
0,20	0,1987	0,9801	0,2027	0,60	0,5646	0,8253	0,6841	1,00	0,8415	0,5403	1,5574
0,21	2085	9780	2131	0,61	5729	8196	6989	1,01	8468	5319	5922
0,22	2182	9759	2236	0,62	5810	8139	7139	1,02	8521	5234	6281
0,23	2280	9737	2341	0,63	5891	8080	7291	1,03	8573	5148	6652
0,24	2377	9713	2447	0,64	5972	8021	7445	1,04	8624	5062	7036
0,25	2474	9689	2553	0,65	6052	7961	7602	1,05	8674	4976	7433
0,26	2571	9664	2660	0,66	6131	7900	7761	1,06	8724	4889	7844
0,27	2667	9638	2768	0,67	6210	7838	7923	1,07	8772	4801	8270
0,28	2764	9611	2875	0,68	6288	7776	8087	1,08	8820	4713	8712
0,29	2860	9582	2984	0,69	6365	7712	8253	1,09	8866	4625	9171
0,30	0,2955	0,9553	0,3093	0,70	0,6442	0,7648	0,8423	1,10	0,8912	0,4536	1,9648
0,31	3051	9523	3203	0,71	6518	7584	8595	1,11	8957	4447	2,0143
0,32	3146	9492	3314	0,72	6594	7518	8771	1,12	9001	4357	0660
0,33	3240	9460	3425	0,73	6669	7452	8949	1,13	9044	4267	1198
0,34	3335	9428	3537	0,74	6743	7385	9131	1,14	9086	4176	1759
0,35	3429	9394	3650	0,75	6816	7317	9316	1,15	9128	4085	2345
0,36	3523	9359	3764	0,76	6889	7248	9505	1,16	9168	3993	2958
0,37	3616	9323	3879	0,77	6961	7179	9697	1,17	9208	3902	3600
0,38	3709	9287	3994	0,78	7033	7109	0,9883	1,18	9246	3809	4273
0,39	3802	9249	4111	0,79	7104	7038	1,0092	1,19	9284	3717	4979
X	sin х	cos x	tg x	X	sin x	cos x	tg x	X	sin x	cos x	tg x

X	sin х	cos x	tg x	X	sin x	cos x	tg x	X	sin x	cos x	tg x
1,20	0,9320	0,3624	2,572	1,60	0,9996	— 0,0292	— 34,233	2,00	0,9093	— 0,4161	— 2,1850
1,21	9356	3530	650	1,61	9992	0392	— 25,495	2,01	9051	4252	1285
1,22	9391	3436	733	1,62	9988	0492	— 20,307	2,02	9008	4342	0744
1,23	9425	3342	820	1,63	9982	0592	— 16,871	2,03	8964	4432	0224
1,24	9458	3248	912	1,64	9976	0691	— 14,427	2.04	8919	4522	— 1,9725
1.25	9490	3153	3,010	1,65	9969	0791	— 12,599	2,05	8874	4611	9246
1,26	9521	3058	113	1,66	9960	0891	— 11,181	2.06	8827	4699	8784
1,27	9551	2963	224	1,67	9951	0990	— 10,047	2,07	8780	4787	8340
1,28	9580	2867	341	1,68	9940	1090	— 9,1208	2,08	8731	4875	7911
1,29	9608	2771	467	1,69	9929	1189	— 8,3492	2,09	8682	4962	7498
1,30	0,9636	0,2675	3,602	1,70	0,9917	— 0,1288	— 7,6966	2,10	0,8632	— 0,5048	— 1,7098
1,31	9662	2579	747	1,71	9903	1388	— 7,1373	2,11	8581	5135	6713
1,32	9687	2482	903	1,72	9889	I486	— 6,6524	2,12	8529	5220	6340
1,33	9711	2385	4,072	1,73	9874	1585	— 6,2281	2,13	8477	5305	5979
1,34	9735	2288	256	1,74	9857	1684	— 5,8535	2,14	8423	5390	5629
1,35	9757	2190	455	1,75	9840	1782	— 5,5204	2,15	8369	5474	5290
1,36	9779	2092	673	1,76	9822	1881	— 5,2221	2,16	8314	5557	4961
1,37	9799	1994	913	1.77	9802	1979	— 4,9534	2,17	8258	5640	4642
1,38	9819	1896	5,177	1,78	9782	2077	— 4,7101	2,18	8201	5722	4332
1,39	9837	1798	471	1,79	9761	2175	— 4,4887	2,19	8143	5804	4031
1,40	0,9854	0,1700	5,798	1,80	0,9738	— 0,2272	— 4,2863	2,20	0,8085	— 0,5885	— 1,3738
1,41	9871	1601	6,165	1,81	9715	2369	— 4,1005	2,21	8026	5966	3453
1,42	9887	1502	6,581	1,82	9691	2466	— 3,9294	2,22	7966	6046	3176
1,43	9901	1403	7,055	1,83	9666	2563	— 3,7712	2,23	7905	6125	2906
1,44	9915	1304	7,602	1,84	9640	2660	— 3,6245	2,24	7843	6204	2643
1,45	9927	1205	8,238	1,85	9613	2756	— 3,4881	2,25	7781	6282	2386
1,46	9939	1106	8,989	1,86	9585	2852	— 3,3608	2,26	7717	6359	2136
1,47	9949	1006	9,887	1,87	9556	2948	— 3,2419	2,27	7654	6436	1892
1,48	9959	0907	10,983	1,88	9526	3043	— 3,1304	2,28	7589	6512	1653
1,49	9967	0807	12,350	1,89	9.495	3138	— 3,0257	2,29	7523	6588	1420
1,50	0,9975	0,0707	14,10	1,90	0,9463	— 0,3233	— 2,9271	2,30	0,7457	— 0,6663	— 1,1192
1,51	9982	0608	16,43	1,91	9430	3327	8341	2,31	7390	6737	0969
1,52	9987	0508	19,67	1,92	9396	3421	7463	2,32	7322	6811	0751
1,53	9992	0408	24,50	1,93	9362	3515	6632	2,33	7254	6883	0638
1,54	9995	0308	32,46	1,94	9326	3609	5843	2,34	7185	6956	0329
1,55	9998	0208	48,08	1,95	9290	3702	5095	2,35	7115	7027	0125
1,56	9999	0108	92,62	1,96	9252	3795	4383	2,36	7044	7098	— 0,9924
1,57	1,0000	0008	1256	1,97	9214	3887	3705	2,37	6973	7168	9728
1,58	1,0000	— 0,0092	— 108,6	1,98	9174	3979	3058	2,38	6901	7237	9535
1,59	0,9998	— 0,0192	— 52,07	1,99	9134	4070	2441	2,39	6828	7306	9346
X	sin х	cos x	tg x	X	sin X	cos x	tg x	X	sin x	cos x	tg x

_______________

Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.

infotables.ru

Таблица значений тригонометрических функций

ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций. В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов. Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов. Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности. Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности. Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс. В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах. Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17. Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи. Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах. Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций. Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций. Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.

cat.convdocs.org

В таблице значений для тригонометрической функции синус приведены значения для следующих углов

ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.

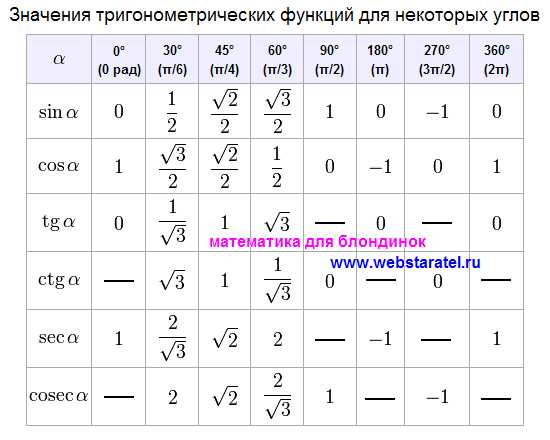
В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов.

Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов.

Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности.

Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.

Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс.

В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.

Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17.

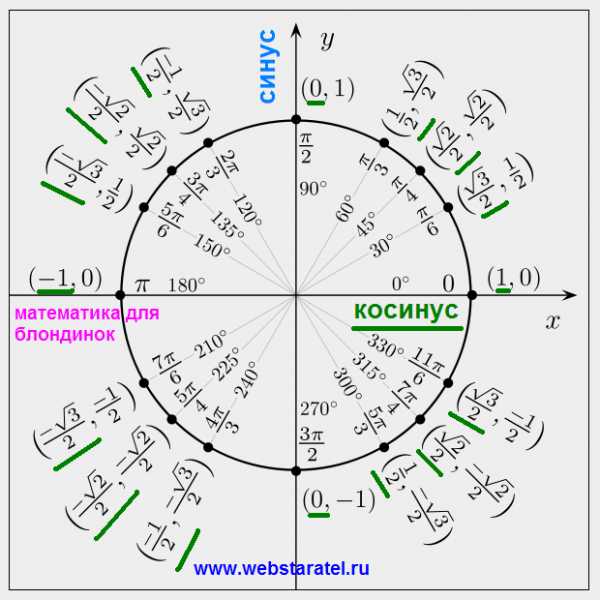
Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.

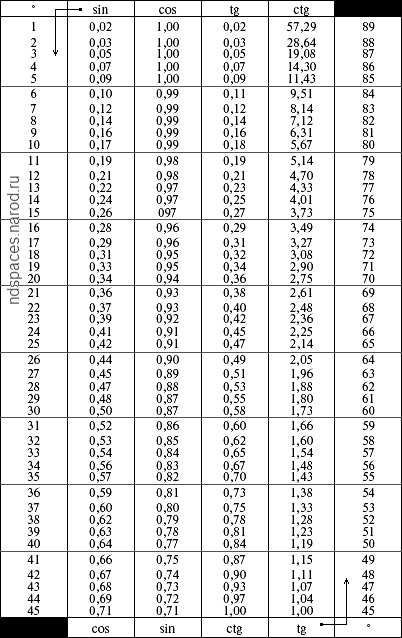
Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах.

Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.

Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.

Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.

textarchive.ru

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия

Таблица значений тригонометрических функций
часто используемых углов

I   четверть
α (рад):   0,   – 2π α (град): 0°,   – 360°
sin α	0
cos α	1
tg α	0
ctg α	не существует
α (рад):   ,    α (град): 30°,   – 330°
sin α
cos α
tg α
ctg α
α (рад):   ,    α (град): 45°,   – 315°
sin α
cos α
tg α	1
ctg α	1
α (рад):   ,    α (град): 60°,   – 300°
sin α
cos α
tg α
ctg α
α (рад):   ,    α (град): 90°,   – 270°
sin α	1
cos α	0
tg α	не существует
ctg α	0
II  четверть
α (рад):   ,    α (град): 120°,   – 240°
sin α
cos α
tg α
ctg α
α (рад):   ,    α (град): 135°,   – 225°
sin α
cos α
tg α	– 1
ctg α	– 1
α (рад):   ,    α (град): 150°,   – 210°
sin α
cos α
tg α
ctg α
α (рад):   π,   – π α (град): 180°,   – 180°
sin α	0
cos α	– 1
tg α	0
ctg α	не существует
III  четверть
α (рад):   ,    α (град): 210°,   – 150°
sin α
cos α
tg α
ctg α
α (рад):   ,    α (град): 225°,   – 135°
sin α
cos α
tg α	1
ctg α	1
α (рад):   ,    α (град): 240°,   –120°
sin α
cos α
tg α
ctg α
α (рад):   ,   α (град): 270°,   – 90°
sin α	– 1
cos α	0
tg α	не существует
ctg α	0
IV  четверть
α (рад):   ,    α (град): 300°,   – 60°
sin α
cos α
tg α
ctg α
α (рад):   ,    α (град): 315°,   – 45°
sin α
cos α
tg α	– 1
ctg α	– 1
α (рад):   ,    α (град): 330°,   –30°
sin α
cos α
tg α
ctg α
α (рад):   2π,  0 α (град): 360°,   0°
sin α	0
cos α	1
tg α	0
ctg α	не существует

Примеры вычисления значений тригонометрических функций

      Пример 1. Найти    sin 15°.

      Решение. Воспользовавшись формулой «Синус разности», получаем:

      Пример 2. Найти    cos 22,5°.

      Решение. Воспользовавшись формулой «Косинус двойного угла», получаем:

      Пример 3. Найти    sin 18°.

      Решение. Поскольку

то, с помощью формул «Синус тройного угла» и «Косинус двойного угла», отсюда получаем:

      Теперь, если ввести обозначение

sin 18° = t ,

то возникает кубическое уравнение

4t³ – 2t² – 3t + 1 = 0 .

      Решим это уравнение, раскладывая его левую часть на множители:

      Поскольку

0 < sin 18° < 1 ,

то первый и второй корни должны быть отброшены. Следовательно,

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Тригонометрические таблицы

Тригонометрические таблицы ● Математика для заочников и не только

Таблица значений тригонометрических функций:

																																											Аргумент
Функция	0																			2										3									5								7									5				4										3	5						7									11										2
		6						4					3						2	3												4								6							6									4				3										2	3								4							6
																																														180																																																		360
		30							45				60						90	120										135									150								210									225				240										270	300						315									330
		1																																						1										1																																				1
										2						3							3											2																								2							3									3								2
sin	0	2																	1																					2						0				2																				–1																2										0
									2					2							2											2																															2									2
																																																									2																							2
													1							1																																											1								1
cos	1				3					2									0																2								3			–1					3							2												0											2								3							1
		2						2					2							2												2								2										2							2						2								2								2							2
tg	0				3			1											–													–1											3			0				3							1													–									–1												3					0
		3											3							3																			3								3																3								3															3
ctg	–							1								3			0						3							–1														–											1							3						0				3					–1																	–
		3											3							3																			3											3										3											3															3

Запоминать эти значения без необходимости не нужно, но полезно знать, что: sin 0 0 , sin2 1, cos 0 1, cos2 0

Это ускорит решение заданий.

Также время от времени требуются формулы по переводу градусов в радианы, и наоборот:

1) Радианы переводятся в градусы по формуле: град рад 180 . Например, переведём в градусырад 6 :град

2) Градусы переводятся в радианы по формуле: рад град . Например, переведём в радианыград 60 :рад 180

© http://mathprofi.ru Высшая математика – просто и доступно!

Распространение данного материала разрешено при условии сохранения копирайта

	Тригонометрические таблицы ● Математика для заочников и не только
	Таблица значений обратных тригонометрических функций:
													Аргумент
	Функция	3		–1			3		2		3		1	0	1	3	2	3	1	3
							2		2		3		2		2	3	2	2
	arcsin		–							Бяка				0		Бяка				–
					2		3		4				6		6		4	3	2
	arccos		–			5		3		Бяка		2				Бяка			0	–
							6		4			3		2	3		4	6
	arctg					Бяка		Бяка				Бяка		0	Бяка		Бяка	Бяка
			3		4						6					6			4	3
	arcctg	5		3		Бяка		Бяка		2		Бяка			Бяка		Бяка	Бяка
			6	4							3			2		3			4	6
	Полезно ознакомиться с графиками и основными свойствами тригонометрических функций и обратных тригонометрических
	функций. Читайте последние параграфы методического материала http://mathprofi.ru/grafiki_i_svoistva_funkcij.html

© http://mathprofi.ru Высшая математика – просто и доступно!

Распространение данного материала разрешено при условии сохранения копирайта

Тригонометрические таблицы ● Математика для заочников и не только

Формулы приведения

Функция						Аргумент
							3	3	2	2
	2	2					2	2
sin	cos	cos			sin	sin	cos	cos	sin	sin
cos	sin	sin			cos	cos	sin	sin	cos	cos
tg	ctg	ctg			tg	tg	ctg	ctg	tg	tg
ctg	tg	tg			ctg	ctg	tg	tg	ctg	ctg
Пример на всякий случай: sin			2		cos

Иногда приходится заглядывать, чаще всего, для того, чтобы упростить предел

© http://mathprofi.ru Высшая математика – просто и доступно!

Распространение данного материала разрешено при условии сохранения копирайта

studfiles.net