Теоремы косинусов и синусов для треугольника – Теорема синусов, теорема косинусов — урок. Геометрия, 9 класс.

Применим теорему косинусов к треугольникам ABC и ABD. Получим $$ АС^2 = АВ^2 + ВС^2 — 2АВ • ВС • cos \beta \\ BD^2 = АВ^2 + AD^2 — 2АВ • AD • cos \alpha $$ Так как $\beta = 180° — \alpha$ , то, складывая эти равенства и замечая, что $\cos \beta = \cos (180° — \alpha) = -\cos \alpha \,; АВ = CD\,; ВС = AD$ , получим $$ АС^2 + BD^2 = АВ^2 + ВС^2 + CD^2 + AD^2 $$

Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.

Видео-решение.

www.wiki.eduvdom.com

Теорема косинусов, синусов. Применение для любых треугольников. Формулы

Рис. 1. Треугольник. Теорема косинусов. Теорема синусов

Для произвольного треугольника существуют две теоремы, позволяющие формульно связать длины сторон и углы треугольника: теорема косинусов и теорема синусов.

Теорема косинусов — соотношение, позволяющее связать стороны и углы в произвольном треугольнике (рис. 1). Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними, или математически:

Теорема синусов — соотношение, позволяющее связать стороны и углы в произвольном треугольнике (рис. 1). Отношение стороны треугольника к синусу противоположного угла есть величина постоянная,  или математически:

Как применять:

• если в вашей задаче необходимо найти сторону треугольника, а известны ещё две стороны и угол между ними, то легче использовать теорему косинусов
• если в вашей задаче необходимо найти сторону треугольника, а известны два угла и любая сторона, то легче использовать теорему синусов
• если в вашей задаче необходимо найти угол треугольника, а известны три стороны, то легче использовать теорему косинусов
• если в вашей задаче необходимо найти угол треугольника, а известны две стороны и любой из углов, то легче использовать теорему синусов

Поделиться ссылкой:

www.abitur.by

Теорема косинусов и синусов. Доказательство и примеры

Тригонометрия широко применяется не только в разделе алгебра — начала анализа, но также и в геометрии. В связи с этим, разумно предположить о существовании теорем и их доказательств, связанных с тригонометрическими функциями. Действительно, теоремы косинусов и синусов выводят очень интересные, а главное полезные соотношения между сторонами и углами треугольников.

Теорема косинусов

С помощью данной формулы можно вывести любую из сторон треугольника:

Доказательство утверждения выводится на основе теоремы Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

Рассмотрим произвольный треугольник ABC. Из вершины C опустим  высоту h к основанию фигуры, в данном случае абсолютно не важна ее длина. Теперь, если рассмотреть произвольный треугольник AСВ, то  можно выразить координаты точки C через тригонометрические функции cos и sin.

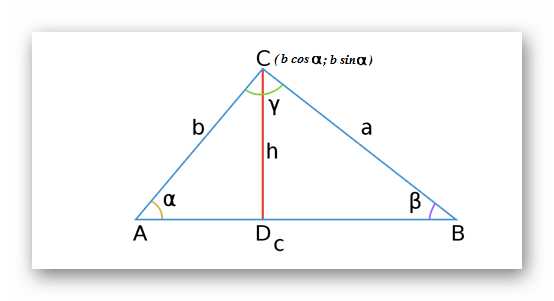
Вспомним определение косинуса и распишем соотношение сторон треугольника ACD: cos α = AD/AC | умножим обе стороны равенства на AC; AD = AC * cos α.

Длину AC примем за b и получим выражение для первой координаты точки С:
x = b * cos⁡α. Аналогично, находим значение ординаты С: y = b * sin α.  Далее применим теорему Пифагора и выразим h поочередно для треугольника ACD и DCB:

Очевидно, что оба выражения (1) и (2) равны между собой. Приравняем правые части и приведем подобные:

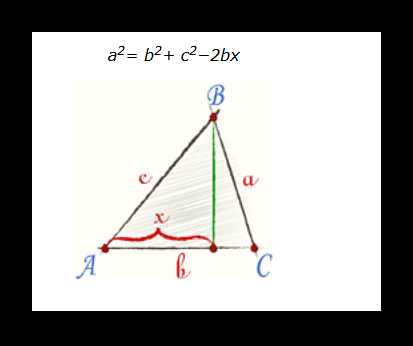
На практике данная формула позволяет найти длину неизвестной стороны треугольника по заданным углам. Теорема косинусов имеет три следствия: для прямого, острого и тупого угла треугольника.

Заменим величину cos α привычной переменной x, тогда для острого угла треугольника ABC получим:

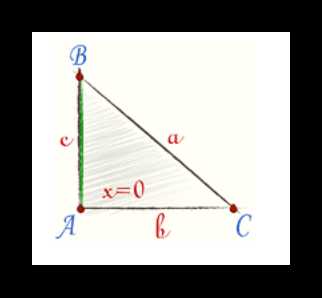
Если же угол окажется прямым, то 2bx исчезнет из выражения, так как cos 90° = 0. Графически второе следствие можно представить следующим образом:

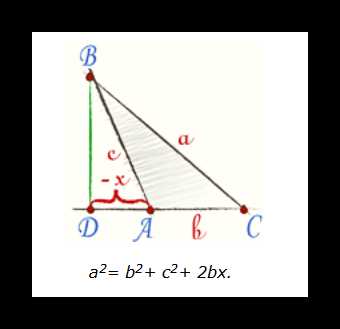
В случае тупого угла знак «-»перед двойным аргументом в формуле сменится на «+»:

Как видно из объяснения, ничего сложного в соотношениях нет. Теорема косинусов есть не что иное, как переложение теоремы Пифагора в тригонометрических величинах.

Практическое применение теоремы

Задание 1.  Дан треугольник ABC, у которого сторона BC = a = 4 см, AC = b = 5 см, а cos α = ½. Необходимо найти длину стороны AB.

Чтобы правильно произвести расчет, нужно определить угол α. Для этого стоит обратиться к таблице значений для тригонометрических функций, согласно которой арккосинус равен 1/ 2 для угла в 60°. Исходя из этого, воспользуемся формулой первого следствия теоремы:

Задание 2. Для треугольника ABC известны все стороны: AB =4√2,BC=5,AC=7. Требуется найти все углы фигуры.

В данном случае не обойтись без чертежа условий задачи.

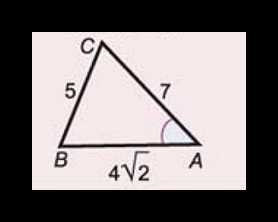
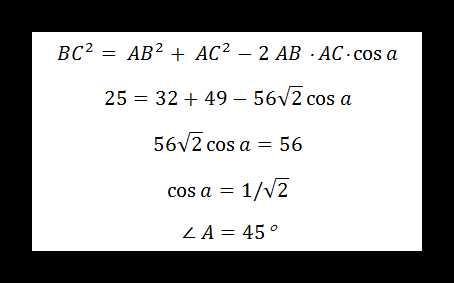
По аналогии нетрудно составить формулы и рассчитать значения и других углов:

В сумме три угла треугольника должны составить 180 °: 53 + 82 + 45 = 180, следовательно, решение найдено.

Теорема синусов

Теорема гласит, что все стороны произвольного треугольника пропорциональны синусам противолежащих углов. Записываются соотношения в виде тройного равенства:

Классическое доказательство утверждения проводят на примере фигуры вписанной в окружность.

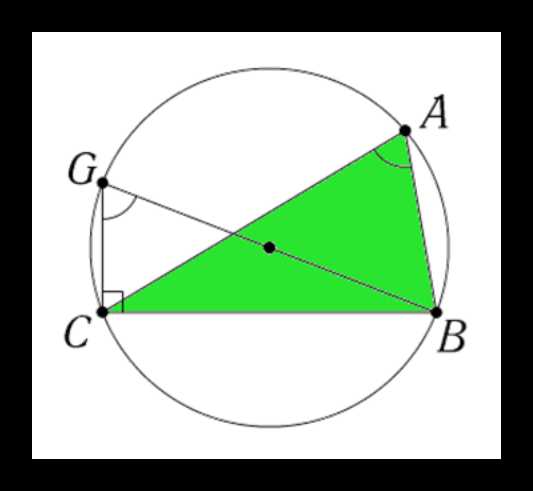
Чтобы убедиться в правдивости высказывания на примере треугольника ABC на рисунке, необходимо подтвердить тот факт, что 2R = BC / sin A. Затем доказать, что и прочие стороны соотносятся с синусами противоположных углов, как 2R или D окружности.

Для этого проводим диаметр круга из вершины B. Из свойства углов вписанных в окружность ∠GCB – прямой, а ∠CGB либо равен ∠CAB, либо (π — ∠CAB).  В случае с синусом последнее обстоятельство не значительно, так как sin (π –α) = sin α.  На основании приведенных умозаключений можно утверждать, что:

sin ∠CGB = BC/ BG или sin A = BC/2R,

2R=BC/sinA.

Если рассматривать другие углы фигуры, получим расширенную формулу теоремы синусов:

Типовые задания на отработку знания теоремы синусов сводятся к поиску неизвестной стороны или угла треугольника.

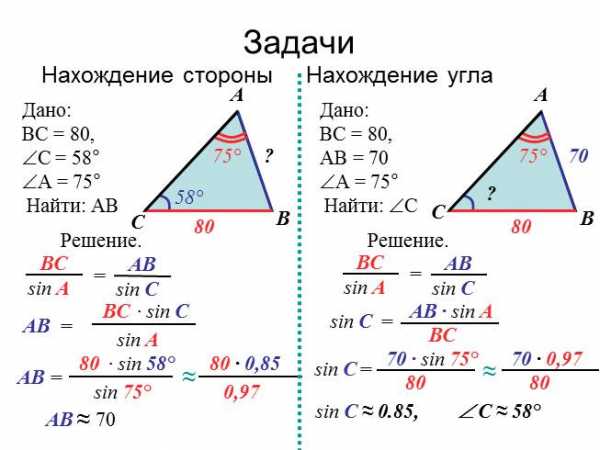
Как видно из примеров, решение подобных задач не вызывает затруднений и заключается в проведении математических расчетов.

Похожие статьи

Рекомендуем почитать:

Тригонометрические функции произвольных углов. Теоремы синусов и косинусов

Тригонометрические функции (синус, косинус, тангенс, котангенс) однозначно определяют острый угол. Это значит, что если нам известно значение хотя бы одной из этих функций, то мы можем найти и сам острый угол, и значение оставшихся трех тригонометрических функций (см. рис. 1).

Рис. 1. Взаимосвязь тригонометрических функций

Взаимосвязь тригонометрических функций:

Например, глядя на определения тангенса и котангенса, легко заметить, что:

Потому что , и наоборот.

Можно переписать в эквивалентном виде:

Если мы знаем, что , то сразу скажем: . Нам даже не надо искать само значение угла.

Кроме того, несложно заметить, что:

И аналогично:

Мы уже почти научились по значению одной тригонометрической функции угла находить остальные. Нужно только связать между собой синус и косинус.

Вспомним, что для прямоугольного треугольника верна теорема Пифагора:

Чтобы перейти к формулам для синуса и косинуса, разделим обе части этого равенства на . Получим:

Откуда, по определению:

Можно получить и другие формулы, связывающие тригонометрические функции одного угла. Например, если мы хотим связать тангенс и косинус, то, взяв формулу

, поделим обе части на , получим:

Откуда:

Аналогично можно получить формулу:

Полученные нами формулы называются основными тригонометрическими тождествами. С их помощью можно, зная значение одной из тригонометрических функций острого угла, найти значения трех остальных. С примером решения такой задачи можно ознакомиться ниже.

Вычисление значений тригонометрических функций

Предположим, что нам известно значение синуса острого угла:

Найдем значения остальных тригонометрических функций этого угла.

Зная синус, несложно найти косинус, используя формулу:

Подставляем, получаем:

Поскольку косинус острого угла, по определению, – это отношение длин двух сторон, то он может принимать только положительные значения. Значит,

Теперь найти тангенс и котангенс не составит проблем:

Можно было действовать и по-другому, например найти котангенс через синус, используя формулу:

Потренируйтесь самостоятельно находить значения остальных тригонометрических функций острого угла по известному тангенсу или котангенсу.

Возникает вопрос: зачем нужно рассматривать целых четыре функции, если можно использовать одну, а все остальные при необходимости выражать через эту одну?

Конечно, можно. Вопрос только в удобстве. Если какая-то конструкция часто используется, то ее удобно обозначить отдельно, а также вывести ее свойства, чтобы использовать их при решении конкретных задач.

К примеру, длину можно было бы измерять только в метрах. Но расстояние между городами или размеры телефона в них измерять не очень удобно. Не говоря уже про размеры бактерий или расстояния между планетами. Поэтому люди используют разные единицы измерения для одной и той же величины (миллиметры, километры, дюймы, мили, световые года и т. д.) в зависимости от удобства при решении той или иной задачи (см. рис. 2).

Рис. 2. Использование различных единиц измерения

Такая же ситуация с тригонометрическими функциями – оказалось, что эти  соотношения используются настолько часто, что удобнее ввести и изучать их отдельно, чем выражать через одно.

Более того, можно ввести и другие тригонометрические функции, но они не прижились именно из-за того, что редко встречаются при решении практических задач. Подробнее о них ниже.

vetkaДругие тригонометрические функции

Наблюдательный человек заметит, что при определении тригонометрических функций мы перебрали не все комбинации (см. рис. 3): можно гипотенузу разделить на каждый из катетов.

Рис. 3. Взаимосвязь тригонометрических функций

Взаимосвязь тригонометрических функций:

Действительно, можно ввести еще две функции – секанс и косеканс:

Несложно заметить, что мы получили функции, обратные синусу и косинусу.

В наше время эти функции практически не используют. Слишком просто их заменить синусом и косинусом. Кстати, по этой причине в некоторой литературе не выписываются свойства для котангенса – считается, что его проще выражать через тангенс.

На самом деле, никакой принципиальности в том, чтобы использовать именно эти, а не другие функции, нет. Просто при решении различных задач чаще встречались именно выражения, содержащие синусы, косинусы, тангенсы и котангенсы, поэтому им дали отдельные названия и их подробно изучают.

Какие значения могут принимать тригонометрические функции? Рассмотрим . Поскольку мы определяли синус для острых углов прямоугольных треугольников, то угол  может принимать значение от  до . Формально, не включая эти значения. Но угол может сколь угодно близко к ним приближаться.

Зафиксируем гипотенузу  и уменьшим угол  почти до нуля (см. рис. 4).

Рис. 4. Уменьшенный почти до  угол  при зафиксированной гипотенузе

Почти до нуля уменьшится и катет . А вместе с ним и :

Поэтому можем определить:

Если начать увеличивать  (см. рис. 5), то будет увеличиваться и катет , а вместе с ним будет увеличиваться и значение синуса.

Рис. 5. Увеличенный почти до  угол

Чем ближе к  будет угол, тем ближе катет  будет к гипотенузе . Значит:

Поэтому можем определить:

Значение синуса не может превышать  – это его максимальное значение. Больше синус быть не может.

Попробуйте самостоятельно провести аналогичные рассуждения для косинуса острого угла и убедиться, что он будет убывать с увеличением угла от  до . И максимальное значение:

Минимальное значение:

Такие выводы можно сделать сразу, используя полученное на прошлом уроке свойство:

Рассмотрим теперь значения тангенса и котангенса. Будем увеличивать угол от  до . Катет  будет меняться от  до . С катетом  все с точностью до наоборот: от  до .

Получается, что:

Поэтому можем определить:

А :

Но мы знаем, что деление на  не определено. Как же быть? Если проследить изменение значений тангенса, то заметно, что они неограниченно растут при приближении угла к . Поэтому можно сказать, что: . Но поскольку у нас нет такого числа, как бесконечность, говорят, что  не существует или, по-другому, не определен.

 не определен

Это вполне согласуется с уже полученными свойствами. Действительно:

Поскольку деление на  не определено, то и  должен быть не определен.

С котангенсом все аналогично. Несложно получить:

 – не определен

Мы ввели тригонометрические функции, чтобы заменить непосредственное измерение углов измерением длин. И сделали это для острых углов, т. к. использовали свойства прямоугольных треугольников.

Вспомним, что математика имеет инструментальный характер. Чтобы инструмент был удобным, мы можем расширять или дополнять его. При этом обычно это делается так, чтобы свойства расширенных инструментов совпадали со свойствами уже существующих (или не противоречили им). Именно поэтому мы расширили значения тригонометрических функций для углов  и , которые не являются острыми.

Но углы могут быть и больше  (например, в тупоугольном треугольнике) (см. рис. 6).

Рис. 6. Угол больше  в тупоугольном треугольнике

И хочется расширить наш удобный инструмент измерения углов с помощью линейных измерений на произвольный угол (от  до ), сохранив при этом все полученные нами свойства (например, основные тригонометрические тождества).

Стороны угла можно продлить сколь угодно далеко. Для измерения длин нам необходимо их ограничить. Когда угол был острый, мы использовали для этих целей прямоугольный треугольник. Для произвольного угла можно использовать еще одну простую фигуру – окружность.

Для острых углов от размера прямоугольного треугольника ничего не зависело, т. к. все прямоугольные треугольники с равным острым углом подобны (см. рис. 7).

Рис. 7. Подобные прямоугольные треугольники с равным острым углом

Поскольку любые две окружности подобны (см. рис. 8), то от размера окружности тоже ничего зависеть не будет.

Рис. 8. Окружности подобны

Поэтому можем выбрать в качестве эталона окружность радиуса  (см. рис. 9) (или, как ее еще называют, единичную окружность).

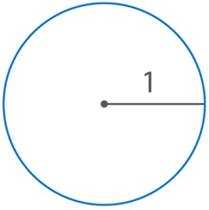
Рис. 9. Единичная окружность

Можно сказать и по-другому: какую бы окружность мы ни взяли – можно обозначить ее радиус за  – значения тригонометрических функций от этого не изменятся.

Итак, начертим единичную окружность с центром в вершине рассматриваемого угла.

Рассмотрим декартову систему координат, начало которой совпадает с центром этой окружности и, соответственно, вершиной угла. А ось  направлена вдоль одной из сторон этого угла (рис. 10).

Рис. 10. Тригонометрическая окружность

Тогда вершины угла – это точки: ,  и подвижная точка  на окружности, координаты которой будут зависеть от величины угла  (рис. 11).

Рис. 11. Точки на тригонометрической окружности

Точка  может двигаться по часовой стрелке к точке  (угол  равен ) (см. рис. 12) или против часовой стрелки до точки  как бы с другой стороны (угол  равен ) (см. рис. 13).

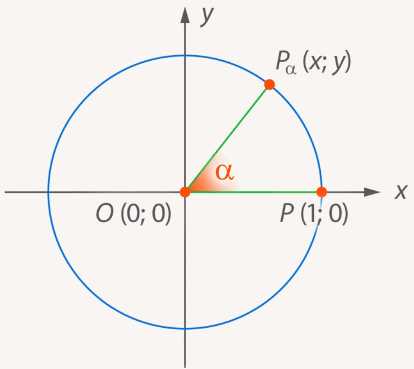
Рис. 12. Точка  двигается по часовой стрелке к точке  (угол  равен )

Рис. 13. Точка  двигается против часовой стрелки до точки  с другой стороны (угол  равен )

Понятно, что точка  однозначно задает угол, и наоборот – каждому углу соответствует ровно одна такая точка. Поэтому нам достаточно следить за положением (координатами) этой точки, чтобы определять величину угла.

Как мы уже говорили, главная задача при расширении инструмента – чтобы сохранялись его свойства. Посмотрим, как будут выглядеть уже известные нам тригонометрические функции острого угла. Понятно, что им соответствует расположение точки  в первой четверти.

Построим прямоугольный треугольник, чтобы воспользоваться определением. Для этого опустим перпендикуляр из точки  на ось  (см. рис. 14).

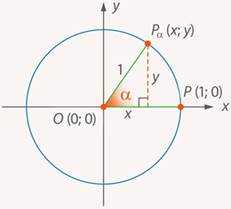
Рис. 14. Построенный прямоугольный треугольник

По определению: синус угла – это отношение противолежащего катета к гипотенузе (радиусу окружности, который мы считаем равным ).

Получаем, что – ордината точки . Аналогично получаем, что  – абсцисса точки .

Таким образом, можно дать новое определение синуса и косинуса угла  – это координаты  и  точки : . Это определение позволяет нам его использовать для любых углов, при этом для острых углов оно совпадает с ранее введенным.

Попробуем вычислить значение синуса и косинуса, например . При пересечении двух прямых образуется четыре угла. Но, как мы знаем, по любому из них можно однозначно восстановить все остальные (см. рис. 15):

Рис. 15. По одному из углов можно восстановить все остальные

Поэтому логично ожидать, что синусы и косинусы таких углов будут обладать какими-то особыми свойствами.

Отметим точку  и точку  (см. рис. 16).

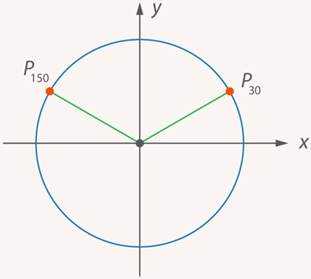
Рис. 16. Отмеченные точки  и

Несложно заметить, что прямоугольные треугольники, которые получились, равны (гипотенузы – радиусы, острые углы по ) (см. рис. 17).

Рис. 17. Полученные равные прямоугольные треугольники

Значит, у этих двух точек равны ординаты и равны по модулю, но противоположны по знаку абсциссы. Используя введенное определение, получаем, что:

Несложно обобщить эти свойства для произвольных углов:

Попробуйте самостоятельно доказать похожие свойства:

Обратите внимание, что, расширив тригонометрические функции на углы больше  мы получили, что значение синуса и косинуса может быть отрицательным. Однако несложно видеть, что в силу определения оно по модулю не может быть больше .

Нас будут интересовать значения тригонометрических функций для углов треугольника, которые могут быть от  до . Им будут соответствовать точки окружности первой и второй четверти (см. рис. 18).

Рис. 18. Первая и вторая четверти тригонометрической окружности

Ординаты этих точки всегда будут положительными, т. е. синус может принимать значения только в интервале , а вот абсцисса точек второй четверти отрицательна. Поэтому косинус острого угла всегда будет положительным, а тупого – отрицательным.

Мы расширили определение синуса и косинуса. А что же с тангенсом и котангенсом?

Как мы уже говорили, расширение инструмента должно сохранять его свойства.

Мы знаем, что:

Раз мы определили: , , то должно выполняться:

Можем принять полученные формулы в качестве определения для тангенса и котангенса.

Мы узнаем, что тангенс и котангенс для острых углов – положительные, несложно получить, что для тупых углов они будут отрицательными (если одно из чисел положительно, другое отрицательно, то их отношение будет отрицательным).

Например:

Обратите внимание, что:

Это неслучайное совпадение:

Мы использовали полученные ранее свойства для синуса и косинуса.

Попробуйте, используя их, самостоятельно вывести аналогичные формулы для:  

Основные тригонометрические тождества

Будут ли верны для расширенных тригонометрических функций основные тождества?

Очевидно, да, т. к. мы через них определили тангенс и котангенс. Перемножим эти два равенства, получим еще одно тождество:

Чуть сложнее с тождеством:

Используем определение (см. рис. 19):

Рис. 19. Тригонометрические функции на единичной окружности

Обратите внимание, что  и  – это длины катетов прямоугольного треугольника для точки  из любой четверти (см. рис. 20).

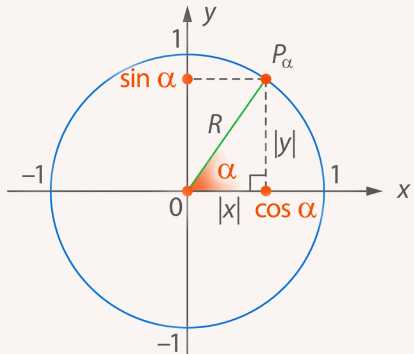
Рис. 20.  и  – длины катетов прямоугольного треугольника для точки  из любой четверти

Значит, для них выполняется теорема Пифагора:

Т. е.:

Значит,

interneturok.ru

Теорема синуса, косинуса. Решение треугольников

Вопросы занятия:

·  вспомнить формулировки и доказательства теорем синуса и косинуса;

·  повторить, что значит «решить треугольник»

Материал урока

И начнём мы с вами с того, что вспомним формулировку теоремы синусов.

Она звучит так:

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

Доказательство.

Расширенная теорема синусов.

Отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности.

Доказательство.

Что и требовалось доказать.

Теперь давайте вспомним теорему косинусов.

Теорема косинусов.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон, умноженное на косинус угла между ними.

Доказательство.

Частным случаем теоремы косинусов является теорема Пифагора.

Давайте рассмотрим прямоугольный треугольник и запишем для него теорему косинусов.

Именно поэтому теорему косинусов называют обобщённой теоремой Пифагора.

Рассмотрим несколько примеров.

Пример.

Рассмотрим ещё один пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Теперь давайте вспомним, что значит решить треугольник.

Определение.

Решить треугольник – это значит найти все его элементы (три стороны и три угла) по каким-нибудь известным трём элементам, определяющим треугольник. К задачам такого плана относятся следующие задачи: решение треугольника по трём сторонам; решение треугольника по трём углам; решение треугольника по двум сторонам и углу между ними; решение треугольника по двум сторонам и углу, не лежащего между ними; решение треугольника по стороне и прилежащим к ней углам; решение треугольников по стороне и произвольным двум углам.

Рассмотрим каждый вид таких задач отдельно.

Начнём с решения треугольника по трём углам.

Запишем теорему синусов и косинусов и подумаем, с помощью какой из них можно решить треугольник.

Обе эти теоремы содержат длины сторон, поэтому зная только углы треугольника нельзя найти длины сторон треугольника. То есть зная только три угла, решить треугольник нельзя.

Попробуем теперь решить треугольник по трём сторонам.

Зная длины всех сторон треугольника, по теореме косинусов можно найти косинусы всех углов треугольника.

А, зная косинус угла, сам угол найти несложно.

Для этого можно воспользоваться либо калькулятором либо таблицами Брадиса.

Значит в этом случае решить треугольник можно с помощью теоремы косинусов.

Следующим мы рассмотрим решение треугольника по стороне и прилежащим к ней углам.

Сразу замечаем, что третий угол найти нетрудно, он равен разности 180 градусов и известных углов.

Запишем теорему синусов.

Из каждого равенства, мы можем найти сторону треугольника. Таким образом, зная длину одной стороны и величину двух прилежащих к ней углов, можно найти все остальные элементы треугольника, используя теорему синусов.

Нетрудно увидеть, что условие: углы прилежащие к стороне здесь не существенно. Поскольку даже если нам известны два любых угла треугольника, то мы всегда можем найти третий угол этого треугольника. Тогда можно сказать, что, зная одну сторону и два любых угла можно решить треугольник с помощью теоремы синусов.

Теперь давайте рассмотрим способ решения треугольника по двум сторонам и углу между ними.

Третью сторону можно найти с помощью теоремы косинусов.

А углы отыскать или с помощью теоремы косинусов, как мы это делали, когда решали треугольник по трём сторонам. Или с помощью теоремы синусов. То есть в таком случае можно решить треугольник используя или теорему синусов или теорему косинусов.

Теперь давайте посмотрим, а можно ли решить треугольник, если мы знаем две стороны и угол, который не лежит между ними. Да, можно. Для этого по теореме синусов надо найти второй угол треугольника, а затем и третий угол и по теореме косинусов найти третью сторону треугольника. То есть и в этом случае треугольник можно решить с помощью теоремы синусов и теоремы косинусов.

Итак, давайте обобщим.

Решим задачу.

Пример.

Итоги урока

Сегодня на уроке мы с вами вспомнили формулировки и доказательства теорем синуса и косинуса. Повторили, что значит решить треугольник.

videouroki.net

Теорема синусов | Треугольники

Теорема синусов.

Стороны треугольника пропорциональны синусам противолежащих углов.

Дано: ∆ ABC,

BC=a, AC=b, AB=c,

∠A=α, ∠B=β, ∠C=γ.

Доказать:

Доказательство:

1) Опустим из вершины C высоту CD.

2) Из прямоугольного треугольника ACD по определению синуса острого угла 

Отсюда

3) Аналогично из треугольника BCD

4) Приравниваем правые части полученных равенств:

Поделив обе части последнего равенства на произведение sinα∙sinβ, получим:

5) Опустим из вершины A высоту AF.

6) Из прямоугольного треугольника ACF по определению синуса

7) Аналогично из треугольника ABF

8) Приравниваем правые части:

делим обе части равенства на произведение sinγ∙sinβ, получаем:

Что и требовалось доказать.

Замечание.

Если треугольник ABC тупоугольный, то все рассуждения и в этом случае сохраняются, поскольку 

Например, из треугольника BCD

В прямоугольном треугольника теорему синусов не принято использовать (достаточно применить определение синуса).

www.treugolniki.ru

Теорема синусов. Теорема косинусов

При решении прямоугольных треугольников используются только основные тригонометрические функции. Для решения же косоугольных треугольников потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.

В дальнейшем мы будем пользоваться следующими обозначениями: a, b и c — стороны треугольника; А, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; r — радиус вписанного круга; h_а, l_а и m_а — высота, биссектриса и медиана, соответствующие стороне а.

Теорема синусов

Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:

Доказательство. Опишем круг около данного треугольника ABC. Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например А; через одну из других вершин, например через В, проведём диаметр ВА’ описанного круга. Вспомогательный треугольник А’ВС прямоугольный, так как вписанный угол А’СВ опирается на диаметр. Из вспомогательного треугольника найдём:

а = 2Rsin A’.

Если угол А острый, то А = А’, так как вписанные углы A и A’ опираются на одну и ту же дугу.
Если угол А тупой, то угол А’ острый, измеряющийся половиной дуги ВАС:

Итак, или A= А’, или A’ =\(\pi\) — A, в обоих случаях sin A’ = sin A, а потому

а = 2R sin A. (1)

Если угол Aпрямой, то а = 2R, sin A= 1 и равенство (1) также справедливо.

Аналогичные равенства найдём и для прочих углов В и С. Итак,

а =2R sin A; b =2R sin В; с = 2R sin С, откуда

Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.

Теорема косинусов

Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:

а² =b² + с² — 2bccosА

b² =c² + a² — 2cacosB

c² =a² + b² — 2abcosC

Доказательство. Докажем первое равенство.

Случай 1. Угол A острый.

Пусть ВН — высота, опущенная из вершины В ; из геометрии известно, что
а² = b² + с²—2b · АН. (1)
Из прямоугольного треугольника АВН найдём
АН = с cos А; подставив в формулу (1), получим доказываемое равенство.

Случай 2. Угол A тупой.
В этом случае а² = b² + с² +2b · АН. (2)

Из треугольника АВН найдём:
АН = с cos∠BAH = с cos(\(\pi\) — A) = — с cosA.

Подставив в формулу (2), получим доказываемое равенство.

Случай 3. Угол А прямой.

В этом случае (по теореме Пифагора):

а² = b² + с²= b² + с² — 2bccosА

(так как cos А = 0).

Итак, во всех случаях

а² = b² + с² — 2bccosА

razdupli.ru