Как найти периметр прямоугольного треугольника
Чтобы узнать как найти периметр прямоугольного треугольника, нужно вспомнить что такое периметр.
Для того, чтобы найти периметр нужно сложить все длины сторон данного треугольника.
Например, если МТЕ — прямоугольный треугольник, и он имеет катеты и и гипотенузу , то его периметр будет равен:
Рассмотрим примеры того, как найти периметр треугольника с прямым углом.
Пример 1.
У прямоугольного треугольника гипотенузы равна 19 дм, а катеты соответственно по 13 дм и 17 дм. Найдем периметр этого треугольника.
Решение.
Воспользуемся формулой для нахождения периметра прямоугольного треугольника:
Подставим известные значения и получим:
(дм).
Ответ. (дм).
Пример 2.
Известны гипотенуза и катет прямоугольного треугольника, длины которых равны соответственно 31 см и 23 см. Найдем периметр заданного треугольника.
Решение.
Согласно условию дан прямоугольный треугольник, у которого есть две известные длины — длина гипотенузы и длина катета. Для того, чтобы найти периметр заданного треугольника, необходимо знать и длину второго катета. Поскольку треугольник является прямоугольным, то мы можем воспользоваться теоремой Пифагора, из которой и найдем неизвестную длину:
(см).
Найдем периметр согласно рассмотренной выше формуле:
(см).
Ответ. (см).
ru.solverbook.com
Периметр прямоугольного треугольника формула | Помощь школьнику
1) у = 2х + 5 2) у = 4 – 3х 3) у = 8х – 2 4) у = 5х 5) у = 0,1х + 8 6) Х = 2 7) У = х – 3, у = 2х + 3 у = -3х + 1 у = 4х – 2 у = 5х + 2 у = 3 у = -х у = -3 + х, 1) 0 2) 0 3) 1 4) 0 5) 1 6) 1 7) Бесконечное множество. с тестами по карточкам. Карточка № 1. А10. Соотнесите функции, заданные формулами с их графиками (рис. 1).
Как найти периметр прямоугольного треугольника?
Прямоугольный треугольник — это частный вид произвольного треугольника. Как и любой другой треугольник он имеет три стороны, но один из его углов обязательно должен составлять 90 градусов. Ка только вы определили, что заданный треугольник является прямоугольным, можно приступить к нахождению его основных величин. Одной из характеристик прямоугольного треугольника является его периметр. Нахождению периметра прямоугольного треугольника посвящено много задач по геометрии.
Где P — периметр треугольника;
A, b, c — стороны треугольника.
Исходя из теоремы Пифагора появилась возможность определять периметр прямоугольного треугольника по его двум любым сторонам известной длины. Если известны длины катетов, то периметр треугольника определяется через нахождение величины гипотенузы по формуле:
Если известен только один из катетов и длина гипотенузы, то периметр треугольника определяется через нахождение величины недостающего катета по формуле:
Если в прямоугольном треугольнике известна только длина гипотенузы с и один из прилегающих к ней острых углов α, то периметр треугольника в данном случае может быть определен по формуле:
В том случае, когда условиями задачи задана длина катета a и величина противолежащего ему острого угла α, то периметр прямоугольного треугольника в данном случае вычисляется по формуле:
Если же задан катет a с прилежащим к нему углом β, то периметр треугольника может быть рассчитан на основе выражения:
Периметр прямоугольного треугольника формула
Как найти периметр прямоугольного треугольника
Прямоугольным треугольником считается такой треугольник, один из углов которого равен 90 градусам, а два других являются острыми углами. Расчет периметра такого треугольника будет зависим от количества известных о нем данных.
В зависимости от случая, знание двух из трех сторон треугольника, а также одного из его острых углов.
Спонсор размещения P&G Статьи по теме «Как найти периметр прямоугольного треугольника» Как найти площадь поверхности пирамиды Как найти периметр если известна площадь Как найти периметр равностороннего треугольника
Способ 1.Если известны все три стороны треугольника, то, независимо от того, прямоугольный ли треугольник или нет, его периметр будет рассчитан так:
P = a + b + c, где, допустим,
Способ 2. Если в прямоугольнике известны только 2 стороны, то, используя теорему Пифагора, периметр этого треугольника можно рассчитать по формуле:
P = v(a2 + b2) + a + b, или
P = v(c2 – b2) + b + с.
Способ 3. Пусть в прямоугольном треугольнике даны гипотенуза c и острый угол?, то найти периметр можно будет таким образом:
P = (1 + sin? + cos?)*с.
Способ 4. Дано, что в прямоугольном треугольнике длина одного из катета равна a, а напротив него лежит острый угол?. Тогда расчет периметра этого треугольника будет вестись по формуле:
P = a*(1/tg? + 1/sin? + 1)
Способ 5. Пускай нам известен катет a и прилежащий к нему угол?, тогда периметр будет рассчитан так:
P = a*(1/сtg? + 1/cos? + 1)
Другие новости по теме:
Площадь и периметр — основные числовые характеристики любых геометрических фигур. Нахождение этих величин упрощается благодаря общепринятым формулам, согласно которым можно также вычислить одно через другое с минимумом или полным отсутствием дополнительных начальных данных. Спонсор размещения P&G
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще. Вам
Периметр треугольника, как и любой другой плоской геометрической фигуры, составляет сумма длин ограничивающих его отрезков. Поэтому, чтобы вычислить длину периметра, надо знать длины его сторон. Но в силу того, что длины сторон в геометрических фигурах связаны определенными соотношениями с
Прямоугольным считается такой треугольник, у которого один из углов прямой. Сторона треугольника, расположенная напротив прямого угла, называется гипотенузой, а две другие стороны — катетами. Чтобы найти длины сторон прямоугольного треугольника, можно воспользоваться несколькими способами. Спонсор
Периметр любой геометрической фигуры, в том числе треугольника, равен совокупной длине границ этой фигуры. Он обозначается заглавной латинской буквой P и легко находится методом сложения длин всех сторон данной фигуры. Спонсор размещения P&G Статьи по теме «Как вычислить периметр треугольника»
Треугольник — это многоугольник, имеющий три стороны и три угла. Как же вычислить его периметр? Спонсор размещения P&G Статьи по теме «Как находить перим
Высота прямоугольного треугольника делит его на треугольники с периметрами 3 и 4. Найдите периметр заданного треугольника.
Способ 1.Анализ. Очевидно, что
Поэтому используя подобие треугольников, выразим через одну переменную стороны и свяжем их, используя данные значения периметров, а так же теорему Пифагора.
Решение. Так как
то
Пусть AH=x, BH=y, CH=h, тогда AC=4-(x+y), CB=3-(y+h).
Учитывая, что
Из треугольника ACH по теореме Пифагора:
Свяжем теперь три стороны, используя периметр и найдем значение h:
Осталось подставить
Ответ: 5.
Способ 2.
Оказывается, что сумма квадратов периметров двух треугольников, на которые высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник, равна квадрату периметра этого треугольника.
Докажем это в общем виде.
Для начала напомню формулу квадрата суммы трех слагаемых:
Рассмотрим треугольники:
Пусть CB=a; AC=b, CH=h, HB=x, тогда AH=c-x. Учитывая, что угол A и угол BCH равны, получаем:Для удобства в дальнейшем доказательстве я обозначила каждое равенство отдельным цветом. Далее находим сумму квадратов периметров «малых» треугольников:
Теперь, очевидно, для нахождения периметра треугольника необходимо
Ответ: 5.
mathrepetitor.blogspot.com
теорема Пифагора и формула косинусов в зависимости от известных сторон
Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.
В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.
Вконтакте
Одноклассники
Мой мир
Возможные методы:
- известны все три стороны равнобедренного или любого другого треугольника;
- как найти периметр прямоугольного треугольника при двух известных его гранях;
- известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.
Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.
Первый метод: известны все стороны фигуры
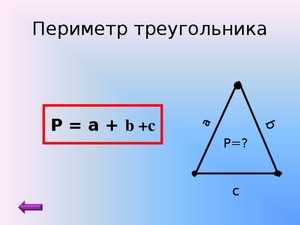Как находить периметра треугольника, когда известны все три грани, необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.
Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.
Данная формула подходит к любому треугольнику, необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.
Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.
Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения.
Это интересно: что понимают под образовательными информационными ресурсами?
Второй метод: прямоугольный треугольник и две известные его стороны
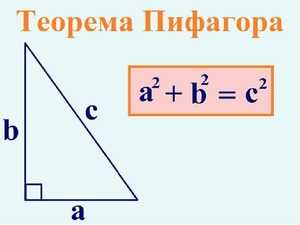В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.
Теорема Пифагора описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:
Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b — катеты фигуры, а c — гипотенуза.
- Гипотенуза. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c.
- Катеты — это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.
Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.
Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется «Египетский треугольник». Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.
Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.
Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.
Третий метод: по двум граням и углу между ними
В старшей школе, а также университете, чаще всего приходится обращаться именно к данному способу нахождения периметра. Если условиями задачи заданы длины двух сторон, а также размерность угла между ними, то необходимо воспользоваться теоремой косинусов.
Данная теорема применима абсолютно к любому треугольнику, что и делает ее одной из наиболее полезных в геометрии. Сама теорема выглядит следующим образом: c^2 = a^2 + b^2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
Задача решена.
obrazovanie.guru
Периметр — прямоугольный треугольник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Периметр — прямоугольный треугольник
Cтраница 1
Периметр прямоугольного треугольника равен 60 см, а высота, проведенная к гипотенузе, равна 12 см. Найти стороны треугольника. [1]
Периметр прямоугольного треугольника равен 2р, а гипотенуза равна с. [3]
Периметр прямоугольного треугольника равен 132, а сумма квадратов сторон треугольника-6050. [4]
Периметр прямоугольного треугольника равен 2 р, а гипотенуза равна с. [5]
Периметр прямоугольного треугольника равен 2р, а гипотенуза равна с. [6]
Периметр прямоугольного треугольника равен 84 см, а его гипотенуза равна 37 см. Найдите площадь этого треугольника. [7]
Периметр прямоугольного треугольника равен 84 см, гипотенуза равна 37 см. Найдите площадь этого треугольника. [8]
Периметр прямоугольного треугольника равен 2р, а гипотенуза равна с. [9]
Периметр прямоугольного треугольника равен 60 дюймам, а длина высоты, перпендикулярной гипотенузе, равна 12 дюймам. [10]
Периметр прямоугольного треугольника ЛВС ( С я / 2) равен, 72 см, а разность между длинами медианы СК и высоты СМ равна 7 см. Найти площадь треугольника ЛВС. [11]
Периметр прямоугольного треугольника ABC ( Z C90) равен 72 см, а разность между длинами медианы С / С и высоты СМ равна 7 см. Найти длину гипотенузы. [12]
Периметр прямоугольного треугольника ABC ( ZLC90) равен 72 см, а разность между длинами медианы С / С и высоты СМ равна 7 см. Найти длину гипотенузы. [13]
Периметр прямоугольного треугольника ЛВС ( С я / 2) равен 72 см, а разность между длинами медианы С / С и высоты СМ равна 7 см. Найти площадь треугольника ЛВС. [14]
Длина периметра прямоугольного треугольника равна Чр, а длина гипотенузы равна С. [15]
Страницы: 1 2
www.ngpedia.ru