Треугольник стороны – Стороны треугольника, формулы и примеры

Стороны треугольника, формулы и примеры

Классификация треугольников по сторонам

Треугольники можно классифицировать по сторонам следующим образом:

Формулы связывающие стороны треугольника

Большая сторона треугольника лежит против большего угла.

В любом треугольнике (рис. 1) его стороны связаны с углами с помощью теоремы синусов:

   

и теоремы косинусов:

   

Площадь треугольника по трем сторонам (формула Герона)

   

где – полупериметр

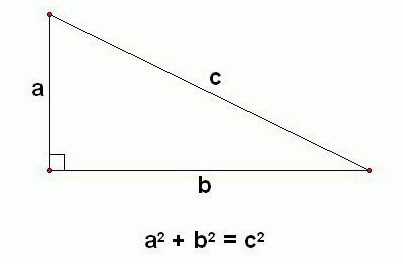
Стороны в прямоугольном треугольнике

В прямоугольном треугольнике (рис. 2) стороны и , образующие прямой угол, называются катетами, а третья сторона – гипотенузой. Связаны стороны прямоугольного треугольника теоремой Пифагора: «Квадрат гипотенузы равен сумме квадратов катетов»

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника.

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника — формулы вычисления, прямоугольный треугольник, равнобедренный треугольник, высота треугольника. Свойства треугольника. Обозначения в треугольнике, Виды треугольников. Формулы площади треугольника. Величины углов треугольника. Основные свойства треугольников, Конгруэнтные (равные) треугольники, Признаки равенства, Равенство прямоугольных треугольников, Подобные треугольники, Признаки подобия, Свойства подобных треугольников, Подобие в прямоугольных треугольниках, Теорема Пифагора, Теорема синусов, Теорема косинусов, Основные линии — Медиана, Биссектриса, Высота треугольника, Срединный перпендикуляр, Средняя линия треугольника, Формулы площади треугольника, в т.ч. формула Герона, Окружности вписанные в треугольники и описанные вокруг треугольников

dpva.ru

Свойства треугольника. В том числе равенство и подобие, равные треугольники, стороны треугольника, углы треугольника, площадь треугольника

Свойства треугольника. Обозначения в треугольнике, Виды треугольников. Формулы площади треугольника. Основные свойства треугольников, Конгруэнтные (равные) треугольники, Признаки равенства, Равенство прямоугольных треугольников, Подобные треугольники, Признаки подобия, Свойства подобных треугольников, Подобие в прямоугольных треугольниках, Теорема Пифагора, Теорема синусов, Теорема косинусов, Основные линии — Медиана, Биссектриса, Высота треугольника, Срединный перпендикуляр, Средняя линия треугольника, Формулы площади треугольника, в т.ч. формула Герона, Окружности вписанные в треугольники и описанные вокруг треугольников Меню Треугольник -это фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами. Для инженера это еще и единственная «жесткая» плоская фигура на свете. Раздел математики, посвященный изучению закономерностей треугольников — тригонометрия. Сумма всех углов в треугольнике равна 180°. Обозначения в треугольнике. Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α, β, γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c). Виды треугольников: (по величине углов) Остроугольный треугольник — это треугольник, в котором все три угла острые, т.е. меньше 90°. Прямоугольный треугольник — это треугольник, содержащий прямой угол. Две сторо

dpva.ru

Какими могут быть стороны треугольника

Какими могут быть стороны треугольника? Могут ли стороны треугольника быть равными данным числам? Существует ли треугольник со сторонами той или иной длины? . Рассмотрим конкретные задачи.

1) Существует ли треугольник со сторонами

а)  1 см, 2 см, 3 см;

б)  7 см, 10 см, 12 см?

Решение:

Согласно неравенству треугольника, длина любой стороны треугольника меньше суммы длин двух других сторон. Проверяем, выполнено ли это условие для каждого отрезка. Для задачи а):

   

   

   

Третье неравенство неверно, следовательно, треугольника со сторонами 1 см, 2 см и 3 см не существует.

б)

   

   

   

Все три условия выполнены, значит, треугольник со сторонами 7 см, 10 см и 12 см существует.

2) Можно ли построить треугольник со сторонами 3 см, 4 см, 8 см?

Решение:

Проверяем, выполняется ли неравенство треугольника для каждого из отрезков:

   

   

   

Последнее неравенство не выполнено, поэтому треугольник со сторонами 3 см, 4 см и 8 см построить нельзя.

3) Какими могут быть стороны треугольника:

а)  5 м, 7 м, 10 м;

б)  11 дм, 15 дм, 30 дм?

Решение:

Проверяем выполнение неравенства треугольника для каждой тройки отрезков:

   

Все три неравенства верны, следовательно, стороны треугольника могут быть равными 5 м, 7 м и10 м.

   

Третье неравенство не является верным, значит, стороны треугольника не могут быть равными 11 дм, 15 дм и 30 дм.

 

www.treugolniki.ru

Треугольник и его виды

Из всех многоугольников треугольники имеют наименьшее количество углов и сторон.

Треугольники можно различать по виду их углов.

Есди все углы треугольника острые, то его называют остроугольным треугольником (рис. 113, а).

Если один из углов треугольника прямой, то его называют прямоугольным треугольником (рис. 113, б).

Если один из углов треугольника тупой, то его называют тупоугольным треугольником (рис. 113, в).

Говорят, что мы классифицировали треугольники по виду их углов.

Треугольники можно классифицировать не только по виду углов, но и по количеству равных сторон.

Если две стороны треугольника равны, то его называют равнобедренным треугольником.

На рисунке 114, а изображен равнобедренный треугольник ABC, у которого AB = BC. На рисунке равные стороны отмечают равным количеством черточек. Равные стороны AB и BC называют боковыми сторонами, а сторону AC − основанием равнобедренного треугольника ABC.

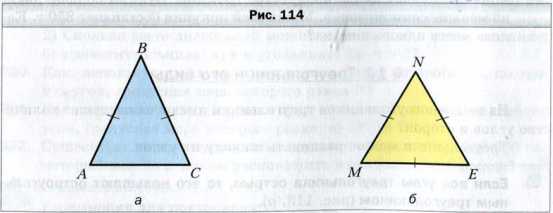
Если стороны треугольника равны, то его называют равносторонним треугольником.

Треугольник, изображенный на рисунке 114, б, − равносторонний, у него MN = NE = EM.

Треугольник, у которого три стороны имеют различную длину, называют разносторонним треугольником.

Треугольники, изображенные на рисунке 113, − разносторонние. Если сторона равностороннего треугольника равна a, то его периметр вычисляют по формуле:

P = 3a

Пример 1. С помощью линейки и транспортира постройте треугольник, две стороны которого равны  3 см и 2 см, а угол между ними − 50°.

Решение.

С помощью транспортира построим угол A, градусная мера которого 50° (рис. 115). На сторонах этого угла от его вершины с помощью линейки отложим отрезок AB длиной 3 см и отрезок AC длиной 2 см (рис. 116). Соединив отрезком точки B и C, получим искомый треугольник ABC (рис. 117).

Пример 2. С помощью линейки и транспортира постройте треугольник ABC, сторона AB которого равна 2 см, а углы CAB и CBA соответственно равны 40° и 110°.

Решение. С помощью линейки строим отрезок AB длиной 2 см (рис. 118). От луча AB с помощью транспортира откладываем угол с вершиной в точке A, градусная мера которого равна 40°. От луча BA в ту же сторону от прямой AB, в которую был отложен первый угол, откладываем угол с вершиной в точке B, градусная мера которого равна 110°(рис. 119).

Найдя точку C пересечения сторон углов A и B, получаем искомый треугольник ABC (рис. 120).

reshalka.com

Треугольники /qualihelpy

Треугольником называют многоугольник, имеющий три вершины (рис. 8.27 – 8.29).

Классификация треугольников по сторонам

1. Если все три стороны треугольника равны, то треугольник равносторонний. Все внутренние углы равностороннего треугольника равны. 

Например, на рисунке 8.27 изображен равносторонний треугольник : ; .

2. Если две стороны треугольника равны, то треугольник равнобедренный. Стороны, имеющие одинаковую длину, называют боковыми сторонами

, а третью сторону – основанием этого треугольника. Углы при основании равнобедренного треугольника равны. 

Например, на рисунке 8.28 изображен равнобедренный треугольник  с боковыми сторонами  и основанием , а .

3. Если все стороны треугольника имеют различную длину, то треугольник разносторонний (произвольный). 

Например, на рисунке 8.29 изображен разносторонний треугольник . 

Длина стороны треугольника меньше суммы длин двух других его сторон, причем, большая сторона треугольника лежит против большего его угла. 

Например: 1) если на рисунке 8.27 , то ; 2) если на рисунке 8.28 , то длина стороны  меньше 8, но больше 4. 

Классификация треугольников по углам

1. Если все углы треугольника острые, то треугольник остроугольный (на рисунке 8.27 треугольник ).2. Если один из углов треугольника тупой, то треугольник тупоугольный (на рисунке 8.28 треугольник ).

3. Если один из углов треугольника прямой, то треугольник прямоугольный. Сторону прямоугольного треугольника, лежащую против прямого угла, называют гипотенузой, две другие стороны – катетами. Например, на рисунке 8.29 треугольник  – прямоугольный, отрезок  – гипотенуза этого треугольника, а отрезки  и  – его катеты.Рассмотрим прямоугольный треугольник, у которого  и  – катеты,  – гипотенуза,  – острый угол (рис. 8.30).

Теорема Пифагора: квадрат гипотенузы треугольника равен сумме квадратов его катетов:

, (8.3)где  – гипотенуза,  и  – катеты.

Например, если катеты треугольника соответственно равны 3 и 4, то гипотенуза этого треугольника равна 5. Такой треугольник называют египетским.  

Соотношения между сторонами и углами в прямоугольном треугольнике

1. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.

2. Косинус острого угла

прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.

3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему катету.

Например, на рисунке 8.30: ; ; . Катет, лежащий против угла , равен половине гипотенузы. Рассмотрим произвольный треугольник, у которого  – стороны,  – соответственно противолежащие им углы (рис. 8.31).

Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих же сторон на косинус угла между ними:

, (8.4)

или 

, (8.4.1)

или 

. (8.4.2)

Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих им углов: 

 (8.5)

или 

, (8.5.1)где  – радиус окружности, описанной около этого треугольника.

Линии в треугольнике

Среди всех линий, которые можно провести в треугольнике выделяют среднюю линию треугольника, биссектрису треугольника, его медиану и высоту. 

Средней линией треугольника называют отрезок, соединяющий середины двух его сторон. 

Свойства средней линии треугольника

1. Средняя линия треугольника равна половине длины его третьей стороны.

2. Средняя линия треугольника параллельна одной из сторон треугольника.

Высотой треугольника называют перпендикуляр, проведенный из вершины треугольника на прямую, содержащую противолежащую сторону. 

Например, на рисунке 8.33 изображены высоты остроугольного треугольника : отрезки  и .На рисунке 8.34 изображена одна из высот тупоугольного треугольника : высота .На рисунке 8.35 изображены три высоты прямоугольного треугольника : высоты  и .

Свойства высоты треугольника

1. В остроугольном и прямоугольном треугольнике три высоты треугольника пересекаются в одной точке (точка  на рисунке 8.33 и точка  на рисунке 8.35). 

2. Если высота треугольника проведена из вершины прямого угла к гипотенузе, то она является средним геометрическим проекций катетов на гипотенузу (рис. 8.5):

, (8.6)где  и  – проекции катетов на гипотенузу.3. Для всякого треугольника зависимость между его высотами , ,  и радиусом вписанной окружности r выражается формулой: . (8.7)

Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. 

Например, на рисунке 8.36 изображены медианы треугольника : отрезки  и .

Свойства медианы треугольника

1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении , считая от вершины. Например, на рисунке 8.36 .

2. Медиана делит треугольник на два равновеликих треугольника (треугольники, имеющие равные площади, называют равновеликими). 

Например, на рисунке 8.36 треугольники  и  равновеликие. 

3. Если медиана проведена к гипотенузе прямоугольного треугольника, то она равна половине гипотенузы. 

Например, на рисунке 8.37 . 

Биссектрисой треугольника называют отрезок биссектрисы внутреннего угла треугольника, заключенный между вершиной треугольника и точкой пересечения биссектрисы угла и стороны треугольника. 

Например, на рисунке 8.38 отрезки  и  – биссектрисы внутренних углов треугольника .

Свойства биссектрисы треугольника

1. Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник. 

Например, точка  на рисунке 8.38.

2. В равностороннем треугольнике все биссектрисы равны и являются высотами и медианами этого треугольника. 

Например, на рисунке 8.39 биссектрисы  – высоты и медианы правильного треугольника  и .

3. Если биссектриса проведена из вершины равнобедренного треугольника к его основанию, то она является высотой и медианой этого треугольника. 

Например, на рисунке 8.40 биссектриса  – высота и медиана равнобедренного треугольника .

4. Биссектриса треугольника делит сторону этого треугольника на отрезки, пропорциональные прилежащим к ним сторонам. 

Например, если  – биссектриса треугольника , изображенного на рисунке 8.41, то .

Формулы для вычисления площади треугольника

Для вычисления площади треугольника можно применять одну из следующих формул: 

, (8.8)где  – сторона равностороннего треугольника; , (8.9)где  – сторона,  – высота, проведенная к стороне  произвольного треугольника; , (8.10)где  и  – катеты прямоугольного треугольника; , (8.11)где  и  – стороны,  – величина угла между ними произвольного треугольника;

Формула Герона: 

, (8.12)где  – стороны,  – полупериметр треугольника;, (8.13)где  — полупериметр треугольника,  — радиус окружности, вписанной в треугольник;, (8.14)где  – стороны,  – радиус окружности, описанной около треугольника.

Два треугольника равны, если все их соответственные стороны и углы равны. 

Признаки равенства треугольников

1. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника. 

Например, на рисунке 8.42 треугольники  и  равны по двум сторонам и углу между ними.

2. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника. 

Например, на рисунке 8.43 треугольники  и  равны по стороне и прилежащим к ней углам.

3. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого треугольника. 

Например, на рисунке 8.44 треугольники  и  равны по трем сторонам.

Признаки равенства прямоугольных треугольников

1. Прямоугольные треугольники равны, если катеты одного треугольника соответственно равны катетам другого треугольника. 

Например, на рисунке 8.45 треугольники  и  равны по двум катетам.

2. Прямоугольные треугольники равны, если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника. 

Например, на рисунке 8,46 треугольники  и  равны по катету и прилежащему острому углу.

3. Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника. 

Например, на рисунке 8.47 треугольники  и  равны по гипотенузе и острому углу.

4. Прямоугольные треугольники равны, если гипотенуза и катет одного треугольника соответствравны гипотенузе и катету другого треугольника. 

Например, на рисунке 8.48 треугольники  и  равны по гипотенузе и катету.

Два треугольника подобны, если все углы одного треугольника соответственно равны углам другого, а все стороны одного пропорциональны соответствующим (сходственным) сторонам другого треугольника.

Признаки подобия треугольников

1. Два треугольника подобны, если два угла одного треугольника равны двум углам другого. 

2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, заключенные между ними, равны. 

3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого. 

Например, на рисунке 8.51 изображены подобные треугольники, так как длины сторон одного из них в два раза больше длин сторон другого. 

Отношение сходственных сторон подобных треугольников называют коэффициентом подобия . Отношение периметров подобных треугольников равно коэффициенту подобия . Отношение площадей подобных треугольников равно квадрату коэффициента подобия .

helpy.quali.me

Как найти стороны прямоугольного треугольника? Основы геометрии

Катеты и гипотенуза – стороны прямоугольного треугольника. Первые – это отрезки, которые прилегают к прямому углу, а гипотенуза является самой длинной частью фигуры и находится напротив угла в 90^о. Пифагоровым треугольником называется тот, стороны которого равны натуральным числам; их длины в таком случае имеют название «пифагорова тройка».

Египетский треугольник

Для того чтобы нынешнее поколение узнало геометрию в том виде, в котором ее преподают в школе сейчас, она развивалась несколько веков. Основополагающим моментом считается теорема Пифагора. Стороны прямоугольного треугольника (фигура известна на весь мир) составляют 3, 4, 5.

Мало кто не знаком с фразой «Пифагоровы штаны во все стороны равны». Однако на самом деле теорема звучит так: c² (квадрат гипотенузы) = a²+b² (сумма квадратов катетов).

Среди математиков треугольник со сторонами 3, 4, 5 (см, м и т. д.) называется «египетским». Интересно то, что радиус окружности, которая вписана в фигуру, равняется единице. Название возникло примерно в V столетии до н.э., когда философы Греции ездили в Египет.

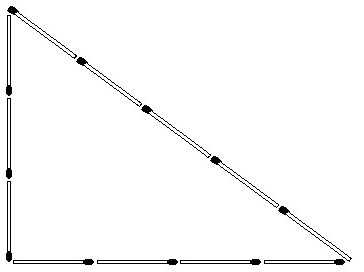
При построении пирамид архитекторы и землемеры пользовались соотношением 3:4:5. Такие сооружения получались пропорциональными, приятными на вид и просторными, а также редко рушились.

Для того чтобы построить прямой угол, строители использовали веревку, на которой было завязано 12 узлов. В таком случае вероятность построения именно прямоугольного треугольника повышалась до 95%.

Признаки равенства фигур

• Острый угол в прямоугольном треугольнике и большая сторона, которые равны тем же элементам во втором треугольнике, – бесспорный признак равенства фигур. Беря во внимание сумму углов, легко доказать, что вторые острые углы также равны. Таким образом, треугольники одинаковы по второму признаку.
• При наложении двух фигур друг на друга повернем их таким образом, чтобы они, совместившись, стали одним равнобедренным треугольником. По его свойству стороны, а точнее, гипотенузы, равны, так же как и углы при основании, а значит, эти фигуры одинаковые.

По первому признаку очень просто доказать то, что треугольники действительно равны, главное, чтобы две меньшие стороны (т. е. катеты) были равными между собой.

Треугольники будут одинаковыми по II признаку, суть которого заключается в равенстве катета и острого угла.

Свойства треугольника с прямым углом

Высота, которую опустили из прямого угла, разбивает фигуру на две равные части.

Стороны прямоугольного треугольника и его медианы легко узнать по правилу: медиана, которая опущена на гипотенузу, равна ее половине. Площадь фигуры можно найти как по формуле Герона, так и по утверждению, что она равна половине произведению катетов.

В прямоугольном треугольнике действуют свойства углов в 30^о, 45^о и 60^о.

• При угле, который равен 30^о, следует помнить, что противолежащий катет будет равен 1/2 самой большой стороны.
• Если угол 45^о, значит, второй острый угол также 45^о. Это говорит о том, что треугольник равнобедренный, и его катеты одинаковы.
• Свойство угла в 60^о заключается в том, что третий угол имеет градусную меру в 30^о.

Площадь легко узнать по одной из трех формул:

1. через высоту и сторону, на которую она опускается;
2. по формуле Герона;
3. по сторонам и углу между ними.

Стороны прямоугольного треугольника, а точнее катеты, сходятся с двумя высотами. Для того чтобы найти третью, необходимо рассматривать образовавшийся треугольник, и тогда по теореме Пифагора вычислить необходимую длину. Помимо этой формулы существует также соотношение удвоенной площади и длины гипотенузы. Наиболее распространенным выражением среди учеников является первое, так как требует меньше расчетов.

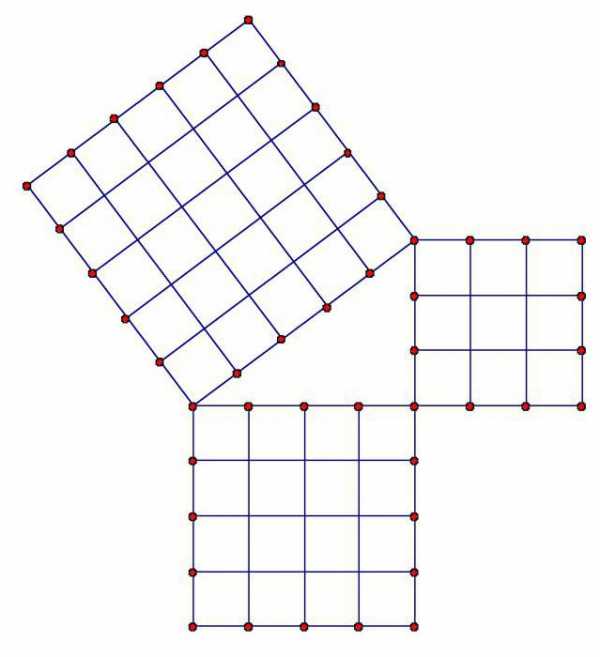
Теоремы, применяемые к прямоугольному треугольнику

Геометрия прямоугольного треугольника включает в себя использование таких теорем, как:

1. Теорема Пифагора. Ее суть заключается в том, что квадрат гипотенузы равен сумме квадратов катетов. В евклидовой геометрии данное соотношение является ключевым. Использовать формулу можно, если дан треугольник, к примеру, SNH. SN – гипотенуза, и ее необходимо найти. Тогда SN²=NH²+HS².
2. Теорема косинусов. Обобщает теорему Пифагора: g²=f²+s²-2fs*cos угла между ними. Например, дан треугольник DOB. Известны катет DB и гипотенуза DO, необходимо найти OB. Тогда формула принимает данный вид: OB²=DB²+DO²-2DB*DO*cos угла D. Существует три следствия: угол треугольника будет остроугольным, если из суммы квадратов двух сторон вычесть квадрат длины третьей, полученный результат должен быть меньше нуля. Угол – тупоугольный, в том случае, если данное выражение больше нуля. Угол – прямой при равенстве нулю.
3. Теорема синусов. Она показывает зависимость сторон к противолежащим углам. Иными словами, это отношение длин сторон к синусам противолежащих углов. В треугольнике HFB, где гипотенузой является HF, будет справедливо: HF/sin угла B=FB/sin угла H=HB/sin угла F.

fb.ru