Тригонометрическая единичная окружность. Функция синуса. Функция косинуса.
Возьмем ось \(x\) и ось \(y\) , и пусть \(0\)-начало координат. Круг с центром в точке \(0\) и радиусом \(1\) называется тригонометрической окружностью или единичной окружностью.
Единичная окружность
Если \(P\)- точка на окружности, а \(A\)-угол между отрезком \(PO\) и \(x\), то:
- \(x\)-координата \(P\) называется косинусом \(A\). мы пишем \(cos (A)\) или \(cos A\);
- \(y\)-координата \(P\) называется синусом \(A\). Мы пишем \(sin (A)\) или \(sin A\);
число \(\frac{sin (A)} { cos (A)}\) называется касательной \(A\) , мы пишем \(tg (A)\) ;
Функция синуса
\(sin: R — > [-1;1]\)
Все тригонометрические функции являются периодическими c периодом \( 2π.\)
Диапазон функции равен \([-1,1]\).
Функция косинуса
\(cos: R — > [-1;1]\)
Период \(2π\).
Функция тангенса
\(tan: R — > R\)
Период диапазона \(π\) функции \(R\) не определен при \( x = \frac{π}{2} + kn, k=0,1,2,…\)
График функции тангенса на интервале \(0 — π\)
Функция котангенс
\(ctg: R — > R\)
Диапазон функции \(R\). период \(π\) и что функция не определена при \( x = kn, k=0,1,2,…\)
myalfaschool.ru
Числовая окружность, тригонометрический круг и единичная окружность
Любая окружность, которую мы соотносим с действительными числами будет числовая. Но на практике (для удобства) используют единичную окружность, т.е. окружность с радиусом = 1 и центром в начале координат.
Ну, и поскольку у каждой точки окружности есть координаты на осях Х и Y, которые являются косинусом и синусом угла β, соответственно круг является тригонометрическим, т.е. связанным с этими самыми функциями из тригонометрии.

Большой плюс, что на тригонометрическом круге можно увидеть разные углы (а не только, как в треугольнике). Ведь неважно, где мы поставим точку на круге, мы всегда сможем определить для нее косинус и синус по абсциссе и ординате даже по самому простому и схематичному рисунку.

Важно только помнить, что угол всегда рисуется от оси OX (называется углом поворота) и получается такая схема, где положительные углы всегда отображаются против часовой стрелки, а отрицательные — по часовой.
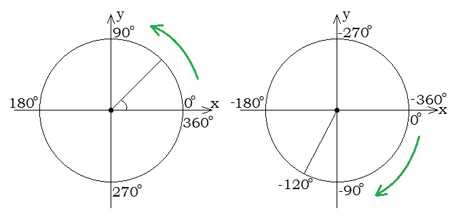
Вместе с положительными углами движется и отсчет четвертей круга:
0° до 90° — I четверть,
90° до 180° — II четверть,
180° до 270° — III четверть,
270° до 360° — IV четверть
Еще лайфхаки с градусами и кругами
Соответственно, если точно помнить, что целый круг — это 360°, то 50° будет в том же месте, где и -310° (проверьте;)
Если нужны углы более 360°, то делим их на 360, отбрасываем целые части и рисуем обычный угол. Например, угол в 795° = (360° * 2) + 75° — значит, просто рисуем угол в 75° и смотрим его синусы/косинусы.
Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно Добавить новость и получить деньгиДобавить анкету репетитора и получать бесплатно заявки на обучение от учеников
uchilegko.info
Тригонометрическая окружность Википедия
Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до n{\displaystyle n}-мерного пространства (n>2{\displaystyle n>2}), в таком случае говорят о «единичной сфере».
Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство x2+y2=1{\displaystyle x^{2}+y^{2}=1}.
Тригонометрические функции[ | ]
Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).
Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)}, получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:
- cosα=x{\displaystyle \cos \alpha =x},
- sinα=y{\displaystyle \sin \alpha =y}.
При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:
- cos2α+sin2α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}.
(Используется следующая общепринятая нотация: cos2x=(cos
ru-wiki.ru
Тригонометрическая таблица и тригонометрический круг
Тригонометрическая таблица и тригонометрический кругИнтерактивная таблица значений тригонометрических функций
| α | |||
| sin α = | cos α = | ||
| tg α = | ctg α = | ||
Пояснения к интерактивной таблице значений тригонометрических функций
- Угол α — это угол между лучом, проведённым из центра единичной окружности с координатами (0;0) через выбранное вами положение указателя компьютерной мыши (эта линия обозначена красными точками), и положительным направлением горизонтальной оси (эта линия обозначена синим цветом).
- Значение синуса угла α обозначено красной точкой на красной прямой.Эта горизонтальная прямая совпадает с осью X декартовой системы координат.
- Значение косинуса угла α обозначено синей точкой на синей прямой. Эта вертикальная прямая совпадает с осью Y декартовой системы координат.
- Значение тангенса угла α обозначено зелёной точкой на зелёной прямой. Эта вертикальная прямая параллельна оси Y и проходит через точку с координатами (1;0).
- Значение котангенса угла α обозначено жёлтой точкой на жёлтой прямой. Эта горизонтальная прямая параллельна оси X и проходит через точку с координатами (0;1).
- Для углов, кратных π/12 или 15 градусов, приведены точные значения тригонометрических функций в виде дроби с корнями. Для остальных углов — приблизительные, округленные до трех знаков после запятой.
Эта красивая тригонометрическая таблица с тригонометрическим кругом взята с сайта Летопись МИФИ без разрешения владельцев. За что приношу им свои извинения и выражаю искреннюю благодарность :)))
05 марта 2011 года.
© 2006 — 2013 Николай Хижняк. Все права защишены.
ndspaces.narod.ru
Единичная окружность — Википедия
Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до -мерного пространства (), в таком случае говорят о «единичной сфере».
Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство .
Тригонометрические функции[править]
Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).
Синус и косинус могут быть описаны следующим образом: соединив любую точку на единичной окружности с началом координат , получается отрезок, находящийся под углом относительно положительной полуоси абсцисс. Тогда действительно:
- ,
- .
При подстановке этих значения в уравнение окружности получается:
- .
(Используется следующая общепринятая нотация: .)
Тут же наглядно описывается периодичность тригонометрических функций, так как угол отрезка не зависит от количества «полных оборотов»:
для всех целых чисел , то есть для .
Комплексная плоскость[править]
В комплексной плоскости единичная окружность — это следующее множество :
Множество является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ).
www.wikiznanie.ru
Единичная окружность — WiKi
Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).
Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)} , получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:
- cosα=x{\displaystyle \cos \alpha =x} ,
- sinα=y{\displaystyle \sin \alpha =y} .
При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:
- cos2α+sin2α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1} .
(Используется следующая общепринятая нотация: cos2x=(cosx)2{\displaystyle \cos ^{2}x=(\cos x)^{2}} .)
Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:
- sin(x+2πk)=sin(x){\displaystyle \sin(x+2\pi k)=\sin(x)}
- cos(x+2πk)=cos(x){\displaystyle \cos(x+2\pi k)=\cos(x)}
для всех целых чисел k{\displaystyle k} , то есть для k∈Z{\displaystyle k\in \mathbb {Z} } .
В комплексной плоскости единичная окружность — это следующее множество G⊂C{\displaystyle G\subset \mathbb {C} } :
- G={z:Re{z}2+Im{z}2=1}={z:z=eiϕ,0≤ϕ<2π}{\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}
Множество G{\displaystyle G} является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ei0=1{\displaystyle e^{i0}=1} ).
www.ru-wiki.org
Тригонометрическая окружность Вики
Единичная окружность — окружность с радиусом 1 и центром в начале координат. Понятие единичной окружности обобщается до n{\displaystyle n}-мерного пространства (n>2{\displaystyle n>2}), в таком случае говорят о «единичной сфере».
Для координат всех точек на окружности, согласно теореме Пифагора, выполняется равенство x2+y2=1{\displaystyle x^{2}+y^{2}=1}.
Тригонометрические функции[ | код]
Все тригонометрические функции угла θ могут быть сконструированы геометрически при помощи единичной окружности.С помощью единичной окружности могут быть наглядно описаны тригонометрические функции (в контексте такого описания единичную окружность иногда называют «тригонометрическим кругом», что не слишком удачно, так как рассматривается именно окружность, а не круг).
Синус и косинус могут быть описаны следующим образом: если соединить любую точку (x,y){\displaystyle (x,y)} на единичной окружности с началом координат (0,0){\displaystyle (0,0)}, получается отрезок, находящийся под углом α{\displaystyle \alpha } относительно положительной полуоси абсцисс. Тогда действительно:
- cosα=x{\displaystyle \cos \alpha =x},
- sinα=y{\displaystyle \sin \alpha =y}.
При подстановке этих значений в уравнение окружности x2+y2=1{\displaystyle x^{2}+y^{2}=1} получается:
- cos2α+sin2α=1{\displaystyle \cos ^{2}\alpha +\sin ^{2}\alpha =1}.
(Используется следующая общепринятая нотация: cos2x=(cosx)2{\displaystyle \cos ^{2}x=(\cos x)^{2}}.)
Тут же наглядно описывается периодичность тригонометрических функций, так как соответствующее углу положение отрезка не зависит от количества «полных оборотов»:
- sin(x+2πk)=sin(x){\displaystyle \sin(x+2\pi k)=\sin(x)}
- cos(x+2πk)=cos(x){\displaystyle \cos(x+2\pi k)=\cos(x)}
для всех целых чисел k{\displaystyle k}, то есть для k∈Z{\displaystyle k\in \mathbb {Z} }.
Комплексная плоскость[ | код]
В комплексной плоскости единичная окружность — это следующее множество G⊂C{\displaystyle G\subset \mathbb {C} }:
- G={z:Re{z}2+Im{z}2=1}={z:z=eiϕ,0≤ϕ<2π}{\displaystyle G=\{z:\mathrm {Re} \{z\}^{2}+\mathrm {Im} \{z\}^{2}=1\}=\{z:z=e^{i\phi },0\leq \phi <2\pi \}}
Множество G{\displaystyle G} является подгруппой группы комплексных чисел по умножению, её нейтральный элемент — это ei0=1{\displaystyle e^{i0}=1}).
См. также[ | код]
ru.wikibedia.ru
