Тригонометрии значения – . .

Значения тригонометрических функций

Значения тригонометрических функций для основных углов: 0, 30, 45, 60, 90, 120, 180, 270 и 360 градусов

Значения тригонометрических функций для основных углов: \(0^\circ\), \(30^\circ\), \(45^\circ\), \(60^\circ\), \(90^\circ\), \(120^\circ\), \(180^\circ\), \(270^\circ\) и \(360^\circ\)  

\(\alpha^\circ\)	\(\alpha\) рад	\(\sin \alpha\)	\(\cos \alpha\)	\(\tan \alpha\)	\(\cot \alpha\)	\(\sec \alpha\)	\(\csc \alpha\)
\(0^\circ\)	\(0\)	\(0\)	\(1\)	\(0\)	\(\infty\)	\(1\)	\(\infty\)
\(30^\circ\)	\(\pi/6\)	\(1/2\)	\(\sqrt 3/2\)	\(1/\sqrt 3\)	\(\sqrt 3\)	\(2/\sqrt 3\)	\(2\)
\(45^\circ\)	\(\pi/4\)	\(\sqrt 2/2\)	\(\sqrt 2/2\)	\(1\)	\(1\)	\(\sqrt 2\)	\(\sqrt 2\)
\(60^\circ\)	\(\pi/3\)	\(\sqrt 3/2\)	\(1/2\)	\(\sqrt 3\)	\(1/\sqrt 3\)	\(2\)	\(2/\sqrt 3\)
\(90^\circ\)	\(\pi/2\)	\(1\)	\(0\)	\(\infty \)	\(0\)	\(\infty\)	\(1\)
\(120^\circ\)	\(2\pi/3\)	\(\sqrt 3/2\)	\(-1/2\)	\(-\sqrt 3\)	\(-1/\sqrt 3\)	\(-2\)	\(2/\sqrt 3\)
\(180^\circ\)	\(\pi\)	\(0\)	\(-1\)	\(0\)	\(\infty\)	\(-1\)	\(\infty\)
\(270^\circ\)	\(3\pi/2\)	\(-1\)	\(0\)	\(\infty\)	\(0\)	\(\infty\)	\(-1\)
\(360^\circ\)	\(2\pi\)	\(0\)	\(1\)	\(0\)	\(\infty\)	\(1\)	\(\infty\)

Значения тригонометрических функций для некоторых нестандартных углов: \(15^\circ\), \(18^\circ\), \(36^\circ\), \(54^\circ\), \(72^\circ\) и \(75^\circ\)  

\(\alpha^\circ\)	\(\alpha\) рад	\(\sin \alpha\)	\(\cos \alpha\)	\(\tan \alpha\)	\(\cot \alpha\)
\(15^\circ\)	\(\pi/12\)	\(\large\frac{{\sqrt 6 — \sqrt 2 }}{4}\normalsize\)	\(\large\frac{{\sqrt 6 + \sqrt 2 }}{4}\normalsize\)	\(2 — \sqrt 3\)	\(2 + \sqrt 3\)
\(18^\circ\)	\(\pi/10\)	\(\large\frac{{\sqrt 5 — 1}}{4}\normalsize\)	\(\large\frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\normalsize\)	\(\large\sqrt {\frac{{5 — 2\sqrt 5 }}{5}}\normalsize\)	\(\sqrt {5 + 2\sqrt 5 }\)
\(36^\circ\)	\(\pi/5\)	\(\large\frac{{\sqrt {10 — 2\sqrt 5 } }}{4}\normalsize\)	\(\large\frac{{\sqrt 5 + 1}}{4}\normalsize\)	\(\large\frac{{\sqrt {10 — 2\sqrt 5 } }}{{\sqrt 5 + 1}}\normalsize\)	\(\large\frac{{\sqrt 5 + 1}}{{\sqrt {10 — 2\sqrt 5 } }}\normalsize\)
\(54^\circ\)	\(3\pi/10\)	\(\large\frac{{\sqrt 5 + 1}}{4}\normalsize\)	\(\large\frac{{\sqrt {10 — 2\sqrt 5 } }}{4}\normalsize\)	\(\large\frac{{\sqrt 5 + 1}}{{\sqrt {10 — 2\sqrt 5 } }}\normalsize\)	\(\large\frac{{\sqrt {10 — 2\sqrt 5 } }}{{\sqrt 5 + 1}}\normalsize\)
\(72^\circ\)	\(2\pi/5\)	\(\large\frac{{\sqrt {10 + 2\sqrt 5 } }}{4}\normalsize\)	\(\large\frac{{\sqrt 5 — 1}}{4}\normalsize\)	\(\sqrt {5 + 2\sqrt 5 }\)	\(\large\sqrt {\frac{{5 — 2\sqrt 5 }}{5}}\normalsize\)
\(75^\circ\)	\(5\pi/12\)	\(\large\frac{{\sqrt 6 + \sqrt 2 }}{4}\normalsize\)	\(\large\frac{{\sqrt 6 — \sqrt 2 }}{4}\normalsize\)	\(2 + \sqrt 3\)	\(2 — \sqrt 3\)

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Поделитесь с другими:

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

calcsbox.com

Формулы по тригонометрии от репетитора по математике — Колпаков Александр Николаевич

by Колпаков А.Н. on 13 сентября 2010

Справочные материалы по тригонометрии. Формулы. Определения и свойства.

Комплект предназначен для слабых и средних по уровню учащихся, для репетиторов по математике и школьных преподавателей. Он специально адаптирован мной для слабых и средних по уровню учеников. В материалах применяются, на мой взгляд, лучшие приемы уменьшения нагрузки на память и упрощения работы с большими объемами информации. Их содержание дает репетитору по математике возможность преподнести тригонометрию в удобной для работы и для запоминания форме. В помощь репетитору по математике, работающему со слабыми учащимися, я специально исключил из списка формул те, которые не входят в основную программу, а также сложные формулы и различные формулы-следствия.

Определение тригонометрических функций: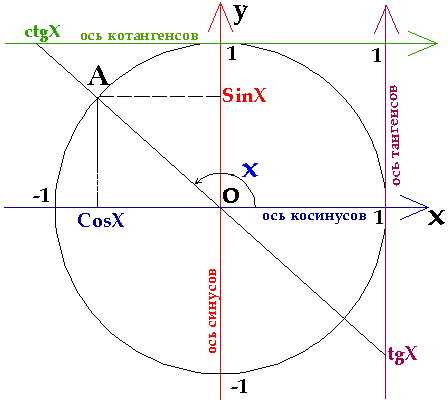

Определение: синусом угла поворота на называется ордината точки, изображающей данный угол.
Определение: косинусом угла поворота называется абсцисса точки, изображающей данный угол.
Определение: тангенсом угла поворота называется отношение ординаты точки, изображающей угол, к ее

абсциссе.
Определение: котангенсом угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате.

Основные тригонометрические свойства:
(основное тригонометрическое тождество)

Четность и нечетность тригонометрических функций:

ankolpakov.ru

Значения тригонометрических функций

Значения тригонометрических функций. Друзья, прошлой статье, при рассмотрении тригонометрических уравнений, я пообещал вам привести алгоритм быстрого «восстановления»  значений тригонометрических функций от 0 до 90 градусов. Решил далеко не откладывать, будущее уже настало )). Если хотите скачать данную теорию в pdf формате, подпишитесь на рассылку (в МЕНЮ вкладка ПОДАРКИ).  Вы получите все прототипы задач базовой части с ответами и теорию систематизированную по группам задач от 1 до 14.

Предлагаю вам алгоритм, благодаря которому вы легко, в течение минуты восстановите в памяти все вышеуказанные значения:

1. Записываем в строчку углы от 0 до 90 градусов. Слева в столбик запишем сначала синус, затем косинус аргумента:

2. Напротив синуса пишем числа от нуля до четырёх (под значениями  углов). Напротив косинуса от 4 до 0:

3. Далее извлекаем корень:

4. Делим на 2:

5. Вычисляем:

Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и  котангенса:

вы сможете найти  значения для указанных углов.

Например: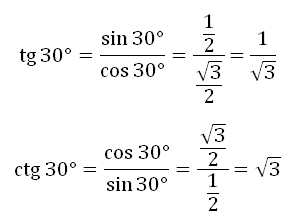

И так для тангенса и котангенса любого угла. Данная шпаргалка представленная выше может выручить.

*Конечно, к пониманию того,  каким значениям  равны тригонометрические функции различных углов (имею виду углы 0, 30, 45, 60, 90, 120 и так далее), какие ставить знаки при этих значениях лучше прийти через понимание тригонометрической окружности.

Кстати, вы можете расширить диапазон углов и записать углы  от 0 до 180 градусов, но тогда напротив синуса и косинуса нужно будет поставить  числа в следующем порядке:

Далее выполняем те же действия, учитывая один нюанс: корень в строке с косинусом извлекаем из положительного числа, минус ставим перед корнем:

Тригонометрическая окружность

 

 

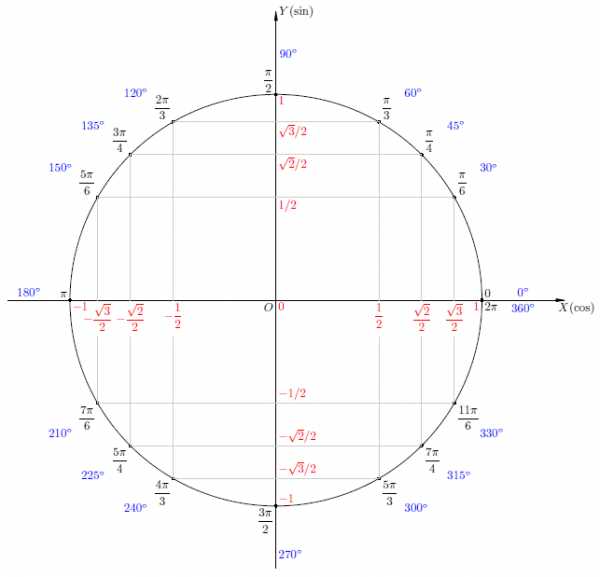
Описывать подробно, как определять значения функций, которые соответствуют определённому  углу здесь не буду, сделаю это в одной из будущих статей, не пропустите!

Объясню лишь принцип: косинус угла – это абсцисса точки на тригонометрической окружности, которая соответствует данному углу; синус угла – это ордината точки на тригонометрической окружности, которая соответствует данному углу.

Например по представленному рисунку видно, что косинус нуля градусов равен 1, косинус 120 градусов равен минус 0,5 и так далее, надеюсь, логику вы уловили.

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Значение слова «тригонометрия»

Тригонометрия

— Соотношения между сторонами и углами треугольников (см.) выражаются при помощи особого рода функций, назыв. тригонометрическими. Этим функциям даны особые названия: синус, косинус, тангенс, котангенс, секанс и косеканс.

Фиг 1.

Предположим, что, приняв точку О за центр, радиусом ОА опишем дугу AB.

Точка А наз. началом дуги AB, а точка В — концом дуги AB. Представим себе угол АОВ, вершина которого находится в точке О, а стороны проходят через точки А и В. При изменении радиуса ОА дуга AB, ограниченная сторонами данного угла, меняется, но отношение AB/OA остается неизменным. Это отношение служит мерою данного угла. Так как равные углы можно отложить по разные стороны прямой ОА, то, для того, чтобы отличить один угол от другого, согласились один из углов выражать числом положительным, а другой числом отрицательным. Если дуги AB и AB’, описанные радиусом ОА равны, то и угол АОВ равен углу АОВ’. Если напр. AB/OA =

1/3, то согласимся говорить, что угол АОВ равен 1/3 и что угол АОВ’ равен (— 1/3). Таким образом всякому отвлеченному числу (положительному или отрицательному) соответствует вполне определенный угол. Если мы из конца дуги В опустим перпендикуляры ВР и BQ на прямую ОА и на прямую ОС, перпендикулярную к ОА, то получим отрезки ОР и OQ (черт. 2), которые назыв. проекциями 0В на ОА и на ОС. Предположим, что угол АОВ не меняется, а изменяется радиус ОА; в таком случае отношения ОР/OA и OQ/OA остаются неизменными.

Черт. 2.

Здесь возможны следующие частные случаи. Проекция 0В на О А может быть направлена в ту же сторону, как и отрезок

ОА или же в сторону противоположную (черт. 3).

Черт. 3.

Точно так же проекция 0В на ОС может иметь направление ОС или направление противоположное (черт. 4).

Черт. 4.

Направление ОС выбрано так, чтобы прямой

угол А ОС был положительный. Если угол АОВ равен α, то синусом α (Sin α) назыв. отношение OQ/OA в случае, если OQ имеет одинаковое направление с ОС. Если же OQ направлено противоположно ОС, то

Sin α = — OQ/OA

Отношение OP/OA назыв. косинусом α, (Cos α) в случае, если ОР одинаково направлено с OA. Если же

ОР имеет противоположное направление с ОА, то

Cos α = — OP/OA

В учебниках Т. можно найти доказательство следующих формул:

Sin (— α) = — Sin α, Cos (— α) = Cos α,

Sin (π /2 — α) = Cos α, Cos (π /2 — α) = Sin α,

Sin (π — α) = Sin α, Cos (π — α) = —Cos α,

Sin (π + α) = — Sin α, Cos (π + a) = —Cos α,

Sin (2 π — α) = — Sin α, Cos (2 π — α) = Cos α,

Sin (2 π + α) = Sin α, Cos (2 π + α) —Cos α.

При помощи этих формул вычисление Sinα и Cosα приводится к случаю, когда α число положительное, не превосходящее π /4

Из формул

Sin (α + β) = Sin α Cosß + Cos α Sinß,

Cos (α + ß) = Cos α Cosß —

Sin α Sinß

следует

Sina + Sinb = 2Sin[(a + b)/2] Cos[(a — b)/2],

Sina — Sinb = 2Sin[(a — b)/2] Cos[(a + b)/2],

Cosa + Cosb = 2Cos[(a + b)/2] Cos[(a — b)/2],

Cosa — Cosb = 2Sin[(a + b)/2] Sin[(a — b)/2].

Функции Sin2 α и Cos2 α выражаются через Sin α и Cos α следующим образом:

Sin2 α = 2Sin α Cos α,

Cos2 α = Cos² α — Sin² α.

Вследствие соотношения

Cos² α + Sin² α = 1

последняя формула принимает следующие виды;

Cos2a = 1 — 2Sin² α или Cos2a = SCos² α — 1.

Здесь для сокращения написано Sin²

α и Cos²a вместо (Sin α)² и (Cos α)². Тригонометри-ческие функции тангенс (tg), котангенс (ctg), секанс (sec) и косеканс (cosec) определяются следующим образом:

tg α = Sin α /Cos α, ctg α = Cos α /Sin α,

sec α = 1/Cos α, cosec α = 1/Sin α

Отметим некоторые свойства тангенса.

tg(α + β) = (tg α + tg β)/(1 — tg α tg β)

tg2 α = (2tg α)/(1 — tg² α)

tg α /2 = Sin α /(1 + Cos α) = (1 — Cos α)/Sin α

Функции обратные тригонометрическим наз. круговыми: арксинус (arc Sin), арккосинус (arc Cos), арктангенс (arc tg), арккотангенс (arc ctg), арксеканс (arc sec) и арккосеканс (arc cosec). Если напр. tg α = a, то α = arc tga. Так как данному числу a соответствует множество различных α, то для большей определенности согласились под arc tga понимать число, лежащее в промежутке (— π /2, π /2). В этом промежутке тангенс может иметь любое значение. Подобным же образом предполагается, что числа arc Sina, arc ctga и arc coseca лежат между — π /2 и π /2, а числа arc Cosa и arc seca между О и π. Тригонометрические функции имеют очень важное значение: они встречаются в очень многих вопросах анализа и геометрии. Так как вычисления облегчаются при помощи логарифмов, то в таблицах помещаются не самые тригонометрические функции, но их логарифмы (см.). Углы в таблицах выражены не числами, а градусами. Если данный угол равен α, то он содержит 180 α / π градусов; 60-ая часть градуса наз. минутой, а 60-ая часть минуты — секундой. Тригонометрические таблицы вычисляются при помощи рядов (см.).

Соотношения между сторонами и углами прямолинейного треугольника (см.) выражаются следующими формулами. Если обозначим углы треугольника через A, В и С, а противолежащие им стороны через a, b и с, то получим

А + B + С = π,

SinA/a = SmB/b = SinC/c

a² = b² + с ² — 2bс.CosA,

a = b.CosC + c.CosB,

tg[(Α — Β)/2] = [(a — b)/(a + b)]Ctg(С/2)

Если периметр треугольника, т. е. а + b + c обозначим для краткости через 2р, то получим

В этих формулах корень квадратный имеет значение положительное. Если s обозначает площадь треугольника, то s = 1/2(ab).Sinc или s = √[p(p — a)(p — b)(p — c)].

Если R радиус круга, описанного около треугольника, а r — радиус круга вписанного, то

R = a/(2SinA) = (abc)/(4s) и r = s/p.

Из перечисленных формул можно вывести другие при помощи перестановки букв. Напр., из формулы

а ² = b² + с ²— 2bс.CosA

следует

b² = а ² + с ²— 2ас. CosB.

При помощи указанных формул по данным частям треугольника вычисляются остальные его части. Подобная задача, называемая решением треугольников, встречается во многих практических вопросах: при геодезических съемках, при определении высот, при нахождении расстояния между неприступными точками и т. д.

Переходим теперь к треугольникам сферическим. Решение этих треугольников составляет предмет сферической тригонометрии. Предположим, что на поверхности шара радиуса R начерчен треугольник, вершины которого суть A, В и С. Соединив центр шара О с точками A, В и С, получим трехгранный угол, содержащий три плоских угла и три двугранных угла. Величины двугранных углов, ребра которых суть ОА, ОВ и ОС, обозначим через А, В и С, а величины противоположных им плоских углов через а, b и с. Будем предполагать, что шесть чисел А, В, С, а, b, с выражены в градусах, и что ни одно из них не превосходит 180°. Между этими числами имеют место следующие основные соотношения:

Cosa = Cosb.Cosс + Sinb. Sinс. CosА,

SinA/Sina = SinB/Sinb = SinC/Sinc

Cosa.Sinb — Sina.Cosb.CosC = Sinc.CosA,

Cosa.SinB — Cosb.CosС.SinА = СоsA.Sin С,

Ctga. Sinb — CtgA.SinC = Cosb.CosC,

CosA = — CosB.CosC + SinB.SinC.Cosa.

Если a + b + c = 2p, то

Сумма углов сферического треугольника содержит более 180°. Число A + В + С — 180° наз. сферическими избытком данного треугольника и обозначается буквою ε. Для определения числа градусов, содержащихся в одной из сторон сферического треугольника, углы которого даны, служат формулы

Площадь сферического треугольника равна (π /180) ε.R², где R радиус шара.

Формула Люилье (l’Huillier) дает возможность вычислить сферический избыток по сторонам треугольника.

Укажем еще на формулы Деламбра:

Sin[(A + B)/2]:Cos[C/2] = Cos[(a — b)/2]:Cos[c/2]

Sin[(A — B)/2]:Cos[C/2] = Sin[(a — b)/2]:Sin[c/2]

Cos[(A + B)/2]:Sin[C/2] = Cos[(a + b)/2]:Cos[c/2]

Cos[(A — B)/2]:Sin[C/2] = Sin[(a + b)/2]:Sin[c/2]

и на формулы Непера:

tg[(A + B)/2] = (ctg[c/2])(Cos[(a — b)/2]/Cos[(a + b)/2])

tg[(A — B)/2] = (ctg[c/2])(Sin[(a — b)/2]/Sin[(a + b)/2])

tg[(a + b)/2] = (tg[c/2])(Cos[(A — B)/2]/Cos[(A + B)/2])

tg[(a — b)/2] = (tg[c/2])(Sin[(A — B)/2]/Sin[(A + B)/2]) Из перечисленных формул получим новых при помощи перестановки букв.

Формулы сферической Т. очень часто применяются в астрономии.

Не перечисляя учебников тригонометрии, укажем на J. A. Serret, «Trait é de Trigonomé trie». Сведения по истории Т. можно найти в сочинении: Moritz Cantor, «Vorlesungen ü ber Geschichte der Mathematik», доведенном до 1759 г. (до года рождения Лагранжа). Кроме того, в 1900 г. появилась первая часть сочинения: A. von Braunm ühl, «Vorlesungen ü ber Geschichte der Trigonometrie», в которой история Т. доведена до половины XVII стол. (до изобретения логарифмов).

Д. С.

how-to-all.com

Значения тригонометрических функций для различных углов · Математика

 /  19 апреля 2006 года  /  Математика  /  Светлана Кабанова

В таблице приведены значения тригонометрических функций (sin x, cos x, tg x, ctg x) для различных углов от 0 до 2π.

ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ДЛЯ РАЗЛИЧНЫХ УГЛОВ
Функция / угол	0 или 0°	π/6 или 30°	π/4 или 45°	π/3 или 60°	π/2 или 90°	2π/3 или 120°	3π/4 или 135°	5π/6 или 150°	π или 180°	3π/2 или 270°	2π или 360°
sin α	0	1/2	√2/2	√3/2	1	√3/2	√2/2	1/2	0	–1	0
cos α	1	√3/2	√2/2	1/2	0	-1/2	-√2/2	-√3/2	–1	0	1
tg α	0	√3/3	1	√3	–	-√3	-1	-√3/3	0	–	0
ctg α	–	√3	1	√3/3	0	-√3/3	-1	-√3	–	0	–

Чтобы узнать значение угла для arcsin α, arccos α, arctg α и arcctg α, просто найдите в таблице нужное число и посмотрите какому значению угла оно соответствует.

Например, вам нужно найти arctg 1, для этого в строке tg α находите 1, поднимаетесь в найденном столбике наверх и видите, что 1 соотвествует углу π/4.

Получаем результат: tg π/4 = 1 и arctg 1 = π/4.

Есть что сказать?   Выразите своё мнение к статье!

Cообщение # 7527, написанное 21-02-2018 в 20:26 МСК, удалено.  # 7278  ·  07-09-2017 в 16:56 МСК  ·  ip адрес записан  ·  наверх ↑  ·  написать мнение Спасибо управляющему сего прекраснаго рессурса, я былъ пораженъ темъ, какъ проста сія таблица и удобна въ использованіи. Искренне благодаренъ темъ, кто создалъ это! Сія табличка помогла мнѣ въ жизни, я сталъ успѣшнымъ предпринимателемъ только благодаря сіей лучшей табличкѣ. Позвольте пожелать вамъ долгой жизни, счастья вашей семьѣ, вашимъ близкимъ, всего самаго наилучшаго желаю я вамъ. Спасибо, спасибо, спасибо! Британский кодекс. Кодекс профессионального поведения института ПР (ИПР) статьи на habit.ru Cообщение # 5071, написанное 26-01-2015 в 09:08 МСК, удалено. Cообщение # 4634, написанное 30-10-2014 в 08:36 МСК, удалено.

Читайте также:

www.habit.ru