Функция y=sinx, ее основные свойства и график. Видеоурок. Алгебра 10 Класс
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).

Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент – это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
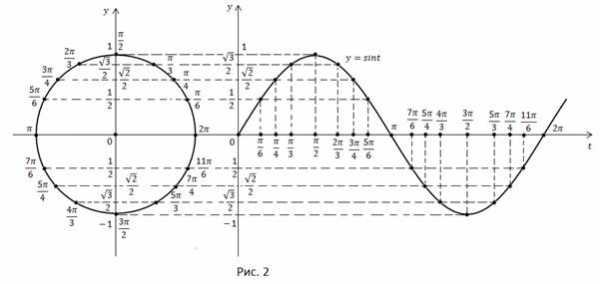
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
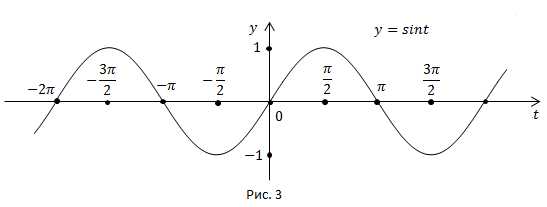
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. –М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
1. Математика (Источник).
2. Интернет-портал Problems.ru (Источник).
3. Образовательный портал для подготовки к экзаменам (Источник).
interneturok.ru
Функция y=sinx, её свойства и график. Видеоурок. Алгебра 9 Класс
Мы рассмотрели функцию числового аргумента , либо углового аргумента От переобозначения смысл не меняется. Переобозначим
. Каждому значению независимой переменной ставится в соответствие только одно значение зависимой переменной.
Рассмотрим свойства функции , для этого построим график.
Рис.1
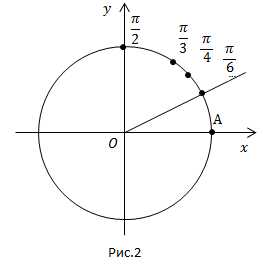
По оси oу функция будет меняться только в пределах от до 1.
Отметим основные точки:
Почему график функции ведет себя таким образом? Рассмотрим единичную окружность в координатной плоскости.
Вспомним закон, по которому каждому значению аргумента
Начнем увеличивать угол. Отметим углы
Если т. А скользит по единичной окружности и угол увеличивается, то ордината тоже увеличивается от 0 до 1.
Если точка скользит по окружности от , ордината уменьшается от 1 до 0. Это же видим на графике.
Итак, если , функция возрастает; а если , то функция убывает;
Далее, сославшись на нечетность функции, можно график симметрично отобразить относительно начала координат.
Но посмотрим, например, что происходит с функцией, когда . Функция уменьшается от 0 до .
Получим значения функции для некоторых точек:
Отметим их на графике (рис.1) и вспомним, как вычисляется синус.
Чтобы найти значение функции для , рассмотрим — прямоугольный.
Найдем значение функции для , для этого рассмотрим прямоугольный треугольник:
Гипотенуза равна 1. Углы равны, значит треугольник равнобедренный и катеты тоже равны. Обозначим катеты m.
По теореме Пифагора .
.
Найдем значение функции для Рассмотрим прямоугольный (рис.4).
Нам известно MN, вычислим ON по теореме Пифагора.
.
Отметим полученные значения на графике и получим плавную кривую – синусоиду.
Мы рассмотрели график функции изобразили ее график, объяснили его построение и с его помощью перечислим основные свойства функции.
1. Область определения
2. Множество значений
Решить уравнение
Уравнение не имеет решений, т.к.
Найти все a,при которых уравнение имеет хотя бы одно решение.
Уравнение имеет хотя бы одно решение при
– минимальный период, т.е.
Таким образом, изучить свойства синуса достаточно на любом отрезке длиной в период–для синуса .
4. Функция — нечетная,
График функции симметричен относительно начала координат, например точка переходит в точку (рис.1).
Можно построить график на участке от 0 до (половина периода), и симметрично отобразив относительно т.О (0;0), получить график на промежутке от до т.е. на участке длиной в период.
5. Если возрастает от 0 до , то возрастает от 0 до 1; если возрастает от до , то убывает от 1 до 0.
6. непрерывная функция, т.е. можно построить график, не отрывая карандаша от бумаги.
Мы рассмотрели функцию и ее важнейшие свойства.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на ресурсы интернет
1. Открытая математика (Источник).
2. РЕШУ ЕГЭ (Источник).
3. РЕШУ ЕГЭ (Источник).
4. РЕШУ ЕГЭ (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№653, 654, 655, 656.
interneturok.ru
y = — sin x
Доброй ночи!
Ваше непонимание — это нормальное явление, так как Вы столкнулись уже немного с другим типом заданий, точнее даже с другой темой. Вы уже должны были строить графики функций. Должны были знакомится с различными видами функций. Так вот, Ваше задание — это и есть функция: y = — sin x, которую называют синусоидой.
Обычно, чтоб справится с таким задание Вам надо всего лишь построить график данной функции, а в этом нет ничего сложного.
Но для начала давайте вспомним основные свойства первоначальной функции, которая имеет такой вид, как y = sin x.
Прежде всего, как впрочем и всегда с графиками, составляется табличка значений.
Следует заметить, что данная функция периодична с периодом 2π. То есть, чтоб нарисовать полностью график данной функции достаточно получившуюся кривую, продолжить влево и вправо периодически с периодом 2π.
Данная функция у = sin х является ограниченной. То есть, все значения, которые она принимает, находятся в интервале от —1 до 1, включая эти два числа.
Также, функция у = sin х является нечетной (то есть синусоида симметрична относительно начала координат)
А табличные значения можете взять такие:
А Ваша функция — это та же самая функция,отображённая симметрично относительно оси Оx.
Но в данном случае, проще преобразовать эту функцию так : -sin x = sin(пи + x) и построить график y = sin x, смещенный на пи единиц влево. Можно перейти к новым осям, построив прямую y = -пи — это новая ось Oy’, ось Ox оставить без изменений. И построить график функции y = sin x в новой системе координат. Это будет график требуемой Вам функции в старой системе координат.
ru.solverbook.com
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
10 класс. Алгебра. Тригонометрические функции. Функции у=sinx, y=cosx, их свойства, графики, типовые задачи. — Функция y=sinx, ее основные свойства, график и типовые задачи.
Комментарии преподавателя
Функция y=sint, её свойства и типовые задачи
На прошлом уроке мы рассмотрели основные свойства функции и сейчас используем их при решении задач.
Подробно рассмотрим поведение функции на промежутке и отметим основные точки (рис. 1).
Теперь те же точки поместим в числовую окружность на отрезке (рис. 2).
Отметим некоторые особенности функции при
1) Монотонное возрастание функции от до
2) Функция пробегает все свои возможные значения,
Рассмотрим несколько задач, при решении которых очень важное значение имеет монотонность функции.
Задача 1.
a) Найти наибольшее значение функции на отрезке
Решение:
Функция монотонно возрастает на указанном промежутке, значит, наибольшее значение принимает на правом конце отрезка, (рис. 3).
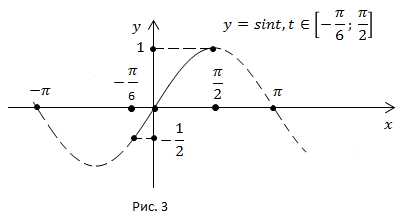
b) Найти наименьшее значение функции на отрезке
Решение:
Функция монотонно возрастает на указанном отрезке, значит, наименьшее значение принимает на его левом конце, (рис. 3).
Ответ: a) 1; b)
Задача 2. Если аргумент меняется в заданных пределах, то найдите, в каких пределах меняется функция . Найти наименьшее и наибольшее значение функции.
a)
Решение:
Функция монотонно возрастает на отрезке значит,
(рис. 4).
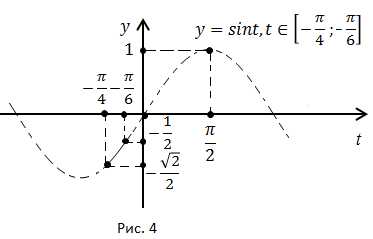
Ответ:
b)
Решение:
На заданном промежутке функция немонотонна (рис. 5).
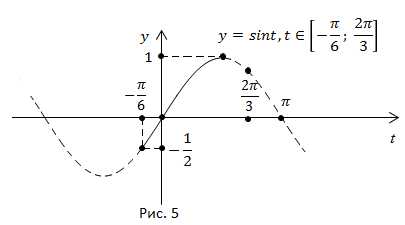
На графике мы видим, что функция меняется в пределах
Ответ:
Задача 3. Найти количество решений уравнения на промежутке
Решение:
На заданном промежутке функция монотонна, значит, каждое свое значение она принимает при единственном значении аргумента (рис. 1). Поэтому уравнение на данном отрезке имеет единственное решение.
Важнейшая особенность функции на отрезке монотонность функции. Поэтому и прямая и обратная задачи тут имеют одно решение.
1. Прямая задача – заданному значению аргумента соответствует единственное значение функции.
Например:
2. Обратная задача – заданное значение монотонной функции достигается только при одном значении аргумента.
Например: Если
Если
www.kursoteka.ru
Помогите построить график функции y=sin x/2
Проще пареной репы!! ! Вы ведь знаете график функции y = sin(x). Это известная всем синусоида. У функции y=sin x/2 такой же график, с той только разницей, что эта синусоида вдвое меньшей частоты. У sin(x) первый максимум в точке x = тт/2, а у sin(x/2) в точке х = тт (действительно, подставим в у=sin(x/2) вместо х величину тт — получим y = sin(тт/2) — это как раз максимум. Так что надо просто вдвое растянуть график синуса. Вот и вся недолга!!
<a href=»/» rel=»nofollow» title=»21168633:##:http://www.fayloobmennik.net/1444537″ target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a> Построен в Excel 2007.
это тоже самое что график y=sinx, те проходит через 0 следующий узел в 2пи, а верхняя точка в пи и 3пи, а по y границы 1 и -1
<a rel=»nofollow» href=»https://steamgifts.co/go/?id=laWpgBU2b» target=»_blank»>https://steamgifts.co/go/?id=laWpgBU2b</a>
touch.otvet.mail.ru
