Углы при двух параллельных прямых и секущей – Углы при параллельных прямых и секущей

Пары углов, образованные параллельными прямыми, пересеченными секущей

Когда есть две параллельные линии (на рисунке внизу), можно выделить две основные области: внутреннюю и внешнюю.

Когда две параллельные линии пересекаются третьей прямой, эта прямая называется секущей. В примере, приведенном ниже, образуются восемь углов, когда параллельные линии m и n пересекаются секущей — прямой t.

Есть несколько пар углов, образованных на этом рисунке. Некоторые пары уже рассмотрены:
      Вертикальные пары:       1 и 4
                                  2 и 3
                                  5 и 8
                                  6 и 7

Напомним, что все пары вертикальных углов равны.
      Смежные углы:       1 и 2
                                            2 и 4
                                            3 и 4
                                            1 и 3
                                            5 и 6
                                            6 and 8
                                            7 and 8
                                            5 and 7
Напомним, что смежные углы это углы, которые дополняют друг друга до 180°. Все эти смежные пары есть линейными парами. Есть и другие пары смежных углов, которые описаны далее в этом разделе. Есть еще три специальные пары углов. Эти пары есть конгруэнтными (равными) парами.

Внутренние накрест лежащие углы это два угла во внутренней области параллельных прямых и на разных сторонах секущей. Внутренние накрест лежащие углы попарно равны.

Внешние накрест лежащие углы это два угла во внешней области параллельных прямых и на разных сторонах секущей. Внешние накрест лежащие углы попарно равны.

Соответственные углы это два угла, один во внешней области, один во внутренней области, и которые лежат на одной стороне секущей. Соответственные углы равны.

Используйте следующие диаграмма параллельных линий, пересеченных секущей, чтобы дать ответы на вопросы в примерах.

Пример:
Чему равен угол 8?
Угол, величина которого на рисунке равна 53° и 8 — внешние накрест лежащие углы. Так как такие углы являются равными, то величина 8 = 53°.
Пример:
Чему равен угол 7?
8 и 7 есть линейной парой; они смежные. Они дополняют друг друга до 180°. Поэтому, 7 = 180° – 53° = 127°.

1. Когда секущая пересекает параллельные прямые, все образующиеся при этом острые углы равны, и все образующиеся тупые углы- равны.

На рисунку вверху1, 4, 5, и 7 есть острыми углами. Они все равны между собой. 1 ≅ 4 есть вертикальными углами. 4 ≅ 5 есть внутренним накрест лежащими углами, и 5 ≅ 7 — вертикальные углы. То же свойство и справедливо для тупых углов на рисунке: 2, 3, 6, и 8 есть равными между собой.

2. Когда секущая пересекает параллельные прямые, один любой образующийся угол и один любой образующийся тупой угол есть смежными.

На рисунке Вы можете видеть, что 3 и 4 являются смежными, потому что они есть линейной парой. Обратите внимание, что 3 ≅ 7, так как они есть соответсвенными углами. Поэтому, вы можете заменить 7 на

www.math10.com

Углы при 2-х параллельных прямых и секущей

Мы знаем, что две прямые параллельны, если при пересечении их третьей прямой равны соответственные углы, или внутренние, или внешние накрест лежащие углы, или сумма внутренних, или сумма внешних односторонних углов равна 2d. Докажем, что верны и обратные теоремы, а именно:

Если две параллельные прямые пересечены третьей, то:

1. соответственные углы равны;
2. внутренние накрест лежащие углы равны;
3. внешние накрест лежащие углы равны;
4. сумма внутренних односторонних углов равна 2d;
5. сумма внешних односторонних углов равна 2d.

Докажем, например, что если две параллельные прямые пересечены третьей прямой, то соответственные углы равны.

Пусть прямые АВ и СD параллельны, а МN — их секущая (рис.). Докажем, что соответственные углы 1 и 2 равны между собой.

Допустим, что ∠1 и ∠2 не равны. Тогда при точке О можно построить ∠МОК, соответственный и равный ∠2 (рис.).

Но если ∠МОК = ∠2, то прямая ОК будет параллельна СD.

Получили, что через точку О проведены две прямые АВ и ОК, параллельные прямой СD. Но этого быть не может.

Мы пришли к противоречию, потому что допустили, что ∠1 и ∠2 не равны. Следовательно, наше допущение является неправильным и ∠1 должен быть равен ∠2, т. е. соответственные углы равны.

Установим соотношения между остальными углами. Пусть прямые АВ и СD параллельны, а МN — их секущая (рис.).

Мы только что доказали, что в этом случае соответственные углы равны. Положим, что какие-нибудь два из них имеют по 119°. Вычислим величину каждого из остальных шести углов. На основании свойств смежных и вертикальных углов мы получим, что четыре угла из восьми будут иметь по 119°, а остальные — по 61°.

Оказалось, что как внутренние, так и внешние накрест лежащие углы попарно равны, а сумма внутренних или внешних односторонних углов равна 180° (или 2d).

То же самое будет иметь место и при любом другом значении равных соответственных углов.

Следствие 1. Если каждая из двух прямых АВ и СD параллельна одной и той же третьей прямой МN, то первые две прямые параллельны между собой.

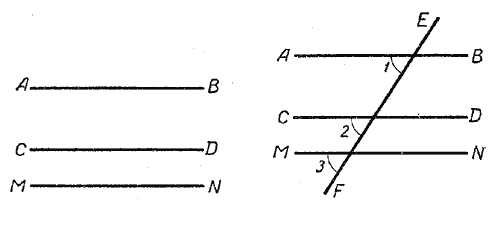
В самом деле, проведя секущую ЕF (рис.), получим:

а) ∠1 = ∠3, так как АВ || МN; б) ∠ 2 = ∠3, так как СО || МN.

Значит, ∠1 = ∠2, а это углы соответственные при прямых АВ и СD и секущей ЕF, следовательно, прямые АВ и СD параллельны.

Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой

.

В самом деле, если ЕF ⊥ АВ, то ∠1 = d; если АВ || СD, то ∠1 = ∠2.

Следовательно, ∠ 2 = d т. е. ЕF ⊥ СD .

razdupli.ru

Накрест лежащие, односторонние и соответственные углы. Признаки параллельности двух прямых.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямых a и b секущей образуются 8 углов. Они имеют специальные названия.

Признаки параллельности двух прямых

Теорема: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема: Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема: Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Аксиома: Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствие 1: Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. 

Следствие 2: Если две прямые параллельны третьей, то они параллельны. 

Обратные теоремы

Теорема 1: Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Теорема 2: Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Теорема 3: Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°

Теорема 4: Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и другой.

Задания

bitreit.ru

Аксиома параллельности

Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Из аксиомы параллельности и признаков параллельности прямых следует теорема: через точку, не лежащую на данной прямой, можно провести ровно одну прямую, параллельную данной.

Названия углов при двух прямых и секущей

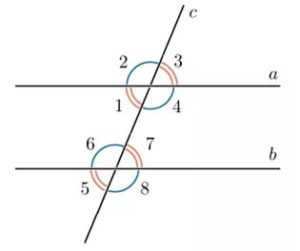
Пусть прямая \(c\) пересекает каждую из прямых \(a\) и \(b\). Образующися при этом пары углов, отмеченных на рисунке, имеют следующие названия.

1 и 5, 2 и 6, 3 и 7, 4 и 8 – соответственные; 3 и 5, 4 и 6 – внутренние накрест лежащие; 4 и 5, 3 и 6 – внутренние односторонние; 1 и 7, 2 и 8 – внешние накрест лежащие; 1 и 8, 2 и 7 – внешние односторонние.

Признаки параллельности прямых

1. Если внутренние накрест лежащие углы при двух прямых и секущей равны, то эти две прямые параллельны.

$$ \angle{1}=\angle{2} \, \Rightarrow \, a||b $$

2. Если сумма внутренних односторонних углов при двух прямых и секущей равна \(180^{\circ}\), то эти две прямые параллельны.

$$ \angle{1}+\angle{2}=180^{\circ} \, \Rightarrow \, a||b $$

3. Если соответственные углы при двух прямых и секущей равны, то эти две прямые параллельны.

$$ \angle{1}=\angle{2} \, \Rightarrow \, a||b $$

4. Если внешние накрест лежащие углы при двух прямых и секущей равны, то эти две прямые параллельны.

$$ \angle{1}=\angle{2} \, \Rightarrow \, a||b $$

5. Если сумма внешних односторонних углов при двух прямых и секущей равна \(180^{\circ}\), то эти две прямые параллельны.

$$ \angle{1}+\angle{2}=180^{\circ} \, \Rightarrow \, a||b $$

6. Если две прямые перпендикулярны третьей прямой, то они параллельны друг другу.

$$ a\perp c, \, b\perp c \, \Rightarrow \, a||b $$

Свойства углов при параллельных прямых и секущей

1. Внутренние накрест лежащие углы при параллельных прямых и секущей равны.

$$ a||b \, \Rightarrow \, \angle{1}=\angle{2} $$

2. Сумма внутренних односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\).

$$ a||b \, \Rightarrow \, \angle{1}+\angle{2}=180^{\circ} $$

3. Соответственные углы при параллельных прямых и секущей равны.

$$ a||b \, \Rightarrow \, \angle{1}=\angle{2} $$

4. Внешние накрест лежащие углы при параллельных прямых и секущей равны.

$$ a||b \, \Rightarrow \, \angle{1}=\angle{2} $$

5. Сумма внешних односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\).

$$ a||b \, \Rightarrow \, \angle{1}+\angle{2}=180^{\circ} $$

6. Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

$$ a||b, \, a\perp c, \, \Rightarrow \, b\perp c $$

tmath.ru

7 класс. Геометрия. Параллельные прямые. Задачи на признаки параллельности прямых. — Параллельные прямые и задачи на углы между ними и секущей.

Комментарии преподавателя

Па­рал­лель­ны­ми на­зы­ва­ют­ся такие пря­мые, ко­то­рые не пе­ре­се­ка­ют­ся.

 – пря­мые, с – се­ку­щая.

Рис. 1

Воз­ни­ка­ет много углов (1, 2, 3, 4, 5, 6, 7, 8).

Эти углы важны для нас, и по­это­му они имеют на­зва­ния:

— на­крест ле­жа­щие углы: ∠3 и ∠5, ∠4 и ∠6;

— од­но­сто­рон­ние углы: ∠4 и ∠5, ∠3 и ∠6;

— со­от­вет­ствен­ные углы: ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.

Ос­нов­ные тео­ре­мы о па­рал­лель­но­сти пря­мых:

Рис. 2

Если на­крест ле­жа­щие углы равны, то пря­мые па­рал­лель­ны. И на­о­бо­рот, если пря­мые па­рал­лель­ны, то на­крест ле­жа­щие углы равны.

Рис. 3

Если со­от­вет­ствен­ные углы равны, то пря­мые па­рал­лель­ны. И на­о­бо­рот, если пря­мые па­рал­лель­ны, то со­от­вет­ствен­ные углы равны.

Рис. 4

Если сумма внут­рен­них углов равна , то пря­мые па­рал­лель­ны. И на­о­бо­рот, если пря­мые па­рал­лель­ны, то сумма внут­рен­них углов равна .

www.kursoteka.ru

Теорема об углах, образованных двумя параллельными прямыми и секущей

Теорема об углах, образованных двумя параллельными прямыми и секущей

Теоремы

1. Если две параллельные прямые пересечены секущей, накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
4. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство

1. Пусть параллельные прямые a и b пересечены секущей MN (c). Докажем, что накрест лежащие углы 3 и 6 равны. Допустим, что углы 3 и 6 не равны. Отложим от луча MN угол PMN, равный углу 6, так, чтобы угол PMN и угол 6 были накрест лежащими углами при пересечении прямых МР и b секущей MN. По построению эти накрест лежащие углы равны, поэтому МР||b. Мы выяснили, что через точку М проходят две прямые (прямые a и МР), параллельные прямой b. Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и угол 3 равен углу 6.

ru.wikiversity.org

Соответственные углы | Треугольники

Соответственные углы — вид углов, образованный при пересечении двух прямых секущей.

Один из пары соответственных углов лежит во внутренней области между прямыми, другой — во внешней, причем оба угла находятся по одну сторону от секущей.

При пересечении двух прямых секущей образуется четыре пары соответственных углов.

    ∠1 и∠5

    ∠2 и∠6

    ∠3 и∠7

    ∠4 и∠8

                                     

— соответственные углы при прямых a и b и секущей c.

 

Наибольший интерес в геометрии представляют соответственные углы при параллельных прямых.

 

Свойство параллельных прямых

Если две параллельные прямые пересечены третьей прямой, то  соответственные углы равны.

Если a ∥ b, то

∠1 =∠2

(как соответственные углы при при a ∥ b и секущей c).

Всего при параллельных прямых и секущей образуется четыре пары равных соответственных углов:

    ∠1 =∠5

    ∠2 =∠6

    ∠3 =∠7

    ∠4 =∠8

                               
Признак параллельных прямых

Если соответственные углы равны, то прямые параллельны.

      ∠1 =∠2

А так как эти углы — соответственные при прямых при a и b и секущей c,

то a ∥ b (по признаку параллельных прямых).

 

Равенство соответственных углов используется, в частности, для доказательства равенства треугольников и подобия треугольников.

 

www.treugolniki.ru