Центральный и вписанный угол, свойства
Центральный угол — это угол, вершина которого находится в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее.
На рисунке — центральные и вписанные углы, а также их важнейшие свойства.

Итак, величина центрального угла равна угловой величине дуги, на которую он опирается.
Значит, центральный угол величиной в градусов будет опираться на дугу, равную , то есть круга. Центральный угол, равный , опирается на дугу в градусов, то есть на шестую часть круга.
Величина вписанного угла в два раза меньше центрального, опирающегося на ту же дугу
Также для решения задач нам понадобится понятие «хорда».
Равные центральные углы опираются на равные хорды.
1. Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Вписанный угол, опирающийся на диаметр, — прямой.
Ответ: .
2. Центральный угол на больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
Пусть центральный угол равен , а вписанный угол, опирающийся на ту же дугу, равен .
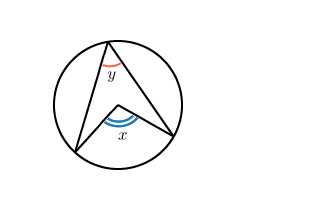
Мы знаем, что .
Отсюда ,
.
Ответ: .
Ты нашел то, что искал? Поделись с друзьями!
3. Радиус окружности равен . Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.
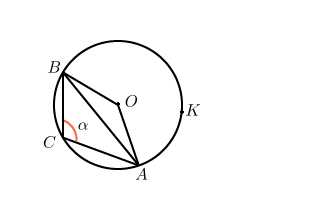
Пусть хорда равна . Тупой вписанный угол, опирающийся на эту хорду, обозначим .
Тогда дуга равна , а дуга равна .
Вписанный угол опирается на дугу и равен половине угловой величины этой дуги, то есть .
Ответ: .
4. Хорда делит окружность на две части, градусные величины которых относятся как . Под каким углом видна эта хорда из точки , принадлежащей меньшей дуге окружности? Ответ дайте в градусах.
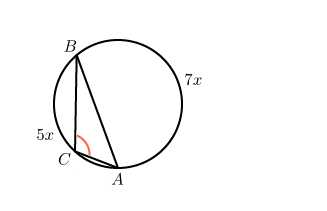
Главное в этой задаче — правильный чертеж и понимание условия. Как вы понимаете вопрос: «Под каким углом хорда видна из точки ?»
Представьте, что вы сидите в точке и вам необходимо видеть всё, что происходит на хорде . Так, как будто хорда — это экран в кинотеатре 🙂
Очевидно, что найти нужно угол .
Сумма двух дуг, на которые хорда делит окружность, равна , то есть
Величина вписанного угла равна половине угловой величины дуги, на которую он опирается, значит, угол равен .
Ответ: .
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Углы | Математика
Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.
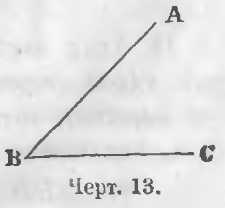
Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.
Стороны угла. Пересекающиеся линии называются сторонами угла.
Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.
Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.
На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.
Таким образом угол ABC есть угол B или
угол ABC = углу B.
Знак угла. Слово угол заменяют иногда знаком ∠.
Таким образом предыдущее равенство изображают письменно:
∠ABC = ∠B
В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.
На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.
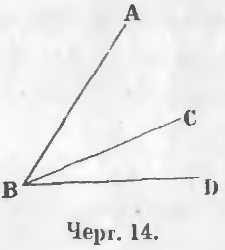
Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.
Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.
Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14
уг. ABD > уг. ABC и уг. CBD < уг. ABD.
Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой. При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.
a) Если линия ED совпадет с линией BA, углы называются равными
уг. ABC = уг. DEF.
b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF
уг. ABC > уг. DEF.
c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF
уг. ABC < уг. DEF.
Сложение, вычитание, умножение и деление углов. Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:
∠ABD = ∠ABC + ∠CBD (a)
Из равенства (а) вытекает равенство:
∠ABC = ∠ABD — ∠CBD
∠CBD = ∠ABD — ∠ABC,
т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.
Углы можно складывать и вычитать.
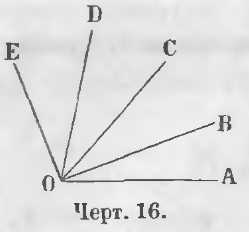
Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если
∠AOB = ∠BOC = ∠COD = ∠DOE,
то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,
∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.
Угол AOD равен трем углам AOB
AOD = 3AOB.
Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.
AOB = ½ AOC = 1/3 AOD = ¼ AOE.
Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число.
Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.
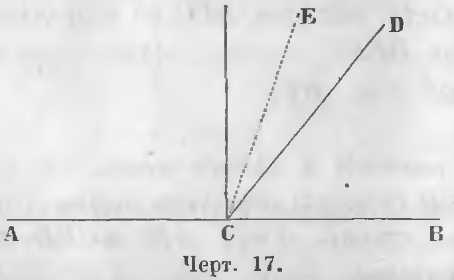
Смежные углы. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.
Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE. Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами.
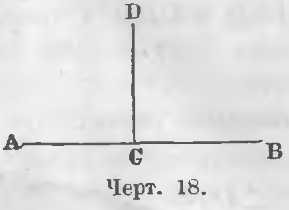
В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.
На чертеже 19 начерчен один прямой угол без другого смежного с ним.
Прямой угол есть один из равных смежных углов.
Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.
На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.
Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.
Подошва перпендикуляра. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.
Точка C (чер. 18) есть подошва перпендикуляра CD.
В каждой точке линии AB можно провести перпендикуляр к линии AB.Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр (черт. 18).
Наклонная линия. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.
На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.
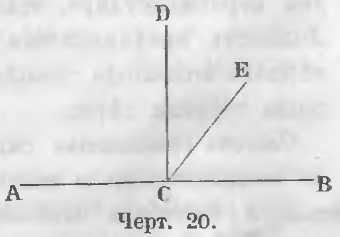
Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.
Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.
Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.
Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.
Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.
Дана прямая AB и на ней точка C (черт. 20).
Требуется доказать, что можно к ней восставить только один перпендикуляр.
Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра
уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.
Если приложить к первой части последнего неравенства угол ECD, получим неравенство
уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.
Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим
уг. DCA > уг. ACE,
неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.
Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.
Теорема 4. Все прямые углы равны.
Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.
Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.
Заключение. Прямой угол есть величина постоянная.
Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.
В таком случае
всякий острый угол < d,
всякий тупой угол > d.
Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.
Теорема 5. Сумма двух смежных углов равна двум прямым.
Даны смежные углы ACD и DCB (черт. 22).
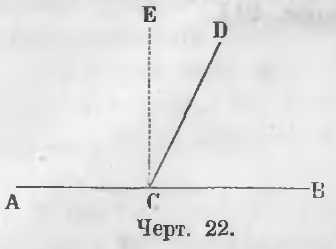
Требуется доказать, что ACD + DCB = 2d.
Доказательство. Из точки C восставим перпендикуляр CE, тогда
ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD
Сложив эти равенства, имеем:
ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).
Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.
Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.
Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.
Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).
ACD + DCB = 2d.
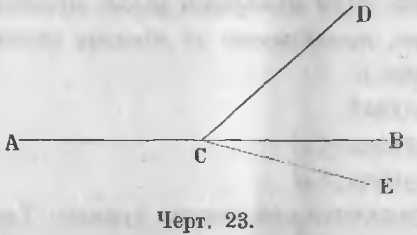
Требуется доказать, что ACB прямая линия.
Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда
ACD + DCE = 2d
Две величины равные одной и той же третьей равны (аксиома 3), следовательно
ACD + DCB = ACD + DCE
откуда выходит при сокращении
DCB = DCE
заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).
Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.
Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).
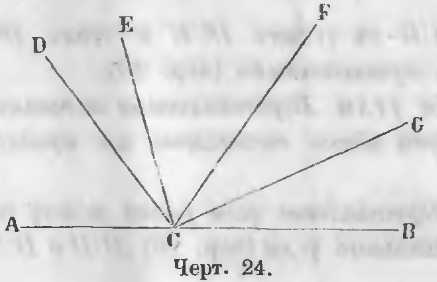
Требуется доказать, что
ACD + DCE + ECF + FCG + GCB = 2d.
Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).
ACF + FCB = 2d.
Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:
ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).
Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.
Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).
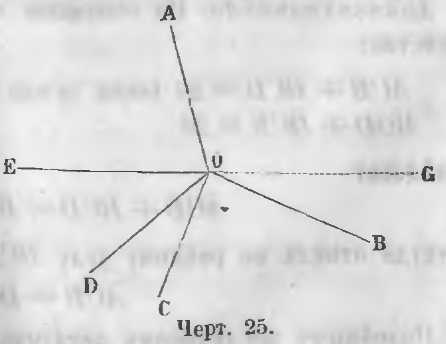
Требуется доказать, что
AOB + BOC + COD + DOE + EOA = 4d.
Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда
EOA + AOG = 2d.
Точно также
GOB + BOC + COD + DOE = 2d.
Сложив эти равенства, имеем:
EOA + AOG + GOB + BOC + COD + DOE = 4d.
Так как AOG + GOB = AOB, то
EOA + AOB + BOC + COD + DOE = 4d (ЧТД).
Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).
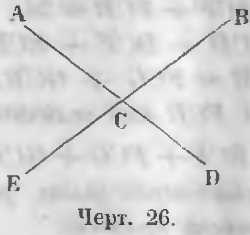
Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.
Теорема 9. Вертикальные углы равны между собой.
Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.
Требуется доказать, что ACB = DCE и BCD = ACE.
Доказательство. На основании теоремы 5 имеют место равенства:
ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d
следовательно,
ACB + BCD = BCD + DCE
откуда, отняв по равному углу BCD, находим
ACB = DCE.
Подобным же образом доказывают, что
∠BCD = ∠ACE.
Равносекущая (биссектриса) есть линия, делящая угол пополам.
На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.
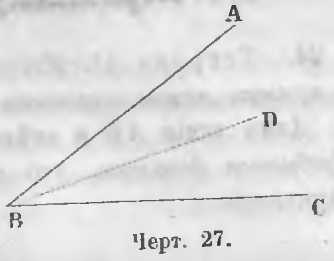
Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.
Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.
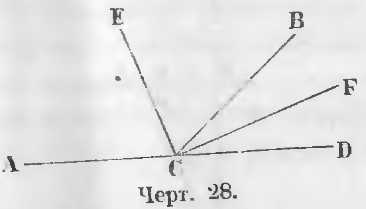
Требуется доказать, что EC ⊥ CF.
Доказательство. По условию
ECB = ½ ACB, BCF = ½ BCD
Сложив эти равенства, имеем:
ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).
Так как ACB + BCD = 2d, то
ECB + BCF = ½ · 2d = d.
Так как ECB + BCF = ECF, то
ECF = d
Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).
maths-public.ru
Определение угла | Треугольники
Что такое угол? Введём определение угла.
Определение.
Угол — это геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Например, вершина угла BAC — точка A, стороны — лучи AB и AC.
Знак угла — ∠ — представляет собой уменьшенное изображение угла.
Запись «∠ABC» читают как «угол ABC».
Угол можно назвать одной или тремя буквами. Если буква одна, то это — вершина угла. Если букв три, то вершина вершина должна стоять посередине, а по бокам — точки, лежащие на сторонах угла:
∠B или ∠ABC или ∠CBA.
Другой способ определить угол: по названию лучей — сторон угла.
∠(a; b) — угол, стороны которого — лучи a и b.
Обозначают угол дужкой.
Два угла называются равными, если они могут быть совмещены так, что совпадут их соответствующие стороны и вершины.
∠BAC=∠MNK.
Равные углы обозначают равным количеством дужек.
Единицы измерения углов — градусы и радианы.
1 градус (1º) равен 1/180 доле развёрнутого угла.
Градусную меру угла измеряют с помощью транспортира.
1 радиан — величина центрального угла, опирающегося на дугу окружности, равной её радиусу.
Наглядное представление об угле в 1 радиан можно получить, если отрезать кусок нити длиной, равной радиусу окружности, и приложить эту нить к окружности. Центральный угол, опирающийся на полученную дугу, — это и есть угол в один радиан:
∠ABC=1 радиану
1 радиан ≈ 57º, π радиан=180º.
Основные свойства измерения углов:
Каждый угол имеет определённую градусную меру, большую нуля.
Развёрнутый угол равен 180 градусам.
Градусная мера угла равна сумме градусных мер углов, на которые они разбиваются любым лучом, проходящим между его сторонами.
Иногда угол определяют как часть плоскости, заключённую между двумя лучами с общим началом.
В тех случаях, когда угол рассматривают как меру поворота луча вокруг его начала до заданного положения, величина угла может принимать любые значения, в зависимости от направления поворота как положительные, так и отрицательные.
www.treugolniki.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.
Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.
Рис.1
Изображенный на рисунке 1 угол можно обозначить тремя способами:
Углы называют равными углами, если их можно совместить.
Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.
Рис.2
Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.3). Точку B называют основанием перпендикуляра AB.
Рис.3
Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.
Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.
Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).
Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».
Таблица 1 – Типы углов в зависимости от величины в градусах
| Прямой угол |
Свойство: Прямой угол равен 90° |
| Острый угол |
Свойство: Острый угол меньше 90° |
| Тупой угол |
Свойство: Тупой угол больше 90°, но меньше 180° |
| Развернутый угол |
Свойство: Развернутый угол равен 180° |
| Угол больший, чем развернутый |
Свойство: Такой угол больше 180°, но меньше 360° |
| Полный угол |
Свойство: Полный угол равен 360° |
| Угол, равный нулю |
Свойство: Такой угол равен 0° |
Таблица 2 – Типы углов в зависимости расположения сторон
| Вертикальные углы |
Свойство вертикальных углов: Вертикальные углы равны |
| Смежные углы |
Свойство смежных углов: Сумма смежных углов равна 180° |
| Углы с соответственно параллельными сторонами |
Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно параллельными сторонами: Сумма углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой |
| Углы с соответственно перпендикулярными сторонами |
Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми |
Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой |
Определение. Биссектрисой угла называют луч, делящий угол пополам.
Задача. Доказать, что биссектрисы смежных углов перпендикулярны.
Решение. Рассмотрим рисунок 4.
Рис.4
На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку
2α + 2β = 180°.
то
α + β = 90°,
что и требовалось доказать.
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Определение центрального угла
Центральным углом называется угол с вершиной в центре окружности.
Центральный угол рассматривается вместе со своей внутренней областью – одной из двух частей, на которые стороны угла разбивают плоскость. Измеряется в пределах \([0^{\circ}; 360^{\circ}]\).
Определение градусной меры дуги окружности
Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла (т. е. центрального угла, который высекает эту дугу на окружности).
$$ \overset{\smile}{AB}=\angle AOB $$
Определение вписанного угла
Угол называется вписанным в окружность, если его вершина лежит на окружности, а стороны пересекают окружность. Говорят, что вписанный угол опирается на дугу, которую он вместе со своей внутренней областью высекает на окружности.
Вписанный угол \(ACB\) опирается на дугу \(AB\).
Теорема о вписанном угле
Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается, и равна половине градусной меры соответствующего этой дуге центрального угла.
$$ \alpha=\frac{1}{2}\beta=\frac{1}{2}\overset{\smile}{AB} $$
Угол, опирающийся на диаметр
Угол, вписанный в окружность, прямой, тогда и только тогда, когда он опирается на диаметр.
\( \angle{ACB}=90^{\circ} \Leftrightarrow \) \(AB\) – диаметр
Признак вписанного четырёхуольника
Если сумма противоположных углов четырёхугольника равна \(180^{\circ}\), то этот четырёхугольник вписанный.
\(\angle{A}+\angle{C}=180^{\circ} \Rightarrow ABCD\) – вписанный
Угол, образованный хордами
Градусная мера каждого из вертикальных углов, образованных двумя пересекающимися хордами, равна полусумме градусных мер дуг, которые эти углы высекают на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{CD}\right) $$
Угол, образованный касательной и хордой
Градусная мера угла, образованного касательной к окружности и хордой с концом в точке касания, равна половине градусной меры дуги окружности, заключённой внутри этого угла.
$$ \alpha=\frac{1}{2}\overset{\smile}{AB} $$
Угол с вершиной на окружности
Пусть вершина угла принадлежит окружности, а одна из его сторон и продолжение другой стороны пересекают окружность. Тогда градусная мера этого угла равна полусумме градусных мер дуг, которые он вместе с вертикальным ему углом высекают на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}+\overset{\smile}{BC}\right) $$
Угол с вершиной в круге
Градусная мера угла, вершина которого принадлежит кругу, равна полусумме градусных мер дуг, которые этот угол вместе с вертикальным ему высекает на окружности.
\( \alpha=\frac{1}{2} ( \)дуга\(_1\) + дуга\(_2 )\)
Угол, образованный секущими
Градусная мера угла, образованного двумя секущими к окружности, равна полуразности градусных мер дуг, которые он высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{CD}\right) $$
Угол, образованный касательными
Градусная мера угла, образованного двумя касательными к окружности, равна полуразности градусных мер дуг, на которые точки касания делят окружность.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{ACB}-\overset{\smile}{ADB}\right) $$
Угол, образованный касательной и секущей
Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$
Признак касания прямой и окружности
Градусная мера угла, образованного касательной и секущей к окружности, равна полуразности градусных мер дуг, которые этот угол высекает на окружности.
$$ \alpha=\frac{1}{2}\left(\overset{\smile}{AB}-\overset{\smile}{BC}\right) $$
Угол с вершиной вне круга
Если вершина угла лежит вне круга, а каждая сторона пересекает круг или касается его, то градусная мера этого угла равна полуразности градусных мер дуг, которые он высекает на окружности.
\( \alpha=\frac{1}{2} ( \)дуга\(_1\) – дуга\(_2 )\)
tmath.ru
Виды углов. Измерение углов
На каждом из рисунков 82, a − г изображены два луча. На каком из рисунков пара лучей образует угол, сторонами которого являются эти лучи?
Поскольку на рисунках 82, а − в начала лучей не совпадают, то они не могут служить сторонами угла. Лучи на рисунке 82, г образуют прямую. При этом начала лучей совпадают, а следовательно, они образуют угол. Такой угол называт развернутым.
Угол, стороны которого образуют прямую, нахывают развернутым.
Углы, как и отрезки, можно измерять. Напомним, что для измерения отрезков мы использовали единичный отрезок (1 мм, 1 см и т.п.).
Однако для измерения углов мы пока не имеем такого единичного угла.
Создать его можно, например, так. Разделим развернутый угол на 180 равных углов (рис. 83). Угол, образованный двумя соседними лучами, выбирают за единицу измерения. Его величину называют градусом (от лат. gradus − «шаг», «ступенька») и записывают 1°.
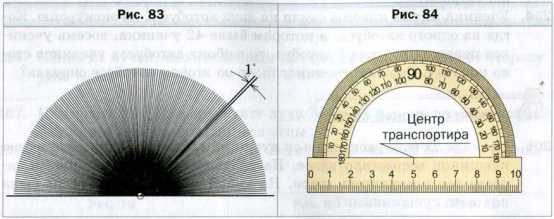
Измерить угол − значит подсчитать, сколько единичных углов в нем помещается.
Тогда величина или, как еще принято говорить, градусная мера развернутого угла равна 180°.
Для измерения углов используют специальный прибор − транспортир (рис. 84). Он состоит, как правило, из полукольца, соединенного с линейкой. Его шкала содержит 180 делений.
Чтобы измерить угол, совместим его вершину с центром транспортира таким образом, чтобы одна из сторон угла прошла по линейке (рис. 85).
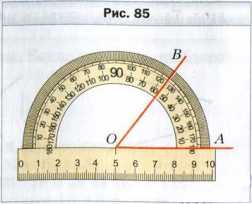
Тогда штрих на шкале, через который пройдет вторая сторона, укажет градусная (величину) этого угла.
Так, на рисунке 85 градусная мера угла AOB равна 55°. Пишут: ∠AOB = 55°. На рисунке 86 имеем: ∠MON = 134°.
Равные углы имеют равные градусные меры. Из двух неравных углов бОльшим будем считать тот, градусная мера которого больше. Например, из трех углов, изображенных на рисунке 87, ∠MON − наибольший. В этом легко убедиться, измерив углы транспортиром.
Величина угла обладает следующим свойством.
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC (рис. 88), т.е.
∠ABC = ∠ABD + ∠DBC.
Угол, градусная мера которого меньше 90°, называют острым (рис. 89, a).
Угол, градусная мера которого равна 90°, называют прямым (рис. 89, б).
На рисунке прямой угол обозначает так: ∟.
Угол, градусная мера которого больше 90°, но меньше 180° называют тупым (рис. 89, в).
Отметим, что биссектриса развернутого угла делит его на два угла, градусная мера каждого из которых равна 90°. Следовательно, биссектриса развернутого угла делит его на два прямых угла (рис. 90).
Пример 1. Дан луч OA. Постройте угол BOA, равный 72°.
Решение.
Совместим центр транспортира с точкой O так, чтобы луч OA прошел по линейке. Выберем на кольце транспортира штрих, который соответствует 72°. Возле этого штриха отметим точку B (рис. 91). Проведем луч OB. Угол BOA − искомый.
Если дан луч OA и построен угол BOA, то говорят, что от луча OA отложен угол BOA.
Пример 2. Из вершины угла ABC проведены два луча BK и BM так, что ∠ABK = 48°, ∠CBM = 72° (рис. 92).
Вычислите величину угла ABC, если ∠MBK = 16°.
Решение.
Имеем: ∠ABM = ∠ABK − ∠MBK, ∠ABM = 48° − 16° = 32°;
∠ABC = ∠ABM + ∠СBM, ∠ABC = 32° + 72° = 104°.
Ответ: 104°.
reshalka.com
Чему равен вписанный угол | Треугольники
Выясним, чему равен вписанный угол окружности и как его величина связана с величиной центрального угла.
Теорема
(О вписанном угле)
Вписанный угол равен половине соответствующего ему центрального угла.
Дано: окружность (O; R),
∠ABС — вписанный,
∠AOС — центральный.
Доказать:
Доказательство:
1) Рассмотрим частный случай, когда одна из сторон угла проходит через центр окружности.
В треугольнике AOB OA=OB (как радиусы). Значит, треугольник AOB — равнобедренный с основанием AB. Следовательно, у него углы при основании равны:∠ABO=∠BAO.
∠AOC — внешний угол треугольника AOB. Внешний угол равен сумме двух внутренних углов, не смежных с ним:
∠AOC=∠ABO+∠BAO=2∙∠ABO. Отсюда,
2) Если центр окружности лежит между сторонами угла.
Проведем из вершины вписанного угла ABC диаметр BF.
Аналогично, ∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и
∠FOC — внешний угол при вершине O равнобедренного треугольника BCO и
3) Если центр окружности лежит вне угла.
Проведем диаметр BF.
∠AOF — внешний угол при вершине O равнобедренного треугольника ABO и
∠СOF — внешний угол при вершине O равнобедренного треугольника BCO и
Что и требовалось доказать.
Замечание.
Дугу окружности можно измерять в градусах. Если центральный угол AOC меньше либо равен 180º, то градусная мера дуги AC равна градусной мере центрального угла AOC:
Если центральный угол AOC больше 180º, то градусная мера дуги AC равна 360º-∠AOC.
Таким образом, сумма градусных мер двух дуг окружности с общими концами равна 360º.
Другая формулировка теоремы о вписанном угле:
Вписанный угол измеряется половиной дуги, на которую он опирается.
www.treugolniki.ru
