угол — Толковый словарь Ушакова
’УГОЛ, угла, об угле, на (в) углу и (мат.) в угле, ·муж.
1. Часть плоскости между двумя прямыми линиями, исходящими из одной точки (мат.). Вершина угла. Стороны угла. Измерение угла градусами. Прямой угол. (90°). Острый угол (менее 90°). Тупой угол (более 90°). Двугранный угол (образованный двумя плоскостями). Многогранный или телесный угол (образованный несколькими плоскостями). В этом угле 30°.
2. Такая фигура как мера для измерения чего-нибудь (спец.). Угол рассеяния света. Угол падения равен углу отражения. Угол прицела. Угол склонения. Угол дрейфа судна. Угол зрения.
3. Место, где сходятся две внешние стороны предмета. Угол стола. Угол дома. Завернуть за угол.
| место пересечения двух улиц. На углу улицы и переулка. Милицейский пост на углу. Выйти на угол. Стоять на углу.
4. Место, где сходятся две внутренние стороны предмета. «Сел в угол и стал смотреть в книгу.» Гончаров. «Старик тыкнул пальцем в другой угол комнаты.» Гоголь. «Мой волк сидит, прижавшись в угол задом.» Крылов. Поставить стол в угол. Стол стоит в углу.
5. Часть комнаты, сдаваемая в наем. «Он сторговал первый встречный угол и через час переехал.» Достоевский. Сдавать углы.
6. Вообще — место, помещение. «Хозяйка! Нет ли в избе другого угла?» Пушкин. «Собеседники, минуя спавшего в передней казачка, разбрелись по своим углам.» А.Тургенев. Искать по всем углам.
| перен. Приют, пристанище, место, где жить. — Он мне угол даст. «Назябся уж я, наголодался.» А.Островский. «Иметь дома свой стол, чай, словом, свой угол — un chez-soi, как говорят французы.» Гончаров. Иметь свой угол. Нет своего угла.
| перен. Местность, обычно отдаленная. «Назови мне такую обитель, я такого угла не видал…» Некрасов. Медвежий угол. (см.
медвежий). Жить в глухом углу.7. В карточных играх — четверть ставки, при объявлении которой *****
Источник: Толковый словарь русского языка Ушакова на Gufo.megufo.me
Угол — это… Что такое Угол?
(мат.). — Если из точки О на данной плоскости проведем прямые ОА и 0В, то получим угол АОВ (черт. 1).
Черт. 1.
Точка 0 наз. вершиною угла, а прямые ОА и 0В сторонами угла.
Предположим, что даны два угла ΒΟΑ и Β1Ο1Α1. Наложим их так, чтобы вершины О и 01 совпали и чтобы сторона O1A1 совпала со стороной ОА. Если при этом сторона О1В
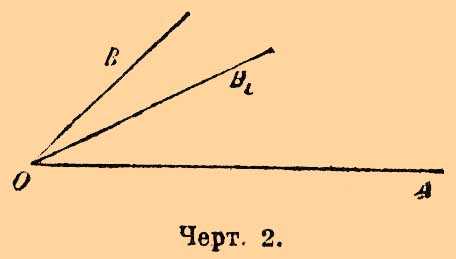
Черт. 2.
Если сторона О1В1 пойдет внутри угла BOA (черт. 2), то угол АОВ больше угла В1О1А1. Если же чертеж имеет вид (черт. 3), то угол АОВ меньше угла А1О1В1.
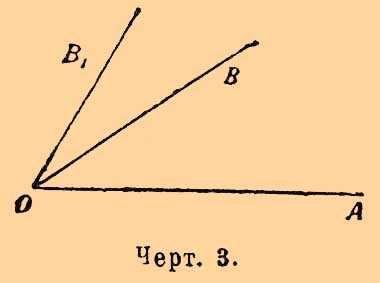
Черт. 3.
Два угла, имеющие общую вершину и общую сторону, наз. прилежащими, таковы, напр., углы АОВ и BOC (черт. 4).
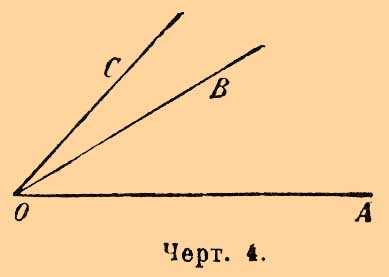
Черт. 4.
Стороны ОА и ОС наз. внешними сторонами прилежащих углов.
Смежными углами наз. такие прилежащие углы, внешние стороны которых составляют одну прямую (черт.
5).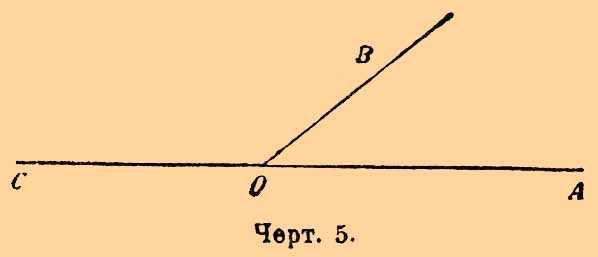
Черт. 5.
Угол наз. прямым, если он равен углу смежному из ним (черт. 6).
Говорят, что прямая ОВ (черт. 6) перпендикулярна к прямой СА, если она образует равные смежные углы АОВ и СОВ.
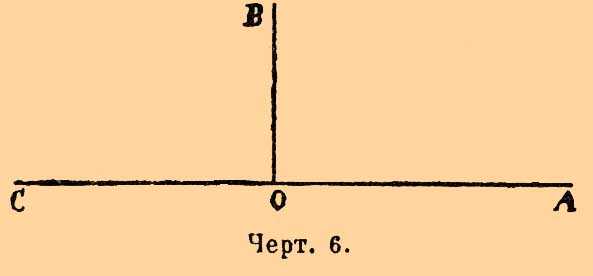
Черт. 6.
Все прямые углы равны между собой. Угол больший прямого наз. тупым, а меньший прямого — острым. Если построим два прилежащих угла так, чтобы один из них равнялся углу АОВ, а другой углу А1О1В1, то внешние стороны этих прилежащих углов образуют угол равный сумме углов АОВ и Α1Ο
Сумма смежных углов равна двум прямым.
Если из точки О на плоскости проведем несколько лучей, напр. ОА, ОВ, ОС, OD и OE (черт. 7), то получим углы ВОА, ВОС, COD, DOE и ЕОА, сумма которых равна четырем прямым.
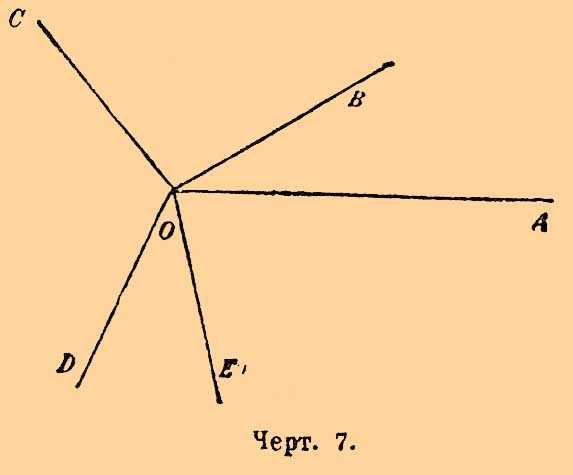
Черт. 7.
Две пересекающиеся прямые AB и CD (черт. 8) образуют четыре угла a, b, с, d.
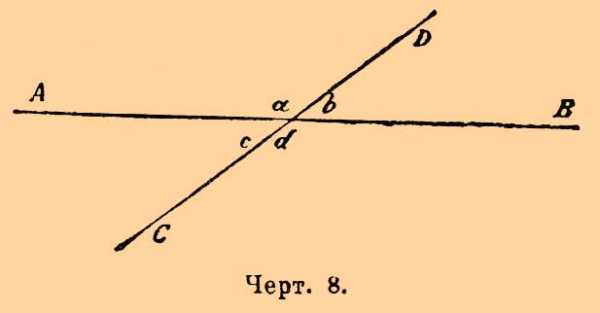
Черт. 8.
Из них а и b смежные; углы же а и d или же b и с наз. вертикальными. Существуют равенства:
а = d и b = с.
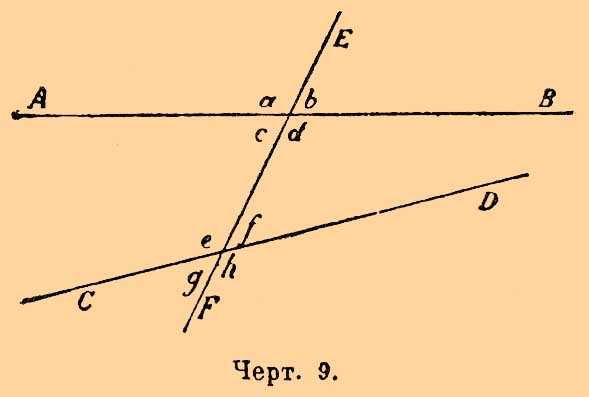
Черт. 9.
Углы, образованные двумя прямыми AB и CD при пересечении третьей прямою EF
(черт. 9) имеют особые названия.Такие углы, как а и е, называются соответственными
Такие углы, как с и f, называются внутренними накрест лежащими
Такие углы, как a и h, называются внешними накрест лежащими
Такие углы, как c и e, называются внутренними односторонними
Такие углы, как a и g, называются внешними односторонними.
Для того чтобы прямые AB и CD были параллельны, необходимо и достаточно, чтобы имело место одно из равенств вида
a = е, с = f, a = h, с + е = двум прямым, а + g = двум прямым.
Представим себе круг, в центре которого О находится вершина угла. Если стороны угла проходит через точки А и B, лежащие на окружности, то угол А ОВ измеряется дугою AB. Мерою угла служит отвлеченное число, равное отношению дуги
Угол, вершина которого находится в центре круга, наз. центральным. Если же вершина угла находится на окружности в точке А, а стороны проходят через точки В и С, лежащие на окружности, то угол ВАС называется вписанным. Этот угол измеряется половиною дуги ВС. Если же вершина угла находится вне круга, а стороны AB и АС касаются круга в точках В и С, то угол называется описанным. Он измеряется полуразностью дуг, заключенных между его сторонами.
Две прямые на плоскости или пересекаются, или параллельны. В пространстве прямые могут не пересекаться и в то же время не быть параллельными. Предположим, что прямые а и b не пересекаются и не параллельны. Углом между этими прямыми назыв. тот угол, который получим, проведя из какой-нибудь точки пространства О прямые ОА и ОВ, параллельные прямым а и b.
Предположим, что прямая AB пересекает плоскость P в точке А (черт. 10).
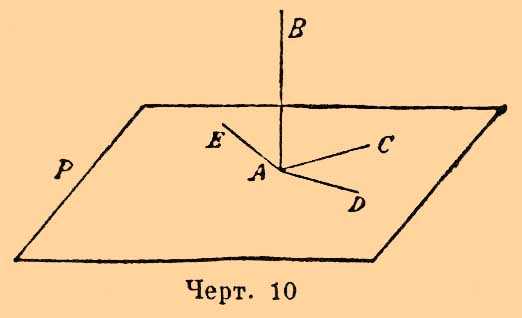
Черт. 10.
Если окажется, что две прямые АС и AD, проведенные на плоскости P через точку А, перпендикулярны к AB, то и всякая прямая АЕ, находящаяся в плоскости Р, будет перпендикулярна к AB. В этом случае говорят, что прямая AB перпендикулярна к плоскости Р.
Две пересекающиеся плоскости образуют двугранный угол. Линия пересечения этих плоскостей назыв. ребром двугранного угла; плоскости, образующие угол, назыв. сторонами угла.
Предположим, что плоскости АР и BQ
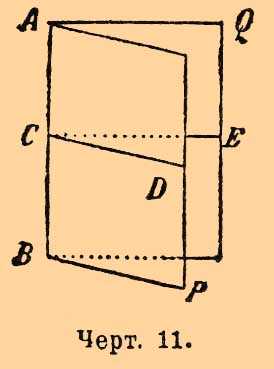
Черт. 11.
Возьмем на ребре AB какую-нибудь точку С и проведем в плоскостях АР и BQ прямые CD и СЕ, перпендикулярные к AB. Получим угол ECD, который назыв. линейным углом двугранного угла QABP.
Двугранный угол измеряется соответствующим ему линейным У. Если угол ECD (черт. 11) прямой, то и двугранный У. прямой. В этом случае говорят, что плоскость АР перпендикулярна к плоскости BQ.
Если прямая AB перпендикулярна к плоскости P (черт. 10), то всякая плоскость, проходящая через AB, будет перпендикулярна к плоскости Р.
Предположим, что дана плоскость P и прямая AB (черт. 12).
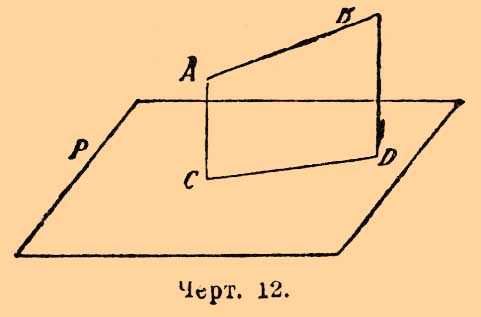
Черт. 12.
Проведем через AB плоскость, перпендикулярную к Р. Пусть эти плоскости пересекаются по прямой CD. Углом прямой AB с плоскостью P назыв. угол, образованный прямыми AB и CD.
Несколько плоскостей, проходящих через точку О и пересекающихся по прямым О А, 0В, ОС, OD и ОЕ, образуют многогранный угол, точка О назыв. вершиной, плоскости BOA, COB, DOC, EOD и ЕОА — гранями, прямые ОА, ОВ, ОС, OD и ОЕ — ребрами, углы BOA, COB, DOC, EOD и ЕОА — плоскими углами многогранного угла.
Многогранный угол назыв. выпуклым, если он весь расположен по одну сторону каждой из его граней.
В трехгранном угле каждый плоский угол меньше суммы двух других плоских углов. Сумма плоских углов выпуклого многогранного угла меньше 4-х прямых.
Д. С.
Углы | Математика
Две прямые линии BA и BC (черт. 13), пересекающиеся в одной и той же точке B, образуют при точке B угол.
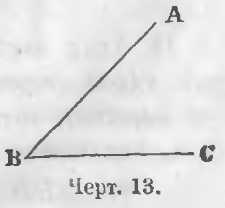
Определение угла. Углом называется неопределенная часть плоскости, ограниченная двумя пересекающимися прямыми линиями. Угол есть величина, определяющая наклонение одной прямой линии к другой.
Стороны угла. Пересекающиеся линии называются сторонами угла.
Вершина угла. Точка пересечения двух прямых называется вершиной угла. Величина угла не зависит от длины сторон, поэтому стороны угла можно неопределенно продолжать.
Название угла. a) Углы называют буквой, стоящей при вершине; так угол на черт. 13 называют углом B. b) Если при вершине несколько углов, то углы называют тремя буквами, стоящими при вершине и двух его сторонах. При этом буква при вершине произносится и пишется в середине.
На черт. 13 угол B называют угол ABC. Линии BA и BC — две стороны, а точка B — вершина угла.
Таким образом угол ABC есть угол B или
угол ABC = углу B.
Знак угла. Слово угол заменяют иногда знаком ∠.
Таким образом предыдущее равенство изображают письменно:
∠ABC = ∠B
В том случае, когда из точки выходит несколько линий, при точке B имеется несколько углов.
На черт. 14 из точки B выходят прямые линии BA, BC, BD и при вершине B имеются углы ABC, CBD, ABD.
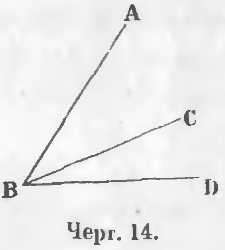
Прилежащие углы. Два угла называются прилежащими, когда они имеют общею вершину, по одной общей стороне, а две другие лежат по обе стороны общей стороны.
Углы ABC и CBD (черт. 14) суть прилежащие углы. Они имеют общую вершину B, общую сторону BC, а две другие стороны BA и BD лежат одна сверху, а другая снизу общей стороны BC.
Углы изменяют свою величину, если изменяется наклонение одной стороны к другой. Из двух углов, имеющих общую вершину, тот угол, внутри которого помещается другой угол, называется большим углом. На чертеже 14
уг. ABD > уг. ABC и уг. CBD < уг. ABD.
Чтобы иметь понятие о взаимной величине двух углов, имеющих разные вершины, накладывают один угол на другой. При наложении совмещают их вершины и по одной стороне, тогда направление другой стороны даст возможность сравнивать их величину. Чтобы сравнить два угла ABC и DEF (черт. 15), накладывают угол DEF на угол ABC так, чтобы сторона EF пошла по стороне BC, точка E совмещалась с точкой B; тогда сторона ED может занять три положения: она может совпасть со стороной BA, упасть внутри и вне угла ABC.
a) Если линия ED совпадет с линией BA, углы называются равными
уг. ABC = уг. DEF.
b) Если линия ED упадет внутри угла ABC и займет положение BG, угол ABC будет больше угла DEF
уг. ABC > уг. DEF.
c) Если же линия ED упадет вне угла ABC по направлению BH, угол ABC меньше угла DEF
уг. ABC < уг. DEF.
Сложение, вычитание, умножение и деление углов. Два прилежащих угла ABC и CBD (чер. 14) образуют один угол ABC. Угол ABD называется суммой углов ABC и CBD. Это выражают письменно равенством:
∠ABD = ∠ABC + ∠CBD (a)
Из равенства (а) вытекает равенство:
∠ABC = ∠ABD — ∠CBD
∠CBD = ∠ABD — ∠ABC,
т. е. угол ABC есть разность углов ABD и CBD, и угол CBD есть разность углов ABD и ABC.
Углы можно складывать и вычитать.
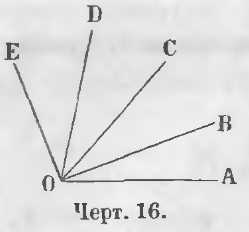
Если при точке O (черт. 16) находится несколько равных прилежащих углов, т. е. если
∠AOB = ∠BOC = ∠COD = ∠DOE,
то угол AOC, равный сумме углов AOB и BOC равен двум углам AOB,
∠AOC = ∠AOB + ∠BOC, след. ∠AOC = 2AOB.
Угол AOD равен трем углам AOB
AOD = 3AOB.
Обратно, угол AOB составляет половину угла AOC, треть угла AOD, четверть угла AOE.
AOB = ½ AOC = 1/3 AOD = ¼ AOE.
Отсюда выводим, что углы как величины можно не только складывать и вычитать, но также умножать и делить на отвлеченное число.
Если из двух прилежащих углов ACD и DCB (чер. 17) две стороны CA и CB лежат на одной прямой, их называют смежными.
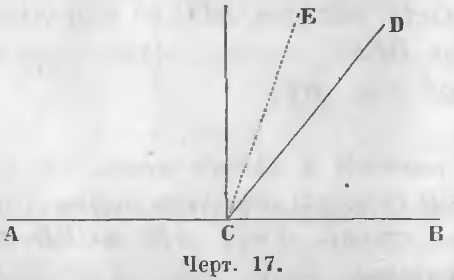
Смежные углы. Смежными называются такие углы, у которых одна сторона общая, а две другие лежат на одной прямой.
Если линия CD, поворачиваясь около точки C, займет положение CE, то угол ACD уменьшаясь обратится в угол ACE, а угол BCD увеличиваясь обратится в угол BCE. Линия CD, продолжая поворачиваться, может принять такое положение, что два смежных угла сделаются равными. Когда два смежных угла ACD и DCB равны (чер. 18), их называют прямыми углами.
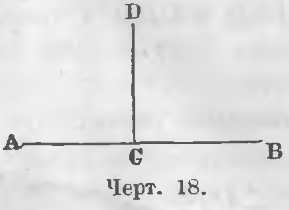
В этом случае линия CD называется перпендикулярной к линии AB или просто перпендикуляром к линии AB.
На чертеже 19 начерчен один прямой угол без другого смежного с ним.
Прямой угол есть один из равных смежных углов.
Перпендикуляр есть прямая линия, образующая с другой линией прямой угол.
На чертеже 18 углы ACD и DCB, оставаясь смежными и равными, получают название прямых углов. Линия DC будет перпендикулярной к линии AB. Такое взаимное отношение двух линий выражают иногда письменно: CD ⊥ AB.
Так как линия AB будет также перпендикулярна к линии CD, то линия AB и CD будут взаимно-перпендикулярны, т. е. если CD ⊥ AB, то и AB ⊥ CD.
Подошва перпендикуляра. Точка взаимной встречи двух перпендикулярных линий называется подошвою перпендикуляра.
Точка C (чер. 18) есть подошва перпендикуляра CD.
В каждой точке линии AB можно провести перпендикуляр к линии AB.
Провести перпендикуляр к линии (AB) из точки, лежащей на линии, значит восставить перпендикуляр. Провести же перпендикуляр (DC) к линии (AB) из точки (D), лежащей вне прямой, значит опустить перпендикуляр (черт. 18).
Наклонная линия. Всякая линия неперпендикулярная к другой называется линией наклонною к ней.
На чертеже 20 линия CE будет наклона к линии AB, а линия CD перпендикулярна к линии AB.
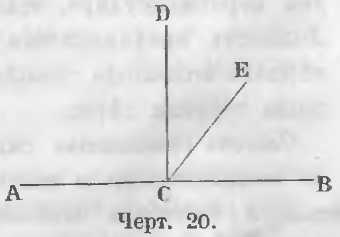
Угол ECB меньше прямого, а угол ACE больше прямого. Угол ECB называется острым, а угол ACE тупым.
Острый угол есть всякий угол меньше прямого, а тупой угол есть угол больший прямого.
Одноименные и разноименные углы. Два острых или два тупых угла называются одноименными, а два угла, из которых один острый, а другой тупой, называются разноименными.
Наклонная линия CE образует (черт. 20) с прямою AB два смежных угла, из которых один меньше, а другой больше прямого, т. е. один острый, а другой тупой.
Теорема 3. Из точки, взятой на прямой линии, можно восставить к ней только один перпендикуляр.
Дана прямая AB и на ней точка C (черт. 20).
Требуется доказать, что можно к ней восставить только один перпендикуляр.
Доказательство. Положим, что можно из точки C к линии AB восставить два перпендикуляра (черт. 20) CD и CE. По свойству перпендикуляра
уг. DCB = уг. ACD (a)
уг. BCE = уг. ACE.
Если приложить к первой части последнего неравенства угол ECD, получим неравенство
уг. BCE + уг. ECD > уг. ACE, или уг. BCD > уг. ACE.
Заменяя в этом неравенстве уг. BCD равным ему углом ACD (a), получим
уг. DCA > уг. ACE,
неравенство очевидно нелепое, ибо часть не может быть более своего целого, следовательно предположение, что можно восставить два перпендикуляра, ведет к нелепости, поэтому оно ложно. Ложность предположения основана на том соображении, что из верного положения нельзя вывести неверного заключения, следовательно, наша теорема верна.
Способ доказывать справедливость данной теоремы указанием на невозможность и нелепость всякого другого предположения называется способом доказательства от противного или способом приведения к нелепости.
Теорема 4. Все прямые углы равны.
Предположим, мы имеем две пары прямых углов: одну пару составляют углы ACD и DCB, а другую углы EGH и HGF, следовательно, CD ⊥ AB и HG ⊥ EF (черт. 21).

Требуется доказать, что прямые углы равны.
Доказательство. Наложим линию EF на линию AB точкой G на точку C, тогда линия GH пойдет по линии CD, ибо из точки C можно восставить только один перпендикуляр, следовательно, прямой угол DCB = прямому углу HGF.
Заключение. Прямой угол есть величина постоянная.
Мера углов. При измерении углов прямой угол, как величину постоянную, принимают за единицу сравнения. Величину его обозначают буквою d.
В таком случае
всякий острый угол < d,
всякий тупой угол > d.
Все углы выражаются при помощи прямого. Так, например, говорят: данный угол равен ½ d, 2/3 d и т. д.
Теорема 5. Сумма двух смежных углов равна двум прямым.
Даны смежные углы ACD и DCB (черт. 22).
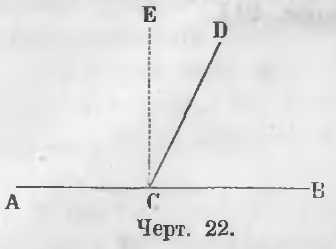
Требуется доказать, что ACD + DCB = 2d.
Доказательство. Из точки C восставим перпендикуляр CE, тогда
ACD = ACE + ECD = d + ECD
DCB = ECB — ECD = d — ECD
Сложив эти равенства, имеем:
ACD + DCB = ACE + ECB = 2d (что и требовалось доказать).
Два смежных угла пополняют один другой до двух прямых и потому называются углами дополнительными.
Из теоремы 5 вытекает следствие. Одна пара смежных углов равна другой паре смежных углов.
Теорема 6 (обратная теореме 5). Если сумма двух прилежащих углов равна двум прямым, то две другие стороны лежат на одной прямой.
Пусть сумма двух прилежащих углов ACD и DCB равна двум прямым (черт. 23).
ACD + DCB = 2d.
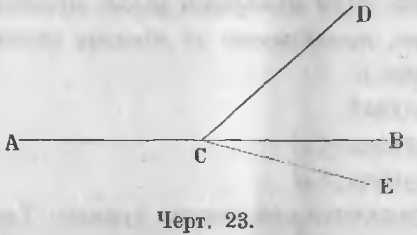
Требуется доказать, что ACB прямая линия.
Доказательство. Допустим, что ACB есть ломаная линия и что продолжение линии AC будет линия CE, тогда
ACD + DCE = 2d
Две величины равные одной и той же третьей равны (аксиома 3), следовательно
ACD + DCB = ACD + DCE
откуда выходит при сокращении
DCB = DCE
заключение нелепое (часть равна целому, см. акс. 1), следовательно линия ACB есть прямая линия (что и требовалось доказать).
Теорема 7. Сумма углов, имеющих вершину в одной точке и расположенных по одну сторону прямой линии, равна двум прямым.
Даны углы ACD, DCE, ECF, FCG, GCB, имеющие общую вершину в точке C и расположенные по одну сторону прямой AB (черт. 24).
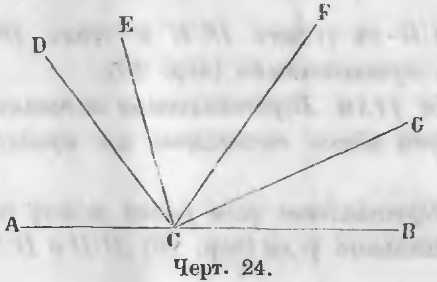
Требуется доказать, что
ACD + DCE + ECF + FCG + GCB = 2d.
Доказательство. МЫ знаем, что сумма двух смежных углов ACF и FCB равна двум прямым (т. 5).
ACF + FCB = 2d.
Так как ACF = ACD + DCE + ECF и FCB = FCG + GCB, то заменяя углы ACF и FCB их величинами, находим:
ACD + DCE + ECF + FCG + GCB = 2d (что и требовалось доказать).
Теорема 8. Сумма всех углов, расположенных вокруг одной точки, равна четырем прямым.
Даны углы AOB, BOC, COD, DOE, EOA, имеющие общую вершину O и расположенные вокруг точки O (черт. 25).
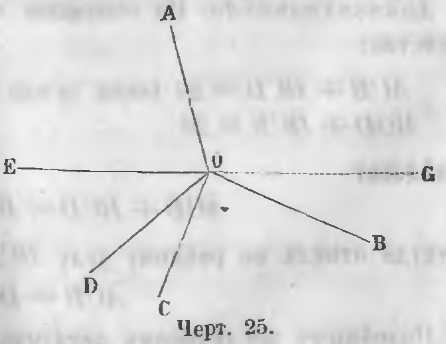
Требуется доказать, что
AOB + BOC + COD + DOE + EOA = 4d.
Доказательство. Продолжим сторону EO по направлению OG (чер. 25), тогда
EOA + AOG = 2d.
Точно также
GOB + BOC + COD + DOE = 2d.
Сложив эти равенства, имеем:
EOA + AOG + GOB + BOC + COD + DOE = 4d.
Так как AOG + GOB = AOB, то
EOA + AOB + BOC + COD + DOE = 4d (ЧТД).
Угол ACB с углом DCE и угол BCD с углом ACE называются вертикальными (чер. 26).
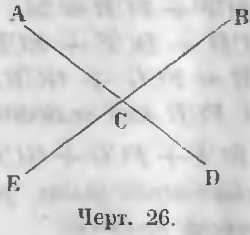
Вертикальные углы. Вертикальными называются такие углы, у которых стороны одного составлены из продолжения сторон другого угла.
Теорема 9. Вертикальные углы равны между собой.
Даны вертикальные углы (чер. 26) ACB и DCE, точно также BCD и ACE.
Требуется доказать, что ACB = DCE и BCD = ACE.
Доказательство. На основании теоремы 5 имеют место равенства:
ACB + BCD = 2d (как сумма двух смежных углов)
BCD + DCE = 2d
следовательно,
ACB + BCD = BCD + DCE
откуда, отняв по равному углу BCD, находим
ACB = DCE.
Подобным же образом доказывают, что
∠BCD = ∠ACE.
Равносекущая (биссектриса) есть линия, делящая угол пополам.
На чертеже 27 BD есть биссектриса, если ∠ABD = ∠DBC.
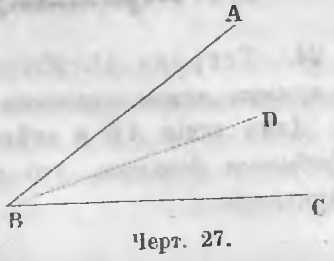
Теорема 10. Биссектрисы двух смежных углов взаимно перпендикулярны.
Даны смежные углы ACB и BCD (чер. 28). Их биссектрисы линии CF и CE делят смежные углы BCD и BCA пополам, следовательно BCF = FCD, ACE = ECB.
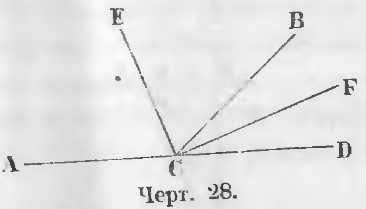
Требуется доказать, что EC ⊥ CF.
Доказательство. По условию
ECB = ½ ACB, BCF = ½ BCD
Сложив эти равенства, имеем:
ECB + BCF = ½ ACB + ½ BCD = ½ (ACB + BCD).
Так как ACB + BCD = 2d, то
ECB + BCF = ½ · 2d = d.
Так как ECB + BCF = ECF, то
ECF = d
Угол ECF прямой, т. е. линии CE и CF взаимно перпендикулярны (ЧТД).
maths-public.ru
угол — это… Что такое угол?
уголёк — угол/ёк/ … Морфемно-орфографический словарь
УГОЛ — муж. перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. Угол линейный, всякие две встречные черты и промежуток их; угол плоскостной или в плоскостях, встреча двух плоскостей или стен; угол толстый, теловой, встреча в одной … Толковый словарь Даля
УГОЛ — угла, об угле, на (в) углу и (мат.) в угле, м. 1. Часть плоскости между двумя прямыми линиями, исходящими из одной точки (мат.). Вершина угла. Стороны угла. Измерение угла градусами. Прямой угол. (90°). Острый угол. (менее 90°). Тупой угол.… … Толковый словарь Ушакова
УГОЛ — (1) атаки угол между направлением воздушного потока, набегающего на крыло самолёта, и хордой сечения крыла. От этого угла зависит значение подъёмной силы. Угол, при котором подъёмная сила максимальна, называется критическим углом атаки. У… … Большая политехническая энциклопедия
УГОЛ — (плоский) геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла). Всякий угол с вершиной в центре некоторой окружности (центральный угол) определяет на окружности дугу АВ, ограниченную точками… … Большой Энциклопедический словарь
угол — глава угла, из за угла, медвежий угол, непочатый угол, по всем углам.. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. угол вершина, угловая точка; пеленг, пристанище, девятина, румб,… … Словарь синонимов
угол — угол, род. угла; предл. об угле, в (на) углу и в речи математиков в угле; мн. углы, род. углов. В предложных и устойчивых сочетаниях: за угол и допустимо за угол (зайти, завернуть и т. п.), с угла на угол (двигаться, располагаться и т. п.), угол… … Словарь трудностей произношения и ударения в современном русском языке
УГОЛ — УГОЛ, угла, об угле, на (в) углу, муж. 1. (в угле.). В геометрии: плоская фигура, образованная двумя лучами (в 3 знач.), исходящими из одной точки. Вершина угла. Прямой у. (90°). Острый у. (меньше 90°). Тупой у. (более 90°). Внешние и внутренние… … Толковый словарь Ожегова
угол — УГОЛ , угла, м. Четверть ставки, при объявлении которой загибается край карты. ◘ Туз и дама пик с углом // Убиты. А .И.Полежаев. День в Москве, 1832. ◘ После обеда рассыпает он червонцы на стол, тасует карты; понтёры трещат колодами,… … Карточная терминология и жаргон XIX века
угол ψ — угол ψ Угол между лучом и плоскостью YOZ. Примечание Угол отсчитывают от плоскости к лучу. [ГОСТ 7427 76] Тематики оптика, оптические приборы и измерения … Справочник технического переводчика
УГОЛ — УГОЛ, мера наклона между двумя прямыми линиями или плоскостями, а также величины вращательного движения. Полный круг делится на 360° (градусов) иди на 2p радиан. Прямой угол составляет 90° или p/2 радиан. Один градус подразделяется на 60 (минут) … Научно-технический энциклопедический словарь
noun_ru.academic.ru
Ответы@Mail.Ru: Что такое угол?
Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки. <img src=»//otvet.imgsmail.ru/download/875a8375f91de049494d6073098e8a2f_270d48d30e55a499e24fdc8033357e3d.jpg»> В зависимости от величины угла их разделяют на следующие виды: Острый угол. Имеет величину от 0 до 90 градусов. Угол равный 90 градусов — прямой. Тупой угол имеет величину 90 и 180 Развернутый угол. Он равен 180 градусам. Если величина угла менее 360, но более 180, такой угол называют невыпуклым. Полный угол равен 360 градусам. Углы не равные 90 и 180 градусам называют косыми. Если углы называют равными, значит, они имеют одинаковую величину. . <img src=»//otvet.imgsmail.ru/download/875a8375f91de049494d6073098e8a2f_0313d46c993310e2a7cbbc77a72c2381.jpg» data-lsrc=»//otvet.imgsmail.ru/download/u_b4d1ca819d0126a63e828efe79b1cb0b_120x120.jpg» data-big=»1″>
Что, никогда в детстве не ставили?
Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла). Плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется плоским углом (или просто углом, если это не вызывает разночтений). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним. Точки плоского угла, не принадлежащие его сторонам, образуют внутреннюю область плоского угла. В другом, эквивалентном варианте определения плоским углом называется часть плоскости, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую лежащую в этой плоскости линию (которая называется линией, стягивающей данный плоский угол). Часто для краткости углом называют также угловую меру, то есть число, определяющее величину угла. Кроме наиболее часто встречающихся плоских углов, в качестве углов могут рассматриваться и более общие объекты — фигуры, образованные пересекающимися дугами, полуплоскостями и другими фигурами как в евклидовой, так и в других типах геометрии в метрических пространствах различной размерности.
Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки.
Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки.
фигура образованная двумя разными лучами
Угол это он <img src=»//otvet.imgsmail.ru/download/247160789_4bba5ff1b7972b458bacd9d2e0a67668_120x120.jpg» data-hsrc=»//otvet.imgsmail.ru/download/247160789_4bba5ff1b7972b458bacd9d2e0a67668_800.jpg»><img src=»//otvet.imgsmail.ru/download/247160789_eeebbad4ca43bf999ce347d3dee91a73_120x120.jpg» data-hsrc=»//otvet.imgsmail.ru/download/247160789_eeebbad4ca43bf999ce347d3dee91a73_800.jpg»>
touch.otvet.mail.ru
