Как перемножить матрицы в Excel

Одной из частых операций, которую выполняют при работе с матрицами, является перемножение одной из них на другую. Программа Excel является мощным табличным процессором, который предназначен, в том числе и для работы над матрицами. Поэтому у него имеются инструменты, которые позволяют перемножить их между собой. Давайте узнаем, как это можно выполнить различными способами.
Процедура перемножения матриц
Сразу нужно сказать, что перемножить между собой можно далеко не все матрицы, а только те, которые соответствуют определенному условию: число столбцов одной матрицы должно быть равным числу строк другой и наоборот. Кроме того, исключается наличие в составе матриц пустых элементов. В этом случае тоже выполнить требуемую операцию не получится.
Способов перемножить матрицы в Экселе все-таки не так уж и много — всего два. И оба они связаны с применением встроенных функций Excel. Разберем в деталях каждый из данных вариантов.
Способ 1: функция МУМНОЖ
Наиболее простым и популярным вариантом среди пользователей является применение функции МУМНОЖ. Оператор МУМНОЖ относится к математической группе функций. Как раз его непосредственной задачей и является нахождение произведения двух матричных массивов. Синтаксис МУМНОЖ имеет такой вид:
=МУМНОЖ(массив1;массив2)
Таким образом этот оператор имеет два аргумента, которые представляют собой ссылки на диапазоны двух перемножаемых матриц.
Теперь давайте посмотрим, как используется функция МУМНОЖ на конкретном примере. Имеется две матрицы, число строк одной из которых, соответствует количеству столбцов в другой и наоборот. Нам нужно перемножить два этих элемента.
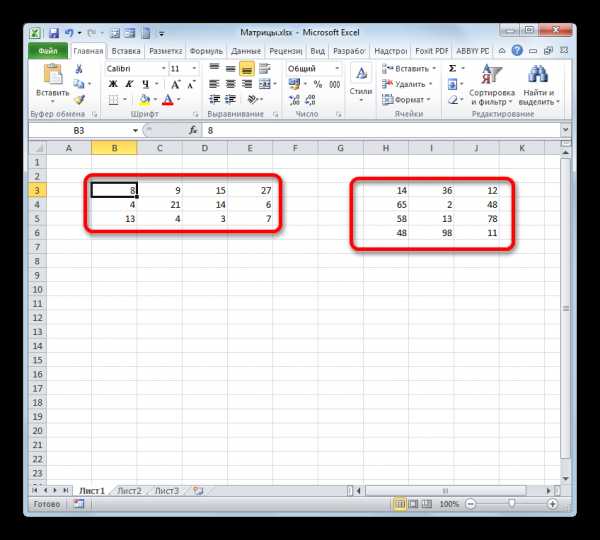
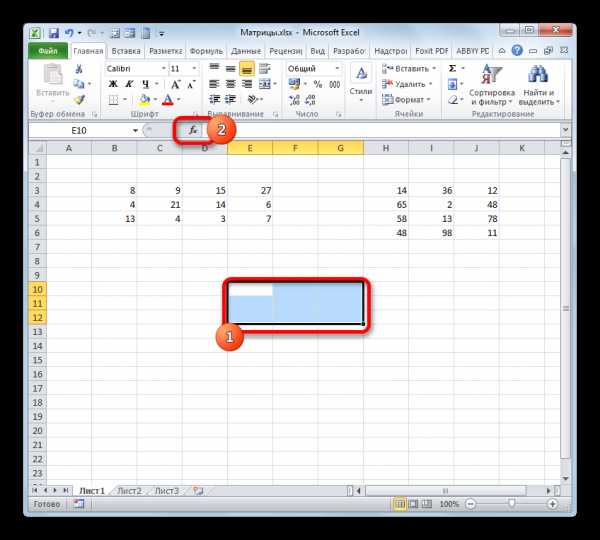
- Выделяем диапазон, где будет отображаться результат умножения, начиная с его верхней левой ячейки. Размер данного диапазона должен соответствовать числу строк у первой матрицы и числу столбцов у второй. Клацаем по пиктограмме «Вставить функцию».
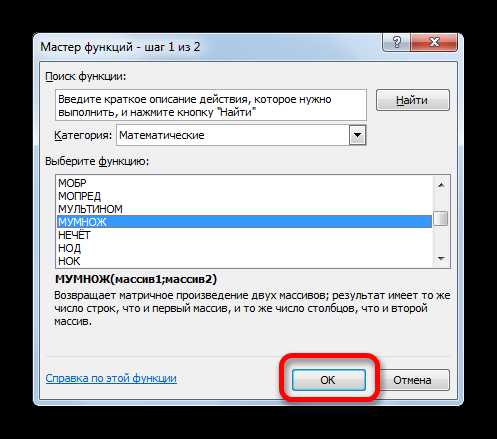
- Активируется Мастер функций. Перемещаемся в блок «Математические», кликаем по наименованию «МУМНОЖ» и клацаем по кнопке «OK» в нижней части окна.
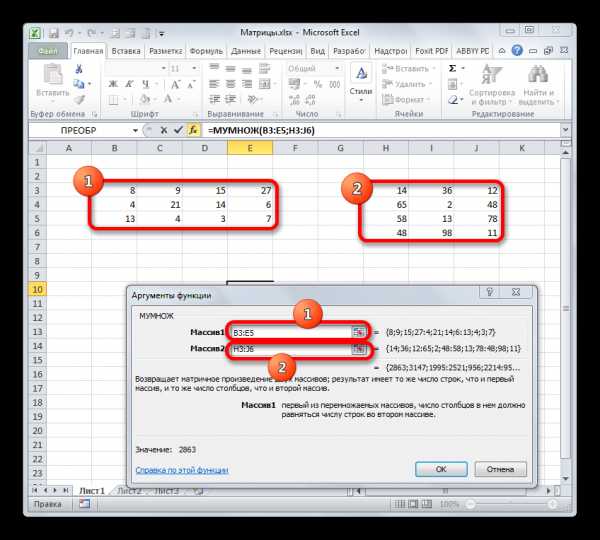
- Будет выполнен запуск окна аргументов требуемой функции. В этом окне имеется два поля для ввода адресов матричных массивов. Ставим курсор в поле «Массив1» и, зажав левую кнопку мыши, выделяем на листе всю область первой матрицы. После этого её координаты отобразятся в поле. Ставим курсор в поле «Массив2» и аналогичным образом выделяем диапазон второй матрицы.
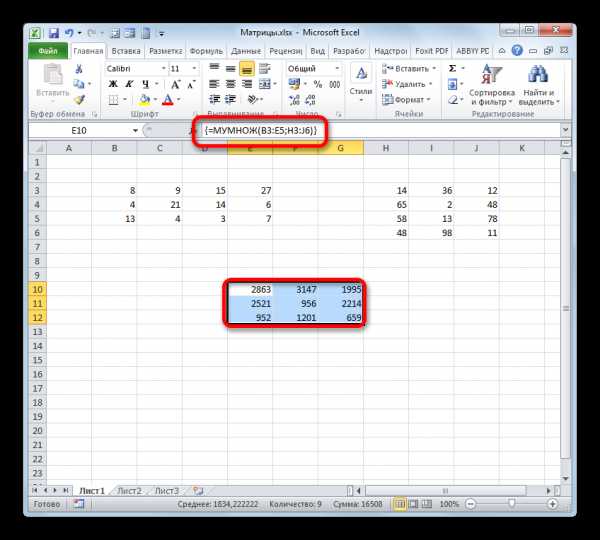
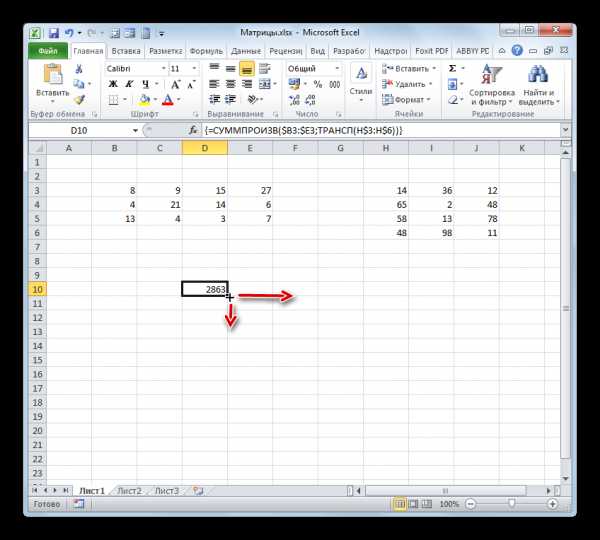
После того, как оба аргумента внесены, не спешим жать на кнопку «OK», так как мы имеем дело с функцией массива, а это значит, что для получения корректного результата обычный вариант завершения работы с оператором не подойдет. Данный оператор предназначен не для того, чтобы выводить результат в одну ячейку, так как выводит его в целый диапазон на листе. Итак, вместо нажатия кнопки
- Как видим, после этого предварительно выделенный диапазон был заполнен данными. Это и есть результат умножения матричных массивов. Если взглянуть на строку формул, после выделения любого из элементов данного диапазона, то мы увидим, что сама формула обернута в фигурные скобки. Это и есть признак функции массива, который добавляется после нажатия сочетания клавиш Ctrl+Shift+Enter перед выводом результат на лист.
Урок: Функция МУМНОЖ в Экселе
Способ 2: использование составной формулы
Кроме того, существует ещё один способ умножения двух матриц. Он более сложный, чем предыдущий, но тоже заслуживает упоминания, как альтернативный вариант. Данный способ предполагает использование составной формулы массива, которая будет состоять из функции СУММПРОИЗВ и вложенного в неё в качестве аргумента оператора ТРАНСП.
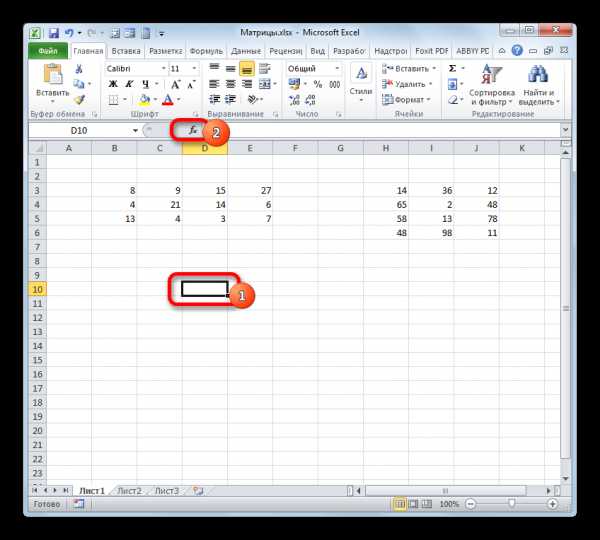
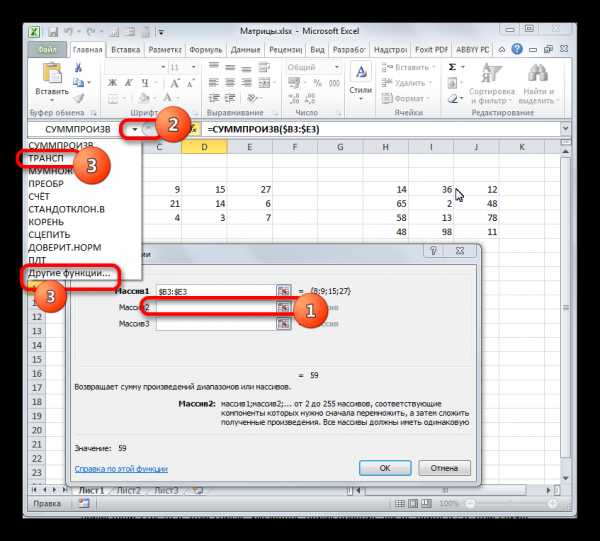
- На этот раз выделяем на листе только левый верхний элемент массива пустых ячеек, который рассчитываем использовать для вывода результата. Щелкаем по значку «Вставить функцию».
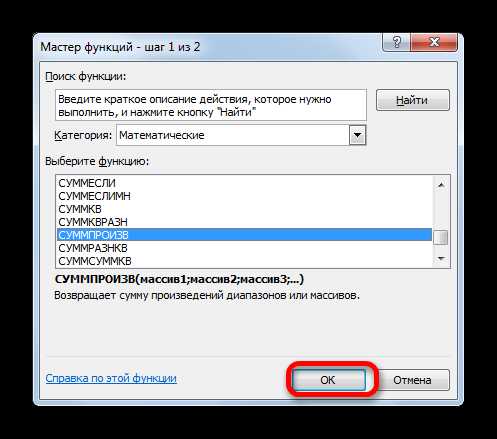
- Мастер функций запускается. Перемещаемся в блок операторов «Математические», но на этот раз выбираем наименование СУММПРОИЗВ. Клацаем по кнопке «OK».
- Происходит открытие окна аргументов вышеуказанной функции. Данный оператор предназначен для перемножения различных массивов между собой. Его синтаксис следующий:
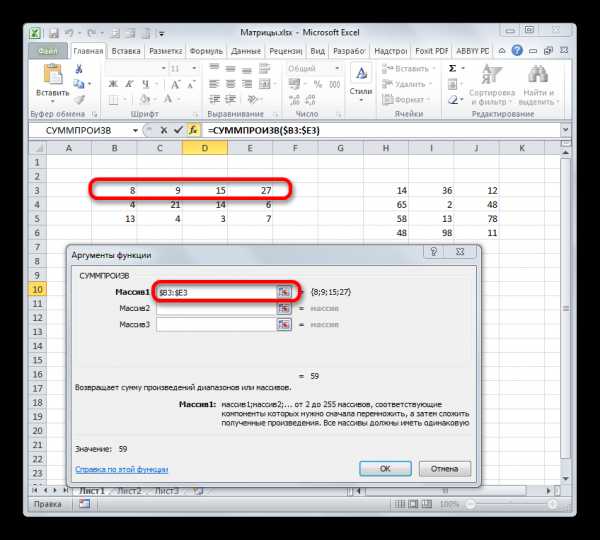
=СУММПРОИЗВ(массив1;массив2;…)В качестве аргументов из группы «Массив» используется ссылка на конкретный диапазон, который нужно перемножить. Всего может быть использовано от двух до 255 таких аргументов. Но в нашем случае, так как мы имеем дело с двумя матрицами, нам понадобится как раз два аргумента.
Ставим курсор в поле «Массив1». Тут нам нужно будет ввести адрес первой строки первой матрицы. Для этого, зажав левую кнопку мыши, нужно просто выделить её на листе курсором. Тут же координаты данного диапазона будут отображены в соответствующем поле окна аргументов. После этого следует зафиксировать координаты полученной ссылки по столбцам, то есть, эти координаты нужно сделать абсолютными. Для этого перед буквами в выражении, которое вписано в поле, устанавливаем знак доллара ($). Перед координатами, отображенными в цифрах (строки), это делать не следует. Также, можно вместо этого выделить всё выражение в поле и трижды нажать на функциональную клавишу F4. В данном случае абсолютными тоже станут лишь координаты столбцов.
- После этого устанавливаем курсор в поле «Массив2». С этим аргументом будет посложнее, так как по правилам умножения матриц, вторую матрицу нужно «перевернуть». Для этого используем вложенную функцию ТРАНСП.
Чтобы перейти к ней, клацаем по значку в виде треугольника, направленного острым углом вниз, который размещен слева от строки формул. Открывается список недавно используемых формул. Если вы в нем найдете наименование «ТРАНСП», то щелкайте по нему. Если же вы давно использовали данный оператор или вообще никогда не применяли его, то в этом списке указанное наименование вы не отыщите. В этом случае требуется нажать по пункту «Другие функции…».
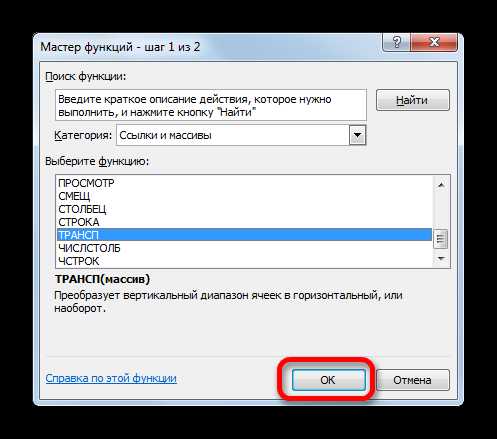
- Открывается уже хорошо знакомое нам окно Мастера функций. На этот раз перемещаемся в категорию «Ссылки и массивы» и выбираем наименование «ТРАНСП». Щелкаем по кнопке «OK».
- Производится запуск окна аргументов функции ТРАНСП. Данный оператор предназначен для транспонирования таблиц. То есть, попросту говоря, он меняет местами столбцы и строки. Это нам и нужно сделать для второго аргумента оператора СУММПРОИЗВ. Синтаксис функции ТРАНСП предельно простой:
=ТРАНСП(массив)То есть, единственным аргументом данного оператора является ссылка на тот массив, который следует «перевернуть». Вернее, в нашем случае даже не на весь массив, а только на его первый столбец.
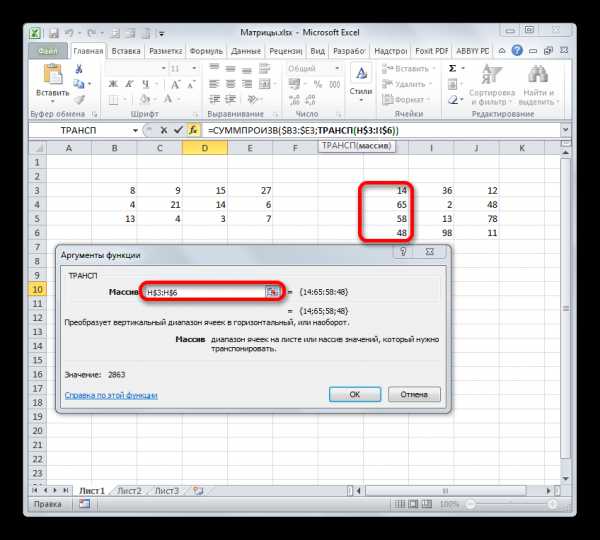
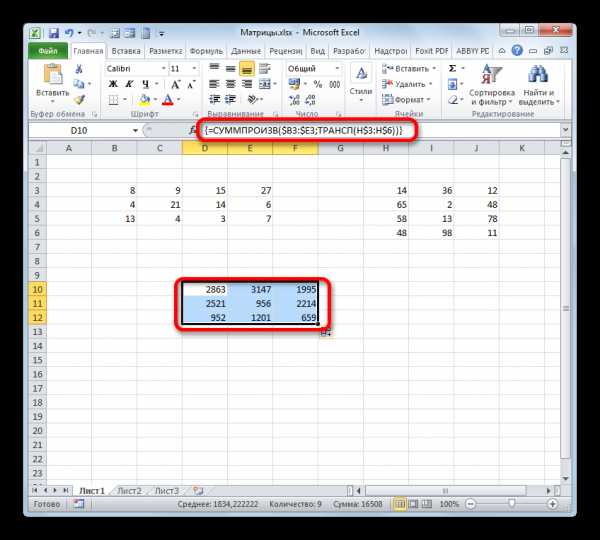
Итак, устанавливаем курсор в поле «Массив» и выделяем первый столбец второй матрицы на листе с зажатой левой кнопкой мыши. Адрес отобразится в поле. Как и в предыдущем случае, тут тоже нужно сделать определенные координаты абсолютными, но на этот раз не координаты столбцов, а адреса строк. Поэтому ставим знак доллара перед цифрами в ссылке, которая отображается в поле. Можно также выделить всё выражение и дважды кликнуть по клавише F4. После того, как нужные элементы стали иметь абсолютные свойства, не жмем на кнопку «OK», а так же, как и в предыдущем способе, применяем нажатие комбинации клавиш Ctrl+Shift+Enter.
- Но на этот раз у нас заполнился не массив, а только одна ячейка, которую мы ранее выделили при вызове Мастера функций.
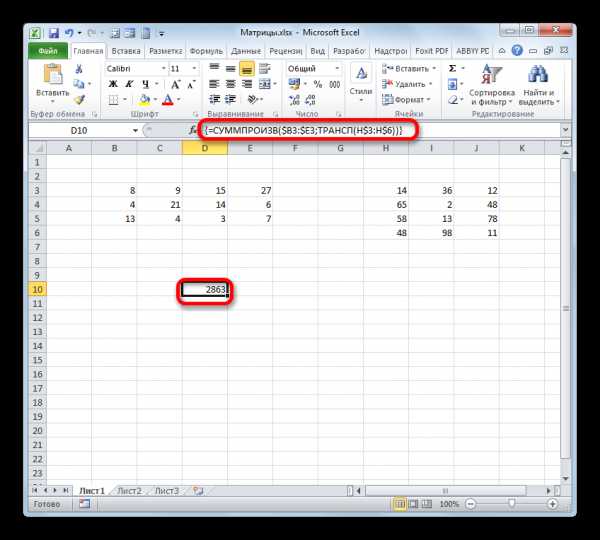
- Нам нужно заполнить данными такой же по размеру массив, как и в первом способе. Для этого следует скопировать формулу, полученную в ячейке, на равнозначный диапазон, который будет равен количеству строк первой матрицы и количеству столбцов второй. В конкретно нашем случае получается три строки и три столбца.
- Как видим, выделенный диапазон заполнен данными. Если их сравнить с тем результатом, который мы получили благодаря применению оператора МУМНОЖ, то увидим, что значения полностью идентичны. Это означает, что умножение двух матриц выполнено верно.
Урок: Работа с массивами в Экселе
Как видим, несмотря на то, что был получен равнозначный результат, использовать функцию для умножения матриц МУМНОЖ значительно проще, чем применять для этих же целей составную формулу из операторов СУММПРОИЗВ и ТРАНСП. Но все-таки данный альтернативный вариант тоже нельзя оставить без внимания при изучении всех возможностей перемножения матриц в Microsoft Excel.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Умножение матриц в MS EXCEL. Примеры и методы
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ(), которую нужно вводить как формулу массива.
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9.
Для этого:
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2)
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо больший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2, исправьте формулу и нажмите CTRL+SHIFT+ENTER.
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)). Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER. Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
excel2.ru
Функция МУМНОЖ в Excel

Как известно, программа Excel обладает множеством инструментов для работы с матрицами. Одним из них является функция МУМНОЖ. С помощью данного оператора у пользователей появляется возможность перемножать различные матрицы. Давайте узнаем, как использовать эту функцию на практике, и в чем заключаются основные нюансы работы с ней.
Использование оператора МУМНОЖ
Основной задачей функции МУМНОЖ, как было сказано выше, является перемножение двух матриц. Она относится к категории математических операторов.
Синтаксис этой функции следующий:
=МУМНОЖ(массив1;массив2)
Как видим, у оператора всего два аргумента – «Массив1» и «Массив2». Каждый из аргументов представляет собой ссылку на одну из матриц, которую следует перемножить. Именно это и выполняет указанный выше оператор.
Важным условием для применения МУМНОЖ является то, что количество строк первой матрицы должно совпадать с количеством столбцов второй. В обратном случае, в результате обработки будет выдаваться ошибка. Также во избежание ошибки ни один из элементов обоих массивов не должен быть пустым, а они полностью должны состоять из чисел.
Умножение матриц
Теперь давайте на конкретном примере рассмотрим, как можно умножить две матрицы, применив оператор МУМНОЖ.
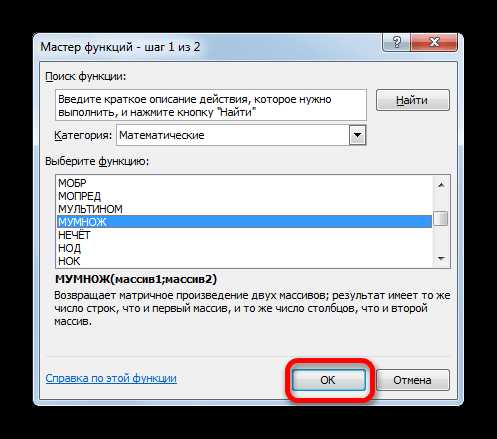
- Открываем лист Excel, на котором уже располагаются две матрицы. Выделяем на нем область из пустых ячеек, которая по горизонтали имеет в своем составе количество строк первой матриц, а по вертикали количество столбцов второй матрицы. Далее жмем на значок «Вставить функцию», который размещен около строки формул.
- Происходит запуск Мастера функций. Нам следует перейти в категорию «Математические» или «Полный алфавитный перечень». В списке операторов нужно отыскать наименование «МУМНОЖ», выделить его и нажать на кнопку «OK», которая размещена в нижней части данного окна.
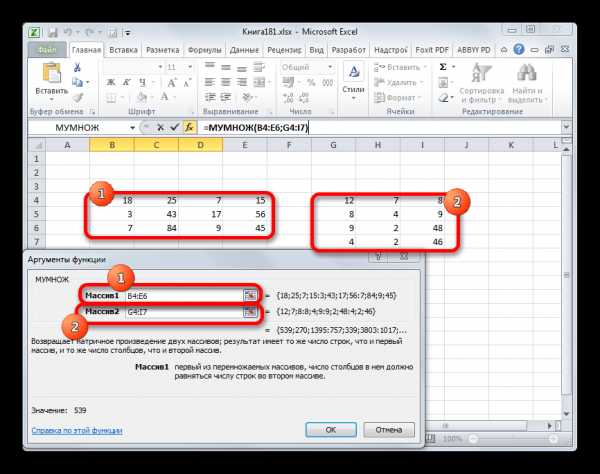
- Запускается окно аргументов оператора МУМНОЖ. Как видим, оно имеет два поля: «Массив1» и «Массив2». В первом нужно указать координаты первой матрицы, а во втором, соответственно, второй. Для того, чтобы сделать это, устанавливаем курсор в первое поле. Затем производим зажим левой кнопкой мыши и выделяем область ячеек, содержащую первую матрицу. После выполнения этой несложной процедуры координаты отобразятся в выбранном поле. Аналогичное действие проводим и со вторым полем, только в этот раз, зажав левую кнопку мыши, выделяем вторую матрицу.
После того, как адреса обеих матриц записаны, не спешим жать на кнопку «OK», размещенную в нижней части окна. Дело в том, что мы имеем дело с функцией массива. Она предусматривает то, что результат выводится не в одну ячейку, как в обычных функциях, а сразу в целый диапазон. Поэтому для вывода итога обработки данных, используя этот оператор, недостаточно нажать на клавишу Enter, расположив курсор в строке формул, или щелкнуть по кнопке «OK», находясь в окне аргументов функции, которое открыто у нас в данный момент. Нужно применить нажатие комбинации клавиш Ctrl+Shift+Enter. Выполняем данную процедуру, а кнопку «OK» не трогаем.
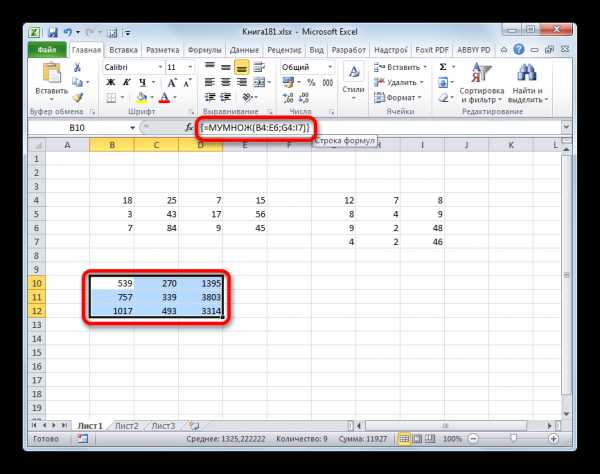
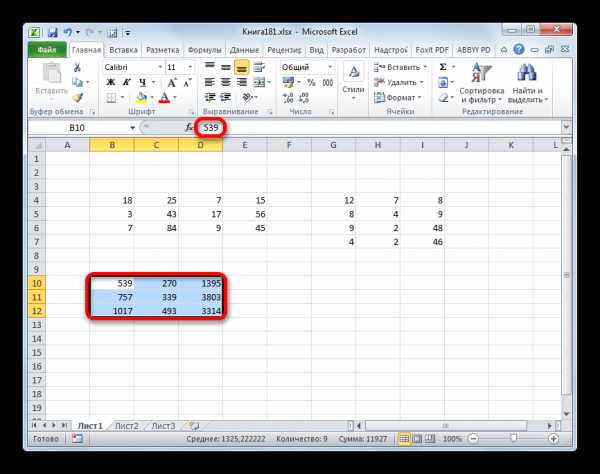
- Как видим, после нажатия указанной комбинации клавиш окно аргументов оператора МУМНОЖ закрылось, а диапазон ячеек, который мы выделили ещё в первом шаге этой инструкции, был заполнен данными. Именно эти значения и являются результатом умножения одной матрицы на другую, которое выполнил оператор МУМНОЖ. Как видим, в строке формул функция взята в фигурные скобки, что означает её принадлежность к операторам массивов.
- Но именно то, что результат обработки функции МУМНОЖ является цельным массивом, мешает дальнейшему его изменению в случае необходимости. При попытке изменить любое из чисел итогового результата пользователя будет ждать сообщение, которое информирует о том, что нельзя изменять часть массива. Чтобы устранить это неудобство и преобразовать неизменяемый массив в обычный диапазон данных, с которым можно работать, выполняем следующие действия.
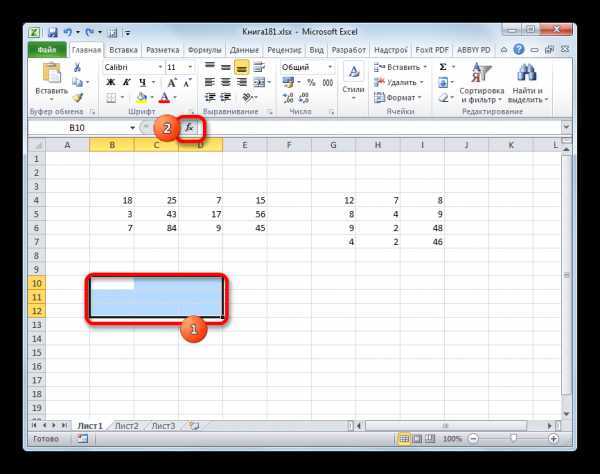
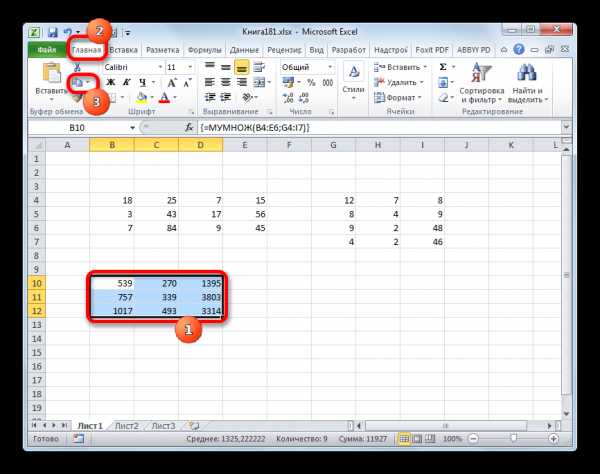
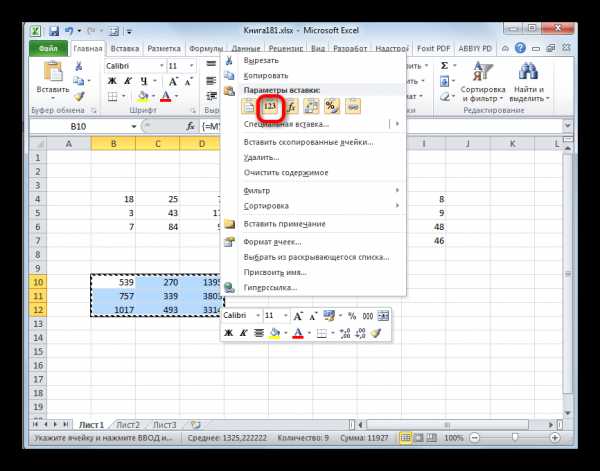
Выделяем данный диапазон и, находясь во вкладке «Главная», кликаем по значку «Копировать», который размещен в блоке инструментов «Буфер обмена». Также вместо этой операции можно применить набор сочетания клавиш Ctrl+C.
- После этого, не снимая выделения с диапазона, кликаем по нему правой кнопкой мыши. В открывшемся контекстном меню в блоке «Параметры вставки» выбираем пункт «Значения».
- После выполнения данного действия итоговая матрица уже не будет представлена как единый неразрывный диапазон и с ней можно производить различные манипуляции.
Урок: Работа с массивами в Excel
Как видим, оператор МУМНОЖ позволяет довольно быстро и легко умножать в Экселе две матрицы друг на друга. Синтаксис этой функции довольно простой и у пользователей не должно возникнуть проблем со вводом данных в окно аргументов. Единственная проблема, которая может возникнуть при работе с этим оператором, заключается в том, что он представляет собой функцию массива, а значит, имеет определенные особенности. Для вывода результата требуется предварительно выделить соответствующий диапазон на листе, а затем уже после ввода аргументов для расчета применить специальную комбинацию клавиш, предназначенную для работы именно с таким типом данных — Ctrl+Shift+Enter.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Умножение матриц в Excel
Поиск ЛекцийУмножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки h5 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
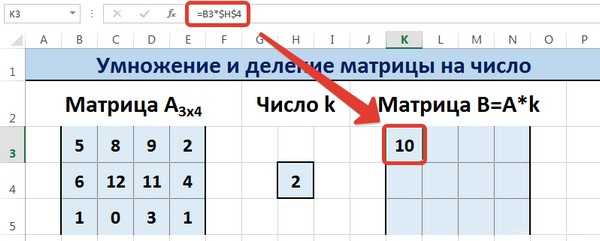
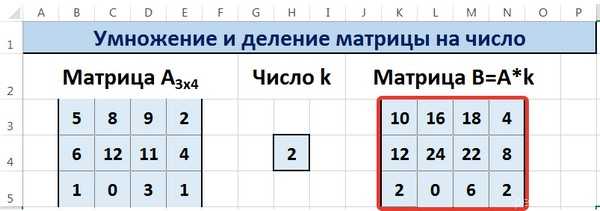
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
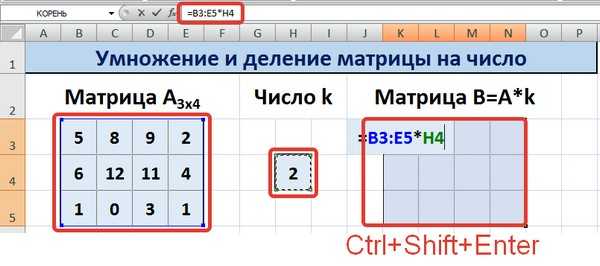
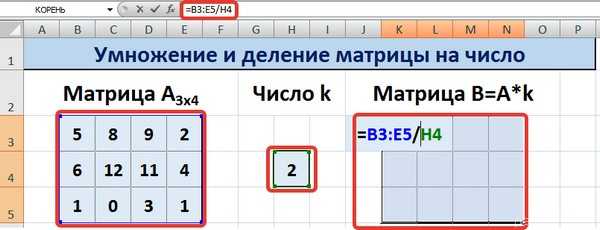
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/h5, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
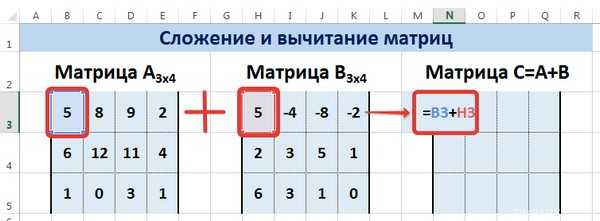
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij =аij + bij.
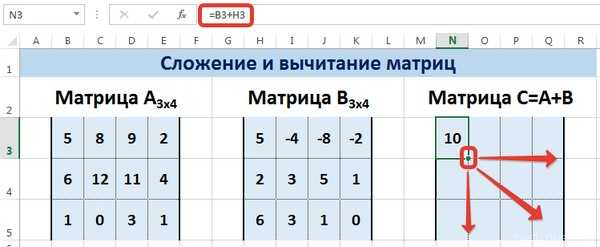
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+h4, где B3 и h4 – первые элементы матриц А и Всоответственно. При этом формула содержит относительные ссылки (В3 и h4), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — h4 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
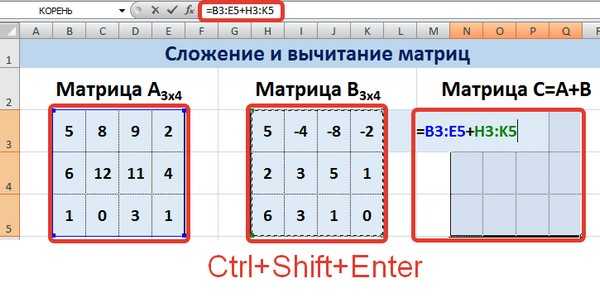
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
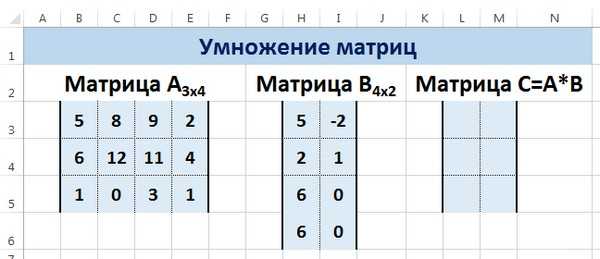
Вычислим произведение этих матриц С=А*Вс помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
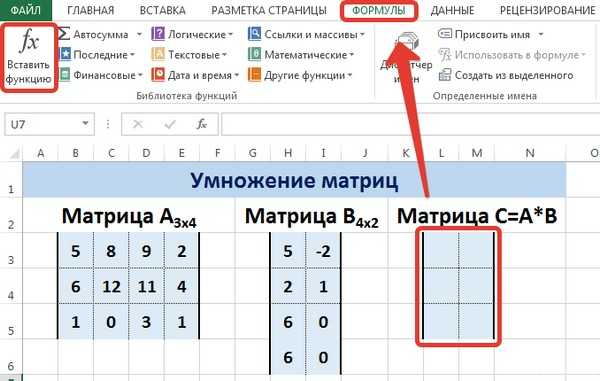
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
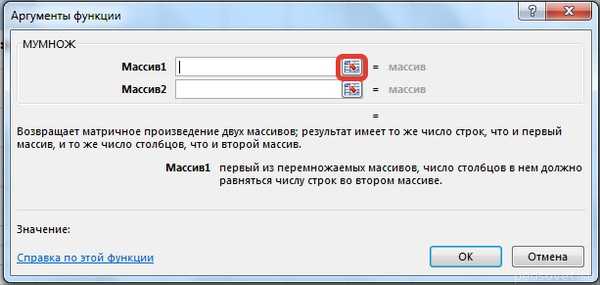
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
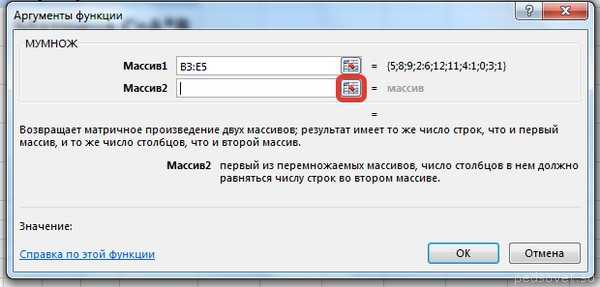
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
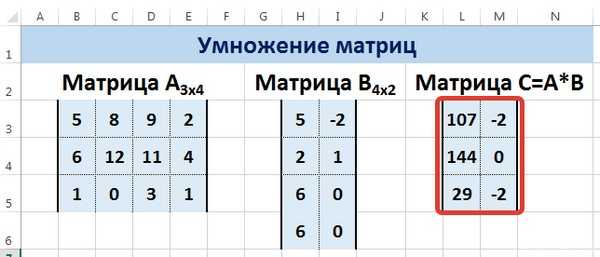
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Операции с матрицами в Excel
РХТУ им. Д.B. Менделеева Кафедра ИКМ Методическое пособие по изучению Excel
Операции с матрицами в Excel
Как и над числами, над матрицами можно проводить ряд операций, причем в случае с матрицами некоторые из операций являются специфическими.
Транспонирование.
Транспонированной называется матрица (AT), в которой столбцы исходной матрицы (А) заменяются строками с соответствующими номерами.
Пример. Пусть в диапазон ячеек А1:Е2 введена матрица размера 2×5. Необходимо получить транспонированную матрицу.
Выделить указателем мыши при нажатой левой кнопке блок ячеек, где будет находиться транспонированная матрица. В нашем примере блок размера 5 x2 в диапазоне А4:В8.
Нажать на панели инструментов Стандартная вставка функции.
В появившемся диалоговом окне Мастер функцийв рабочем полеКатегориявыбратьСсылки и массивы, а в рабочем полеФункция– имя функции ТРАСП (рис.1)
рис.1
Появившееся диалоговое окно ТРАСП мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:Е2 в рабочее поле Массив(указателем мыши при нажатой левой кнопке). После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER(рис.2)
Если транспонированная матрица не появилась в заданном диапазоне А4:В8, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне А4:В8 появится транспонированная матрица.
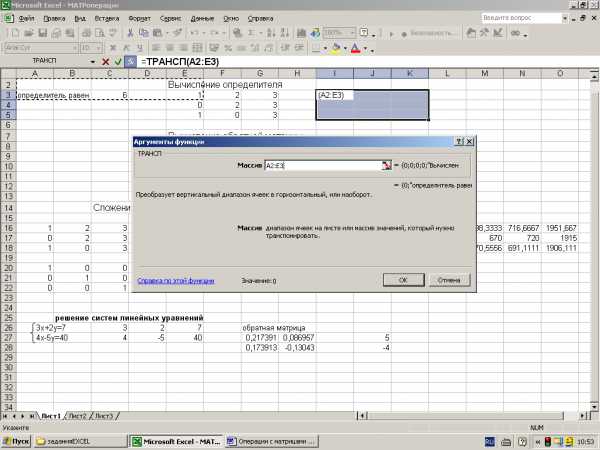
Рис.2
Вычисление определителя матрицы
Пусть в диапазон А1:С3 введена матрица. Необходимо вычислить определитель матрицы
Табличный курсор поставить в ячейку, в которой требуется получить значение определителя, например. В А4.
Нажать на панели инструментов СтандартнаякнопкуВставка функции
В появившемся диалоговом окне Мастер функцийв рабочем полеКатегориивыбратьМатематические,а в рабочем полеФункция– имя функции МОПРЕД. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МОПРЕД мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:С3 в рабочее поле Массив(указателем мыши при нажатой левой кнопке). После чего нажать кнопку ОК.
В ячейке А4 появится значение определителя матрицы.
Нахождение обратной матрицы
Пусть в диапазон А1:С3 введена матрица. Необходимо в диапазоне А5:С7 получить обратную матрицу.
Выделить блок ячеек под обратную матрицу (в нашем примере А5:С7)
Нажать на панели инструментов СтандартнаякнопкуВставка функции
В появившемся диалоговом окне Мастер функцийв рабочем полеКатегориивыбратьМатематические,а в рабочем полеФункция– имя функции МОБР. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МОБР мышью отодвинуть в сторону от исходной матрицы и ввести диапазон исходной матрицы А1:С3 в рабочее поле Массив(указателем мыши при нажатой левой кнопке). После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER
Если обратная матрица не появилась в заданном диапазоне А1:С3, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне А1:С3 появится обратная матрица.
Сложение и вычитание матриц, умножение и деление матрицы на число
Складывать (вычитать) матрицы можно одного размера. В Excelдля выполнения операция сложения (вычитания) матриц используются формулы, вводимые в соответствующие ячейки.
Пример. Пусть матрица А введена в диапазон А1:С2, а матрица В – в диапазон А4:С5. Необходимо найти матрицу С, являющуюся их суммой, в диапазоне Е1:G2.
С = А + В
Табличный курсор установить в левый верхний угол результирующей матрицы – ячейку Е1.
Ввести формулу для вычисления первого элемента результирующей матрицы =А1+А4 (предварительно установить английскую раскладку клавиатуры)
Скопируйте введенную формулу в остальные ячейки результирующей матрицы.
В результате в ячейках E1:G2 появится матрица, равная сумме исходных матриц.
Подобным образом вычисляется разность матриц, только в формуле вместо знака +, ставится знак -.
Если необходимо умножить (разделить) матрицу А на число k, то формула будет иметь вид =А1*k.
Рис.3
Умножение матриц
Произведение двух матриц определено, если число столбцов первой матрицы произведения равно числу строк второй матрицы произведения.
Пример. Пусть матрица введена в диапазонA1:D3, а матрица В – в диапазон А4:В7. Необходимо найти произведение этих матриц С=Аx В.
Выделить блок ячеек указателем мыши при нажатой левой кнопке под результирующую матрицу. Если матрица А имеет размерность 3 x 4, а матрица В имеет размерность 4 x 3, то результирующая матрица С имеет размерность 3 x 3. Поэтому следует внимательно следить, чтобы размерность матрицы С в точности соответствовала определению произведения двух матриц. Пусть матрица С будет размещаться в диапазонеF1:G3.
Нажать на панели инструментов СтандартнаякнопкуВставка функции
В появившемся диалоговом окне Мастер функцийв рабочем полеКатегориивыбратьМатематические,а в рабочем полеФункция– имя функции МУМНОЖ. После этого нажать на кнопку ОК.
Появившееся диалоговое окно МУМНОЖ мышью отодвинуть в сторону от исходной матрицы и ввести диапазон первой матрицы А1:D3 в рабочее полеМассив1(указателем мыши при нажатой левой кнопке), а диапазон матрицы В – А4:В7 ввести в рабочее полеМассив2. После чего, не нажимая кнопку ОК, нажать сочетание клавишCTRL+SHIFT+ENTER(рис.3)
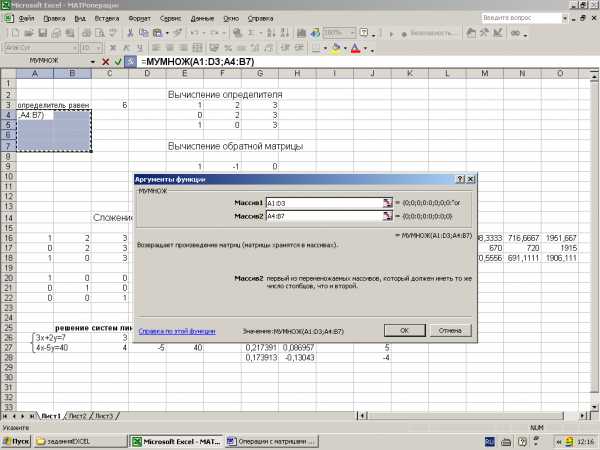
Рис.4
Если произведение матриц не появилось в заданном диапазоне А1:С3, то надо щелкнуть указателем мыши в строке формул и повторить нажатие клавиш CTRL+SHIFT+ENTER.
В результате в диапазоне F1:G3 появится обратная матрица.
studfiles.net
Вычисление обратной матрицы в MS EXCEL. Примеры и методы
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE.
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
Матрица А-1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А-1*А=Е и А*А-1=Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР().
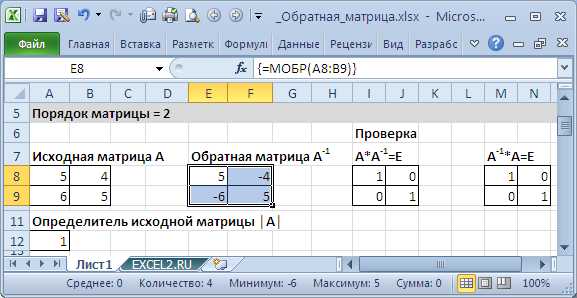
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера):
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9, например, Е8:F9
- в Cтроке формул ввести формулу =МОБР(A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР({5;4: 3;2}). Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон.
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ()), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР().
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
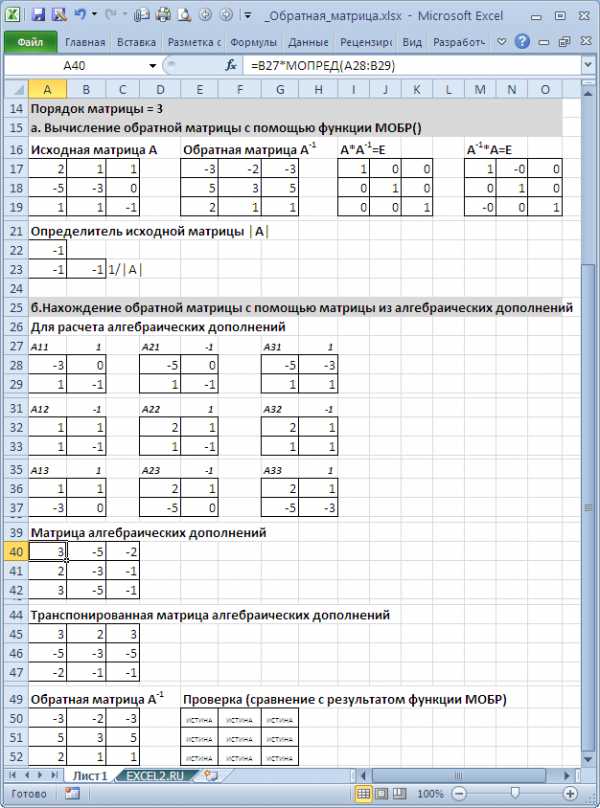
Порядок действий при вычислении обратной матрицы:
В качестве проверки можно перемножить исходную и обратную матрицы. В результате должна получиться единичная матрица.
excel2.ru
11. Действия с матрицами на компьютере в excel
Рассмотрим применение табличного процессора EXCEL для работы с матрицами.
Процессор EXCEL работает с числовыми матрицами и может осуществлять следующие операции:
сложение (вычитание) матриц, умножение матриц на число,
преобразования матрицы с целью получения нулей,
вычисление определителя матрицы,
транспонирование матрицы,
нахождение обратной матрицы.
Сложение матриц, умножение матрицы на число, преобразование матрицы осуществляются с помощью строки формул. Для нахождения определителя матрицы, транспонированной матрицы, обратной матрицы, а также для умножения матриц следует пользоваться соответствующими встроенными функциями: МОПРЕД; ТРАНСП; МОБР; МУМНОЖ. К сожалению, нет встроенной функции для определения ранга матрицы. Ранг придется находить переходом к эквивалентной матрице. Такой же переход полезен и для исследования линейных систем.
Сложение матриц.
Рис.3
В ячейки 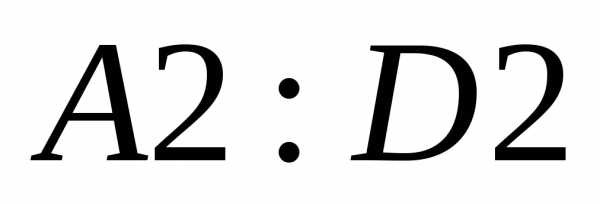 введена матрица
введена матрица .
.
В ячейки 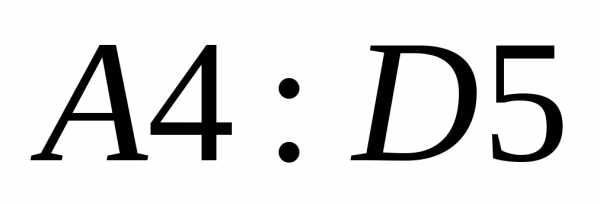 введена матрица
введена матрица .
.
В ячейку  введена формулаи скопирована в диапазон
введена формулаи скопирована в диапазон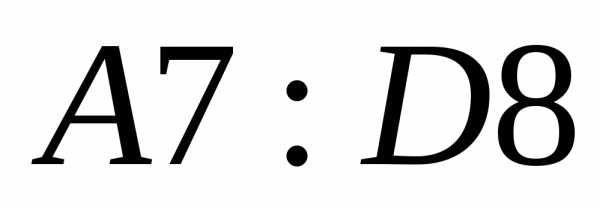 .
.
Умножение матрицы на число.
Рис.4
В ячейки 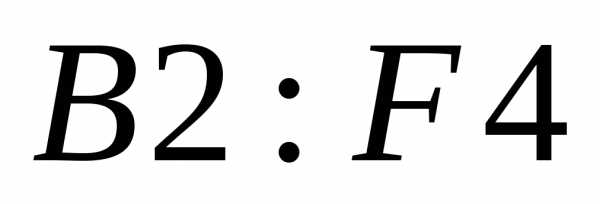 введена матрица
введена матрица ,
,
В ячейку 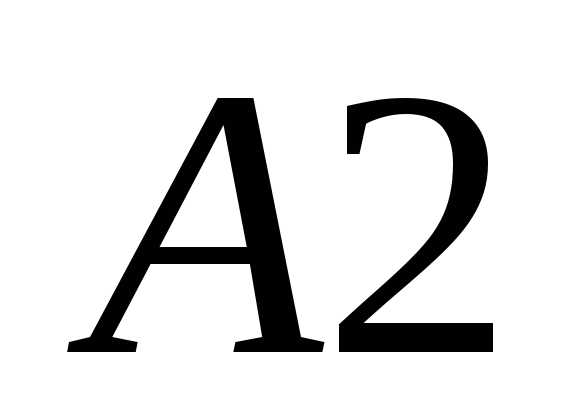 введено число
введено число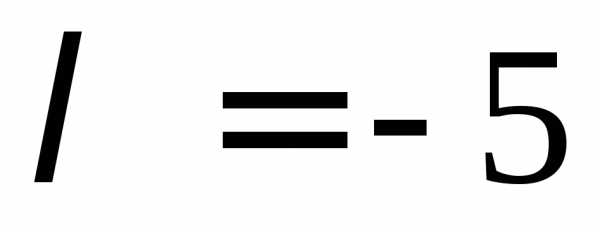 .
.
В ячейку  введена формулаи скопирована в диапазон
введена формулаи скопирована в диапазон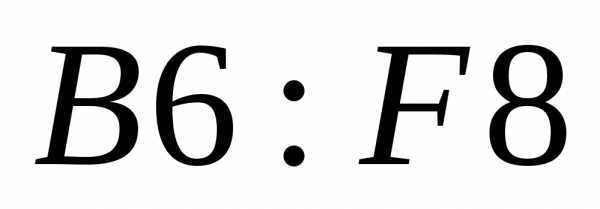 .
.
Вычисление определителя, транспонирование, нахождение обратной матрицы.
Перечисленные операции проводятся с помощью соответствующих встроенных функций. При выполнении операций транспонирования, умножения матриц, нахождения обратной матрицы необходимо предварительно выделить диапазон ячеек для записи результата. Результат получается нажатием клавиш (ввод массива).
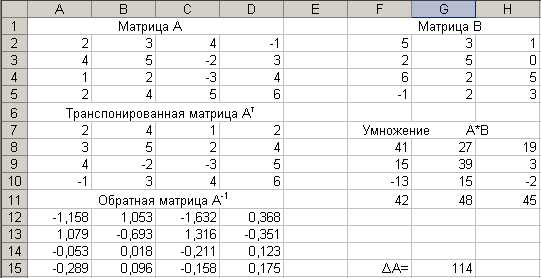
Рис.5
В ячейки 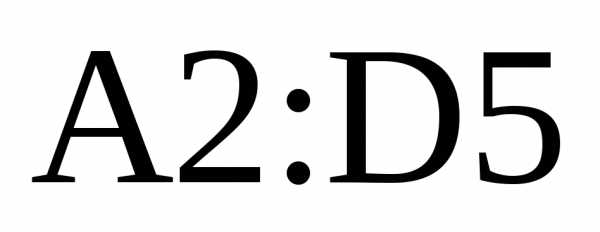 введена матрица
введена матрица ,
в ячейки
,
в ячейки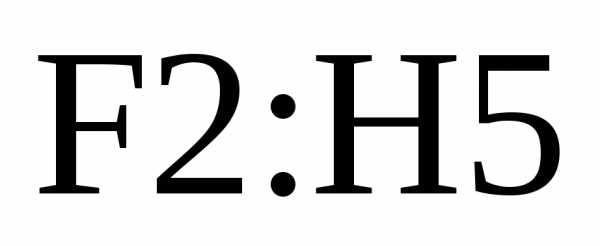 — матрица
— матрица .
.
В ячейку  введем формулу
введем формулу =МОПРЕД,
заполним поле значений аргумента
=МОПРЕД,
заполним поле значений аргумента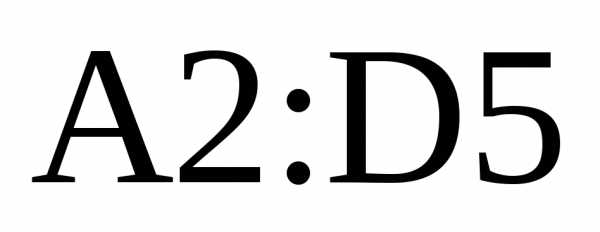 ,
получаем значение определителя матрицы
,
получаем значение определителя матрицы .
.
Пример 16. Вычислить обратную матрицу для 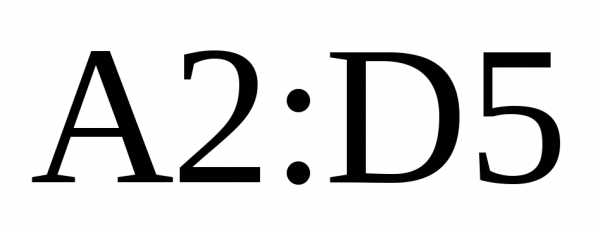 .
.
Выделим диапазон
ячеек
для записи обратной матрицы. Теперь
надо вызвать Мастер функций, выбрать
имя функции МОБР, ввести в поле значений
аргумента функции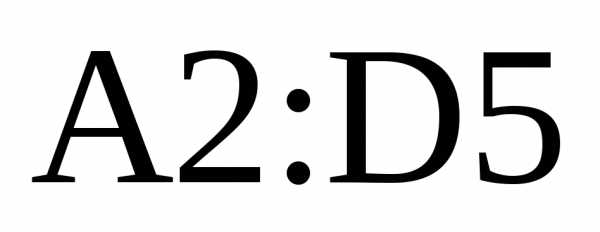 и нажать клавиши(ввод
массива).
и нажать клавиши(ввод
массива).
Пример 17.
Умножить матрицы  и
и .
.
Определим размерность
матрицы 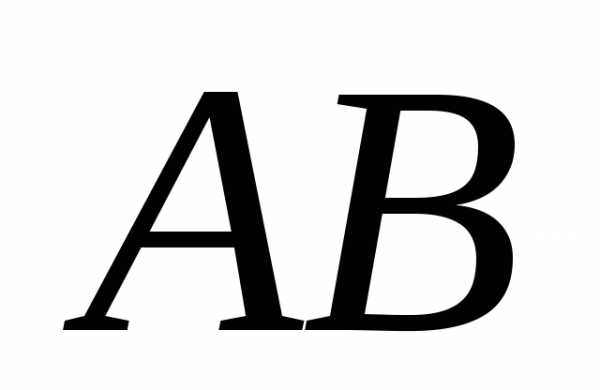 (результата
умножения):
(результата
умножения):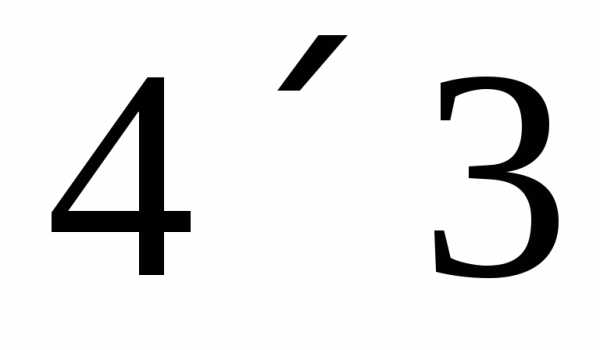 ,
и выделим диапазон
,
и выделим диапазон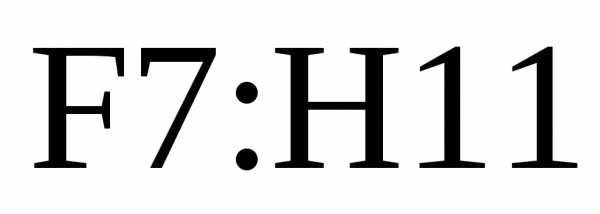 для записи этой матрицы.
для записи этой матрицы.
Для умножения
надо вызвать Мастер функций, выбрать
имя функции МУМНОЖ, ввести в поле значений
1 аргумента функции первую матрицу, в
поле 2 – вторую матрицу, и нажать клавиши
(ввод
массива). В ячейках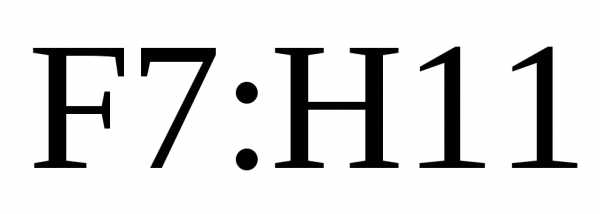 − результат умножения.
− результат умножения.
Вычисление ранга матрицы.
Будем последовательно получать нули в первом, втором и т.д. столбцах ниже диагональных элементов.
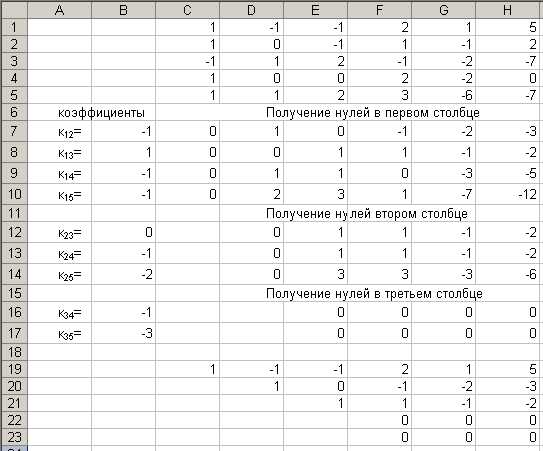
Рис.6
В ячейки 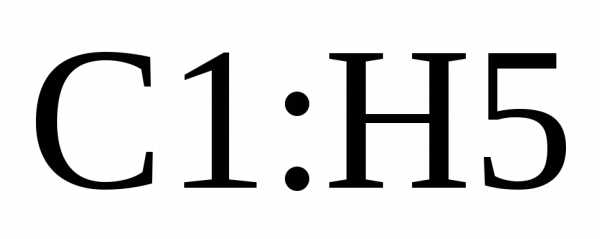 введем матрицу (пример 11).
введем матрицу (пример 11).
Получим нули в
первом столбце матрицы 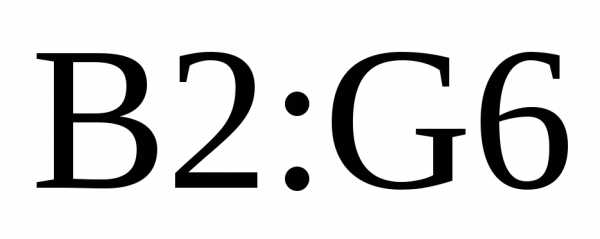 .
Для этого в ячейку
.
Для этого в ячейку введем формулуи скопируем ее в ячейки,
в ячейку
введем формулуи скопируем ее в ячейки,
в ячейку введем формулуи скопируем ее в ячейки
введем формулуи скопируем ее в ячейки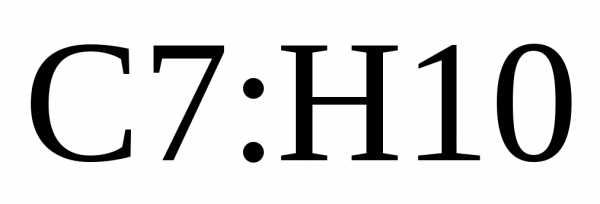 .
.
Аналогично получаем
нули во втором столбце. В ячейку 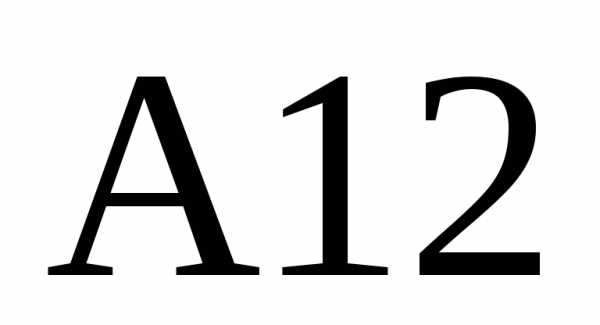 введем формулуи скопируем ее в ячейку.
В ячейку
введем формулуи скопируем ее в ячейку.
В ячейку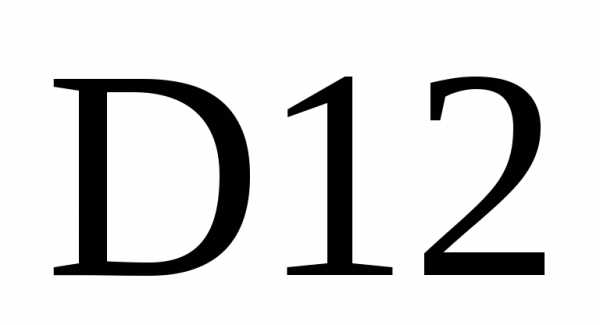 введем формулуи скопируем ее в ячейки.
введем формулуи скопируем ее в ячейки.
Дальше получаем
нули в третьем столбце. В ячейку 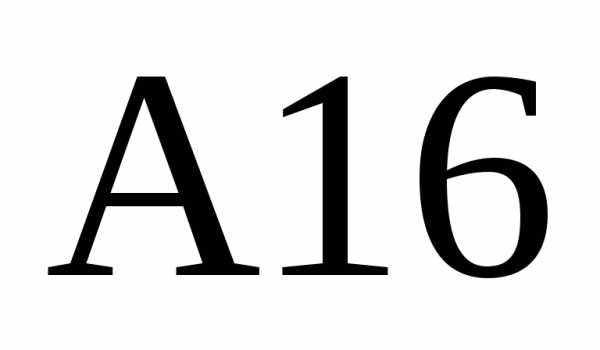 введем формулуи скопируем ее в ячейку.
В ячейку
введем формулуи скопируем ее в ячейку.
В ячейку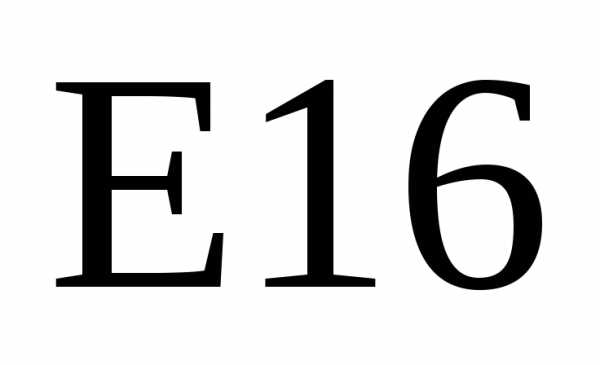 введем формулуи скопируем ее в ячейки.
введем формулуи скопируем ее в ячейки.
Получили полностью нулевые строки. Ниже копированием значений (специальная вставка) записана преобразованная матрица (нули ниже диагонали опущены). Следовательно, ранг матрицы равен трем.
studfiles.net
