2.3 Сложение некоторых КПВ | Экономика для школьников
Как можно складывать некоторые КПВ? (уровень муниципального этапа)- Рассчитываем суммарные крайние точки (или одну крайнюю точку)
- Рассматриваем $AC$ какого-нибудь товара на всех участках всех КПВ
- Располагаем эти участки в соответствии с законом возрастающей $AC$
Пример 1
Найдите суммарную КПВ двух стран:
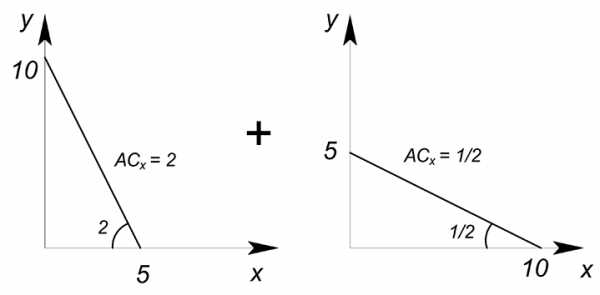
Данные КПВ являются линейными функциями.
Рассчитаем суммарные крайние точки данных КПВ: по $y$: $10+5=15$, по $x$: $5+10=15$.
Рассмотрим $AC_x$: первая функция обладает постоянной (ибо функция линейная) $AC_x=\dfrac{10}{5}=2$; вторая функция обладает также постоянной $AC_x$, но уже равной $\dfrac{5}{10}=\dfrac{1}{2}$. Первый участок суммарной КПВ будет представлен функцией с меньшей $AC_x=\dfrac{1}{2}$, а на втором участке $AC_x=2$.
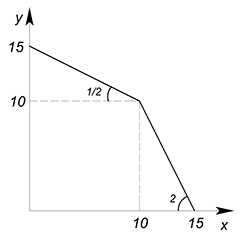
Найдите суммарную КПВ двух стран:
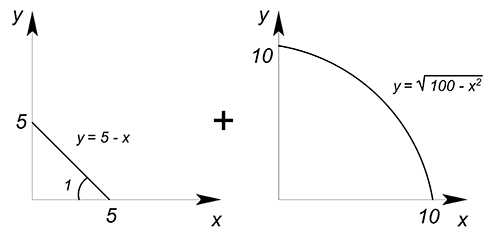
В данном случае мы имеем одну линейную и одну вогнутую КПВ.
Крайние точки суммарной КПВ: по $y$: $5+10=15$, по $x$: $5+10=15$.
Теперь перейдем к оценке альтернативной стоимости. У линейной функции она постоянна и по $x$ равна $\dfrac{5}{5}=1$. $AC_x$ вогнутой функции не является константой. Она возрастает на при движении вдоль оси $x$ ($tg$ углов наклона касательных, проведенных к каждой точке данного графика возрастают). Для построения суммарной КПВ необходимо расположить участки в соответствии с законом возрастающей альтернативной стоимости. Поэтому нам надо найти на вогнутой КПВ участки, где $AC_x>1$ и где $AC_x<1$. Найдем точку, в которой $AC_x=1$. $tg$ угла наклона касательной, взятый по модулю, в ней должен равняться $1$, производная данной функции в этой точке тоже должна быть равна $1$:
$y(x)= \sqrt{100-x^2}$
$y'(x)=|\dfrac{-x}{\sqrt{100-x^2}}|=|-1|$
$x^2=100-x^2$
$x^2=50$
$x=5\sqrt{2}$
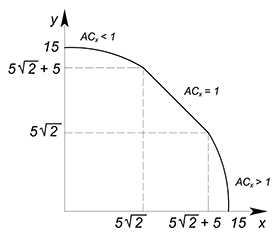
Очевидно, что $AC_x$ на участке, располагающемся слева от этой точки меньше $1$, а на находящемся справа больше.
Размещаем наши фрагменты двух КПВ по правилу, получаем: первый кусочек с $AC_x<1$ является частью вогнутой функции, второй есть линейная функция с $AC_x=1$, третий — оставшийся фрагмент вогнутой функции с $AC_x>1$.
При совместном производстве благ тот или иной товар будет производить тот субъект, у которого это получается лучше всего (то есть с наименьшими альтернативными издержками). В такой ситуации ресурсы каждого производителя будут использоваться максимально эффективно, ибо они будут задействованы в создании того блага, для которого подходят лучше всего (например, если мы выращиваем морковь и ловим рыбу, то в данном случае лопатой будут копать, а не использовать её вместо весла). Поэтому, работая вместе, две страны смогут произвести больше благ, чем при индивидуальной работе.
iloveeconomics.ru
Pract_1_BI
Задачи по курсу Тема 1. Базовые экономические понятия
Экономическая теория и институциональная экономика
Часть I. Микроэкономика
Кривая производственных возможностей (КПВ)
Фермер имеет два поля одинаковой площади, на которых может выращивать капусту и свеклу. Земля на каждом поле однородна. Максимальный урожай, который можно получить с первого поля, составляет 120 тонн капусты или 60 тонн свеклы. Относительно второго поля известно, что максимально возможный урожай капусты составляет 240 тонн, а альтернативная стоимость производства одной тонны свеклы равна 3 тонны капусты.
Построить КПВ для каждого поля и написать их уравнения.
Определить альтернативную стоимость выращивания 1 тонны капусты и 1 тонны свеклы на каждом поле.
Определить, какое поле имеет сравнительное преимущество в выращивании капусты, а какое – в выращивании свеклы; решить аналогичный вопрос об абсолютных преимуществах.
Построить совокупную КПВ.
Используя совокупную КПВ, определить альтернативную стоимость выращивания 80 тонн свеклы, альтернативную стоимость выращивания 300 тонн капусты.
Иван работает 40 часов в неделю и может производить 3 продукта – А, В, и С, затрачивая на производство единицы каждого из них 4, 2 и 5 часов соответственно.
Определить максимально возможный выпуск каждого продукта в неделю.
Построить двумерную КПВ для продуктов А и В и написать ее уравнение, считая что Иван должен выпускать ровно 2 единицы продукта С в неделю и определить альтернативную стоимость производства единицы продуктов А и В.
Построить трехмерную КПВ, написать ее уравнение.
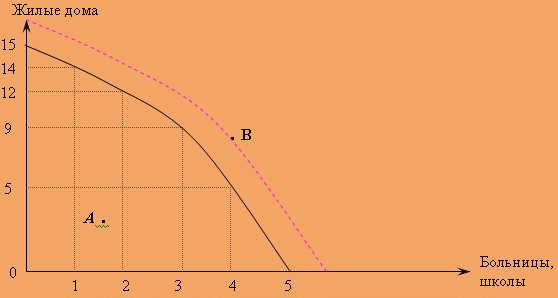
На рисунке изображены две кривые производственных возможностей. Построить совокупную КПВ. Ответ обосновать.
Андрей и Олег работают в мастерской и производят столы и табуретки. Андрей затрачивает 6 часов на производство стола и 40 минут на производство табуретки. Олег на производство стола тратит 3 часа, а одну табуретку делает за 30 минут.
Определить, кому следует производить табуретки, а кому столы, если Андрей и Олег решат распределить обязанности. В какой пропорции Андрей и Олег могут обмениваться столами и табуретками, чтобы данный обмен был взаимовыгоден? Какова пропорция безубыточного обмена?
Исходя из 48 часов рабочего времени, построить КПВ для Андрея и Олега, написать их уравнения.
Построить КПВ совместного труда Андрея и Олега. Определить альтернативную стоимость производства 120 табуреток, альтернативную стоимость производства 20 столов.
Предположим, что страна производит только два товараX и Y. Единственный ресурс, используемый в производстве товаров X и Y – труд, который имеется в размере 64 единиц. Производственные функции1 для товаров X и Y:
где X,Y – количества товаров X и Y,
6*. Точки A, B, C и D лежат на одной кривой производственных возможностей. У точек A и C известны обе координаты: A(2,8) и C(6,3). У точек B и D известна только одна координата: В(3,b) и D(7,d). Каким ограничениям должны удовлетворять неизвестные координаты b и d? Решение обосновать.
1Производственная функция показывает зависимость объема производства товара от объемов используемых ресурсов.
Николаева Т.П. 2012 – 2013 уч. год
studfiles.net
2.4 Оптимизация на КПВ | Экономика для школьников
Нахождение максимальной выручкиИмеем: КПВ некоторый страны задана функцией $x^2+y^2=100$, цены товаров $x$ и $y$ соответственно равны $10$ и $5$, найти при каком объёме производства данных товаров выручка от их продажи будет максимальной.
Построим КПВ:
$x^2+y^2=100$
$y^2=100-x^2$
$y=\sqrt{100-x^2}$
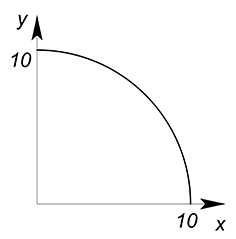
Теперь разберемся с функцией выручки (выручка обозначается буквами $»TR»$ (от англ «total revenue»)):
$TR=PQ$, где $P$ — цена товара, $Q$ — его количество.
В данном случае у нас $2$ товара, поэтому функция $TR$ будет зависеть от двух переменных $Q_x$ и $Q_y$:
$TR=P_xQ_x+P_yQ_y=10Q_x+5Q_y$
Далее для простоты будем писать не $Q_x$, $Q_y$, а просто $x$, $y$
Данная функция выручки может быть построена в трехмерной плоскости. Что мы можем сделать с этой функцией, чтобы перевести её в двухмерное пространство? В первую очередь можно выразить $y$ через $2$ другие переменные ($TR$;$x$):
$y=\dfrac{TR}{5}-2x$.

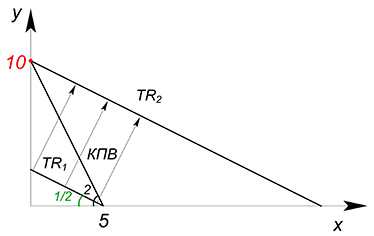
Так как значение $TR$ нам не задано, мы можем сами выбрать оптимальную для нас величину выручки. Будем фиксировать значение $TR$ на разных уровнях (будем преходить на более высокие графики — увеличивать значение выручки), пока не достигнем оптимального ($TR_1 \to TR_2 \to TR_3$). $TR_3$ будет оптимальной величиной, ибо точка, в которой функция выручки касается графика КПВ, будет на границе нашей области производственных возможностей, следовательно, точка касания будет приносить максимальную выручку, а график выручки будет занимать самое высокое положение из всех доступных (выручка будет наибольшей из всех возможных). Если бы мы выбрали меньшее значение выручки, то мы недополучили бы часть денег — мы смогли бы произвести ещё больше товаров $x$ и $y$ и продать их (в этом случае у нас была бы возможность улучшения ситуации). Если бы выбрали большее значение переменной $TR$ ($TR_4$), то не смогли бы произвести соответствующий ей объём товаров, ибо нет такой точки (с точки зрения производства), в которой мы бы получили такую выручку.
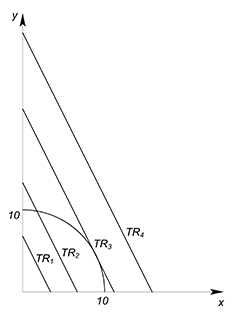
Как мы уже выяснили, оптимальная точка будет лежать на графике КПВ. Её положение на данной линии будет зависеть от соотношения цен товаров $x$ $y$, которые и задают наклон функции выручки.
Линейная функция $y=\dfrac{TR}{5}-2x$ будет иметь постоянный $tg$ угла наклона, равный по модулю $2$. Чтобы найти положение оптимальной точки на графике КПВ необходимо взять производную функции КВП (обычно это делается по переменной $x$) и приравнять её к производной функции выручки (взятой также по $x$ — $y'(x)$) . То есть угол наклона касательной в оптимальной точке должен совпадать с углом наклона функции выручки.
КПВ:
$y=\sqrt{100-x^2}$
$y'(x)=\dfrac{-x}{\sqrt{100-x^2}}$
$TR$:
$y=\dfrac{TR_3}{5}-2x$
$y'(x)=-2$
$\dfrac{-x}{\sqrt{100-x^2}}=-2$
Отсюда находим $x$ и соответствующее ему значение $y$:
$x=4\sqrt5$
$y=2\sqrt5$
Считаем выручку:
$TR=10\cdot{4\sqrt5}+5\cdot{2\sqrt5}=50\sqrt5$
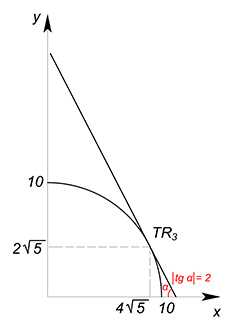
У этой задачи есть более легкое и быстрое решение: подставляем функцию КПВ вместо переменной $x$ в функции выручки:
$TR=10x+5\sqrt{100-x^2}$
Получаем функцию, зависимую от одной переменной. Максимизируем данную функцию обычным способом, беря производную и приравнивая её к 0.
В общем виде:
КПВ:
$y=f(x)$
$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$
Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:
$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$
Берем производные функций КПВ и выручки, приравниваем их:
$f'(x)=-\dfrac{P_x}{P_y}$
Находим оптимальные $x$, $y$, $TR$
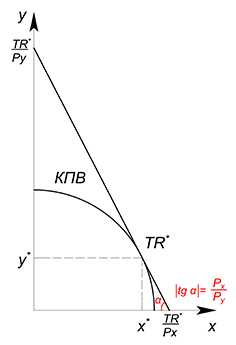
Особого внимания заслуживает случай с линейной функцией КПВ (аналогично поступаем и с выпуклой).
Имеем: КПВ задана функцией $y=10-2x$; $P_x=5$, $P_y=10$. Найти максимальную выручку.
В данном случае у нас нет возможности провести касательную к графику функции КПВ, но мы также можем воспользоваться методом фиксации значения $TR$ и поиска оптимальной точки.
$TR=5x+10y$
$y=\dfrac{TR^*}{10}-\dfrac{x}{2}$
Точно также будем двигать в право функцию выручки, пока она не займет наивысшее положение из всех возможных — пока значение выручки, приносимой комбинациями $x$ и $y$, не станет максимальным из всех доступных. Максимальную выручку в данном случае мы можем получить в точке $y=10$, $x=0$. Считаем $TR=10\cdot{10}=100$. При линейной функции КПВ метод тот же, но функция выручки уже не будет касательной.
Также интересен случай с функцией КПВ, имеющей излом. Воспользуемся тем же методом, что и в двух предыдущих случаях, только опять же здесь функция выручки не будет касательной, проведенной к графику КПВ.
Имеем: график КПВ состоит из двух участков, заданных функциями $y=15-\dfrac{x}{2}$ при $x$ принадлежащем $[0;10]$, $y=30-2x$ при $x$ принадлежащем $[10;15]$. $P_x=P_y=5$.
$TR=5x+5y$
$y=\dfrac{TR}{5}-x$
Двигаем график выручки вправо, пока он не займет максимально доступное значение. В данном случае это значение оказалось в точке излома графика КПВ (такое бывает не всегда). Так случилось, потому что угол наклона графика выручки был меньше угла наклона одной из функций КПВ, но больше угла наклона второй.
$x=y=10$
$TR=5\cdot{10}+5\cdot{10}=100$
 В общем виде:
В общем виде:
КПВ:
$y=f(x)$
$TR$:
$TR=P_x\cdot{x}+P_y\cdot{y}$
$y=\dfrac{TR}{P_y}-\dfrac{P_xx}{P_y}$
Фиксируем $TR$=$TR^*$ на некотором оптимальном уровне:
$y=\dfrac{TR^*}{P_y}-\dfrac{P_x\cdot{x}}{P_y}$
Двигаем функцию выручки вправо, пока не достигнем наибольшего уровня $TR$ из всех возможных. Находим соответствующие точке пересечения значения $x$, $y$, $TR$.
Вообще весь данный метод поиска максимальной выручки основан на фиксации переменной $TR$ и её движении вправо до того момента, пока мы не достигнем максимально высокого уровня графика, которому соответствует максимально возможное значение выручки и оптимальные $x$ и $y$. Просто методы подсчета этих оптимальных значений товаров различны для различных функций КПВ.
Еще одним распространённым типом задач является поиск оптимальных объёмов производства товаров при заданной пропорции их потребления.
КПВ некоторой страны задана функцией $x^2+y^2=100$. Жители потребляют товары $x$ и $y$ только в пропорции $\dfrac{1}{2}$. Найти оптимальные объёмы производства данных благ.
Как обычно начнем с построения КПВ
Далее у нас имеется ограничение — потребление $x$ и $y$ в определенной пропорции. Если $\dfrac{x}{y}=\dfrac{1}{2}$, то $y=2x$. Все точки, для которых верна пропорция $\dfrac{x}{y}=\dfrac{1}{2}$, будут лежать на одной прямой, являющейся лучом решений.
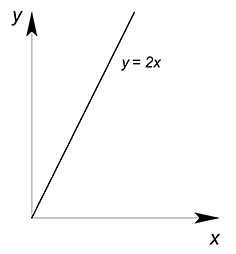
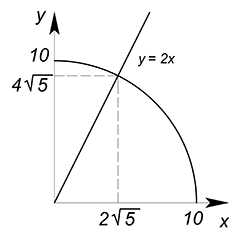
Как известно, эффективная точка будет лежать на границе производственных возможностей. Одновременно он будет принадлежать лучу решений. Найдем её:
$y=\sqrt{100-x^2}=2x$
Из уравнения находим $x$ и соответствующий ему $y$:
$x=2\sqrt{5}$
$y=4\sqrt{5}$
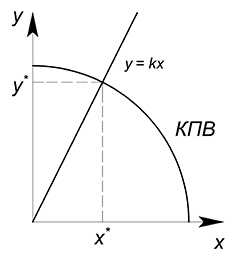
 В общем виде:
В общем виде:
КПВ:
$y=f(x)$
Пропорция производства товаров:
$y=kx$
Отсюда находим $x$ и $y$
iloveeconomics.ru
2.5 Кое-что о кривой торговых возможностей
Определение 1Экономика страны, осуществляющей торговлю с другими странами, называется открытой. Если страна живет изолированно и ни с кем не торгует, её экономика соответственно будет называться закрытой(это будет автаркия).
Страна, участвующая в процессе обмена благами, может обладать абсолютным или сравнительным преимуществом в их изготовлении.
Концепция абсолютного преимущества (Адам Смит)
Абсолютное преимущество — это возможность сделать товар, потратив на его производство меньшее количество ресурсов. Согласно данной теории страна продаёт то благо, в производстве которого имеет абсолютное преимущество. Но ведь некоторые страны могут иметь абсолютное преимущество в производстве обоих благ. Зачем им тогда обмениваться товарами с другими государствами? На этот вопрос может ответить концепция сравнительного преимущества.
Концепция сравнительного преимущества (Давид Рикардо)
Страна продает то благо, в производстве которого имеет сравнительное преимущество, то есть тот товар, который она может производить с меньшими альтернативными издержками.
Взаимовыгодная торговля расширяет набор различных комбинаций благ, доступных для потребления, ибо при торговле страна может специализироваться на производстве того товара, который получается у неё лучше всего, то есть с меньшими альтернативными издержками.
Определение 2
Кривая торговых возможностей показывает все возможные комбинации двух благ, которые страна может получить с учетом взаимовыгодной торговли.
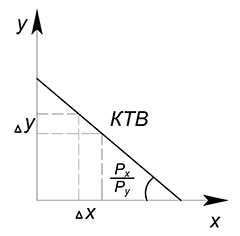
Обычно кривая торговых возможностей представляет собой прямую линию с отрицательным наклоном. Почему отрицательным? Чтобы увеличить количество одного блага, нам необходимо отказаться от какого-то количества другого блага — обменять второе благо на первое. Следовательно, если мы хотим увеличить количество блага $x$ ($\Delta x$), например, нам придется обменять какое-то количество блага $y$ ($\Delta y$) на желаемый объём товара $x$ — положительный прирост аргумента повлечет за собой отрицательный прирост значения функции.
Наклон прямой КТВ определяется пропорцией обмена благ на мировом рынке — отношением цены первого блага, выраженной в единицах второго блага, к единице второго блага (если, например, на мировом рынке мы обмениваем 1 единицу $x$ на 4 единицы $y$, то тангенс угла наклона прямой КТВ будет равен $\dfrac{P_x}{P_y}=\dfrac{4y}{y}=\dfrac{x}{0{,}25x}=4$).
Теперь рассмотрим основные принципы построения КТВ на примере двух наиболее распространенных в задачах случаев — когда у нас линейная КПВ и когда у нас вогнутая КПВ.
Задача 1. КПВ линейна
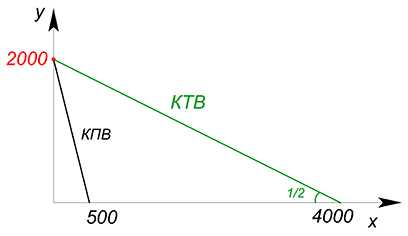
В стране А производится 2000 единиц товара $y$ и 500 единиц товара $x$ с постоянными альтернативными издержками. На мировом рынке единица товара $y$ стоит $2$ единицы товара $x$. Построить КТВ.
Для начала построим КПВ.
КПВ задается функцией $y=2000-4x$.
Теперь разберемся с КТВ. КТВ будет иметь наклон, равный $\dfrac{P_x}{P_y}=\dfrac{x}{2x}=\dfrac{1}{2}$. Обратимся к графику КПВ: нарисуем на нем прямую КТВ с наклоном 0,5 и начнем двигать её вправо, пока на не достигнет наивысшего положения из всех возможных, то есть пока нам не станет доступным наибольшее количество комбинаций товаров $x$ и $y$. Данное движение линии КТВ аналогично методу поиска максимальной выручки. Сначала мы продаём всё, что произвели, потом покупаем все товары на вырученные деньги. Для максимума потребления нужно на продаже заработать максимальное количество денег. Точкой специализации будет точка с координатами (0;2000) (там, где КТВ пересекает КПВ).
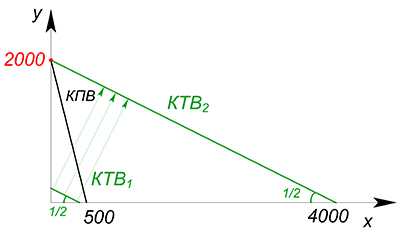
Мы будем производить только благо $y$, ибо альтернативные издержки его производства меньше, чем отношение цен товаров на мировом рынке. Произведя 2000 единиц данного товара, мы можем продать все или часть. Зная угол наклона прямой и координаты 1 крайней точки, можно найти координаты второй и вывести уравнение прямой. Крайние точки нашей максимально высокой КТВ будут иметь координаты (0;2000) (4000;0). Максимальное количество товара $x$, которое можно получить, обменяв максимально возможное количество блага $y$, составляет 4000.
 Задача 2. Вогнутая КПВ
Задача 2. Вогнутая КПВ
В целом принцип построения КТВ в данном случае схож с принципом построения КТВ, рассмотренном в предыдущем пункте. В данной ситуации также необходимо взять прямую с углом наклона, равным соотношению цен товаров, и двигать её вправо до достижения максимально высокого уровня. Точкой специализации здесь в большинстве случаев является точка касания графика КПВ и прямой КТВ.
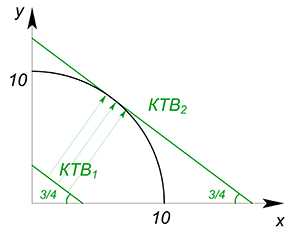
Пусть КПВ некоторой страны задана функцией $y=\sqrt{100-x^2}$, за 1 единицу товара $x$ необходимо отдать $\dfrac{4}{3}$ единицы товара $y$. Построить КТВ.
Построим график КПВ. Теперь КТВ. Данная прямая обладает углом наклона, равным по модулю $\dfrac{3x}{4x}=0{,}75$.
Нарисуем КТВ на одном графике с КПВ, начнем двигать её вверх, пока она не займет максимально высокую позицию. Нетрудно догадаться, что в наивысшем положении она будет касаться графика КПВ. Эта точка касания и будет оптимальной (если мы выберем более низкое положение КТВ, то тем самым мы сократим область возможных комбинаций потребления двух благ, располагающуюся под КТВ, что не очень хорошо). Найдем эту точку — точку специализации.
$КПВ'(x)=y'(x)=\dfrac{-x}{\sqrt{100-x^2}}$
$\dfrac{x}{\sqrt{100-x^2}}=\dfrac{3}{4}$
$x=6$
$y=8$
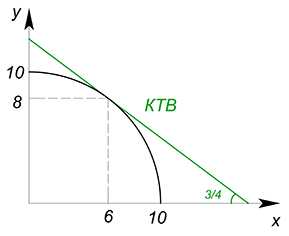
При движении влево вдоль КПВ мы обмениваем $x$ на $y$, при движении вправо, соответственно, $y$ на $x$.
iloveeconomics.ru
Как построить кривую производственных возможностей
Автор КакПросто!
Кривая производственных возможностей — это обычная модель, с помощью которой можно отразить, от какого количества одного блага нам придется отказаться, чтобы получить некоторое количество другого блага. Так как же построить такую модель?
Статьи по теме:
Вам понадобится
- Бумага, текст задачи, линейка, ручка, карандаш, ластик.
Инструкция
Внимательно изучите условие задания. Оно может быть разным. Постарайтесь выяснить, что именно от вас требует автор задачи. В задании может требоваться просто нарисовать примерный график кривой производственных возможностей или построить точный график и по нему найти какие-либо значения в заданной точке. Во всех случаях необходимо сначала построить сам график. График выполняют в декартовой плоскости. Это значит, на графике будет два луча — горизонтальный и вертикальный, выходящих из начала координат. Отметьте нулевую точку, обозначив ее буквой О. Из нее проведите два луча. На одном будет отмечаться количество одного блага, а на втором другого. На концах лучей подпишите, какое именно благо на нем будет отмечаться. Выберите масштаб для чертежа. Намного проще чертить рисунок на клетчатой бумаге, так как каждые два квадратика — это один сантиметр. Для наглядности можно цифры написать ручкой красного цвета. Сам график лучше всего чертить простым карандашом, чтобы в случае ошибки можно было легко стереть и исправить. Теперь обратитесь к тексту задачи и найдите, в каком виде дана кривая производственных возможностей. Она может быть дана в виде линейного уравнения. Тогда необходимо начертить маленькую табличку, в которой внести все данные функции при заданном значении аргумента. После этого по данным таблице постройте график.В задаче могут быть просто даны значения. Тогда нужно просто нанести их на график точками и построить график. Также можно сначала получить уравнение и по нему построить график.
Источники:
- задачи по производственным возможностям
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Альтернативная стоимость и КПВ | Экономика для школьников
1 $y=18-3x$1.1 Найдем $AC_x$ в точке $x=3$ (чему равна $AC$ в точке, и откуда это берется, подробнее можно узнать в подборке $2.1$).
$y'(x)=-3$
Альтернативная стоимость товара $x$ в данном случае постоянна и равна $3$ единицам товара $y$.
1.2 Сейчас мы находимся в точке с координатами $(3;9)$. Максимально возможный объём производства товара $y$ равен $18$. Ищем разницу между максимально возможным количеством производств товара $y$ ($18$) и фактическим производством этого товара в данной точке ($9$): $18-9=9$. Альтернативная стоимость трех единиц продукции $x$ равна $9$ единицам продукции $y$.
1.3 Теперь проделаем тоже самое с товаром $y$. Для удобства можно выразить переменную $x$ через переменную $y$:
$y=18-3x$
$3x=18-y$
$x=6-\dfrac{y}{3}$
Находим производную данной функции:
$x'(y)=-\dfrac{1}{3}$
Альтернативная стоимость товара $y$ в данном случае постоянна и равна $\dfrac{1}{3}$ единицы товара $x$.
1.4 Если мы производим $3$ единицы товара $y$, то максимально можно произвести только $5$ единиц товара $x$. Всего же можно произвести $6$ единиц товара $x$, при $y=0$; $6-5=1$
Альтернативная стоимость трех единиц продукции $y$ равна $1$ единице продукции $x$.
2 $y=100-2x^2$
2.1 $y'(x)=-4x$
$AC_ {5й.ед. x}=4\cdot5=20$
$AC$ пятой единицы товара $x$ равна 20 единицам продукции $y$.
2.2 $y_{max}=100$ (при $x=0$)
$y(5)=100-2\cdot5^2=50$
$100-50=50$
$AC$ пяти единиц товара $x$ равна $50$ единицам товара $y$
2.3 $y(x)=100-2x^2$
$x(y)=\sqrt{50-0{,}5y}$
$x'(y)=\dfrac{-0{,}5}{2\sqrt{50-0{,}5y}}$
$x'(5)=-\dfrac{1}{4\sqrt{47{,}5}}$
$AC$ пятой единицы товара $y$ равняется $\dfrac{1}{4\sqrt{47{,}5}}$ единиц товара $x$
2.4 $x_{max}=5\sqrt 2$ примерно равно $7{,}07$
$x(5)=\sqrt{47{,}5}$, что примерно $6{,}89$
$AC$ пяти единиц товара $y$ составляет $7{,}07-6{,}89=0{,}18$ единиц товара $x$
3 $y=\sqrt{100-x^2}$
3.1 $y'(x)=- \dfrac {x}{\sqrt{100-x^2}}$
$y'(6)=-0{,}75$
Альтернативная стоимость шестой единицы товара $x$ равна $0{,}75$ единицы товара $y$
3.2 Всего можно произвести $10$ единиц продукта $y$. Если $x=6$, $y=8$. $10-8=2$. Альтернативная стоимость шести единиц товара $x$ равна $2$ единицам товара $y$
3.3 Выразим $y$ через $x$:
$x(y)=\sqrt{100-y^2}$
Данная функция такая же как и исходная функция, следовательно, ответы к пунктам $3.3$, $3.4$ аналогичны
iloveeconomics.ru
Акимов — Решение задач — Стр 4
Ответ: производство манго, не уменьшая производства :киви, можно увеличить до 76,67 т за счет выращивания всех :киви в восточной части.
19. Альтернативная стоимость одного часа отдыха в первые
2 °
5 часов составляет 2 рыбки {1: = 2) или 4 :кокоса{ 5 = 4). Альтерна
тивная стоимость | одного часа отдыха во вторые 5 часов составляет |
1,6 рыбки { = | 1,6) или 2,2 :кокоса{151 = 2,2). В последние |
5 часов альтернативная стоимость одного часа отдыха равна 0,8 рыбки
{-i = 0,8) или 1,6 :кокоса{ = 1,6). Поскольку Робинзон один час
отдыха оценивает выше, чем одну рыбку или два :кокоса, то отсюда следует, что в последние 5 часов он однозначно предпочтет отдых.
Пусть Х — :количестворыбок, необходимых для приготовления :ко:кофишбургера, тогда 2Хсоответствующее :количество :кокосов. Тогда 2Х+ Х= 24, та:к :ка:к Робинзон способен употребить не более 24 единиц собранной продукции Х= 8. Следовательно, за день Робинзон будет добывать 16 :кокосов и 8 рыбок: в течение первых пяти часов он добывает 16 :кокосов и 2 рыбки, в течение 3,75 часа из последующих 5 часов добываются остальные 6 рыбок.
Ответ: Р= 8; К= 16.
20. Точка, в :которой производится 100 т фасоли, соответствует верхнему участку КПВ, отражающему производственные возмож ности одного из полей. Из графи:ка КПВ следует, что на этом поле можно произвести либо 150 т фасоли, либо 30 т риса (150120 =30). Следовательно, альтернативные издержки производства 1 т риса со-
ставят 5 т фасоли ( 1 50 = 5).
30
Ответ: 5 т фасоли.
21. а) Поскольку у страныА имеется в наличии 400 единиц тру довых ресурсов, то ее экономика может производить 4000 единиц блага Х (10· 400 = 4000) либо 3200 единиц благаУ (8· 400 = 3200).
Альтернативные издержки производства блага Х в стране А состав-
( 3200
ляют 0,8 единиц блага У 4000 = 0,8). СтранаВ располагает 1000
единиц труда, экономика страны В может производить 24 000 единиц блага Х (24• 1000 = 24 000) либо 30 000 единиц благаУ
studfiles.net
