РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ — ПриМат
Матричные уравнения бывают трех типов.
Пример 1. Чтобы решить уравнение первого типа нужно обе части уравнения умножить на обратную к матрице слева.
,
, полученную матрицу транспонируем и умножим на . Обратная матрица к равна .
, . Сделаем проверку . Уравнение решили правильно.
Пример 2. Чтобы решить уравнение второго типа нужно обе части уравнения умножить на обратную к матрице справа.
Матрица обратная к равна .
Пример 3. Чтобы решить уравнение третьего типа нужно обе части уравнения умножить на обратную к матрице справа и на обратную матрице слева.
. Обратная матрица к равна обратная матрица к равна . .
Проверка .
Пример 4. Случай когда обратная матрица не существует.
.
Матрицу запишем как , .
\begin{cases}
3 \cdot x_{1}+4 \cdot x_{2} = 2\\
6 \cdot x_{1}+8 \cdot x_{2} = 4\\
6 \cdot x_{3}+8 \cdot x_{4}=18
\end{cases}
Эта система эквивалентна
\begin{cases}
3 \cdot x_{1}+4 \cdot x_{2} = 2\\
3 \cdot x_{3}+4 \cdot x_{4} = 9
\end{cases}
Решив данную систему получим общей вид решения
Литература
Решение матричных уравнений
Лимит времени: 0
Навигация (только номера заданий)
0 из 2 заданий окончено
Вопросы:
- 1
- 2
Информация
Обращение матриц. Решение матричных уравнений
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 2
Ваше время:
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Нет рубрики 0%
Загрузка
Имя: E-Mail: Капча:- 1
- 2
- С ответом
- С отметкой о просмотре
Задание 1 из 2
1.
Количество баллов: 1Решите матричное уравнение
$$X \cdot \begin{pmatrix} 5 & 3 & 1 \\ 1 & -3 & -2 \\ -5 & 2 & 1 \end{pmatrix}=\begin{pmatrix} 1 & -3 & 0 \\ 10 & 2 & 7 \\ 10 & 7 & 8 \end{pmatrix}$$- $$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & -9 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 2 & -3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}$$
Правильно
Неправильно
Задание 2 из 2
2.
Количество баллов: 1Решите матричное уравнение
$$\begin{pmatrix} 2 & -3 & 1 \\ 14 & -5 & 2 \\ 5 & -7 & 3 \end{pmatrix} \cdot X \cdot \begin{pmatrix} 9 & 7 & 6 \\ 1 & 1 & 2 \\ 1 & 1 & 1 \end{pmatrix}=\begin{pmatrix} 2 & 0 & -2 \\ 18 & 12 & 9 \\ 23 & 15 & 11 \end{pmatrix}$$- $$ \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 2 & -3 & 1 \end{pmatrix}$$
- $$ \begin{pmatrix} 1 & 1 & -1 \\ 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$$
Правильно
Неправильно
Таблица лучших: Решение матричных уравнений
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Поделиться ссылкой:
- Нажмите здесь, чтобы поделиться контентом на Facebook. (Открывается в новом окне)
- Нажмите, чтобы поделиться на LinkedIn (Открывается в новом окне)
- Нажмите, чтобы поделиться на Twitter (Открывается в новом окне)
- Нажмите, чтобы поделиться на Reddit (Открывается в новом окне)
- Нажмите для печати (Открывается в новом окне)
Похожее
ib.mazurok.com
Матричные уравнения
Любая система
линейных уравнений может быть легко
переписана в матричной
форме: 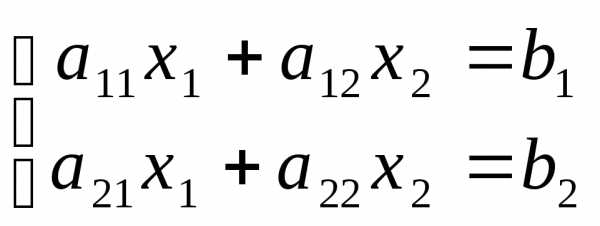

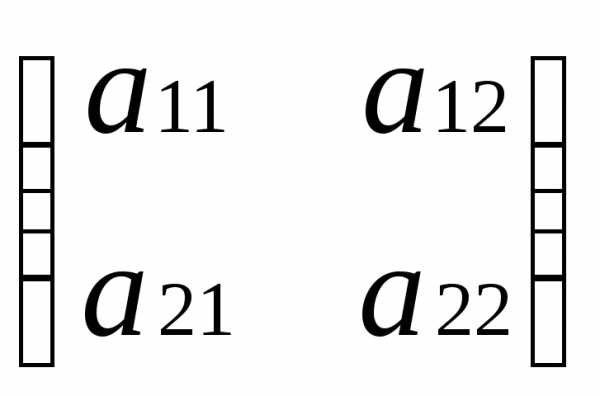
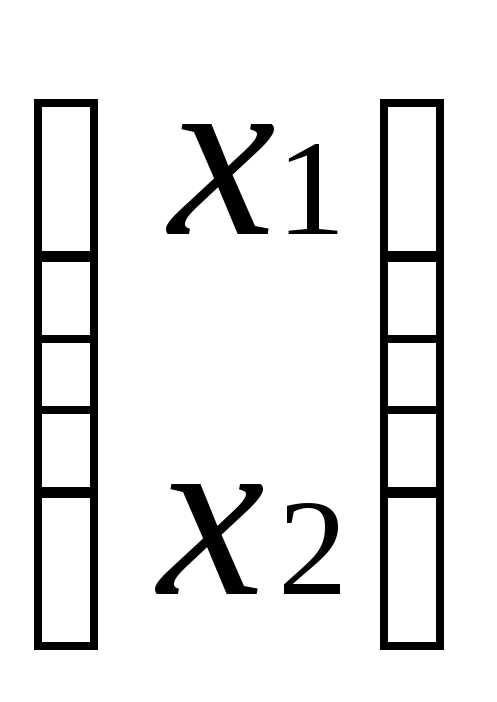 =
= или А
или А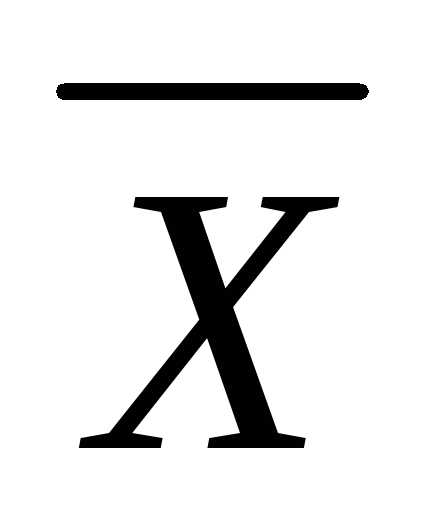 =
=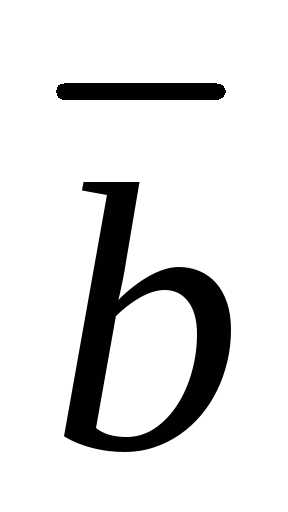 .
.
Умножим
полученное матричное уравнение на
матрицу А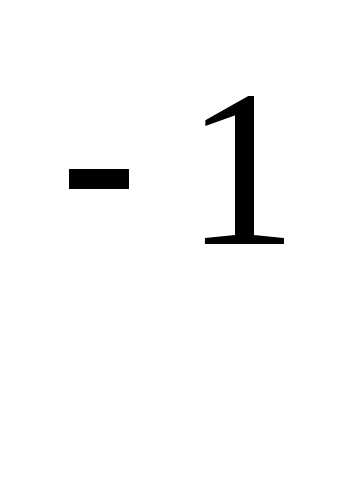 слева: А
слева: А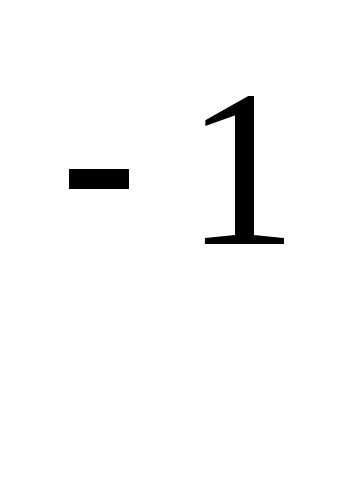 А
А =
А
=
А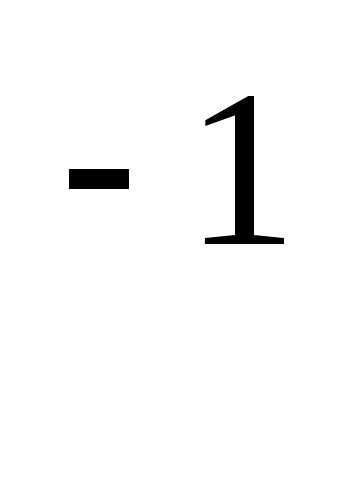
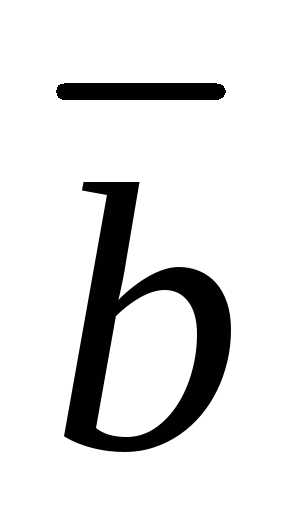 ,
откуда
,
откуда 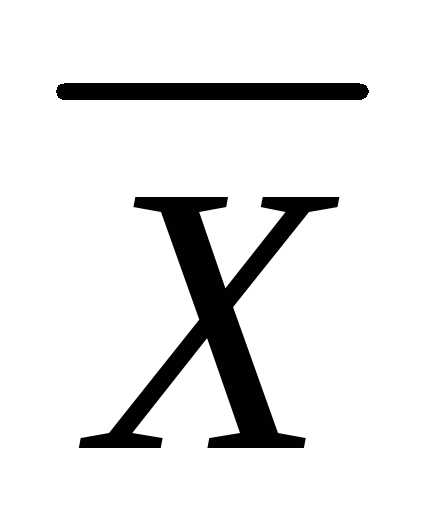 =
А
=
А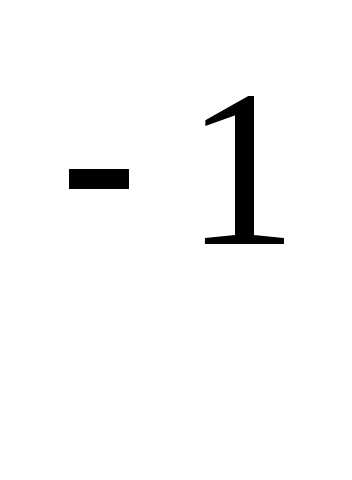
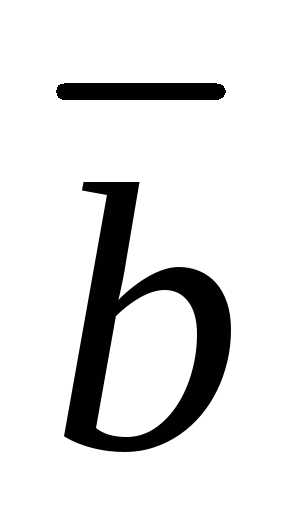 ,
т.е. при известной матрице А
,
т.е. при известной матрице А можно получить решение
можно получить решение 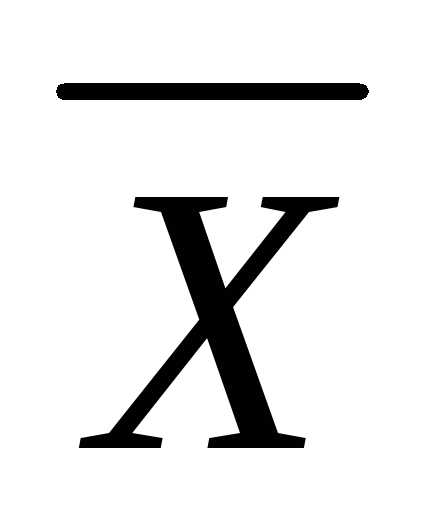 для произвольных
значений bв
векторе
для произвольных
значений bв
векторе  .
Относительно привычного нам вектора
.
Относительно привычного нам вектора 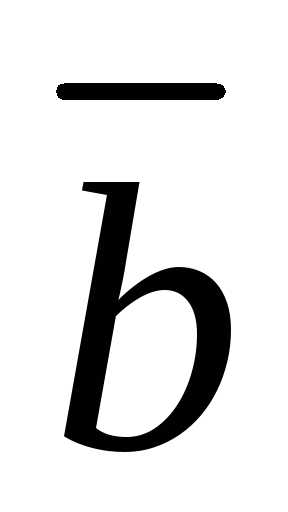 отметим, что
можно решать и самые общие уравнения,
в которых неизвестными являются уже не
векторы, а матрицы, причем не всегда
квадратные: АХ=В
отметим, что
можно решать и самые общие уравнения,
в которых неизвестными являются уже не
векторы, а матрицы, причем не всегда
квадратные: АХ=В  Х= АВ; ХА=В
Х= АВ; ХА=В  Х= В А
Х= В А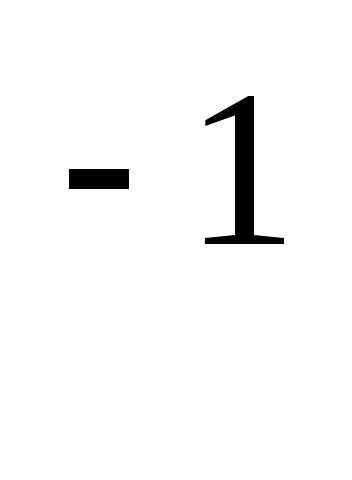 — здесь для
получения ответа надо умножить уравнение
на А
— здесь для
получения ответа надо умножить уравнение
на А справа.
справа.
Степень и функции матриц
Для
квадратных матриц целая степень матрицы определяется так же, как и для
обычных чисел: А=ААА…А(n сомножителей). При этом полагается: А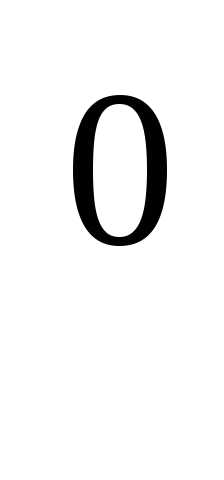 =Е; А
=Е; А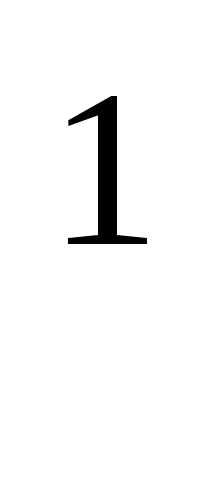 =А.
=А.
В
целом ряде случаев необходимо использовать
отрицательную степень матрицы. Она
может быть введена по правилу: А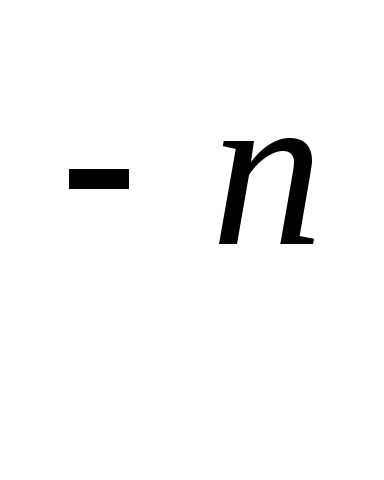 =(А
=(А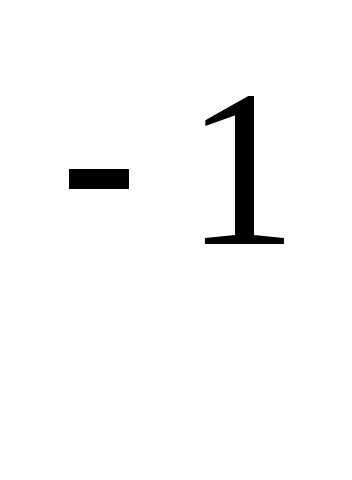 )
)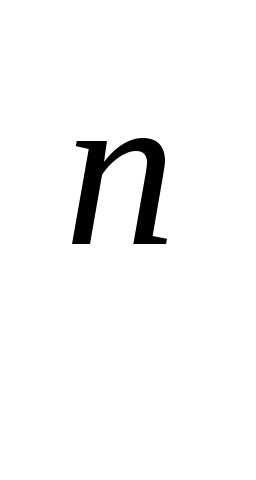 .
.
С
помощью этих формул можно решать задачи
типа: если известен закон изменения f(x), то: определить f(A)
— функцию
от матрицы.
Например, если f(x)=2x -3x+5,
тоf(A)=
2A
-3x+5,
тоf(A)=
2A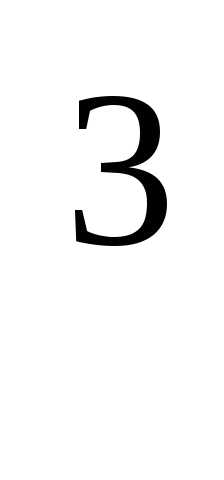 -3A+5E.
Если f(x)=4x
-3A+5E.
Если f(x)=4x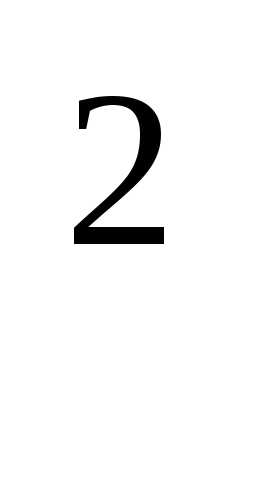 +
+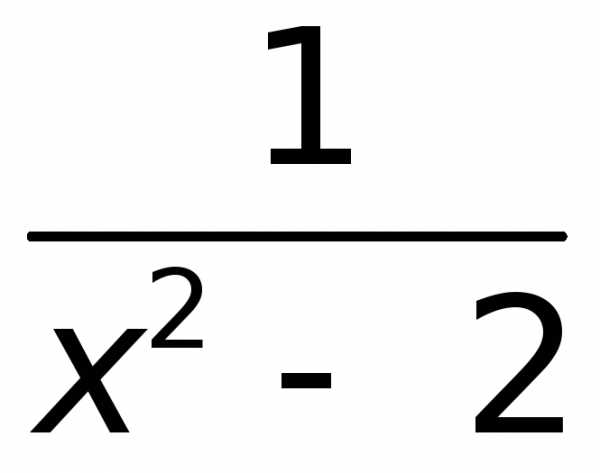 , тоf(A)=4A
, тоf(A)=4A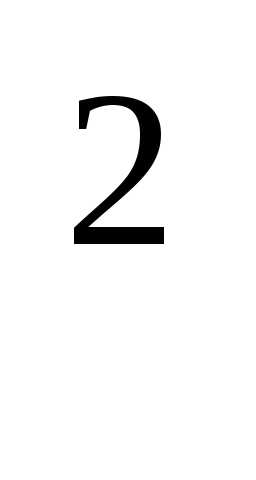 +(A
+(A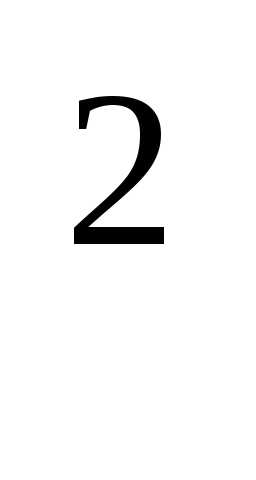 —2E)
—2E) .
.
Ясно, что матрица А должна быть такой, чтобы все операции имели смысл. Единичная матрица Е использована для формального преобразования обычных чисел к матричной записи. По размерности она должна соответствовать матрице А.
Понятие о проблеме собственных значений матрицы
В большом ряде моделей процессов и в задачах анализа требуются как оценка имеющегося объекта, так и сравнение между собой различных моделей. Так как матрицы — один из наиболее распространенных способов описания экономических процессов и объектов, то использование их универсальных характеристик удобно для задач эталонного сравнения. Собственные значения и векторы и представляют собой такие характеристики.
Собственным
вектором квадратной матрицы А называется вектор 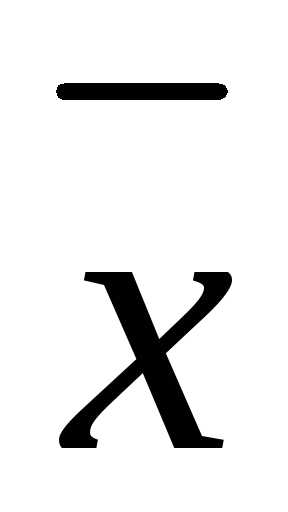
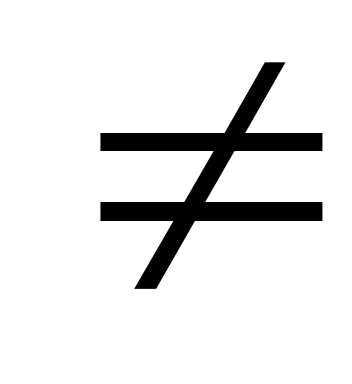 0,
удовлетворяющий матричному уравнениюА
0,
удовлетворяющий матричному уравнениюА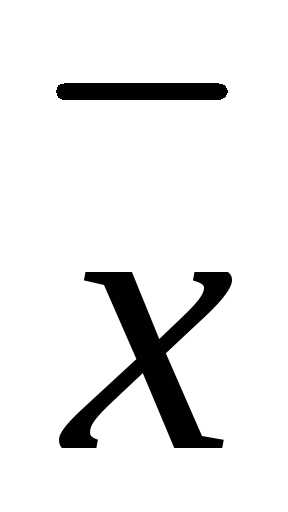 =
=
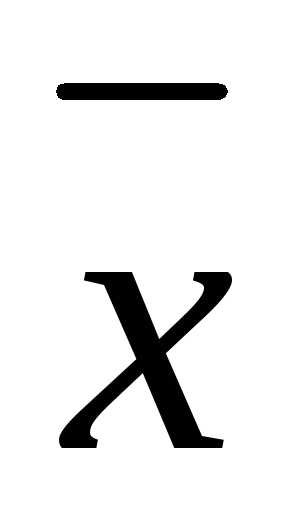 ,
где
,
где — собственное значение матрицы,
соответствующее вектору
— собственное значение матрицы,
соответствующее вектору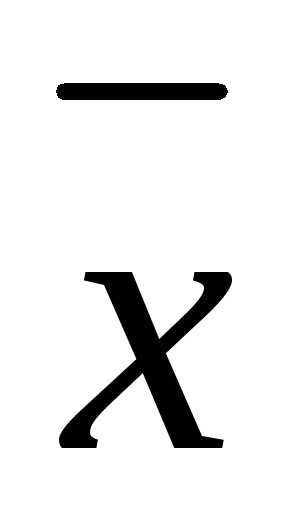 .
.
Представим это равенство в виде
(А- Е)
Е) 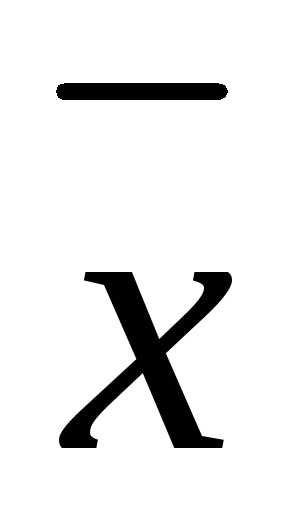 =0.
=0.
Чтобы
это однородное матричное уравнение
имело ненулевые решения 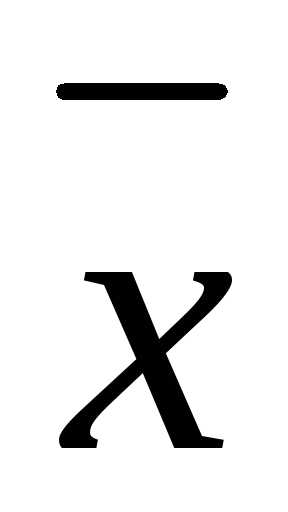 ,
необходимо и достаточно равенство нулю
определителя
,
необходимо и достаточно равенство нулю
определителя
D(А- Е)=0.
Е)=0.
Это — характеристическое уравнение (степени n) для матрицы А.
Отсюда
получаем сначала собственные
значения  ,
а затемсобственные
векторы
,
а затемсобственные
векторы 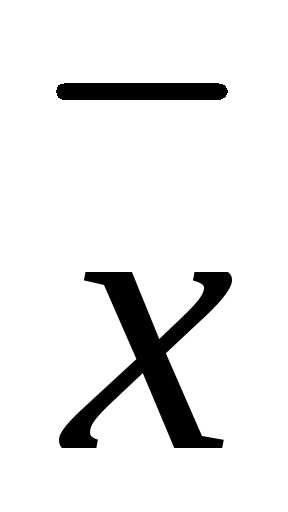 .
Общее число этих характеристик равно
порядкуn матрицы А.
.
Общее число этих характеристик равно
порядкуn матрицы А.
Рассмотрим
пример: определить собственные значения
матрицы А=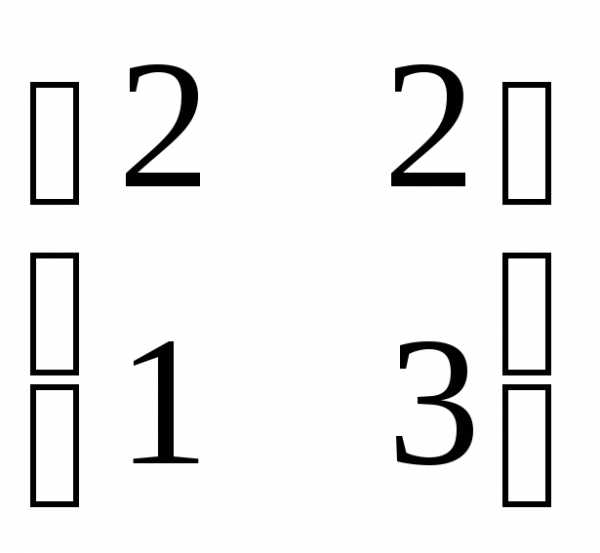 .
.
Составим: А- Е=
Е= —
— 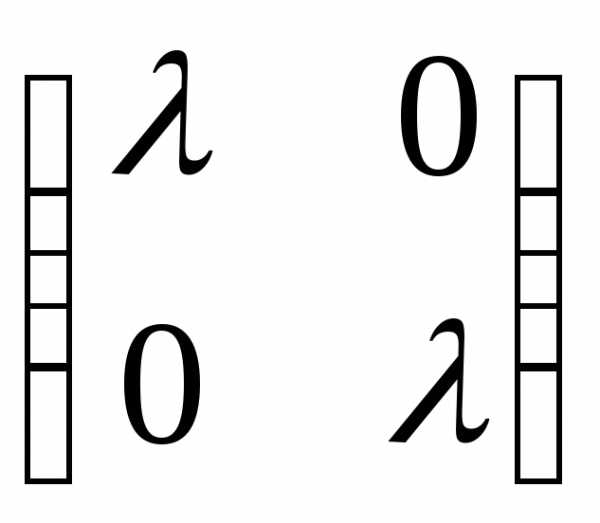 =
= 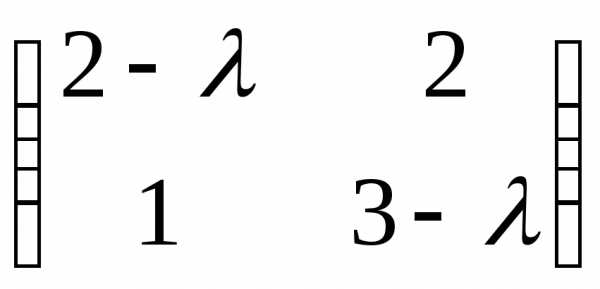 ;
D(А-
;
D(А- Е)
=
Е)
= 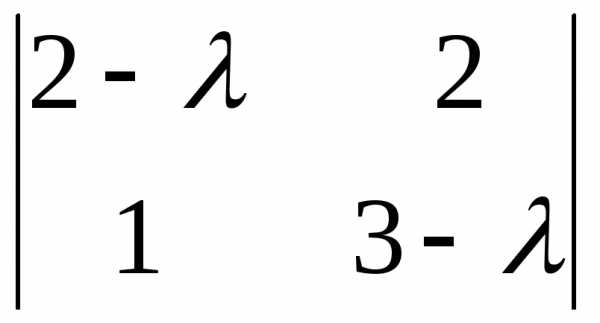 =
0 или
=
0 или
(2- )(3-
)(3- )-2=0,
откуда получим два собственных значения:
)-2=0,
откуда получим два собственных значения:
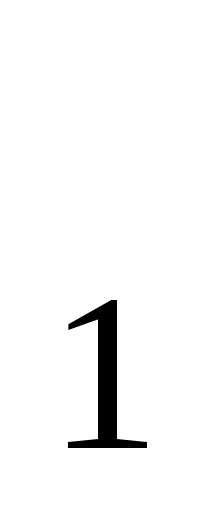 =1;
=1;
 =4.
=4.
Определим
собственные векторы для каждого  :
:
1.  =1
=1
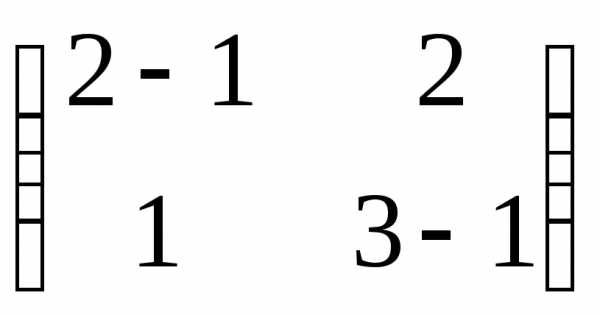
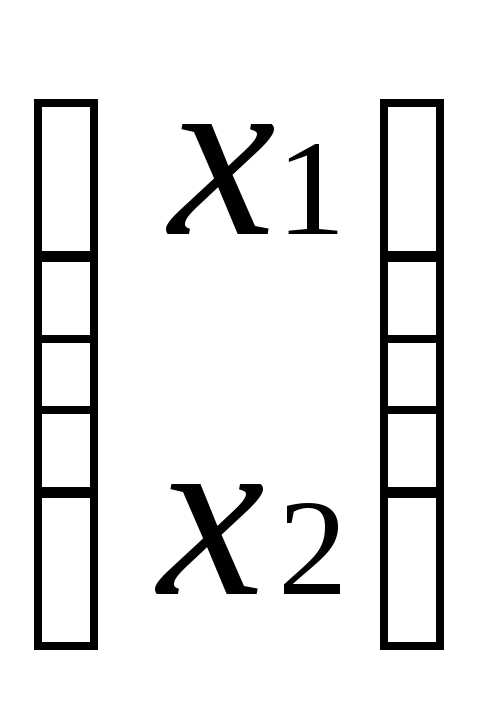 =0,
т.е.
=0,
т.е. 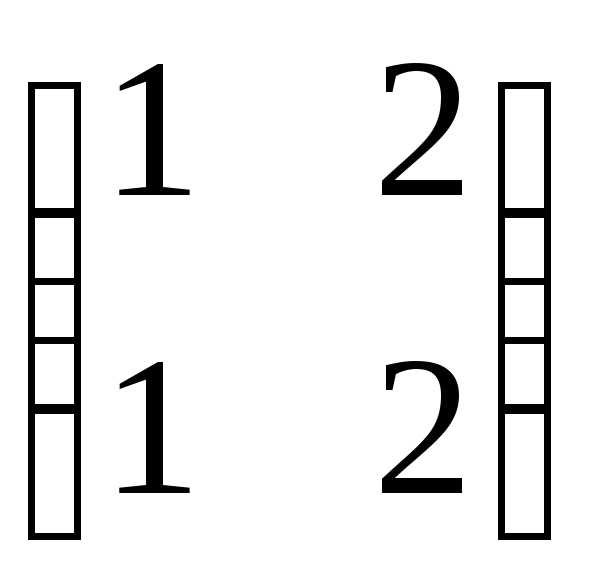
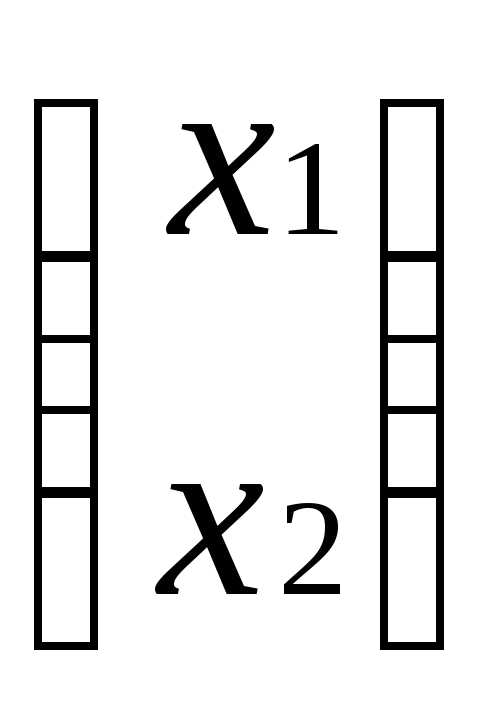 =0
или х
=0
или х +2х
+2х =0.
=0.
Собственный
вектор определится с точностью до
постоянного множителя с. Положим х =1,
тогда х
=1,
тогда х =
-2 и
=
-2 и
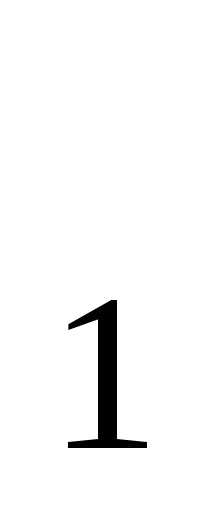 =с
=с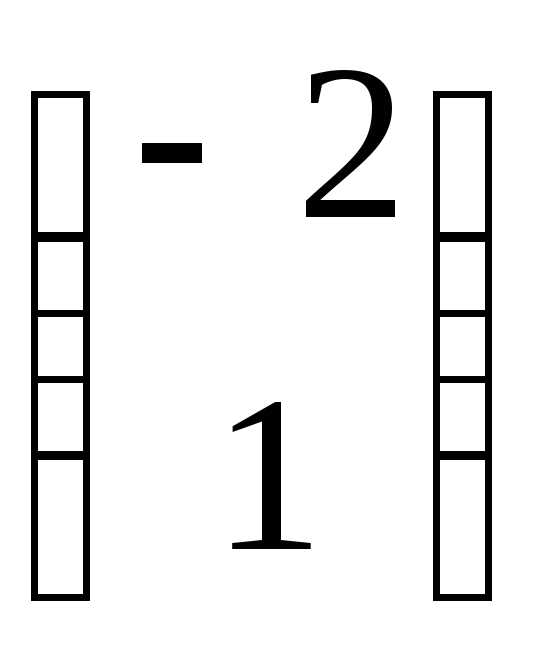 .
.
2.  =4
=4
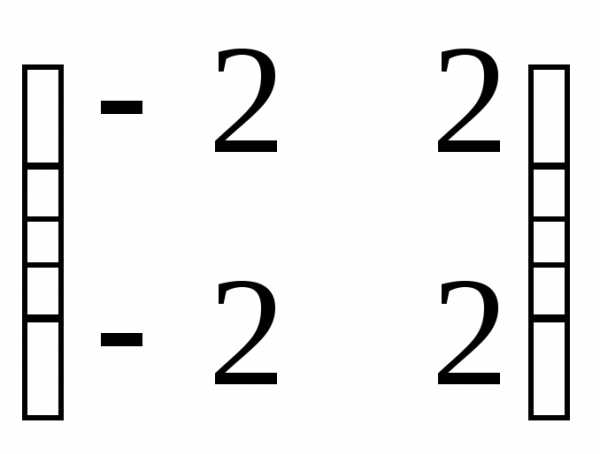
 =0
и х
=0
и х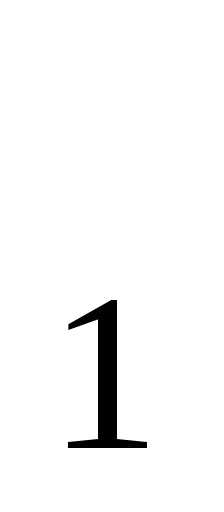 +2х
+2х =0.
Полагая х
=0.
Полагая х =1,
получим х
=1,
получим х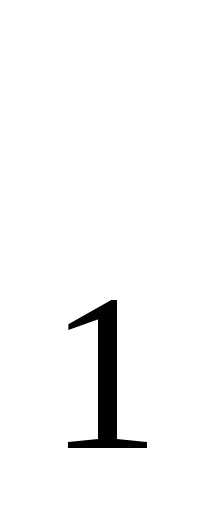 =1
и вектор
=1
и вектор 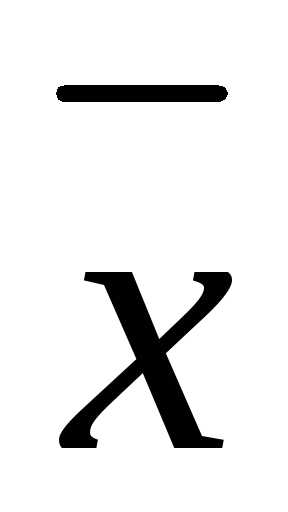
 =с
=с .
.
Вычисленные собственные значения обычно проверяются по их свойствам:
1. Сумма собственных значений равна сумме
диагональных элементов матрицы А (следу матрицы А):  +
+
 +…
+…
 =а
=а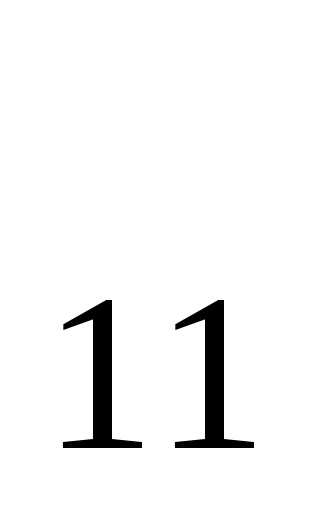 +а
+а +…+а
+…+а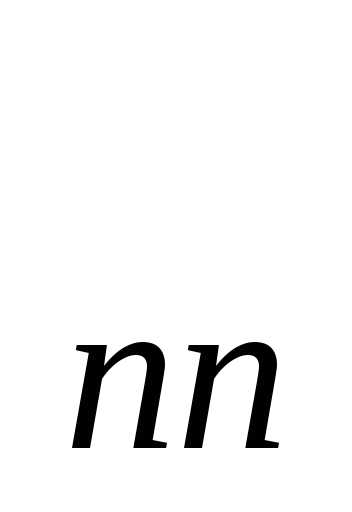 .
.
2. Произведение собственных значений связано с
определителем D(A)
матрицы А формулой: 

 …
…
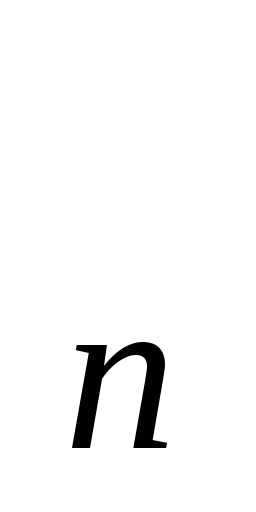 =(-1)
=(-1)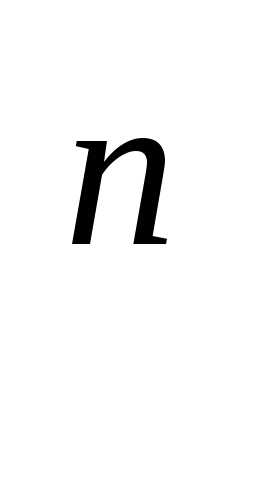 D(A).
D(A).
3.
Если матрица А симметрична,
то ее собственные значения всегда
действительны, т.е. 
 R.
R.
Описанное выше, в целом, представляет
собой полную
проблему собственных значений — определяются
все  и
и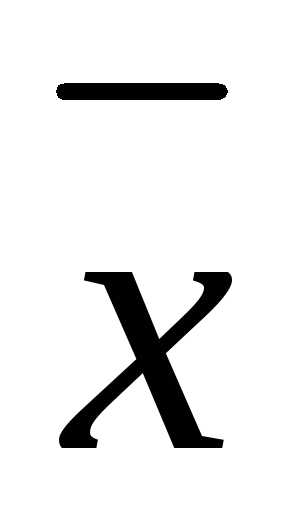 для
матрицыА.
В большинстве же практических задач
это не нужно — итоговое заключение
делается по минимальному (или максимальному)
собственному значению и соответствующему
ему вектору. При этом нет необходимости
решать сложное характеристическое
уравнение полностью — надо найти только
один нужный корень. Такая задача
называется частичной
проблемой собственных значений. Для ее решения
имеются достаточно простые и быстрые
методы.
для
матрицыА.
В большинстве же практических задач
это не нужно — итоговое заключение
делается по минимальному (или максимальному)
собственному значению и соответствующему
ему вектору. При этом нет необходимости
решать сложное характеристическое
уравнение полностью — надо найти только
один нужный корень. Такая задача
называется частичной
проблемой собственных значений. Для ее решения
имеются достаточно простые и быстрые
методы.
studfiles.net
Матрица и характеристическое уравнение
| Вы ввели следующие элементы массива |
| Полиминальная функция от матрицы, массива |
Давайте зададимся задачей, которая формулируется так:
Существует функция от одной переменной, которая задана в матричном виде.
Не думайте что таких функций не существуют. Самый первый пример который приходит на ум это практические задачи по экономике.
Но речь в общем то не о том, что бы приводить конкертные примеры из жизни.
Теперь стоит задача, а как в общем то исследовать такую матричную функцию на максимумы, минимумы?
Конечно, можно подставляя вместо неизвестного параметра какое либо числовое значение, узнавать значение функции и двигаясь так, можно медотом приближения, вернее «методом тыка» обнаружить минимумы и максимумы, а также корни этого матричного уравнения.
Второй вариант, это разложить эту матрицу в полиминальную функцию. Да это самый разумный, но не самый простой способ, хотя в нашем примере такое решение можно применить.
Сократим и получим наше окончательной ответ
Неплохо, но что делать если матрица иметт размерность в 4, 5 или десять столбцов?
Неуверен что кто то в твердой памяти возьмется решить матрицу 5*5 при например 12 неизвестных.
А если элементы матрицы являются комплексными?? Тот-же..
Для того, что бы не ломать мозги, а также легко превращать матричные функции в полиноминальные и создан этот бот
Update 17.08.2015: То что мы вычисляем в этом материале ,в высшей математике широко применяется и называется характеристическим уравнением. Такие характеристические уравнения например используются для приведения кривой или поверхности второго порядка в канонический вид.
Синтаксис
Для тех кто использует XMPP клиентов то достаточно ввести команду poly_m элементы матрицы
Элементы матрицы — должны быть разделены пробелом. Элеметны могут любыми числами или функциями. В том числе и комплексными
Считаем матрицы только не больше 8*8. Будьте внимательны в расчетах.
Пример
Сразу возьмем для примера тот случай который мы привели выше.
Итак дана функция
и 9 неизвестных ячеек которые равны x. Привести данную функция в полиноминальную
Ну что, решите ручками? 🙂
Попробуем скормить эту матрицу нашему боту
poly_m x 8 x x 6 -4 9 x x 0 2 -2 0 1 -3 -1 x x x 0 5 -2 -7 0 x
В ответ получаем
это и есть наша полиноминальная функция от матрицы.
Такой вид, предоставляет совсем другие возможности. Эту функцию проще исследовать, и на основе анализа принимать те или иные решения.
Проверим? Да запросто
определим чему равна полученная функция ну например для x=3, и определим чему равен детерминант матрицы если в матрице мы все неизвестные x заменим значением -3
И в том и другом случае мы получим значение 900. Что доказывает что расчеты произведены верно.
Усложним нашу задачу и матрица у нас будет комплексная
Даем боту вот такую строку 0:1 x -2 0:-1 0:1 0:-1 9 x x 0 2 -2 0 1 -3 -1 x -x 3*x 0 x 0:-2 -7:1 x 2
Ответ не заставит нас долго ждать и следующая функция и будет ответом
Давайте проверим и её
Пусть х= 1-i
Функция дает ответ -680.0000000001-1248i
Если в матрице мы заменим все неизвестные на это число и посчитаем детерминанат то получим тоже самое значение.
- Метод Горнера. Деление многочлена. >>
abakbot.ru
