Линейное уравнение с двумя переменными и его график. Видеоурок. Алгебра 7 Класс
На данном уроке мы рассмотрим уравнение с двумя переменными, дадим его определение и построим график.
Тема: Линейная функция
Урок: Линейное уравнение с двумя переменными и его график
Мы познакомились с понятиями координатной оси и координатной плоскости. Мы знаем, что каждая точка плоскости однозначно задает пару чисел (х; у), причем первое число есть абсцисса точки, а второе – ордината.
Мы будем очень часто встречаться с линейным уравнением с двумя переменными, решением которого и есть пара чисел, которую можно представить на координатной плоскости.
Уравнение вида:
, где a, b, с – числа, причем
Называется линейным уравнением с двумя переменными х и у. Решением такого уравнения будет любая такая пара чисел х и у, подставив которую в уравнение мы получим верное числовое равенство.
Пара чисел будет изображаться на координатной плоскости в виде точки.
У таких уравнений мы увидим много решений, то есть много пар чисел, и все соответствующие точки будут лежать на одной прямой.
Рассмотрим пример:
Пример 1:
; ; ;
Чтобы найти решения данного уравнения нужно подобрать соответствующие пары чисел х и у:
Пусть , тогда исходное уравнение превращается в уравнение с одной неизвестной:
,
То есть, первая пара чисел, являющаяся решением заданного уравнения (0; 3). Получили точку А(0; 3)
Пусть . Получим исходное уравнение с одной переменной: , отсюда , получили точку В(3; 0)
Занесем пары чисел в таблицу:
Построим на графике точки и проведем прямую: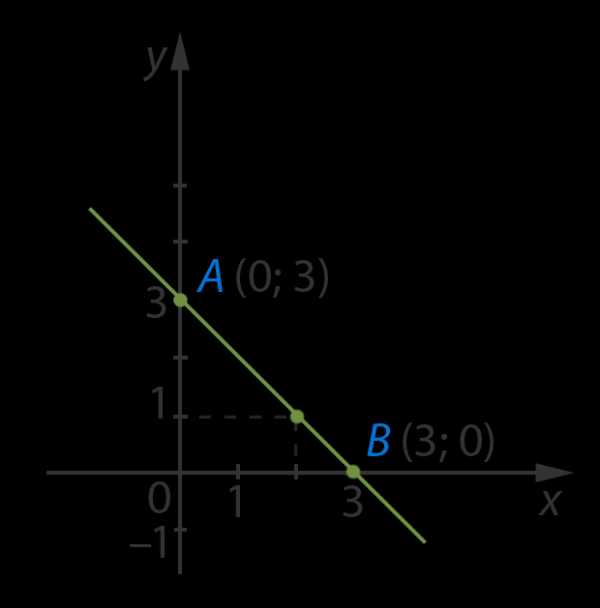
Отметим, что любая точка на данной прямой будет решением заданного уравнения. Проверим – возьмем точку с координатой и по графику найдем ее вторую координату. Очевидно, что в этой точке
interneturok.ru
Система линейных уравнений с двумя переменными. Методы решения систем уравнений.
Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как можно решить систему уравнений с двумя переменными?
Системы уравнений с двумя переменными можно решить методом подстановки:
Пример 1. Решить систему уравнений методом подстановки \(\begin{equation*} \begin{cases} 2x+y=15 \\ 3x-y=5 \end{cases} \end{equation*}\)
Решим систему методом подстановки: выразим y из второго уравнения и подставим в первое уравнение. Подставим x в первое уравнение и найдем y:
Системы уравнений с двумя переменными можно решить методом сложения:
Пример 2. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решение:
Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений. Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.
Выводы:
- Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
- Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
- Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
- Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными
Что такое линейное уравнение с двумя переменными?
С линейными уравнениями с двумя переменными мы имеем дело в 7, 8 классах и в более старших.
Линейное уравнение с двумя переменными определение
Определение линейного уравнения с двумя переменными
Уравнение вида ax + by = c называется линейными уравнениями с двумя переменными.
Здесь a, b и c – числа, x и y – переменные.
Линейное уравнение с двумя переменными пример
Пример линейного уравнения с двумя переменными
8x + 4y = 5
В этом уравнении две переменные x и y, a = 8, b = 4, c = 5.
Линейное уравнение с двумя переменными
Решением линейного уравнения с двумя переменными является пара значений переменных, при подстановке которых в уравнение оно обращается в истинное равенство.
Решите линейное уравнение с двумя переменными
Как решать линейные уравнения с двумя переменными?
Пример. Решите уравнение
8x + 4y = 5
Выразим переменную игрек через переменную икс.
Для этого перенесем 8x в правую часть уравнения, поменяв знак на противоположный
4y = -8x + 5
Разделим обе части уравнения на четыре
y = -2x + 1,25
Выбираем произвольное значение икса, пусть это будет 7.
Подставляем 7 вместо икса и находим значение игрека
y = -2 * 7 + 1,25 = −12,75
Теперь у нас есть пара значений переменных x = 7 и y = −12,75, обычно эту пару чисел записывают в скобках (7; −12,75), при подстановке которых в уравнение оно обращается в верное равенство.
Таким образом решением нашего уравнения является пара чисел (7; −12,75).
Есть ли другие решения уравнения?
Есть и их бесконечно много. Выбирая произвольно значения икса мы расчитываем соответствующее значение игрека и получаем очередное решение уравнения.
Например, если взять x = 2, то
y = -2 * 2 + 1,25 = −2,75
Мы получили новую пару чисел (2; −2,75), которая является решенеием уравнения.
www.sbp-program.ru
Конспект урока на тему «Линейные уравнения с двумя переменными
КОНСПЕКТ УРОКА
Линейные уравнения с двумя переменными
Класс: 7
УМК: Алгебра 7 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н.Г. Миндюк и др.]; под ред. С.А. Теляковского. – 2-е изд. – М.: Просвещение, 2014
Тема: Линейные уравнения с двумя переменными
Цели: Познакомить учащихся с понятиями линейного уравнения с двумя переменными и его решения, научить выражать из уравнения х через у или у через х.
Формируемые УУД:
Познавательные: выдвигать и обосновывать гипотезы, предлагать способы их проверки
Регулятивные: сличать способ и результат своих действий с заданным эталоном, обнаруживать отклонения и отличия от эталона; составлять план и последовательность действий.
Коммуникативные: устанавливать рабочие отношения; эффективно сотрудничать и способствовать продуктивной кооперации.
Личностные: формирование навыков организации анализа своей деятельности
Оборудование: компьютер, мультимедийный проектор, экран
Ход урока:
I Организационный момент
— Послушайте сказку про Деда-Равняло и догадайтесь, о чем мы сегодня будем говорить
Сказка «Дед-Равняло»
Жил в избушке на лесной опушке дед по прозвищу Равняло. Любил он с числами подшучивать. Возьмет дед выстроит по обе стороны от себя числа, соединит их знаками, а самые резвые в скобки возьмет, но следит, чтобы одна часть равнялась другой. А потом какое-нибудь число спрячет под маской «икс» и попросит своего внука, маленького Равнялку, найти его. Равнялка хоть и мал, но дело свое знает: быстро перегонит все числа, кроме «икса», в другую сторону и знаки не забудет у них изменить на противоположные. А числа слушаются его, быстро выполняют по его приказу все действия, и «икс» известен. Дед смотрит на то, как ловко у внучка все получается и радуется: хорошая ему смена растет.
— Итак, о чем идет речь в этой сказке? (об уравнениях)
II. Давайте вспомним всё, что мы знаем о линейных уравнениях и попробуем провести параллель между известным нам материалом и новым материалом.
Какой тип уравнения нам известен? (линейное уравнение с одной переменной)
Вспомним определение линейного уравнения с одной переменной.
Что называется корнем линейного уравнения с одной переменной?
Сформулируем все свойства линейного уравнения с одной переменной.
Заполняется 1 часть таблицы
ах=в, где х – переменная, а,в- числа.Пример: 3х = 6
Значение х, при котором уравнение обращается в верное равенство
1) перенос слагаемых из одной части уравнения в другую, изменив их знак на противоположный.
2) обе части уравнения умножить или разделить на одно и тоже, не равное нулю число.
Линейное уравнение с двумя переменной.
ах + ву = с, где х,у – переменные, а,в.с – числа.
Пример:
х – у = 5
х + у = 56
2х + 6у =68
Значения х, у, обращающие уравнение в верное равенство.
х=8; у=3 (8;3)
х=60; у = — 4 (60;-4)
Верны свойства 1,2.
3) равносильные уравнения:
х-у=5 и у=х-5
(8;3) (8;3)
После того, как заполнили первую часть таблицы, опираясь на аналогию, начинаем заполнять вторую строку таблицы, тем самым узнавать новый материал.
III. Обратимся к теме: линейное уравнение с двумя переменными. Само название темы наталкивает на мысль, что нужно вводить новую переменную, например у.
Существует два числа х и у, одно больше другого на 5. Как записать соотношение между ними? (х – у = 5) это и есть линейное уравнение с двумя переменными. Сформулируем по аналогии с определением линейного уравнения с одной переменной определение линейного уравнения с двумя переменными (Линейным уравнением с двумя переменными называется уравнение вида ax + by = c, где a,b и c – некоторые числа, а x и y –переменные).
Уравнение x – y = 5 при x = 8, y = 3 обращается в верное равенство 8 – 3 = 5. Говорят, что пара значений переменных x = 8, y = 3 является решением этого уравнения.
— Сформулируйте определение решения уравнения с двумя переменными (Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство)
Пары значений переменных иногда записывают короче: (8;3). В такой записи на первом месте пишут значение x а на втором — y.
Уравнения с двумя переменными, имеющие одни и те же решения (или не имеющие решений), называются равносильными.
Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:
Если в уравнении перенести любой член из одной части в другую, изменив его знак, то получится уравнение равносильное данному.
Если обе части уравнения умножить или разделить на одно и то же число(не равное нулю), то получится уравнение равносильное данному.
Пример 1. Рассмотрим уравнение 10x + 5y = 15. Используя свойства уравнений, выразим одну переменную через другую.
Для этого сначала перенесем 10x из левой части в правую, изменив его знак. Получаем равносильное уравнение 5y = 15 — 10x.
Разделим каждую часть этого уравнения на число 5, получим равносильное уравнение
у = 3 — 2x. Таким образом, мы выразили одну переменную через другую. Пользуясь этим равенством, для каждого значения x можно вычислить значение y.
Если x = 2, то y = 3 — 2· 2 = -1.
Если x = -2, то y = 3 — 2· (-2) = 7. Пары чисел (2; -1), (-2; 7) – решения данного уравнения. Таким образом, данное уравнение имеет бесконечно много решений.
Из истории. Проблема решения уравнений в натуральных числах подробно рассматривалась в работах известного греческого математика Диофанта (III в.). В его трактате «Арифметика» приводятся остроумные решения в натуральных числах самых разнообразных уравнений. В связи с этим уравнения с несколькими переменными, для которых требуется найти решения в натуральных или целых числах, называют диофантовыми уравнениями.
Пример 2. Мука расфасована в пакеты по 3 кг и по 2 кг. Сколько пакетов каждого вида надо взять, чтобы получилось 20 кг муки?
Допустим, что надо взять x пакетов по 3 кг и y пакетов по 2 кг. Тогда 3x + 2y = 20. Требуется найти все пары натуральных значений переменных x и y, удовлетворяющих этому уравнению. Получаем:
2y = 20 — 3x
у =
Подставляя в это равенство вместо x последовательно все числа 1,2,3 и т.д., найдем при каких значениях х, значения y являются натуральными числами.
Получаем: (2;7), (4;4), (6;1). Других пар, удовлетворяющих данному уравнению нет. Значит надо взять либо 2 и 7, либо 4 и 4, либо 6 и 1 пакетов соответственно.
IV. Работа по учебнику (устно) № 1025, № 1027(а)
Самостоятельная работа с проверкой в классе.
1. Выпишите линейно уравнение с двумя переменными.
а ) 3х + 6у = 5 в) ху = 11 б) х – 2у = 5
2. Является ли пара чисел решением уравнения?
2х + у = -5 (-4;3), (-1;-3), (0;5).
3. Выразите из линейного уравнения
4х – 3у = 12 а) х через у б) у через х
4. Найдите три, каких либо решения уравнения.
х + у = 27
V. Итак, подведем итог:
Дать определение линейного уравнения с двумя переменными.
Что называется решением (корнем) линейного уравнения с двумя переменными.
Сформулировать свойства линейного уравнения с двумя переменными.
Выставление оценок.
Домашнее задание: п. 40, № 1028, №1032
infourok.ru
«Линейные уравнения с двумя переменными».
7 класс.
Тема урока: «Линейные уравнения с двумя переменными».
Тип урока: урок изучения нового.
Цели урока:
Образовательные: ввести понятия линейного уравнения с двумя переменными, решения уравнения.
Развивающие: Сформировать умение осознанно проводить обобщение и анализ.
Воспитательные: воспитывать интерес к математике.
Структура урока:
Актуализация знаний.
Мобилизующее начало урока, сообщение учителя о планируемой работе на уроке. (1 мин)
Устный опрос с целью проверки домашней работы, и актуализации опорных знаний. (4 мин)
Обсуждение задачи с практическим содержанием с целью построения модели, и создания проблемной ситуации. (5 мин)
Подведение итогов, постановка проблемы и учебной задачи. (1 мин)
Формирование новых знаний и способов действий.
Беседа, с целью подготовки и введения определения линейного уравнения с двумя переменными.(6 мин)
Устное решение задач с целью усвоения определения (5 мин)
Эвристическая беседа, с целью подготовки и введения определения решения линейного уравнения с двумя переменными. (4 мин)
Устное решение задач с целью усвоения понятия «решение уравнения с двумя переменными».(2 мин.)
Эвристическая беседа, с целью получения алгоритма решения линейного уравнения с двумя переменными. (6 мин)
Беседе, с целью введения понятия графика линейного уравнения с двумя переменными и отыскания способа построения графика этого уравнения. (5 мин)
Применение знаний, формирование умений и навыков.
Решение задач, с целью усвоения материала. (если останется время)
Подведение итогов, постановка домашнего задания (2 мин)
Ход урока
Актуализация знаний.
Мобилизующее начало урока, сообщение учителя о планируемой работе на уроке.
Учитель: Здравствуйте ребята! (проверка отсутствующих).
Сегодняшний урок мы построим следующим образом, сначала проверим домашнее задание, затем приступим к изучению новой темы, а если останется время, то порешаем задачи по новой теме.
Проверка домашнего задания с целью актуализации опорных знаний,
Учитель: Домой вам было задано 3 задачи. Есть ли какие-то вопросы по домашнему заданию? Все ли справились с домашним заданием?
Проверим №695, как выполняли и какой ответ? (спрашиваю 1 ученика). У кого не так?
Проверим №698, как выполняли и какой ответ? (спрашиваю 1 ученика). У кого не так?
Проверим №799, какая фигура получилась? (спрашиваю 1 ученика) У кого не так?
Обсуждение задачи с практическим содержанием и построение модели, с дальнейшим созданием проблемной ситуации.
Учитель: Ребята, в математике существует много видов уравнений. Уравнения помогают нам решать задачи. И с некоторыми вы уже знакомы, например, уравнения 5х-2=0 или 0,3х + 9=0 Умеете ли вы решать такие уравнения?
Ученики: Да, умеем.
Учитель: В математике для того, чтобы дать определение какому-либо виду уравнения его записывают в общем виде.
Чтобы это сделать уравнения нужно сравнить, т.е. выявить их сходство и различия. Посмотрим на эти уравнения у каждого из них первое слагаемое в левой части – число, умноженное на х, второе слагаемое – просто число, а в правой части – 0. Это их общие свойства. А различия в том, что числа эти разные. Если теперь эти числа мы обозначим буквами а и в, то получим уравнение вида ах+в=0. Чем в данном уравнение являются а,в, чем х?
Ученики: а и в — это числа, х- неизвестное (переменная).
Учитель: Верно! Такое уравнение, т.е. уравнение вида ах+b=0 называется линейным уравнением с одной переменной.
Мы с вами знаем, что линейные уравнения могут являться математической моделью реальной ситуации. Сегодня мы убедимся в том, что математической моделью могут быть не только линейные уравнения с одной переменной.
Решим такую задачу: Из городов А и В, расстояние между которыми 500 км, навстречу друг другу вышли 2 поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3ч после выхода второго поезда они встретились. Чему равны скорости поездов?
Составим математическую модель задачи. Пусть х км/ч- скорость 1-го поезда, у км/ч – скорость 2-го поезда. Первый был в пути 5ч и, значит прошел путь 5х км. Второй поезд был в пути 3ч т.е. прошел путь 3у км. Их встреча произошла в пункте С. (можно изобразить рисунок). На алгебраическом языке эту задачу можно записать в виде следующего уравнения: 5х+3у=500
Можем ли мы его решить?
Ученики: Нет.
Учитель: Почему не можем решить, что в нем нового?
Ученики: в этом уравнение уже 2 переменные, а мы умеем решать только уравнения с одной переменной.
Учитель: верно.
Подведение итогов, постановка учебной задачи.
Учитель: Так вот задача нашего урока – изучить этот новый вид уравнений, дать ему определение и научиться его решать.
Формирование новых знаний и способов действий.
Беседа, с целью подготовки и введения определения линейного уравнения с двумя переменными.
Учитель: вернемся к полученному уравнению, 5х+3у-500=0.
Назовите неизвестные этого уравнения.
Ученики: неизвестные х,у.
Учитель: Какие известные числа имеются в этом уравнении?
Назовите их.
Ученики: Три. 5, 3, 500.
Как связаны эти числа с неизвестными?
— 5 и 3 это коэффициенты при неизвестных.
Учитель: Посмотрите на такое уравнение 3х+7у+18=0
И сравните его с предыдущим. Что у них общего? Чем они отличаются?
Ученики: В этом уравнении тоже 2 неизвестных х и у, и тоже 3 числа, два из которых коэффициенты (т.е. множители) при неизвестных, только числа другие.
Учитель: Можем ли мы обобщить вид таких уравнений, т.е. записать их в общем виде? Что для этого нужно сделать?
Ученики: Обозначить числа в этом уравнении буквами.
Учитель: Если мы обозначим множитель перед х – через а, множитель перед у – в, и оставшееся число через с. Какое уравнение получим?
Ученики: Получим уравнение ах+ву+с=0
Учитель: Мы получили новый вид уравнения, такой вид уравнения называется линейным уравнением с двумя переменными. Давайте попробуем дать определение такому уравнению. Какое уравнение будем называть линейным уравнением с двумя переменными?
Ученики: Уравнение вида ах+ву+с=0 где а,в,с,- числа и а,в не равны 0 называется линейным уравнением с двумя переменными.(1 ученик повторяет)
Устное решение задач.
Учитель: Теперь нам нужно научиться узнавать такие уравнения.
Задачи: на распознавание. №803-804
Задачи: а= 5, в= 7, с=6, (а=-2, в= 1, с= -9) составить лин.ур. с двумя переменными.
Эвристическая беседа, с целью подготовки и введения определения решения линейного уравнения с двумя переменными.
Учитель: вспомним, что значит решить линейное уравнение с одной переменной?
Ученики: Это значит, что нам нужно найти такое х, при подстановке которого в наше уравнение получится верное равенство.
Учитель: Как мы решали например уравнение 3х-15=0
Ученики: …..
Учитель: Хорошо. Можно ли таким же способом найти решение линейного уравнение с двумя переменными?
Ученики: нет, у нас ведь ещё есть одно неизвестное.
Учитель: верно ребята, тут нам нужно найти уже 2 значения и х, и у. Если мы подберем такие х,у что наше равенство будет верно, можно ли сказать что мы нашли решение линейного уравнения с двумя неизвестными?
Ученики: Да.
Учитель: Давайте проверим и подберем решения уравнения
3х+4у=24 Какой х и у нужно взять чтобы получилось верное равенство?
Ученики: х=4 и у=3
Учитель: А ещё можно подобрать?
Ученики: да, (0,6) или( 8,0)
Учитель: Из этого мы видим что решение данного уравнения будет не единственное. Давайте же сделаем вывод и дадим определение решению линейного уравнения с 2 переменными.
Ученики: Решением уравнения вида ах+ву+с=0 называется пара чисел, при подстановке которых в уравнение мы получаем верное равенство, и эта пара будет не единственная.
Учитель: Проверим, является ли пара (1;4) решением уравнения 7х+5у=23?
Ученики: …..
Учитель: Как найти решение уравнения 2х+3у=24? Можно заметить, что угадывать решения линейного уравнения с двумя неизвестными совсем не просто. Поэтому нам нужно научиться находить их решения.
Эвристическая беседа, с целью поиска решения линейного уравнения с двумя переменными.
Учитель: Вспомните, что нужно сделать, чтобы решить уравнение с одной переменной. Ну, например, уравнение 10х+4=14
Какие шаги надо выполнить, чтобы получить х?
Ученики: Надо 1)4 перенести в левую часть с противоположным знаком.
2)затем из 14 вычесть 4
3)обе части уравнения поделить на 10
Получается х=1
Учитель: Верно! Можно ли таким алгоритмом пользоваться и при решении уравнения вида ах+ву+с=0?
Ученики: нет т.к. у нас 2 неизвестных.
Учитель: верно. Для того чтобы решить уравнение вида ах+ву+с=0 нам необходимо знать значение одной переменной, это значение мы можем брать произвольно (т.е. как хотим), а затем, подставив выбранное значение этой переменной в уравнение мы сможем найти вторую переменную.
Учитель: Рассмотрим такой пример: Решите уравнение 8х+6у-11=0
Значение какой либо переменной нам не дано, поэтому сами произвольно его выбираем. Пусть х=2.
Тогда мы в наше уравнение вместо х подставляем 2 , что получили?
Ученики: 16+6у-11=0
6у+5=0 т.е. мы получили линейное уравнение с одной переменной.
Учитель: такой вид уравнения вы уже умеете решать, что получилось? Чему равен у?
Ученики: у=-5/6
Учитель: Правильно. А если бы мы взяли значение у. Что тогда надо было бы сделать?
Ученики: Надо было вместо у поставить это значение, посчитать и найти х.
Учитель: хорошо. Проделайте это самостоятельно возьмите у=3 Что получилось?
Построение графика линейного уравнения с двумя переменными.
Учитель: Мы с вами выяснили. Что решением линейного уравнения с двумя переменными является множество пар чисел (х;у).
Давайте вспомним, что можно задать с помощью пары чисел?
Ученики: Можно задать точку в координатной плоскости.
Учитель: Следовательно, любое решение уравнения с двумя переменными можно изобразить в виде соответствующей точки в координатной плоскости. Т.е. решения уравнения задают координаты точек координатной плоскости. Это обстоятельство позволяет получить график такого уравнения.
Учитель:. Вернемся к заданию где вы находили решения уравнения 2х+3у=24 вы получили пары (3,6), (6,4), (0,8), (-3,10). Построим координатную плоскость и отметим на ней эти точки.
Посмотрите внимательно, как расположены эти точки друг относительно друга?
Соединим отмеченные точки. Что получилось?
Ученики: Прямая.
Учитель: Нам нужно выяснить, будут ли координаты всех точек полученной прямой удовлетворять данному уравнению. Возьмём какую-то другую точку на полученной прямой, будет эта точка являться решением нашего уравнения. Проверьте. Например точку (4,5; 5)
Ученики: Да и эта точка является решением нашего уравнения.
Учитель: Тогда можно предположить, что какую бы точку мы не взяли на этой прямой ее координаты будут решением уравнения 2х+3у=24. Это действительно так.
Итак, множество всех решений линейного уравнения с двумя переменными можно изобразить в координатной плоскости в виде прямой линии.
Полученную таким образом прямую называют графиком линейного уравнения с двумя переменными.
Подумаем, что нужно сделать, чтобы построить график линейного уравнения с двумя переменными?
Но надо ли нам строить много точек для того чтобы построить прямую на плоскости? Сколько достаточно иметь точек, чтобы можно было построить прямую?
Ученики: Для того чтобы построить прямую на плоскости нам достаточно 2 точек.
Учитель: Верно.
Выполним такое задание: Изобразить график линейного уравнения х+у-3=0 на координатной плоскости.
Надо найти решения этого уравнения. Мы сегодня выяснили, что решением такого вида уравнения является пара чисел, и при том, она не единственная. Но мы уже знаем что графиком линейного уравнения с двумя неизвестными является прямая и поэтому нам надо найти только 2 решения. Найдём их. Как мы будем это делать?
Ученики: Дадим конкретное значение х, например х=3, затем выразим у. Получим пару чисел (3,0)
Дадим второе конкретное значение х, например х=6, выразим у. Получим (6,3)
Учитель: верно, так мы с вами получили координаты двух точек.
Теперь нам эти точки нужно изобразить на координатной плоскости.
Провести прямую, через полученные точки.
Итак, мы получили прямую, которая является графиком линейного уравнения с двумя неизвестными х+у-3=0
Сделаем вывод. Чтобы построить график линейного уравнения с двумя переменными нужно:
Ученики:
Дать конкретное значение х и выразить у через х. Так мы получили координаты первой точки.
2. Аналогично найти координаты второй точки.
3. Провести через эти точки прямую.
Итак подведем итог нашего сегодняшнего урока, вспомним что нового мы сегодня изучили, а для этого вам предстоит ответит на следующие вопросы:
1.Какое уравнение называется линейное уравнение с 1 переменной?
2. Какое уравнение называется линейное уравнение с 2 переменными?
3. Что является решением линейного уравнения с 2 переменными?
4.Что является графиком линейного уравнения с 2 переменными?
5. Повторим алгоритм построения графика линейного уравнения с 2 переменными.
3. Применение знаний, формирование умений и навыков.
3.1. Решение задач, с целью усвоения материала. (если останется время) №816, №820(б,в)
3.2. Подведение итогов, постановка домашнего задания.
Учитель: Какой новый вид уравнения вы сегодня узнали?
Что является решением такого уравнения?
Что является графиком такого уравнения?
Молодцы ребята, спасибо за работу!
Запишите домашнее задание: №805,№810,813( а,б), №820(а,г)
infourok.ru
§ 1. Линейные уравнения с двумя переменными
2010-2011уч. год., № 3, 8 кл. Математика. Системы уравнений.
Впервом задании мы рассмотрели линейные уравнения с одной пе-
ременной. Например, уравнения 2x +5 = 0, 3x +(8x −1)+9 = 0 являются линейными уравнениями с переменнойx. Уравнение, содер-
жащее переменные x и | y, называется уравнением с двумя перемен- | |||
ными. Например, уравнения 2x −3y =5, | x2 + xy− y2 | = 7 являются | ||
уравнениями с двумя переменными. |
|
|
| |
Уравнение вида ax +by = c называется | линейным | уравнением с | ||
двумя переменными, где | x и y −переменные, | a, b, c −некоторые чис- | ||
ла. | 2x+ y=3, x− y= 0 |
|
| |
Например, уравнения | являются линейными | |||
уравнениями с двумя переменными.
Решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.
Например, x =3, y = 4 является решением уравнения2x +3y =18, будем эту пару чисел записывать так(3; 4). Очевидно, что пара чисел
(4;3) не является решением уравнения, т.к.2 4 +3 3 =17 ≠18. При
нахождении решений с двумя переменными на первом месте в паре чисел пишем значение для переменной x, а на втором месте – значение
переменной y.
Если каждое решение одного уравнения является решением второго уравнения и обратно, то данные уравнения называются равносильными. Например, решения уравнений 2x + y =3 и4x +2 y =6 совпада-
ют, следовательно, эти уравнения равносильные.
Справедливы следующие правила при решении уравнений с двумя переменными:
1)если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;
2)если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.
©2010, ФЗФТШ при МФТИ. Составитель: Яковлева Тамара Харитоновна
studfiles.net
Линейное уравнение с двумя переменными
Вопросы занятия:
· повторить что такое линейное уравнение с одной переменной и сколько решений может иметь такое уравнение;
· ввести понятия «линейное уравнение с двумя переменными», «решение уравнения с двумя переменными», «равносильные уравнения».
Материал урока
Ранее мы с вами рассматривали линейное уравнение с одной переменной.
Вспомним, что:
Сегодня на уроке мы познакомимся с линейным уравнением, но уже с двумя неизвестными.
Давайте рассмотрим ситуацию
Полученное равенство содержит две переменные. А поэтому такие равенства называют уравнениями с двумя переменными (или с двумя неизвестными).
Посмотрите на примеры уравнений с двумя переменными
Сформулируем определение:
Определение.
Линейным уравнением с двумя переменными называется уравнение вида:
Вернёмся к задаче
То есть пара значений переменных (x = 60, y = 110) является решением этого уравнения. Отметим, что эти корни были найдены методом подбора, причём это не единственная пара чисел, удовлетворяющих нашему уравнению.
Определение.
Решением уравнения с двумя переменными называется пара значений переменных, которая обращает это уравнение в верное равенство.
Вспомним, что при изучении уравнений с одной переменной, мы говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.
Аналогично можем сказать, что уравнения с двумя переменными, имеющие одни и те же решения, называются равносильными.
Причем уравнения с двумя переменными, не имеющие решений, также являются равносильными.
Равносильные уравнения обладают следующими свойствами:
Свойство 1.
Если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнения, равносильное данному;
Свойство 2.
Если обе части уравнения умножить (или разделить) на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Снова вернёмся к нашему уравнению
Но здесь важно знать, значение какой из переменных стоит на первом месте, а какой – на втором. Так в нашем случае сначала записано значение переменной x, а затем переменной y.
При этом пара чисел (150; — 25) являясь решением уравнения, не удовлетворяет условию задачи, так как скорость автомобиля не может быть отрицательной.
И давайте рассмотрим ещё одну задачу.
Пример.
Решение уравнений в целых числах, то есть когда надо найти только целые значения переменных, подробно рассматривал древнегреческий математик Диофант.
Поэтому уравнения с несколькими переменными, которые надо решить в целых числах, называют диофантовыми уравнениями. То есть уравнение, составленное в предыдущей задаче, является диофантовым, так как для него мы отыскивали только натуральные решения.
И давайте рассмотрим примеры.
Пример.
И ещё пример.
Пример.
Итоги урока
Итак, на этом уроке мы рассмотрели линейное уравнение с двумя переменными и один из способов решения таких уравнений.
videouroki.net
