Аналитическая геометрия
Аналитическая геометрия
Задача 1. Дан треугольник АВС: А(2,1), В(-1,3), С(-4,1). Найти:
уравнение и длину высоты АD; уравнение и длину медианы СЕ; внутренний угол В; систему линейных неравенств, определяющую треугольник. Сделать чертеж.
Решение. Сделаем чертеж.
Y
D
B
3
E
C 1 A
-4 -1 0 2 X
1. Составим уравнения всех сторон треугольника, используя уравнение прямой, проходящей через две данные точки.
.
Так как точки А и С имеют одинаковую ординату, используем данное уравнение в преобразованном виде:
.
2. Найдем длину высоты АD. Используем формулу расстояния от точки до прямой:
.
Приведем уравнение ВС к общему уравнению прямой.
.
3. Составим уравнение высоты АD. Она проходит через точку А(2,1) и перпендикулярна прямой ВС, kBC=2/3. Из условия перпендикулярности kAD=-1/kBC=-3/2. Воспользуемся уравнением прямой, проходящей через данную точку в данном направлении:
.
4. Для нахождения длины и уравнения медианы СЕ найдем координаты точки
Точка Е (1/2,2).
5. Найдем внутренний угол В. Он отсчитывается в положительном направлении от прямой ВС к прямой АВ. kBC=2/3, kAB=-2/3.
6. Составим систему линейных неравенств, определяющую треугольник. Запишем уравнения сторон в виде
AB: 2x+3y=7,
BC: 2x-3y=-11,
AC: y=1.
Подставим точку с координатами (-1, 2), лежащую внутри треугольника, в левые части равенств.
2x+3y=-2+6=4<7,
2x-3y=-2-6=-8>-11,
y=2>1.
Следовательно, система неравенств, описывающая треугольник, имеет вид
Задача 2. Составить каноническое уравнение гиперболы, если известно, что ее эксцентриситет равен 1,25 и гипербола проходит через точку .
Решение. Каноническое уравнение гиперболы имеет вид . Так как гипербола проходит через точку А (8; ), то ее координаты удовлетворяют уравнению гиперболы, т.е. . Так, как = 1,25, то = 1,25, но , тогда = 1,5625или .
Итак, получаем систему двух уравнений с двумя неизвестными а и b.
Решая эту систему, находим = 16 и = 9, следовательно, каноническое уравнение гиперболы имеет вид .
Задача 3. Составить уравнение прямой, проходящей через вершину параболы и центр окружности .
Решение. Найдем координаты вершины параболы и координаты центра окружности. Для этого выделим полные квадраты по каждой переменной.
Уравнение параболы: ;
уравнение окружности: .
Следовательно, вершина параболы имеет координаты В (2;3), а центр окружности имеет координаты С (-2; 1).
Тогда уравнение искомой прямой составим по формуле
.
Получим , или .
lms2.sseu.ru
Пример 1. Аналитическая геометрия на плоскости
А(1;7), В(-3;-1), С(11;-3)Решение
1) Уравнение прямой АВ:
4(y-7)=8(x-1)
8x-4y+20=0
2x-y+5=0– общее уравнение прямой АВ
2) СНАВ =>
2x-y+5=0=> и
Уравнение высоты CH:
y+3= (x-11)
2у+6= -х+11
x+2y-5=0 – общее уравнение высоты CH.
Найдем длину высоты CH как расстояние от точки С до прямой АВ, общее уравнение которой Ax+By+C=0, А=2, В=-1, С=5
CH=
CH=
1) Найдем координаты точки М как середины отрезка ВС:
,
М()
Уравнение медианы АМ
3(y-7)= -9(x-1)
9x+3y-30=0
3х+y-10=0- общее уравнение медианы АМ
2) Найдем точку пересечения N медианы АМ и высоты CH:
N(3;1)
5) Так как прямая параллельна АВ, то её угловой коэффициент равен . Найдем её уравнение по формуле:
y+3=2 (x-11)
2x-y-25=0 – общее уравнение прямой, параллельной прямой АВ и проходящей через точку С.
3) Косинус внутреннего угла при вершине А:
(-3-1;-1-7)=(-4;-8)
(11-1;-3-7)=(10;-10)
Косинус внешнего угла при вершине С:
(-10,10)
(-3-11;-1+3)=(-14;2)
Ответ:
1) 2x-y+5=0
2) x+2y-5=0, CH=
3) 3х+y-10=0
4) 2x-y-25=0
5) ,
primer.by
Математика 1 (6)
8Даны вершины треугольника. Найти:
длину стороны ВС;
уравнение высоты ВС;
уравнение высоты, проведённой из вершины А;
длину высоты, проведённой из вершины А;
угол В.
Сделать чертёж.
Дано: А(-8;3), В(4;-2), С(7;2).
РЕШЕНИЕ
Длину стороны ВС находим по формуле . По условию имеем В(4;-2), С(7;2).
Найдём уравнение стороны ВС. Найдём уравнение прямой, на которой лежит сторона ВС. Используем уравнение прямой, проходящей через две точки
 ,
полагая
,
полагая
Найдём уравнение высоты, проведённой из вершины А. При составлении уравнения прямой, на которой лежит высота треугольника, воспользуемся формулой и условием перпендикулярности двух прямых

Определим угловой коэффициент прямой ВС. Для этого разрешим уравнение стороны ВС относительно у:
Следовательно, высота, проведённая из
точки А, имеет угловой коэффициент 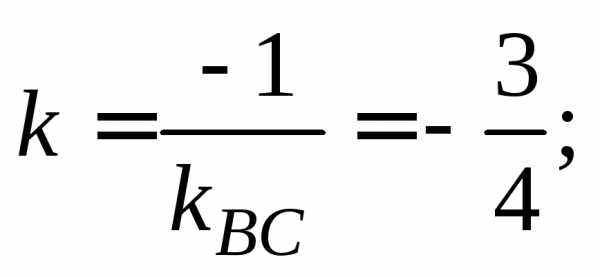
Тогда, уравнение высоты, опущенной из вершины А(-8;3) на сторону ВС:
Найдём длину высоты, проведённой из вершины А. Она равна расстоянию от точки А(-8;3) до прямой ВС заданной уравнением . По формуле
 вычисляем расстояние от точки А до
прямой ВС, полагая
вычисляем расстояние от точки А до
прямой ВС, полагая
Найдём угол В. Угол В равен углу между прямыми ВС и АВ и может быть найден с помощью формулы
. Найдём угловой коэффициент прямой АВ по формуле: .
Угловой коэффициент прямо ВС известен
и равен
.
Угловой коэффициент прямо ВС известен
и равен
Тогда получаем,
И угол равен
Выполним чертёж. В прямоугольной декартовой системе координат хОу строим исходные точки и получаем треугольник АВС. Затем из вершины А опустим перпендикуляр на сторону ВС, получим АК.
18
Даны координаты вершин пирамиды А1А2А3А4. Найти:
координаты вектора
 и длину ребра
и длину ребра ;
;угол между рёбрами и
 ;
;площадь грани
 ;
;объём пирамиды;
уравнение плоскости
 ;
; ;
;угол между ребром
 и гранью
и гранью ;
;уравнение высоты, опущенной из вершины
 на грань
на грань ;
;
Сделать чертёж.
Дано: А1(7;2;2), А2(5;7;7), А3(5;3;1), А4(2;3;7).
РЕШЕНИЕ
Вектор
 равен
равен
Длину ребра  можно найти как расстояние между двумя
точкамии,
оно равно
можно найти как расстояние между двумя
точкамии,
оно равно
Получаем
Угол между рёбрами
 и
и найдём как угол между векторами
найдём как угол между векторами и
и .
.
Вектор
Таким образом, имеем два вектора и, угол между ними найдём по формуле:
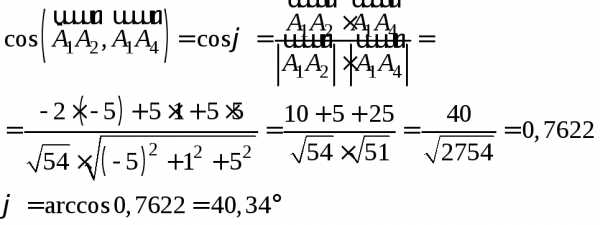
Скалярное произведение двух векторов в числителе дроби находили как сумму произведений одноимённых координат (проекций).
Площадь грани
 равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника
равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника можно вычислить через векторное
произведение
можно вычислить через векторное
произведение
Координаты вектора или
Векторное произведение вычислим через определитель 3-го порядка, разложив его по элементам первой строки:
Модуль векторного произведения
Объём треугольной пирамиды А1А2А3А4 можно рассматривать как одну шестую часть объёма параллелепипеда, построенного на векторах
 ,
, и
и как на рёбрах:
как на рёбрах:
Смешанное произведение трёх векторов равно
Уравнение плоскости
 имеет вид
имеет вид
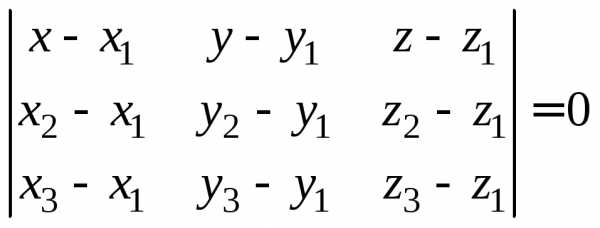
или для нашей задачи
Разложим определитель по элементам первой строки:
Уравнения прямой
 найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точкии:
найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точкии:
,
Углом ψ между ребром
 и гранью
и гранью будет острый угол между прямой
будет острый угол между прямой и её проекцией на плоскость
и её проекцией на плоскость .
Для нахождения угла ψ воспользуемся
формулой
.
Для нахождения угла ψ воспользуемся
формулой
Канонические уравнения прямой 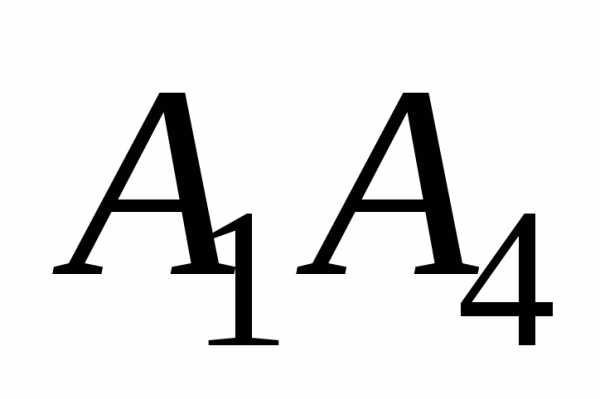 получим как:
получим как:
Отсюда l=5;m=1;n=-5, гдеl,m,n–
координаты направляющего вектора прямой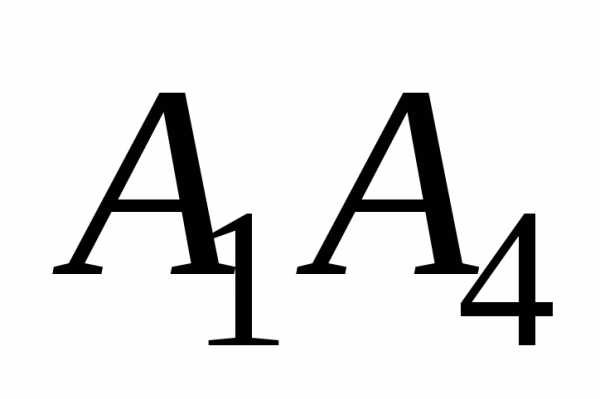 :
:
;
Уравнение плоскости  было получено в пункте 5:
было получено в пункте 5:
Отсюда А=5; В=7; С=-4, где А, В, С – координаты
нормального вектора плоскости 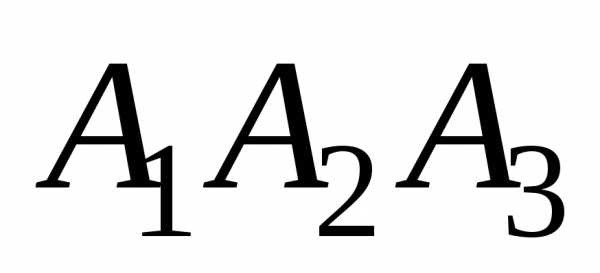 :
:
Тогда получаем
Уравнения высоты, опущенной из вершины
 на грань
на грань .
.
Канонические уравнения прямой, проходящей
через точку  ,
имеют вид,
гдеl,m,n– координаты направляющего вектора
прямой.
,
имеют вид,
гдеl,m,n– координаты направляющего вектора
прямой.
Так как высота перпендикулярна плоскости 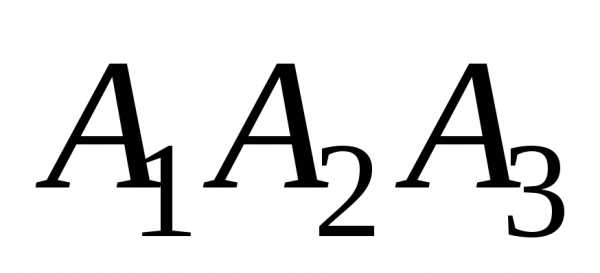 ,
то из условия перпендикулярности прямой
и плоскости
,
то из условия перпендикулярности прямой
и плоскости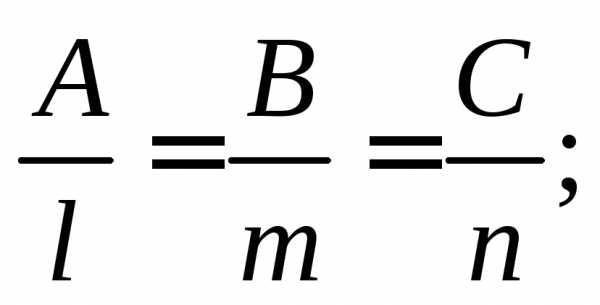 координаты направляющего вектора
прямой, перпендикулярной плоскости
можно заменить координатами нормального
вектора плоскостиl=A=5;m=B=7;n=C=-4.
координаты направляющего вектора
прямой, перпендикулярной плоскости
можно заменить координатами нормального
вектора плоскостиl=A=5;m=B=7;n=C=-4.
Окончательно получим

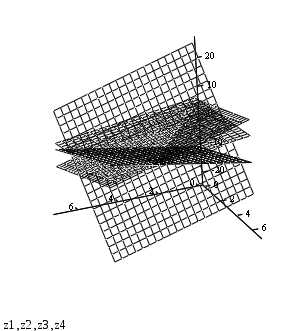
Выполним чертёж пирамиды как пересечения плоскостей её граней:
Грань А1А2А4:
Грань А1А2А3:
Грань А1А3А4:
Грань А2А3А4:
28
Составить уравнение и построить линию,
каждая точка которой равноотстоит от
оси ординат и от окружности 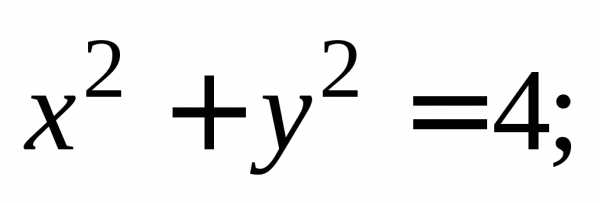
РЕШЕНИЕ
В системе координат хОу строим ось
ординат х=0 и окружность 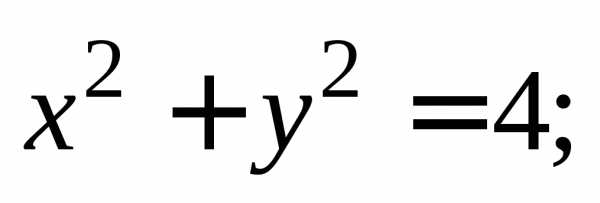
Пусть точка М(х; у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляры на ось ординат и на окружность.
Тогда расстояние от произвольной точки
М(х; у) до оси ординат 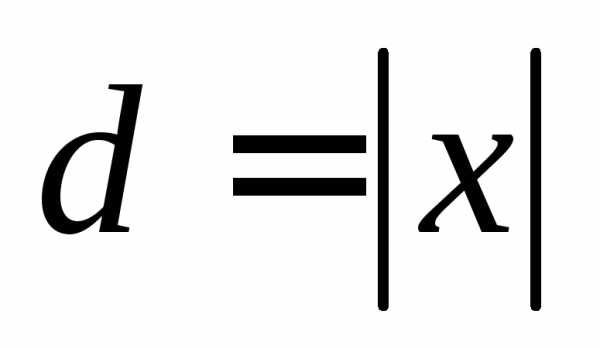 –
абсцисса точки М(х; у), а расстояние от
точки М(х; у) до окружности
–
абсцисса точки М(х; у), а расстояние от
точки М(х; у) до окружности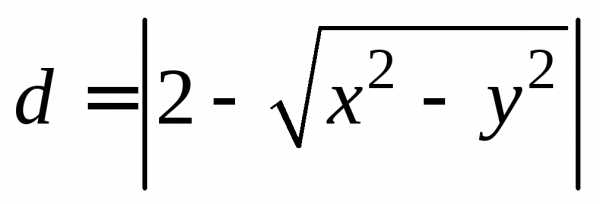 .
Приравнивая эти расстояния и снимая
знак модуля, получаем
.
Приравнивая эти расстояния и снимая
знак модуля, получаем
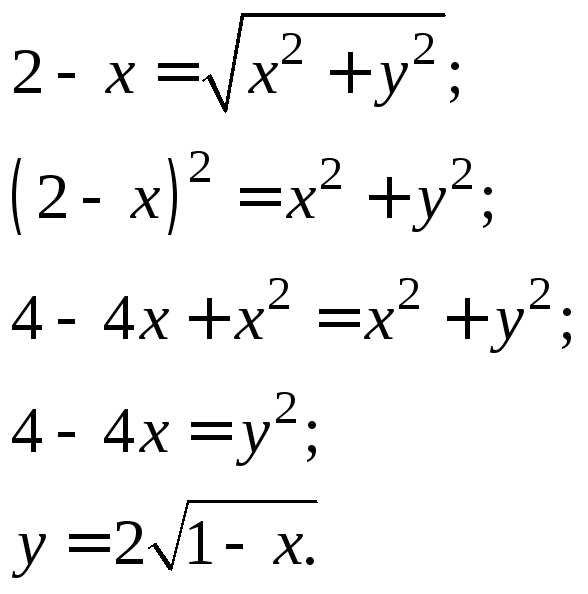
Получили уравнение параболы, строим верхнюю часть окружности и параболы, так как чертёж симметричный:
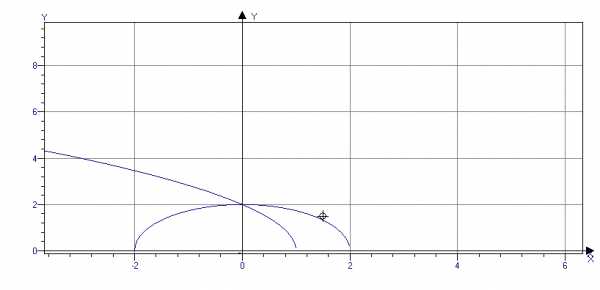
studfiles.net
как найти уравнение высоты треугольника,зная координаты всех его вершин?:)
1. Рассмотрим треугольник ABC 2. Рассмотрим вектор BC(Xc-Xb;Yc-Ya) 3. На векторе возьмем точку D так, что вектор AD(Xd-Xa;Yd-Ya) будет перпендикулярен вектору BC(Xc-Xb;Yc-Ya) 4. Свойство: их скалярное произведение равно нулю => (Xc-Xb)*(Xd-Xa)+(Yc-Ya)*(Yc-Ya)=0 Здесь неизвестные только Xd и Yd. Решив данное уравнение получишь иравнение высоты, опущенной на BC. Аналогично и для других сторон треугольника. При 3-х координатной системе добавится только Zd. Удачи!
найти длины сторон и углы, дальше через синусы косинусы
взять две точки, найти уравнение прямой, затем изменить коэфицент на обратный и с противоположным знаком. т. е. если было k, то будет -1/k, и подставить координаты 3ей точки
touch.otvet.mail.ru
Уравнение — высота — Большая Энциклопедия Нефти и Газа, статья, страница 1
Уравнение — высота
Cтраница 1
Уравнение высоты BD составим по точке и угловому коэффициенту АС. [1]
Составить уравнение высоты, опущенной из вершины С на сторону АВ, и вычислить ее длину. [2]
Составить уравнение высоты, опущенной из вершины С на сторону АВ, и вычислит. [3]
Составить уравнение высоты, опущенной из вершины В. [4]
Составить уравнение высоты, опущенной:: першины А на сторону ВС. [5]
Составить уравнение высоты, опущенной из вершины В на сторону АС. [6]
Составить уравнение высоты треугольника, проведенной из вершины С. [7]
Чтобы составить уравнение высоты, проведенной из точки В на сторону АС, необходимо знать угловой коэффициент этой высоты. [8]
Рассчитанные по этому уравнению высоты газожидкостного слоя на тарелках моделей-спутников приемлемо совпадают с экспериментальными значениями только при низких плотностях орошения и скоростях газа. При плотности орошения выше 40000 кг / ( м2 — ч) и скорости газа больше 1 5 м / с расчетные значения высоты газожидкостного слоя в 2 — 3 раза выше экспериментальных. [9]
В треугольнике ABC даны уравнения высоты AN: 4 — 50 — 3 0, высоты BN: х 4 — 0 — 1 0 и стороны АВ: 4 30 — 1 т О, Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты. [10]
Требуется: 1) составить уравнения высот; 2) убедиться в том, что все высоты пересекаются в одной точке. [11]
В настоящей работе делается попытка вывода уравнения высоты, эквивалентной единице переноса, при ректификации в спиральном вращающемся канале при следующих условиях его работы: с отбором дистиллята, турбулентном течении пара при ректификации смесей углеводородных газов. [12]
Кинетические свойства веществ определяются с помощью уравнения высоты, эквивалентной теоретической тарелке. [13]
Не определяя координат его вершин, составить уравнения высот этого треугольника. [14]
В, равный -: -, написать уравнение высоты, опущенной из вершины А на сторону ВС. [15]
Страницы: 1 2
www.ngpedia.ru

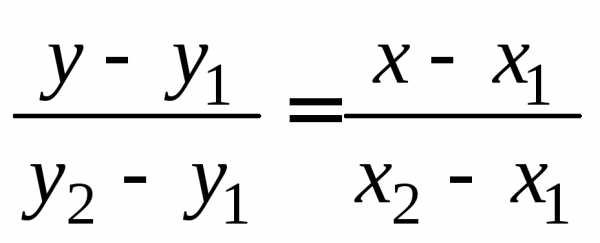 ,
полагая
,
полагая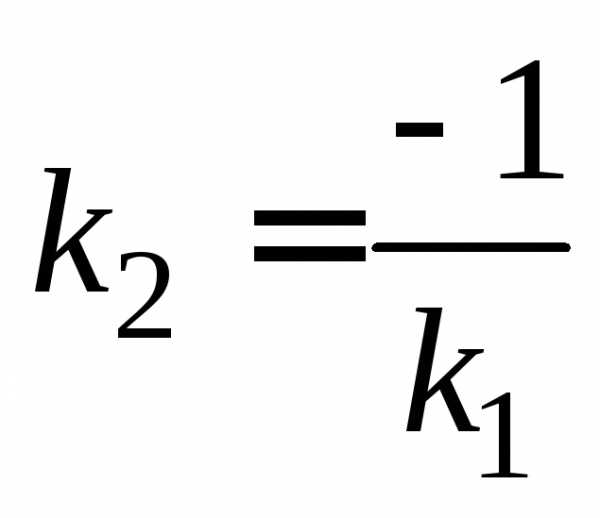
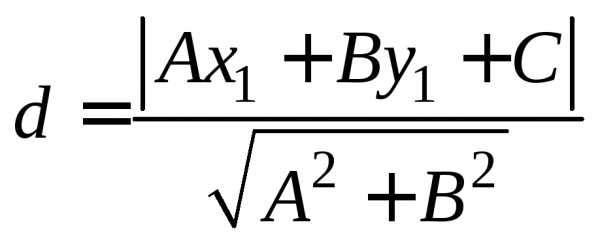 вычисляем расстояние от точки А до
прямой ВС, полагая
вычисляем расстояние от точки А до
прямой ВС, полагая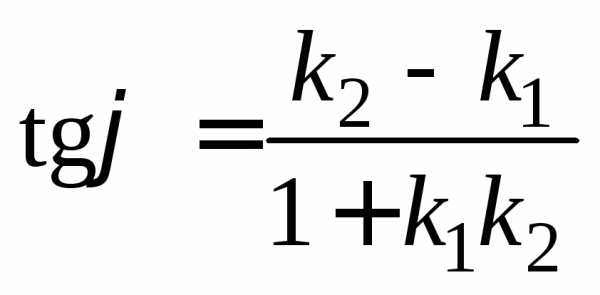 .
Угловой коэффициент прямо ВС известен
и равен
.
Угловой коэффициент прямо ВС известен
и равен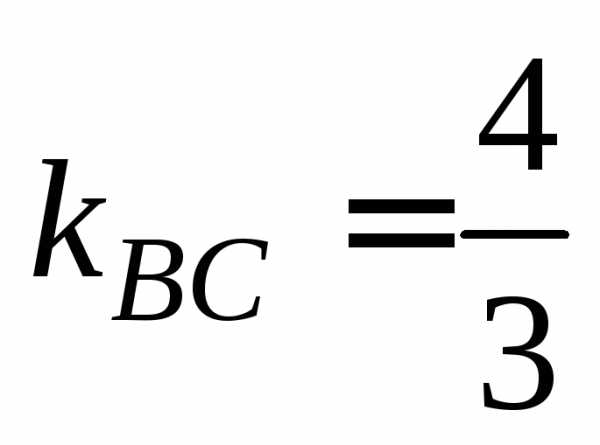
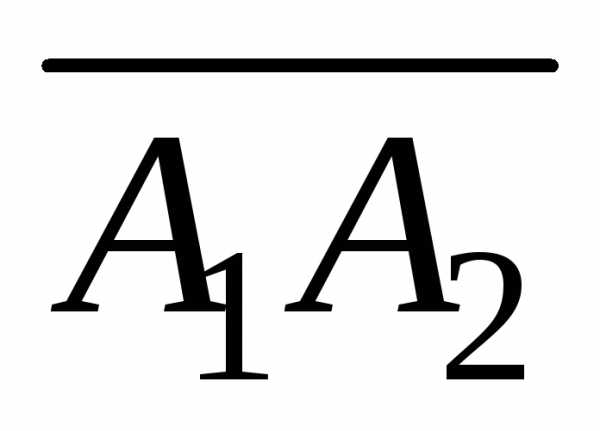 и длину ребра
и длину ребра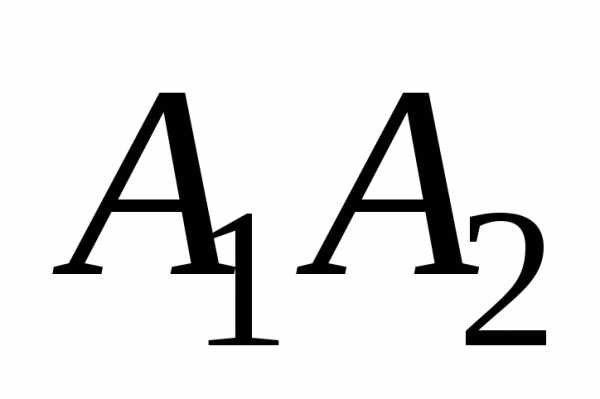 ;
;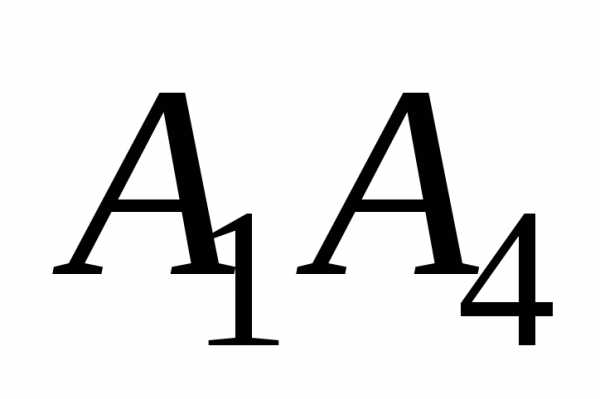 ;
;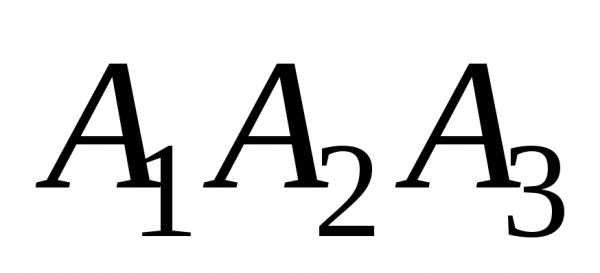 ;
;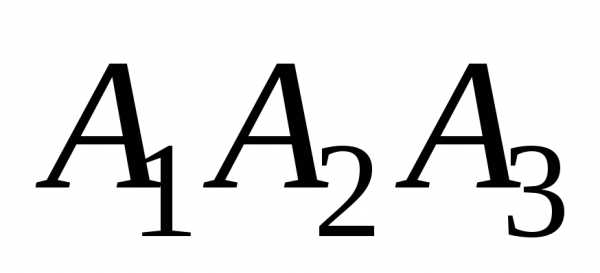 ;
;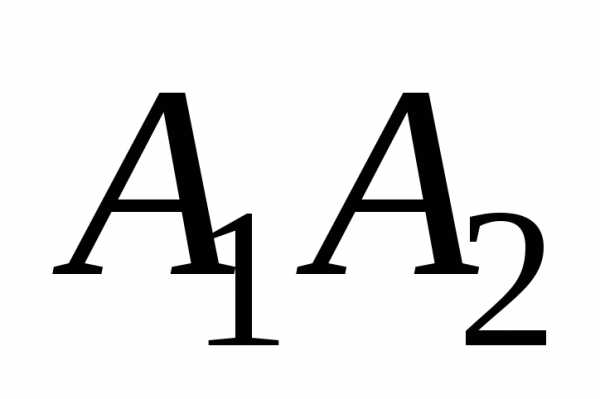 ;
;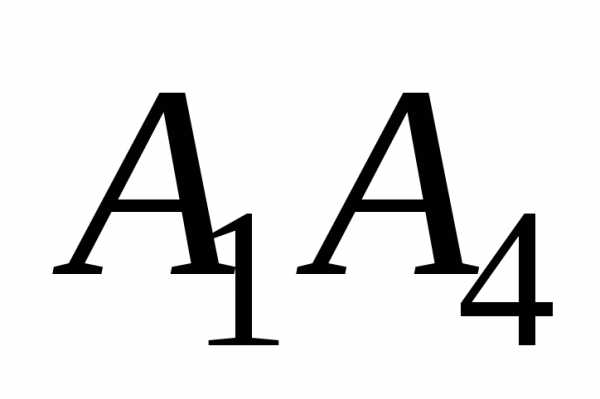 и гранью
и гранью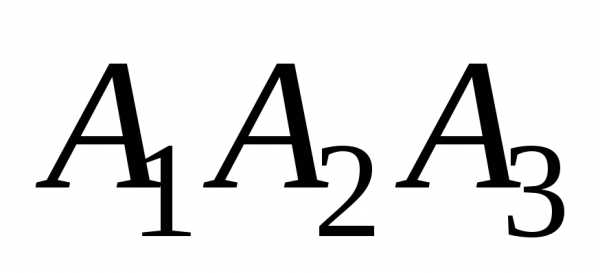 ;
; на грань
на грань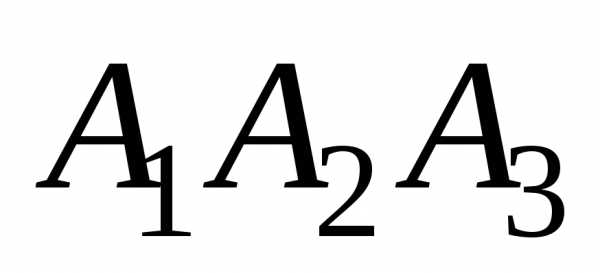 ;
;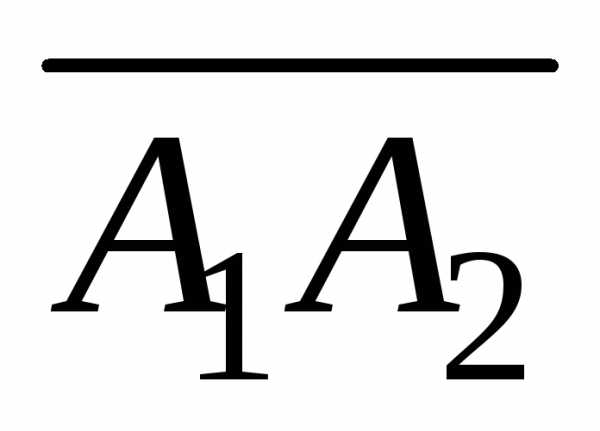 равен
равен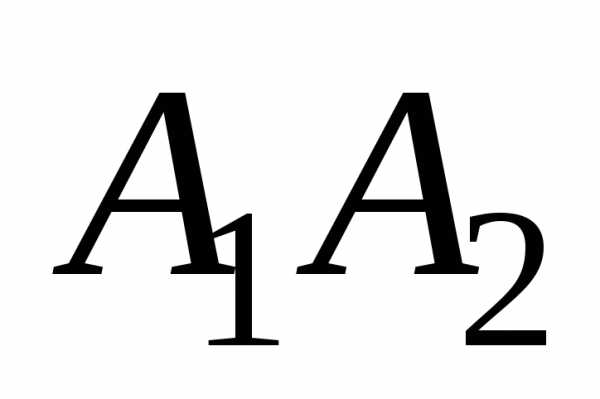 и
и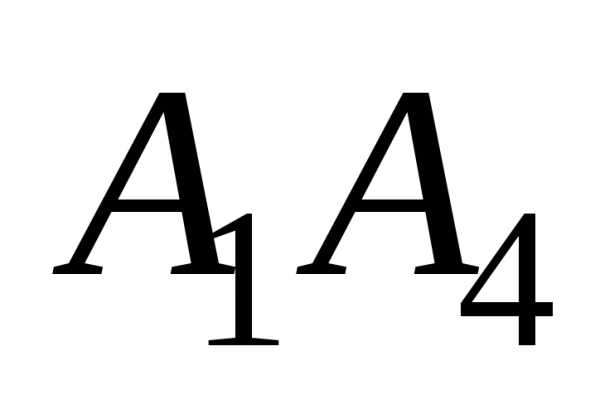 найдём как угол между векторами
найдём как угол между векторами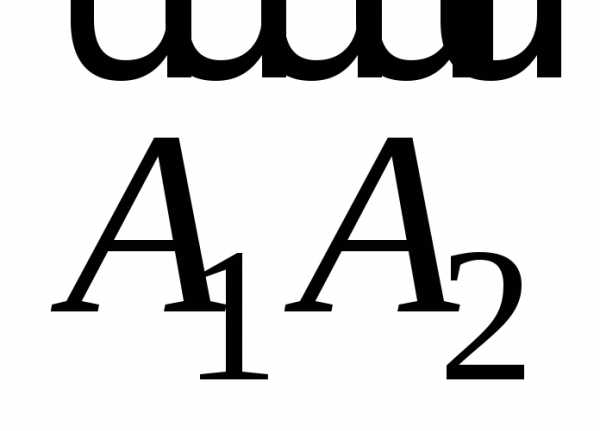 и
и .
.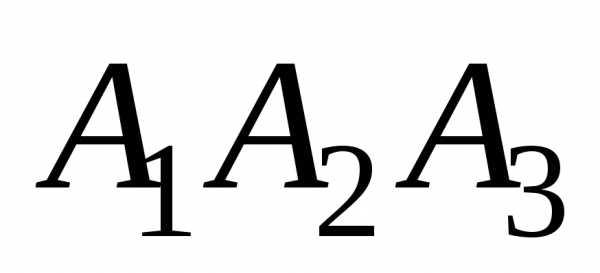 равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника
равна половине площади параллелограмма,
построенного на векторах, как на
сторонах. И площадь треугольника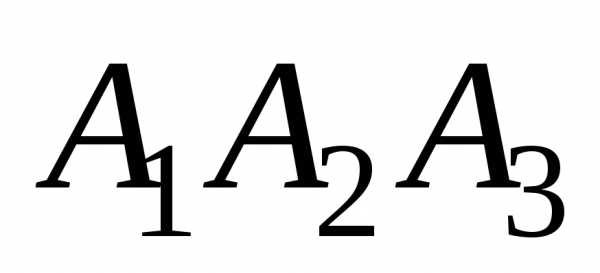 можно вычислить через векторное
произведение
можно вычислить через векторное
произведение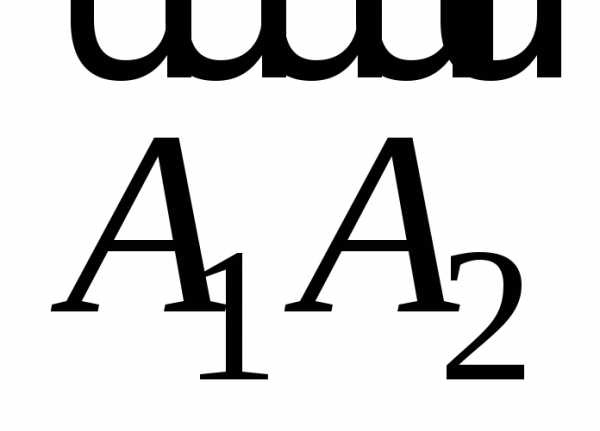 ,
, и
и как на рёбрах:
как на рёбрах: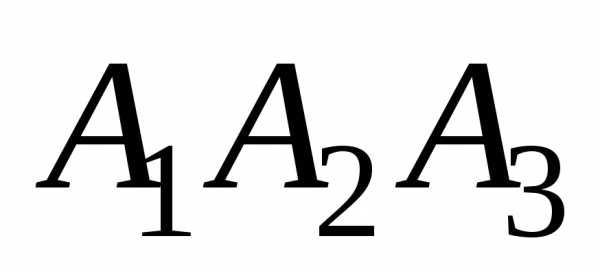 имеет вид
имеет вид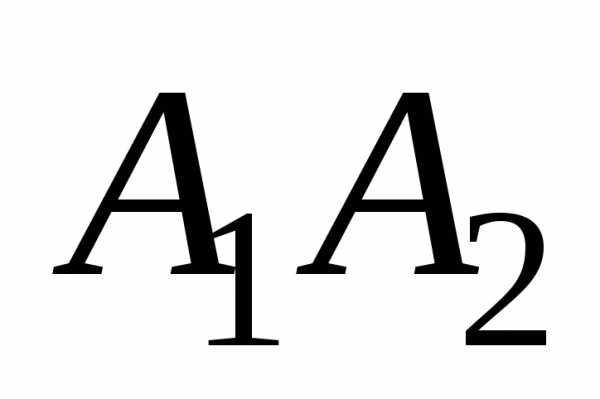 найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точкии:
найдём в канонической форме, для этого
воспользуемся уравнением прямой,
проходящей через две заданные точкии: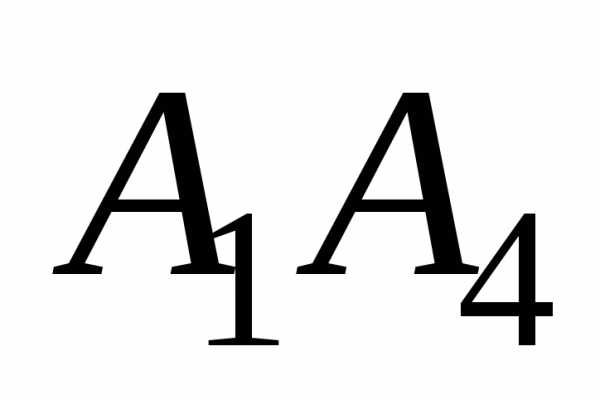 и гранью
и гранью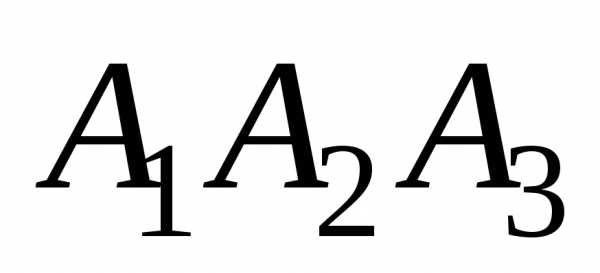 будет острый угол между прямой
будет острый угол между прямой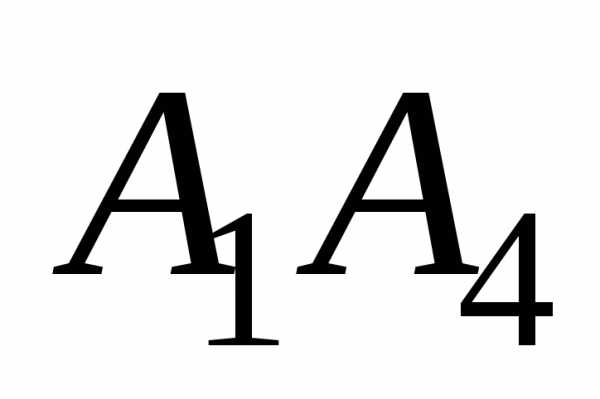 и её проекцией на плоскость
и её проекцией на плоскость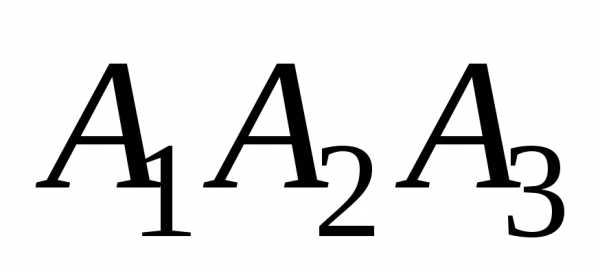 .
Для нахождения угла ψ воспользуемся
формулой
.
Для нахождения угла ψ воспользуемся
формулой на грань
на грань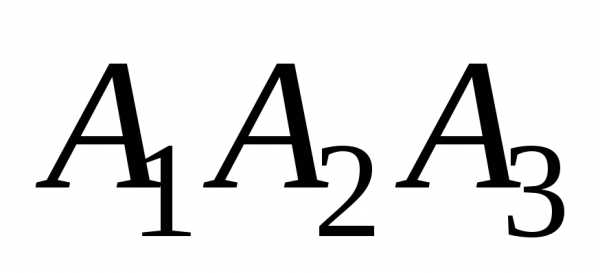 .
.